引言

准地转理论(the quasi-geostrophic theory，Q-G理论)是近代动力气象学的核心(霍尔顿, 1972)。中高纬度大气的许多基本现象都可以使用准地转理论加以描述, 因此它是中高纬度天气学，或者说是中高纬度地区天气预报的主要理论依据。从某种角度讲，中高纬常规的经验天气预报就是这一理论的定性应用(穆穆等，2011；董林等，2012；孟雪峰等，2012；端义宏等，2010)。

天气现象与高空槽脊、急流和低空气旋等影响天气的各种天气系统关系密切。从预报的思路看，通常是“先形势，后要素”；“先高空、后地面”；“先强度、后移动”(孙干生等，2006)。在对天气形势和天气系统移动发展的业务预报中，最常考虑的是温度平流、涡度平流、非绝热加热作用及地形影响，其中温度平流与涡度平流可看成是影响大气运动变化的内在因子，非绝热加热作用及地形影响可看成是外在因子。来自于准地转运动理论的准地转位势倾向方程和准地转垂直运动方程，可以将位势倾向和垂直运动都定性地表示成涡度平流和温度平流及其垂直变化的形式，因此它们既可以用于对中高纬度天气尺度斜压系统进行诊断分析，同时也成为利用天气图制作中高纬度短期天气预报的重要理论基础。

只有对严谨理论的基本假设有足够了解，才能将其科学地用于解释天气现象产生的机制并做出预报(孙继松等，2012；陶祖钰，2012；陶祖钰等，2012a)。准地转理论具有完整的大气动力学理论体系，但在推导过程中涉及到一些基本假定，因此准确地理解其中的基本问题尤其重要。对准地转理论的科学意义及应用价值已有介绍(陶祖钰等，2012b)。本文立足于基础动力学知识，回顾了准地转理论中的基本近似以及在天气图上应用准地转理论的范畴等基本问题；讨论了斜压二层模式框架下，如何判断高空槽脊和地面气旋的移动发展；如何考虑非绝热加热和地形等对天气系统演变的影响。

1 准地转理论的概念

利用控制大气运动的物理规律描述天气系统的移动和发展机制是大气动力学的主要任务之一。完整的大气运动方程组由动量方程、热力学能量方程、连续方程及状态方程组成，由于方程组的高度非线性，无法得到其理论上的解析解(柳崇健，1988)。通过利用符合观测事实的基本特征而作出的某些近似，如准地转近似，则可以定性地得到合理的与中高纬度大尺度大气运动基本观测事实相符的理论解释。

1.1 准地转运动定义

18世纪，荷兰气象学家白贝罗根据观测事实，提出了描述大尺度天气系统中风场与气压场关系的白贝罗定律，即地转风关系。

地转风是地球旋转作用的反映，描述的是气压梯度力与地转偏向力平衡时的水平运动。其数学表达式为：

$\begin{gathered} {u_g} = - \frac{1}{{f\rho }}\frac{{\partial p}}{{\partial y}} \hfill \\ {v_g} = \frac{1}{{f\rho }}\frac{{\partial p}}{{\partial x}} \hfill \\ \end{gathered} $

(1)

它是由不考虑摩擦时的水平运动方程：

$\begin{gathered} \frac{{{\text{d}}u}}{{{\text{d}}t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + fv \hfill \\ \frac{{{\text{d}}v}}{{{\text{d}}t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} - fu \hfill \\ \end{gathered} $

(2)

略去水平加速度项得到。地转风关系的重要性就在于揭示了风场和气压场之间的最简单也是最基本的联系，这种运动称为地转运动。由于略去了水平加速度项，所以地转运动是不随时间变化的定常运动，故它只能解释风场和气压场之间的联系，但不能用来预报风场和气压场的变化。

垂直运动方程为

$\frac{{{\text{d}}w}}{{{\text{d}}t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} - g$

(3)

对于大尺度运动，垂直加速度项比垂直气压梯度力项小8个数量级(杨大升等，1980)，故可以略去并转变为静力平衡关系

$\frac{{\partial p}}{{\partial z}} = - \rho g$

(4)

实际大气中，静力学关系有很高的精度，所以在天气分析中可以利用压高公式，用气压坐标代替高度坐标。由式(1) 和式(4) 可看出，当运动满足地转关系和静力平衡近似时，水平运动方程和垂直运动方程中都不出现含有垂直速度的项，所以是纯粹的水平运动。准地转运动定义来自于对大尺度运动满足地转平衡和静力平衡的综合。即中高纬自由大气大尺度运动，除具有准水平运动的性质外，还近似地满足地转风关系，故又称为准地转运动。

1.2 准地转近似定义

水平运动方程左边的加速度项比右边的强迫项小一个数量级，所以不能在经验预报中直接使用。将p坐标水平运动方程变形为表征水平运动场旋转特性的垂直涡度方程，对大尺度运动，根据量级分析忽略扭转项后，其形式为(杨大升等，1980)：

$\begin{gathered} \frac{{\partial {\zeta _p}}}{{\partial t}} = - u\left( {\frac{{\partial {\zeta _p}}}{{\partial x}}} \right) - v\left( {\frac{{\partial {\zeta _p}}}{{\partial y}}} \right) - \hfill \\ \quad \quad \quad f\left[ {\left( {\frac{{\partial u}}{{\partial x}}} \right) + \left( {\frac{{\partial v}}{{\partial y}}} \right)} \right] - v\left( {\frac{{\partial f}}{{\partial y}}} \right) \hfill \\ \end{gathered} $

(5)

由于方程左边的涡度倾向项和右边的强迫项具有相同的数量级，所以这是一个可用于预报的方程。它表示对于中高纬度天气尺度运动，涡度的局地变化主要由涡度平流、南北运动和水平辐合辐散所决定，其中后两项与地转参数及其随纬度的变化有关。

对大尺度运动，引入准地转运动定义，涡度方程可写为(杨大升等，1980)：

$\frac{{\partial {\zeta _g}}}{{\partial t}} + {u_g}\frac{{\partial {\zeta _g}}}{{\partial x}} + {v_g}\frac{{\partial {\zeta _g}}}{{\partial y}} + \beta {v_g} = {f_0}\frac{{\partial \omega }}{{\partial p}}$

(6)

其中做了如下假定：(1) 除水平散度场外，涡度场和风场都取了地转近似；(2)f处于系数地位时用f₀代替，即地转参数不随纬度改变。由于地转风的散度恒等于零，为了保留散度项，水平散度项中的u、v分量不能用地转风代替，所以式(6) 被称为准地转涡度方程。

两个水平运动方程作变形后，应该分别为垂直涡度方程与水平散度方程。实际上地转风关系即是散度方程的0级近似，因此准地转涡度方程可以看成是两个水平运动方程的综合。

引入准地转运动定义，不考虑非绝热加热项的热力学方程在静力平衡条件下可改写成(杨大升等，1980)：

$\left( {\frac{\partial }{{\partial t}} + {u_g}\frac{\partial }{{\partial x}} + {v_g}\frac{\partial }{{\partial y}}} \right)\frac{{\partial \mathit{\Phi }}}{{\partial p}} + \sigma \left( p \right)\omega = 0$

(7)

其中做了如下假定：(1) 水平平流项取地转风近似；(2)σ只是p的函数(水平微商等于零，或不参与水平微商)。

在上述准地转涡度方程和准地转热力学方程的近似中，水平运动取地转近似，则称为准地转近似。f处于系数地位时用f₀代替，实际上是部分考虑地球曲率影响的中纬β平面近似。

因此，准地转运动方程组即为：

$\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\zeta _g}}}{{\partial t}} + {u_g}\frac{{\partial {\zeta _g}}}{{\partial x}} + {v_g}\frac{{\partial {\zeta _g}}}{{\partial y}} + \beta {v_g} = {f_0}\frac{{\partial \omega }}{{\partial p}}} \\ {\left( {\frac{\partial }{{\partial t}} + {u_g}\frac{\partial }{{\partial x}} + {v_g}\frac{\partial }{{\partial y}}} \right)\frac{{\partial \mathit{\Phi }}}{{\partial p}} + \sigma \left( p \right)\omega = 0} \end{array}} \right.$

(8)

如上所述，准地转运动指的是大气的运动特征，而准地转近似指的是涡度方程和热力学方程中平流风用地转风代替的方法。

1.3 准地转运动理论的完备性

在准地转近似假定下，绝热、无摩擦时的大气运动方程组简化为准地转运动方程组。准地转运动方程组[式(8)]是准地转理论的核心内容。在所作假定下，可以写为：

$\left\{ {\begin{array}{*{20}{l}} \begin{gathered} \frac{{\partial {\nabla ^2}\mathit{\Phi }}}{{\partial t}} - \frac{1}{{{f_0}}}\frac{{\partial \mathit{\Phi }}}{{\partial y}}\frac{{\partial {\nabla ^2}\mathit{\Phi }}}{{\partial x}} + \frac{1}{{{f_0}}}\frac{{\partial \mathit{\Phi }}}{{\partial x}}\frac{{\partial {\nabla ^2}\mathit{\Phi }}}{{\partial y}} + \hfill \\ \quad \quad \frac{\beta }{{{f_0}}}\frac{{\partial \mathit{\Phi }}}{{\partial x}} = f_0^2\frac{{\partial \mathit{\Phi }}}{{\partial p}} \hfill \\ \end{gathered} \\ {\left( {\frac{\partial }{{\partial t}} - \frac{1}{{{f_0}}}\frac{{\partial \mathit{\Phi }}}{{\partial y}}\frac{\partial }{{\partial x}} + \frac{1}{{{f_0}}}\frac{{\partial \mathit{\Phi }}}{{\partial x}}\frac{\partial }{{\partial y}}} \right)\frac{{\partial \mathit{\Phi }}}{{\partial p}} + \sigma \left( p \right)\omega = 0} \end{array}} \right.$

(9)

其中 $\sigma \left( p \right) = \frac{{{R^2}T}}{{{p^2}g}}\left[ {{\gamma _d} - \gamma \left( p \right)} \right]$ 为静力稳定度参数。

准地转运动方程组的完备性体现在两个方面。一是式(9) 中两个方程只有两个未知数ω和Φ，不需要增加新的方程即可对式(9) 求解。二是在绝热、无摩擦，且在σ仅取为p的函数的情况下，式(9) 中的位能和动能之和是守恒的。这样避免了对大气运动基本方程组进行简化时可能出现的虚假的能源或能汇。

总之，准地转运动方程组简化了数学上的问题，使得求解简化后的大气运动方程组成为可能。

2 准地转运动理论的应用范畴

中高纬度大尺度运动的重要特征是大尺度运动具有准水平、静力平衡、准地转平衡和准水平无辐散的特征(杨大升等，1980)。在准地转运动方程组的推导过程中，将静力平衡和地转平衡近似合理地引入到大气运动方程组中，尽管对大气中可能出现的一些运动形式加以了限制(如滤去重力惯性波)，但方便了对大尺度运动系统的描述和解释。

2.1 大尺度运动定义

实际大气运动的水平范围有着宽广的空间尺度，从分子平均自由程(约0.1 μm)到地球的周长(约40000 km)。尺度分类的方法众多，天气学上最常用的是Orlanski(1975)和Fujita(1981)的分类法。Orlanski的大尺度分类指的是水平尺度为2000 km以上的运动；Fujita的大尺度分类指的是水平尺度为400 km以上的运动。Markowski等(2010)指出尺度的划分必须要有动力学意义，如对大尺度运动，可以忽略垂直加速度项和非地转风平流的作用等。这与动力气象学中的定义是一致的，在动力气象学尺度分析理论中(杨大升等，1980)，将10⁶ m水平尺度的运动称为大尺度运动，10⁷ m水平尺度的运动称为行星尺度运动。

2.2 准地转运动理论的范畴

准地转运动是大气动力学中一个十分重要的概念。对准地转运动而言，由尺度分析知，最主要的特征是Rossby数小于1(杨大升等，1980)。Rossby数是惯性力与科氏力的比值，表示惯性力和科氏力在运动中的相对重要性，尺度越大，地球自转的作用越大，Rossby数越小。对于中高纬度大气运动，Rossby数的大小取决于运动的水平尺度。

在动力学上，也可以根据运动的水平尺度将准地转运动分成二类：第一类准地转运动，指运动的水平尺度小于地球半径，这类准地转运动实际上是指中高纬度天气尺度运动，或水平尺度小于地球半径的大气长波；第二类准地转运动，指运动的水平尺度L与地球半径a相当，这类准地转运动指的是中高纬度行星尺度运动，亦即超长波运动。要注意的是，第一类准地转运动和第二类准地转运动的涡度方程形式是不同的(吕美仲等，2004)。

综上所述，狭义地说，准地转运动理论指的是以准地转涡度方程和热力学方程为基础的理论体系，它可以用于研究中高纬度大尺度天气系统，如大型气旋与反气旋、锋面和斜压波。广义地说，准地转运动理论指的是Rossby数小于1的运动，除可用于研究中高纬度大尺度天气系统外，还可用于研究中高纬度行星尺度运动。为明确起见，本文所指的准地转运动理论是前一种，即动力学上的第一类准地转运动。

2.3 天气图上的大尺度运动

天气图分析是通过分析等压面图上各种气象要素分布，来认识天气系统的结构和性质并进而判断其未来的演变趋势。由于天气观测的空间间隔一般为200~300 km，实际的天气形势可以看成是大尺度要素场和中尺度扰动要素场的叠加(Markowski et al，2010)。

在进行实际天气图分析时，如不作中尺度滤波(Markowski et al，2010；贺哲，2006)，直接分辨出不同尺度运动特征有一定难度，需要有丰富的经验。如，夏季500 hPa风场上的西风带中出现几个偏北风测站，经验丰富的预报员会以偏北风为标志推论出大尺度运动短波槽所代表的冷空气活动。

2.4 准地转运动理论与短期天气预报的关系

短期天气预报指的是时效为24~72 h的预报。其预报思路为：分析和判断近期大型环流背景及主导系统；分析、判断影响本地的天气系统及其影响部位的主要特征；考察其中可能引发的中小尺度系统的条件；分析局地的天气实况和气象条件。生命史长度为3~5 d的天气尺度系统(包括地面的气旋、反气旋与锋面以及与之相关联的高空斜压波)的发展演变直接或间接决定了未来1~3 d的天气变化，而准地转理论揭示了天气尺度系统发展机理，所以是短期天气预报思路的理论基础。

在逐日天气图上，不论是高空还是地面天气图，天气系统的运动形式大多呈涡旋状或波状，即低压、高压和槽脊都与气旋、反气旋及高空西风带的波动相对应。在准地转近似下，由式(8) 得到的准地转位势倾向方程和准地转垂直运动方程中，大尺度天气系统的位势高度变化和垂直运动都可以用涡度平流和温度平流来定性表示，因而在天气图上可直接利用等温线和等高线的特征及其配置定性地判断气旋、反气旋和高空槽脊的变化趋势以及相伴随的垂直运动分布。

3 准地转位势倾向方程及其实际应用 3.1 位势与位势倾向

气象上用位势高度代替几何高度。空间某一点的位势高度是将单位质量空气从海平面(位势取为0) 抬高到空间某高度克服重力所作的功，此功又称为重力位势，简称位势，用Φ表示。在等压面图上用H表示位势高度，则以位势米表示的位势高度为 $H = \frac{\mathit{\Phi }}{{9.8}}$ 。采用位势高度的好处是在实际计算时可以把重力加速度g当作常数来处理，虽然g随纬度和海拔高度实际上有微小的变化。

$\frac{{\partial \mathit{\Phi }}}{{\partial t}}$ 称为位势倾向，即Φ随时间的局地变化。如海平面(或1000 hPa等压面)位势取为0，500 hPa上某点的位势倾向大于0，意味着500 hPa的位势高度要升高。如果此处为槽，则槽将减弱；如果此处为脊，则脊将增强。

3.2 准地转位势倾向方程及其定性表达式

在经典的理论推导中，没有给出准地转位势倾向和准地转垂直运动方程中涡度平流和温度平流及其垂直变化在天气图上的具体使用方法，特别是如何选择等压面的层次(杨大升等，1980；吕美仲等，2004)。“斜压二层模式”框架下的准地转理论则可以解决这个问题。

“斜压二层模式”(刘式适等，1991)由于其简明性，对揭示许多斜压大气动力学问题非常有效，它是将整个大气层(大气层顶p=0，地面p=1000) 按Δp=500 hPa二等分，再用250 hPa等压面代表上半层，用750 hPa等压面代表下半层。所以在斜压二层模式中共有4层等压面。

将准地转涡度方程[式(6)]写在第二层500 hPa等压面上，准地转热力学方程[式(7)]写在第一和三(分别为250和750 hPa)层等压面上。假设Φ₀、Φ₄不随时间变化，静力稳定度参数为常数。由式(6) 和式(7) 可求得(王秀明等，2013)：

$\begin{gathered} - \left( {\frac{{\partial {\mathit{\Phi }_2}}}{{\partial t}}} \right) \propto - {f_0}{\mathit{\boldsymbol{V}}_{g2}} \cdot \nabla \left( {{\zeta _{g2}} + f} \right) + \hfill \\ \quad \frac{{f_0^2}}{{2\Delta p{\sigma _2}}}\left[ {{\mathit{\boldsymbol{V}}_{g1}} \cdot \nabla {{\left( {\frac{{\partial \mathit{\Phi }}}{{\partial p}}} \right)}_1} - {\mathit{\boldsymbol{V}}_{g3}} \cdot \nabla {{\left( {\frac{{\partial \mathit{\Phi }}}{{\partial p}}} \right)}_3}} \right] \hfill \\ \end{gathered} $

(10)

将上式写成定性表达式，则为：

500 hPa位势高度的下降 ∝

   500 hPa的(绝对)涡度平流

   250 hPa层的暖平流

   750 hPa层的冷平流

3.3 高空槽脊发展的判断

这里所指的高空槽脊即500 hPa的槽脊。由式(9) 可知，500 hPa位势高度的变化取决于500 hPa以下层次和以上层次的温度平流的差异和本层的(绝对)涡度平流。

首先考虑式(9) 中的上下层温度平流之差的作用。如图 1所示，状态(1) 为大气初始状况。假设z与z+2Δz固定不变(即推导过程中的Φ₀、Φ₄不随时间变化)，如果500 hPa以下层有冷平流，则由状态(1) 发展到状态(2)，即p-Δp面的高度下降。反之，若下层有暖平流，则由状态(1) 发展到状态(3)，即p-Δp面的高度上升(周小刚等，2010)。

在实际大气中，由热成风关系，在500 hPa以上的层次中，等温线与等高线趋于一致，因此可以认为500 hPa槽脊的发展或减弱主要取决于所对应的500 hPa以下层次的温度平流。此即为通常所认为的温度平流决定槽脊的发展。

考虑式(9) 中的涡度平流的作用。绝对涡度平流可以分成相对涡度平流和牵连涡度平流两部分。在对称性槽或脊上，相对涡度平流和牵连涡度平流都为0，在这个意义上，认为绝对涡度平流对槽脊的发展不起作用。此即为通常所认为的涡度平流对槽脊的发展不起作用。

因此，对于发展的理想斜压系统模型可以归纳为：500 hPa脊的下方如果为暖平流，则脊将加强；500 hPa槽的下方如果为冷平流，则槽将加强。

3.4 高空槽脊移动的判断

实际观测资料计算得到的长波槽脊中辐散辐合随高度变化的一般特点为：(1) 长波槽后脊前，对流层上层是辐合的，下层是辐散的；(2) 长波槽前脊后，对流层上层是辐散的，下层是辐合的；(3) 高层最大辐散辐合在对流层顶左右，低层最大辐散辐合在地面附近；(4) 高低层的辐合辐散相互抵消；散度为0的过渡层(无辐散层)，高度在600 hPa左右。

如果认为500 hPa层是无辐散层，则涡度方程可以化成正压无辐散的涡度方程形式：

$\frac{{{{\text{d}}_h}\left( {{\zeta _{g2}} + f} \right)}}{{{\text{d}}t}} = 0$

(11)

由式(11)，可求出著名的Rossby波速公式为：

$c = \bar u - \frac{\beta }{{{k^2}}}$

(12)

在中高纬度，假设槽以平均西风风速(10 m·s^-1)移动，则由式(11) 可求出槽脊约一天移动10~15个经度，此即可作为500 hPa槽脊移动的基本外推值(王秀明等，2013)。

将 $L = \frac{{2\pi }}{k}$ 代入式(9)，则可求得L=6000 km时为静止波。L＜6000 km为前进波；L＞6000 km为后退波。因此也可以认为本文所讨论的准地转理论是限于1000~6000 km尺度的运动。

事实上，并不是所有大于6000 km波长的系统都能观测到后退(Bluestein, 1993)。这是因为大气长波公式是由正压无辐散的涡度方程求出的，仅仅考虑了相对涡度和地球自转涡度平流的作用，而没有考虑热力因子的作用。

在槽附近(有限纬度范围)还可以观测到，当最强的风在槽的上游时，槽有向南移动(北半球)的倾向；当最强的风在槽的下游时，槽有向北移动(北半球)的倾向(Bluestein, 1993)。这些观测事实可以用准地转运动理论来解释：假定槽附近的风速近似为地转的，在西风带中，如果最大风速在槽的上游，则与槽相联系的涡度最大值也在槽的上游，因此最大气旋式涡度平流和高度下降区是在靠近槽线的南端，而不是像对称槽一样在槽的东部，故槽有向南运动的分量。同样，在西风带中，当最大风速在槽的下游时，与槽相联系的涡度最大值也在槽的下游，因此最大气旋式涡度平流和高度下降区是靠近槽线的北端，槽有向北运动的分量。

4 准地转垂直运动方程及其应用

大气中的垂直运动有中小尺度对流性垂直运动和大尺度的系统性垂直运动之分。中小尺度对流性垂直运动与大气的静力不稳定有关，大尺度系统性垂直运动的发生与大尺度天气系统有关，如高压、低压和槽脊等。这两类垂直运动具有完全不同的性质，不可混淆。尽管系统性的垂直运动很小，只有cm·s^-1的量级。但由于其范围大，持续时间较长，对天气的形成和变化有很大影响。

4.1 准地转垂直运动方程的优点

理论上，大尺度的垂直运动可以由大气运动方程组中的垂直运动方程、连续方程及热力学方程这三条可能途径来估算(丁一汇，1989)。第一条途径，由于大尺度运动具有静力平衡特性，决定了其垂直速度不能由垂直运动方程的垂直加速度来计算。第二条途径，由于大尺度运动具有的准无辐散特性，一方面决定了实际垂直运动小于由连续方程估计出的垂直速度，另一方面由于风的观测值中包括大大小小各种尺度的运动，精度有限，因此用连续方程估计的垂直速度误差非常大，与垂直速度本身的量级相同而无法使用。第三条途径，在利用大尺度热力学方程计算垂直速度时，只能是在绝热假定下根据温度局地变化反算垂直速度，由于大气中实际存在的各种各样非绝热过程对计算结果的影响非常大而无法使用。准地转垂直运动方程综合考虑了运动学方程与热力学方程的作用，是一个在理论上完备的诊断方程，能够揭示产生大尺度垂直运动的动力学机理，故其结果较为合理可信。

4.2 准地转垂直运动方程及其定性表达式

利用斜压二层模式，假设ω₁、ω₄=0，静力稳定度参数取为常数。则垂直运动可写为(周小刚等，2010)：

$\begin{gathered} - {\omega _2} \propto \frac{1}{\sigma }{\nabla ^2}\left[ { - {\mathit{\boldsymbol{V}}_{g2}} \cdot \nabla {{\left( {\frac{{\partial \mathit{\Phi }}}{{\partial p}}} \right)}_2}} \right] + \hfill \\ \quad \frac{{f_0^2}}{{2\Delta p\sigma }}\left[ { - {\mathit{\boldsymbol{V}}_{g1}} \cdot \nabla \left( {{\zeta _{g1}} + f} \right) + {\mathit{\boldsymbol{V}}_{g3}} \cdot \nabla \left( {{\zeta _{g3}} + f} \right)} \right] \hfill \\ \end{gathered} $

(13)

将上式写成定性表达式，则为：

$\begin{array}{*{20}{c}} {500\;{\text{hPa}}\;{\text{上升运动}}}& \propto &\begin{gathered} 500\;{\text{hPa}}\;{\text{的暖平流}} \hfill \\ 250\;{\text{hPa}}\;{\text{层的正涡度平流}} \hfill \\ 750\;{\text{hPa}}\;{\text{层的负涡度平流}} \hfill \\ \end{gathered} \end{array}$

4.3 大尺度垂直运动的判断

由式(13) 可知，500 hPa上升运动取决于500 hPa的温度平流和500 hPa以下层次和以上层次的上下层涡度平流之差。

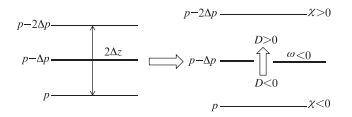
首先考虑温度平流的作用。如图 2所示，图中χ为等压面高度的位势倾向，如果p与p-2Δp间有暖平流区，则2Δz会增加。即p-2Δp处，χ>0；p处，χ＜0。此时如果p与p-2Δp处的ω=0(即推导中假定的ω₁、ω₄=0)，则中间会有ω＜0，即p-2Δp(500 hPa)有上升运动。此时p面产生辐合，p-Δp面则形成辐散，中间会有D=0。

考虑式(13) 中的上下层涡度平流之差的作用。先看250 hPa层的正涡度平流作用，由式(13)，250 hPa层的正涡度平流作用对应对流层中层为上升运动，其原因是高空正涡度平流引起高空辐散。类似地，对于高空急流附近的辐合辐散区(丁一汇，2005)，可以很容易从涡度平流得到解释，即：高空急流入口区的右侧、出口区的左侧为高空正涡度平流区，也为高空辐散区；高空急流入口区的左侧、出口区的右侧为高空辐合区。

考虑到500 hPa以下层次(750 hPa)涡旋状分布相对明显，且风速低于高层，因此上下层涡度平流之差可主要考虑高空涡度平流项。

直接分析准地转垂直运动方程，可以得出涡度平流与温度平流会有部分抵消(周小刚等，2011)，去掉抵消后的项，准地转垂直运动方程可写成准地转Q矢量的形式。但由于它不如判断温度平流和涡度平流方便，目前主要是用于诊断计算。

4.4 地面气旋发展与移动的判断 4.4.1 地面气旋系统的形成和发展

在推导准地转位势倾向方程时，假定了Φ₀、Φ₄不随时间变化，因此，地面气旋的发展不能由准地转位势倾向方程得到。结合前面提到的长波槽脊中辐散辐合随高度变化的一般特点，可以通过由准地转垂直运动方程决定对流层中层(500 hPa)是上升还是下沉运动来判断地面气旋的发展与移动。若对流层中层为上升运动，低层辐合，引起地面气旋发展；若对流层中层为下沉运动，低层辐散，则引起地面反气旋发展。这与利用位涡守恒对气旋发展的解释也是一致的(许健民等，2008；帕特里克·桑特里特等，2008)。

对于地面气旋或反气旋的形成和发展，在通过式(13) 来作判断时，除考虑温度平流与涡度平流外，还必须考虑地形和非绝热加热的作用。在非绝热变化中，对气旋发生发展影响最大的是凝结释放的潜热。凝结潜热由上升运动引起，反过来它又加快了上升速度，这种正反馈作用往往在中层达到最大。因此，凝结潜热的释放对气旋的发展有重要作用，降水越大，这种作用越强。其他一些非绝热加热、冷却作用也是不能忽视的。如冷的大陆性气团移到相对暖的水面上时，向气团的感热传输有利于低压槽的形成；相对暖的空气移到冰面或雪面时，有利于反气旋的形成。

地面的影响有两方面。一是地面摩擦的作用，它也有两方面的作用，摩擦的直接作用是消耗动能，即削弱地面气旋，也消弱反气旋；而摩擦的间接作用使风向偏向低压方向，造成气旋辐合、反气旋辐散，气旋和反气旋涡度都增强，同时气压梯度力做功使动能增加。二是地形的影响，如果地表面是倾斜的，即使无其他准地转强迫项，也会形成气旋与反气旋。如山脉背风坡的下沉运动导致背风槽的形成。

综上所述，有利于地面气旋发展的特征是：对流层高层(250 hPa)正涡度平流；对流层中层(500 hPa)暖平流；下坡(地形项)；冬季内陆包围的暖水面(非绝热加热项)；冬季低压入海(非绝热加热、摩擦项)。

由于对气旋发展的判断是间接使用了准地转垂直运动方程。除准地转垂直运动方程中固有的上下层涡度平流之差与温度平流的抵消项(周小刚等，2011)外，还可能有温度平流和非绝热加热的抵消，如当冷空气移到暖水面时(即水面上有冷平流)，与非绝热加热相关的地面气压降低受到冷平流的抑制；摩擦和非绝热加热项的抵消，如果考虑行星边界层的作用，假设在摩擦层中有气旋式地转风涡度，则在摩擦层里有上升运动；如果大气是条件不稳定且有充足的水汽，由与摩擦层气旋相联系的Ekman抽吸可以触发积云对流；积云对流触发后，则水汽凝结潜热释放引起的非绝热加热将导致高层上升运动和地面辐合，使地面气压下降；倾斜上升或下沉运动与上下层涡度平流之差的抵消，如在高空脊前，背风坡倾斜下沉运动要导致背风槽或低压形成，则要克服上下层涡度平流之差的作用。

4.4.2 地面气旋系统的移动

地面气旋、反气旋并不是由高空气流引导的刚体，它们的移动实质上是低压和高压中心的传播。具体说：地面高压系统(反气旋)，是从气压下降区移向气压升高区，即移向变压升度方向。地面低压系统(气旋)，是从气压上升区移向气压下降区，即移向变压梯度方向。地面气压升高区也是近地面的高度上升和辐散区。根据连续方程，辐合层伴随上层上升运动，辐散层伴随上层下沉运动。因此地面气压系统的移动规则有：地面气旋是从下沉运动区移向上升运动区；地面反气旋是从上升运动区移向下沉运动区。

因此，地面气旋移动特征：移向正涡度平流(250 hPa)更大的区域、移向暖平流(500 hPa)更大的区域、下坡向南移动或移向非绝热加热更大的区域(周小刚等，2010)。地面气旋的移动是由上述影响共同决定的。具体而言，冷暖平流对气压系统移动的作用是：通常在地面气旋的东北部有暖平流，西南部有冷平流，因此温度平流的作用是使地面气旋向东北移动。而地面反气旋中通常是东南部为冷平流，西北部为暖平流，因此温度平流的作用是使地面反气旋向东南方向移动。在西风带中，气旋通常形成于500 hPa槽前脊后，反气旋通常形成于500 hPa槽后脊前，因而高空流场的方向与所分析的气旋和反气旋的移动方向是一致的，高空引导气流正是在这个意义上提出来的。上下层涡度平流之差对气压系统移动的作用不容易概括。如果地面低压正好是最大涡度平流随高度愈加气旋式的区域，则气旋将加深，但上下层涡度平流之差无法判断其移动方向。如果最大涡度平流随高度愈加气旋性的区域位于地面低压上游(下游)，则上下层涡度平流之差的作用是减弱(加强)向东的移动分量。地形对地面系统的移动也有显著影响，如气旋在西风带中移到有一定坡度的山脉附近，下坡时气旋向南一侧的气压下降，故气旋下坡南落。

5 结语

准地转运动理论是在尺度分析的基础上针对中高纬度大尺度运动提出来的动力学理论。准地转理论的目的是利用控制方程组解释天气尺度运动的观测结构，认识天气系统的变化机理。

在经典的推导中，未涉及具体针对哪个层次来考察涡度平流和温度平流，用之来确定高空天气系统和地面天气系统的移动和发展有不确定性。由斜压二层模式得到的准地转位势倾向方程可用于判断500 hPa槽脊的发展和移动；准地转垂直运动方程可用于判断对流层中层最大的系统性垂直运动，并可用于地面气旋或反气旋发展和移动的判断。涡度平流与温度平流是系统发展和移动的内部因子，非绝热加热作用和地形作用作为外部因子对系统的发展和移动也有影响。值得注意的是上述四个因子的部分抵消作用，如在气旋发展过程中，除考虑上下层涡度平流之差与温度平流有抵消外，还要注意温度平流和非绝热加热的抵消及摩擦和非绝热加热项的抵消作用。

实际上，准地转位势倾向方程和准地转垂直运动方程是通过严谨的数学推导获得的描述中高纬度大尺度天气系统发展因子和垂直运动的数学表达式。这两个方程都是没有解析解(一般解)的微分方程，只能用迭代法在一定的边界条件下求出数值解。由于绝热和无摩擦的假定，其数值解本身存在较大的误差，主要用来区分两个强迫因子贡献的大小。在数值预报有了长足进步的今天，准地转动力学理论为我们提供了认识模式预报的天气过程的定性分析方法。它的意义在于使我们能够深刻认识中高纬度大尺度系统的生成和发展的机理。因此，即使在计算机广泛应用、数值天气预报水平不断提高的今天，对准地转理论的认识和应用仍然是重要的。

致谢：本文的一些基本问题来源于与中国气象局举办的各级预报员培训班学员的讨论，在此表示感谢。