2. 北京文泽智远信息技术有限公司,北京 100081;
3. 广州数鹏通科技有限公司,广州 510650
2. Beijing Wenzezhiyuan Information Technology Co., Ltd., Beijing 100081;
3. Guangzhou Shupengtong Technology Co., Ltd., Guangzhou 510650
预报检验与评估,是气象预报发展过程中不可或缺的重要组成部分。通过检验评估可以了解不同预报的偏差特征,促进数值模式和主客观预报的改进(Jolliffe and Stephenson, 2016;韦青等,2019)。随着气象预报精细化要求的提升,预报产品制作流程和算法日益复杂,天气预报全流程业务包含从数值模式预报出发,经过各种后处理订正、多种模式及多种客观算法的集成、主客观融合再到国、省产品融合,以及最终发布精细化网格预报(唐健等,2018;金荣花等,2019)等数字化的业务流程。其中,每一个制作环节不仅会带来预报的改进,也可能引入新的误差,通过检验可以更好地评估每个环节的实际贡献(Roberts and Mittermaier, 2015)。天气预报“研究型业务”对检验评估也提出了更高的要求,检验不仅限于统计一组评分指标,而是要对各种要素的空间分布、季节变化及日变化等特征进行对比分析(Chen et al, 2016)。譬如,通过检验不同影响系统下的降水预报偏差,可为降水预报的改进提供更多的参考价值(宫宇等, 2018)。
在国际上,欧洲中期天气预报中心及其成员国、美国、澳大利亚和加拿大等都在发展业务预报检验系统(韦青等, 2019; Yadav et al, 2014)。英国气象局建立了一套全流程检验评估系统,评估预报流程各环节的价值,以促进预报质量的提高(Roberts and Mittermaier, 2015)。然而,在国内,国家级、省级和地市级气象部门的检验业务和系统主要是针对最终预报产品的常用检验指标进行统计(姚文等,2010;杨辉等,2014;杨阳等,2017),缺少精细化检验分析,也很少涉及中间产品的检验。
当前,开展全流程精细化检验的主要障碍在于缺乏适应业务环境的通用检验算法库,各级气象部门的检验系统都要从底层的检验算法开始搭建(符凤平等, 2015; 李新庆等,2016),导致重复建设、效率低下和标准难以统一。2007年,美国国家大气研究中心(National Center for Atmospheric Research,NCAR)数值预报发展试验中心(Developmental Testbed Center,DTC)开发了检验工具库(Model Evaluation Tools,MET),集成了站点检验、格点检验和MODE空间检验等功能(Brown et al, 2021)。MET不足之处在于灵活性较差以及不适应国内业务环境,基于它很难开展分季节、分地域或者分影响系统的精细化检验评估,同时还存在计算效率较慢和学习成本较高的问题(潘留杰等,2016)。
考虑到现有的工具对检验评估的支撑能力不足,国家气象中心组织研发了天气预报全流程检验评估程序库(Meteorological Evaluation Program Library, 简称MetEva),并通过PyPI开源发布。文章首先介绍了MetEva程序库的设计目标和系统架构;第二部分介绍了程序库的关键技术,即统一的数据结构、模块化的检验流程以及并行化的计算技术;第三部分围绕检验流程的6个步骤进行了功能函数介绍;第四部分给出了MetEva集成的预报检验算法以及相对于传统编程思路在计算流程上的改进;最后以温度和降水为例说明MetEva在精细化检验评估中的应用效果,以帮助用户对该系统有更深入的理解。
1 系统设计 1.1 设计目标MetEva是一款采用Python语言开发的软件工具,旨在为“从数值模式、精细化网格预报产品研发到预报产品应用”的天气预报产品制作的全流程提供检验技术支持。具体的目标包括以下两部分。
MetEva第一个设计目标是检验评估算法的全流程覆盖。MetEva要覆盖不同预报制作流程和环节所需的检验算法,以提升各环节(或部门)的检验评估程序(系统)的开发效率。
MetEva第二个设计目标是检验评估结果的可对比性。MetEva按照检验规范提供统一的数据处理流程、检验算法和结果呈现形式,保证检验评估的数据样本和算法的一致性,使不同业务部门或不同流程和环节的预报产品的检验结果具有可对比性,从而评估不同环节对最终预报准确率的贡献。
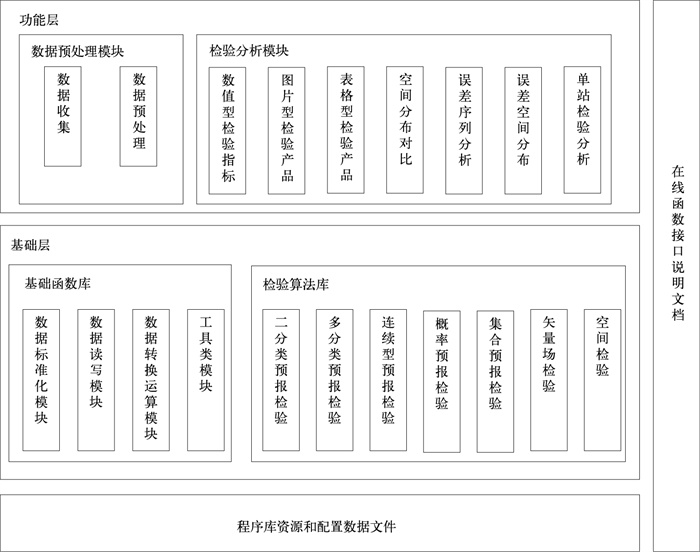
1.2 系统架构MetEva采用分层架构设计(图 1),可分为基础层和功能层。其中,基础层包含基础函数库和检验算法库,功能层包括数据预处理模块和检验分析模块。基础函数库提供数据结构定义、数据读写、数据选取、数据分组、插值和图形绘制等功能;检验算法库则包含具体的检验运算功能;数据预处理模块功能是基于基础函数库封装的数据整理的应用模块;检验分析模块则基于整理后的数据进行检验计算和图表绘制。功能层依赖于基础层,但同一层的各功能采用模块化设计,直接依赖关系弱,方便扩展。
|
图 1 MetEva的模块及分层结构示意图 Fig. 1 The module and hierarchical structure of MetEva |
MetEva设计了一套统一的包含完整时空信息的数据结构,包括站点数据和网格数据两种结构,具体如下。
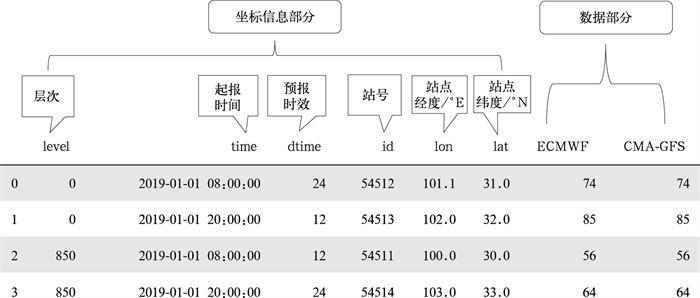
站点数据:如图 2所示,采用pandas.Dataframe表格(https://pandas.pydata.org/)作为基础数据结构。表格中的每一行记录一个时空坐标点上的预报和观测。表格可横向划分为坐标信息和数据两部分。坐标信息有6列,依次为level、time、dtime、id、lon和lat,分别为数据样本的层次、时间、预报时效、站号、站点经度、站点纬度,其中观测数据的预报时效设为0。数据部分从第7列开始,一种数据置于一列,列名代表数据的名称。
|
图 2 站点数据结构 Fig. 2 Structure of site data |
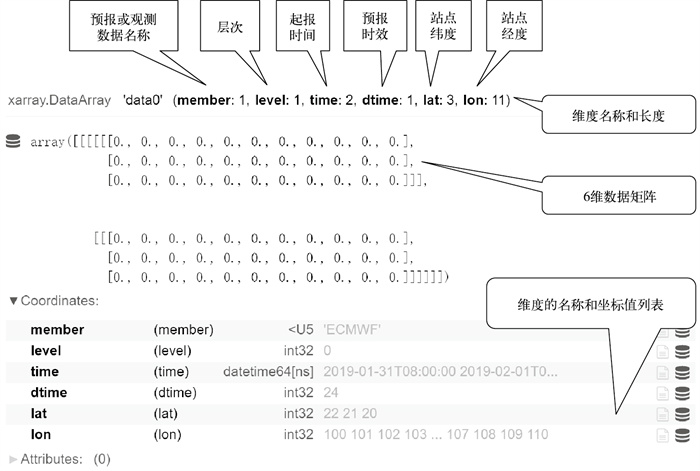
网格数据:如图 3所示,采用带有6维坐标信息的xarray.DataArray矩阵(http://xarray.pydata.org/)作为基础数据结构。维度次序为member、level、time、dtime、lat和lon,分别记录预报(或观测)数据名称、垂直层次、起报时间、预报时效、站点的经度和纬度信息,其中水平方向为等经纬度坐标。数据内容部分采用6维的数组记录。
|
图 3 网格数据结构 Fig. 3 Structure of gridded data |
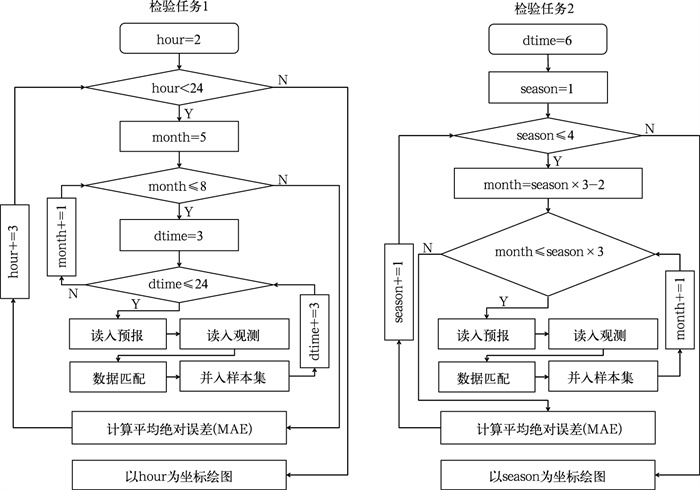
传统检验程序通常包含不同的分支和循环结构,以满足多样的检验需求。流程结构的差异导致程序难以模块化,是制约检验程序(系统)开发效率的主要原因。为了具体地解释上述问题,本文以一个示例加以说明。例如,针对2020年全国范围内08时起报的24 h时效内逐3 h的2 m温度预报,有两项不同的检验任务:
检验任务1:统计5—8月温度预报平均绝对误差的日变化;
检验任务2:统计14时温度预报平均绝对误差的四季变化。
图 4展示了针对上述两项检验任务的传统计算流程,由于两项任务需要的数据样本和分类统计方式不同,两个计算流程在数据的读取、匹配和分类统计等环节包含了不同的判断和循环结构。
|
图 4 针对两项检验任务示例的传统计算流程 Fig. 4 Traditional calculation process for two examples of verification tasks |
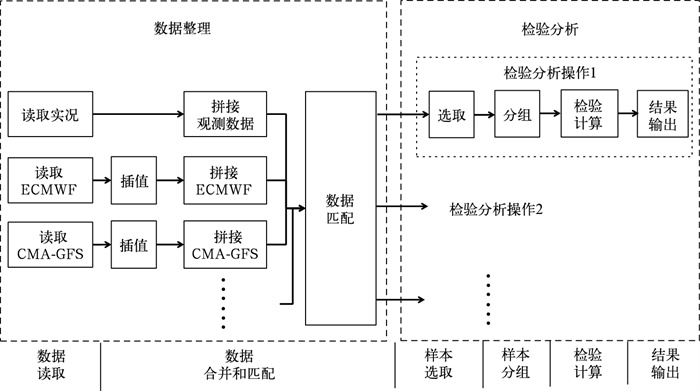
为了提升检验程序的模块化程度,本文给出了统一的检验流程,其结构如图 5所示。该流程包括数据整理和检验分析两大步骤。其中数据整理步骤包括观测数据读取和拼接,预报数据读取、插值和拼接及数据匹配部分。检验分析步骤依次包括样本选取、样本分组、检验计算和结果输出四个步骤,通过调整其中的参数来完成不同的检验任务。
|
图 5 基于MetEva的检验程序流程图 Fig. 5 Flow diagram of the verification program based on MetEva |
针对上述两个检验任务的数据整理程序可以完全一致,即读取全国范围内2020年全年逐3 h的观测和预报数据,并完成匹配。在检验分析步骤,两个任务所需的函数功能也完全一致,只是调用参数有所差异。任务1的选取参数是月份属于集合[5, 6, 7, 8],分组参数是观测时间;任务2的选取参数是时效等于6;分组参数是月份,并指定将月份划分到季节的参数。
在图 5所示的新流程图中,各预报数据的收集模块是并列关系,可以任意增删预报数据。各检验分析模块也是并列关系,也可任意增删,且它们可以共用数据整理的结果,避免重复收集数据。围绕上述新流程,MetEva开发了数据读取、数据合并和匹配、样本选取、样本分组、检验计算和结果整合输出等6类功能函数(详见第3节)。
对于图 5中每个步骤,MetEva提供的功能函数都采用上述统一数据结构作为输入和输出,因此观测和预报数据的完整时空信息在计算流程中被保留。基于数据中的时空信息,各类函数可以分别完成插值、匹配、选取、分组等功能。如果输入数据不包含时间信息,则分类检验依赖的分组函数就无法根据时间相关量(年、月和日等)对数据样本进行分组,此时就需要在程序中通过循环流程来实现,这也正是传统检验程序包含循环结构的原因。
2.3 并行化的计算技术传统的检验程序没有设计可并行的检验算法,然而,在大规模预报数据检验中,如果数据规模超出内存大小,则必须采用分块的方式,并通过并行计算来进一步提升效率。
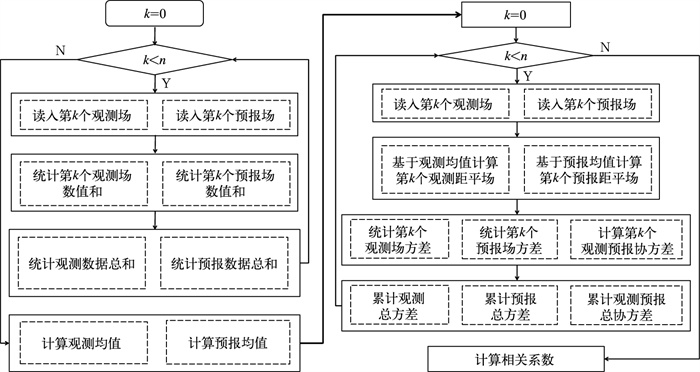
以常用的相关系数为例,当数据规模较小时,可以直接调用numpy等程序库中的函数功能来完成计算。当数据规模非常大时,通常采用分块计算流程来实现。图 6给出了计算相关系数的传统分块计算流程,在该流程中需要先循环读取所有数据以求取观测和预报的平均值,之后再重新读取数据计算观测和预报的方差和协方差。可见,这种传统的分块计算流程是顺序执行的,需要重复2次读取观测和预报数据,执行效率较低。
|
图 6 相关系数的传统分块计算流程 Fig. 6 Traditional block calculation process of correlation coefficient |
为了进一步提升大规模数据检验计算的效率,MetEva为大部分检验算法(详见第4节)提供了并行计算方案,通常包含3个部分:(1)基于分块数据,统计分块统计量;(2)将分块统计量合并成总体统计量;(3)基于总体统计量计算最终检验指标。其中,第一部分是决定计算效率的主要部分,可以采用并行的方式进行计算。第二部分中,对于大部分检验指标而言,将分块统计量累加就可以得到总体统计量,但有少部分检验指标需要设计专门的合并函数来实现分块统计量的合并。
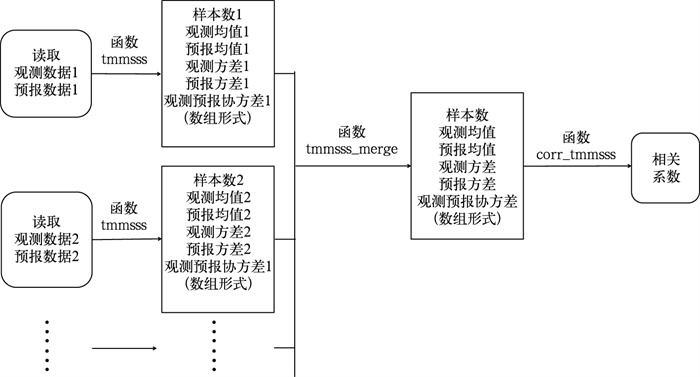
仍以相关系数为例,基于MetEva的相关系数并行计算流程如图 7所示。在该流程中,函数tmmsss计算分块数据的6项中间统计量(样本数、观测均值、预报均值、观测方差、预报方差和观测预报协方差),与上述第一部分对应。函数tmmsss_merge用于中间统计量的合并(具体计算公式见本文附录),对应第二部分。函数corr_tmmsss对应第三部分,即基于观测方差、预报方差和观测预报协方差计算相关系数。
|
图 7 基于MetEva的相关系数并行计算流程 Fig. 7 Parallel computing process of correlation coefficient based on MetEva |
基于图 7所示的并行计算流程,只需1次读取观测和预报数据,更重要的是,基于MetEva的并行方案可以充分利用已有的分块统计量实现检验指标的快速计算。例如,为了计算全年的相关系数,已经计算并保存了逐日的分块统计量,如果要按月分类统计,可根据逐日的分块统计量快速合并出逐月的总体统计量,然后计算逐月的相关系数。而基于图 6所示的传统流程,则必须重新读取原始数据并重新统计计算。
总之,MetEva区别于传统检验程序的关键技术是采用了统一的包含完整时空信息的数据结构,并基于该数据结构设计了统一的模块化的检验计算流程。因为数据和计算流程统一,MetEva提供的各类功能函数具有很好的可复用性,加上MetEva为大规模数据场景提供的检验并行计算方案,从而可以有效地提升检验效率。
3 主要功能截至目前,MetEva(V1.5)提供了402个可供用户调用的功能函数,并且通过在线说明文档网站提供相应的参数说明和调用示例。本节针对检验评估中的实际问题和解决方案,围绕检验流程中数据整理和检验分析的6个主要步骤对其主要功能进行阐述,帮助用户理解相关功能函数的实践应用。
3.1 数据读取我国气象业务的数据存储方式多样,包括以GRIB、NETCDF和MICAPS等格式文件存储和以MICAPS分布式数据库和“天擎”气象大数据云平台等数据库方式存储等。不同的数据存储方式有各自的优缺点、配套的软件系统以及下游应用,短期内难以实现数据存储方式的统一,因此检验需要面对预报观测数据种类繁多的问题。为此,MetEva集成了19种数据读取接口(表 1),以方便用户将各种方式存储的预报观测数据读取到统一的数据结构中。
|
|
表 1 MetEva集成的数据读取功能 Table 1 Data reading function integrated in MetEva |
实践中,检验需要的预报和观测数据通常是分散存储在文件或数据库中,接口函数一次只能读入部分数据。为此,MetEva集成了数据合并功能,将依次读入的数据合并成一个整体。同时,用户需通过要素匹配、空间匹配和时间匹配等操作来为每条预报数据匹配相应的实况。
首先是要素匹配。例如,用户需要检验相对湿度,但读入的是温度和露点温度数据,或者需检验变温,但读入的是温度数据,亦或者需检验逐3 h降水,但读入的是逐小时降水等,此时需要进行转换操作。对此,MetEva集成了要素之间相互转换、时间序列的滚动求和、求最大、求最小以及求变化量等功能。
第二是空间匹配。目前预报数据通常是网格数据,而实况通常是站点数据,用户需要通过插值实现两者的匹配。为此,MetEva集成了目前常用的邻近点插值、双线性插值及CRESSMAN插值等算法。考虑到温度和地形高度关系密切,而网格点同站点的海拔高度差异可能带来插值结果的不合理性,MetEva增加了插值结果的地形高度订正功能,其中温度垂直递减率设置为常数6℃·km-1。
最后是时间匹配。采用预报数据的起报时间加上预报时效得到观测数据的时间,为每条预报数据找到对应的观测数据。基于MetEva的匹配功能,只需输入观测数据集和预报数据集,即可自动地完成时间匹配,形成完整的检验数据集。
3.3 统计样本选取在数据准备环节,用户可尽量收集得到更完整的数据集,但一次检验并不总是对所有的数据样本进行统计。此时,基于MetEva的数据选取功能,传入一个字典参数即可提取出所需的样本子集。例如,通过传入参数s ={“dtime”: 24, “id”: [54511, 53759]}可以从全集中选取站号为54511或53759、预报时效为24 h的样本子集。类似的,数据选取功能还支持用户按层次、经纬度的范围、起报时间、以及起报时间中的年份、月份和日期等方式选取数据。
此外,数据选取功能也支持按照任意列的取值范围来选取数据,据此可以实现按天气系统来选取数据的功能。例如,当需要检验副热带高压影响范围内的地面温度预报时,可以将500 hPa位势高度值一并记录在数据集当中,然后选取位势高度取值大于5 880 gpm的样本即可挑选所需样本。
3.4 统计样本分类分类检验是实现精细化检验评估的基本技术手段。例如,通过按月的分类检验可揭示预报性能的季节变化特征,按站点位置的分类检验可揭示预报偏差的空间分布特征。为此,基于MetEva的数据分组功能可实现将数据样本按不同方式进行分类。
MetEva支持的分组方式包括按照层次、时间、时效、站号等基本坐标列的取值进行分组,也包括按照预报起报时间的年份、月份和日期的取值作为分组依据。在统计检验指标的日变化特征时,可以选用观测时间的小时值作为分组的依据。分组功能返回的结果包括分组的数据样本和分组的标签,例如将全年的数据按月分组得到12个数据集,每组标签则为相应的月份。
3.5 检验计算该步骤是调用检验算法对数据样本进行统计运算。MetEva集成了54种常用检验算法,并对它们的计算流程进行了改进(详见第4节),用户既可以直接调用这些算法函数,也可以将算法名称用作集成检验函数的参数(详见第3.6节)。
3.6 结果整合和输出MetEva通过集成检验函数将数据选取、数据分组、检验计算和图形绘制功能封装在一起。当检验数据包括多种预报,用户输入了分组参数时,该函数会自动循环调用检验算法统计不同预报不同分组的检验指标,并将计算的结果存储到数组当中,和分组标签一并作为函数结果返回。若用户还指定了绘图参数,则可进一步将检验结果绘制成图形输出。若选取的是只能返回图片结果的检验算法(如相对作用特征,以下简称为ROC)(Mason, 1982),集成检验功能则会循环调用算法,将不同预报不同分组数据的检验图表批量输出至指定的文件夹当中。
4 检验算法检验算法可分为二分类预报检验、多分类预报检验、连续量预报检验、概率和集合预报检验及空间检验等几类(Jolliffe and Stephenson, 2016)。表 2中按该分类方法列出了MetEva(V1.5)集成的检验算法(共54种),其中包含了世界气象组织推荐的大部分检验方法(Brown et al, 2008),以及MODE(Davis et al, 2006a; 2006b; 2009; 尤凤春等,2011)和SAL(Wernli et al, 2008; 金小霞等,2020)等常用空间检验方法。
|
|
表 2 MetEva集成的预报检验算法 Table 2 Verification algorithms integrated in MetEva |
在业务中,检验方法又常被笼统地划分为两大类,第一类是常规检验算法,它包括表 2所示的前4种类型,第二大类是空间检验方法。MetEva对两类检验方法都做了改进,其中对前者的改进主要是计算效率的优化,对后者的改进主要是增加了辅助分析功能。
4.1 常规检验算法除了应用本文2.3节所述的并行技术之外,MetEva还对常规的检验算法的计算流程进行了改进,采用矩阵运算的方法进一步提升计算效率。下面以TS评分为例对MetEva中常规检验算法的实现方法加以说明。
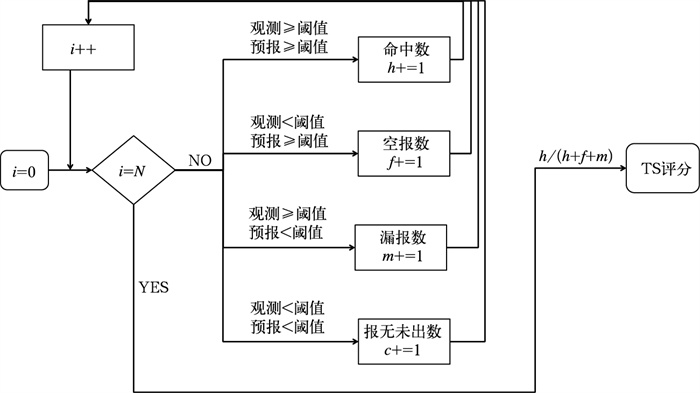
二分类预报的完整表现可用表 3所示的列联表呈现,其评价指标都可以表述为关于命中数(h)、空报数(f)、漏报数(m)和报无未出数(c,预报不发生实况也未发生)的函数,例如,TS=h/(h+f+m)。图 8显示了TS评分的传统算法流程,其中循环判断了每一对观测和预报数据是否超过阈值,由此判断它属于命中、空报、漏报还是报无未出的情况,并在相应的数目上增加1,从而统计出列联表,再计算出TS评分。
|
|
表 3 二分类预报检验列联表 Table 3 Contingency table for deterministic binary forecasts evaluation |
|
图 8 TS评分的传统算法流程 Fig. 8 Traditional algorithm flow of TS score |
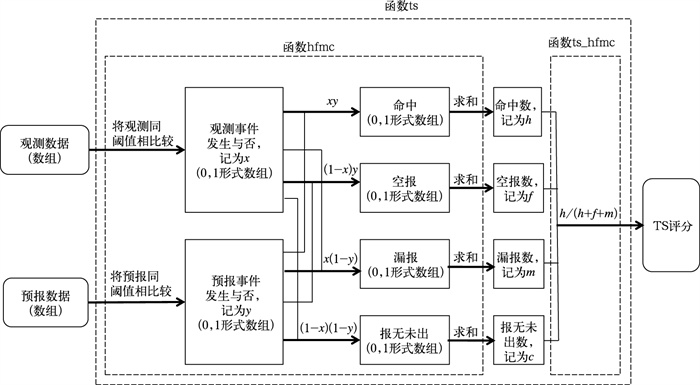
考虑到在Python中采用循环计算的效率非常低,MetEva对TS评分的计算流程进行了改进。改进后的计算流程(图 9)同样包含统计列联表和计算评分两大步骤,但在统计列联表时先将预报和观测整体转换为0, 1形式,再通过预报和观测的与(或)运算获得0, 1形式的命中、空报、漏报和报无未出,最终通过对各项求和获得列联表。改进后的流程步骤都可以通过numpy的矩阵计算实现。以1 000 000个样本的TS评分计算为例,改进前需耗时1 s,改进后的耗时约为0.05 s,效率提升约20倍。
|
图 9 MetEva中TS评分算法流程 Fig. 9 Algorithm flow of TS score in MetEva |
空间检验方法在高分辨率预报检验中有重要的应用价值。基于Python语言,MetEva实现了MODE、SAL、Variogram、FSS和Rigider等几种常用的空间检验方法,它们都是对照Gilleland(2019)研发的R语言版本空间检验程序库中的算法逻辑来实现的。为方便用户调用及帮助用户快速了解检验中间过程和最终结果,空间检验模块也采用2.1节提到的统一数据结构,同时增加了一些辅助绘图功能(图略)。譬如,为更好地发挥空间检验方法在检测雨带位置和强度预报偏差方面的价值,MetEva为MODE等空间检验方法提供了批量检验结果的辅助分析功能。
5 应用效果以下根据业务中的实际需求,将MetEva的综合检验功能应用于2021年7—8月数值模式和精细化网格的温度和降水预报的检验评估中,以说明MetEva在精细化检验评估中的应用效果。
5.1 温度预报检验目前,我国精细化网格温度预报制作流程包括三个部分,首先是数值模式预报,其核心是中国气象局全球同化预报系统(以下简称CMA-GFS);其次为中央气象台网格预报指导报(以下简称SCMOC),是以CMA-GFS和ECMWF模式输出的2 m温度预报作为数据源的统计订正预报;最后是国省融合网格预报(以下简称SMERGE),省级气象台站将指导报和本地主观或客观预报融合,以进一步提升预报的准确率。
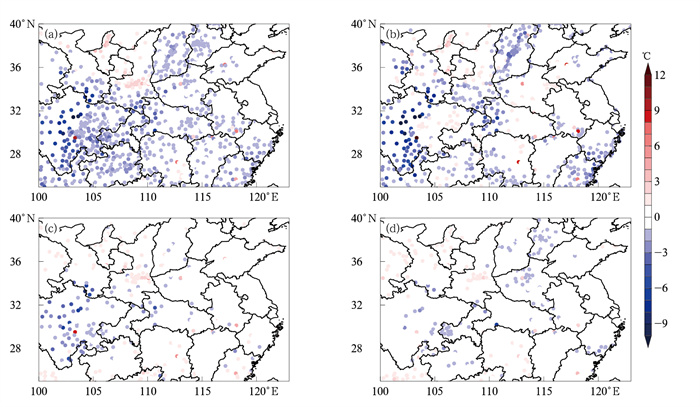
图 10显示25°~40°N、100°~123°E范围内ECMWF、CMA-GFS、SCMOC和SMERGE温度预报平均误差的空间分布,统计样本包含2021年7月24日20时至8月1日08时逐12 h起报的72 h时效内逐3 h预报。从图 10可以看出,在分析时段内CMA-GFS模式偏差幅度小于EMCWF模式,但两者具有相似的分布特征,在四川西部、山西中部、湖北西部、浙江南部和福建北部有较大的负偏差,而SCMOC对模式偏差有明显订正效果,SMERGE相对SCMOC又有进一步改善。上述示例直观展示了数值模式误差的时空特征,以及不同流程环节对预报质量的改进情况。
|
图 10 2021年7月24日20时至8月1日08时逐12 h起报的72 h时效内逐3 h温度预报平均误差的空间分布(a)ECMWF, (b)CMA-GFS, (c)SCMOC, (d)SMERGE(填色散点对应的是各站点的所有起报时间和预报时效的样本的统计结果) Fig. 10 Spatial distribution of average errors of 3 h temperature forecasts with 72 h leadtime initiated every 12 h from 20:00 BT 24 July to 08:00 BT 1 August 2021 (a) ECMWF, (b) CMA-GFS, (c) SCMOC, (d) SMERGE (Colored scatter points are correspond to statistical results of all samples of starting time and valid time at each station) |
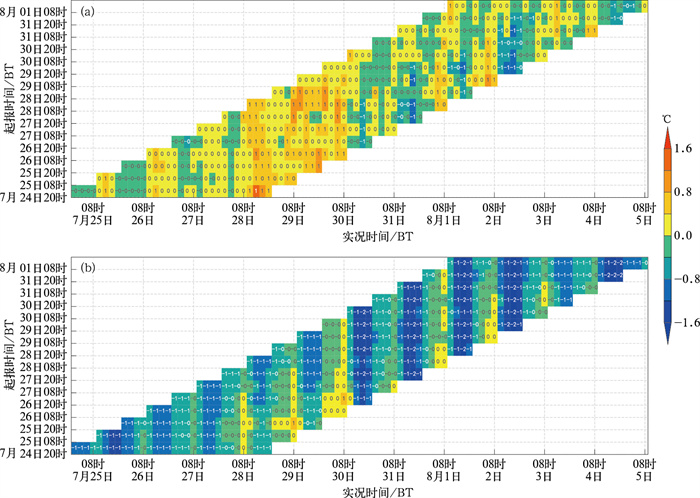
为对比SMERGE在时间维度上对系统性偏差的改进情况,图 11给出了全国范围内SMERGE温度预报的平均误差随起报时间和预报时效的变化,并和ECMWF模式的预报误差进行对比分析。图中统计样本包含2021年7月24日20时至8月1日08时逐12 h起报的96 h时效内逐3 h预报,每个填色(填值)是全国范围2411个国家站的平均误差。可以清楚地看到,ECMWF不同起报时间大部分预报时效误差都小于0℃,即预报存在系统性的负偏差;同时,预报偏差还存在明显的日变化特征,早晨时段预报偏差小幅高于0℃,下午时段预报偏差大幅低于0℃,即预报日较差小于实况;而SMERGE预报正、负偏差的样本比较均衡,且误差没有明显规律,说明SMERGE已消除了明显的系统性偏差。
|
图 11 2021年7月24日20时至8月1日08时逐12 h起报的96 h时效内逐3 h全国范围内(a)SMERGE和(b)ECMWF模式温度预报的平均误差随起报时间和预报时效的变化(实况时间:起报时间+预报时效) Fig. 11 Changes in average errors with starting time and valid time for (a) SMERGE and (b) ECMWF 3 h temperature forecasts with 96 h leadtime nationwide initiated every 12 h from 20:00 BT 24 July to 08:00 BT 1 August 2021 (observation time: starting time+valid time) |
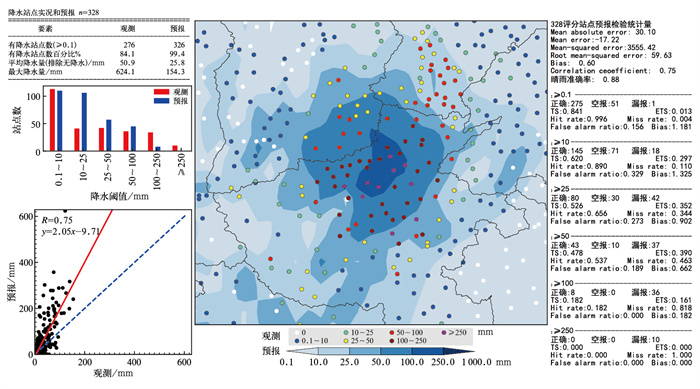
图 12是基于MetEva制作的降水综合检验图,检验的对象是CMA-GFS模式的2021年7月20日08时起报的24 h降水量预报(0~24 h时效)。其中,空间分布图显示出CMA-GFS模式暴雨预报落区和实况基本吻合,但强度明显偏弱。同样,散点回归图也显示出预报和观测之间存在线性关系,但预报值明显低于观测。此外,最大值、平均值和频率等统计图表信息定量显示了观测和预报的降水强度差异。进一步的,各等级的TS评分和漏报率等指标显示CMA-GFS模式对暴雨以下降水等级有较好的预报准确率,但在大暴雨及以上级别漏报率较大,预报技巧很低。从该示例可以看出,应用MetEva可以方便地对降水预报做出综合性的检验评估。
|
图 12 CMA-GFS模式2021年7月20日08时起报的24 h时效降水量(预报: 填色, 观测: 散点; 左侧是统计对比的表格和图形,右侧是各类检验指标构成的表格) Fig. 12 An example of comprehensive verification chart of precipitation forecast, comparison map of spatial distribution of forecast (colored) and observation (scattered point) (On the left are the table and graphs of statistical comparison, and on the right are the table composed of various verification scores) |
为推进天气预报检验向全流程和精细化方向发展,针对“从数值模式、客观方法、精细化网格预报到预报产品应用”整个天气预报产品制作流程的检验需求,研发了天气预报全流程检验评估程序库(Met-Eva)。
MetEva以检验算法的全流程覆盖和检验结果的可对比性为目标,采用基础层(基础函数库和检验算法库)和功能层(数据预处理和检验分析模块)的分层架构设计,基于统一的包含完整时空信息的数据结构,设计了统一的模块化检验计算流程。围绕检验流程中数据整理和检验分析的6个主要步骤,即数据读取、数据合并和匹配、样本选取、样本分组、检验计算和结果整合输出等,MetEva开发了相应的6类400项以上功能函数。
MetEva集成的检验算法包括二分类预报检验、多分类预报检验、连续量预报检验、概率和集合预报检验及空间检验等5类共54种,其中包含了大部分世界气象组织推荐的检验方法和国内业务规范中的检验算法。MetEva对大部分检验算法的计算流程进行了改进,并采用矩阵计算方式和并行算法来提升检验程序的计算效率。
以2021年7—8月数值模式和精细化网格的温度和降水预报的检验评估为例,对MetEva的功能和使用方法进行了简要说明,揭示了SCMOC、SMERGE对数值模式温度预报偏差的订正作用,以及CMA-GFS模式在一次强降水预报中的综合表现,展示了MetEva在精细化检验评估方面的应用价值。
目前,该程序库已开源发布,可以有效支撑全国各级气象部门开展天气预报全流程检验评估工作,并由此推动气象预报的发展。但该程序库仍存在诸多不足之处,如该程序库主要支持了要素预报的常规检验,集成的空间检验算法种类仍然较少,未来将逐步改进和完善。
附录: 相关系数检验中间量的合并算法设有一组观测数据序列(O)和与之匹配的一组预报数据序列(F)。将它们都分割为两部分:O1和F1以及O2和F2。关于O1和F1的统计量(样本数,观测均值,预报均值,观测方差,预报方差,观测和预报的协方差)记为(n1,μ1,υ1,ρ1,σ1,s1),类似的O2和F2的统计量记为(n2,μ2,υ2,ρ2,σ2,s2),则关于O和F的统计量可以用如下公式计算:
| $ n=n_1+n_2 $ | (1) |
| $ \mu=p_1 \mu_1+p_2 \mu_2 $ | (2) |
| $ v=p_1 v_1+p_2 v_2 $ | (3) |
| $ \rho=p_1\left[\rho_1+\left(p_2 \mu_1-p_2 \mu_2\right)^2\right]+p_2\left[\rho_2+\left(p_1 \mu_1-p_1 \mu_2\right)^2\right] $ | (4) |
| $ \begin{gathered} \sigma=p_1\left[\sigma_1+\left(p_2 v_1-p_2 u_2\right)^2\right]+p_2\left[\sigma_2+\left(p_1 v_1-p_1 v_2\right)^2\right] \\ s=s_1+s_2+n_1\left[\left(1-p_1\right) \mu_1-p_2 \mu_2\right]\left[\left(1-p_1\right) v_1-p_2 v_2\right]+ \end{gathered} $ | (5) |
| $ n_2\left[\left(1-p_2\right) \mu_2-p_1 \mu_1\right]\left[\left(1-p_2\right) v_2-p_1 v_1\right] $ | (6) |
式中:p1和p2是两部分数据在总数据集中的占比:
| $ p_1=n_1 /\left(n_1+n_2\right) $ | (7) |
| $ p_2=n_2 /\left(n_1+n_2\right) $ | (8) |
符凤平, 吴哲红, 高如玉, 2015. 精细化预报的自动检验与技巧评分系统[J]. 贵州气象, 39(5): 14-18. Fu F P, Wu Z H, Gao R Y, 2015. Automatic inspection and techniques scoring system for precise forecast[J]. J Guizhou Meteor, 39(5): 14-18 (in Chinese). DOI:10.3969/j.issn.1003-6598.2015.05.003
|
宫宇, 代刊, 徐珺, 等, 2018. GRAPES-GFS模式暴雨预报天气学检验特征[J]. 气象, 44(9): 1148-1159. Gong Y, Dai K, Xu J, et al, 2018. Synoptic verification characteristics of operational GRAPES-GFS model heavy rain event forecast[J]. Meteor Mon, 44(9): 1148-1159 (in Chinese).
|
金荣花, 代刊, 赵瑞霞, 等, 2019. 我国无缝隙精细化网格天气预报技术进展与挑战[J]. 气象, 45(4): 445-457. Jin R H, Dai K, Zhao R X, et al, 2019. Progress and challenge of seamless fine gridded weather forecasting technology in China[J]. Meteor Mon, 45(4): 445-457 (in Chinese).
|
金小霞, 俞剑蔚, 刘梅, 等, 2020. 基于SAL方法对一次区域性大暴雨过程多模式预报空间检验及误差分析[J]. 气象科学, 40(6): 791-801. Jin X X, Yu J W, Liu M, et al, 2020. SAL quantitative verification and error analysis for multi-model forecast of a regional heavy rain process[J]. J Meteor Sci, 40(6): 791-801 (in Chinese).
|
Jolliffe I T, Stephenson D B, 等, 2016. 预报检验——大气科学从业者指南: 第2版[M]. 北京: 气象出版社. Jolliffe I T, Stephenson D B, et al, 2016. Forecast Verification: A Practitioner's Guide in Atmospheric Science: 2nd ed[M].
Beijing: China Meteorological (in Chinese).
|
李新庆, 岳勇, 陈玉华, 等, 2016. 基于FineUI的气象预报检验评估系统构建研究[J]. 软件, 37(7): 94-98. Li X Q, Yue Y, Chen Y H, et al, 2016. The construction of meteorological forecast verification and evaluation system based on FineUI[J]. Comput Eng Softw, 37(7): 94-98 (in Chinese). DOI:10.3969/j.issn.1003-6970.2016.07.019
|
潘留杰, 张宏芳, 薛春芳, 等, 2016. 数值模式评估系统MET及其初步应用[J]. 气象科技进展, 6(4): 37-43. Pan L J, Zhang H F, Xue C F, et al, 2016. Numerical weather prediction model testing and evaluation systems MET and application[J]. Adv Meteor Sci Technol, 6(4): 37-43 (in Chinese).
|
唐健, 代刊, 宗志平, 等, 2018. 主客观融合定量降水预报方法及平台实现[J]. 气象, 44(8): 1020-1032. Tang J, Dai K, Zong Z P, et al, 2018. Methods and platform realization of the national QPF master blender[J]. Meteor Mon, 44(8): 1020-1032 (in Chinese).
|
韦青, 李伟, 彭颂, 等, 2019. 国家级天气预报检验分析系统建设与应用[J]. 应用气象学报, 30(2): 245-256. Wei Q, Li W, Peng S, et al, 2019. Development and application of national verification system in CMA[J]. J Appl Meteor Sci, 30(2): 245-256 (in Chinese).
|
杨辉, 黄思先, 鲁建军, 2014. "湖北省乡镇精细化气象要素预报订正及检验平台"研发和实施[J]. 气象水文海洋仪器, 31(4): 88-91. Yang H, Huang S X, Lu J J, 2014. Development and implementation of Hubei township refined meteorological forecast and test platform[J]. Meteor Hydrol Mar Instrum, 31(4): 88-91 (in Chinese).
|
杨阳, 王连仲, 周晓珊, 2017. 东北区域业务模式预报产品检验评估系统的建立及应用[J]. 气象与环境学报, 33(4): 21-28. Yang Y, Wang L Z, Zhou X S, 2017. Establishment and application of the verification and evaluation system of operational model forecast products in Northeast China[J]. J Meteor Environ, 33(4): 21-28 (in Chinese).
|
姚文, 陈海涛, 张晶, 等, 2010. 营口地区乡镇天气预报和实况对比检验系统[J]. 河北农业科学, 14(6): 170-172. Yao W, Chen H T, Zhang J, et al, 2010. Comparative inspection system between township weather forecast and actual data in Yingkou[J]. J Hebei Agric Sci, 14(6): 170-172 (in Chinese).
|
尤凤春, 王国荣, 郭锐, 等, 2011. MODE方法在降水预报检验中的应用分析[J]. 气象, 37(12): 1498-1503. You F C, Wang G R, Guo R, et al, 2011. The application analysis of MODE method to the rainfall forecast test[J]. Meteor Mon, 37(12): 1498-1503 (in Chinese).
|
Brown B, Atger F, Brooks H, et al, 2008. Recommendations for the verification and intercomparison of QPFs and PQPFs from operational NWP models-Revision 2 October 2008[R]. Switzerland: WMO.
|
Brown B, Jensen T, Gotway J H, et al, 2021. The model evaluation tools (MET): more than a decade of community-supported forecast verification[J]. Bull Am Meteor Soc, 102(4): E782-E807.
|
Chen H M, Yu R C, Shen Y, 2016. A new method to compare hourly rainfall between station observations and satellite products over central-eastern China[J]. J Meteor Res, 30(5): 737-757.
|
Davis C, Brown B, Bullock R, 2006a. Object-based verification of precipitation forecasts. Part Ⅰ: methodology and application to mesoscale rain areas[J]. Mon Wea Rev, 134(7): 1772-1784.
|
Davis C, Brown B, Bullock R, 2006b. Object-based verification of precipitation forecasts. Part Ⅱ: application to convective rain systems[J]. Mon Wea Rev, 134(7): 1785-1795.
|
Davis C A, Brown B G, Bullock R, et al, 2009. The method for object-based diagnostic evaluation (MODE) applied to numerical forecasts from the 2005 NSSL/SPC spring program[J]. Wea Forecasting, 24(5): 1252-1267.
|
Gilleland E, 2019. SpatialVx: Spatial forecast verification, version 0.7. R package[EB/OL]. https://cran.r-project.org/package5SpatialVx.
|
Mason I B, 1982. A model for assessment of weather forecasts[J]. Aust Meteor Mag, 30: 291-303.
|
Roberts N, Mittermaier M, 2015. A post-processing and verification strategy for the future[C]. MOSAC and SRG Meetings.
|
Wernli H, Paulat M, Hagen M, et al, 2008. SAL-A novel quality measure for the verification of quantitative precipitation forecasts[J]. Mon Wea Rev, 136(11): 4470-4487.
|
Yadav B P, Kumar N, Rathore L S, 2014. Operational weather forecast verification at India meteorological department[C]//6th International Verification Methods Workshop.
|
 2023, Vol. 49
2023, Vol. 49 
