引言

经过50年的发展，我国风云卫星已经形成了静止轨道和极轨轨道两个系列，并且静止轨道卫星在近5年实现了更新换代，搭载仪器的能力也有了全面升级(杨军等, 2011)。2018年6月5日21：07，中国风云二号H星(FY-2H)在西昌卫星发射中心成功发射，作为中国第一代静止轨道气象卫星的最后一颗，FY-2H继承了风云二号系列卫星技术成熟、运行稳定等特点。基于风云卫星的发展和实力，利用风云气象卫星遥感资料，服务“一带一路”沿线国家的重要决策。同时世界气象组织及亚太空间合作组织希望中国能将新发射的FY-2H定点位置向西布局，更广泛惠及成员国，确定将FY-2H定点位置从原定的86.5°E移至79°E，使我国静止轨道气象卫星观测范围向西扩展到4°E附近。监测范围包括亚洲50个国家、非洲41个国家、欧洲39个国家、大洋洲9个国家，“一带一路”沿线64个国家(王新等，2020)。

“一带一路”沿线区域多高山、沙漠、海洋等无人区域，气象资料匮乏，同时是影响这我国天气系统的上游，FY-2H对该区域进行观测并获取有效的气象观测数据，有助于提高影响我国的灾害天气系统的预报准确率和“一带一路”沿线国家的防灾减灾能力。其上的主要载荷为扫描辐射计(stretched visible and infrared spin scan radiometer, VISSR-2)和空间环境监测器(space environment monitor, SEM)。VISSR-2上有5个通道，其中1个可见光和4个红外通道，包括了从可见光(VIS，0.66 μm)到热红外(IR，12.0 μm)的波长范围，同时区域扫描数据的时空分辨率大大提高，其中VIS通道具有1 km和5 km两种空间分辨率数据，红外通道的空间分辨率为5 km，时间分辨率为6 min(周鑫等，2019)。相较于前序FY-2，FY-2H的图像质量有了较大提升，在轨测试结束后已投入业务运行，可以实现最快半小时一次的全圆盘观测，实现每日28次对“一带一路”地区的观测，生成针对“一带一路”地区实时可见光、红外和水汽云图、空间天气和卫星所处空间环境的精细化服务产品。考虑到水资源短缺问题也是“一带一路”沿线多数国家面临的重要问题：沿线65个国家中，33个将面临中等或极端水危机, 其中28个国家将在2040年面临极端水危机; 因此，“一带一路”大气可降水(total precipitable water，TPW)产品应用是风云气象卫星服务能力建设的相关行动方案中重要的一项工作内容。

TPW是指从地表延伸到大气顶部的单位截面垂直柱中所含水汽的总量，是表征大气中水汽含量的重要指示因子(吴琼等，2020)。水汽作为地球大气中最丰富的温室气体，表现较为活跃，其变化是天气和气候变化的主要驱动力。了解其空间分布对研究全球、区域和局地的水循环、能量收支以及气候变化都有很重要的意义(Held and Soden, 2000；Trenberth et al，2005；Wagner et al, 2006)。在卫星遥感地表参数反演中，大气订正是关键环节，而水汽是主要影响因子，所以对地表参数的准确反演有极其重要的作用(Li et al，2013；Qin et al，2001；Sobrino et al，1993)。相比其他观测资料，利用卫星数据反演的水汽数据在空间分布连续、空间范围广等方面优于无线电探空数据，具有更为广泛的应用价值。

目前，由于缺乏近红外和微波波段的观测，地球静止轨道卫星的TPW反演算法主要基于热红外数据(Cziczo et al，2013；Julien et al，2015；Schroedter-Homscheidt et al，2008；Sobrino and Romaguera, 2008; Suggs et al，1998)。在过去的几十年里，基于分裂窗通道内的水汽差分吸收这一原理，已经提出了许多热红外反演算法，主要分为线性分裂窗算法、分裂窗协方差方差比方法、物理分裂窗(physical split-window，PSW)算法和查找表方法(Dalu, 1986; Guillory et al, 1993; Labbi and Mokhnache, 2015; Ottle et al, 1997; Schroedter-Homscheidt et al, 2008; Sobrino et al, 2002)。这些算法的精度在干燥的大气条件下，易受到地表发射率不确定性、初猜场误差、仪器噪声和定标误差的影响(Barton and Prata, 1999；Knabb and Fuelberg, 1997；Hulley et al, 2012；Sun et al, 2013)。传统的PSW算法在被用于反演FY-2系列卫星的TPW产品后，闵文彬等(2015)用FY-2E VISSR在青藏高原上进行了TPW验证，在干燥月份与无线电探空水汽数据的相对误差高达780.45%，这一结果表明利用PSW反演算法所得到的干燥条件下的FY-2 VISSR TPW产品的质量亟需改善。针对此，Liu et al(2017)利用FY-2G VISSR数据，提出了一种改进的物理分裂窗反演算法，通过增加水汽通道观测值，在干燥大气条件下显著降低了由地表发射率不确定性、初猜场不确定性和观测误差所引起的水汽反演误差。Hu et al(2019)基于FY-2F VISSR通道数据，利用改进的PSW算法进行了水汽反演，研究表明这种新算法可以显著提高当前FY-2F VISSR TPW产品的质量，特别是在水汽值低于15 mm的区域。

FY-2H VISSR TPW产品的生成也使用了这种改进的PSW算法，但目前还未有学者对FY-2H VISSR TPW的质量进行评估。本文以“一带一路”区域为研究区，对FY-2H TPW的精度和稳定性两个方面进行评价，证明FY-2H在对空中水资源进行高精度实时监测的同时，也能为“一带一路”沿线国家的气象、生态等研究的数据选择提供必要的参考。为此，我们对研究区现状、检验数据、FY-2H大气可降水的产品生成进行了介绍；并主要针对卫星大气可降水产品的检验结果进行了图示和分析。

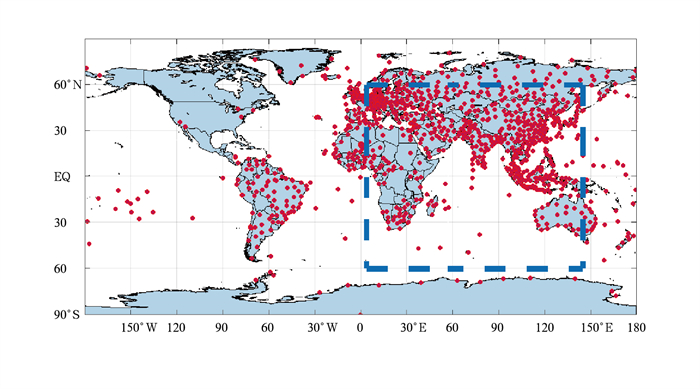
1 数据与方法 1.1 研究区检验数据介绍

“一带一路”沿线区域经纬度范围位于60°~60°N、4°~145°E，该区域多高山、沙漠、海洋等无人区域，气象资料匮乏，自然灾害严重，灾害相对损失是全球平均值的两倍以上，且以气象灾害居多。同时，水资源短缺问题也是“一带一路”沿线多数国家面临的重要问题。为验证FY-2H对该区域观测并获取的气象观测数据的准确性，考虑使用高空观测数据中的大气温度和湿度廓线计算的水汽数据，因此本文利用了Wyoming大学网站(http://weather.uwyo.edu/upperair/Sounding.html)提供的探空水汽数据。下载了全球1067个站点(站点分布如图 1所示，虚线框内区域为试验区域)在2019年整年的数据。提取数据记录中00 UTC和12 UTC整层大气水汽含量的水汽值，经过筛选，保留水汽值有效的记录，用于卫星数据的匹配检验工作。与卫星数据对比时，通过站点经纬度匹配，查找相同时间卫星数据像元反演值。

1.2 FY-2H TPW生成及介绍

FY-2H TPW产品的反演计算，采用了扫描辐射计VISSR提供的两个红外分裂窗通道(10.8 μm和12.0 μm)和一个水汽通道(6.9 μm)的观测数据，具体的算法如下。在晴朗的天空条件下，在卫星上观测到的大气层顶部的辐射可以通过下式表示：

$ \begin{array}{c} I(\lambda) = \varepsilon (\lambda){\tau _s}(\lambda)B\left({\lambda, {T_s}} \right) + \\ \int_{{p_s}}^0B\left({\lambda, {T_p}} \right)\frac{{\partial \tau (\lambda, p)}}{{\partial p}}{\rm{d}}p + \\ {[1 - \varepsilon (\lambda)]_{{\tau _s}}}(\lambda)\int_0^{{p_s}}B\left({\lambda, {T_p}} \right)\frac{{\partial \tau (\lambda, p)}}{{\partial p}}{\rm{d}}p \end{array} $

(1)

式中：I(λ)是在该波长下的光谱辐射，ε是地表发射率，τ是大气透射率，τ_s大气从表面到大气顶部的透射率，T_s是地表温度，T_p是气压p下的大气温度，B(λ, T_s)是普朗克函数。通过在该波长下设置大气上行辐射，上式可以简化为：

$ {I_\lambda } = {\tau _{\lambda, s}}{B_\lambda }\left({{T_{g\lambda }}} \right) + I_\lambda ^ \uparrow $

(2)

式中：τ_{λ, s}为大气透过率，T_gλ为该波长下的表面亮温，I_λ^↑为大气上行辐射。假设真实水汽廓线与猜测的水汽廓线具有相同的垂直结构，则可由猜测的水汽廓线乘某一尺度因子得到。

$ \gamma = \frac{{w'(p)}}{{w(p)}} = \frac{{PW'}}{{PW}} $

(3)

式中：γ为尺度因子，w(p)为初始值的水汽混合比剖面，w′(p)为真实水汽分布，PW′和PW是w′(p)和w(p)剖面的总可降水量，可以通过从地表到大气顶部的水汽廓线积分得到。在猜测中，由于传感器辐射产生了扰动，可以将比例因子和陆面温度的扰动值写为：

$ \delta {I_\lambda } = B\left({{T_{g\lambda }}} \right)\frac{{\partial {\tau _{\lambda, s}}}}{{\partial r}}\delta r + \frac{{\partial I_\lambda ^ \uparrow }}{{\partial r}}\delta r + \frac{{\partial B\left({{T_{g\lambda }}} \right)}}{{\partial {T_s}}}\delta {T_s}{\tau _{\lambda, s}} $

(4)

$ \begin{array}{c} \delta {I_\lambda } = \delta r\left[ {B\left({{T_{g\lambda }}} \right)\frac{{\partial {\tau _{\lambda, s}}}}{{\partial r}} + \frac{{\partial I_\lambda ^ \uparrow }}{{\partial r}}} \right] + \\ \delta {T_s}\left[ {\frac{{\partial B\left({{T_{g\lambda }}} \right)}}{{\partial {T_s}}}\partial {\tau _{\lambda, s}}} \right] \end{array} $

(5)

$ {C_\lambda } = B\left({{T_{g\lambda }}} \right)\frac{{\partial {\tau _{\lambda, s}}}}{{\partial r}} + \frac{{\partial I_\lambda ^ \uparrow }}{{\partial r}};\;\;\;\;\;{D_\lambda } = \frac{{\partial B\left({{T_{g\lambda }}} \right)}}{{\partial {T_s}}}\partial {\tau _{\lambda, s}} $

(6)

将式(6)中的C_λ, D_λ代入式(4)和式(5)，则可以得到一个关于δT_s, δλ的线性方程。通过将线性方程应用于两个或两个以上的通道中，可以得到δT_s和δλ的解：

$ \left\{ {\begin{array}{*{20}{l}} {\delta {I_{\lambda 1}} = \delta r{C_{\lambda 1}} + \delta {T_s}{D_{\lambda 1}}}\\ {\delta {I_{\lambda 2}} = \delta r{C_{\lambda 2}} + \delta {T_s}{D_{\lambda 2}}}\\ \cdots \\ {\delta {I_{\lambda n}} = \delta r{C_{\lambda n}} + \delta {T_s}{D_{\lambda n}}} \end{array}} \right\} $

(7)

利用辐射传输模型的先验信息可以计算出系数C和D，一般将初始场的尺度因子γ设置为1，通过求解式(7)方程组得到δT_s和δλ，反演的PWV就等于PW×(1+δγ)。

利用上述反演方法，FY-2H VISSR提供了观测区域内空间分辨率为5 km，时间分辨率为3 h的标称格式晴空大气可降水产品，该产品给出了晴空无云条件下的白天和夜晚，海洋和陆地上空水汽值。

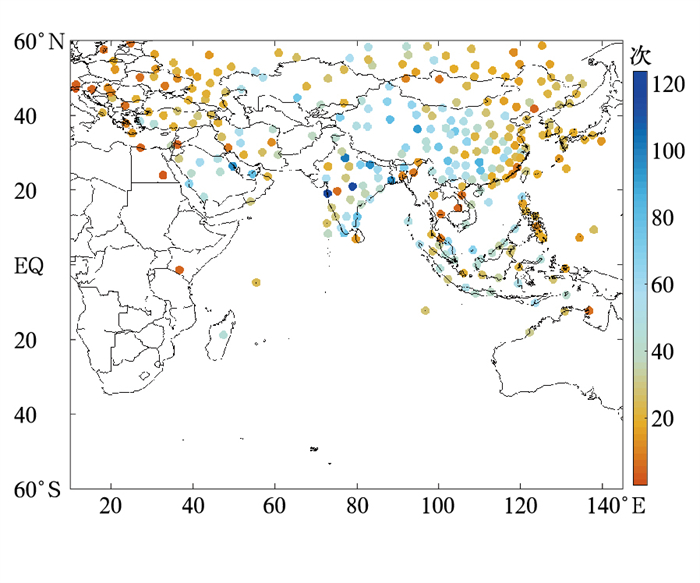
2 检验结果 2.1 产品精度检验

选取2019年1、4、7、10月4个月的每月前7天的数据来进行产品的精度检验，在验证时间段内，提取每日00 UTC和12 UTC两个时次的探空数据，对每一条探空记录，分别遍历与探空时间相同的FY-2H VISSR TPW。根据卫星数据的经纬度信息，通过查找与探空站点经纬度距离最小的像元，匹配到此探空记录对应的FY-2H TPW。图 2显示了风云卫星数据与探空数据匹配到的探空站点分布，散点的颜色表示该站点匹配到的记录次数。

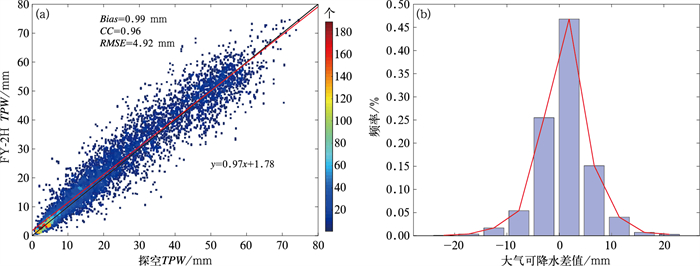
卫星数据与探空数据匹配结果统计如表 1所示，全天时段记录了两个时刻所有的数据，相对偏差(Bias)为0.99 mm，均方根误差(RMSE)为4.92 mm，与探空数据的相关系数(CC)达到0.96。图 3为FY-2H TPW与探空数据匹配的散点密度和误差分布直方图，色标代表该区域数据的密度。不难发现，散点相对y=x线的分布比较均匀，整体来看在水汽较低时FY-2H TPW的值要高于探空水汽值，从误差直方图的正负频率来看，正误差的频率要高于负误差的频率，这与散点密度所呈现出来的趋势相一致。

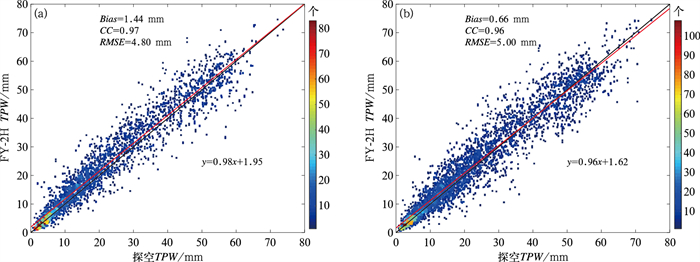
另外，为研究白天与夜间FY-2H TPW的差异性，将00 UTC认定为夜间数据，12 UTC为日间数据，分别进行了匹配统计。从匹配的结果来看，日间时段记录到的有效样本数比夜间时段记录到的有效样本数少了近两千个，但日间时段的FY-2H TPW与探空数据的相关系数和均方根误差与夜间时段相差不大，因此两个时段都具有较高的精度。

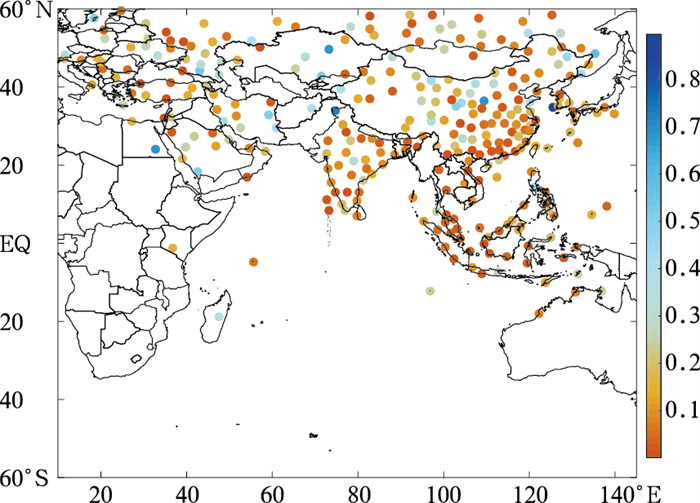
为了评价精度是否受站点的分布影响，将匹配到的数据按照站点经纬度进行划分，根据式(8)计算每个匹配到的站点的相对误差的平均值(RE)：

$ RE = \frac{1}{N}\sum\limits_{i = 1}^N {\left({\left| {\frac{{TP{W_{{\rm{sat }}}} - TP{W_{{\rm{raob }}}}}}{{TP{W_{{\rm{raob }}}}}}} \right|} \right)} $

(8)

式中: N表示该区间内统计到的个数，TPW_sat表示FY-2H反演水汽值，TPW_raob表示无线电探空值。首先计算各个站点的绝对相对误差, 根据统计到的各站点重复匹配的点数计算得到平均相对误差，计算结果如图 5所示。图中指出了相对误差的分布情况，点的颜色代表了FY-2H TPW平均相对误差的大小。总体来看，FY-2H TPW在整个区域内的相对误差分布均匀，无论是在高水汽区域还是低水汽区域，相对误差大体都在0.3以下，说明FY-2H TPW反演时受背景场差异的影响较小。

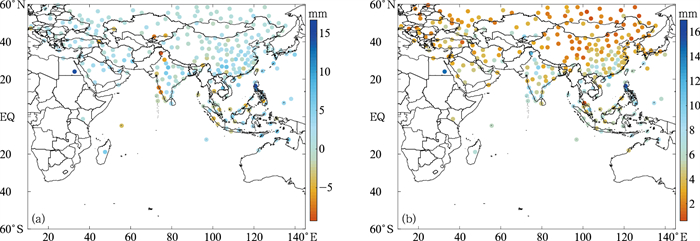
根据匹配到的站点，将匹配得到的结果进行了统计处理，得到了FY-2H TPW与探空数据对比误差的空间分布(图 6)。图 6a指出了匹配的平均偏差分布，从图中能够看到在大部分试验区内的偏差基本在±4 mm以内，整体偏差较小。图 6b指出了匹配的均方根误差分布，表明均方根误差可能与水汽含量的大小有关。在高于30°N的区域，RMSE大多小于5 mm，20°S~30°N的区域内，RMSE值变动较大。结合两图，以印度和东南亚各国为例，发现在海岸线附近误差的值普遍较大，推测可能是由于海陆交界区域的水汽变化大有关。

2.2 产品稳定性评价

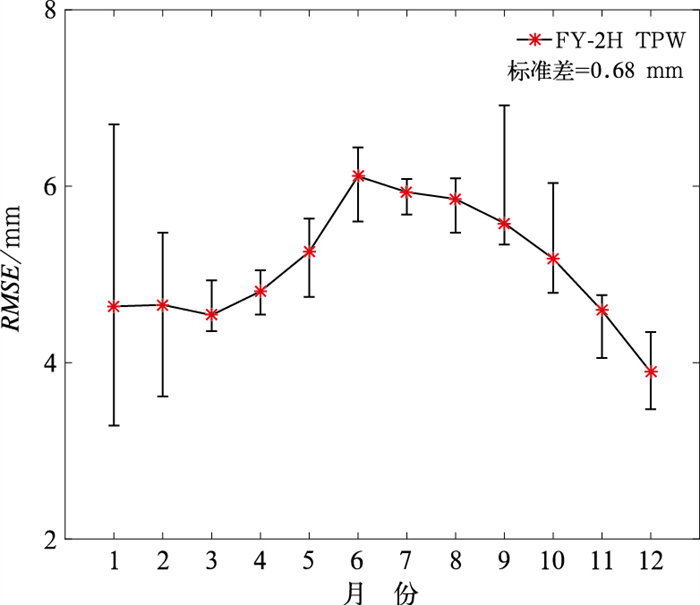
利用2019年全年的探空数据进行产品的稳定性评价，将每日的探空数据与FY-2H TPW进行匹配，计算日均方根误差，以此求得月平均RMSE及每月RMSE的最大、最小值，从而绘制得到图 7均方根误差时间序列。图 7显示了12个月FY-2H TPW均方根误差的时间分布。误差棒的中间点代表每个月的月平均RMSE值，上下边界代表该月RMSE的最大、最小值。结合图分析，月平均均方根误差值所连成的折线随月份的增大先增后减，变化幅度在±2 mm之内，同时折线的变化趋势表现出一定的季节波动性。在6—8月要高于别的月份，6月最高，超过了6 mm，其他月份均低于6 mm。而从误差棒上下界之间的跨度来看，除了1月的RMSE最大、最小值差值超过了2.5 mm外，其他月份均在1.5 mm之内，这体现了各月份的FY-2H TPW与探空数据的一致性较好，误差在可控范围内且波动不大。研究能够反映FY-2H水汽产品在2019年内具有较好的稳定性。

2.3 产品时空特征分析

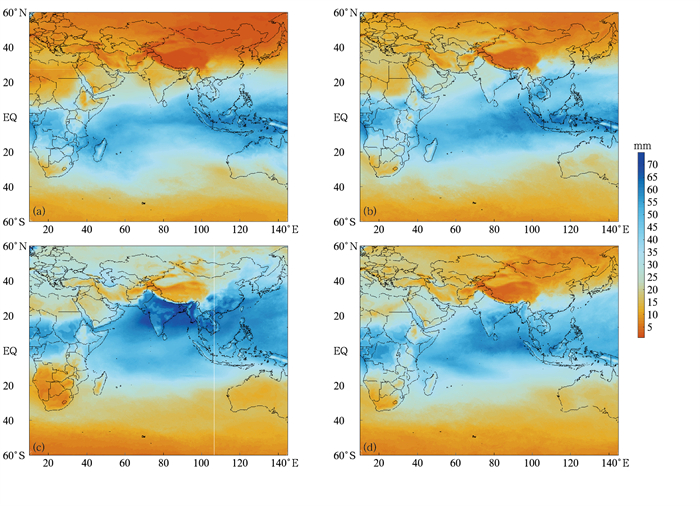
FY-2H观测数据为每3 h记录一次，每日得到8个观测数据文件，经过处理得到日平均数据，将一个月内所有日数据平均可得到月平均数据。研究合成处理了2019年1、4、7、10月4个月的FY-2H大气可降水数据，在FY-2H观测覆盖区域内月平均大气可降水空间分布如图 8所示，图中色标代表了水汽含量的大小。

从空间分布上看，卫星月平均水汽分布整体都是呈两极到赤道水汽含量逐渐递增的趋势，符合水汽在高纬度地区低于低纬度地区的特点。20°S~20°N的区域靠近赤道，为高水汽地区，常年受到赤道低压带的控制，因此常年多雨，平均水汽偏大。在南北回归线附近区域，陆地东岸区域可降水要多于陆地西岸区域。在中纬度地区的可降水分布情况为沿海区域大于内陆区域。

从时间分布上看，平均水汽的分布具有一定的季节性规律。在观测范围内，7月的平均水汽要远高于其他3个月，尤为明显地体现在陆地上空的分布情况，这主要是北半球在7月处于夏季，降水多所引起的。观察图 8我们发现，非洲南部区域似乎不符合这种季节性规律。分析原因，在非洲南部区域，在1月的平均水汽要高于7月的平均水汽，该区域地处副热带高压带和西风带，受两者的影响，所以会在夏季炎热干燥、冬季温和多雨；而在青藏高原区域的大气可降水量分布，整体水汽值偏低，夏季水汽含量最高，但终年保持偏低状况。这是由于海拔过高，空气稀薄，加之印度洋板块与亚欧板块相互挤压而隆起的喜马拉雅山脉阻挡了来自于印度洋的水汽，造成了青藏高原区域终年水汽偏低。

为验证FY-2H TPW能否正确反映区域降水的空间分布特点，本研究将2019年1、4、7月和10月等4个月的探空水汽资料做了进一步处理，得到探空水汽数据在“一带一路”区域的水汽分布散点，结果如图 9所示，散点颜色代表了水汽含量的大小。

对比图 8和图 9，FY-2H TPW比探空水汽的连续性更好，在大致变化趋势上两者具有较高的契合度。在个别变化明显的区域，例如青藏高原区和非洲南部，探空水汽与FY-2H水汽的分布相似度很高。这也验证了在个别特殊区域下，FY-2H TPW产品依然能够提供准确的数据，相较探空水汽具备更广泛的使用能力。由此可见FY-2H反演得到的TPW产品经过合成处理，可以发展为区域时间尺度更长的水汽产品，这也丰富了“一带一路”沿线区域内的气候变化等研究中的数据选择。同时，在大区域中，高时效性、高连续性的水汽数据能够为数据同化和数值预报提供良好的初始数据。

3 结论

本文在介绍了FY-2H卫星及水汽产品生成和算法的基础上，利用了Wyoming大学网站提供的探空水汽数据评价了FY-2H VISSR TPW的精度和稳定性两个方面的质量。

首先利用2019年1、4、7月和10月每月前7天的水汽数据进行了时空匹配，并分别针对全天时段、日间和夜间三个时段进行了分别统计，整体来说三个时段都具有较高精度，与探空数据匹配的全天时段的相关系数分别达到0.96、0.97、0.96。

对比误差的空间分布，FY-2H TPW的平均相对误差分布均匀，且误差大多小于0.3，说明该产品的误差受地表类型的不同影响较小；在匹配区域内平均偏差普遍较小，而均方根误差的大小可能与水汽含量的高低有关，水汽高的区域RMSE要大于水汽低的区域。但两者在海岸线附近的误差较陆地区域变化都较为明显，可能与海陆交界处的水汽变化波动大有关。

利用2019年12个月的探空数据和FY-2H TPW产品数据对比，分析了这12个月内的产品误差和月均方根误差的时间序列。结果显示误差值在不同月份均会有所波动，6—8月高于其他月份，12个月的月均方根误差的标准差为0.68 mm，在2019年中FY-2H TPW数据波动较小，稳定性较优。

通过合成月平均水汽数据，FY-2H VISSR TPW较为准确地反映了大区域水汽分布的特点。利用探空站点的月平均水汽合成，验证了在观测区域及特殊地区，FY-2H TPW产品仍然能够提供可靠观测数据。

FY-2H VISSR TPW产品精度除受自身算法的影响，还受限于定标精度、地表发射率精度、光学传感器精度、云检测精度等多方面因素的影响。单从检验的结果来看，经过前7颗实验星数据产品的基础上发展和测试，FY-2H VISSR TPW产品精度较高，且质量稳定，具备天气和气候等方面的广泛应用能力，可以为“一带一路”沿线国家和地区提供高精度高频次区域观测的大气可降水数据。