引言

台风带来的狂风暴雨、洪涝、城市积涝等气象灾害和泥石流、山体滑坡等次生灾害严重威胁着人民的生命和财产安全。台风路径和强度预报的准确性直接影响到台风的总体预报效果，是台风预报中最受关注的预报内容，也是难点问题(陈联寿等，2012；张定媛等，2018)。台风数值预报技术是提高台风预报水平的一个有效途径(马雷鸣，2014；端义宏等，2020)，而初始场的准确性是提升数值预报性能的一个关键所在(Lorenz, 1965；2004)。能否在初始场中合理描述台风所处的大气环流背景，并且较为准确地描述出台风的结构(这一过程被称为台风涡旋初始化)，对台风路径和强度预报都显得尤为重要(Hendricks et al, 2013)。

数值模式初始化(包括资料同化、台风涡旋初始化)是基于观测和背景场资料通过动力和热力约束形成数值模式初始场的过程。由于台风生命史中绝大部分时间处于海上，而洋面上缺乏观测资料，普通的资料同化对台风涡旋的改进有限。早期的研究直接剔除模式背景场中的初始涡旋，加入人造台风涡旋(简称bogus)实现台风初始化(Kurihara et al, 1990; Lord, 1991; 王国民等，1996)。Kurihara et al(1993; 1995)利用滤波方法将台风背景场分解为环境场、对称涡旋场和非对称涡旋场，利用bogus技术对对称涡旋场进行替换，最后合成新的初始场。针对上述方法存在台风初始条件和模式的物理过程以及动力学不平衡的问题，Zou and Xiao(2000)提出了BDA(bogus data assimilation)方案，把四维变分同化与bogus相结合，有效改进了初始台风结构。黄燕燕等(2010)验证了BDA方案可以更好地预报台风海棠的路径和中心强度变化。此外，涡旋重定位技术在近些年得到了发展并在GFS预报系统中进行了应用(Kurihara et al, 1995; Liu et al, 2006)。涡旋重定位技术将模式预报的涡旋移动到观测的位置而不是植入一个人造涡旋，该方法减小了初始场与模式不协调的问题(Hsiao et al, 2010)。瞿安祥等(2009a; 2009b)利用模式自身产生的台风涡旋，通过重定位和强度调整发展了一套完整可行的台风初始化数值方案，该方案更多的是依靠数值模式自身的动力和物理过程来协调约束产生三维空间的涡旋结构，预报效果较好。但这些研究或基于bogus涡旋及其衍生技术，或基于模式自身预报的涡旋，业务上实现的技术难度较大。

浙江是我国受台风灾害影响较大的省份之一，提升台风数值预报精细化水平是浙江现代气象业务面临的迫切任务。目前浙江业务运行的浙江省中尺度数值预报业务系统(ZJWARMS)使用GFS模式预报产品作为初始场和背景场，在台风影响期间提供0~72 h的逐小时路径和强度预报(陈锋等，2012)。实际应用表明，ZJWARMS由于缺乏有效的台风初始化方案，对台风路径和强度预报存在较大的误差。陈国民等(2018; 2019)对2016年和2017年台风业务预报评估发现，美国GFS全球预报系统对台风路径的预报总体不如欧洲中期天气预报中心ECMWF模式，但在强度预报上优于ECMWF模式。针对模式资料各有优势的情形，Wang and Yang(2008)融合了NECP/DOE R2和ERA40两种再分析资料作为侧边界条件驱动WRF模式，对减小模式不确定性有较大的作用。受此类工作启发，结合前述台风涡旋初始化技术的进展，充分利用不同模式资料(如GFS模式和ECMWF模式)各自优势、吸收有限的观测资料，尝试从基于全球模式评估结果的角度开展台风初始场重建技术研究，通过为中尺度数值天气预报模式提供更优的台风初始场来提升其预报性能是值得探索的一个可行的途径。

综上所述，本文从实际应用需求出发，基于GFS和ECMWF两个全球模式台风预报优势，结合台风观测资料，利用台风涡旋分离、涡旋重定位以及最大风速调整等方法研制台风初始场重建技术，试图改进浙江省中尺度数值预报系统台风预报性能，为精细化台风数值预报提供科技支撑。

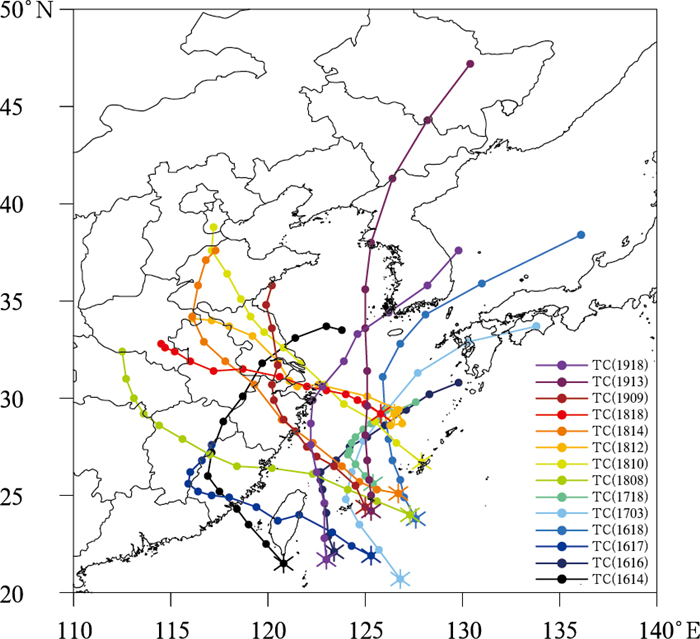
1 全球模式对影响浙江台风路径和强度的预报评估

本文选取2016—2019年期间14个影响浙江的台风个例(1614莫兰蒂、1616马勒卡、1617鲇鱼、1618暹芭、1703南玛都、1718泰利、1808玛莉亚、1810安比、1812云雀、1814摩羯、1818温比亚、1909利奇马、1913玲玲、1918米娜)，并收集中国气象局下发的全球数值预报模式ECMWF和GFS对上述台风的0~72 h预报数据。ECMWF模式在每日00时和12时(世界时，下同)起报，产品垂直层数为19层，空间分辨率为0.125°×0.125°，时间分辨率为3 h。GFS模式起报时间和产品时间分辨率与ECMWF模式相同，但其垂直层数为34层，空间分辨率为0.5°×0. 5°。结合台风影响浙江时段，提前24~36 h，选定14个台风个例的模式起报时间，将模式起报时间开始的0~72 h作为研究时段。图 1是研究时段内的逐6 h台风路径实况，台风强度实况见表 1，数据来源于中国气象局热带气旋最佳路径数据集(Ying et al, 2014)，该数据集提供了台风强度标记、纬度、经度、中心最低气压、2分钟平均近中心最大风速。

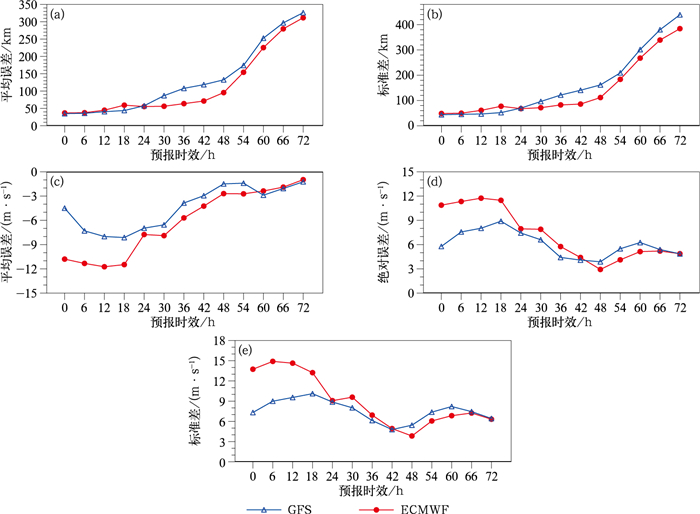
选用中心最低海平面气压进行数值预报台风的定位，使用近中心最大风速进行定强，对全球模式ECMWF、GFS开展上述14个台风个例的路径和强度预报性能评估。从路径上来看，对比近4年影响浙江台风的逐6 h预报累积误差，有64.3%(9个)的个例，ECMWF模式预报的台风路径优于GFS模式；有28.6%(4个)的个例，ECMWF与GFS模式预报的台风路径相当；仅有7.1%(1个)的个例，GFS模式预报的台风路径优于ECMWF模式。图 2给出了两个模式0~72 h台风路径和强度预报的误差分析，标准差的大小反映了模式预报误差的离散度。由图 2a可知，两个模式的路径预报误差均随着预报时效的延长而增大，尤其是在48 h以后，误差明显加大。两个模式对0~24 h以内的台风路径预报较好，平均误差均在50 km左右，而对24~72 h的台风路径预报，ECMWF模式要明显优于GFS模式，平均误差值分别为157 km和187 km。图 2b显示ECMWF模式预报误差的标准差在24~72 h期间明显低于GFS模式，说明ECMWF模式的预报误差比GFS模式更为稳定(离散度更小)。从强度的逐6 h预报累计绝对误差来看，14个台风个例中有64.3%(9个)的个例，GFS模式预报的台风强度优于ECMWF模式；有7.1%(1个)的个例，GFS与ECMWF模式预报的台风强度相当；仅有28.6%(4个)的个例，ECMWF模式预报的台风强度优于GFS模式。由图 2c可知，GFS和ECMWF模式对台风强度预报均存在低估，0~72 h平均误差分别为-4.4 m·s^-1和-6.3 m·s^-1，结合平均绝对误差(图 2d)可知，GFS模式对0~42 h的台风强度预报要明显优于ECMWF模式。图 2e表明GFS模式0~42 h的强度预报离散度较ECMWF模式明显偏低，预报更稳定。

综上所述，ECMWF模式对影响浙江台风的路径预报总体优于GFS模式，其原因可能和ECMWF模式对500 hPa高度场的形势预报具有较高的预报准确率，且对副热带高压系统南侧的引导气流刻画较准有关(关月，2016；任宏昌，2017)。GFS模式进行了台风初始化处理(Liu et al, 2006)，ECMWF模式未做相关处理，因此GFS模式对台风强度预报把握更好，但仍存在初始强度估计偏低的问题。

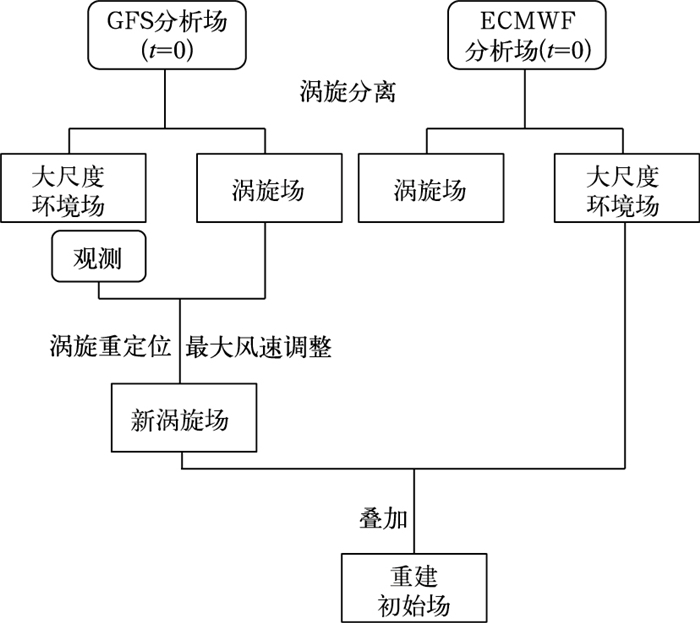
2 重建方案与试验设计 2.1 台风初始场重建方案

根据全球模式的评估结果，制定台风初始场重建方案，主要思路为：充分发挥ECMWF模式对大尺度环境场和GFS模式对台风涡旋场刻画的优势，利用涡旋分离技术，将从GFS分析场中分离得到的涡旋场经过重定位和最大风速调整后，与从ECMWF分析场中分离得到的大尺度环境场重新叠加融合，重建一个强度、位置均和实况比较接近的新的台风初始场(具体流程如图 3所示)。

2.1.1 涡旋分离及重定位技术

本文采用Kurihara et al(1995)提出的涡旋分离技术，表征如下

$H' = {H_{\rm{E}}} + H{' _{\rm{V}}} = H - {H_{\rm{V}}} + H{' _{\rm{V}}}$

(1)

式中：H′为重定位以后的模式背景场，H为模式预报的背景场，H_E为大尺度环境场，H_V为涡旋场，H′_V为重定位后的涡旋场。

相应计算过程简述如下：

(1) 确定台风涡旋环流范围。首先，利用850 hPa位势高度场确定台风中心位置，并在极坐标下计算得到切向平均风速；其次，自台风中心开始随着半径增长，取切向平均风速在减弱过程中第一次小于等于3 m·s^-1时对应的半径(Kurihara et al, 1995)，即为台风尺度半径r₀，从而确定台风涡旋环流范围。

(2) 利用变化平滑系数的3点平滑算子将背景场H分离为基本场和扰动场，平滑系数为

$a = \frac{1}{2}{(1 - \cos \frac{{2{\rm{ \mathsf{ π} }}}}{m})^{ - 1}}$

(2)

式中：取m=2, 3, 4, 2, 5, 6, 7, 2, 8, 9, 2，先沿纬向再沿经向做滤波，得到扰动场H_D。

(3) 对扰动场H_D做柱形滤波分离出涡旋环流，公式如下

${H_{\rm{V}}}\left({r, \theta } \right) = \left[ {1 - E\left(r \right)} \right][{H_{\rm{D}}}\left({r, \theta } \right) - \overline {{H_{\rm{D}}}({r_0})} ]$

(3)

式中：$ \overline {{H_{\rm{D}}}({r_0})} $是H_D在台风尺度半径r₀处的角度平均，柱形滤波函数E(r)由式(4)计算而得。

$E\left(r \right) = \frac{{\exp [ - {{({r_0} - r)}^2}/{l^2}] - \exp [ - r_0^2/{l^2}]}}{{1 - \exp [ - r_0^2/{l^2}]}}$

(4)

式中：r为距离涡旋中心的半径，l为控制E(r)形状的参数，本文取l=r₀/5。

(4) 进一步计算得到大尺度环境场H_E

${H_{\rm{E}}} = H - {H_{\rm{V}}}$

(5)

将得到的涡旋环流场H_V的环流中心平移移动到观测的台风中心位置，得到重定位后的涡旋环流H′_V，然后与大尺度环境场H_E进行叠加，得到新的台风初始场H′。

2.1.2 最大风速调整技术

根据徐道生等(2019)提出的最大风速调整技术方案，得到式(6)，重新定位以后的背景水平风场可写成

$\left\{ {\begin{array}{*{20}{l}} {u' = {u_{\rm{E}}} + u{' _{\rm{V}}}}\\ {v' = {v_{\rm{E}}} + v{' _{\rm{V}}}} \end{array}} \right.$

(6)

式中：u′和v′是重定位后的背景场H′的水平风场，u_E和v_E是大尺度环境场H_E的水平风场，u_V′和v′_V是重定位后的涡旋环流H′_V的水平风场。

通过对涡旋分量乘以系数β实现最大风速调整

$\left\{ {\begin{array}{*{20}{l}} {u{' _c} = {u_{\rm{E}}} + \beta {\rm{ }}u{' _{\rm{V}}}}\\ {v{' _c} = {v_{\rm{E}}} + \beta {\rm{ }}v{' _{\rm{V}}}} \end{array}} \right.$

(7)

式中：u′_c和v′_c分别为经过最大风速调整后的风场分量，调整以后的最大风速等于观测风速V_obs

$\begin{array}{*{20}{l}} {u{' _{c, {r_0}}}^2 + v{' _{c, {r_0}}}^2 = {{\left({{u_{\rm{E}}} + \beta {\rm{ }}u{' _{\rm{V}}}} \right)}^2} + {{\left({{v_{\rm{E}}} + \beta v{' _{\rm{V}}}} \right)}^2}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {V_{{\rm{obs}}}}} \end{array}$

(8)

式中：u′_{c, r0}和v′_{c, r0}是最大风速所在点的水平风场分量，根据式(9)计算得到β

$\beta = \frac{{ - ({u_{\rm{E}}}u{' _{\rm{V}}} + {v_{\rm{E}}}v{' _{\rm{V}}}) + \sqrt {{{({u_{\rm{E}}}u{' _{\rm{V}}} + {v_{\rm{E}}}v{' _{\rm{V}}})}^2} - (u{' _{\rm{V}}}^2 + v{' _{\rm{V}}}^2)({u_{\rm{E}}}^2 + {v_{\rm{E}}}^2 - {V_{{\rm{obs}}}}^2)} {\rm{ }}}}{{(u{' _{\rm{V}}}^2 + v{' _{\rm{V}}}^2)}}$

(9)

值得注意的是，这里计算的是地面层的β，在实际应用时，需要对其乘以一个权重系数使得低层的风速做较大订正，而高层较小。

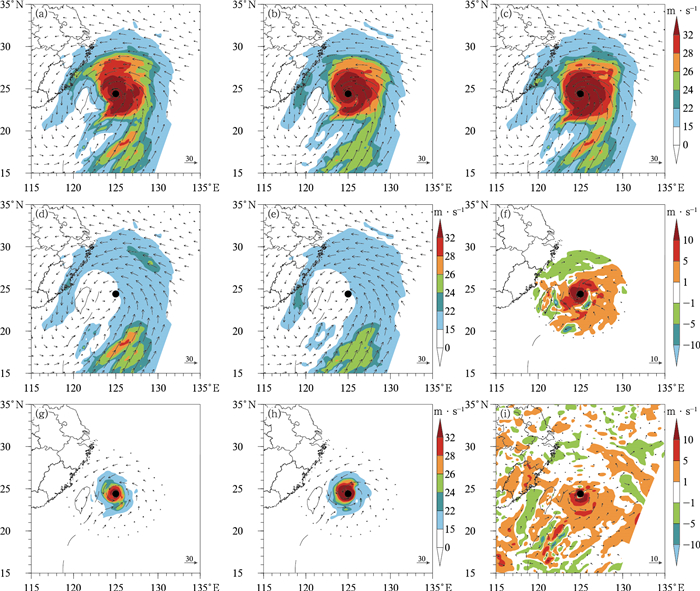
2.1.3 台风初始场重建

以1909号超强台风利奇马为例，进行初始场重建。图 4a和4b分别为2019年8月8日12时ECMWF和GFS分析场的850 hPa全风场，经过涡旋分离，得到大尺度环境场(图 4d，4e)和涡旋场(图 4g，4h)，由图可知，两个模式的大尺度环境场在台风中心附近主要为南风和东南风，而在涡旋场展示出了完整的气旋式环流，可见中心附近的气旋式环流均被较好地分离出来，这表明采用上述涡旋分离技术是可行的。进一步对比得到，ECMWF分析场分离得到的大尺度环境场其南侧的西南风和北侧的偏东风气流较GFS更为强盛，而GFS分析场分离得到的涡旋场表征的台风中心附近环流风速较ECMWF偏强。根据观测得到的台风中心位置(24.4°N、125°E)和近中心最大风速(62 m·s^-1)，将GFS分析场分离得到的涡旋场进行重定位和最大风速调整，然后叠加到ECMWF分析场分离得到的大尺度环境场，即得到重建初始场(图 4c)。由重建初始场与全球模式全风场差值分布(图 4f，4i)可知，经过最大风速调整后的重建初始场对台风中心附近的气旋式环流明显强于ECMWF分析场，略强于GFS分析场。同时，重建初始场对大尺度环流场较GFS分析场有所调整。基于上述方法，对本文研究的14个台风均进行了初始场重建。

2.2 模式介绍和试验设计 2.2.1 模式介绍

浙江省中尺度数值预报业务系统框架(ZJWARMS)采用WRF 3.7.1为预报模式，选用单层嵌套，区域大致范围为10°~55°N、80°~130°E，水平分辨率为9 km，垂直层数为51层。模式使用的物理过程包括：微物理方案采用WSM 6-Class方案(Hong et al, 2004)，陆面过程使用Noah方案(Chen and Dudhia, 2001)，行星边界层采用Yonsei University(YSU)参数化方案(Hong and Pan, 1996)，表面层使用基于Monin-Obukhov的MM5相似理论(Jiménez et al, 2012)，长波、短波辐射选用RRTMG快速辐射传输方案(Iacono et al, 2008)，不采用积云参数化方案。

2.2.2 试验设计

为了探讨台风初始场重建对路径、强度预报的影响，对本文研究的14个台风，开展如下三组回报试验：(1)TESTEC：利用ECMWF模式预报数据提供初、边界条件，驱动ZJWARMS；(2)TESTGFS：利用GFS模式预报数据提供初、边界条件，驱动ZJWARMS；(3)TESTCOM：利用重建的14个台风初始场，结合ECMWF模式预报场作为边界条件，驱动ZJWARMS。

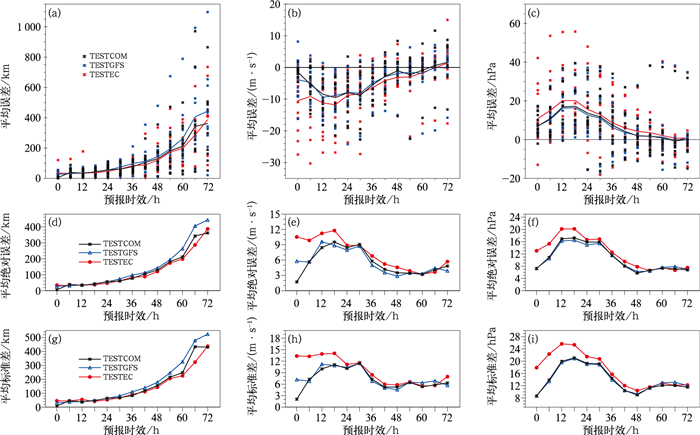
3 结果分析 3.1 台风初始场重建对路径、强度的影响

选用海平面最低气压进行数值预报台风的定位，选用中心最低海平面气压和近中心最大风速分别进行定强，对三组试验开展台风路径和强度预报的检验评估。从路径上来看，对比近4年14个影响浙江台风的逐6 h预报累计误差，有64.3%(9个)的个例，TESTCOM试验预报的台风路径优于TESTGFS试验，另有57.1%(8个)的个例，TESTCOM试验优于TESTEC试验。图 5给出了三组试验对14个台风0~72 h路径和强度预报的误差散点分布及平均误差分析。由图 5a、5d和5g可知，经过涡旋重定位后，TESTCOM试验在初始时刻的台风中心位置基本和实况一致，在24 h以后TESTCOM试验的路径预报较TESTGFS试验的优势开始体现，尤其是在第60~72小时的预报明显占优，平均误差减少65.3 km，标准差降低72.5 km。三组试验(TESTEC、TESTGFS和TESTCOM)所有预报时刻平均的路径误差分别为122、148和127 km，标准差分别为141.9、177.1和150.5 km。可见，TESTCOM试验预报路径平均误差较TESTGFS试验减少21 km，平均标准差较TESTGFS试验降低26.6 km。14个台风个例的误差散点分布进一步表明(图 5a)，对TESTGFS试验路径预报误差较大的台风个例，TESTCOM试验得到有效改进。从强度预报累计绝对误差来看，有78.6%(11个)的个例，TESTCOM试验预报的近中心最大风速较TESTEC试验有改进，另有50%(7个)的个例，TESTCOM试验较TESTGFS试验有改进；有64.3% (9个)的个例，TESTCOM试验预报的中心最低海平面气压累计绝对误差小于TESTEC试验，另有50%(7个)的个例，TESTCOM试验小于TESTGFS试验。由图 5b、5e和5h可知，经过最大风速调整后，TESTCOM试验初始时刻的近中心最大风速误差接近于0。除个别时刻外，TESTCOM试验的平均误差、绝对误差和误差离散度均明显小于TESTEC试验，尤其在第0~18小时的台风强度预报，TESTCOM试验绝对误差改进4 m·s^-1以上，标准差改进6 m·s^-1以上。进一步计算得到，所有预报时刻平均的TESTEC、TESTGFS和TESTCOM试验预报近中心最大风速平均绝对误差分别为7.2、5.6和5.5 m·s^-1，平均标准差分别为9.5、7.7和7.2 m·s^-1。可见，TESTCOM试验预报近中心最大风速平均绝对误差较TESTEC试验减少1.7 m·s^-1，平均标准差较TESTEC试验降低2.3 m·s^-1。从中心最低海平面气压来看(图 5c、5f和5i)，TES- TCOM试验0~72 h预报较TESTEC试验更接近实况，预报更稳定。平均来看，TESTEC、TESTGFS和TESTCOM试验预报最低气压平均绝对误差分别为12.3、10.5和10.6 hPa，平均标准差分别为16.9、14.1和14.1 hPa。计算得到，TESTCOM试验预报中心最低海平面气压平均绝对误差较TESTEC试验减少1.7 hPa，平均标准差较TESTEC试验降低2.8 hPa。14个台风个例的误差散点分布进一步表明(图 5b和5c)，对TESTEC试验强度预报误差较大的台风个例，TESTCOM试验得到有效改进。

上述结果表明，经过初始场重建的TESTCOM试验的台风路径预报能力与TESTEC试验相当，较TESTGFS试验有了较大改进；TESTCOM试验的强度预报能力与TESTGFS试验相当，较TESTEC试验有明显优势。可见，重建台风初始场后的模式预报结果兼顾了ECMWF模式的路径预报优势以及GFS模式的强度预报优势，有效改进了台风的路径和强度预报，本文提出的初始场重建方案可投入实际业务使用。

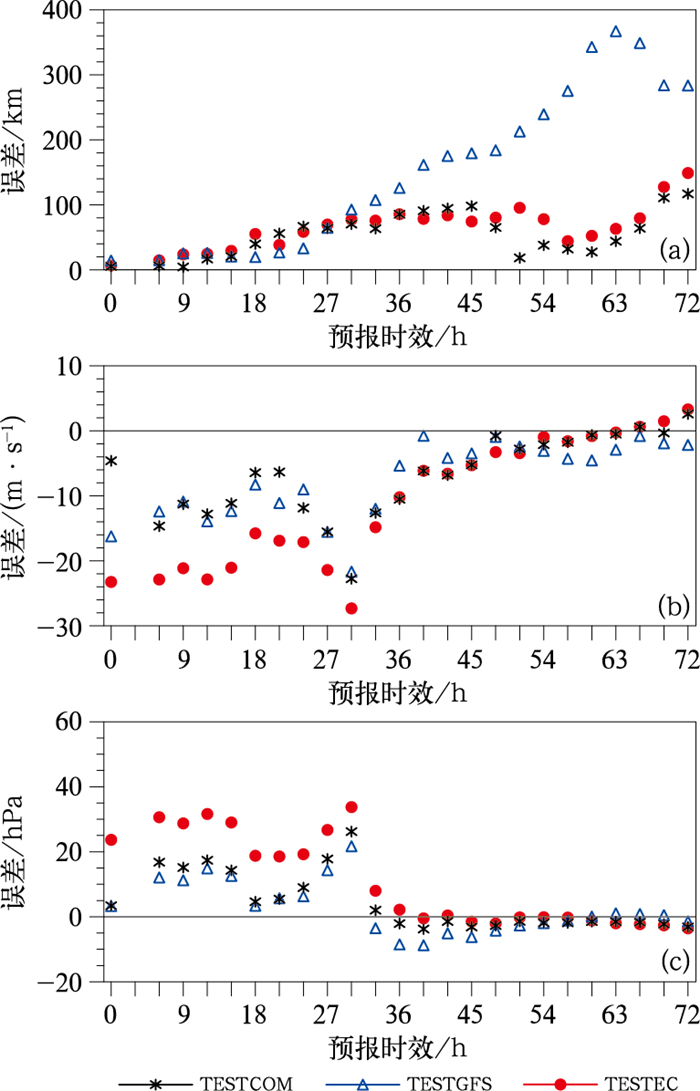
3.2 台风利奇马个例分析

继续以台风利奇马2019年8月8日12时起报的三组试验结果为例，进一步探讨不同初始化方案对台风预报的影响。从路径误差来看(图 6a)，经过初始场重建的模式预报路径与实况最为接近，尤其是对48~72 h的预报结果，TESTCOM试验改进最为显著，平均预报误差较TESTGFS试验降低200 km以上。由强度误差可知(图 6b和6c)，TESTCOM试验较TESTEC试验占优，尤其对0~33 h的预报改进较明显，TESTCOM试验最大风速预报误差较TESTEC试验平均降低9 m·s^-1左右，最低气压预报误差较TESTEC试验平均降低12 hPa左右。总的来说，台风初始场重建技术对台风利奇马的路径和强度预报具有显著的正效应。

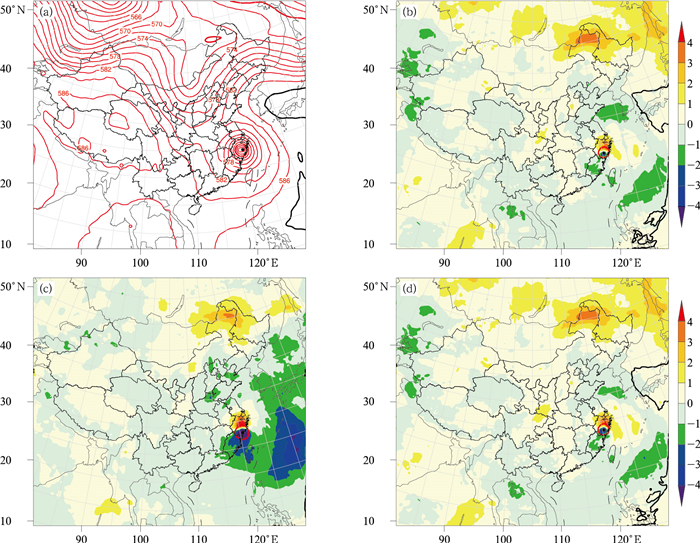
本文拟从三组试验预报的大气环流特征来分析初始场重建后的模式预报台风路径占优的原因。利用NCEP/NCAR FNL(每日4次，水平分辨率为1°×1°)再分析资料作为实况。从8日12时的大气环流分布来看(图略)，三组试验初始时刻500 hPa等压面中纬度是两槽两脊的形势，西太平洋副热带高压(以下简称副高)588 dagpm等值线西伸脊点位置位于33°N、124°E附近，与再分析资料得到的结果基本一致。从10日00时(模式起报后36 h)再分析资料的结果来看(图 7a)，副高西伸脊点位置较8日12时有所东退北抬，脊点位于36°N、128°E附近，TESTEC和TESTCOM两组试验准确预报出了副高的位置变化(图 7b，7d)，588 dagpm等值线西伸脊点与图 7d所示的位置接近，但图 7c表明，TESTGFS试验预报副高整体偏弱，副高西伸脊点大幅东撤至135°E以东，正是从该时刻开始，TESTGFS试验的路径误差逐渐加大，而TESTEC和TESTCOM试验的误差相对较小。可见，经过初始场重建的中尺度模式预报对环流形势把握较好。

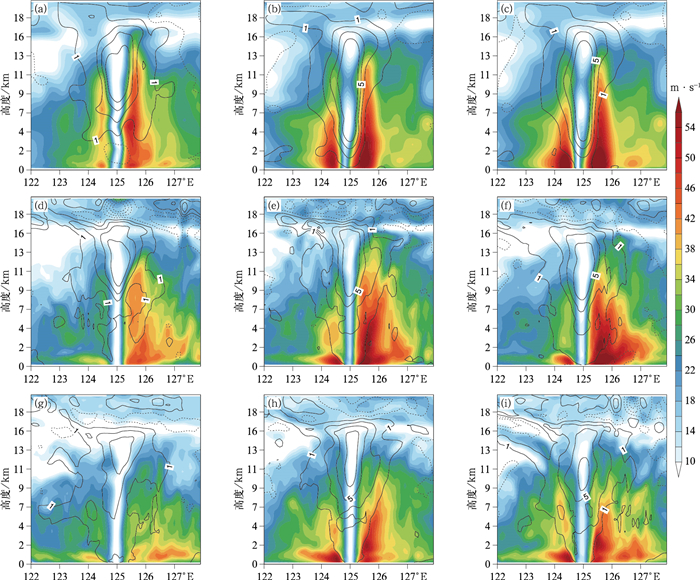
为分析初始化方案对台风结构的影响，给出三组试验第0小时、第6小时、和第12小时预报的沿台风中心的风速和温度距平垂直剖面(温度距平为当前格点温度值与同一高度层台风环流区域平均温度值之差，图 8)。由图 8a~8c可知，经过初始场重建的TESTCOM试验初始时刻的台风近中心最大风速为57.4 m·s^-1，大风速区在垂直方向深厚发展，较TESTGFS试验(45.8 m·s^-1)和TSETEC试验(38.8 m·s^-1)，风速得到明显增强。此外，三组试验在初始时刻台风暖心结构的温度距平数值相当，都达到了10 K。从第6小时的预报结果看(图 8d~8f)，TESTCOM试验的最大风速(43.3 m·s^-1)及暖心结构(9.6 K)预报结果较TESTEC试验(35.1 m·s^-1和8.8 K)要强，与TESTGFS试验(45.6 m·s^-1和9.4 K)接近。再对第12小时的结果进行分析(图 8g~8i)，TESTCOM试验的最大台风风速预报降至42.2 m·s^-1，温度距平为8.1 K，同时TESTGFS试验为41.1 m·s^-1和8.2 K，TESTEC试验为32.1 m·s^-1和6.6 K，TEST- COM试验的预报结果仍占优。上述分析可知，模式预报台风暖心结构和台风强度变化趋势一致，TESTCOM试验对台风强度预报较TESTEC试验有了明显改进，这与暖心结构预报的改进相匹配。从12 h以后的预报结果来看(图略)，TESTCOM试验对台风结构预报较TESTEC试验仍有明显优势，与TESTGFS试验水平相当。可见，初始场重建后的模式预报对台风垂向风场和暖心结构预报把握较好。

4 结论与讨论

为提升区域中尺度数值模式台风预报性能，本文基于ECMWF和GFS两个全球模式对2016—2019年影响浙江台风的路径和强度预报的评估结果，提出了一种新的台风初始化方案，并开展了在14个台风个例回报试验中的应用和评估，主要结论如下：

(1) ECMWF模式对影响浙江台风的路径预报总体优于GFS模式，而GFS模式对台风强度预报更具优势。

(2) 基于ECMWF和GFS分析场及洋面台风观测资料，利用台风涡旋分离、涡旋重定位以及最大风速调整等方法研制了可吸收各模式优势的台风初始场重建技术。

(3) 台风初始场重建技术在浙江省中尺度数值天气预报模式的应用表明，经过初始化处理过的模式预报结果兼顾了ECMWF模式的路径预报优势和GFS模式的强度预报优势，有效改进了台风的路径和强度预报性能。相较于GFS模式驱动的中尺度模式预报结果，新方法的模式路径预报绝对误差减少21 km，标准差降低26.6 km。相较于ECMWF模式驱动的中尺度模式预报结果，新方法的模式强度预报绝对误差减少1.7 m·s^-1，标准差降低2.3 m·s^-1。对典型个例超强台风利奇马进一步分析表明初始场重建技术对大气环流特征和台风暖心结构模拟均有较好的修正能力。

经过对14个影响浙江的台风个例的业务试验表明，本方法在实际业务中具有较强的实践可行性，对提高台风路径和强度的预报有较好作用。诚然，本方案还存在一定的不足，首先，初始化方案依赖于ECMWF模式路径预报优于GFS模式，GFS模式强度预报优于ECMWF模式这一检验结论，因此对于不支持该结论的台风个例预报，进行初始场重建后预报效果可能会更差，今后在实时业务中可以考虑在初始场重建之前对模式资料进行动态评估，且模式资料不局限于ECMWF和GFS全球模式资料，也可以利用如区域模式自身的预报资料，动态选择适合该台风个例的模式资料进行融合。其次，本方案仅对涡旋场的风速进行调整，并未考虑调整后对其他要素场的影响，重建的初始场可能会造成动力-物理过程相互不协调。下一步，我们将进一步加强这方面的改进研究，借鉴考虑模式动力和热力平衡、多种地形条件影响等台风动力初始化方案(许晓林等，2019；Cha and Wang, 2013; Liu et al, 2018)，改进台风业务数值预报准确率。