2. 中国气象局数值预报中心, 北京 100081;
3. 中国气象科学研究院, 北京 100081
2. CMA Numerical Weather Prediction Centre, Beijing 100081;
3. Chinese Academy of Meteorological Sciences, Beijing 100081
大气运动是一个具有混沌特性的非线性动力系统, 初始条件或模式的微小误差会使得单一数值预报模式存在不确定性(Leith, 1974; 陈静等, 2002; 杜钧, 2002; 杜钧和陈静, 2010; 王婧卓等, 2018; 张涵斌等, 2019)。此外, 区域模式侧边界条件误差也会导致区域模式具有不确定性。因此, 研究初值、模式、侧边界扰动技术, 是目前区域集合预报的重要方向。
侧边界扰动对区域集合预报性能提高非常重要, 假若没有扰动侧边界条件, 区域集合预报的离散度会降低(Hou et al, 2001)。通过扰动侧边界条件, 向区域模式传入大尺度扰动信息, 有助于提高区域集合预报离散度(Nutter et al, 2004a; 2004b)。同时, 引入侧边界扰动能降低集合预报均方根误差(RMSE)(Saito et al, 2010; 2012), 不仅如此, 侧边界扰动对离散度增长的影响时间多于初值扰动, 并且侧边界不确定性的传播特征依赖于天气形势的发展(Vié et al, 2011)。
近年来, 国内外学者对区域集合预报侧边界扰动方法进行了大量研究。侧边界扰动方法可归纳为三类。第一类方法是随机扰动方法, 陈静和薛纪善(2004)设计了随机扰动法扰动常规观测资料, 获得模式侧边界扰动的计算方案, 对降水集合预报有正面影响。孙凤娟(2009)对水平侧边界内位温扰动项进行随机扰动, 有助于提高离散度; 第二类是尺度化滞后平均法(scaled lagged average forecasting, SLAF), Hou et al(2001)在ARPS模式中使用SLAF产生侧边界扰动和初值扰动, Kong et al(2006;2007)也在区域模式中使用SLAF产生侧边界扰动, 得到了较好的预报效果; 第三类是通过全球集合预报动力降尺度产生, 动力降尺度是指利用全球集合预报扰动成员, 通过例如线性插值等方法获得区域集合预报的初值扰动和侧边界扰动(Marsigli et al, 2005; 张涵斌等, 2017)。目前全球各大业务中心区域集合预报侧边界扰动主要采用第三类动力降尺度方法产生, 例如美国NCEP的区域集合预报系统SREP(Wei et al, 2008; Bishop et al, 2009)和区域集合预报系统IAP-REFS(Zhu et al, 2012; 2013);奥地利气象局的区域集合预报ALADIN-LAEF(Wang et al, 2011); 英国气象局的MOGREPS区域集合预报系统(Bowler and Mylne, 2009); 日本气象厅的热带气旋区域集合预报的侧边界扰动也来源于全球集合预报系统, 区域集合预报离散度较单一侧边界条件提高50%, 均方根误差有所减小(Saito et al, 2010; 2012);中国气象局区域集合预报系统GRAPES-REPS使用的侧边界扰动来源于T639全球集合预报业务系统(张涵斌等, 2014)。总体而言, 采用动力降尺度侧边界扰动方法获得的区域集合预报侧边界扰动, 能够有效地提高集合离散度和降低均方根误差, 已在业务中获得了较好的应用效果。
对于高分辨率区域集合预报, 侧边界条件的误差是导致预报不确定性的重要因素, 在区域集合预报中引入侧边界扰动是代表区域模式侧边界条件不确定性的有效方法, 但是目前国内这方面研究较少。因此, 有必要深入开展侧边界不确定性对区域集合预报的影响研究, 本文构造了动力降尺度侧边界扰动方案(DOWN方案)和尺度化滞后侧边界扰动方案(SLAF方案), 重点分析两种方案对GRAPES-REPS区域集合预报扰动质量和整体预报性能的影响, 讨论与评估两种侧边界扰动方案的效果, 获得两种侧边界扰动方法的概率预报特征, 为改进GRAPES-REPS区域集合预报侧边界扰动的质量提供依据。
1 方法介绍和试验方案 1.1 SLAF侧边界扰动方法SLAF侧边界扰动方法是利用尺度化因子δ缩放过去时刻预报场与分析场的差值, 将其叠加到侧边界上(Ebisuzaki and Kalnay, 1991), 其数学表达式为:
| $ \begin{array}{l} LBC = LBC(t = 0) \pm \delta \times [LBC(t = - k) - \\ \;\;\;\;\;\;\;\;\;\;\;LBC(t = 0)] \end{array} $ | (1) |
式中, LBC(t=0)为起始时刻控制预报的侧边界, LBC(t=-k)为滞后预报的侧边界, k∈{1, 2, …, n}。Ebisuzaki and Kalnay(1991)认为各预报时间的侧边界扰动振幅需要保持与LBC(t=-1)的预报误差基本相当的量值, 根据天气时间尺度内预报误差呈线性增长的认识, 当k=1, 将尺度化因子δ设置为1, 当k=2时, 为了与k=1时的扰动量值相当, 将δ设置为1/2, 当k=3时, 则设置为1/3, 其余类推。
Kong et al(2006;2007)分析预报误差发现, 其增长不完全符合传统的天气时间尺度内预报误差呈线性增长的特征, 研究结果显示, 预报误差在前6 h快速增长并基本达到饱和, 其后保持基本稳定, 因此对尺度化因子δ计算方法进行了改进; 提出了基于扰动振幅调整的集合预报成员尺度化因子δ计算方法:以6 h预报扰动为基准, 则第一对集合预报成员的扰动采用滞后6 h预报扰动, 故δ为±10;第二对集合预报成员采用滞后12 h预报扰动, 故δ为6 h与12 h预报扰动的比值; 第三对集合预报成员采用滞后18 h预报扰动, 故δ为6 h与18 h预报扰动的比值, 以此类推。
1.2 GRAPES-REPS的SLAF侧边界扰动设计本文参考Kong et al(2006;2007)提出的方法计算δ, 在GRAPES集合预报中, 为了增加集合成员, 将式(1)中右端中第三项LBC(t=0)进行扩展, 如下式所示:
| $ \begin{array}{l} LBC = LBC(t = 0) \pm \delta \times [LBC(t = - k) - \\ \;\;\;\;\;\;\;\;\;\;\;LBC(t = - j)] \end{array} $ | (2) |
式中, k∈{1, 2, 3, 4}, j∈{0, 1}, k=0为当前预报时刻, k=1, 2, 3, 4分别为滞后6、12、18、24 h预报。
表 1为SLAF方案产生的2015年7月2日无量纲气压PI、纬向风U、经向风V、比湿Q、位温Th等变量对应的尺度化因子δ。
|
|
表 1 SLAF方案集合成员的尺度化因子 Table 1 The δ for ensemble members of the SLAF scheme |
设计两组侧边界扰动方案:动力降尺度侧边界扰动方案(简称DOWN), 侧边界扰动从中国气象局数值预报中心的T639全球模式获得; 尺度化滞后侧边界扰动方案(简称SLAF)。
选取2015年7月2, 7, 12, 17, 22, 27日共6 d进行集合预报质量评估, 起报时刻为00:00 UTC, 预报时效为60 h, 试验采用GRAPES-REPS区域集合预报模式, 包含1个控制预报和14个扰动成员共15个集合成员, 模式水平分辨率0.15°×0.15°, 水平格点数502×330, 垂直坐标为地形追随高度坐标, 垂直层次为51层, 预报模拟区域15°~65°N、70°~145°E, 覆盖中国范围。两种方案的初值扰动由T639全球集合预报系统动力降尺度产生, 模式扰动采用模式物理参数化倾向随机扰动方案(袁月等, 2016)。等压面和地面要素的检验资料为GRAPES-Meso中尺度模式分析场, 降水观测资料采用国家气象信息中心的站点分析资料。
1.4 检验方法评估一个集合预报系统的效果, 可采用一组概率预报检验评分。本文采用RMSE、集合离散度、连续分级概率评分CRPS(Continuous Ranked Probability Score)、离群值Outlier、BS评分、TS评分、AROC等进行检验(Brier, 1950; Hersbach, 2000; Jolliffe and Stephenson, 2003; 彭相瑜等, 2014; 赵琳娜等, 2015), 检验对象选取高层200 hPa, 中层500 hPa, 低层850 hPa气象要素U、V、T、H以及近地面要素2 m温度和10 m风速。表 2给出检验方法的介绍。
|
|
表 2 集合预报检验方法 Table 2 Verification method of ensemble forecast |
扰动能量演变可以体现出预报误差随预报时效的变化。Palmer et al(1998)提出了适用于资料同化和天气预报研究的集合扰动总能量的表达式:
| $ \begin{array}{l} P(i, j, k) = \frac{1}{2}\left[ {{u^{\prime 2}}(i, j, k) + {v^{\prime 2}}(i, j, k)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{c_p}}}{{{T_{\rm{r}}}}}{T^{\prime 2}}(i, j, k) \end{array} $ | (3) |
式中, u′、v′、T′分别代表纬向风U、经向风V、温度T的扰动, 扰动值为集合成员的预报与集合平均的差值, Tr是参考温度, cp是干空气的定压比热, i、j、k分别为水平及垂直点数。
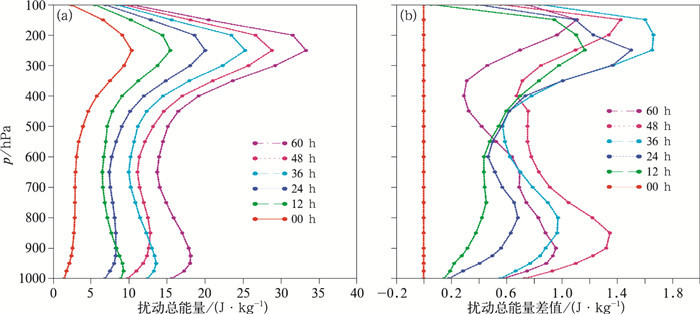
图 1是2015年7月2日、7日、12日、17日、22日、27日平均的扰动总能量及差值的垂直分布。从图 1a可以看出, DOWN方案的各层扰动总能量随预报时效的延长而增长, 能够表示预报误差的增长。其次, DOWN方案的扰动总能量在垂直方向分布不均, 扰动总能量最大值位于250 hPa, 即急流轴附近, 扰动总能量包含的动能较多, 与Bowler et al(2008)的研究结果吻合。最小值位于650 hPa, 次大值位于低层950 hPa。图 1b为DOWN与SLAF方案的扰动总能量的差值, 预报初始时刻, DOWN和SLAF方案的扰动总能量一致, 随着预报时效延长, 二者对扰动总能量的影响具有显著差异:DOWN方案的扰动总能量明显大于SLAF方案。而在36 h预报时效, 高层250 hPa扰动总能量差值达到最大, 差值约为1.7 J·kg-1。两个方案的总能量差异, 可以初步说明DOWN方案的集合离散度更大, 集合扰动的整体性能更优。这可能是由于DOWN方案的侧边界初始扰动直接通过降尺度得到, 保持了原来大尺度扰动的合理结构和扰动大小, 而SLAF方案中, 时间距离较大的两个时刻的预报误差偏大, 从而导致离散度结构不合理, 在预报过程中, 不合理的侧边界扰动很快由模式过滤, 导致集合离散度偏小。
|
图 1 2015年7月2、7、12、17、22、27日平均的扰动总能量的垂直分布 (a)DOWN, (b)DOWN与SLAF的差值 Fig. 1 Temporally averaged vertical distributions of perturbation total energy from 2, 7, 12, 17, 22 and 27 July 2015 (a) DOWN experiment, (b) difference of DOWN experiment and SLAF experiment |
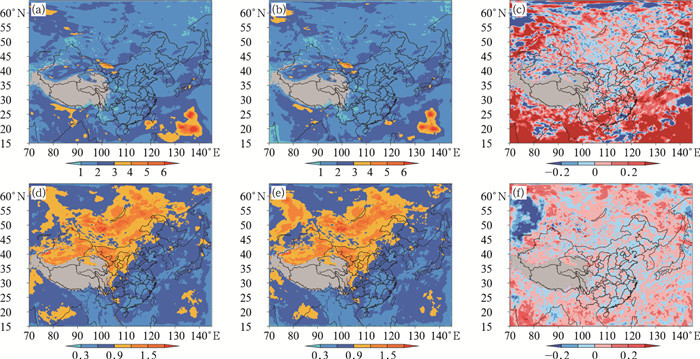
图 2为两种方案的平均850 hPa纬向风和温度水平24 h预报时效的离散度分布及差值, 对于低层850 hPa纬向风, DOWN方案(图 2a)的离散度分布大值区域集中在20°~30°N、130°~140°E的太平洋, 与SLAF方案的离散度大值区类似。侧边界扰动对于边界上的离散度分布影响较大, DOWN与SLAF方案(图 2b)在边界上的离散度分布差异较大, 而中心区域差异较小。为了进一步分析两种侧边界扰动对离散度的影响, 图 2c给出DOWN与SLAF方案的离散度差值分布, 可以看出, 区域边界上离散度差值分布多为红色和蓝色, 这说明侧边界扰动对离散度的影响很大, 不仅如此, 在边界上离散度分布红色多于蓝色, 红色为正值, 说明DOWN方案的离散度在边界上大于SLAF方案。其余层次(500、200 hPa)纬向风离散度分布特征类似, 不再赘述。对于低层850 hPa温度离散度分布, 从图 2d, 2e可以看出, DOWN和SLAF方案的850 hPa温度离散度大值区分布于中国新疆、内蒙古以及西伯利亚。图 2f给出DOWN与SLAF方案离散度差值的分布, 与图 2c类似, 图 2f中离散度差值在边界上多为较大的正值(红色), 说明侧边界扰动对离散度的影响较大, DOWN方案能使离散度更快地增长。
|
图 2 DOWN方案(a, d)和SLAF方案(b, e)6 d平均的24 h预报的850 hPa纬向风(a~c)、温度(d~f)离散度及两方案的差值(c, f) (图中灰色阴影为地形) Fig. 2 DOWN experiment (a, d) and SLAF experiment (b, e) 6 d average 24 h forecast 850 hPa zonal wind (a, b, c), temperature (d, e, f) dispersion and the difference (c, f) between the two experiments (Gray shadow is the terrain) |
图 3是两组试验结果离散度和均方根误差随预报时效的演变图。由图 3a~3f所示, 对于风场U、V来说, DOWN方案的离散度略大于SLAF方案, 例如图 3b为500 hPa纬向风, 在24 h, DOWN、SLAF方案离散度分别为2.43、2.3。在36 h预报时效内, DOWN方案的RMSE与SLAF方案几乎重合, 36 h预报时效后, DOWN方案的RMSE略小于SLAF方案, 两方案的RMSE均小于控制预报。这表明, DOWN方案的侧边界扰动对于风场U、V的预报效果优于SLAF方案, 且在24、36、48、60 h分别通过了0.05、0.05、0.25、0.25的显著性水平t检验。图 3g~3i为温度场的离散度和RMSE变化特征, 两组试验的变化趋势一致, 表明两方案的预报效果相当, 而且在12、36 h通过了0.25的显著性水平t检验。图 3j~3l是高度场的离散度和RMSE变化特征, 由图可知, 在高层200 hPa(图 3j), DOWN方案离散度在预报时效36 h为15.63, RMSE为16.4;而SLAF方案离散度为15.44, RMSE为16.8, 这表明, 在高度场DOWN方案优于SLAF方案的预报效果, 且在12、24、36、48 h分别通过了0.05、0.05、0.25、0.25的显著性水平t检验。总体上看, 对于等压面要素U、V、T、H, DOWN方案的侧边界扰动方法略优于SLAF方案。

|
图 3 DOWN方案和SLAF方案的试验结果U(a, b, c)、V(d, e, f)、T(g, h, i)、H(j, k, l)的离散度和均方根误差随预报时效演变 (a, d, g, j)200 hPa, (b, e, h, k)500 hPa, (c, f, i, l)850 hPa Fig. 3 The spread and root mean square error (RMSE) of the U (a, b, c), V (d, e, f), T (g, h, i), H (j, k, l) of DOWN experiment and SLAF experiment test results along with changes of forecast lead time a, d, g, j) 200 hPa, (b, e, h, k) 500 hPa, (c, f, i, l) 850 hPa |
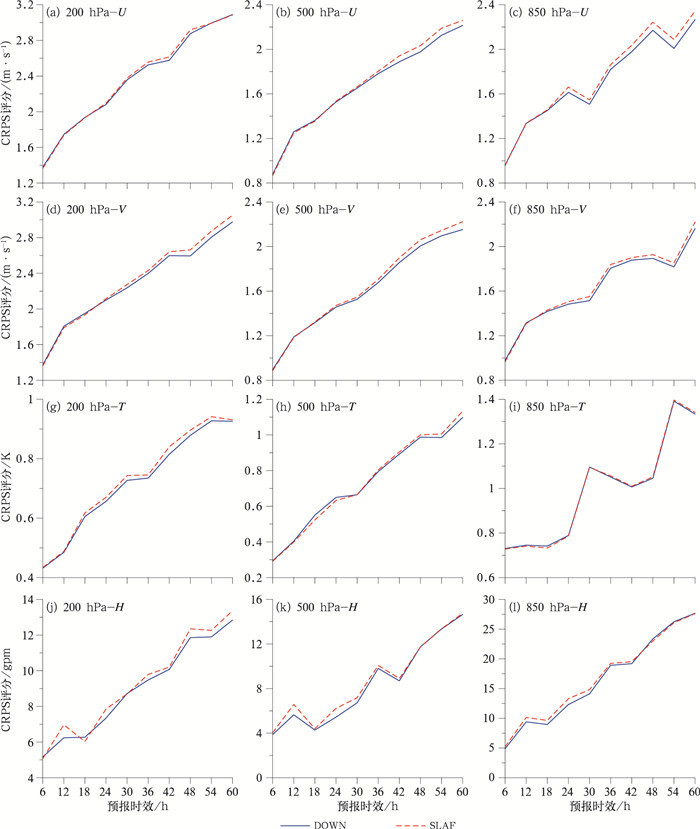
图 4是两组试验结果的连续分级概率评分(CRPS)随预报时效演变, CRPS是一种负定向的评分值, 值越小表示集合预报系统的概率预报性能越好。由图 4a~4f所示, 对于风场来说, DOWN方案的CRPS值在36 h内与SLAF方案几乎重合, 36 h后, DOWN方案的CRPS值逐渐略小于SLAF, 例如500 hPa纬向风(图 4b), 在48 h, DOWN、SLAF方案的CRPS值分别为1.97、2.03。因此, 对于风场U、V来说, DOWN方案略优于SLAF方案且在24、36和60 h均通过了0.25的显著性水平t检验。图 4g~4i为温度场的CRPS变化特征, 对于500 hPa温度场, DOWN、SLAF方案在24 h的CRPS值分别为0.65、0.63, 这表明, 对于温度场DOWN方案预报效果略优于SLAF方案; 200、850 hPa温度场变化趋势大致相同, 不再赘述。图 4j~4l是高度场的CRPS变化特征, 例如200 hPa高度场(图 4j), DOWN、SLAF方案在24 h的CRPS值分别为7.34、7.84, 随着预报时效延长, CRPS的差值逐渐增大, 这表明在高度场, DOWN方案侧边界扰动方法略优于SLAF方案。总体上看, DOWN方案略优于SLAF方案。
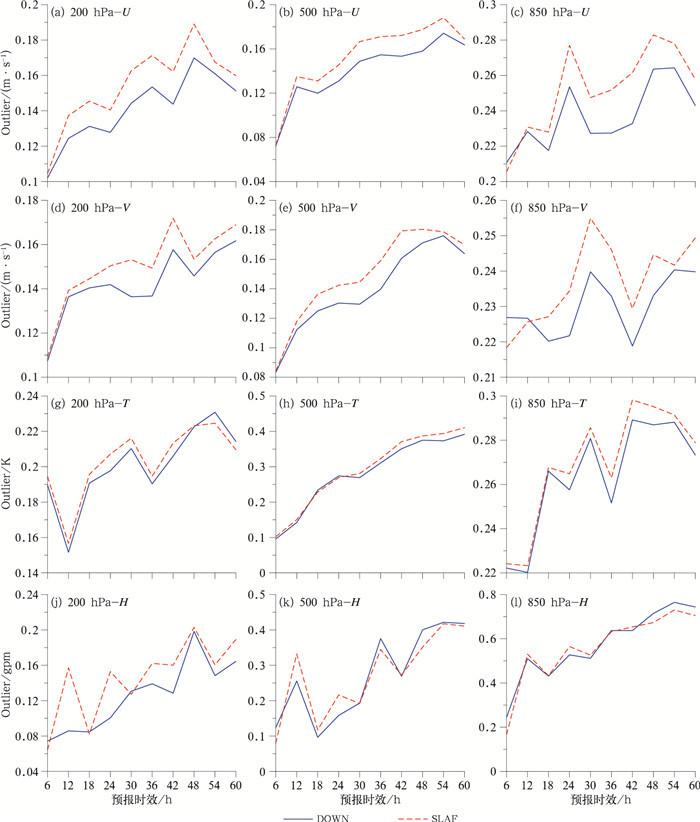
图 5是两组试验结果离群值(Outlier)分布特征。Outlier指观测落在集合预报成员之外的频率, 其值越低, 说明集合成员预报分布越可靠, 图 5a~5l所示, 对于各个等压面要素U、V、T、H, DOWN方案的Outlier值小于SLAF方案, 例如图 5a为200 hPa纬向风Outlier值随预报时效演变, 在36 h, DOWN、SLAF方案的Outlier值分别为0.15、0.17;这说明DOWN方案的预报效果更好, 构造的侧边界扰动更优, 且U、V、T、H各要素Outlier的减少在12、24、48 h均通过了0.05的显著性水平t检验, 在36和60 h通过了0.25显著性水平t检验。分析DOWN方案Outlier评分优于SLAF方案的原因, 可能是由两者离散度差异导致, DOWN方案各层次的离散度高于SLAF方案, 因此其集合预报包含实况的可能性更高, 所以Outlier评分更低。
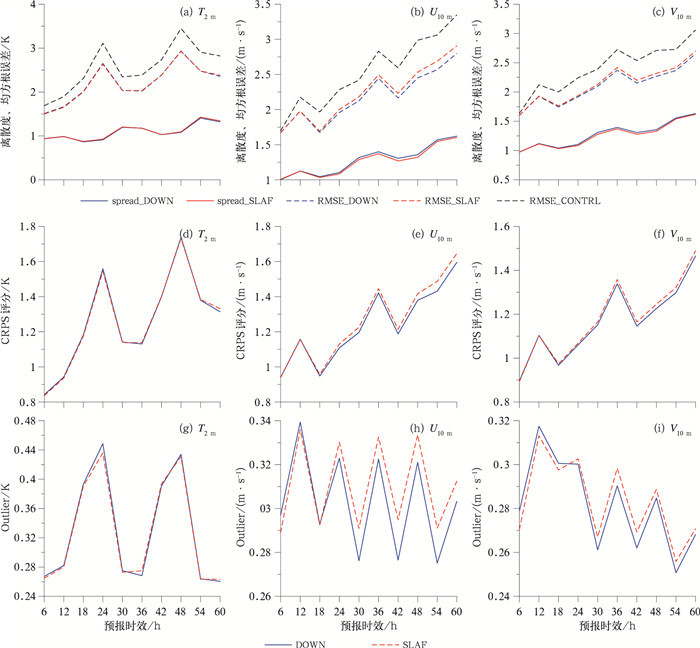
2.3 地面要素2 m温度、10 m风图 6是地面要素2 m温度、10 m纬向、经向风的集合均方根误差和集合离散度、CRPS评分、离群值Outlier分布特征。对于2 m温度来说, DOWN方案的离散度、RMSE、CRPS和Outlier等评分(图 6a、6d、6g)与SLAF方案几乎重合。例如2 m温度的离散度和RMSE(图 6a), 在36 h, DOWN方案的离散度为1.177, RMSE为2.02;SLAF方案的离散度为1.174, RMSE为2.03。而对于地面要素10 m风(图 6b、6c、6e、6f、6h、6i), 在24 h预报时效内, DOWN方案的RMSE、CRPS、Outlier评分与SLAF方案保持一致, 随着预报时效延长, DOWN方案逐渐小于SLAF方案, 如对于10 m纬向风(图 6e), DOWN方案的CRPS值在36 h为1.42, 而SLAF方案的为1.44。
|
图 6 DOWN方案和SLAF方案的T2 m(a, d, g), U10 m(b, e, h), V10 m(c, f, i)概率预报检验结果 (a, b, c)均方根误差和离散度, (d, e, f)CRPS评分, (g, h, i)Outlier Fig. 6 Ensemble verification results of T2 m (a, d, g), U10 m (b, e, h), V10 m (c, f, i) of DOWN experiment and SLAF experiment (a, b, c) RMSE and spread, (d, e, f) CRPS, (g, h, i) Outlier |
这表明对于地面要素2 m温度, DOWN与SLAF方案预报效果相当, 由于2 m温度没有通过t检验。而对于10 m风, DOWN方案略优于SLAF方案, 且在24、36、48、60 h分别通过了0.05、0.05、0.25、0.25的显著性水平检验。
2.4 降水降水预报能力高低的是衡量区域集合预报系统优劣的重要指标。本文采用一系列降水评分方法对DOWN和SLAF方案的逐6 h累计降水预报进行检验, 所采用的评分为BS评分、TS评分、AROC。
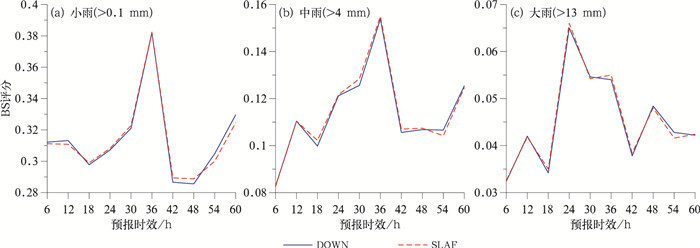
图 7给出了DOWN和SLAF方案两组侧边界扰动试验的逐6 h降水BS评分在小雨、中雨、大雨不同量级上随预报时效的变化。在小雨量级(>0.1 mm)(图 7a), 在0~48 h, DOWN方案的BS评分与SLAF方案持平, 随着预报时效的增长, DOWN方案在60 h的BS评分为0.329, SLAF方案的为0.324, 可以看出DOWN方案的BS值逐渐大于SLAF方案。而对于中雨量级(>4 mm, 图 7b)和大雨量级(>13 mm, 图 7c), BS评分随时间变化特征与小雨的基本一致。BS评分的差异在预报时效60 h内没有通过显著性水平t检验。
|
图 7 DOWN和SLAF方案两组试验结果的BS评分随预报时效演变 Fig. 7 The BS score of the DOWN experiment and SLAF experiment test results as a function of forecast lead time |
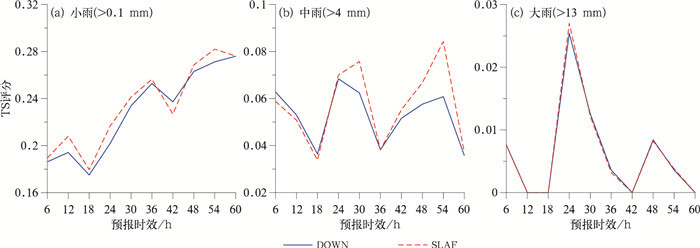
图 8给出了DOWN和SLAF方案两组侧边界扰动试验的逐6 h降水TS评分。对于小雨量级(图 8a)和中雨量级(图 8b), SLAF方案的TS评分在大多数时间内高于DOWN方案, 如, DOWN方案在12 h的TS评分为0.194, 而SLAF方案的为0.208。对于大雨量级(图 8c), 两者的评分几乎重合。但是SLAF方案在小雨和中雨上TS评分的提高在60 h内也没有通过t检验。
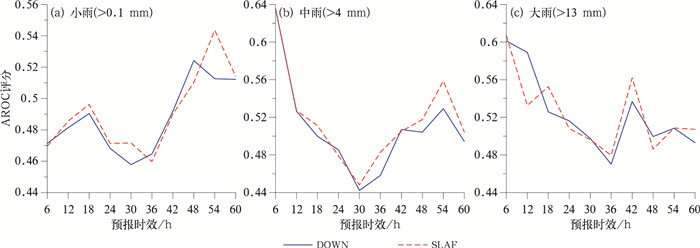
图 9给出了两组侧边界扰动试验的逐6 h降水AROC评分。对于小雨量级(图 9a), DOWN方案在30 h的AROC值为0.457, SLAF方案的为0.471。对于中雨量级(图 9b), 与图 9a类似, SLAF方案的AROC值在大多数时间内高于DOWN方案。而对于大雨量级(图 9c), DOWN方案在12 h的AROC值为0.589, SLAF方案的为0.532, 随着预报时效延长, SLAF方案的AORC值有逐渐超越DOWN方案的趋势, DOWN方案在42 h的AROC值为0.536, SLAF方案的为0.562。SLAF方案在小雨和中雨上AROC的提高在60 h内没有通过显著性水平t检验。
综合上述3种评分结果, 对于降水的预报, 虽然SLAF方案评分具有一定优势, 但评分的提高没通过显著性水平检验, 因此可认为两种方案预报效果相当。
3 结论与讨论中国气象局数值预报中心自2014年建立了GRAPES-REPS业务系统, 其侧边界扰动一直由全球集合预报系统DOWN方案侧边界扰动方法得到, 为了深入了解侧边界扰动对GRAPES区域集合预报的影响, 本文基于15 km水平分辨率的GRAPES-REPS区域集合预报模式, 使用SLAF方案侧边界扰动方法和DOWN方案侧边界扰动方法, 对2015年7月进行6 d集合预报试验, 分析了两种方案的扰动分布与量级特征、并利用集合均方根误差、集合离散度、CRPS评分、Outlier、BS评分、TS评分、AROC等概率预报检验方法, 分析了两种方案的GRAPES-REPS区域集合预报扰动质量和整体预报性能, 讨论与评估了两种侧边界扰动方案的效果, 主要得出以下结论:
(1) DOWN方案的扰动总能量在各垂直层次均大于SLAF方案, 使得边界上前者的离散度大于后者, 集合扰动增长更为合理。综合DOWN和SLAF方案的等压面要素和地面要素的概率预报评分, DOWN方案的离散度、Outlier和CRPS等评分优于SLAF方案, 说明DOWN方案构造的侧边界扰动更加合理。
(2) 在降水概率预报技巧方面, SLAF方案侧边界扰动在TS和AROC评分上具有一定优势, 但评分的提高没有通过显著性检验, 因此认为两种方案对降水预报改进相当。
对于两种方案在等压面要素和地面要素评分的差异, 分析其可能存在的原因, 是由于DOWN方案的侧边界初始扰动直接通过降尺度得到, 保持了原来大尺度扰动的合理结构和扰动大小, 而SLAF方案中, 时间距离较大的两个时刻的预报误差偏大, 导致离散度结构不合理, 从而在预报过程中, 不合理的侧边界扰动很快由模式过滤, 导致SLAF方案的预报技巧偏差。
陈静, 陈德辉, 颜宏, 2002. 集合数值预报发展与研究进展[J]. 应用气象学报, 13(4): 497-507. Chen J, Chen D H, Yan H, 2002. A brief review on the development of ensemble prediction system[J]. J Appl Meteor Sci, 13(4): 497-507 (in Chinese).
|
陈静, 薛纪善, 2004.水平侧边界条件对中尺度暴雨集合预报的影响[C]//数值天气预报新理论新方法及应用学术研讨会论文摘要汇编.乌鲁木齐: 中国气象学会. Chen J, Xue J S, 2004.Influence of lateral boundary conditions on ensemble mesoscale heavy rain prediction[C]//National Science Seminar on New Theory and Application of Numerical Weather Prediction.Urumqi: Chinese Meteorological Society(in Chinese).
|
邓国, 龚建东, 邓莲堂, 等, 2010. 国家级区域集合预报系统研发和性能检验[J]. 应用气象学报, 21(5): 513-523. Deng G, Gong J D, Deng L T, et al, 2010. Development of mesoscale ensemble prediction system at National Meteorological Center[J]. J Appl Meteor Sci, 21(5): 513-523 (in Chinese).
|
杜钧, 2002. 集合预报的现状和前景[J]. 应用气象学报, 13(1): 16-28. Du J, 2002. Present situation and prospects of ensemble numerical prediction[J]. J Appl Meteor Sci, 13(1): 16-28 (in Chinese).
|
杜钧, 陈静, 2010. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 36(11): 1-11. Du J, Chen J, 2010. The corner stone in facilitating the transition from deterministic to probabilistic forecasts-ensemble forecasting and its impact on numerical weather prediction[J]. Meteor Mon, 36(11): 1-11 (in Chinese).
|
马旭林, 计燕霞, 周勃旸, 等, 2018. GRAPES区域集合预报尺度混合初始扰动构造的新方案[J]. 大气科学学报, 41(2): 248-257. Ma X L, Ji Y X, Zhou B Y, et al, 2018. A new scheme of blending initial perturbation of the GRAPES regional ensemble prediction system[J]. Trans Atmos Sci, 41(2): 248-257 (in Chinese).
|
马旭林, 薛纪善, 陆维松, 等, 2008. GRAPES全球集合预报的集合卡尔曼变换初始扰动方案初步研究[J]. 气象学报, 66(4): 526-536. Ma X L, Xue J S, Lu W S, et al, 2008. Preliminary study on ensemble transform Kalman filter-based initial perturbation scheme in GRAPES global ensemble prediction[J]. Acta Meteor Sin, 66(4): 526-536 (in Chinese).
|
彭相瑜, 代刊, 金荣花, 等, 2014. 欧洲中心集合预报在中国区域中期时效离散度预报技巧关系分析[J]. 气象, 40(7): 777-786. Peng X Y, Dai K, Jin R H, et al, 2014. Analysis of spread skill relations using the ECMWF ensemble prediction in medium term period over China[J]. Meteor Mon, 40(7): 777-786 (in Chinese).
|
孙凤娟, 2009.风暴尺度集合预报侧边界扰动技术研究[D].南京: 南京信息工程大学. Sun F J, 2009.Study on the lateral boundary condition perturbation method for storm-scale ensemble forecast[D].Nanjing: Nanjing University of Information Science & Technology(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1462395
|
王婧卓, 陈静, 庄照荣, 等, 2018. GRAPES区域集合预报模式的初值扰动增长特征[J]. 大气科学, 42(2): 367-382. Wang J Z, Chen J, Zhuang Z R, et al, 2018. Characteristics of initial perturbation growth rate in the regional ensemble prediction system of GRAPES[J]. Chin J Atmos Sci, 42(2): 367-382 (in Chinese).
|
袁月, 李晓莉, 陈静, 等, 2016. GRAPES区域集合预报系统模式不确定性的随机扰动技术研究[J]. 气象, 42(10): 1161-1175. Yuan Y, Li X L, Chen J, et al, 2016. Stochastic parameterization toward model uncertainty for the GRAPES mesoscale ensemble prediction system[J]. Meteor Mon, 42(10): 1161-1175 (in Chinese).
|
张涵斌, 陈静, 智协飞, 等, 2014. 基于GRAPES_Meso的集合预报扰动方案设计与比较[J]. 大气科学学报, 37(3): 276-284. Zhang H B, Chen J, Zhi X F, et al, 2014. Design and comparison of perturbation schemes for GRAPES_Meso based ensemble forecast[J]. Trans Atmos Sci, 37(3): 276-284 (in Chinese).
|
张涵斌, 范水勇, 陈敏, 等, 2019. 区域集合预报基于SKEB和多物理过程的混合模式扰动方法研究[J]. 气象, 45(1): 17-28. Zhang H B, Fan S Y, Chen M, et al, 2019. Study on a synthetic model perturbation method based on SKEB and multi physics for regional ensemble forecast[J]. Meteor Mon, 45(1): 17-28 (in Chinese).
|
张涵斌, 李玉焕, 范水勇, 等, 2017. 基于动力降尺度的区域集合预报初值扰动构建方法研究[J]. 气象, 43(12): 1461-1472. Zhang H B, Li Y H, Fan S Y, et al, 2017. Study on initial perturbation construction method for regional ensemble forecast based on dynamical downscaling[J]. Meteor Mon, 43(12): 1461-1472 (in Chinese).
|
赵琳娜, 刘琳, 刘莹, 等, 2015. 观测降水概率不确定性对集合预报概率Brier技巧评分结果的分析[J]. 气象, 41(6): 685-694. Zhao L N, Liu L, Liu Y, et al, 2015. Impact of observation uncertainty of precipitation on the Brier skill score of global ensemble prediction system[J]. Meteor Mon, 41(6): 685-694 (in Chinese).
|
Bishop C H, Holt T R, Nachamkin J, et al, 2009. Regional ensemble forecasts using the ensemble transform technique[J]. Mon Wea Rev, 137(137): 288-298.
|
Bowler N E, Arribas A, Mylne K R, et al, 2008. The MOGREPS short-range ensemble prediction system[J]. Quart J Roy Meteor Soc, 134(632): 703-722.
|
Bowler N E, Mylne K R, 2009. Ensemble transform Kalman filter perturbations for a regional ensemble prediction system[J]. Quart J Roy Meteor Soc, 135(640): 757-766.
|
Brier G W, 1950. Verification of forecasts expressed in terms of pro-bability[J]. Mon Wea Rev, 78(1): 1-3.
|
Ebisuzaki W, Kalnay E, 1991.Ensemble experiments with a new lagged average forecasting scheme[C]//Research Activities in Atmospheric and Oceanic Modeling Rep.15, WMO, 423pp.
|
Hersbach H, 2000. Decomposition of the continuous ranked probability score for ensemble prediction systems[J]. Wea Forecasting, 15(5): 559-570.
|
Hou D C, Kalnay E, Droegemeier K K, 2001. Objective verification of the SAMEX '98 ensemble forecasts[J]. Mon Wea Rev, 129(1): 73-91.
|
Jolliffe I T, Stephenson D B, 2003. Forecast Verification:A Practitioner's Guide in Atmospheric Science[M].
Hoboken: Wiley.
|
Kong F Y, Droegemeier K K, Hickmon N L, 2006. Multiresolution ensemble forecasts of an observed tornadic thunderstorm system.Part Ⅰ:comparsion of coarse- and fine-grid experiments[J]. Mon Wea Rev, 134(3): 807-833.
|
Kong F Y, Droegemeier K K, Hickmon N L, 2007. Multiresolution ensemble forecasts of an observed tornadic thunderstorm system.Part Ⅱ:storm-scale experiments[J]. Mon Wea Rev, 135(3): 759-782.
|
Leith C E, 1974. Theoretical skill of Monte Carlo forecasts[J]. Mon Wea Rev, 102(6): 409-418.
|
Marsigli C, Boccanera F, Montani A, et al, 2005. The COSMO-LEPS mesoscale ensemble system:Validation of the methodology and verification[J]. Nonlinear Processes Geophys, 12(4): 527-536.
|
Nutter P, Stensrud D, Xue M, 2004a. Effects of coarsely resolved and temporally interpolated lateral boundary conditions on the dispersion of limited-area ensemble forecasts[J]. Mon Wea Rev, 132(10): 2358-2377.
|
Nutter P, Xue M, Stensrud D, 2004b. Application of lateral boundary condition perturbations to help restore dispersion in limited-area ensemble forecasts[J]. Mon Wea Rev, 132(10): 2378-2390.
|
Palmer T N, Gelaro R, Barkmeijer J, et al, 1998. Singular vectors, metrics, and adaptive observations[J]. J Atmos Sci, 55(4): 633-653.
|
Saito K, Kuroda T, Kunii M, et al, 2010. Numerical simulation of Myanmar cyclone Nargis and the associated storm surge Part Ⅱ:ensemble prediction[J]. J Meteor Soc Japan, 88(3): 547-570.
|
Saito K, Seko H, Kunii M, et al, 2012. Effect of lateral boundary perturbations on the breeding method and the local ensemble transform Kalman filter for mesoscale ensemble prediction[J]. Tellus, 64(1): 1-4.
|
Vié B, Nuissier O, Ducrocq V, 2011. Cloud-resolving ensemble simulations of mediterranean heavy precipitating events:Uncertainty on initial conditions and lateral boundary conditions[J]. Mon Wea Rev, 139(2): 403-423.
|
Wang Y, Bellus M, Wittmann C, et al, 2011. The Central European limited-area ensemble forecasting system:ALADIN-LAEF[J]. Quart J Roy Meteor Soc, 137(655): 483-502.
|
Wei M Z, Toth Z, Wobus R, et al, 2008. Initial perturbations based on the ensemble transform (ET) technique in the NCEP global ope-rational forecast system[J]. Tellus A:Dyn Meteor Oceanogr, 60(1): 62-79.
|
Zhu J S, Kong F Y, Lei H C, 2012. A regional ensemble forecast system for stratiform precipitation events in northern China.Part Ⅰ:a case study[J]. Adv Atmos Sci, 29(1): 201-216.
|
Zhu J S, Kong F Y, Lei H C, 2013. A regional ensemble forecast system for stratiform precipitation events in the northern China Region.Part Ⅱ:seasonal evaluation for summer 2010[J]. Adv Atmos Sci, 30(1): 15-28.
|
 2019, Vol. 45
2019, Vol. 45