引言

洋面10 m风是海洋气象预报的重要要素之一，其预报主要依据数值预报，而单一确定性的数值模式中的10 m风速预报产品是由物理方程直接计算得到，因模式自身分辨率及计算精度等的影响，数值模式中的10 m风速预报产品存在着不可避免的系统性误差(Toth et al，2001)。常用的风速订正方法有局地非参数的加权回归订正方法(Rozas-Larraondo et al，2014)、MOS预报法(荣艳敏等，2015)、风速的高斯统计预报方法(Monahan，2013)、神经网络方法(黄凤新等，2013)等，但这些订正方法均是针对陆地观测站点密集、观测资料多的情况下开展的技术方法，洋面10 m风由于受洋面观测资料少的限制，对其的数值预报订正技术一直没有进展。集合预报技术在过去的二十多年取得了巨大进步，现已成为数值天气预报的重要组成部分，相比于确定性模式，集合预报不仅能够提供更多的概率信息，而且集合成员的初始扰动信息可以很好地诠释预报偏差，并且可以量化由初始误差或模式误差引起的不确定性，因此被广泛应用于实际业务预报中，同时也部分地弥补了海洋观测资料的不足。越来越多的基于集合预报的客观订正方法被广泛地应用于温度、降水等气象要素及台风(路径)、暴雨等灾害性天气预报之中(李莉等，2011；王敏等，2012；钱奇峰等，2014；杜钧和李俊，2014)，基于集合预报10 m风速订正方法的研究工作开展相对较少(赖鑫等，2016)。集合预报中常用的10 m风速预报产品主要有风速最大值、平均值、百分位数等，这些产品只是对集合预报10 m风速预报产品的简单释用，并不能从根本上降低集合预报10 m风速预报产品的系统性误差。

本文基于ECMWF集合预报数据，利用集合预报的概率特性，采用众数方法，建立适用于我国近海海域风速客观预报订正方法，减小集合预报受初始值扰动引起的系统偏差，提高风速的预报准确率，为我国近海风速预报提供参考。

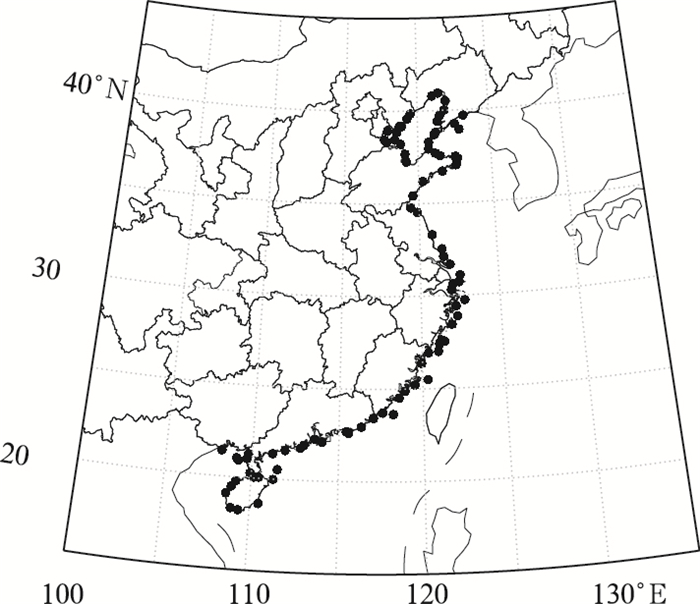
1 资料

本文采用2013—2015年ECMWF集合预报10 m风场资料，起报时刻为12 UTC(世界时)，分辨率0.5°×0.5°，预报时效为12~120 h，间隔12 h。2013—2015年地面风速实况观测资料采用中央气象台近海风速质量检验办法中的88个沿岸及近海代表站点作为洋面风速预报检验代表站(图 1)。利用2013—2014年ECMWF集合预报10 m风场资料进行误差特征分析及订正方程中误差参数的计算，2015年ECMWF集合预报10 m风场资料用于回算检验和订正效果分析。

2 方法 2.1 众数

众数是指统计分布中具有明显集中趋势点的数值，体现集合预报的概率特性。集合预报中的众数可以反映出各个预报成员的集中趋势，即预报概率最大的位置，相比于中位数和平均值，众数受极值的影响相对较小，表现更为稳定(时娟，2002)。集合预报众数经验公式已在温度要素的预报中得到了应用，此经验公式仅适用于准正态分布，而风速分布呈现明显的右偏分布，即变量在高值处比低值处有较大的偏离中心的趋势(茆诗松和贺思辉，2010)，不适用众数求解的经验公式。由于风速分布的右偏和众数可能不存在或者多于一个的特性，因此，基于集合预报10 m风速众数的订正方法需要对集合预报各个成员按照风速大小排序并进行分组，参照下限公式(罗晓娟，2003)求解唯一的众数值。众数求解的下限公式如下：

$ {{M}_{0}}=L+\frac{{{f}_{0}}-{{f}_{1}}}{\left({{f}_{0}}-{{f}_{1}} \right)+\left({{f}_{0}}-{{f}_{2}} \right)}K $

(1)

式中，L表示众数组(众数所在区间)下限值，f₀、f₁、f₂分别表示众数组及与众数组相邻的前一组及后一组的频数，K表示众数组的组距。众数组的划分对于平均误差及偏差概率的计算有较大的影响，众数组划分过大会导致订正效率的降低，而众数组划分过小又不能反映出众数的特性，因此需要根据样本量大小及观测范围选用合理的区间划分。经过样本统计计算，计算风速众数采用等间距分组，组距为3 m·s^-1。对于如何更准确地确定众数在众数组中的位置，目前仍存在着一定的争议。因此在使用上述众数求解公式时需要基于众数组内数据是均匀分布的假设(张保林，2014)，即假设众数组内各个预报成员为均匀分布。风是矢量，不利于众数的求解与平均误差的确定，因而本文仅考虑基于风速的订正，风向则采用集合预报的平均风向。

2.2 订正方法

基于集合预报10 m风速众数订正方程可以表示为如下：

$ Y={{M}_{0}}+f\left({{{{M}'}}_{0}} \right) $

(2)

式中，Y为订正后风速值，M₀为所预报时刻集合预报众数值。f(M′₀)为订正误差，M′₀为求解集合预报历史数据中的众数。对于不同预报时效、不同风速量级，预报的偏差概率及偏差程度均不相同，对应的订正量也不同。同时，为避免对M₀造成盲目订正，通过集合预报历史数据中风速众数值的预报概率将众数进行分组，计算不同等级风速、不同预报时效的f(M′₀)，按照预报正确、预报偏大、预报偏小3种情况分别进行考虑。将f(M′₀)写成如下分段函数：

$ f\left({{{{M}'}}_{0}} \right)=\left\{ \begin{align} &0 \\ &-{{e}_{\text{d-1}}}\ \ \ \ {{M}_{0}}\in \left({{L}_{1}}, {{L}_{1}}+{{P}_{\text{d}}}\cdot K \right)\ \\ &-{{e}_{\text{x+1}}}\ \ \ \ {{M}_{0}}\in \left({{L}_{2}}-{{P}_{\text{x}}}\cdot K, {{L}_{2}} \right) \\ \end{align} \right. $

(3)

式中，e_d-1和e_x+1分别为集合预报历史数据中众数在某一预报时效中对某一量级风速的相邻量级风速预报的平均偏大误差和平均偏小误差，L₁和L₂分别表示该级别风速上限及下限值，P_d和P_x分别表示历史数据中众数值对该量级、该预报时效预报的偏大概率和偏小概率，K表示组距宽度(取3 m·s^-1)。当偏大概率或偏小概率越大时，所对应的区间宽度也就越大，表明众数预报偏大或偏小的可能性也就越大，因此对其订正的概率也就越大；当众数不在偏大或偏小区间内时，则认为众数预报正确，不进行订正。一个较大的风速实况通常对应一个较小的众数预报值，而一个众数值却对应多个可能出现的实况观测值。为了使统计误差具有明显的规律性，需要以实况为基准计算众数的误差，但是将这种误差直接带回公式是不合理的，因此假设众数落在订正区间是由相邻风速量级预报偏大、偏小造成。偏大概率及偏小概率计算公式如下：

$ {{P}_{\text{d}}}=\frac{N{{B}_{k}}}{N{{A}_{k}}+N{{B}_{k}}+N{{C}_{k}}} $

(4)

$ {{P}_{\text{x}}}=\frac{N{{C}_{k}}}{N{{A}_{k}}+N{{B}_{k}}+N{{C}_{k}}} $

(5)

式中，P_d和P_x为预报偏大概率和预报偏小概率，NA_k为预报正确次数，NB_k为预报偏大次数，NC_k为预报偏小次数。平均偏大误差及平均偏小误差则根据平均误差及平均绝对误差计算得到，公式如下：

$ {{e}_{\text{d}}}=\frac{\bar{b}+|\bar{b}|}{2} $

(6)

$ {{e}_{\text{x}}}=|\bar{b}|-{{e}_{\text{d}}} $

(7)

式中，e_d和e_x分别表示平均偏大误差及平均偏小误差，b和|b|则分别为历史预报数据中众数的平均误差和平均绝对误差。

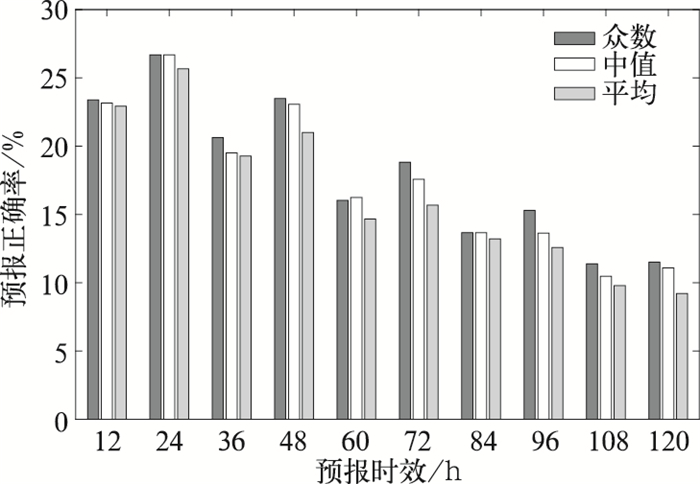
2.3 众数预报特性分析

利用2013—2014年集合预报数据进行相应的预报误差及预报概率的检验，集合预报风速数据按照3 m·s^-1组距进行划分。众数在各个预报时效的预报准确率均略高于中值、平均值，中期预报时效表现相对明显。如图 2所示，在96~120 h预报时效，众数预报正确率高于中值，明显高于集合平均，因此基于众数进行风速订正要优于基于中值或平均值，可以有效提高订正后的预报效果。

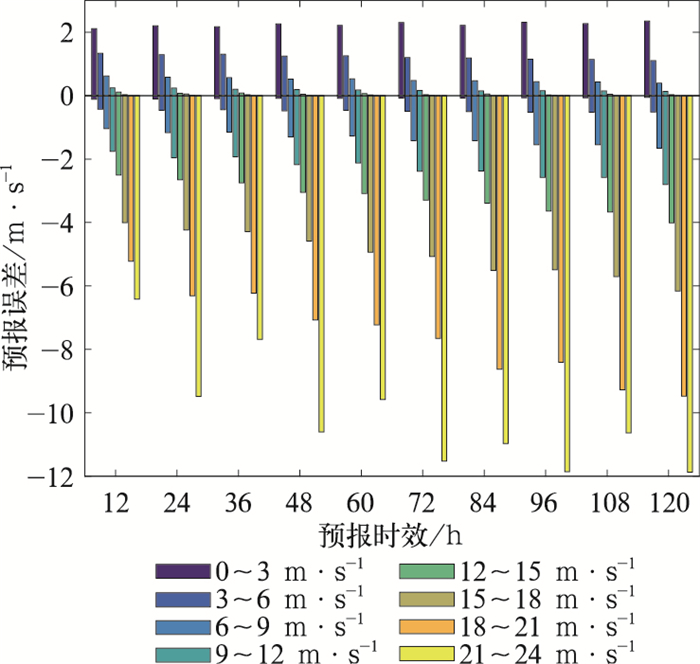
众数对于小于9 m·s^-1的风速预报存在0.4~2.4 m·s^-1的平均偏大误差，大于9 m·s^-1风速的预报明显偏小，并随预报时效延长、量级的增加，偏小的程度加大。18 m·s^-1以上风速的预报，偏小误差均在5 m·s^-1以上，当预报时效增加到84 h时，偏小误差可达8 m·s^-1以上(图 3)。众数预报的平均偏小概率同样随风速量级增大、预报时效延长而增加，15 m·s^-1以上的风速预报其偏小概率基本达到90%及以上，对于21 m·s^-1以上风速的预报，预报偏小概率为100%(表 1)。在短时效或风速较小时，预报偏差由预报偏大和偏小共同造成；但当预报时效延长或所预报风速增大时，预报偏差主要由预报偏小造成。

3 结果与检验 3.1 站点检验

利用2015年ECMWF集合预报10 m风场资料及代表站点对于订正后结果进行检验，并按照风速级分别为2~3级、4~5级、6~7级、8~9级的划分计算订正前(M₀)与订正后(Y)的平均误差及TS评分。

通过计算订正前后平均偏小误差的减小率可以看出(表 2)：风速2~3级和4~5级的订正效果并不明显，平均偏小误差的的减小率基本为0，而对于风速6~7级和8~9级的风速偏小误差有明显改进，其中12~120 h预报时效的6~7级风速预报的偏小误差减小率平均为21%，8~9级风速偏小误差减小率平均为55%。订正效果与众数预报误差是相一致的，众数对于2~3级和4~5级风速的预报效果相对较好，订正后效果不明显；但众数对于6~7级和8~9级预报效果较差，订正后偏小误差改进效果较大。

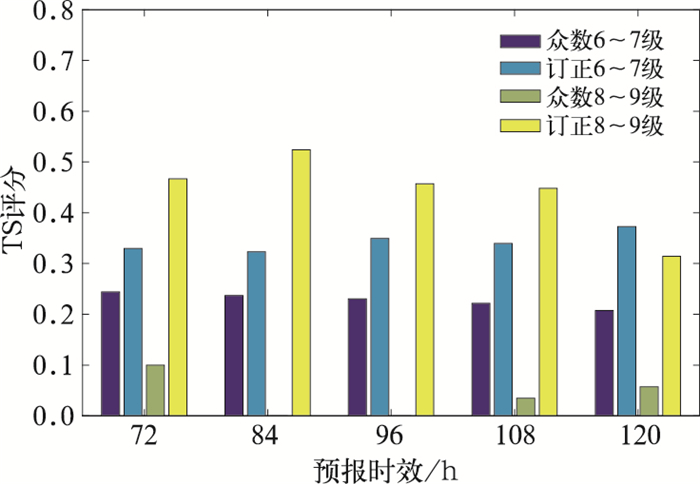
利用代表站点进行订正前后TS评分对比结果(图 4)表明，订正后对大于72 h预报时效的6级以上风速的TS评分提高明显。订正后72~120 h预报时效的6~7级和8~9级风速预报的TS评分明显高于订正前。6~7级风速预报的平均TS评分由0.23提高到0.34；8~9级风速的订正效果更为明显，平均TS评分由0.04提高到0.44。

3.2 个例检验

为了进一步验证该订正方法对于我国近海大风过程的预报性能，选取2015年11月6—7日冷空气及2015年10月3日1522号台风彩虹洋面大风天气过程进行对比分析。

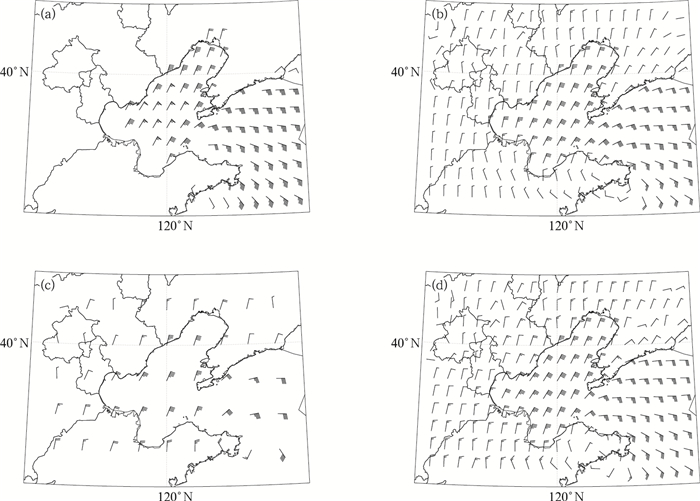
2015年11月6—7日，受入海气旋及冷空气的影响，造成我国渤海、渤海海峡、黄海等海域出现大风天气过程，观测的最大平均风速达9级。图 5为15年11月7日08时(北京时，下同)实况观测及10时ASCAT卫星反演风场。ASCAT卫星反演风场已被逐渐应用于洋面风的业务预报(张增海等，2014；姚日升等，2016)，以弥补洋面实况观测资料的稀少。由于ASCAT的反演原理及风的瞬时性，导致ASCAT反演风场与实况会存在一定的偏差。杨晓君和张增海(2014)利用北方海域的6个观测站点进行ASCAT反演风场的对比检验，当风力在6~7级时卫星呈现出低估现象，风力在8级以上时卫星低估现象明显加剧。在图 5中，我国渤海海域出现了较大范围20 m·s^-1的ASCAT反演风场，因而实际中渤海海域风速要大于20 m·s^-1。对比业务预报中使用的日本、GFS、EC确定性模式36 h预报可以看出(图 6b、6c和6d)，3家模式对渤海海域大风预报明显偏弱。用众数订正风场的36 h预报(图 6a)在渤海地区预报出了较大范围的20~22 m·s^-1的风速区域，与ASCAT反演风场更为接近，可以更有效的对此次大风天气过程起到预报指示作用。

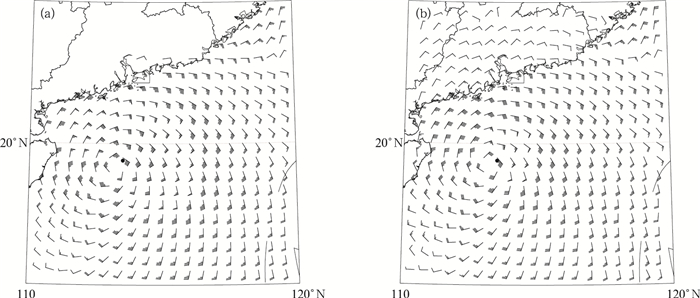
2015年10月3日20时，1522号台风彩虹中心位于19.4°N、113.5°E，中心附近最大风速38 m·s^-1。通过对比订正后风场与EC确定性模式2日20时24 h预报风场可以看出(图 7)，众数方法订正后台风中心的风场预报为32 m·s^-1，EC确定性模式的预报为26 m·s^-1，订正后的风速与实况更为接近。

4 结论

集合预报10 m风速众数在各个预报时效的预报正确率要高于集合中值及平均值，基于集合预报众数建立的洋面风速订正方法可以对集合预报产品有更好的释用。综合考虑历史数据的预报概率及集合预报各个成员的分布情况进行客观订正，可减少不必要的订正或错误订正的出现。

风速的订正效果与众数预报误差特征相对应，订正后72~120 h预报时效的6~7级和8~9级风速预报的TS评分明显高于订正前。6~7级风速预报的平均TS评分由0.23提高到0.34，8~9级风速的订正效果更为明显，平均TS评分由0.04提高到0.44，能够有效提高中长期时效和大量级风速的预报能力。该订正方法中的订正参数均是由沿岸及近海的代表站点统计得到，因此代表站点的选取对于订正效果有着重要影响，在实际业务中应根据不同的适用区域选用合理的代表站点。