2. 河海大学水文水资源学院,南京 210098;
3. 河海大学水文水资源与水利工程科学国家重点实验室,南京 210098;
4. 江苏省水文水资源勘测局, 南京 210029;
5. 淮河水利委员会水文局(信息中心), 蚌埠 233001
2. College of Hydrology and Water Recourses, Hohai University, Nanjing 210098;
3. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098;
4. Hydrology and Water Resources Investigation Bureau of Jiangsu Province, Nanjing 210029;
5. Bureau of Hydrology, Huaihe Water Conservancy Committee, Bengbu 233001
洪水灾害是自然态洪水异常变化造成的,威胁国民经济发展与社会进步,是给国家与人民群众造成生命财产损失最常见和危害最大的自然灾害之一(Sapir et al,2004)。洪水预报作为一项重要的防洪非工程措施,是根据洪水运动规律与形成机理,借助流域地形地貌、气象、水文等信息,预测洪水发生与过程变化,是减少洪灾损失的最重要手段和方法之一(Anderson and Burt, 1985;Maidment,1993)。随着近三十年来的定量降水预报、降雨径流预报、“3S”以及计算机等技术快速发展,融入预见期降水的气象水文耦合的洪水预报方法已成为江河流域防汛、中小河流洪水与山洪灾害防治的最主要的措施之一(Warner et al,1991;Bae et al,1995;Schaake et al,2006;Pappenberger et al,2008;陶诗言等,2003;崔春光等,2010;刘志雨等,2010;王莉莉等,2012;包红军等,2016)。
目前,数值天气预报技术已经成为流域格点化定量降水预报(15 d)的主要依据(张利平和夏军,2000;陶诗言等,2003;姜晓曼等,2014;胡淳焓等,2015;Hólm et al,2016;刘艳等, 2016)。在我国,全球模式预报性能提升促使中短期业务预报能力得到不断增强,但对于容易引发灾害的中小尺度天气系统降水难以捕捉(毛冬艳等,2014)。而对于洪水预报而言,降水预报的时段、雨带位置与量级的微量偏差都可能引起截然不同的洪水效应。在我国,中央气象台预报员的主观预报降水在这一方面要高于世界上先进的数值天气预报模式(毕宝贵等,2016;代刊等,2016),但发布的业务产品往往以落区等级预报为主,难以定量化与格点化(端义宏和金荣花,2012)。
大流域内往往存在水库、闸坝、行蓄洪区等多种水利工程,流域水文系统的降雨径流与洪水过程预报是一个十分复杂的问题。其随机性和非线性在复杂大流域尤为明显(葛守西,1999;包红军等,2009)。国内外学者针对流域洪水预报的复杂性,往往引入流域降水预报作为预见期内的降水输入强迫,驱动流域水文模型进行气象水文耦合的洪水预报,旨在提升预报精度与延长预报的预见期(Pappenberger et al,2005;Cloke and Pappenberger, 2009;Bao et al,2011;Bao and Zhao, 2012;李致家等,2004;宋星原等,2007;崔春光等,2010;包红军和赵琳娜,2012a)。目前,在大流域中,多种水利工程干预下的流域产汇流过程已经发生较大改变,流域洪水预报单元需要被精细化细分,对高分辨率格点化的定时、定点、定量的降水预报产品需求进一步提升,并且包括行蓄洪区在内的水利工程本身在流域产汇流计算中的处理方式对洪水预报精度也有较大的影响;国内水文业务预报中用于降雨径流预报的水文模型有新安江水文模型(赵人俊,1984)、经验预报API模型、陕北模型(赵人俊,1984)等,在我国湿润、半湿润地区新安江模型具有广泛的适用性与预报精度;进行河道洪水水位预报的传统水文学方法经验性较强,模拟精度往往不高,而一维、二维非恒定流水动力学方法能较好地解决水位模拟,但其对河道断面等资料要求较高,计算较为繁琐,水文水力学耦合模型是解决的主要方法(包红军,2009)。目前如何在复杂大流域洪水预报中,实现精细化降水预报与水文水动力学耦合,以有效提高流域洪水预报精度与延长预报预见期是洪水预报的技术难点与重点。
本研究以淮河鲁台子以上流域为例,建立复杂大流域气象水文耦合的洪水预报模型。模型利用基于主客观融合降水反演、降水统计降尺度、降水时间拆分等技术的高分辨率格点化定量预报降水(曹勇等,2016),作为流域洪水预报预见期内驱动降水,以河道汇流为主线, 流域源头和支流采用降雨径流预报的分布式结构进行流域洪水预报。其中,降雨径流模拟采用新安江水文模型;淮河干流王家坝至鲁台子区间(具有行蓄洪区的复杂河系洪水)采用水文水动力学耦合方式,建立基于扩散波与水文学柱蓄和楔蓄理论的Muskingum-Cunge水位流量演算模型进行预报。淮河钐岗分流量利用分流曲线推求,引入虚拟线性水库法用来解决大洪水时支流顶推作用,临淮岗水利工程作为内边界处理,利用分流比概化行洪过程,行洪区内进行一维水流演算,蓄洪区不考虑洪水演进,只进行水量平衡计算。以2016年淮河流域汛期洪水进行预报检验。
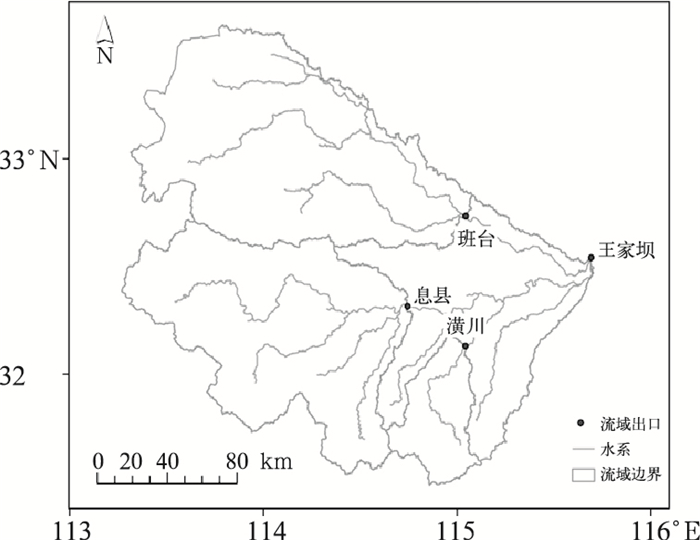
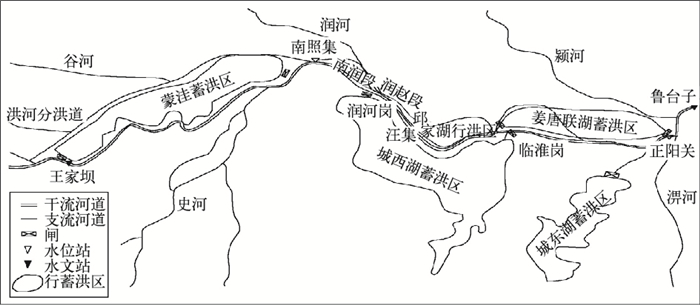
1 试验流域概况淮河流域发源于河南省桐柏山,在江苏省境内三江营注入长江,干流全长约1000 km。淮河流域分上、中、下游,洪河口以上为上游,落差大、水流急;洪河口至三河闸为中游,河道坡降平缓,沿干流两侧多湖泊洼地,淮河中游洪水在此蓄滞回旋;三河闸以下为下游。鲁台子处于中游,鲁台子以上流域汇水面积为8.86万km2。王家坝以上为淮河上游,王家坝站是上游的总控制站,集水面积为30672 km2。根据流域内水文站的布设和自然流域的边界,将流域划分为4个子流域:息县子流域、班台子流域、潢川子流域以及3个子流域至王家坝区间子流域(图 1)。干流王家坝至鲁台子段河系洪水预报是河道汇流为主线,源头及区间流域采用降雨径流预报的分布式结构(图 2)。淮河干流王家坝至鲁台子属中游河段,该河段内支流多、水量大量集中,集中淮河水量达80%;地形复杂、位置重要,有3个行洪区:南润段、润赵段、邱家湖,4个蓄洪区:蒙洼、城西湖、城东湖、姜唐联湖。淮河中游一直是淮河流域防汛的重点。将上游王家坝站洪水预报过程作为淮河中游干流王家坝至鲁台子河道洪水演算模型的上边界条件,对中游具有行蓄洪区的河系进行洪水预报。
|
图 1 淮河上游流域概化图 Fig. 1 Sketch of the upper stream of Huaihe River |
|
图 2 淮河中游王家坝至鲁台子河系概化图 Fig. 2 Sketch of the river basin from Wangjiaba to Lutaizi Stations of Huaihe River |
由于数值模式不断地发展和成熟,其降水预报的准确率也在逐步提升(Lalaurette et al,2009),通过模式后处理技术,降水预报的准确率在模式基础上又进一步提高(赵声蓉等,2012;Yuan,2007),但因大气固有的混沌效应、模式初值的误差及物理过程参数化等原因(Lorenz,1972),定量降水预报依旧需要预报员根据自身对大气物理过程的认识和经验,以及对模式误差特性的了解,进行主观订正。这也是当前国内外定量降水预报业务中提高降水预报准确率的主要方法。为了减少预报员主观订正后的降水落区预报的精细化程度降低、空间精细分布丢失,中央气象台格点化定量预报降水产品通过一系列统称为降水信息恢复技术的应用,在预报员主观等级落区预报的基础上,采用主客观融合降水反演、降水统计降尺度和降水时间拆分技术,恢复降水分布的局部信息和特征,提高降水预报的精细化程度(曹勇等,2016)。
主客观融合降水反演技术主要实现与业务模式分辨率相当的粗网格格点化定量降水预报产品。利用等级识别算法,结合预报员主观等级落区预报,识别空白格点场的每个格点降水所在等级并标记;采用分等级反距离权重客观分析算法保证客观分析结果严格遵守预报员的主观落区预报,避免分析结果出现跨等级违背预报员预报意图的情形;最后使用主客观融合算法将预报格点靠近预报员的落区等值线时给予主观格点预报更大权重,远离预报员的落区等值线时给予参考客观格点预报更大权重。
降水降尺度目的是获取更精细空间尺度的降水格点场。传统的双线性插值方法难以考虑气象意义,动力降尺度依赖于数值模式性能与计算机资源(Tobin et al,2011;Pavlik et al,2012),统计降尺度已经成为实际预报业务中提高降水空间分辨率的捷径方法(Schaake et al, 2004)。中央气象台格点化降水产品采用降尺度比例矢量技术,利用粗分辨率与细分辨率的定量降水估测产品,建立大尺度降水到小尺度降水的气象统计关系并确定降尺度比例矢量,体现不同空间尺度降水的气象关系。
降水时间拆分技术主要是提高降水预报的时间分辨率,能将预报员的订正信息合理地分配于各个精细化预报时段内,在提高降水预报时间分辨率的同时也提高精细化时段内的降水预报准确率。其原理是:假定业务预报参考的模式降水能够较好反映降水过程分布,仅是预报量级上精度不够,可以把预报员的精细化降水与数值预报模式降水高分辨率时间尺度相结合,提高时间分辨率。
2.2 流域降水径流预报流域降水径流模拟采用新安江水文模型,考虑到流域汇流时间,王家坝站的洪水预报预见期在3 d左右,鲁台子站在5 d以上,本研究的时间步长取为6 h。
2.2.1 有资料流域新安江水文模型率定上游淮北片班台以上流域由于流域水利工程和调度方式复杂, 受人为影响较大, 对资料条件较好的10场洪水进行率定。对阜阳区间流域, 考虑周口以及茨河铺闸人为控制的放水流量, 选择1984—2010年12场完整的典型洪水进行模型率定与检验。淮河上游息县子流域、潢川子流域、王家坝子区间流域、史河蒋家集流域、淠河横排头流域等5个子流域分别选取1991—2010年的15~25场不等的典型洪水进行基于人工试错法的模型参数率定与检验(表 1为各个子流域模型率定参数取值表)。根据《水文情报预报规范》(中华人民共和国国家质量监督检验检疫总局等,2009), 除了阜阳流域为乙等精度标准以外,均达到甲级精度标准。
|
|
表 1 淮河鲁台子站以上流域各子流域水文模型参数率定表 Table 1 Model parameters calibration results of sub-basins in the Upper Reaches of Huaihe River above Lutaizi Station |
班台流域内水库控制面积占总流域面积的二分之一,并且流域下垫面土壤有明显的三层分布,即上层壤质较为松散,易于降水下渗,下层壤质密实,不易渗透,中间层为降水难以下渗的犁地层。在上层土壤蓄满后,中间层形成的水流分为三部分:其一沿大孔隙补给地下水,其二下渗给下层土壤, 剩余的侧向运动形成壤中流。在这类地区,虽然在雨量大时或雨强大时会以蓄满或超渗两种方式形成地表径流,也有上述的壤中流,但由于土层中大孔隙的存在,地下径流所占比例可达总径流量的60%左右,土壤水和地下水的蒸发也比较多。因此水文模型要能反映这个特点。本研究中,考虑到属于洼地较多的平原坡水区,新安江模型的SM和K都比一般情况下的数值要大,Muskingum法中的参数X值应比较小,来弥补结构上的差异。实践证明,模型的模拟效果良好, 尤其在大水时, 模型结构差别的影响相对来说就不太显著了(包红军,2009;包红军等,2009)。图 3为班台流域20060720次洪水预报过程。

|
图 3 班台流域20060720次洪水预报过程图 Fig. 3 Forecasts hydrograph of Bantai Basin (Flood number 20060720) |
蒋家集至干河汇合处、谷河、润河集以及阜阳、模排头至干河的区间面积有8730 km2,占鲁台子以上流域总面积的8.7%。为了解决这部分地区的产汇流计算,这里借鉴文献(包红军,2009)的研究成果:选淮北王市集小流域为代表性流域,用新安江模型进行产汇流计算,而后把参数移置到区间上。
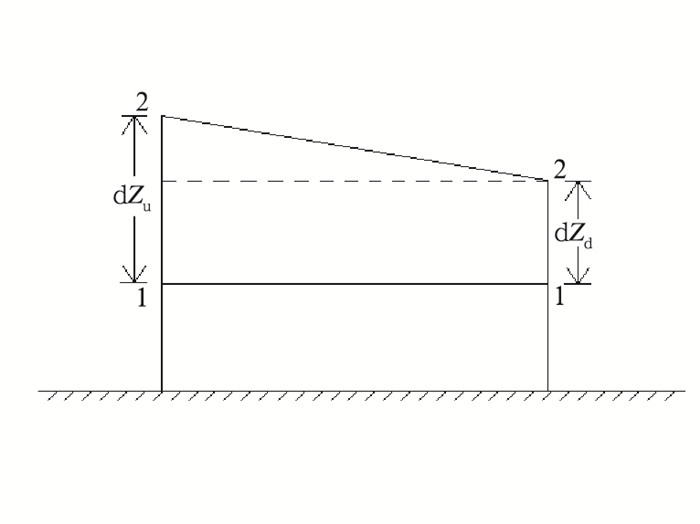
2.3 复杂水系洪水预报模型 2.3.1 基于扩散波与柱蓄和楔蓄理论的Muskingum-Cunge水位流量预报法Muskingum-Cunge法的参数基于河道物理特征推求,这就避免了Muskingum法对大量历史数据的需求(包红军,2009),但其不能直接进行河道水位预报。本研究以Muskingum-Cunge法为基础,结合水文学柱蓄和楔蓄理论与扩散波非线性水位法,建立考虑行蓄洪的Muskingum-Cunge水位流量预报法。主要思路是首先通过Muskingum-Cunge法模拟出河道各断面流量,然后根据水文学柱蓄和楔蓄理论推导得到的水位流量关系计算出上边界(或下边界)水位,再用扩散波非线性水位法计算出其余河道断面水位。该法优势是在有限的资料条件下能解决传统水文学方法较难解决的水位模拟问题,而且与水动力学方法相比,又具有计算简便、断面资料要求少等优越性,在往往缺少河道断面与水文资料的气象部门有很好的适用性。Muskingum-Cunge法与扩散波非线性水位法请参见文献(Maidment,1993;包红军,2009),这里只给出根据水文学柱蓄和楔蓄理论推导水位流量关系过程。在图 4中,设河道的起始水面线为1-1,经dt时间后水面变为2-2,河道槽蓄量增量dW为:
| $ {\rm{d}}\mathit{W}{\rm{ = }}{\mathit{B}_{\rm{w}}}{\mathit{L}_{\rm{l}}}{\rm{d}}{\mathit{Z}_{\rm{d}}}{\rm{ + }}{\mathit{B}_{\rm{w}}}{\mathit{L}_{\rm{l}}}\mathit{x}{\rm{(d}}{\mathit{Z}_{\rm{u}}}{\rm{ - d}}{\mathit{Z}_{\rm{d}}}{\rm{)}} $ | (1) |
|
图 4 柱蓄和楔蓄图 Fig. 4 Sketch of columbar storageand wedge storage |
通过积分可得
| $ \begin{array}{l} \mathit{W}{\rm{ = }}{{\mathit{\bar B}}_{\rm{w}}}{\mathit{L}_{\rm{l}}}{\mathit{Z}_{\rm{d}}}{\rm{ + }}{{\mathit{\bar B}}_{\rm{w}}}{\mathit{L}_{\rm{l}}}\mathit{x}\left({{\mathit{Z}_{\rm{u}}}{\rm{ - }}{\mathit{Z}_{\rm{d}}}} \right){\rm{ - }}\\ \;\;\;\;\;\;{{\mathit{\bar B}}_{\rm{w}}}{\mathit{L}_{\rm{l}}}\mathit{x}{\rm{(}}{\mathit{Z}_{{{\rm{u}}_{\rm{0}}}}}{\rm{ - }}{\mathit{Z}_{{{\rm{d}}_{\rm{0}}}}}{\rm{) + }}{\mathit{W}_{\rm{0}}} \end{array} $ |
式中,x为反映水面形状的系数;Bw与Ll分别为水面宽及河长(单位:m),Bw为河段平均水面宽;Zu0和Zd0分别为河段上、下断面的河底高程(单位:m)。假定W′=BwLlxZu0+BwLl(1-x)Zd0和Z=xZu+(1-x1)Zd,考虑到非棱柱河道中断面沿程变化,令FV=BwLl,F为河道水面面积(单位:m2),V为非棱柱河道中断面沿程的变化,结合物理意义得到的W0=0,则:
| $ \mathit{W}{\rm{ = }}{\mathit{F}^\mathit{V}}\mathit{\bar Z}{\rm{ - }}\mathit{W'} $ | (2) |
根据假定水面线近似为直线,涨水与落水时中断面水位不变为恒定流水位Z(单位:m),河道蓄量又可表示为(Li et al,2008):
| $ \mathit{W}{\rm{ = }}{\mathit{F}^\mathit{V}}{\mathit{Z}_{\rm{u}}}\left[ {{\rm{1 + }}\frac{{{\mathit{L}_{\rm{l}}}{\rm{(}}{\mathit{i}_{\rm{0}}}{\rm{ + }}{\mathit{i}_{\rm{\Delta }}}{\rm{)}}}}{{{\rm{2}}{\mathit{Z}_{\rm{d}}}}}{\rm{ - }}\mathit{W'}} \right] $ | (3) |
式中,i0为河底比降,iΔ为洪水波的附加比降。综合式(2) 与式(3),可以得到得:
| $ {\mathit{Z}_{\rm{u}}}{\rm{ = }}\mathit{\bar Z}{\rm{ - }}\frac{{{\mathit{L}_{\rm{l}}}{\mathit{i}_{\rm{0}}}{\rm{(1 + }}\frac{{{\mathit{i}_{\rm{\Delta }}}}}{{{\mathit{i}_{\rm{0}}}}}{\rm{)}}}}{{\rm{2}}} $ | (4) |
在特征河长公式中
| $ {\mathit{Z}_{\rm{d}}}{\rm{ = }}\mathit{\bar Z}{\rm{ - }}\frac{{{\mathit{L}_{\rm{l}}}{\mathit{i}_{\rm{0}}}}}{2}{\rm{ + }}\frac{{{\mathit{L}_{\rm{l}}}{\mathit{i}_{\rm{0}}}}}{2}\mathit{E}\frac{{{\rm{\Delta }}\mathit{Q}}}{{\mathit{Q}_0^{^\mathit{\beta }}}} $ | (5) |
式中Qu和Qd分别是河段上、下断面的流量(单位:m3·s-1)。这样,与Muskingum-Cunge法结合,实现水位模拟。
2.3.2 钐岗分流与旁侧入流处理钐岗的分流量由王家坝与钐岗的分流关系曲线确定。王家坝闸的分流量根据闸门运行方式和水流的实际形态,采用恰当的水力学公式计算。钐岗的分流曲线采用统计实测期(1996—2004年汛期)内的资料拟合成如下分流关系:
| $ \begin{array}{l} {\rm{若}}{\mathit{Q}_{{\rm{王家坝总}}}} \ge {\rm{300}}{{\rm{m}}^{\rm{3}}}{\rm{\cdot}}{{\rm{s}}^{{\rm{ - 1}}}}{\rm{, }}\\ {\rm{则}}{\mathit{Q}_{{\rm{钐岗}}}}{\rm{ = 334}}{\rm{.1154 - 32}}{\rm{.8561 \times }}\mathit{Q}_{{\rm{王家坝总}}}^{{\rm{0}}{\rm{.5}}}{\rm{ + 0}}{\rm{.8138 \times }}{\mathit{Q}_{{\rm{王家坝总}}}} \end{array} $ | (6) |
| $ {\rm{若}}{\mathit{Q}_{{\rm{王家坝总}}}}{\rm{ < 300}}{{\rm{m}}^{\rm{3}}}{\rm{\cdot}}{{\rm{s}}^{{\rm{ - 1}}}}{\rm{, 则}}{\mathit{Q}_{{\rm{钐岗}}}}{\rm{ = 0}} $ | (7) |
王家坝至鲁台子河段全长约155.16 km。根据中间的水文水位站支流的汇入位置和行蓄洪区位置情况,河段共分10段(图 5)。

|
图 5 王家坝至鲁台子河段概化图 Fig. 5 Sketch of channel partition from Wanjiaba to Lutaizi Stations of Huaihe River |
把钐岗分流后与地理城的流量作为旁侧入流合并,从断面5演算至淮河干流。此外,中游支流蒋家集、阜阳和横排头也分别作为旁侧入流从断面4、断面10演算至淮河干流。为了解决大洪水时支流洪水受干流顶托作用,直至退水期才能进入干流,这里借鉴文献(包红军等,2011)的做法:在支流末端与干流交汇处设虚拟线性水库法,即支流洪水必须经过水库调蓄后才能进入干流。
考虑到流域下垫面变化情况,选取淮河1996—2007年汛期洪水资料进行检验。对于Muskingum-Cunge水位流量演算模型而言,当河道比降大时,属于运动波,先计算出上边界水位,反之先计算出下边界条件。淮河干流河道比降较低,因而采用扩散波非线性水位法自下游向上游推求水位。通过在1996—2007年洪水的检验,该处理方式具有一定的效果,洪水模拟精度较高(表 2)。
|
|
表 2 王家坝至鲁台子河段洪水模拟结果表 Table 2 Flood simulation results of the channel between Wangjiaba to Lutzizi Stations |
2016年汛期(6—7月),淮河鲁台子站以上流域在6月1—2、5—8、21—22、24—25、7月1—2、5—8、13、15—16和18—22日等发生多次强降水过程,分别形成6月30日至7月8日,7月18—30日两次明显的洪水涨落过程(洪号分别记为20160630与20160718),特别是后者,致使王家坝水文站于7月22日01时达到警戒水位27.50 m,并持续上涨。洪峰水位出现在7月22日14时,为27.86 m,洪峰流量出现在7月22日08时,为3570 m3·s-1,并形成了2016年淮河第一号洪水,给淮河流域防汛减灾造成较大的压力。
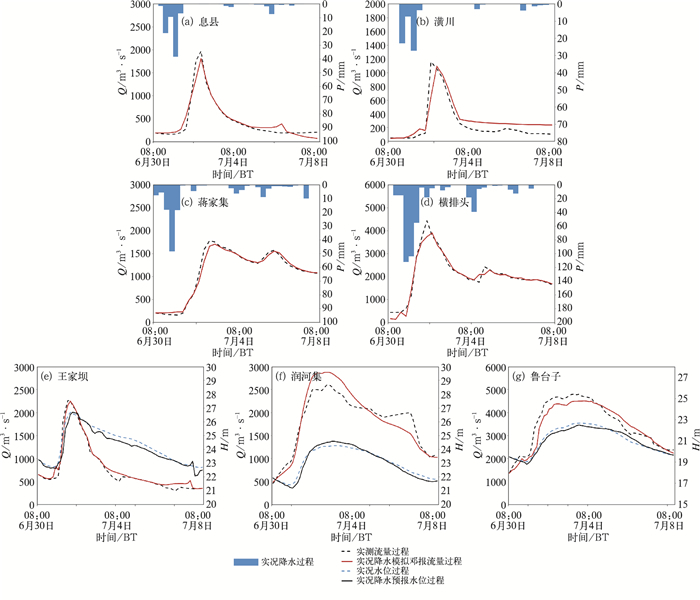
7月1—8日的强降水主要在研究流域的上游与右岸,上游息县站、潢河潢川站、史河蒋家集站、淠河横排头站以及干流王家坝站、润合集站、鲁台子站均形成了洪水过程,而流域偏北的洪汝河班台站、颍河阜阳站没有形成洪水过程。图 6a~6g分别是上述流域的洪水模拟预报过程(起报时间6月30日08时),表 3和表 4为本次洪水预报统计特征值。由模拟结果可以看出,模型预报的7个断面的洪峰误差均小于20%,峰现时间误差都在1个时间步长以内,6个预报断面的径流深误差<10%,7个预报断面的确定性系数均大于0.70,并且有5个预报断面的确定性系数>0.90;其中潢川站径流量模拟预报误差>20%,主要表现在洪水退水上模拟偏大,主要原因是潢川流域前期降水相对不多,本次洪水是流域2016年度第一次较大量级的洪水过程,流域降水累计也只有70.5 mm,其中一部分降水用于流域土壤缺水补给,这在模型中没有被充分考虑到,这也是该流域洪水预报技术下一步需要着重改进的。对于水位模拟预报,3个干流断面的最高水位出现时间误差均在1个时间步长以内,最高水位误差在0.07~0.31 m,水位确定性系数都大于0.90,可见,所建模型对本次洪水过程预报效果较好。
|
图 6 淮河鲁台子以上流域20160630次洪水模拟图 Fig. 6 Flood simulation results of the Upper Reaches of Huaihe River above Lutaizi Station (Flood number 20160630) |
|
|
表 3 20160630次洪水子流域预报统计特征值表 Table 3 Simulation results of sub-basins in Huaihe River (Flood number 20160630) |
|
|
表 4 20160630次洪水干流预报统计特征值表 Table 4 Simulation results of the main channel in Huaihe River (Flood number 20160630) |
7月18—30日的强降水主要在研究流域的上游与左岸,上游息县站、潢河潢川站、洪汝河班台站、颍河阜阳站以及干流王家坝站、润合集站、鲁台子站均形成了洪水过程,而流域偏南的史河蒋家集站、淠河横排头站没有形成洪水过程。表 5和表 6为各个预报断面预报统计特征值(起报时间7月18日08时)。由表结果可以看出,模型预报的6个断面的洪峰误差和径流深误差均小于20%,6个预报断面的峰现时间误差都在1个时间步长以内且确定性系数均大于0.80,并且有3个预报断面的确定性系数>0.90;对于水位模拟预报,3个干流断面的最高水位出现时间误差均在1个时间步长以内,最高水位误差在0.13~0.34 m,确定性系数都大于0.70。从这两场洪水的模拟预报结果分析可以得出,所建模型在2016年7月的两场淮河洪水模拟预报中取得的精度较高,说明了模型的合理性与可信性。
3.2 洪水实时滚动预报中检验
为了进一步检验基于格点化降水预报的淮河气象水文耦合洪水预报模型在流域2016年汛期洪水预报中的预报性能,选择2016年形成淮河汛期第一号洪峰的洪水过程进行实时预报,格点化降水资料选择中央气象台实时定量降水预报产品(时间步长为6 h,空间分辨率为3 km×3 km),驱动淮河预报模型进行逐日滚动预报(以每日08时为例),分析断面选择息县、王家坝、润河集和鲁台子站。
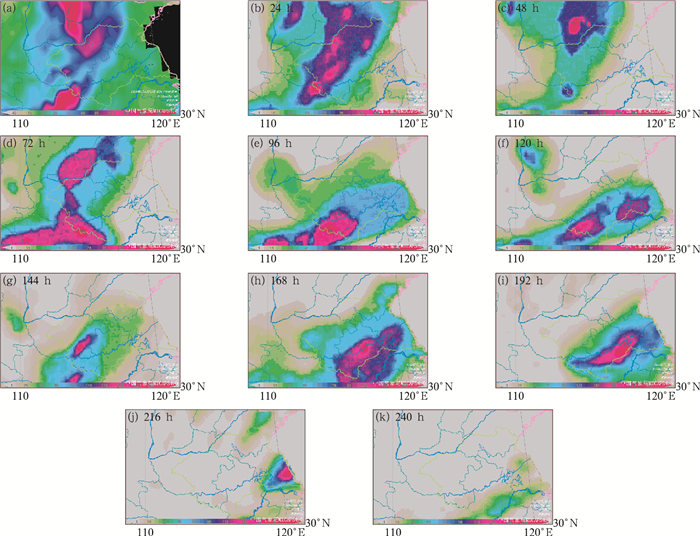
7月18—22日的降水过程的最强日降水发生在7月19日08时至20日08时,淮河鲁台子以上流域的上游与干流北部流域普遍出现了暴雨以上量级的降水,最大降水点出现在上游的鸡公山站,为189 mm。图 7a为降水实况图(分析方法选择CRESSMAN方法),图 7b~7k分别为预报该24 h降水的24~240 h预报时效的格点化降水产品。由图 7可见,在预报时效72 h之内,都能够较为准确地捕逐到研究流域的强降水中心,量级上也比较贴近;96~192 h预报时效内,对上游的强降水的位置与量级有一定的预报能力,但明显低于0~72 h预报时效的精度,对研究流域北侧的强降水出现漏报,预报的强降水偏南;216~240 h预报时效内,对7月19日08时至20日08时的强降水几乎无预报能力。
|
图 7 2016年7月19日08时至20日08时降水实况(a)与不同预报时效预报结果(b~k) Fig. 7 Precipitation observation (a) and forecasts (b-k) in different lead time from 08:00 BT 19 to 08:00 BT 20 July 2016 |
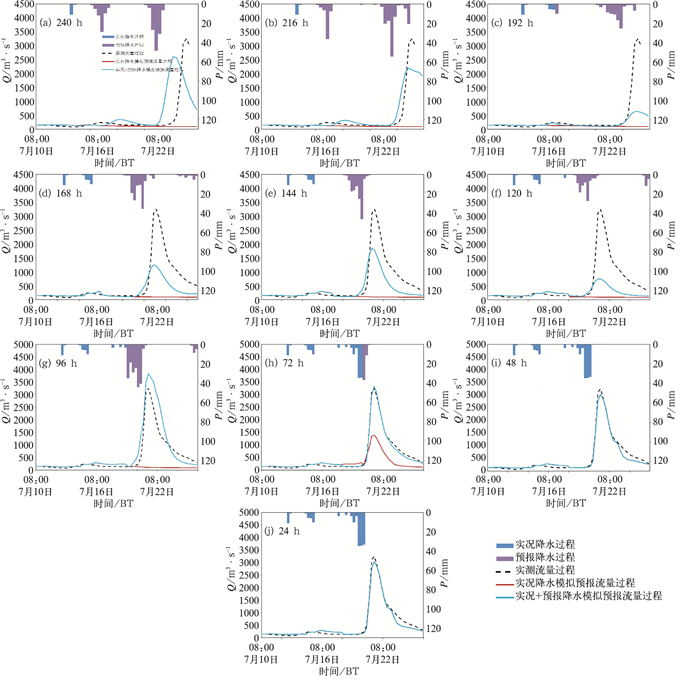
7月18—22日流域强降水过程致使淮河王家坝水位在2016年7月22日超过了警戒水位,并且上游息县站、潢河潢川站、班台站、颍河阜阳站以及干流润河集站、鲁台子站均形成了洪水过程,本研究以此过程进行洪水实时作业预报。降水产品选择7月13日08时至22日08时(逐日08时)预报的240 h预报时效的逐3 h格点化降水。图 8和图 9是不同预见期的息县、王家坝站洪水过程预报过程线。表 7是息县、王家坝、润河集和鲁台子4个断面预报结果统计特征值表。可以得到,对于息县站,在120~240 h预报预见期内,息县洪水过程基本形态是可以预报出来的,但在量级与出现时间还有较大的误差,而不考虑预见期内降水的洪水预报,直到72 h预见期内才有息县洪水过程基本形态的预报,在这一点上提前了168 h。在0~96 h预报预见期以内,息县的洪水过程比较准确地被预报出来,无论在洪水量级、洪峰出现时间上都比较准确,洪峰误差与径流深误差均小于20%,峰现时间误差均为0,确定性系数>0.80,随着预见期的临近,洪水预报的精度在逐步提高。由于在预见期48 h内,无论7月21日08时起报的48 h降水预报与7月22日08时起报的24 h降水预报在息县流域都没有预报降水(图 10和图 11),对洪水径流过程作贡献的降水都是前期实况降水,这也导致在24与48 h预见期的实况和实况加预报的降水模拟预报息县站流量过程线重合。而且,相对于不考虑预见期内降水的洪水预报,洪水预报的预见期从48 h延长至96 h,延长了48 h。
|
图 8 息县站不同预报时效预报结果 Fig. 8 Flood forecasts in different lead time at Xixian Station |

|
图 9 王家坝站不同预报时效预报结果图 Fig. 9 Flood forecasts in different lead time of Wangjiaba Station |
|
|
表 7 2016年淮河汛期洪水预报统计特征值表 Table 7 Flood forecasting results of Huaihe River in rainfall season of 2016 |
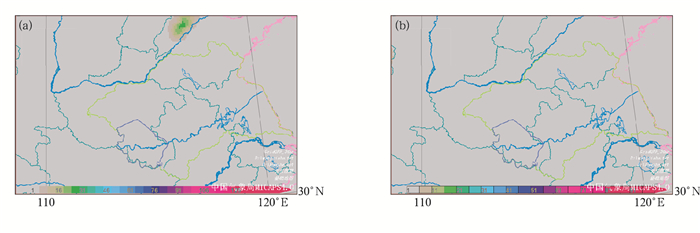
|
图 10 2016年7月21日08时起报的淮河流域24 h(a)和48 h(b)预报时效定量降水预报图 Fig. 10 Grid-based quantitative precipitation forecasts for Huaihe River Basin in the lead time of 24 h (a) and 48 h (b) starting from 08:00 BT 21 July 2016 |
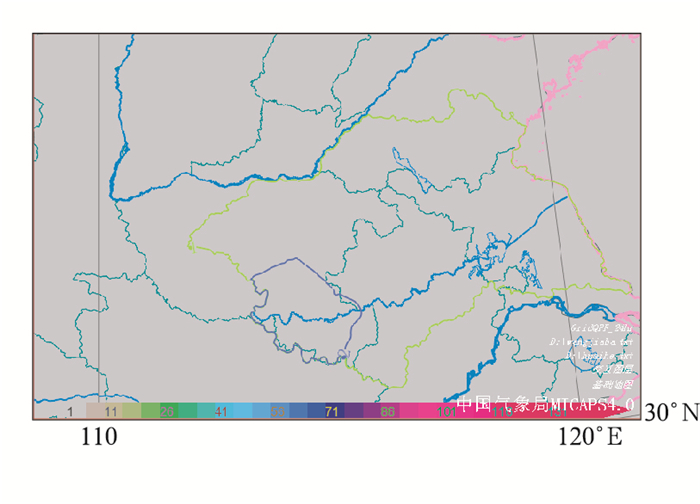
|
图 11 2016年7月22日08时起报淮河流域的24 h预报时效定量降水预报图 Fig. 11 Grid-based quantitative precipitation forecasts for Huaihe River Basin in the lead time of 24 h starting from 08:00 BT 22 July 2016 |
对于王家坝站,也有类似的预报结果:在216~240 h预报预见期内,王家坝站的洪峰已经能够被预报出来,量级上有一定程度上的偏小与提前;在120~192 h预报预见期内,王家坝的洪水过程形状已经能预报出来,峰现时间误差控制在2个时间步长以内,但量级上偏小32.8%~53.8%;24~96 h预报时效内,王家坝的洪水过程已经能够较为准确地被模拟出来,洪峰误差在4.8%~20%,径流量误差为1.5%~19.8%,流量确定性系数为0.93~0.99,达到作业预报的精度要求。与息县预报结果同样原因:由于在预见期48 h内,无论是7月21日08时起报的48 h降水预报,还是7月22日08时起报的24 h降水预报,在淮河王家坝以上流域都没有预报降水(图 10和图 11),对洪水径流过程作贡献的降水都是前期实况降水,这也导致在预见期24与48 h预见期时的实况与实况加预报的降水模拟预报的王家坝站流量过程线重合。而且,相对于不考虑预见期内降水的洪水预报,王家坝洪水预报的预见期从48 h延长至96 h,延长了48 h。王家坝站水位是淮河流域行蓄洪区等水利工程调度等,即防汛减灾措施使用的重要指标之一。
王家坝水位预报中,在120~240 h预报预见期内,水位预报的量级与最高水位出现时间均有较大的误差,至24~96 h预报预见期以内,随着洪水预见期逐渐临近,水位预报精度迅速提升,最高水位出现时间误差也控制在1个时间步长以内,水位确定性系数均在0.85以上。同样的预报效果出现在干流润河集站和鲁台子站。120~240 h预报时效内,流量与水位预报的量级与峰现时间均有较大的误差,至24~96 h预报时效以内,随着洪水预见期逐渐临近,预报精度逐渐提升,峰现时间误差也控制在1个时间步长以内。
4 结论与讨论在洪水预报中引入降水预报信息,采用气象水文耦合方法延长预报预见期,可为防洪减灾赢得更多的应急响应时间。预见期内的降水预报精度是影响洪水预报精度与有效预见期长短的关键因素。本研究针对复杂大流域的洪水预报,以淮河为例,基于中央气象台的业务化格点降水产品驱动,以河道汇流为主线,流域源头和区间采用降雨径流预报分布式结构的气象水文耦合预报模型进行洪水预报。其中,降雨径流模拟采用新安江水文模型;淮河干流王家坝至鲁台子区间具有行蓄洪区的复杂河系洪水预报采用水文水动力学耦合方式,建立基于扩散波与水文学柱蓄和楔蓄理论的Muskingum-Cunge水位流量演算模型进行预报。并针对包括行蓄洪区等水利工程的影响运用较为合理的处理方式。模型在2016年的淮河汛期洪水进行预报检验,取得了较高的预报精度,与不考虑预见期内降水预报的洪水预报相比,流域上游洪水预报预见期延长了48 h,为同类流域的洪水预报提供一定的借鉴。作者认为,针对此类复杂大流域的洪水预报技术,仍需要进行进一步的研究:
(1) 本次研究使用的预报降水是融合预报员降水主观预报、气候背景、精细化地形以及数值模式产品等信息的综合格点化降水预报产品,精度在不同程度上高于原降水预报源。但在实际应用中,对降水不确定性,以及洪水预报的贡献(在本次研究中对预见期延长了48 h)还是不够。随着集合预报技术的不断发展,利用集合预报来考虑降水预报的不确定性也是提高降水预报与洪水预报精度的重要手段。如何结合多模式集合预报与能够捕捉局地中小尺度系统的中尺度模式,形成面向流域洪水预报的高分辨率区域集合预报降水,是提高洪水预报精度与延长洪水预报预见期的重要手段。
(2) 流域水文模型是洪水预报与调度的核心部分。本研究使用的水文模型是在中国洪水预报作业中应用最广泛的新安江水文模型。目前,水文模型的发展已经进入分布式水文模型的阶段。随着大型计算能力、GIS、遥感等新技术不断进步,融合概念性降雨-径流模型和具有物理基础汇流技术的栅格型分布式水文模型是面向洪水预报的水文模型发展方向。如何在大流域的洪水预报中使用分布式水文模型,考虑模型不确定型与参数化方案选择,实时获取每个格点上水文预报要素及其同化技术,是下一步在洪水预报中使用分布式水文模型的重要研究点之一。
(3) 对于考虑行蓄洪区的河系洪水预报,本研究采用的是基于扩散波与柱蓄和楔蓄的Muskingum-Cunge水位流量预报法,行洪区内考虑洪水演进,蓄洪区作为水库处理,只考虑水量平衡处理,本研究对于干流洪水的顶托作用采用较为简单的线性水库概化,取得一定的预报效果。但这样复杂河系的洪水预报,行洪区内洪水演算属于二维水力学范畴,河水顶托是个非常复杂的水流演算问题。另外,河道预报实时校正技术是提高洪水预报精度,特别是提高水位预报精度的另一项重要技术(包红军和赵琳娜,2012b)。这些也是大流域洪水预报下一步需要着重解决的问题。
包红军, 2009. 基于EPS的水文与水力学相结合的洪水预报研究[D]. 南京: 河海大学.
|
包红军, 李致家, 王莉莉, 2009. 具有行蓄洪区的复杂水系实时洪水预报研究[J]. 水力发电学报, 28(4): 5-12. |
包红军, 王莉莉, 沈学顺, 等, 2016. 气象水文耦合的洪水预报研究进展[J]. 气象, 42(9): 1045-1057. DOI:10.7519/j.issn.1000-0526.2016.09.002 |
包红军, 赵琳娜, 2012a. 基于集合预报的淮河流域洪水预报研究[J]. 水利学报, 43(2): 216-224. |
包红军, 赵琳娜, 2012b. 基于Kalman滤波糙率反演模型的河道洪水实时预报研究[J]. 水力发电学报, 31(3): 59-64. |
包红军, 赵琳娜, 李致家, 2011. 淮河具有行蓄洪区河系洪水预报水力学模型研究[J]. 湖泊科学, 23(4): 635-641. DOI:10.18307/2011.0421 |
毕宝贵, 代刊, 王毅, 等, 2016. 定量降水预报技术进展[J]. 应用气象学报, 27(5): 534-549. DOI:10.11898/1001-7313.20160503 |
曹勇, 刘凑华, 宗志平, 等, 2016. 国家级格点化定量降水预报系统[J]. 气象, 42(12): 1476-1482. DOI:10.7519/j.issn.1000-0526.2016.12.005 |
崔春光, 彭涛, 沈铁元, 等, 2010. 定量降水预报与水文模型耦合的中小流域汛期洪水预报试验[J]. 气象, 36(12): 56-61. DOI:10.7519/j.issn.1000-0526.2010.12.008 |
代刊, 曹勇, 钱奇峰, 等, 2016. 中短期数字化天气预报技术现状及趋势[J]. 气象, 42(12): 1445-1455. DOI:10.7519/j.issn.1000-0526.2016.12.002 |
端义宏, 金荣花, 2012. 我国现代天气业务现状及发展趋势[J]. 气象科技进展, 2(5): 6-11. |
葛守西, 1999. 现代洪水预报技术[M]. 北京: 中国水利水电出版社.
|
胡淳焓, 黄娟, 王益琴, 等, 2015. 基于强度尺度法的雷达和数值模式定量降水预报检验对比[J]. 热带气象学报, 31(2): 273-279. |
姜晓曼, 袁慧玲, 薛明, 等, 2014. 北京"7.21"特大暴雨高分辨率模式分析场及预报分析[J]. 气象学报, 72(2): 207-219. DOI:10.11676/qxxb2014.024 |
李致家, 董增川, 梁忠民, 等, 2004. 大流域洪水预报与洪水调度管理方法研究[J]. 水力发电, 30(1): 12-15. |
刘艳, 薛纪善, 张林, 等, 2016. GRAPES全球三维变分同化系统的检验与诊断[J]. 应用气象学报, 27(1): 1-15. DOI:10.11898/1001-7313.20160101 |
刘志雨, 杨大文, 胡健伟, 2010. 基于动态临界雨量的中小河流山洪预警方法及其应用[J]. 北京师范大学学报(自然科学版), 46(3): 317-321. |
毛冬艳, 朱文剑, 樊利强, 等, 2014. GRAPES_MESO V3.3模式强天气预报性能的初步检验[J]. 气象, 40(12): 1429-1438. DOI:10.7519/j.issn.1000-0526.2014.12.001 |
宋星原, 李允军, 余海燕, 等, 2007. AREM模式预报技术在洪水预报中的应用[J]. 武汉大学学报(工学版), 40(3): 1-4. |
陶诗言, 赵思雄, 周晓平, 等, 2003. 天气学和天气预报的研究进展[J]. 大气科学, 27(4): 451-467. |
王莉莉, 陈德辉, 赵琳娜, 2012. GRAPES气象-水文模式在一次洪水预报中的应用[J]. 应用气象学报, 23(3): 274-284. |
张利平, 夏军, 2000. 短期定量降水预报研究进展[J]. 武汉大学学报(工学版), 33(1): 63-67. |
赵人俊, 1984. 流域水文模拟[M]. 北京: 水利电力出版社.
|
赵声蓉, 赵翠光, 赵瑞霞, 等, 2012. 我国精细化客观气象要素预报进展[J]. 气象科技进展, 2(5): 12-21. |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2009. 水文情报预报规范: GB/T 22482—2008[S]. 北京: 中国标准出版社.
|
Anderson M G, Burt T P, 1985. Hydrological Forecasting[M].
New York: John Wiley & Sons.
|
Bae D H, Georgakakos K P, Nanda S K, 1995. Operational forecasting with real-time databases[J]. J Hydraulics Division, 121(1): 49-60. DOI:10.1061/(ASCE)0733-9429(1995)121:1(49) |
Bao Hongjun, Zhao Linna, 2012. Development and application of an atmospheric-hydrologic-hydraulic flood forecasting model driven by TIGGE ensemble forecasts[J]. Acta Meteor Sin, 26(1): 93-102. DOI:10.1007/s13351-012-0109-0 |
Bao Hongjun, Zhao Linna, He Yi, et al, 2011. Coupling Ensemble weather predictions based on TIGGE database with Grid-Xinanjiang model for flood forecast[J]. Adv Geosci, 29: 61-67. DOI:10.5194/adgeo-29-61-2011 |
Cloke H L, Pappenberger F, 2009. Ensemble flood forecasting: a review[J]. J Hydrology, 375(3/4): 613-626. |
Hólm E, Forbes R, Lang S, et al, 2016. New model cycle brings higher resolution[J]. ECMWF Newsletter, (147): 14-19. |
Lalaurette F, Ferranti L, Ghelli A, et al, 2009. Verification statistics and evaluations of ECMWF forecasts in 2008-2009[R/OL].http://www.ecmwf.int/sites/default/files/elibrary/2003/10635-verification-statistics-and-evaluations-ecmwf-forecasts-2002-2003.pdf.
|
Li Zhijia, Bao Hongjun, Xue Cangsheng, et al, 2008. Real-time flood forecasting of Huai River with flood diversion and retarding areas[J]. Water Sci Eng, 1(2): 10-24. |
Lorenz E, 1972. Predictability: does the flap of a butterfly's wing in Brazil set off a tornado in Texas?[R].Washington D C: 139th Annual Meeting, Am Ass Adv Sci.
|
Maidment D R, 1993. Hydrology Handbook[M].
New York: McCraw-Hill.
|
Pappenberger F, Bartholmes J, Thielen J, et al, 2008. New dimensions in early flood warning across the globe using grand-ensemble weather predictions[J]. Geophy Res Let, 35(10): L10404. DOI:10.1029/2008GL033837 |
Pappenberger F, Beven K J, Hunter N, et al, 2005. Cascading model uncertainty from medium range weather forecasts (10 days) through a rainfall-runoff model to flood inundation predictions within the European Flood Forecasting System (EFFS)[J]. Hydrol Earth Syst Sci, 9(4): 381-393. DOI:10.5194/hess-9-381-2005 |
Pavlik D, Söhl D, Pluntke T, et al, 2012. Dynamic downscaling of global climate projections for Eastern Europe with a horizontal resolution of 7 km[J]. Environ Earth Sci, 65(5): 1475-1482. DOI:10.1007/s12665-011-1081-1 |
Sapir D G, Hargitt D, Hoyois P, 2004. Thirty years of natural disasters 1974-2003: The Numbers[M].
Belgium: Presses universitaires de Louvain.
|
Schaake J, Henkel A, Cong S, 2004. Application of PRISM climatologies for hydrologic modeling and forecasting in the western U.S.[C]//18th Conference on Hydrology. Seattle: American Meteorological Society.
|
Schaake J, Franz K, Bradley A, et al, 2006. The hydrological ensemble prediction experiment (HEPEX)[J]. Hydrol Earth Sys Sci, 3(5): 3321-3332. DOI:10.5194/hessd-3-3321-2006 |
Tobin C, Nicotina L, Parlange M B, et al, 2011. Improved interpolation of meteorological forcings for hydrologic applications in a Swiss Alpine region[J]. J Hydrology, 401(1): 77-89. |
Warner T T, Kibler D F, Steinhart R L, 1991. Separate and coupled testing of meteorological and hydrological forecast models for the Susquehanna River basin in Pennsylvania[J]. J Appl Meteor, 30(1): 1521-1533. |
Yuan Huiling, 2007. Analysis of precipitation forecasts from the NCEP global forecast system[C]//22nd Conference on Weather Analysis and Forecasting/18th Conference on Numerical Weather Prediction. Boulder: NOAA/ESRL/GSD and NRC.
|
 2017, Vol. 43
2017, Vol. 43 