2. 湖北省黄石市气象局,黄石 435002;
3. 中国气象局北京城市气象研究所,北京 100089;
4. 国网湖北省电力公司黄石供电公司,黄石 435000
2. Huangshi Meteorological Office of Hubei Province, Huangshi 43500;
3. Institute of Urban Meteorology, CMA, Beijing 100089;
4. State Grid Huangshi Power Supply Company of Hubei Province, Huangshi 435000
随着经济社会发展和人民生活水平提高,我国的电能需求不断上升,而电力产能还无法随时随地完全满足各类用户的需求,“电荒”带来的人为限电时有发生,给经济发展及居民生活带来极大的不便。
气象要素对电力负荷具有显著影响(杨静等,2009;Hernández et al, 2012;Selakov et al, 2014),尤其在夏季,大量使用空调而带来的调温负荷被证明同气温、湿度等要素密切相关(马瑞等,2015;高赐威等,2015)。当前针对该问题的研究多集中在两方面:一是小时级别上的精细化研究(Deihimi et al, 2013;宋易阳等,2014;雷绍兰等,2014)。该类研究通常将气象要素、大用户负荷、特定事件等诸多要素进行综合分析,以期了解特定时期最为翔实的电力负荷变化成因;二是较长序列的逐日电力负荷分析(鹿翠华等,2014; 付桂琴等,2015;罗慧等,2016)。由于气象因子可引起30%左右的电力负荷上升(廖峰等,2012),该类研究着重讨论不同气象因子所带来的影响。受各方面条件制约,该类研究中通常存在一些亟待解决的通用问题,如电力负荷分解过程不够精细、金融危机对电力负荷的影响常被忽略等(荣秀婷等,2014;张贲等,2013),这将必然影响最终结果的准确性。
此外,可以表征多个气象要素共同影响的综合指标同电力负荷具有更高的关联度(张伟,2013;杜翼等,2013)。但综合指标的应用过程仍存在一定不足,如将综合指标应用于电力负荷分解阶段的研究尚鲜见报道;当前定量衡量“1℃效应”的许多研究,其出发点仍为气温(贺芳芳和史军,2011;张自银等,2011)等。因此,有必要扩展综合指标的应用领域,并定量分析综合指标变化对电力负荷产生的影响。
黄石市地处湖北省东南部,长江中游南岸,气候特征为典型的亚热带大陆性气候,雨量充沛,夏季湿热。作为非中心城市,金融危机所带来的影响更为显著。因此本文以黄石市长序列的夏季电力负荷为研究对象,分析气象因子对其影响,尝试给出具有较好表征意义的综合指标,并定量讨论该指标的适用性。
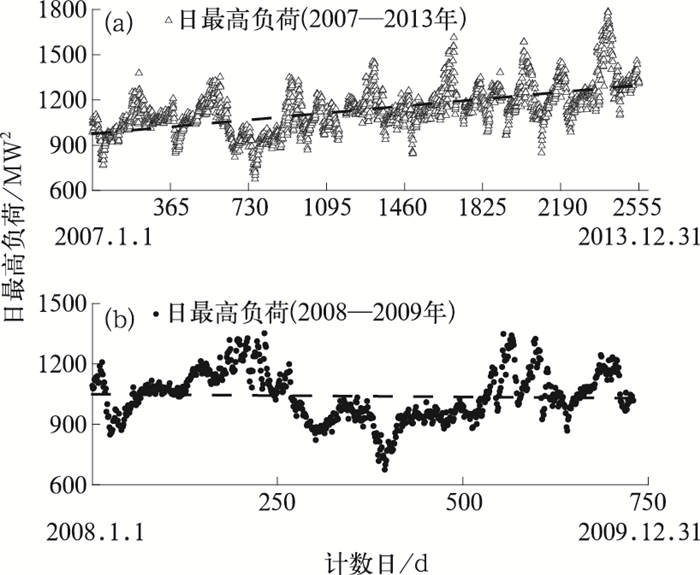
1 资料与方法 1.1 电力数据及质量控制本文所用电力数据为黄石市供电公司提供的2007年1月1日至2013年12月31日逐15 min电力负荷资料,即每日可获得96个电力负荷数据,选取其中最大值作为当日最高电力负荷,在此基础上采用比较滤波法(王雁平和乐春峡,2007)对逐日最高负荷数据进行质量控制,剔除、修正错误数据,最终得到有效样本2477个。研究时段内的逐日最大电力负荷如图 1所示。
|
图 1 2007—2013年(a)和2008—2009年(b)黄石市逐日最大电力负荷 Fig. 1 Trend of daily power load from 2007 to 2013 (a) and from 2008 to 2009 (b) in Huangshi City |
本文所用气象数据为黄石市气象局提供的质控后2007年1月1日至2013年12月31日逐日气象资料,包括日平均气温、最高气温、最低气温、降水量、平均相对湿度和平均风速。
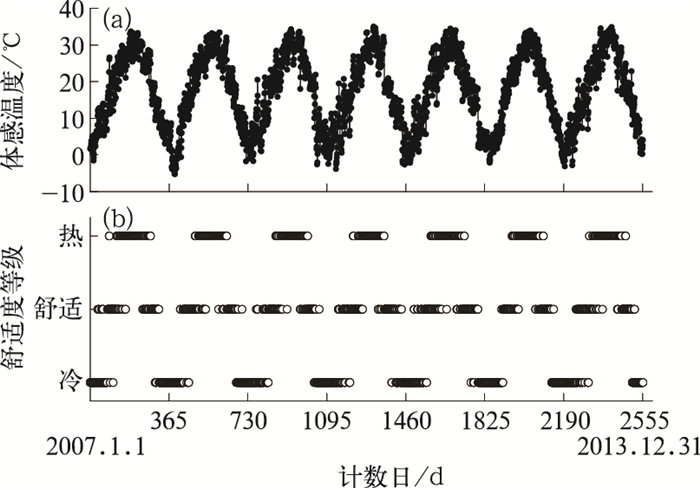
讨论气象因子对电力负荷影响的研究中,温湿指数和体感温度等指标被认为比单纯的气象因子具有更好的指示意义(曹磊和祖蓓,2011)。本文采用王式功等(2013)提出的人体舒适度算法计算研究时段内黄石市逐日体感温度,并依照张志薇等(2014)基于上述算法给出的舒适度等级划分方法,将每日的舒适度划分为“舒适”、“热不舒适”和“冷不舒适”三大类。研究时段内逐日体感温度及舒适度等级如图 2所示。
|
图 2 2007—2013年逐日体感温度(a)及舒适度等级(b)情况 Fig. 2 Daily sensitive temperature (a) and comfort level (b) in Huangshi City from 2007 to 2013 |
电力负荷(L)通常可分为三个分量(方鸽飞等,2010;洪国平等,2013):
| $ L = {L_t} + {L_m} + \varepsilon $ | (1) |
式中,Lt为受经济发展影响的基础负荷,Lm为受气象要素影响的气象敏感负荷,ε为随机分量,包括节假日因素、工业检修和电网调价等不确定因素。受资料限制,本文仅考虑节假日因素带来的影响。
一般情况下,基础负荷随经济发展逐年提高,研究认为基础负荷随时间线性增长(贺芳芳等,2008;李嘉龙等,2013),即:
| $ {L_t} = a + bt $ | (2) |
式中,t为样本序列,系数a和b可通过最小二乘法进行计算获得。
另一方面,电网运行调度中更为关心气象负荷率的变化情况(胡江林等,2002;刘红亚和曹亮,2013),故本文将重点讨论气象因子对其影响。气象负荷率的计算公式如下:
| $ R = {L_m}/{L_t} $ |
由图 1可知,研究时段内黄石市每日最大电力负荷基本呈线性增长,但受金融危机影响,2008—2009年电力负荷呈下降趋势,这与国内非中心城市观测到现象相一致(廖峰等,2012;武辉芹等,2013)。因此,有必要分时段确定不同时期的基础负荷。具体方法如下。
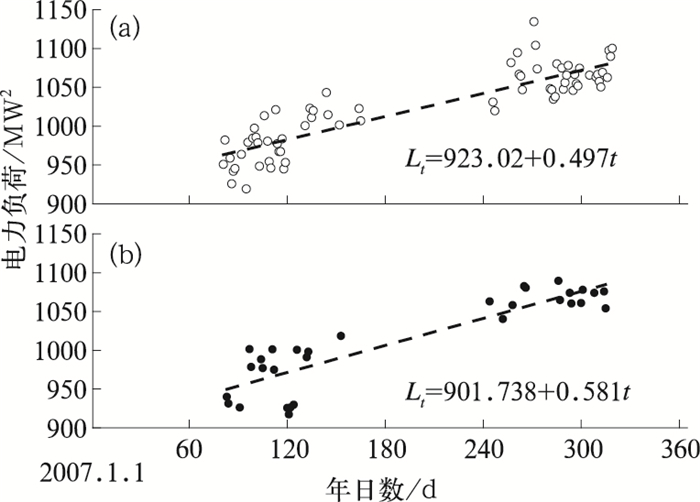
夏季气象敏感负荷主要源自居民降温需求带来的调温负荷(任志超等,2014),节假日因素亦会对电力负荷造成一定影响(叶殿秀等,2013),人体感觉舒适时,总负荷中几乎不包含气象负荷。因此本文参照1.2节中计算出的每日舒适度级别,当一年中第一次连续3 d舒适度等级为“舒适”时,将第一天视作全年第一个“舒适日”,选取自该日起全年所有“舒适日”的最高电力负荷作为样本,并进一步细化为“工作日”和“节假日”两大类。由于国庆、春节长假时段内电力负荷明显低于其他时段(罗森波等,2007),故上述时段内的数据不作为研究样本。在此基础上,以式(2) 计算除2008、2009年以外每一年的基础负荷,以2007年为例,当年基础负荷的求解方程如图 3所示。
|
图 3 2007年基础负荷计算结果(a)工作日, (b)节假日 Fig. 3 Trend of basic power load in weekdays (a) and holidays (b) in 2007 |
对2008和2009年而言,有必要首先明确金融危机造成影响的具体时段。本文对2008—2009年“热不舒适日”的最大负荷建立新的时间序列,采用M-K检验法确定可能存在的间断点。由于所有样本均存在气象敏感负荷,可在一定程度上降低系统性变化带来的干扰。检验结果如图 4所示。

|
图 4 2008年(a)和2009年(b)“热不舒适”日最高负荷M-K检验结果 (两条虚线内的交点为通过0.01显著性水平检验的间断点) Fig. 4 The M-K test of maximum power load from 'thermal discomfort days' in 2008 (a) and 2009 (b) (The intersections within the dashed lines are discontinuous points having passed the 0.01 significance level test) |
|
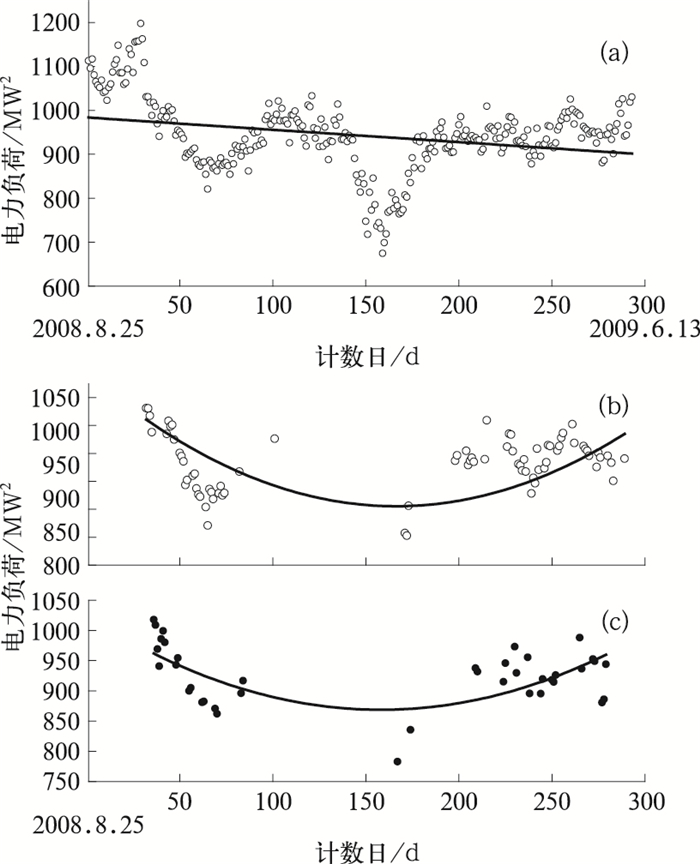
图 5 2008年8月25日至2009年6月13日逐日电力负荷变化趋势(a)、基础负荷工作日(b)和节假日(c)拟合曲线 Fig. 5 The trend of daily power load (a), the fitting results of basic power load in weekdays (b) and holidays (c) |
由图 4可知,在2008年的第93个“热不舒适”日(2008年8月25日)甄别出一个不显著的间断点,在2009年的第17个“热不舒适”日(2009年6月13日)甄别出一个通过0.01显著性水平检验的间断点。2008年8月25日为周一,但当天最高电力负荷低于临近的周末。考虑到节假日因素带来的影响,该间断点虽不显著,但仍可认为是电力负荷下滑的起始点。据此,本文将2008—2009年细化为3个时段:2008年1月1日至8月24日、2008年8月25日至2009年6月12日和2009年6月13日至12月31日。
金融危机期间(2008年8月25日至2009年6月12日),电力负荷整体呈下降趋势,在2009年春节之后,电力负荷开始缓慢回升。故该时段内的基础负荷并非一般认为的线性增长,而呈二次型变化。
依据黄石市常年入季时间(夏季平均5月2日,秋季平均9月12日),本文选取每年的5月1日至9月30日作为黄石市的夏季,2007—2013年夏季敏感负荷及气象负荷率结果如图 6所示。由图 6a和6b可知,黄石市夏季敏感负荷呈线性增长,且节假日增幅[线性倾向率6 MW2·(100 d) -1]略大于工作日[线性倾向率4 MW2·(100 d) -1]。另一方面,气象负荷率的增幅并不显著,工作日气象负荷率的线性倾向率约为0.2 %·(100 d)-1,而节假日则约为0.5 %·(100 d)-1。
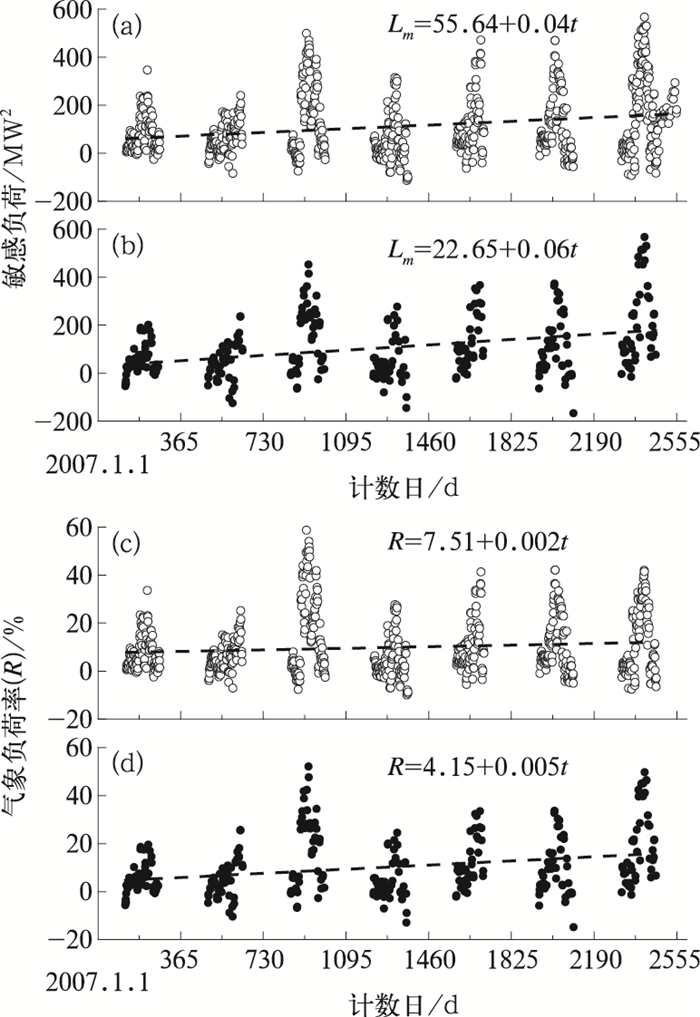
|
图 6 2007—2013年黄石市夏季敏感负荷(a, b)及气象负荷率(c, d) (a, c)工作日,(b, d)节假日 Fig. 6 Trend of sensitive load (a, b) and meteorological load rate (c, d) |
建筑学上通常认为日平均气温超过26℃即会因开启空调而产生额外的电力负荷(中华人民共和国住房和城乡建设部,2001)。但空调是否开启则取决于体感温度,因此,本文尝试计算体感温度阈值。
本文给出2007—2013年黄石市夏季体感温度同气象负荷率对应关系散点图,并在此基础上以气象负荷率(R)为因变量,体感温度(Tg)为自变量,区分工作日和节假日后,对两者进行非线性拟合,结果如图 7所示。由图 7可知,不论是工作日或节假日,在Tg∈ [13.7,34.9]℃的区间内(研究时段内最低、最高体感温度分别为13.7℃和34.9℃,下同),气象负荷率随体感温度近似呈二次型变化。故当R=0时,可分别求得两个体感温度阈值,其中高值即为影响夏季气象负荷率的体感温度阈值。当体感温度高于该值时,气象负荷率即有可能>0。
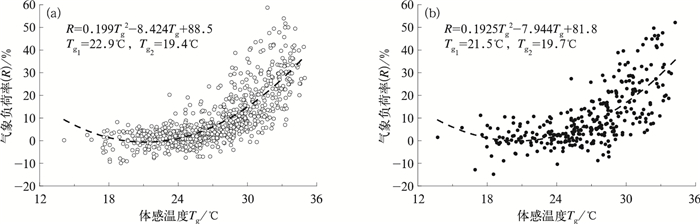
|
图 7 工作日(a)及节假日(b)体感温度同气象负荷率对应关系散点图 Fig. 7 Scatter diagram of meteorological load rate and sensitive temperature in weekdays (a) and holidays (b) |
采用上述方法求解出的黄石市夏季体感温度阈值分别为22.9℃(工作日)和21.5℃(节假日)。结合图 6c和6d给出的气象负荷率变化趋势可知,自2010年起,节假日的气象负荷率即开始高于工作日,且两者间差值呈增大趋势,即随着国民经济水平的提高,空调保有量逐渐增加,居民夏季降温需求亦逐渐增加,空调连续运作的时间随之增加。节假日时,即使在气温较低的夜间,也会由于白天的影响而继续开启空调,故节假日体感温度阈值低于工作日。
3.2 体感温度适用性验证本文利用灰色关联算法(黄治勇等,2011;廖峰等,2011;Jin et al, 2012; 常蕊等,2013;焦润海等,2013;罗毅和李昱龙,2013;Bahrami et al, 2014)比对不同气象因子增量(最高气温、最低气温、平均气温和体感温度)与气象负荷率增量ΔR的关联度,以讨论体感温度的适用性,结果如表 1所示。由表 1可知,不论工作日或节假日,体感温度同气象负荷率均具有最高的关联度,体感温度作为衡量气象负荷率变化的影响因子具有较好适用性。
|
|
表 1 2007—2013年黄石市夏季不同气象要素同气象负荷率的灰色关联度 Table 1 Gray correlation of meteorological load rate to different weather factors in Huangshi City from 2007 to 2013 |
依据第2节结果,研究时段的样本可细化为三类:Ⅰ,2008年8月25日至2009年6月12日,该时段样本表征了金融危机背景下体感温度的影响;Ⅱ,2007年5月1日至2010年9月30日中除Ⅰ时段外的样本,该样本表征了金融危机前,电力负荷缓慢增长背景下体感温度的影响;Ⅲ,2011年5月1日至2013年9月30日,该时段的样本表征了金融危机过后,电力负荷迅速增长背景下,体感温度带来的影响。
最终得到不同时段体感温度变化量同气象负荷率的关系如图 8所示。两者间拟合方程如表 2所示。其中,2013年的样本作为验证数据使用,故时段Ⅲ仅采用2011—2012年的数据进行建模。
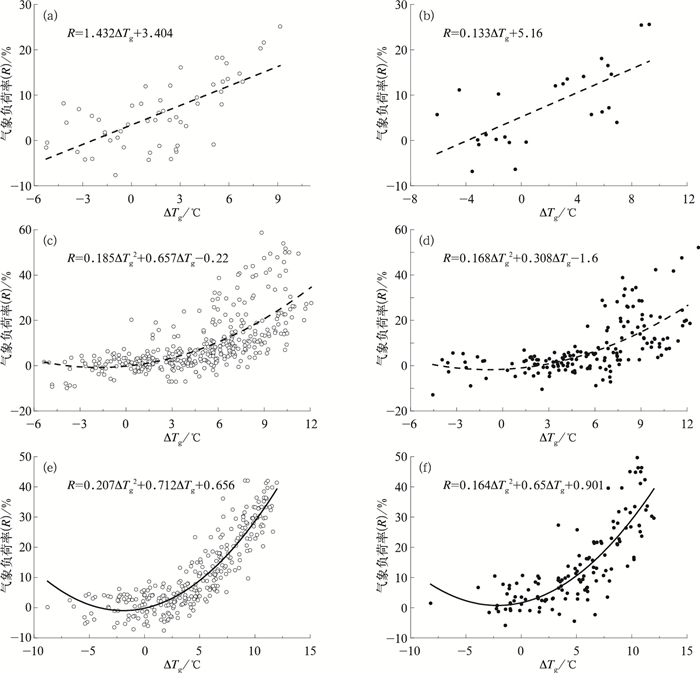
|
图 8 2007—2012年黄石市夏季不同时段工作日(a, c, e)和节假日(b, d, f)体感温度变化量与气象负荷率散点图(a, b)时段Ⅰ, (c, d)时段Ⅱ, (e, f)时段Ⅲ Fig. 8 Scatter diagram of the increasement of sensitive temepature and meteorological load rate in weekdays (a, c, e) and holidays (b, d, f) form 2007 to 2012 (a, b) Period Ⅰ, (c, d) Period Ⅱ, (e, f) Period Ⅲ |
|
|
表 2 2007—2013年黄石市夏季工作日和节假日气象负荷率同体感温度变化量的拟合方程 Table 2 Fitting equations describing the relationship between meteorological load rate and increasement of sensitive temepature in weekdays and holidays of summer |
综合图 8及表 2可知,在时段Ⅰ,气象负荷率随体感温度的升高线性增长,而在时段Ⅱ和Ⅲ,气象负荷率则随体感温度的升高呈二次型增长,即金融危机使得气象负荷率的增速放缓。
对表 2中的拟合方程求一阶导数,即可得到不同时段体感温度升高1℃时,气象负荷率的变化情况:
对时段Ⅰ而言,体感温度增加1℃,气象负荷率的增长为定值,在工作日和节假日分别会增加1.432%和1.33%;
对时段Ⅱ而言,拟合方程的一阶导数分别为R′=0.37ΔTg+0.657(工作日)和R′=0.336ΔTg+0.308 (节假日)。即气象负荷率的增量不再是定值,而是随体感温度的增量线性变化。结合整个研究时段体感温度最高值34.9℃进行分析可知,时段Ⅱ内,视体感温度具体值的不同,1℃的体感温度增量将会引起ΔR∈[1.027,50.97] %(工作日)和ΔR∈ [0.644,4.81]%(节假日)的气象负荷率增量。
时段Ⅲ的拟合方程一阶导数分别为R′=0.414ΔTg+0.712(工作日)和R′=0.328ΔTg+0.65 (节假日)。而1℃的体感温度变化将会引起ΔR∈[1.126, 5.68] %(工作日)和ΔR∈[0.978, 5.05] %(节假日)的气象负荷率变化。
时段Ⅱ和时段Ⅲ的结果再一次证实,金融危机前,工作日的气象负荷率对体感温度的响应更为敏感;而金融危机后,节假日的气象负荷率对体感温度的变化更敏感。其主要原因即在于节假日开启空调的体感温度阈值更低,相同的体感温度在工作日和节假日具有不同的ΔTg,而不同的ΔTg最终引起了ΔR的差异。
本文利用2013年的气象负荷率样本对上述结果进行验证(图 9)。由图 9可知,通常情况下,该方法可对夏季气象负荷率进行较好预测,预测结果平均绝对误差约为2.03%,工作日平均绝对误差约为0.71%。但在突发高温时的节假日期间存在预测值偏小的情况。这与构建模型时,节假日样本远少于工作日样本存在一定联系。
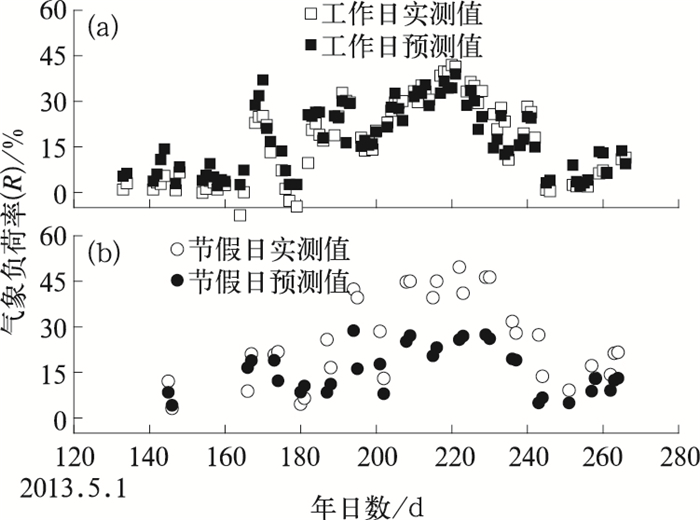
|
图 9 2013年夏季工作日(a)和节假日(b)气象负荷率预测值与实测值比较结果 Fig. 9 Comparation of forecast and real values of summer meteorological load rate in 2013 (a) weekdays, (b) holidays |
综上所述,本文得到以下结论:
(1) 对黄石市2007—2013年电力负荷变化趋势的分析结果表明,研究时段内逐日最大电力负荷总体呈线性增长,但受金融危机影响,在2008年8月25日至2009年6月12日时期内,电力负荷呈下降趋势。同时,2010年之前,工作日的气象负荷率高于节假日,但自2011年起,该现象出现了反转,且差值逐渐增大。
(2) 体感温度及扩展得到的人体舒适度等级在讨论气象因子对电力负荷的影响研究中具有较好适用性:利用该算法可对电力负荷进行更为精细的分解,获得更为准确的气象敏感负荷及气象负荷率。同时,由于可以表征多个气象要素的综合情况,体感温度也被证明是同气象负荷率具有最高关联度的因子。
(3) 分析气象负荷率对体感温度的响应情况表明,当体感温度高于22.9℃(工作日)或21.5℃(节假日)时即会产生气象敏感负荷。1℃的体感温度变化在不同时段产生不同的气象负荷率。其中,在2008年8月25日至2009年6月12日时段内为定值,1℃的体感温度增量会分别引起1.432%(工作日)和1.33%(节假日)的气象负荷率变化;而在其他时段,气象负荷率随体感温度呈二次型变化。研究时段内,体感温度升高1℃最多可引起6%以上的气象负荷率增加。
(4) 利用2013年的数据对体感温度的适用性情况进行验证,结果表明利用体感温度可较好预测气象负荷率,预测结果的平均绝对误差约2.03%,但在高温突发的节假日存在预测值偏小的情况。
曹磊, 祖蓓, 2011. 夏季温湿指数与气象敏感电力负荷的研究[J]. 现代电力, 28(5): 41-45. |
常蕊, 朱蓉, 柳艳香, 等, 2013. 基于均生函数的风电场风速短临预报模型[J]. 气象, 39(2): 226-233. DOI:10.7519/j.issn.1000-0526.2013.02.012 |
杜翼, 方鸽飞, 王玉芬, 2013. 考虑气象信息的短期负荷预测[J]. 华东电力, 41(05): 1051-1055. |
方鸽飞, 胡长洪, 郑奕辉, 等, 2010. 考虑夏季气象因素的短期负荷预测方法研究[J]. 电力系统保护与控制, 38(22): 100-104. DOI:10.7667/j.issn.1674-3415.2010.22.019 |
付桂琴, 尤凤春, 曹欣, 等, 2015. 积温效应在电力日峰谷负荷中的应用及检验[J]. 应用气象学报, 26(4): 492-499. DOI:10.11898/1001-7313.20150411 |
高赐威, 李倩玉, 苏卫华, 等, 2015. 短期负荷预测中考虑积温效应的温度修正模型研究[J]. 电工技术学报, 30(4): 242-248. |
贺芳芳, 史军, 2011. 上海地区夏季气温变化对用电负荷的影响[J]. 长江流域资源与环境, 20(12): 1462-1467. |
贺芳芳, 徐家良, 周伟东, 等, 2008. 上海地区高温期气象条件对用电影响的评估[J]. 高原气象, 27(S1): 210-217. |
洪国平, 胡宗海, 闫敏慧, 等, 2013. 夏季湖北电网气象敏感负荷预测模型研究[J]. 气象科学, 33(4): 424-429. DOI:10.3969/2012jms.0115 |
胡江林, 陈正洪, 洪斌, 等, 2002. 华中电网日负荷与气象因子的关系[J]. 气象, 28(3): 14-18. DOI:10.7519/j.issn.1000-0526.2002.03.003 |
黄治勇, 张文, 陈璇, 等, 2011. 湖北省乡镇温度预报方法初探[J]. 气象, 37(12): 1578-1583. DOI:10.7519/j.issn.1000-0526.2011.12.015 |
焦润海, 苏辰隽, 林碧英, 等, 2013. 基于气象信息因素修正的灰色短期负荷预测模型[J]. 电网技术, 37(3): 720-725. |
雷绍兰, 古亮, 杨佳, 等, 2014. 重庆地区电力负荷特性及其影响因素分析[J]. 中国电力, 47(12): 61-65,71. DOI:10.3969/j.issn.1007-0079.2014.12.030 |
李嘉龙, 李小燕, 刘思捷, 等, 2013. 考虑气温累积效应的短期负荷预测[J]. 华北电力大学学报(自然科学版), 40(1): 49-54. |
廖峰, 刘清良, 贺辉, 等, 2011. 基于改进灰色模型与综合气象因素的母线负荷预测[J]. 电网技术, 35(10): 183-188. |
廖峰, 徐聪颖, 姚建刚, 等, 2012. 常德地区负荷特性及其影响因素分析[J]. 电网技术, 36(7): 117-125. |
刘红亚, 曹亮, 2013. 上海市电力负荷与气象因子关系及精细化预报[J]. 应用气象学报, 24(4): 455-463. DOI:10.11898/1001-7313.20130408 |
鹿翠华, 张立强, 陈连侠, 等, 2014. 枣庄电网日负荷与气象因素的关系及其预测[J]. 中国人口.资源与环境, (S3): 354-356. |
罗慧, 徐军昶, 肖波, 等, 2016. 气象因子对西安城市用电量的影响研究及中长期系统化预测[J]. 气象, 42(1): 54-60. DOI:10.7519/j.issn.1000-0526.2016.01.006 |
罗森波, 纪忠萍, 马煜华, 等, 2007. 2002—2004年广东电力负荷的变化特征及预测[J]. 热带气象学报, 23(2): 153-161. |
罗毅, 李昱龙, 2013. 基于熵权法和灰色关联分析法的输电网规划方案综合决策[J]. 电网技术, 37(1): 77-81. |
马瑞, 周谢, 彭舟, 等, 2015. 考虑气温因素的负荷特性统计指标关联特征数据挖掘[J]. 中国电机工程学报, 2015(01): 43-51. |
任志超, 杜新伟, 王海燕, 等, 2014. 调温负荷的估算方法及影响因素研究[J]. 现代电力, 31(3): 80-85. |
荣秀婷, 葛斐, 王海超, 等, 2014. 一种新的最大负荷分解方法[J]. 现代电力, 31(4): 44-46. |
宋易阳, 李存斌, 祁之强, 2014. 基于云模型和模糊聚类的电力负荷模式提取方法[J]. 电网技术, 38(12): 3378-3383. |
王式功, 马盼, 尚可政, 等, 2013. 一种基于黄金分割法构建人体舒适度计算方法: 中国, CN201210596366. 0[P]. 2013-05-15.
|
王雁平, 乐春峡, 2007. 电力系统负荷建模的数据预处理技术[J]. 电网技术, 31(S2): 292-294. |
武辉芹, 张金满, 曲晓黎, 2013. 河北省南部电网夏季电力负荷特征及与气象因子的关系[J]. 气象科技, 41(5): 945-948,964. |
杨静, 郝毅, 陈冬梅, 等, 2009. 新疆农业区电力负荷与天气的关系[J]. 气象, 35(1): 114-118. DOI:10.11898/1001-7313.20090115 |
叶殿秀, 张培群, 赵珊珊, 等, 2013. 北京夏季日最大电力负荷预报模型建立方法探讨[J]. 气候与环境研究, 18(6): 804-810. DOI:10.3878/j.issn.1006-9585.2013.12146 |
张伟, 2013. 基于人体舒适度指数的配电网短期负荷预测方法[J]. 电力系统保护与控制, 41(9): 74-79. DOI:10.7667/j.issn.1674-3415.2013.09.012 |
张贲, 史沛然, 蒋超, 2013. 气象因素对京津唐电网夏季负荷特性影响分析[J]. 电力自动化设备, 33(12): 140-144. DOI:10.3969/j.issn.1006-6047.2013.12.023 |
张志薇, 孙宏, 蒋薇, 等, 2014. 南京地区人体舒适度及其与居民循环系统疾病死亡关系的研究[J]. 气候变化研究进展, 10(1): 67-73. |
张自银, 马京津, 雷杨娜, 2011. 北京市夏季电力负荷逐日变率与气象因子关系[J]. 应用气象学报, 22(6): 760-765. DOI:10.11898/1001-7313.20110615 |
中华人民共和国住房和城市建设部, 2001. 夏热冬冷地区居住建筑节能设计标准: JGJ75-2012[S]. 北京: 中国建筑工业出版社.
|
Bahrami S, Hooshmand R A, Parastegari M, 2014. Short term electric load forecasting by wavelet transform and grey model improved by PSO (particle swarm optimization) algorithm[J]. Energy, 72(7): 434-442. |
Deihimi A, Orang O, Showkati H, 2013. Short-term electric load and temperature forecasting using wavelet echo state networks with neural reconstruction[J]. Energy, 57(3): 382-401. |
Jin M, Zhou X, Zhang Z M, et al, 2012. Short-term power load forecasting using grey correlation contest modeling[J]. Expert Systems with Applications, 39(1): 773-779. DOI:10.1016/j.eswa.2011.07.072 |
Hernández L, Baladrón C, Aguiar J M, et al, 2012. A study of the relationship between weather variables and electric power demand inside a smart grid/smart world framework[J]. Sensors, 12(9): 11571-11591. |
Selakov A, Cvijetinović D, Milović L, et al, 2014. Hybrid PSO-SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank[J]. Applied Soft Computing, 16(3): 80-88. |
 2017, Vol. 43
2017, Vol. 43 