引言

在近年来全球变暖和快速城市化的背景下，高温热浪事件频发，中国东部当前遭遇极端高温事件的概率比20世纪50年代高出60倍(Sun et al，2014；谢志清等，2015)。在城市热岛效应研究方面，目前国外主要侧重于采用卫星遥感及数值模拟技术来研究城市热岛效应。例如Hughes and Balling(1996)研究了城市对南非气温变化趋势的影响。Jones et al(1990)评估了城市化对大陆气温序列的影响。Adebayo(1987)和Schmidlin(1989)分析了城市热岛强度夜间大于白天。Voogt and Oke(2003)分析了在晴天无云、无风的晚上，城市和郊区的辐射降温差异大，热岛现象明显。Park(1986)分析了热岛强度随城市规模和人口规模的增加而增大。国内基于分析单个城市或者相邻的几个城市组成的区域城市群的热岛效应比较多。如周淑贞(1990)分析了上海地区秋、冬季节热岛较强，夏季热岛较弱。董李丽等(2015)利用逐日气温资料和东亚大气环流再分析资料研究了我国春季气温的时空变化特征。东高红等(2015)研究了天津地区城市热岛环流与海风环流相互作用。刘伟东等(2014)分析了城市化对北京地区秋季气温变化影响最大。王喜全等(2006)利用北京自动气象站资料分析了北京热岛效应，发现热岛效应在夏季最强，秋、冬季次之，春季最弱。王君等(2013)分析了近30年城市化对北京极端气温的影响。白莹莹等(2015)分析了城市化进程对重庆高温日数的影响。刘伟东等(2016)统计了京津冀城市群热岛强度，发现京津冀城市群热岛强度冬季强，而夏季弱。曾侠等(2004)分析了珠三角地区城市热岛效应呈现中间强周围弱的空间格局。黄宏涛等(2016)分析了城市化对珠三角地区气温和气温日较差的影响。周军芳等(2012)和董娟(2005)定性分析了城市化对珠三角部分城市温度场和热岛强度的影响。由于受气象资料或城市集群化发展资料的限制，以上研究大多定性地分析城市化对气温或者热岛强度的影响，而采用定量模型模拟城市集群化发展指标对气温和热岛强度的研究并不多见。因此，本文根据灰色关联度排序，筛选出对气温和热岛强度影响较大的城市发展指标，采用灰色模型初步分析城市集群化发展指标与气温和热岛强度之间的定量关系，从而为识别城市集群化发展指标对气温和热岛强度影响的关键因子提供参考，也可为珠三角城市区域规划和城市防灾减灾提供技术依据。

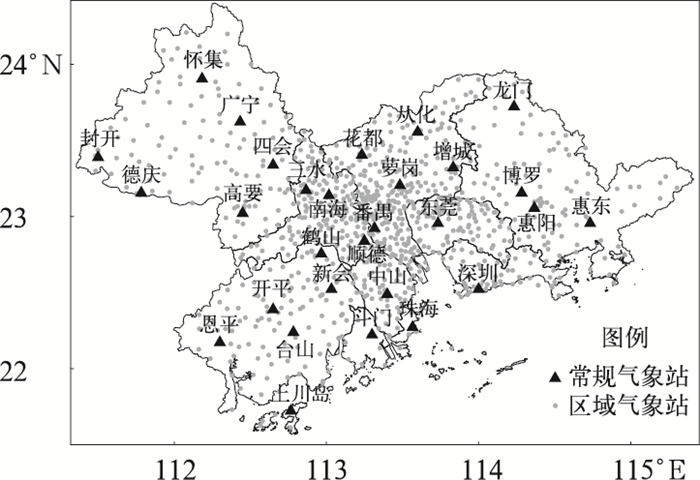
1 资料与方法 1.1 资料

收集珠三角城市群9个地级市1985—2012年城市空间、人口、建设、资源和经济共5大类21项指标，资料来源于广东省统计信息网(http://www.gdstats.gov.cn/)，详见表 1。为分析珠三角地区气温和热岛强度的空间分布规律，收集珠三角范围内研究期间观测资料相对完整的944个区域自动气象站2012—2013年的气温资料，区域气象站平均间距6~8 km，气象资料来源于广东省气象局，气象站分布见图 1。

1.2 方法 1.2.1 郊区代表站的选择和热岛强度计算

采用实测气温标准化方法，即:

$ {\mu _i} = \frac{{{x_i} - \overline x }}{{{\sigma _i}}} $

式中，μ_i为归一化标准差，x_i为第i个气象站气温，x为研究范围内气象站平均气温，σ_i为第i个气象站气温标准差。取-2＜μ_i≤0.5的气象站作为郊区站的选取依据之一，且研究区域内的气象站距离相差不大，具有相近的下垫面条件，在研究时段内气象站周边未发生明显的城市化，则第i站被选定为郊区代表站(丁硕毅等，2015)。由于珠三角地区南北跨度大，为便于反映城市小气候复杂的热岛强度空间分布，在分析热岛强度的空间分布时，将珠三角地区划分为1°×1°的经纬度网格，分别计算各网格内的气象站的热岛强度。在分析珠三角地区热岛强度空间分布时，采用Surfer 8.0的克里格网格化法对各气象站之间进行差值，其误差取决于气象站站点的密度和下垫面的性质。

城区代表站点的平均气温(T_u)与郊区代表站点的平均气温(T_s)之差计算珠三角地区城市热岛强度(urban heat island intensity，UHII)，即

$ UHII = {T_{\rm{u}}} - {T_{\rm{s}}} $

(1)

1.2.2 灰色关联分析

采用灰色关联分析法(邓聚龙，1987)，找出影响气温和UHII的城市集群化发展指标。具体计算步骤如下：

第一步：构建时间数列。设有m个城市集群化发展指标的n个评价样本组成的时间数列为：

$ \begin{array}{l} {X_i} = \{ {X_i}\left(k \right)|k = 1, 2, \ldots, n;\\ i = 0, 1, 2, \cdots, m - 1\} \end{array} $

(2)

式中，i为数列分类，X₀为参考数列，其他为比较数列；k为时刻。

第二步：时间数列标准化

$ X{'_{ij}} = {\rm{ }}\frac{{{X_{ij}} - {{\overline X }_j}}}{{{\sigma _j}}} $

(3)

式中，X_ij和X′_ij分别为第i行第j列的原始数据和归一化标准差；X_j和σ_j分别为第j列的算术平均值和均方差。

第三步：灰色关联系数计算。灰色关联系数ξ_i(k)的计算公式为：

$ \begin{array}{l} {\xi _i}\left(k \right) = \frac{{\mathop {{\rm{min}}}\limits_i \mathop {{\rm{min}}}\limits_k |{x_0}\left(k \right) - {x_i}\left(k \right)| + 0.5\mathop {{\rm{max}}}\limits_{i} \mathop {{\rm{max}}}\limits_k |{x_0}\left(k \right) - {x_i}\left(k \right)|}}{{|{x_0}\left(k \right) - {x_i}\left(k \right)| + 0.5\mathop {{\rm{max}}}\limits_{i} \mathop {{\rm{max}}}\limits_k |{x_0}\left(k \right) - {x_i}\left(k \right)|}}\;\;\;\;k = 1, 2, \cdots, n \end{array} $

(4)

式中，ξ_i(k)为因素i在k时刻的关联系数；${|{x_0}\left(k \right) -{x_i}\left(k \right)|}$表示k时刻参考数列与比较数列的绝对差值；${\mathop {{\rm{min}}}\limits_i \mathop {{\rm{min}}}\limits_k |{x_0}\left(k \right) -{x_i}\left(k \right)|}$和${\mathop {{\rm{max}}}\limits_{i} \mathop {{\rm{max}}}\limits_k |{x_0}\left(k \right) -{x_i}\left(k \right)|}$分别表示在参考数列与所有比较数列每个时刻绝对差中的最小值和最大值。

第四步：求灰色关联度r_i，其计算公式为:

$ {r_i} = \frac{1}{N}\sum\limits_{k = 1}^N {{\xi _i}\left(k \right)} $

(5)

第五步：根据灰色关联度r_i的大小排序。

1.2.3 灰色GM(1, N)模型建模

根据灰色关联度排序，挑选对气温和UHII影响较大的前7项城市发展指标作为自变量，采用GM(1，N)灰色模型(韩玮和苏敬，2014)拟合城市发展指标对气温及UHII的影响，具体计算步骤如下：

第一步：数学建模。

构建m行n列矩阵，其中m为年份序列，n为指标序列，用如下矩阵描述：

$ \mathit{\boldsymbol{X}}_n^{\left(0 \right)} = \left[ {\begin{array}{*{20}{c}} {x_1^{\left(0 \right)}\left(1 \right)}&{{\rm{ }}x_2^{\left(0 \right)}\left(1 \right)}& \ldots &{x_n^{\left(0 \right)}\left(1 \right)}\\ {{\rm{ }}x_1^{(0)}\left(2 \right)}&{x_2^{\left(0 \right)}\left(2 \right)}& \ldots &{x_n^{\left(0 \right)}\left(2 \right)}\\ \vdots&\vdots&\vdots&\vdots \\ {x_1^{\left(0 \right)}\left(m \right)}&{x_2^{\left(0 \right)}\left(m \right)}& \ldots &{x_n^{\left(0 \right)}\left(m \right)} \end{array}} \right] $

(6)

计算一次累加矩阵：

$ \mathit{\boldsymbol{X}}_n^{\left(0 \right)} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^2 {x_1^{\left(0 \right)}\left(1 \right)} }&{\sum\limits_{i = 1}^2 {x_2^{\left(0 \right)}\left(1 \right)} }& \cdots &{\sum\limits_{i = 1}^2 {x_n^{\left(0 \right)}\left(1 \right)} }\\ {\sum\limits_{i = 1}^3 {x_1^{\left(0 \right)}\left(1 \right)} }&{\sum\limits_{i = 1}^3 {x_2^{\left(0 \right)}\left(1 \right)} }& \cdots &{\sum\limits_{i = 1}^3 {x_n^{\left(0 \right)}\left(1 \right)} }\\ \vdots&\vdots&\vdots&\vdots \\ {\sum\limits_{i = 1}^m {x_1^{\left(0 \right)}\left(1 \right)} }&{\sum\limits_{i = 1}^m {x_2^{\left(0 \right)}\left(1 \right)} }& \cdots &{\sum\limits_{i = 1}^m {x_n^{\left(0 \right)}\left(1 \right)} } \end{array}} \right] $

(7)

再计算X ₁⁽¹⁾的一次相邻内插数列的相反数。

第二步：参数估计。

构造矩阵X(A, B)=B，即：

$ \begin{array}{l} \mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} { - \frac{1}{2}[\mathit{x}_1^{\left( 1 \right)}\left( 2 \right) + \mathit{x}_1^{\left( 1 \right)}\left( 1 \right)]}&{\mathit{x}_2^{\left( 1 \right)}\left( 2 \right)}& \cdots &{\mathit{x}_n^{\left( 1 \right)}\left( 2 \right)}\\ { - \frac{1}{2}[\mathit{x}_1^{\left( 1 \right)}\left( 3 \right) + \mathit{x}_1^{\left( 1 \right)}\left( 2 \right)]}&{\mathit{x}_2^{\left( 1 \right)}\left( 3 \right)}& \cdots &{\mathit{x}_n^{\left( 1 \right)}\left( 3 \right)}\\ \vdots&\vdots&\vdots&\vdots \\ { - \frac{1}{2}[\mathit{x}_1^{\left( 1 \right)}\left( m \right) + \mathit{x}_1^{\left( 1 \right)}\left( {m - 1} \right)]}& \cdots &{\mathit{x}_2^{\left( 1 \right)}\left( m \right)}&{\mathit{x}_n^{\left( 1 \right)}\left( m \right)} \end{array}} \right]\\ \;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{Y}}_\mathit{m}} = {[\mathit{x}_1^{\left( 0 \right)}\left( 2 \right),\mathit{x}_1^{\left( 0 \right)}\left( 3 \right), \cdots ,\mathit{x}_1^{\left( 0 \right)}\left( m \right)]^\rm{T}} \end{array} $

(8)

采用最小二乘法求灰参数$\hat {\boldsymbol{a}}$：

$ \mathit{\boldsymbol{\hat a = }}\left[ {\begin{array}{*{20}{c}} a\\ {{b_1}}\\ \vdots \\ {{b_{n - 1}}} \end{array}} \right] = {\left({{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{Y}}_\mathit{m}} $

(9)

式中，a为发展系数；b₁，b₂，…，b_n-1为灰色作用量。

第三步：预测模型，将式(9)中的灰参数代入时间响应函数中。

$ \begin{array}{l} {{\hat x}^{\left(1 \right)}}\left({t + 1} \right) = \sum\limits_{i = 1}^n {\frac{{{b_{i - 1}}}}{a}x_i^{\left(1 \right)}\left({t + 1} \right)} + \\ \;\;\;\;\;\left[ {{x^{\left(0 \right)}}\left(1 \right) - \sum\limits_{i = 2}^n {\frac{{{b_{i - 1}}}}{a}x_i^{\left(1 \right)}\left({t + 1} \right)} } \right]{{\rm{e}}^{\mathit{ - at}}} \end{array} $

(10)

第四步：模型检验。

求生成数据序列计算值$\hat x$⁽¹⁾(t)，然后再对$\hat x$⁽¹⁾(t)求导，还原为$\hat x$⁽⁰⁾(t)，并计算$\hat x$⁽⁰⁾(t)与$\hat x$⁽⁰⁾(t)之差，即为残差ε⁽⁰⁾(t)以及相对误差E(t)。

2 结果与分析 2.1 城市发展阶段划分

根据城市建成区面积和工业总产值的变化来划分城市化进程的不同阶段。由图 2可见，2000年前后两时期比较，后一阶段的城市建成区面积和工业总产值的上升速率分别是前一时期的5.9和8.7倍。样本均值差异的显著性水平检验表明，珠三角的城市建成区面积和工业总产值在2000年前后两个时期的差异均通过了0.01显著性水平检验(魏凤英，2007)。根据上述城市化速率的变化，将1985—2012年划分为1985—2000和2001—2012年两个时期，1985—2000年为城市化进程的缓慢增长期，2001—2012年为城市化快速增长期。本文将分析珠三角地区城市化进程中上述两个阶段的UHII特征。

2.2 UHII的时间变化

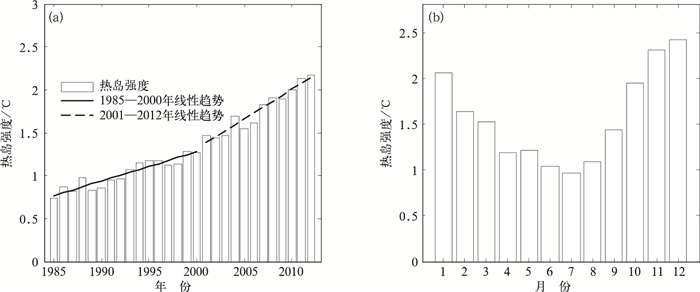
根据气温标准差法并结合《城市热岛效应评估技术指南》(陈新光，2014)，从珠三角地区常规气象站中选取远离城区的具有代表性的花都、增城和恩平等气象站作为郊区站，选取距离城区较近的南海、顺德和番禺等11个测站作为城区站。以市区站平均值与郊区站平均值的差值作为珠三角城市热岛效应的平均强度，计算得到珠三角城市群平均UHII为1.6℃，其中1990、2000和2010年城市热岛效应的平均强度分别为：0.9、1.3和2.0℃。珠三角城市群UHII年、月变化见图 3，珠三角城市群UHII经历两个过程：1985—2000年UHII增加缓慢，UHII增温趋势为0.34 ℃·(10 a)^-1，而2001—2012年UHII增加明显，UHII增温趋势为0.69 ℃·(10 a)^-1。说明2000年前城市建设面积和工业总产值增长缓慢，而2000年后，UHII增速是城市缓慢增长期的2倍，这与这一时期快速城市化有关，城镇的快速发展，造成珠三角地区城市建筑面积不断增大，原有的农田、山地和水塘被水泥地面所取代，城区潜热通量减少，感热通量增大(Oke, 1988; Owen et al, 1998)，增温效应明显。珠三角地区UHII月变化规律明显，呈现明显的“V”字形变化，UHII最强的月份出现在低温干燥的12月，最弱的UHII出现在空气潮湿对流旺盛的7月。

2.3 UHII的空间分布

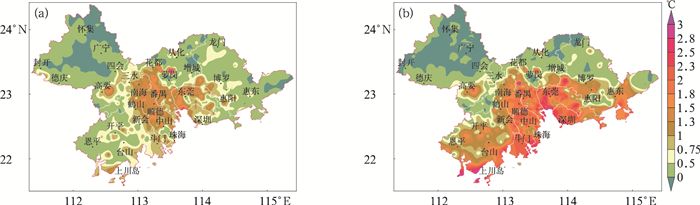
由于珠三角地区气候季节变化不明显，而气候干季和湿季却非常明显，本文参考陈创买等(1997)提出的广东干季和湿季的划分法，即广东10月到翌年1月为干季，4—9月为湿季，而珠三角地区降水也主要集中在前汛期即4—6月和后汛期即7—9月，因此研究珠三角地区雨季和干季UHII变化很有必要。由于珠三角地区从1992年开始陆续建设了区域自动气象站，在研究UHII空间分布时，选用区域气象站密集且覆盖面广、气温观测资料相对完整的2012年作为珠三角城市UHII雨季和干季空间分布分析的基础，能较好体现城市集群化发展导致城区气温高于外围郊区的小气候现象，经过插值得到珠三角地区2012年雨季和干季UHII空间分布(图 4)，由图可见珠三角地区的雨季和干季UHII区域变化明显，雨季珠三角地区只有东莞、广州和佛山的部分工业区热岛达到较强等级，而珠三角中心地带如广州、佛山、东莞、中山和江门的东部地区多为弱等级热岛区域，而珠三角西北部和东北部则属于无热岛区域。干季热岛面积明显扩大，热岛面积在湿季的基础上，向东延伸至惠州的惠东，向西扩展到江门的恩平；UHII明显增强，广州、佛山、东莞、深圳、中山、珠海和高要等地均达到强等级UHII。珠三角城市热岛的空间分布格局与城市建设用地和绿地的分布格局一致。在工业和商业密集区温度较高，UHII大；而在绿地、农田、水库、自然保护区等地区UHII较弱。

2.4 影响UHII的天气因素分析

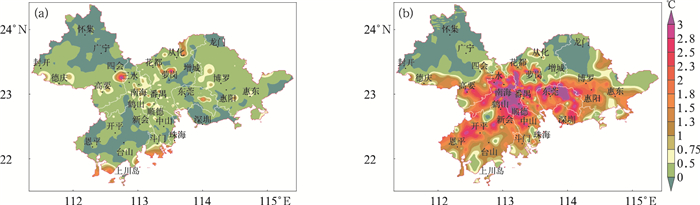
为研究影响城市UHII的典型天气类型，根据2.2节的统计结果，最弱UHII出现在7月，最强UHII出现在12月，因此选取2012年连续强降水过程的7月25日08时作为雨天UHII分析的基础(图 5a)，2012年7月25日前后连续5 d持续暴雨天气，全天中低云量9成以上，降水强度达到暴雨级，风速为5 m·s^-1，相对湿度为95%，全天能见度不到0.2 km，珠三角地区只有高要、顺德、南海和博罗的极个别区域存在较弱的热岛区域，大部分地区为无热岛或者弱热岛区域。这与珠三角地区强对流天气有关，强对流天气有利于中低云量形成，使得到达地面的有效辐射减弱；强对流天气有利于近地层的热量随水汽蒸发带到高空，近地层大风则有利于水汽和热量的水平输送，同时持续降水有利于近地层热量的被吸收，对热岛效应形成有抑制作用。

为分析强热岛形成的气象条件，选取2012年12月16日20时，分析该时次珠三角地区UHII分布情况(图 5b)。该时次珠三角地区气象条件为：风速为0.5~2.7 m·s^-1、风向为东北风，低云量为4成，空气相对湿度65%。12月16日前后没有冷空气过境，天气晴好。江门、佛山、广州、中山、东莞、惠州和深圳均出现极强热岛，肇庆和珠海部分地区出现了强热岛区域。由于16日前没有冷空气侵扰，空气干燥、大气稳定，大气污染物容易聚集，傍晚低空有云层遮挡，大气逆辐射较强，造成城区近地层气温偏高，有利于热岛形成。同时近地层盛行弱的东北风，造成东莞、广州城区近地层累积的热量向下风向的佛山、江门等城市扩散，从而使得珠江东岸城市如东莞、深圳热岛面积小于城市化程度低的江门市；而同一城市也会造成西部UHII强于东部，如惠州，惠阳UHII强于东部的惠东和博罗等地。

2.5 影响UHII的城市因素探讨

城市扩张对大气环境的影响主要表现在土地利用、人为热排放、大气污染物浓度和城市建筑结构的改变，直接影响到城市下垫面反照率，大气热量的收支平衡进而引起城市区域小气候变化，因此研究城市集群化发展指标对气温和UHII的影响十分必要。本文采用灰色关联分析法，对气温和城市发展指标采取标准化无量纲处理，分别计算城市集群化发展指标与气温和UHII的关联度，灰色关联度大小见表 2。

如表 2所见，城市建成区面积是影响平均气温和UHII最重要因子，工业总产值、常住人口、机动车拥有量、公路通车里程、全年总用电量和液化石油气供气总量等也是重要影响因素。根据相关分析，以上因子均与年平均气温和UHII呈正相关。影响气温变化的气象因子很多，但是城市建成区面积增加，城市下垫面的粗糙度增加，地表和太阳的多次反射使吸收的太阳辐射增加，机动车拥有量、公路通车里程、全年总用电量、液化石油气供气总量与能源消耗有关，这些因素造成能源消耗增加，人为排放热增加，从而直接造成气温升高和UHII增加。

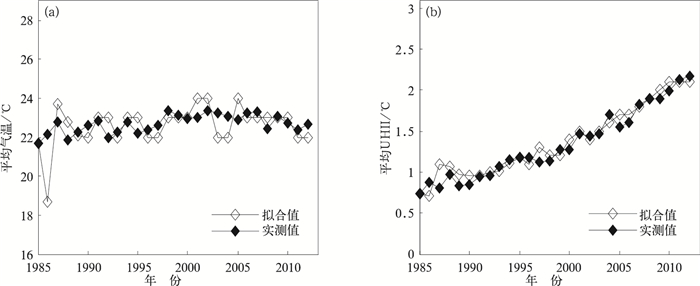
从中挑选出前7项城市集群化发展因子，分别为城市建成区面积、工业总产值、常住人口、机动车拥有量、公路通车里程、全年总用电量和液化石油气供气总量，它们与气温的灰色关联度为0.69~0.79，与UHII的灰色关联度为0.757~0.94，运用GM(1，N)预测模型模拟出1985—2012年珠三角城市集群化发展指标对年平均气温和年平均UHII的影响，气温和UHII的拟合值与实测值之间的对比如图 6所示，可以看到，拟合结果与实测结果的变化趋势是比较接近的，气温的拟合平均相对误差为2.7%，参照灰色模型拟合精度检验等级表，灰色模型对气温拟合相对误差不大于5%，达到拟合精度检验等级的二级，拟合精度较好；灰色模型拟合UHII的平均相对误差为7.0%，达到拟合精度检验等级的三级，拟合精度一般。从城市集群化发展指标对气温和UHII的拟合效果分析，城市集群化发展指标对气温拟合效果要优于UHII，原因可能与UHII的确定与郊区站的选取有关，随着城市集群化发展，郊区站在不同程度上受城市热岛的影响进而影响模型的拟合效果。但总体看灰色模型既全面考虑了各城市因子的影响，又通过关联度排序剔除了对城市集群化发展指标影响相对较小的因子，因此拟合效果较好。分析可见利用灰色模型拟合城市集群化发展因子对气温和UHII的影响具有一定的可行性。

3 结论

(1) 珠三角地区UHII年变化规律明显，2000年前城市UHII增温趋势为0.34 ℃·(10 a)^-1；而2000年后UHII增温趋势为0.69 ℃·(10 a)^-1，UHII增温率是2000年前的2倍。珠三角地区UHII年变化规律明显，UHII最强的月份出现在气温低、空气干燥的12月，UHII最弱月出现在气温高、降水充沛的7月。珠三角地区UHII雨季和干季变化明显，雨季UHII偏弱，热岛面积小，而干季UHII强、热岛面积也大。

(2) 影响UHII的天气因素主要有降水、空气湿度、云量和风速，在对流发展旺盛、多云、持续性大风和强降水天气形势下，UHII较弱；而在微风、晴朗干燥的天气下，UHII较强。此外风向也会影响UHII的空间分布，尤其在干季影响明显，位于城市下风向的区域UHII明显偏大。

(3) 珠三角地区城市集群化发展因子对气温和UHII的影响可用灰色关联度分析，结果表明影响气温和UHII的城市集群化发展指标主要有城市建成区面积、工业总产值、常住人口、机动车拥有量、公路通车里程、全年总用电量和液化石油气供气总量，城市集群化发展对气温和UHII的影响可采用灰色模型建模评估，该模型在刻画珠三角地区城市集群化发展指标对气温和UHII的影响时具有较高的精度。