2. 国家气象中心,北京 100081
2. National Meteorological Centre, Beijing 100081
大气运动是一个高度非线性的动力系统,具有混沌特性(Lorenz,1963),这使得数值预报对初值误差具有高度敏感性。即使模式完美无缺,这样的初值误差也会使预报技巧在几周后几近为零(Toth et al,1993;麻巨慧等,2011),况且数值预报模式并非完备,离散化的大气模式仅仅是真实大气在数学和物理上的近似。对物理过程等描述的不准确等带来的模式误差(穆穆等,2011;李莉等,2011),同初始误差一样,会影响预报技巧。因此,初值的误差、模式的误差及大气的混沌特性使天气预报存在不确定性(李泽椿等,2002;陈静等,2002;邓国等,2010)。针对大气的混沌行为,考虑对不确定性进行全面的模拟,对大气未来的发展情况做出集合预报。Epstein(1969)首先提出集合预报理论,目的在于给出大气未来可能发展情况的整个概率分布。Leith(1974)用蒙特卡罗(Mante Carlo Forecasting,MCF)的预报方法首先进行了集合预报试验。但由于受到计算资源的限制,直至20世纪90年代初,集合预报才在业务数值天气预报中得以实现。1992年集合预报系统(Ensemble Prediction System,EPS)分别在欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)和美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)投入业务使用(Molteni et al,1996;Toth et al,1993),随后,加拿大、日本、中国等国也先后建立了各自的集合预报系统。
集合预报不仅可以用来确定最有可能发生的结果,滤去预报中不可预测的部分,提高预报的精度;而且提供了预报要素的整个概率密度分布函数(Probability Density Function,PDF)的估计,对于某些极端天气事件具有早期预警能力(Buizza et al,2000)。同时,集合预报由于其成员的模式特性和所用的初始条件都彼此不同,能够真实地反映大气的不确定性,可用来分析大气的可预报性,预测天气预报的技巧,为预报可信度的判断提供依据。目前国内外对于集合预报的预报技巧的预测,通常利用不同表征的离散度作为预测量来预测预报技巧(Eugenia et al,1987;Buizza et al,1998;Jeffrey et al,1998;Houtekamer,1998;谭燕,2006;章国材等,2007;陈丽芳等,2010),这是因为离散度作为集合预报不确定性的量度指标(毛恒青等,2002;杜钧,2002;段明铿等,2004),体现预报的不确定性、置信度和集合成员间总体变率程度。一般而言,集合离散度大,则可预报性低,预报技巧差,反之亦然(Molteni et al,1996;Buizza et al,1998;Simon,2002;路建方,2009;杜钧等,2010)。但是,国外学者研究发现,表征离散度的方法不同,所得到的离散度与预报技巧之间的相关性也各有不同(Timonthy,1991;Lance et al,1991;Buizza,1997;Jeffrey et al,1998;Simon et al,2004),因此,对于集合预报系统,全面分析不同离散度表征方法与预报技巧之间的关系,是科学预测和认知集合预报的预报技巧的必要前提。
目前,我国尚没有对集合预报系统的离散度-预报技巧关系进行系统的研究,本文基于ECMWF全球集合预报系统的2007—2011年500 hPa高度场和850 hPa温度场预报数据,针对中国区域,采取两种不同表征的离散度表征方法,对中期预报时效离散度与预报技巧的相关性进行对比分析,以期分析结果能为集合预报在中期时效预报技巧预测方面提供定性和定量的参考。
1 资料说明本文采用ECMWF的全球中期集合预报系统数据,研究时间范围为2007—2011年。研究中使用的资料分为两类:ECMWF的集合预报资料和ECMWF的再分析资料。ECMWF集合预报资料,选取要素为全球500 hPa高度预报场和850 hPa温度预报场,包括51个成员(1个控制预报,50个扰动预报)。覆盖时段为2007年1月1日至2011年12月31日,起报时刻为12 UTC(世界时),预报时效为0~360 h时效,间隔为24 h。ECMWF再分析资料(Uppala et al,2005)为每日00、06、12、18 UTC的500 hPa高度场(Z500) 和850 hPa温度场(T850)。覆盖时段为1980年1月1日至2012年1月15日。再分析资料用于预报技巧检验的实况分析场和构建距平相关中的气候平均值(1980—2009年)。考虑研究整个中国地区,选取14°~60°N和70°~140°E,格点距离为2°×2°,格点数为24×36=864个,所分析的预报时效为96、168、240、360 h。
2 方法 2.1 预报技巧检验预报技巧反映了预报能力的强弱(Palmer et al,1988;Piero et al,2001;杨学胜,2001;Legg et al,2002;皇甫雪官,2002)。本文中所考虑的预报技巧表征方法是均方根差(Root Mean Square Error,RMSE)和距平相关(Anomaly Correlation,AC)。这两种方法在确定性天气模式预报技巧评估中普遍使用,但是在集合预报系统中,其表达公式有所不同,简要介绍如下。
2.1.1 均方根差(RMSE)RMSE表征统计区域内误差幅度的平均状况(刘还珠等,1992)。对于确定性模式,RMSE公式如下:
| $RMSE=\sqrt{\frac{1}{M}\sum\limits_{m=1}^{M}{{{({{y}_{m}}-{{o}_{m}})}^{2}}}}$ | (1) |
式中,ym和om分别是所考虑的空间网格上相应变量的预测值和观测值,M代表网格数。当预报和观测完全一致,即为一个完美的预报时,RMSE的值才等于零,否则结果均大于零。RMSE的值越小,说明预报的准确性越好,反之亦然。对于集合预报而言,定义集合均方根误差RMSENS:
| $RM{{S}_{ENS}}=\frac{1}{N}\sum\limits_{i=1}^{N}{RMS{{E}_{i}}}$ | (2) |
式中,N代表集合预报成员数。
2.1.2 距平相关(AC)AC是两组数据间的空间位相差的量度(Henry et al,1991)。对于确定性模式而言,AC公式如下(Wilks,1995):
| $AC=\frac{\sum\limits_{m=1}^{M}{[({{y}_{m-{{C}_{m}}}})({{o}_{m}}-{{C}_{m}})]}}{\sqrt{[\sum\limits_{m=1}^{M}{{{({{y}_{m}}-{{C}_{m}})}^{2}}\sum\limits_{m=1}^{M}{{{({{o}_{m}}-{{C}_{m}})}^{2}}}}]}}$ | (3) |
式中,ym和om分别是所考虑的空间网格上相应变量的预测值和观测值,Cm是观测变量om的气候平均值,M代表网格数。
| ${{C}_{m}}=\frac{1}{n}\sum\limits_{k=1}^{n}{{{o}_{m}}(k)}$ | (4) |
式中,n代表气候平均值的时间长度。AC大约为0.60是预报的低限。Murphy等(1989)指出,AC值为0.6意味着真实技巧评分大约为0.2,也就是与完全精确的预报相距20%。
由于AC分布是非正态的,可通过费歇尔Z变换,使其具有近似的正态分布(Ledermann,1984)。于是,定义集合距平相关ACENS。
费歇尔Z变换:
| ${{z}_{j}}=1.513\cdot {{\log }_{10}}\frac{1+A{{C}_{j}}}{1-A{{C}_{j}}}$ |
平均:
| $\bar{z}=\frac{1}{N}\sum\limits_{j=1}^{N}{{{z}_{j}}}$ |
逆变换:
| $A{{C}_{ENS}}\frac{{{10}^{\bar{z}/1.513}}-1}{{{10}^{\bar{z}/1.513}}+1}$ | (5) |
式中,N代表集合成员数。经过费歇尔Z变换后,ACENS值越大,说明预报技巧越好,预报的准确性越好,反之亦然。ACENS值的大小所代表的意义与RMSENS值相反。
2.2 集合离散度表征方法集合预报离散度一般定义为相对集合平均(Ensemble Mean,EM)或者相对控制预报的标准差(Timonthy,1991),也有学者定义它为熵、众数(Ziehmann,2001)。所有典型的离散度方法都有其局限性,并与地理位置、年度循环、预报时效和概率分布中预报值的位置等密切相关(Zoltan et al,2001)。本文同样以均方根误差和距平相关表征集合离散度。
2.2.1 RMSE离散度RMSE离散度(SPRMSE)是通过每一个集合预报成员与其余所有成员的RMSE的总和的平均构造而成。SPRMSE被定义:
| $S{{P}_{RMSE}}=\frac{1}{\frac{N(N-1)}{2}}\cdot \Delta ,$ |
| $\Delta =\underbrace{\sum\limits_{i}{\sum\limits_{j}{{{T}^{(i)(j)}}}}}_{i<j}$ |
| ${{T}^{(i)(j)}}=RMSE(\overline{{{W}^{i}}},\overline{{{W}^{j}}})$ | (6) |
式中,Wi和Wj代表N个成员的M个格点网格的物理场,i,j分别代表第i,j个成员。这种离散度的定义没有标准成员或统计量(如控制预报或者EM),所以其优势便显示在每个集合均为一个“中心”,同时也包含着极端成员也具有相同的重要性。
2.2.2 AC离散度AC离散度(SPAC)的定义如下:
| $\underbrace{S{{P}_{AC}}\equiv \frac{{{10}^{\bar{z}/1.513}}-1}{{{10}^{\bar{z}/1.513}}+1}}_{\text{反向费歇尔Z变换}}$ |
| $\bar{z}=\frac{1}{\frac{N(N-1)}{2}}\cdot \Delta $ |
| $\Delta =\underbrace{\sum\limits_{i}{\sum\limits_{j}{{{z}^{(i)(j)}}}}}_{i<j}$ |
| $\underbrace{{{z}_{(i)(j)}}=1.513\cdot {{\log }_{10}}(\frac{1+{{T}^{(i)(j)}}}{1-{{T}^{(i)(j)}}})}_{费歇尔Z变换}$ |
| ${{T}^{(i)(j)}}=\underbrace{AC(\overline{{{W}^{i}}},\overline{{{W}^{j}}})}_{i<j}$ | (7) |
SPAC的含义类似于SPRMSE,同样没有标准参量(如控制预报或者EM),每个集合都是一个“中心”,极端成员也具有相同的重要性。
2.3 去除季节因素气候时间序列通常具备一个季节循环特征。比如温度和位势高度,冬季(夏季)温度低(高)、位势高度低(高)。所以,我们更加关注偏离常态的差值。这也是去除季节循环的原因。由于只有5年的数据,年度循环、偶然成分、谐波成分和极端事件等因素(Grieser et al,2002),因此不可能确定一个完全可靠的气候平均值。于是简单地去除季节因素的方法是减去其滑动平均值,本文研究中选取的滑动值为15 d,以去除天气系统的波动(Simon,2002)。
3 集合预报系统预报技巧的变化特征为探讨集合预报系统预报技巧的季节性和年际变化特征,首先,对预报时效分别为96、168、240、360 h ECMWF全球模式的集合预报系统基于Z500在2007—2011年预报技巧的时间演变序列进行分析。
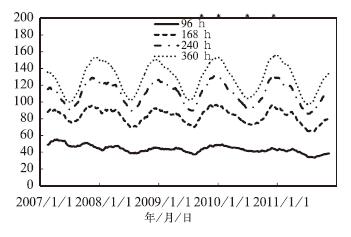
图 1a是以RMSE为表征的预报技巧(RMSENS)的时间演变序列,显示值为91 d的滑动平均——滑动值的选取参考Simon(2002)对预报技巧和离散度时间演变序列的研究,即滑动区间长度取3个月,约为91 d。由图 1a可见,RMSENS值存在一个明显的季节循环,冬(夏)季RMSENS值大(小)。此外,随着预报时效的延长,一是RMSENS值变大,360 h的RMSENS值明显比96 h的RMSENS值大,即预报技巧变低;二是季节循环的波动振幅加大。
|
图 1 ECMWF的500 hPa高度场RMSENS的时间序列(单位:gpm)(a)RMSENS的时间序列, (b)持续性预报的RMSENS的时间序列(实线、虚线、点划线和点线分别代表 96、168、240和360 h,*表示重要的模式升级) Fig. 1 RMSENS time series of ECMWF of the Z500 (unit: gpm)(a) RMSENS time series, (b) RMSENS time series of the persistence forecast(Solid, dashed, stippled, dotted respectively represent 96, 168, 240, 360 h, * indicates important model upgrade) |
持续性预报是根据现有气象状况所作的持续趋势的预报,虽预报不出天气的转折性变化,但反映天气预报的固有变化特征,所以有必要作持续性预报的RMSENS的时间序列,用以理解RMSENS的时间演变序列中所存在的季节循环。其计算方法是用集合预报中各成员零时刻的预报值作为所有时效的预报值,即式(1) 中预报值ym用持续性预报来代替。从图 1b中可见,持续性预报的RMSENS同样具有一个季节性的循环特征,可以认为,RMSENS所具备的季节循环是大气内在固有特性。此外,在不同的预报时效,持续性预报的RMSENS值差别不大,也说明持续性预报在中期时效预报中无技巧可言。
另外,从年际变化来看,2008年冬季各预报时效的RMSENS值明显小于2010年冬季,这可能由当年的大气环流特征所决定的。
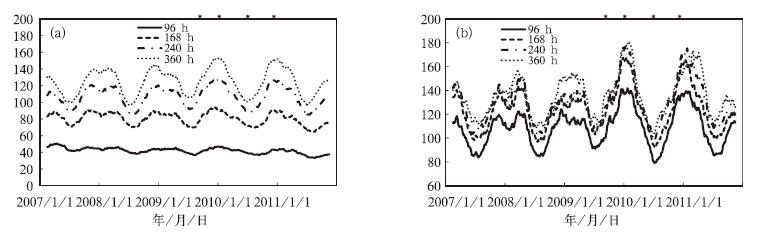
同样,分析了ACENS的变化特征,见图 2。同RMSENS相比,ACENS值也表现出一定的季节循环特征,但相对较弱,冬(夏)季ACENS值大(小)。随着预报时效的延长,ACENS值减小,预报技巧变低。若以0.6为有效预报的AC临界值,96和168 h预报都是有效的。持续性预报的ACENS的时间序列见图 2b,图 2b中,其时间序列显示了一个非常不规则的变化,并不具备一个季节循环特征,所以,ACENS没有显著的内在季节变化特征,模式系统的预报表现的弱的季节性变化并非内在特性。此外,ACENS值均较小,即使在96 h,其值也小于有效预报的AC临界值0.6,表明采用持续性预报在中期预报时效内无预报技巧可言。

|
图 2 ECMWF的500 hPa高度场ACENS的时间序列(a)ACENS的时间序列, (b)持续性预报的ACENS的时间序列(实线、虚线、点划线和点线分别代表 96、168、240和360 h,*表示重要的模式升级) Fig. 2 ACENS time series of ECMWF of the Z500 (a) ACENS time series, (b) ACENS time series of the persistence forecast (Solid, dashed, stippled, dotted respectively represent 96, 168, 240, 360 h, * indicates important model upgrade) |
综合图 1和图 2可以看出,利用RMSE和AC两种统计量(RMSENS和ACENS)来评估预报技巧,其变化特征具有较大的差异。这种差异是由于验证方法内在的特性所决定的。另外还需注意的是,低RMSENS值主要归因于不同的季节,也可能是由模式性能的改变或者大气流场的内在性质所决定的。所以,预报的检验结果依赖于检验方法的选择和所处的季节。
4 集合预报系统离散度的变化特征同样分析了离散度表征方法的变化特征。图 3和图 4显示基于Z500的SPRMSE和SPAC的时间演变序列。
图 3和图 4中可知,随着预报时效的延长,SPRMSE值变大,SPAC值变小,均代表着离散度增加。与RMSENS和ACENS的时间序列所表现的特征类似,SPRMSE也存在一个明显的季节循环(图 3),冬(夏)季SPRMSE值大(小),离散度大(小)。预报时效越长,季节循环的振幅越强,冬夏季所表示的离散度差异也越大,且SPRMSE的变化在冬季强于夏季。模式预报的SPAC具备一个较弱的季节循环特征(图 4),冬(夏)季SPAC值大(小),离散度小(大)。
另外,在850 hPa温度场中,SPRMSE也存在一个季节性的变化,与高度场类似,但没有高度场明显。在850 hPa温度场中,可以看到在2010年11月后,SPRMSE显著减小,这可能是由于集合预报系统性能的升级而引起离散度的减小。回顾ECMWF全球集合预报系统的发展概况,在2010年11月,系统升级了参数化的扰动方案,可以认为这是SPRMSE减小的重要原因。
5 两种集合预报离散度-预报技巧关系对比分析 5.1 散点关系定性分析通过前面部分对预报技巧和离散度变化特征的分析,得知RMSENS和SPRMSE存在一个季节性的循环,冬(夏)季值大(小),ACENS和SPAC不存在内在的季节循环特征,但是模式系统的预报显示出一个弱的季节循环特征,冬(夏)季值大(小)。所以,分别运用RMSE和AC方法来表示集合离散度-预报技巧关系时,若直接将SPRMSE和RMSENS、SPAC和ACENS结合,其关系所表示结果可比性较差,于是采用去除季节性因素和标准化的处理方法,再对两种离散度-预报技巧关系进行对比分析。两种表征的离散度-预报技巧关系的散点图见图 5和图 6。
|
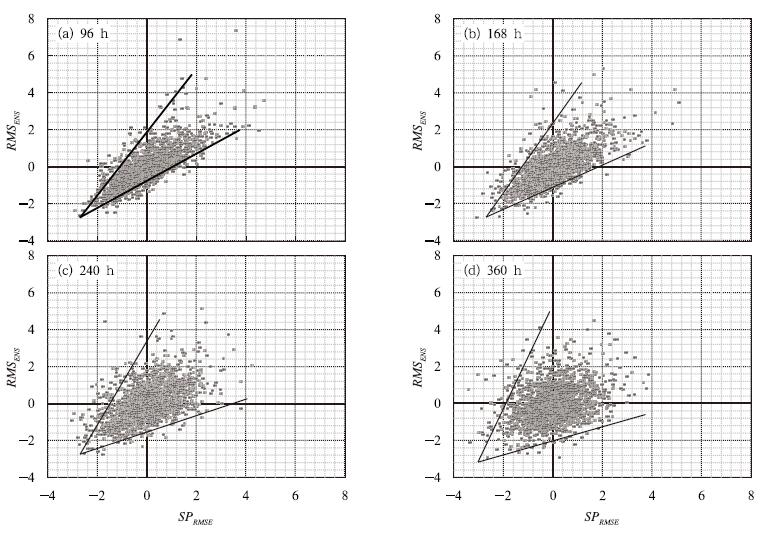
图 5 ECMWF的500 hPa高度SPRMSE-RMSENS关系的散点关系图 Fig. 5 Scatter plots of SPRMSE-RMSENS relations of ECMWF of the Z500 |
|
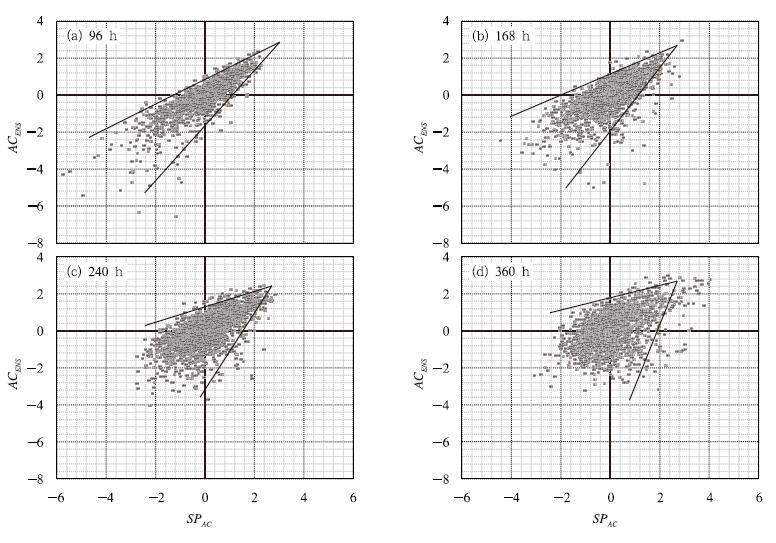
图 6 ECMWF的500 hPa高度SPAC-ACENS关系的散点关系图 Fig. 6 Scatter plots of SPAC-ACENS relations of ECMWF of the Z500 |
散点关系图可以简单直观定性地看出集合离散度-预报技巧关系。对于理想集合预报系统,一般而言,用于表示预报不确定性的集合离散度越大,则可预报性越低,预报技巧越差;集合离散度越小,则可预报性越高,预报技巧越好(Molteni et al,1996;Buizza et al,1998;Simon,2002)。在散点图中,对于SPRMSE-RMSENS关系,期望更多的散点分布在第三象限和第一象限,即小离散度高预报技巧(第三象限)和大离散度低预报技巧(第一象限)。对于SPAC-ACENS关系,由于反相关关系,期望散点分布在第一象限和第三象限,即小离散度高预报技巧(第一象限)和大离散度低预报技巧(第三象限)。上述两种关系,对于不同预报时效而言,随着预报时效的延长,散点逐渐分散,整体呈“扇形”,说明了离散度-预报技巧关系的相关性逐渐地弱化而变得不确定性增大。
从图 5可以看出,SPRMSE-RMSENS关系相对预报时效96、168、240 h,其散点分布均呈现出一个清晰的扇形,扇形张角逐渐增大,即离散度小,预报技巧高,离散度大,预报技巧可能低,并且随着时效的延长对预报技巧预测的不确定性增大。预报时效为360 h,小(大)离散度与高(低)的预报技巧之间有一定的对应关系,但参考意义已经不十分明显。
图 6是以AC为表征的离散度-预报技巧关系(SPAC-ACENS)散点图,预报时效96、168、240和360 h均呈现出“倒”扇形,扇形张角逐渐增大,但扇形角度均比同时效图 5中的扇形角度小,这表明SPAC-ACENS表征的离散度-预报技巧关系比SPRMSE-RMSENS表征的离散度-预报技巧关系更紧密。
进一步采用相关系数统计分析离散度-预报技巧关系,计算结果通过α=0.05的显著性水平检验,结果见表 1。通过对比两种离散度-预报技巧关系的相关系数,可以看出,基于Z500(T850) 的SPAC-ACENS关系的相关系数为0.84~0.49(0.84~0.66),SPRMSE-RMSENS关系的相关系数为0.75~0.33(0.72~0.28),在各预报时效下,SPAC-ACENS关系的相关系数均比SPRMSE-RMSENS关系的相关系数大,同时,基于Z500(T850) 的SPAC-ACENS关系的相关系数在360 h比96 h减少42%(21%),而SPRMSE-RMSENS关系的相关系数在360 h比96 h减少56%(61%),可见,SPRMSE-RMSENS关系的相关系数减少得更多。由此可见,无论是基于Z500还是T850,均显示以AC为表征的离散度与预报技巧的关系(SPAC-ACENS)的相关性更紧密,更能反映中期时效的预报技巧,且T850较Z500反映的离散度-预报技巧关系更强。
|
|
表 1 ECMWF离散度-预报技巧关系的相关系数 Table 1 Correlation coefficients of spread-skill relations of ECMWF |
列联表分析可用来定量判断预报技巧和离散度两种属性之间的关联性,按预报技巧高、低和离散度大、小排列组合为四类关系,统计分析四类关系的相关性,以列联表形式给出统计结果。本文所统计的四类关系,采用散点图中位于不同象限的点占总样本数的百分比。相比散点图分析,该方法客观定量和全面。表 2为ECMWF全球模式的集合预报系统基于Z500的离散度-预报技巧关系列联表,其中划线数据表示理想的集合预报系统中离散度和预报技巧的对应关系。
|
|
表 2 ECMWF的500 hPa高度的离散度-预报技巧关系列联表 Table 2 Contingency table of spread-skill relations of ECMWF of the Z500 |
从表 2中样本百分比表明,ECMWF的集合预报系统在各预报时段的SPRMSE-RMSENS(SPAC-ACENS)关系所表现的小离散度高预报技巧和大离散度低预报技巧之和(划线数值之和)所占百分比为79%~61%(84%~66%)。对比两种表征的离散度-预报技巧关系,SPRMSE-RMSENS关系所表现的理想集合预报系统下的离散度-预报技巧关系(即离散度小预报技巧高,离散度大预报技巧低)没有SPAC-ACENS关系所表现得强。与前面相关系数的统计分析结果相同,SPAC-ACENS关系更能反映集合离散度-预报技巧关系。
分别讨论小离散度高预报技巧的百分比和大离散度低预报技巧的百分比,可以得出在各预报时段SPRMSE-RMSENS(SPAC-ACENS)关系所表示的小离散度高预报技巧所占百分比为44%~33%(51%~30%);SPRMSE-RMSENS(SPAC-ACENS)关系所表示的大离散度低预报技巧所占百分比为35%~28%(34%~36%)。可见,小离散度高预报技巧的百分比普遍更高,且随着预报时效的延长,小离散度高预报技巧所占百分比与大离散度低预报技巧所占百分比之间的差异也逐渐减小。
对于SPAC-ACENS关系,小离散度体现高的预报技巧的关系从96~360 h时效百分比下降了20%左右,而在大离散度的情况下离散度-预报技巧关系相对弱一些,但随预报时效的延长样本百分比没有显著的降低。
5.3 离散度的一致性由于SPRMSE和SPAC的时间演变序列具有不同的特征(图 3和图 4),所以讨论两种离散度方法的一致性,首先采取相关系数分析SPRMSE和SPAC的一致性。表 3是ECMWF全球模式的集合预报系统SPRMSE和SPAC关系的相关系数,计算结果通过α=0.05的显著性水平检验。
|
|
表 3 ECMWF的SPRMSE-SPAC关系相关系数 Table 3 Correlation coefficients of SPRMSE-SPAC relations of ECMWF |
从表 3可知,基于Z500的SPRMSE-SPAC关系去除季节因素及标准化的线性相关系数范围为-0.44(96 h)至-0.26(360 h)。去除季节性因素及标准化与仅标准化处理对比,去除季节因素及标准化的SPRMSE-SPAC关系的相关系数绝对值(0.44~0.26) 大于仅标准化的SPRMSE-SPAC关系的相关系数绝对值(0.37~0.13),相关性有所提高,SPRMSE和SPAC的一致性增加,在96、168、240和360 h时效相对仅标准化的处理,相关系数绝对值分别增加了0.07、0.23、0.18和0.13。这是因为SPRMSE和SPAC具有完全不同的季节特征,所以去除季节因素和标准化处理后其相关性有所提高。
同理,采取列联表表示SPRMSE和SPAC的一致性。从表 4可以看出,基于Z500在中期时段各时效的SPRMSE和SPAC的一致的样本(划线数值之和)占61%~53%。通过去除季节因素和标准化处理后,其一致的样本性占66%~59%,可见,去除季节因素和标准化比仅标准化所代表的SPRMSE和SPAC的一致性有所提高,这与相关系数计算结果相同。从样本百分比的数值上来看,未显示较高的一致性特征。另外,对于去除季节因素和标准化处理所代表的SPRMSE和SPAC的一致性,随着预报时效的延长,SPRMSE和SPAC一致代表大离散度的百分比逐渐增加,一致代表小离散度的百分比逐渐减小,在240 h以前,SPAC和SPRMSE一致代表小离散度的百分比大于一致代表大离散度的百分比。
|
|
表 4 ECMWF的500 hPa高度的SPRMSE-SPAC关系列联表 Table 4 Contingency table of SPRMSE-SPAC relation of ECMWF of the Z500 |
本文针对中期时效预报技巧的预测研究,关注中国区域,利用ECMWF全球模式的集合预报系统对比分析两种集合离散度-预报技巧关系,得出以下结论:
(1) 以均方根误差为表征的预报技巧(RMSENS)和离散度(SPRMSE)表现出季节循环特征,即冬(夏)季值高(低),且随预报时效的延长季节变化幅度增大,是大气内在性质的表现。而以距平相关为表征的预报技巧(ACENS)和离散度(SPAC)没有显著的内在季节变化特征。
(2) 对于两种不同表征的离散度-预报技巧关系,散点图和相关系数分析显示,SPRMSE-RMSENS关系和SPAC-ACENS关系散点图分别呈现一个扇形和“倒”扇形,即离散度小,预报技巧高,离散度大,预报技巧可能高也可能低;且随着预报时效的延长,散点图逐渐发散,扇形的张角逐渐增大,对预报技巧预测的不确定性增大。相关系数统计分析显示,SPAC-ACENS表征的离散度-预报技巧关系比SPRMSE-RMSENS表征的离散度-预报技巧关系更紧密,更能反映中期时效的预报技巧,且T850较Z500反映的离散度-预报技巧关系更强。
(3) 定量分析离散度-预报技巧关系,统计结果表明在小离散度情况下更能体现高的预报技巧,但这种关系从96~360 h样本百分比下降了20%左右,而在大离散度情况下离散度-预报技巧关系相对弱一些,但随预报时效的延长样本百分比没有显著的降低。另外,小离散度情况下高预报技巧的百分比普遍更高,且随着预报时效的延长,小离散度高预报技巧所占百分比与大离散度低预报技巧所占百分比之间的差异也逐渐减小。
(4) 样本统计显示中期各时效SPRMSE和SPAC二者一致的样本占59%~66%,并没有显示较高的一致性特征。SPAC和SPRMSE所代表的小的离散度情况所表示的一致性普遍比大的离散度情况下更高。
本研究仅利用ECMWF全球模式的集合预报系统对中国中期时效预报技巧的预测方法进行研究,数据稍显单一,今后我们将在上述研究工作的基础上,加入NCEP和中国集合预报系统(T213模式)综合讨论分析;另外,我国集合预报系统拟升级为T639模式系统,有待进一步针对我国最新的集合预报系统进行讨论分析;还可以尝试使用更多的检验评估方法、构造综合的离散度表征方法深入探讨分析。
陈静, 陈德辉, 颜宏, 2002. 集合数值预报发展与研究进展[J]. 应用气象学报, 13(4): 497-507. |
陈丽芳, 陈勇明, 2010. 集合预报方法在不同类型天气中的预报性能评估[J]. 科技通报, 26(3): 331-338. |
邓国, 龚建东, 邓莲堂, 等, 2010. 国家级区域集合预报系统研发和性能检验[J]. 应用气象学报, 21(5): 513-523. DOI:10.11898/1001-7313.20100501 |
杜钧, 2002. 集合预报的现状和前景[J]. 应用气象学报, 13(1): 16-28. |
杜钧, 邓国, 2010. 单一值预报向概率预报转变的价值:谈谈概率预报的检验和应用[J]. 气象, 36(12): 10-18. DOI:10.7519/j.issn.1000-0526.2010.12.002 |
段明铿, 王盘兴, 2004. 集合预报方法研究及应用进展综述[J]. 南京气象学院学报, 27(2): 279-288. |
皇甫雪官, 2002. 国家气象中心集合数值预报检验评价[J]. 应用气象学报, 13(1): 29-36. |
李莉, 李应林, 田华, 等, 2011. T213全球集合预报系统性误差订正研究[J]. 气象, 37(1): 31-38. DOI:10.7519/j.issn.1000-0526.2011.01.004 |
李泽椿, 陈德辉, 2002. 国家气象中心集合数值预报业务系统的发展及应用[J]. 应用气象学报, 13(1): 2-14. |
刘还珠, 张绍晴, 1992. 中期数值预报的统计检验分析[J]. 气象, 18(9): 50-54. DOI:10.7519/j.issn.1000-0526.1992.09.012 |
路建方, 2009. 集合预报系统中关键技术的研究与实现[M]. 湖南: 国防科学技术大学.
|
毛恒青, 陈谊, 陈德辉, 2002. 基于神威中期集合数值预报系统的产品开发[J]. 应用气象学报, 13(1): 47-55. |
麻巨慧, 朱跃建, 王盘兴, 等, 2011. NCEP、ECMWF及CMC全球集合预报业务系统发展综述[J]. 大气科学学报, 34(3): 370-380. |
穆穆, 陈博宇, 周菲凡, 等, 2011. 气象预报的方法与不确定性[J]. 气象, 37(1): 1-13. DOI:10.11676/qxxb2011.001 |
谭燕, 2006. 中尺度强降水天气集合预报技术的研究[M]. 北京: 中国气象科学研究院.
|
杨学胜, 2001. 业务集合预报系统的现状及展望[J]. 气象, 27(6): 3-9. DOI:10.7519/j.issn.1000-0526.2001.06.001 |
章国材, 矫梅燕, 李延香, 等, 2007. 现代天气预报技术和方法[M]. 北京: 气象出版社, 292-293.
|
Buizza R, 1997. Potential forecast skill of ensemble prediction and spread and skill distributions of the ECMWF ensemble prediction system[J]. Mon Wea Rev, 125(1): 99-119. DOI:10.1175/1520-0493(1997)125<0099:PFSOEP>2.0.CO;2 |
Buizza R, Hollingsworth A, 2000. Severe weather prediction using the ECMWF EPS[J]. ECMWF Newsletter, No.89, Winter 2000/01: 2-12. |
Buizza R, Palmer T N, 1998. Impact of ensemble size on ensemble prediction[J]. Mon Wea Rev, 126: 2502-2518. |
Epstein E S, 1969. Stochastic dynamic prediction[J]. Tellus, 21: 739-759. |
Eugenia K, Amnon D, 1987. Forecasting Forecast Skill[J]. Mon Wea Rev, 115: 349-356. DOI:10.1175/1520-0493(1987)115<0349:FFS>2.0.CO;2 |
Grieser J, Tromel S, Schonwiese C D, 2002. Statistical time series decomposition into significant components and application to European temperature[J]. Theor Appl Climatal, 71: 171-183. DOI:10.1007/s007040200003 |
HenryR S, LaurenceJ W, WilliamR B, 1991. 气象学中常用检验方法概述[M]. 北京: 气象出版社, 1-94.
|
Houtekamer P L, 1998. Global and local skill forecasts[J]. Mon Wea Rev, 121: 1834-1846. |
Jeffrey S W, Andrew F L, 1998. The Relationship between ensemble spread and ensemble mean skill[J]. Mon Wea Rev, 126: 3292-3302. DOI:10.1175/1520-0493(1998)126<3292:TRBESA>2.0.CO;2 |
Lance M L, Greg J H, 1991. Predicting regional forecast skill using single and ensemble forecast techniques[J]. Mon Wea Rev, 119: 425-435. DOI:10.1175/1520-0493(1991)119<0425:PRFSUS>2.0.CO;2 |
Ledermann W. 1984. Statistics. Handbook of Applicable Mathematics. Vol.6, J. Wiley and Sons, 942.
|
Legg T P, Mylne K R, Woolcock C, 2002. Use of medium-range ensembles at the Met Office 1: PREVIN-a system for the production of probabilistic forecast information from the ECMWF EPS[J]. Meteorol Appl, 9: 255-271. DOI:10.1017/S1350482702003018 |
Leith C E, 1974. Theoretical skill of Mont e Carlo forecasts[J]. Mon Wea Rev, 115: 409-418. |
Lorenz E N, 1963. Deterministic Nonperiodic Flow[J]. J Atmos Sci, 20: 130-141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
Molteni F, Buizza R, Palmer T N, et al, 1996. The ECMWF ensemble prediction system: Methodology and validation[J]. Meteorol Soc, 122: 73-119. DOI:10.1002/(ISSN)1477-870X |
Murphy A H, Epstein E S, 1989. Skill scores and correlation coefficients in Model verification[J]. Mon Wea Rev, 117: 572-581. DOI:10.1175/1520-0493(1989)117<0572:SSACCI>2.0.CO;2 |
Palmer T, Tibaldi, 1988. On the prediction of forecast Skill[J]. Mon Wea Rev, 116: 2453-2480. DOI:10.1175/1520-0493(1988)116<2453:OTPOFS>2.0.CO;2 |
Piero A C, Francois L, 2001. Verification of the ECMWF ensemble prediction system forecasts: A study of large-scale patterns[J]. Wea Forecasting, 16: 611-619. DOI:10.1175/1520-0434(2001)016<0611:VOTEEP>2.0.CO;2 |
Simon C S, 2002. Skill Prediction for Medium-Range Weather Forecasts[J]. Swiss Federal Institute of Technology. |
Simon C S, Cheistof A, 2004. Analysis of the spread-skill relations using the ECMWF ensemble prediction system over Europe[J]. Wea Forecasting, 19: 552-565. DOI:10.1175/1520-0434(2004)019<0552:AOTSRU>2.0.CO;2 |
Timonthy W B, 1991. The relations between spread and forecast error in extended-range forecasts[J]. J Climate, 4: 733-742. DOI:10.1175/1520-0442(1991)004<0733:TRBSAF>2.0.CO;2 |
Toth Z, Kalnay E, 1993. Ensemble forecasting at NMC: The generation of perturbations[J]. Bull Amer Meteor Soc, 74: 2317-2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2 |
Uppala S M, Kallberg P W, Simmons A J, et al, 2005. The ERA-40 re-analysis[J]. Quart J Roy Meteor Soc, 131: 2961-3012. DOI:10.1256/qj.04.176 |
Wilks D S, 1995. Statistical Methods in the Atmosphere[J]. International Geophysics Series, Vol.59, Academic Press: 467. |
Ziehmann C, 2001. Skill prediction for local weather forecasts based on the ECMWF ensemble[J]. Nonliner Processes in Geophysics, 8: 419-428. DOI:10.5194/npg-8-419-2001 |
Zoltan T, Yuejian Z, Timothy M, 2001. The use of ensemble to identify forecasts with small and large uncertainty[J]. Wea Forecasting, 16: 463-477. DOI:10.1175/1520-0434(2001)016<0463:TUOETI>2.0.CO;2 |
 2014, Vol. 40
2014, Vol. 40