引言

随着观测资料和模式状况的日益改善，数值预报技术得到了迅速的发展，预报水平不断提高，但也存在不小的误差^[1]。模式误差是预报误差的主要来源之一。正面改进模式各个环节来发展模式非常重要，但模式终究不能达到完美，发展经验性方法来减小模式误差对预报的影响是非常必要的。目前的模式误差订正大体可分为两种^[2]：一是后验(或事后)订正，另一是过程订正^[3]。对于后验订正，只在整个积分完成后对预报结果进行订正处理，如在许多业务预报单位成功运用的MOS(model output statistics)方法就是一个后加工的典型，它利用数值预报的输出结果通过回归方程来预报局地天气要素^[4]。贺皓^[5]曾对位势高度场和温度场采用不同时间权重和空间平滑的订正方案，风场采用动力订正方案，湿度场采用平流(风场)订正方案，取得了令人满意的效果。魏文秀^[6]用卡尔曼滤波技术对欧洲中期天气预报中心(ECMWF)500 hPa位势高度场进行多种订正试验，证明卡尔曼滤波双因子订正对于提高暴雨中期预报能力是有效的。杨松等^[7]用根据误差的特性，根据不同的物理量建立回归模型，去除模式的随机误差，取得了较好的效果。任宏利等^[8]根据大气相似性原理，提出了利用历史资料的相似信息估计模式误差的反问题，并发展了一种将统计和动力两种方法有机结合的相似性误差订正方法。李莉等^[9]利用一种统计学方法对T213降水预报进行订正，减少T213降水预报的系统性误差，订正后雨带的位置和轮廓更加接近降水实况。马清等^[10]利用类似卡尔曼滤波的自适应误差订正法对不同业务中心的区域集合预报模式2 m温度预报做订正，订正后温度预报的各项检验指标都显示出不同程度的改善。邵爱梅等^[11]提出了一种利用SVD修正模式预报误差的变分方法，并利用浅水方程模式和模式资料对它进行检验，表明当预报误差明显超过分析误差时，订正能够明显改进预报。李莉等^[12]针对模式系统性误差一直存在的现状，研究使用卡尔曼滤波的自适应误差订正方法对国家气象中心业务全球集合预报模式的系统性误差进行估计和订正，结果表明，订正后的高层形势场集合预报和2 m温度集合预报的均一性、集合平均的均方根误差和距平相关系数都得到了改善，系统性偏差得到了不同程度的订正，对于存在较大系统性误差的2 m温度预报，订正效果尤其显著。

与此同时，集合预报作为一种估计天气预报的不确定性和制作概率预报的技术近年来得到了很大的进步^[13-14]。但是集合预报对资料的共享和计算条件都有较高的要求，对于较低一级的暂时不具备条件的台站，可以采取类似poor man的集成方法^[15-16]对多模式集合预报成员或单模式不同时效的预报结果进行集成，以得到更优的决定性预报，改善预报结果。本文提出了针对单个模式预报结果后处理的订正方案，既是对模式输出结果的事后订正，也是对单模式不同时效预报结果进行集成订正预报的试验。以ECMWF模式地面气温预报为例，首先评估了该模式在中国东部地区对地面气温的预报能力，再充分利用模式已有的预报结果，并结合观测资料采取多元线性回归订正方法和多时效消除偏差平均订正方法将模式多个时效的预报结果进行集成。此外，还考察了它们相应的一元订正方法。

1 资料和方法 1.1 资料

本文所用资料为欧洲中期天气预报中心(ECMWF)的确定性预报输出资料以及中国东部地区台站观测资料。

(1) ECWMF资料：选取ECMWF预报模式2007年1月1日至2010年12月31日每天00时，12时(世界时，下同)起报的地面气温资料，预报区域取为中国100°E以东陆地区域，分辨率为1.0°×1.0°经纬网格，预报时效为12~240 h，间隔为12 h。

(2) 台站观测资料：选取中国东部地区687站2007年1月11日至2010年12月31日每天00时，12时的台站观测资料，作为观测值，用于检验预报效果。采用Cressman客观分析法插值出分辨率为1.0°×1.0°经纬网格，扫描半径为10、7、4和1个网格格距，共叠代4次。

1.2 方法 1.2.1 线性回归订正方案

多元线性回归订正方法(MLR)把选取的时间序列分为两部分，即训练期和预报期。在训练期使用订正预报值与观测值做多元线性回归分析，确定参与回归分析的各预报时效(预报因子)的权重(回归)系数，权重随空间、时间变化，相应的权重系数用于预报期的多元线性回归订正预报。

类似于多模式超级集合预报技术^[17-19]，该订正预报模型由方程(1) 构建。在一个给定的格点上，对于某一预报时效某一气象要素：

${{C}_{t}}=\bar{O}+\sum\limits_{i=1}^{m}{{{a}_{i}}({{F}_{i,\text{ }t}}-{{{\bar{F}}}_{i}})}$

(1)

式中，C_t为订正预报值，O为训练期观测值平均，F_{i, t}为第i个预报时效的预报值，F_i为第i个预报时效在训练期的预报值平均，a_i为回归系数(权重)，m为参与集成的因子总数，t为时间。

在训练期，回归系数a_i由式(2) 中的误差项G最小化计算获得：

$G=\sum\limits_{i=1}^{N}{{{({{C}_{t}}-{{O}_{t}})}^{2}}~}$

(2)

式中，O_t为观测值，N为训练期时间样本总数。在用订正预报值与观测值做多元线性回归分析时，要使G最小在计算中应用最小二乘法原理，误差协方差矩阵SS为

$\begin{align} & \mathit{\boldsymbol{SS}}=\left[ \mathit{\boldsymbol{S}}{{\mathit{\boldsymbol{S}}}_{i,j}} \right]=\left[ \sum\limits_{i=1}^{N}{F{{\prime }_{i,t}}F{{\prime }_{j,t}}} \right] \\ & \quad \quad \quad \left( i,j=1,2,\cdots ,n \right) \\ \end{align}$

(3)

式中，F′_i，t和F′_j，t分别是第i个因子和第j个因子的预报值距平。

建立线性代数方程：

$\left[ \mathit{\boldsymbol{S}}{{\mathit{\boldsymbol{S}}}_{i,j}} \right]\cdot \left[ {{\mathit{\boldsymbol{a}}}_{i}} \right]=\left[ \mathit{\boldsymbol{\tilde{O}}}_{i}^{'} \right]$

(4)

式中，$\tilde O_i^{'} = \sum\limits_{t = 1}^N {O_i^{'}F_{i,t}^{'}} ,O_t^{'}$为观测值距平，[SS_i，j]为(m×m)的矩阵，[a_i]为(m×1) 的矩阵，$\left[ \mathit{\boldsymbol{\tilde{O}}}_{i}^{'} \right]$为(m×1) 的矩阵。应用Gauss-Jordan消除法求解式(4) 中的[a_i]，得到a_i代入到式(1) 中。对其他格点也做同样的计算，在预报期即可利用求得的a_i进行订正预报。

由于随着预报时效的缩短，预报准确率逐步提高，因此有必要考察加入更长预报时效的结果进行多元线性回归分析的必要性，即长时效的预报结果是否会带来负面作用。可采取只考虑最新的预报结果(即当前最好的)进行一元线性回归订正(ULR)的试验，该方案由方程(5) 构建，求解方法同多元线性回归。

${{C}_{t}}=\bar{O}+a({{F}_{t}}-\bar{F})$

(5)

1.2.2 消除偏差订正方案

多时效消除偏差平均订正方案(MBR)可由式(6) 定义：

${{C}_{t}}=\bar{O}+\frac{1}{m}\sum\limits_{i=1}^{m}{({{F}_{i,t}}-{{{\bar{F}}}_{i}})}$

(6)

比较式(1) 与式(6)，消除偏差平均给予参与集成的各个时效的预报相同的权重，近的预报时效与远的预报时效对集成预报的贡献相同，而多元线性回归订正通过各个预报时效在训练期表现给予不同的权重来量化它们对集成预报的贡献。

同样，为便于比较，也引入仅考虑当前最新的预报结果进行单时效消除偏差(UBR)的试验，即在方程(6) 中，令m=1。

考虑到地面气温具有显著的日变化，因此以上4种订正方案均分别按模式对00时和12时的预报独立地进行订正。

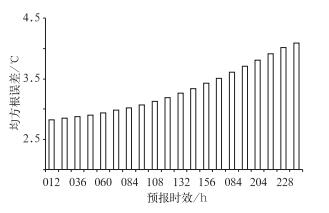
2 ECMWF预报模式地面气温预报误差评估

以温度预报的均方根误差作为衡量预报效果的指标，计算2007年1月11日至2010年12月11日ECWMF预报模式不同预报时效在中国东部地区(100°E以东陆地区域)的区域平均均方根误差。如图 1所示，对于中国东部地区，ECWMF模式预报的均方根误差随预报时效延长而增大，从12 h预报到240 h预报均方根误差增加了1.3℃左右。从地理分布上(图略)来看，ECMWF模式地面气温预报误差在中国东北地区普遍较大，24 h预报达到了3℃以上，另一个较大的区域是四川西部，24 h预报均方根误差在6℃以上。在中部和东部大部分地区误差较小，24 h预报误差均在3℃以下，个别区域不到2℃，168 h预报误差也基本上都在4℃以下。对于任一个格点上的任意一次预报，长时效预报的误差并不是总比短时效预报的大。从ECWMF模式逐日地面气温预报的均方根误差上看(图略)，虽然随着预报时效的延长，地面气温的预报均方根误差总体上呈增大的趋势，但是在某些时次，某些时效较长的预报区域平均均方根误差反而比时效较短的预报误差要小。因此，这些长时效的预报可能包含了部分短期预报中没有的预报信息，在做新的短期预报时具有一定的参考价值。因此能否采用多元线性回归或者多时效消除偏差平均的方法提取有用的预报信息，而摒弃那些由于积分时间长而导致的错误信息？

3 四种订正预报与ECMWF模式预报的比较

针对2007—2010年ECMWF预报模式在中国东部地区的地面气温预报，分别对预报时效为12~240 h(间隔12 h)，选取从2007年1月11日至3月11日共60天120个时次开始并随着预报时间的滑动顺次向后滑动(即预报时间前60天)为训练期，以2007年3月12日至2010年12月11日为预报期，以台站观测资料为观测值，进行订正预报试验。其中，多元线性回归订正方案和多时效消除偏差平均订正方案均选取当前最近的4个预报结果进行集成(216 h订正预报为3个预报结果进行集成，即216、228和240 h，而228和240 h分别为两个和一个预报结果进行订正)。

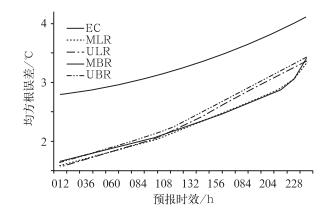
图 2给出了2007年3月12日至2010年12月11日ECMWF模式和4种订正预报结果在中国东部地面气温预报的区域平均均方根误差，预报时效为12~240 h。从中可见，从12~240 h，4种订正预报都大大地改善了模式预报的结果。在72 h时效以前一元线性回归订正方法(ULR)的均方根误差最小，在72 h时效以后多元线性回归(MLR)的订正效果最好，对于168 h及更长的预报时效，多时效消除偏差(MBR)平均在部分时间要略优于多元线性回归，但非常有限，一般不超过0.05℃。单时效消除偏差(UBR)总体效果最差。从12~240 h，最好的订正方案对预报误差的改进都在0.7至1.2℃之间，随着预报时效的延长，改进幅度有减小的趋势。同时，在短期预报(24~72 h预报)，只考虑最新的预报结果的一元线性回归订正方法效果最好，而在72 h预报之后，两种考虑最近4个预报时效的多元集成预报方法要明显优于两种仅对最新预报结果进行订正的方法。这可能是因为随着预报时间的延长，模式的预报能力逐渐下降，误差增大，不同时效预报的离散度增加，而多个时效的集成订正方法考虑了最近48小时的预报结果，并分别利用多元线性回归和消除偏差平均的方法进行集成，比仅考虑单个时效的订正方法提高了预报的稳定性。随着预报时效的延长，这种优势更加明显，因此在更长时效的中期预报或延伸期预报中，多预报时效的集成订正方法将有更大的应用价值。同时，我们也发现随着预报时效的延长，多时效消除偏差平均的预报技巧逐渐接近多元线性回归方法。因此对于24~72 h预报，可选择只考虑最新预报结果的一元线性回归订正和单时次消除偏差的订正方法；对于96~168 h预报，可选择考虑最近4个预报时效集成的多元线性回归和多时效消除偏差平均的订正方法。

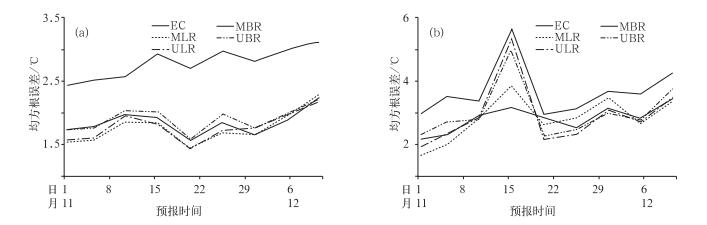
图 3给出了2010年11月1日至12月11日24和168 h 4种订正预报与ECMWF模式对应预报时效的地面气温预报在中国东部的区域平均均方根误差。12~240 h预报(除24 h外其他时效图略)在预报期大部分时间里，4种订正后的预报均方根误差要明显小于模式预报，比模式预报的误差降低了将近1.0℃。24 h预报在大部分时间里，多元线性回归订正方法效果要略优于一元线性回归。对于168 h预报，从4种方法的逐日订正预报均方根误差来看，没有哪一个方法始终最优，但是总体看来，多元线性回归和多时效消除偏差平均能够更加稳定地降低误差，尤其是在模式预报误差较大时，如11月中旬。

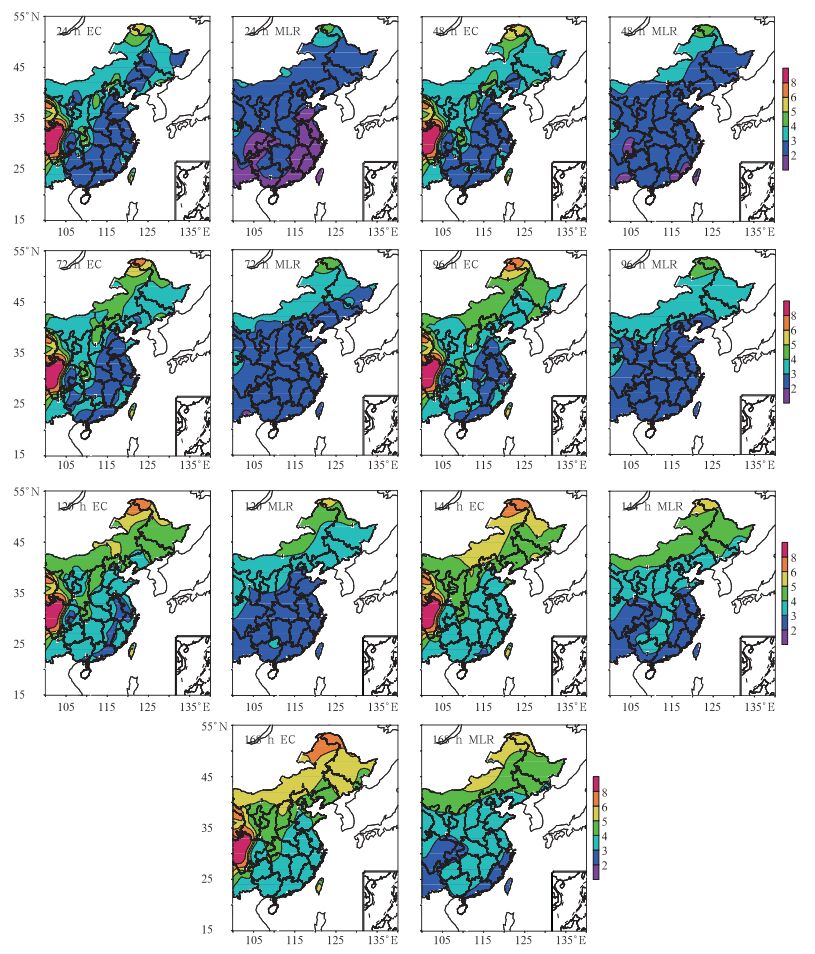
图 4给出了12月ECMWF模式和多元线性回归的订正预报在中国东部地面气温预报均方根误差的地理分布，预报时效为24~168 h(间隔24 h)。从中可见，不同预报时效的订正后预报较ECMWF模式预报都明显降低了预报误差，降低幅度基本上都为一个等级(1℃)。对于24 h预报，我国华东和华南地区的预报误差基本都降到了2℃以下，模式预报误差较大的东北地区大于3℃的区域也明显减少，均方根误差基本上都降低到了3℃以下。同样误差较大的四川西部大值区也被消除。在40°N以南地区，120 h订正后预报误差基本已降低到了3℃以下。从均方根误差的地理分布上看，4种订正结果(其他图略)的比较与前面类似。

4 结论与讨论

本文对ECMWF模式2007年1月至2010年12月的12~240 h中国东部地区的地面气温预报进行了评估，并提出了两种线性回归订正方法和消除偏差订正方法用于模式输出结果的事后订正，得到以下几点结论：

(1) 2007年1月至2010年12月，ECMWF模式地面气温预报随着预报时效的增加，误差也随之增大，12~240 h预报增幅为1.3℃左右。具体到某一天的预报，长时效预报的区域平均均方根误差并不总比短时效预报的大。

(2) 从4年的统计平均状态来看，对于ECMWF模式的短期预报，仅考虑最新预报结果的一元订正方法要优于引入多个时效的多元订正方案；而对于中期预报，考虑多时效集成预报的多元订正方法效果更优。

(3) 四种订正方法都明显改善了相同时效的ECMWF模式预报。总体来看，当模式预报误差较大时，多时效集成的订正方法能更加稳定地降低误差。

通过对以上4种订正方法的比较，我们可采取分时效对单模式预报结果进行后处理的方案，即在短期预报(24~72 h)订正时利用一元线性回归订正方法，在中期预报(96~240 h)订正时利用多元线性回归或者多时效消除偏差平均的订正方法。该订正方案简单易行，充分利用模式已有的预报结果和实测场。这些预报订正方法也可以运用到其他物理量场的订正，如风场、高度场和降水等。