引言

准确的强对流天气预报一直以来是预报员们面临的最大难题之一，强对流过程中伴随的雷暴大风、冰雹、龙卷以及带有强烈雷暴现象的短时强降水等灾害性天气的形成、发展、移动的机理也就成为气象学家们的重点研究内容。就天气预报的本质而言，预报员在天气预报过程中的思维过程(或者说，预报思路的建立过程)就是对未来可能出现的天气现象酝酿、生成、发展、消亡等物理过程的理解，如果对任何一种天气现象产生的物理机制不清楚，其预报结果必然存在一定的盲目性。

通过最近几年来中国气象局组织的各级预报员岗位培训、各种层面的技术交流以及日常的预报会商、学术研究论文撰写等过程中所反映的现象来看，预报员在天气预报思路和天气分析过程中，存在的问题主要表现在以下几个方面：(1) 知其然而不知其所以然，造成许多基本概念被不恰当应用；(2) 忽视某些严谨理论的基本假设，造成有些明显不满足基本约束条件的物理诊断量被广泛滥用；(3) 天气系统中的“尺度混淆”，用大尺度天气动力学理论解释中小尺度天气过程形成机理等。这些现象不仅在日常天气预报过程中经常出现，造成天气预报分析过程的逻辑性漏洞，而且在某些的分析论文中“似是而非”的现象也时有发生^[1-3]。

上述问题在各级预报员中广泛存在，无论是首席预报员、研究员、博士，还是普通岗位的预报员。随着一大批高学历人才逐步充实到预报员队伍中，追求“创新”的思想已经渗透到天气预报领域的各个环节。我们认为，创新思维是推动科技进步的根本力量，但是创新的基础是传承而不是颠覆，传承的精髓是科学地使用并不断完善基础理论。对于天气预报而言，创新的前提是求实。如何把天气动力学中成熟的理论研究成果简明直观地应用到实际天气预报业务中去，依然是全体气象工作者首先需要解决的问题。本文试图从天气分析中经常被预报员不当使用的某些基本概念出发，以一个预报员的视角来审视强对流天气预报分析中的若干基本问题。

1 与降水有关的两个基本问题 1.1 与湿度相关的问题

降水现象的发生或者说降水的本质是空气中的水汽被凝结，降水量的大小取决于大气中的水汽含量、凝结效率和持续时间。

分析大气中的水汽状况包括水汽含量的分布和水汽的输送量。水汽含量通常有多种表达方式：比湿(q)为单位质量湿空气中的质量，故它的单位为g·kg^-1；水汽压(e)为湿空气中水汽的分压力，单位为hPa。比湿和水汽压都代表了大气中的绝对水汽含量，因此被称为绝对湿度。相对湿度(RH)被预报员广泛应用，也是数值预报输出的一个表征水汽含量的基本物理参量。“相对”的含义是指空气的湿度距离达到饱和的程度，它用实际比湿和饱和比湿之比来表示，单位为%，相对湿度实质上是温度露点差(T-T_d)的一种另类表述：当空气中的水汽达到完全饱和时，则温度露点差为零，相对湿度为100%。而这种饱和现象可以是由温度下降接近露点温度时形成，如夜间地面长波辐射冷却造成地面气温下降而形成雾，或未饱和的湿空气上升因绝热冷却而形成云；也可以是由水汽增加造成露点温度上升而接近气温时而形成，如未饱和的湿空气平流到水面或潮湿陆地上时，由于下垫面上水的蒸发而逐渐达到饱和。因此，相对湿度不能确切地说明大气中的水汽质量，同样是相对湿度100%，或T-T_d等于零，由于南方和北方温度差别很大，它们水汽含量有非常显著的差别。

从对应的天气现象来看，在近地面层，相对湿度很好地表征了雾的浓密程度，在对流层内表现为是否有云以及云的密实程度。因此，在没有明显逆温背景下，同一时刻850与700 hPa上相同数值的相对湿度所表明的水汽绝对含量，在这两个水平气压场上是存在巨大差异的；同理，在同一水平气压面上，某地冬季和夏季相同数值的相对湿度所对应的水汽含量也是存在巨大差异。这样，我们就能很好地理解，为什么尽管近地面水汽含量在夏季一般是远大于春季或秋季，而夏季大雾现象一般远远少于这两个季节。

1.2 关于冷空气在降水过程中的作用

在当前天气分析中，特别是在降水预报中，是否存在冷空气的侵入被预报员提升到了极端重要的地位。在具体讨论冷空气在降水过程中的作用之前，首先要明确“冷”、“暖”空气的概念是相对的。在等压面图上，冷空气是指水平方向上温度比四周低的空气，因此温度本身的数值不能决定是不是冷空气，是不是冷空气取决于温度对比，即温度梯度。

在明确了“冷”空气概念之后，“冷空气侵入”的概念也就明确了，它是指等压面上温度较低的空气取代温度较高的空气，即冷平流(温度平流小于零)，在天气图上表现为风向和等温线有交角，从冷侧吹向暖侧。冷平流造成冷空气取代暖空气，一定与局地温度降低相联系，即等压面图上出现负变温。

既然冷空气的确切含义是存在温度对比或者说斜压性，那么它在降水过程中的作用就是显而易见的。要产生降水，必须有“水汽被凝结”。在降水过程中，冷空气的唯一作用就是“水汽被凝结”。动态来看，冷空气有强迫抬升作用，这一过程的结果是“水汽被凝结”，即冷空气的强迫抬升作用造成暖空气“被抬升”而发生凝结现象。我们知道，大气中的绝大部分的水汽集中在对流层的低层，然而，在同一温度的气团内，水汽很难被凝结成直径足够大的水滴而产生降水，但是当有相对“冷”的气团侵入时造成本地气温下降就可能出现凝结现象，这就是降水一般出现在锋面附近的主要原因之一；从动态的角度来看，大多数冷气团是“锲”形移动的，这样暖气块被强迫抬升到高处，气块上升的过程是替换气块上方的空气而气块温度本身不会变为上方空气的温度，由于高处气温明显低于气团原来的环境温度造成水汽凝结而出现降水。有一点需要特别强调，降水过程中被抬升凝结的是暖空气中的水汽而不是冷空气中的水汽，因为大气动力学告诉我们，是暖平流引起了强迫抬升，而冷平流引起的是强迫下沉，所以在降水过程中冷空气侵入的作用只表明斜压的重要性。由于暖平流强迫上升是水汽被凝结的基本原因，所以暖平流的强度和落区才是大尺度降水预报最重要的预报因子之一。

在对流性降水中，冷空气侵入的作用与大尺度降水中不同。高空冷平流的作用是使高空降温，温度垂直递减率变大，增加大气的不稳定性从而导致对流性降水的发生。

在夏季，即便是中纬度，大气的斜压性往往也很弱，等压面图上的冷平流并不清晰，也没有明显的负变温。在降水过程中常常出现测站风转为西北风或等高线表现出向南弯曲的小槽是否也可认为存在冷空气的侵入？上述情况显然冷空气不强，使用“侵入”不很恰当，只能称作弱冷空气活动。它虽然不会引起显著的强迫抬升，但它所伴随的低空扰动很可能会起到触发对流的作用，因此也不可忽视。但由于这种冷空气活动非常弱，它在对流性降水过程中的作用还有待仔细的分析加以确认。

总之，“冷”、“暖”空气的概念是相对的，降水过程中的“凝结效率”取决于气团之间的“相对温差”——即温度梯度，而不是气温的绝对值。温度梯度不仅反映在水平方向(斜压性)上，同时也反映在垂直梯度(静力稳定度)上，温度的水平梯度和垂直梯度的性质有着巨大的不同：水平温度梯度的重要性在于它是决定动力强迫抬升的主要因子之一(斜压性)。垂直温度梯度的重要性在于它是决定对流有效位能CAPE的主要因子之一。前者是动力强迫问题，后者是静力稳定度问题。实际大气层结不存在超绝热层结，所以不存在绝对不稳定的情况(贴地层除外)。之所以出现静力不稳定，即气块(或称空气微团)温度高于环境大气温度，是由于水汽凝结造成的潜热释放。因此，水汽在对流降水中，既提供了降水的物质来源，也提供了降水的能量来源。

从上面的分析可以看到，冷空气的侵入在降水过程中有着重要作用。但是，并不是所有的降水过程甚至暴雨过程都一定需要冷空气的侵入：当低层的水汽由于流场的水平辐合产生的上升运动而被强迫抬升到凝结高度以上时就会发生凝结作用而出现降水，进一步抬高到对流凝结高度以上时，就可能发生对流现象，而对流过程往往伴随着强烈的上升运动，如果凝结率是上升速度和凝结函数的乘积，则对流活动就越强烈，降水强度就越大；另外一种情形是，当低层被强烈加热时，尽管对流层中低层没有“冷空气”侵入(或者说整层大气中各等压面上都没有降温过程)，热力作用也将造成低层气块迅速上升，由此产生剧烈的对流活动。

2 与强对流有关的几个问题

对流是大气中常见的物理过程，如阵雨、阵雪、一般性雷暴等。一般认为，只有雷暴大风、冰雹、龙卷以及伴随有强烈雷电现象的短时强降水等灾害性天气才可以被称为“强对流天气”。从对流高度来说，只有深对流过程才能被称为强对流，因此常用云顶亮温(TBB)或雷达强回波顶高来判断是否发生了强对流过程。

2.1 不稳定的分类

我们知道，强对流的发生发展是与大气不稳定密切相关的。“不稳定”包含两个基本概念，即热力不稳定和动力不稳定。

热力不稳定，也称静力不稳定或层结不稳定，它与温度、湿度的垂直分布廓线(即温湿层结)有关。热力不稳定之所以又称为静力不稳定，是因为气块垂直位移中发生的热力学过程使气块所受到的浮力(重力和垂直气压梯度力之差)方向和位移的方向相同而越来越远离其初始位置。热力不稳定的产生大体上有四种机制：

(1) 在干大气中，静力稳定度是与温度垂直分布的现状相关联。在天气分析中，常用位温的垂直递减率(∂θ/∂z)来判断，即：∂θ/∂z大于0、等于0或小于0时，分别对应的是稳定、中性或不稳定层结。它相当于温度垂直递减率γ小于、等于或大于干绝热递减率γ_d(＝9.8℃·km^-1)。为了简化和方便计算，预报员也经常用850与500 hPa高度上的温度差来表征这种层结稳定度。在实际大气中，∂θ/∂z总是大于0，也就是说，上层大气一般总是比低层大气暖，即“上轻下重”，所以是静力稳定的。

(2) 对于湿大气，必须用“条件性静力稳定度”来判断层结是否稳定；在天气分析中常用假相当位温的垂直递减率来判断，即∂θ_se/∂z大于0、等于0或＜0时，分别对应的是稳定、中性或不稳定, 同样为了简化和方便计算，预报员经常用850与500 hPa高度上的假相当位温差来表征这种温度不稳定层结。因此，这种热力不稳定的产生既与温度的垂直递减率有关，也与湿度的垂直递减率有关，特别是当低层的湿度非常大的时候。所谓“条件性不稳定”是指只有在达到饱和及发生凝结以后才变为现实的静力不稳定。凝结所释放的潜热是使垂直位移的气块获得浮力的原因。实际大气中发生的对流都有对流云或降水产生，所以都是条件性不稳定的结果。

(3) CISK(第二类条件性不稳定)，是指大尺度环流与积云对流的正反馈机制产生的条件性不稳定，气象学家们用它来解释热带风暴(台风)的发展过程，即潜热释放和涡旋强度之间的正反馈机制。这类不稳定中也包含动力学反馈，所以不是纯粹的热力学不稳定。

(4) WAVE-CISK(移动性第二类条件不稳定)，是指中尺度过程之间的正反馈过程产生的条件性不稳定。例如，对流的自激过程以及对流单体之间相互作用而形成线状对流体的过程一般与WAVE-CISK机制有关。

需要特别注意的是，大多数热力不稳定是一种“潜在不稳定”，当没有不稳定能量释放机制存在，这种不稳定是没有意义的；另外，热力不稳定能量的释放过程是快速完成的。因此大多数热力层结不稳定参数的大小只与对流的初始强度有关，与对流能否继续发展和维持无关。例如，众多的不稳定参数都和CAPE的大小有密切关系，在对流发生阶段，CAPE往往由最大值迅速减小——即浮力能迅速转化为动能，此后对流的发展和维持机制只用局地的CAPE来解释是不够的。要维持对流云的发展，必须有来自于云体外的CAPE的输入。由于热力不稳定是不断变化的，在实际天气分析过程中，需要“动态”地看待稳定度变化——热力不稳定层结分析只有在降水或对流发生前才有意义。在对流降水过程中，大气一般处于中性热力层结；降水趋于结束时，大气一般处于稳定层结。

动力不稳定是由于密度的不连续性、水平风切变、垂直风切变产生的，因此，又被称为切变不稳定，与热力稳定度不同，它是与大气流场的水平或垂直结构直接对应的。在实际天气分析过程中，热力不稳定往往受到预报员的足够重视而忽略了动力不稳定的作用，实质上，动力不稳定是对流能否发展和维持的关键因素，不同的强对流天气现象的发展、移动大多与动力稳定度有直接关系，例如，低空垂直风切变是强对流发展和维持的重要条件：在物理本质上，可以理解为强的垂直风切变破坏了雷暴的自毁机制，使对流得以较长时间的维持和发展，因此，龙卷、大雹、强烈的雷暴大风一般在低空强烈的垂直切变环境中发展，因此，从某种意义上讲，在强对流临近预报过程中，动力不稳定显得尤为重要。

动力不稳定大体可分为四类：

(1) 惯性不稳定：是与涡度或水平风切变对应的不稳定，惯性不稳定本质上属于“涡层”不稳定，是指由于速度不连续引起的交界面两侧的一个强风切变层^[4]。

(2) K-H(开尔文-亥姆霍茨)不稳定：本质上属于重力内波不稳定，与垂直切变对应。

(3) 对称不稳定(SI，又称斜升不稳定)：从理论上讲，对称不稳定产生的环境是等熵面与等角动面之间的夹角要足够大^[5]，或者说，它是等熵面上的惯性不稳定。从天气分析角度，我们可以简单将对称不稳定理解为斜升不稳定，这种中尺度不稳定在等压面坐标系中，产生于既存在水平切变环境，同时又存在垂直切变环境中：低空的水平切变环境造成气块产生向上运动，由于垂直风切变的存在，在气块向上运动过程的同时受到不同高度上水平风速甚至风向改变而发生水平运动，因此，这种环境下的运动过程必然是倾斜的^[6]。如果垂直方向不存在风切变，这种不稳定演变为惯性不稳定；如果不存在水平风切变，这种不稳定演变为K-H不稳定。

(4) 条件性对称不稳定(CSI)：它是指湿空气的斜升不稳定。

从理论上讲，无论是热力稳定度还是动力稳定度，都可以化为Richardson数(Ri)的形式来表示，这实质上也说明，热力不稳定与动力不稳定在一定条件下是可以相互转化的，而Richardson数本质上是一个热力稳定度与动力稳定度的组合参量，即： $Ri = \frac{{Ns{e^2}}}{{{{\left( {{\rm{d}}u/{\rm{d}}z} \right)}^2}}}$ ，或者采用粗Richardson数表示为： $Ri = \frac{{CAPE}}{{{{\left( {{\rm{d}}u/{\rm{d}}z} \right)}^2}}}$ 。

2.2 探空与稳定度参数

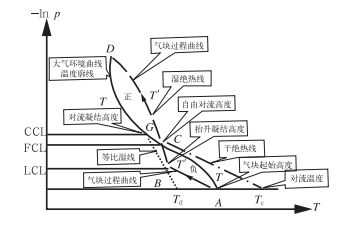
单站探空是我们分析本地大气环境的热力稳定度、动力稳定度的重要手段(如图 1)。

从探空分析图中，我们可以很容易直观地看到热力层结稳定度、风的垂直切变状况。上述T-lnp图中的各个稳定度参数都具有明确物理意义：

(1) 抬升凝结高度(LCL)、对流凝结高度(CCL)虽然都是表示水汽发生凝结的高度，但是两者物理意义是完全不同的，前者为层云云底的高度，后者为午后热对流的云底的高度。

(2) 自由对流高度(FCL)表示气块温度与环境温度之差由负值转为正值的高度，它是一个判断对流现象是否容易发生的一个重要参数。因为，在自由对流高度之下，气块上升需要外力抬升作用，即克服对流抑制能量(CIN，状态曲线与层结曲线围成的负面积)作功，而在自由对流高度之上，气块将获得能量(CAPE)在浮力作用下自动上升。

(3) 对流有效位能(CAPE)是一个具有非常明确物理意义的热力不稳定参量，它与T-lnp图上的正面积对应：表示自由对流高度与平衡高度(图中的D点)之间, 气快由正浮力作功而将势能转化为动能的“能量”大小，因此，CAPE越大，对流发展的高度就越高或者说对流就越强烈。尽管如此，CAPE计算起来并不容易，或者说，我们其实很难获得对流发生前CAPE真实值的大小，这是由于以下两个方面的原因。

其一，CAPE的大小与气块开始抬升高度有很大的关系，或者说那一个高度上的气块是对流发生的主要参与者，在实际过程中是难以确定的。Smith^[7]的分析表明，CAPE是气块起始抬升高度的函数，也就是说，CAPE的大小随起始抬升高度不同而存在显著差异。为了克服这一问题，在实际分析过程中，一般有两种订正办法：(1) 将起始抬升高度定在逆温层顶，其隐含的物理意义是对流开始时，逆温层已消失。(2) 用当天预报的最高气温对探空时的地面温度进行订正，抬升高度从订正后的地面温度开始计算。其隐含的物理意义是，近地面气块是对流过程的主体，而且对流发生在地面温度最高的最不稳定时刻。这种办法虽然存在夸大CAPE值的可能性，但经验表明，它可能是一种比较好的订正方法。

如上所述，目前绝大多数情况下仍是以地面为起始抬升高度，只有极少数所谓高架对流除外。CAPE是起始高度的函数这个问题实际上来源于探空时间距离对流发生时刻很长，如我国08时的探空，此时850 hPa以下的层结往往非常稳定，不得不改为逆温层顶或700 hPa以下相当位温最大点的高度作为起始高度。而对流发生时气块实际上从哪个高度开始上升是一个几乎无法解决的问题。

其二，CAPE值与对流发生前夕的层结曲线有关。由于大多数对流发生前，我们无法真实地得到大气的层结曲线变化，即便是我们能够确定气块的起始抬升高度，我们也无法准确地计算出CAPE的大小。08时和20时的探空，在大多数情况下不能代表对流发生前夕的大气层结。多数对流发生在午后到傍晚之间，这显然与大气层结的日变化有密切的关系。

(4) 地形对热力不稳定的影响。在天气分析过程中，气象工作者对地形的强迫抬升作用造成的降水增幅作用有一定的认识，但是对地形造成的热力不稳定的影响认识明显不足。对应于图 1，如果山体的高度为H，对应的对流温度是A₁，在一般情况下，A₁对应的气温明显低于平原地区的对流温度T_C。但是，如果在弱下沉气流作用下，山上的实际最高气温甚至高于平原地区，也就是说，山上的热力状况更容易满足发生热对流的条件^[8]；另一方面，山上气块的起始抬升高度明显高于平原地区，由此获得的净浮力更大。因此，我们经常发现许多局地对流云的生成发生在山区，研究也表明，山区发生冰雹等深对流过程要远多于平原地区^[9]。

(5) 地形对动力不稳定的影响。假设，基本气流的方向垂直于山体的脊线，由于地形的阻滞作用，山前的水平风速将迅速减小甚至出现较大范围的“死水区”，而“死水区”以上则出现气流加速现象，因此，地形的存在将加强水平风速的垂直切变，这也是山区容易激发出强对流单体可能的动力学原因之一^[10]。

2.3 热力学参数应用中的其他问题

我们经常使用的热力学参数并不都是如“对流稳定度”、CAPE等这样严谨的物理意义。严格讲这些参数应称为稳定度指标，例如沙氏指数(SI指数)、K指数(气团指数)等。其中：

SI指数：SI=T₅₀₀-T_S，其中T₅₀₀是指500 hPa的实际温度，T_S是指气块从850 hPa开始先沿干绝热线上升到凝结高度，再沿湿绝热线抬升到500 hPa的温度；因此，SI指数本质上是指850 hPa处的“保守”气块被抬升500 hPa时，与环境温度的差异，可以定性地用来判断对流层中层(850~500 hPa)是否存在热力不稳定层结。它不能反映对流层底层的热力状况，反过来说，它的优点是受日变化的影响相对较小，而与CAPE有较好的正相关，与自由对流高度以上的浮力大小有关。

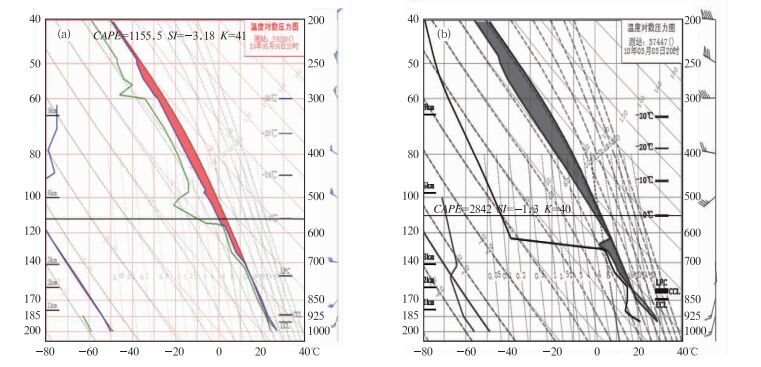
K指数：K=[T₈₅₀-T₅₀₀]+[T_d]₈₅₀-[T-T_d]₇₀₀, 它侧重反映对流层中下层(700~850 hPa)的湿度廓线，湿度越大，K值越大，越不稳定。热带暖湿气团中的K很大，所以也叫做气团指数。然而，K指数只能在判断强对流潜势时定性使用，例如图 2中的两种不同层结，它们对应的K指数分别为41和40℃，数值很接近，但对应的强对流现象完全不同。前者对应强降水(2010年5月6日夜间广州对流性暴雨)，而后者对应雷暴大风和冰雹(2010年5月5日重庆的风雹灾害)。

尽管大多数经常被使用的热力不稳定参量存在很强的相关性，但是，由于每一种热力不稳定参数的设计方案都存在局限性，没有一种热力不稳定参数能够“包打天下”。例如，虽然CAPE和SI指数存在很强的相关性，然而我们可以从图 2所示的两种探空中可以看出它们之间的巨大差异：后者CAPE值是前者的两倍以上，而前者SI指数所表现出的不稳定更强。因此预报员经常使用不同的组合方案来判断可能发生的对流强度，并根据不同强对流现象对各种参数的敏感程度来预判可能出现的天气现象^[11-12]。

2.4 螺旋度与动力不稳定的关系

螺旋度最早是用来研究流体力学中的湍流问题的，1986年Lilly等将这一概念用到强对流风暴研究中^[13-15]，后来，人们发现，螺旋度对雷暴、龙卷、冰雹、大范围暴雨、某些沙尘暴的发生有一定的指示作用^[16-20]。

就大气运动来说，螺旋度是一个描述对流风暴内部三维气流结构的一个物理量。螺旋度本质上是一个“伪”标量，也就是说，它本身是有指向性的，即： $h = u\left( {\frac{{\partial w}}{{\partial y}} - \frac{{\partial v}}{{\partial z}}} \right) + v\left( {\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right) + w\left( {\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}}} \right)$ ，可以看到，螺旋度密度公式右边三项分别表述了i(x)，j(y)，k(z)三个方向上的螺旋度密度。由于在强对流环境中，一般认为涡度的垂直分量一般比垂直切变小一个量级以上，因此，在强对流发生前，可以认为垂直运动的水平方向上的变化(即 $\frac{{\partial w}}{{\partial y}},\frac{{\partial w}}{{\partial x}}$ )比垂直切变小，垂直运动本身也比水平运动小，于是便简化为^[21]： $h = u\frac{{\partial u}}{{\partial z}} - \frac{{\partial v}}{{\partial z}}$ 。但是，在强对流发生、发展过程中，云中的上升运动基本上与水平风速处于同一个量级，垂直运动的水平方向上的变化(即 $\frac{{\partial w}}{{\partial y}},\frac{{\partial w}}{{\partial x}}$ )的量级也并不比垂直切变小，甚至更大，因此，在强对流已经发展起来后，利用简化公式来说明螺旋度的分布是存在很大误差甚至是错误的。

从螺旋度的表达式可以看到，它本质上是一个表述动力稳定度的参量，如果从“场”的视角来看，螺旋度的水平分布特征其实即反映了水平风速的变化(风速本质上可以分解为辐散风和旋转风)，也反映了垂直切变的变化：如果在垂直切变相对均匀的环境下，螺旋度水平分布的梯度是与水平切变或涡度对应的；如果水平风速是相对均匀的，螺旋度水平分布的梯度是与不同格点上的垂直切变或者说与K-H不稳定对应的；在一个水平风速不连续的垂直切变环境中，它是与对称不稳定对应的；螺旋度的垂直分量(即第三项)是与惯性不稳定对应的。因此，从某种意义上看，螺旋度与惯性不稳定、K-H不稳定、对称不稳定有内在物理联系。

2.5 湿位涡与条件性对称不稳定

湿位涡、湿位涡守恒原理是在研究湿对流过程中常用到的概念。在无摩擦、湿绝热大气中，在静力近似条件下，并且假定垂直运动速度的水平变化比水平速度的垂直切变小得多，p坐标下的湿位涡具有守恒性^[22]，即：

$ - g\left( {\zeta + f} \right)\frac{{\partial {\theta _{se}}}}{{\partial p}} - g(\frac{{\partial u}}{{\partial p}}\frac{{\partial {\theta _{se}}}}{{\partial y}} - \frac{{\partial v}}{{\partial p}}\frac{{\partial {\theta _{se}}}}{{\partial x}}) = {\rm{常数}}$

于是，在湿位涡守恒的制约下，倾斜涡度(SVD)发展的必要条件是：大气水平风速的垂直切变或者湿斜压性增加，即：

${C_d} = \frac{{MPV2}}{{\partial {\theta _{se}}/\partial p}} > 0$

其中， $MPV2 = - g(\frac{{\partial u}}{{\partial p}}\frac{{\partial {\theta _{se}}}}{{\partial y}} - \frac{{\partial v}}{{\partial p}}\frac{{\partial {\theta _{se}}}}{{\partial x}})$ 。

我们可以看到，MPV2本质上是一个判断条件性对称不稳定(CSI)或者说湿斜升不稳定的一个判椐： $\left( {\frac{{\partial u}}{{\partial p}},\frac{{\partial v}}{{\partial p}}} \right)$ 是水平风速的垂直切变，而 $\left( {\frac{{\partial {\theta _{se}}}}{{\partial y}},\frac{{\partial {\theta _{se}}}}{{\partial x}}} \right)$ 对应湿斜压锋区，在中纬度大气中，湿斜压锋区往往对应着水平风速切变。

由于湿位涡守恒只有在一系列约束条件下才能成立，对中尺度对流系统而言，这种约束条件经常被破坏，于是出现所谓的湿位涡异常^[23-24]。除了热力强迫、质量强迫造成的湿位涡守恒被破坏以外，还应该注意到，在强烈发展的对流过程中，由于对流系统的垂直运动存在强烈的水平梯度，即垂直运动速度的水平变化可能与水平速度的垂直切变相当，甚至更大，此时将出现强烈的位涡异常现象。因此，在实际强对流分析过程中，虽然MPV2可以用来诊断强对流发展的潜势或者说用来讨论倾斜不稳定的发展，但是在强对流发生、发展过程中，用湿位涡守恒原理来讨论位涡下传或上传过程是缺乏物理逻辑的。

总之，应用湿位涡概念来讨论对流性暴雨时需要非常谨慎，切不可滥用，这是因为：(1) 对流是静力不稳定的结果，有浮力产生的垂直加速度，所以静力学假定不适合；(2) 湿位涡理论为了追求守恒性，其理论的假定是为了满足数学推导的需要，而不是根据问题的物理本质，企图简单地用守恒性取代对物理机理认识的必要性。

3 与辐合线、垂直运动有关的问题

近地面的水平辐合必然伴随上升运动，这是由质量连续方程(质量守恒定律)决定的。但是，同样是由于连续方程，大气中层的水平辐合运动与上升运动不一定有对应关系，因为连续方程给出的是垂直速度的垂直微商而不是垂直速度本身。

水平散度与垂直运动的“互为因果关系”只是对变化缓慢的大尺度天气系统而言的。也就是说，并不是在所有情况下，只有发生水平辐合辐散运动才能“产生”出垂直运动。在变化剧烈的中尺度对流系统中，由于大气中发生了强烈的上升或下沉运动，大气的水平补偿作用也将出现水平“辐合”或“辐散”运动，即可以出现垂直运动强迫出水平散度。例如，浮力作用下的对流活动(剧烈的上升运动)引起抽吸作用将造成近地面层的强烈辐合，而强对流中降水粒子拖曳的下沉气流(下击暴流)造成地面强烈的辐散气流。因此，并不是所有的地面辐合线都一定是对流的触发因子。在对流发生前，可以认为地面辐合线是对流的触发因子，在对流初期(对流云发展阶段)的地面辐合线往往是垂直上升运动的结果而不是原因；而在对流发展的旺盛阶段，而雷暴中的强烈下沉运动(对应雷暴高压)必然形成近地面层的强烈水平辐散运动，与此同时，雷暴高压的出流与环境大气之间可能形成新生辐合线，新生辐合线的抬升作用可能诱发新生对流，这种物理过程是雷暴的一种重要传播机制，于是我们看到地面辐合线的移动总是与雷暴的移动方向一致。

从大尺度资料或再分析资料中诊断出的上升速度不代表中尺度强对流系统内部的上升运动。前者诊断出的垂直运动只能代表环境大气，它在强对流过程中的作用，主要体现为抬升(即大尺度强迫上升)，也就是说，这种抬升作用使得参与对流的气块获得了外力作用，产生了克服CIN所需要的能量。一般状况下，它的量级(1~10 cm·s^-1)要比水平运动小得多，它比实际对流过程中的上升运动或下沉运动也要弱得多。这是由于中尺度对流系统中的垂直运动主要是浮力产生的——即由CAPE转化而来，在强对流过程中，它的量级与水平运动量级相当甚至更大，一系列的观测研究表明，超级单体内6~7 km高度上的上升运动速度可达40~50 m·s^-1[25-27]。

4 天气型与强对流的关系

天气分型、天气概念模型是预报员进行灾害性天气预报的重要手段，从本质上来看是一种相似预报方法，然而，世界上没有两次天气过程是完全重复的。天气系统的空间配置从某种意义上决定了灾害性天气酝酿、发生、发展的环境条件，但是，灾害性天气能否发生本质上取决于这种天气系统空间配置背后的物理条件而不在天气型本身。这一节，我们以“前倾槽”和“后倾槽”配置下的不同强对流现象预报为例，来说明“天气概念模型”与强对流之间存在的内在物理机制。

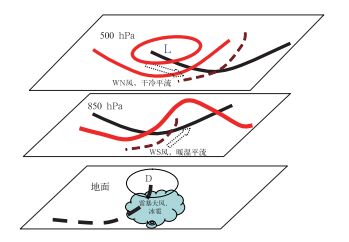
如果天气系统是自西向东影响到预报区域，“前倾槽”是指锋面结构的垂直剖面随高度向东倾斜，也就是说，500 hPa上的西风槽位于850 hPa槽或地面锋面以东(如图 3)；如果高空冷空气较快的从北向南移动，“前倾槽”就是锋面结构是随高度向南倾斜的。

有经验的预报员一般都知道，“前倾槽”结构的天气系统往往预示可能发生雷暴大风、冰雹等强对流天气现象。这是由于这种空间配置结构的天气系统，在大多数情况下，存在满足上述强对流发生的热、动力学特征和启动机制。

(1) 热力不稳定加强机制：在对流层中，温度槽一般是落后气压槽的，因此，图 3所示的空间配置下，意味着500 hPa槽后显然存在较强烈的干冷平流，而对流层低层仍然处于暖湿区或暖湿平流控制下，形成所谓“上干冷、下暖湿”的层结(如图 2b)，这种结构非常有利于热力不稳定层结加强；

(2) 垂直切变维持机制：在大多数情况下，西风槽后一般是西北气流，槽前是西南气流，因此“前倾槽”结构有利于对流层中低层垂直切变的维持；

(3) 低层抬升机制：低空槽或水平风切变、锋面本身就提供了较强的抬升条件，而对流层上层往往对应高空辐散场，对流不稳定很容易被触发；

(4) 对流层中上层的冷平流有利于0℃、-20℃等特性层的降低，为雹胚的生长提供了良好的形成环境。

从上面的分析可以看到，并不是所有的“前倾槽”结构配置的天气系统就一定对应着雷暴大风或冰雹等强对流天气过程。例如，在有些情况下，500 hPa上的温度槽位于西风槽前，这样的结构将造成热力不稳定层结趋于弱化。

对大多数斜压结构的天气系统而言，是“后倾槽”结构的。与“前倾槽”结构不同，虽然有时也存在强烈的对流现象，但是往往对应的是短时暴雨现象，发生冰雹的概率相对小得多，这是由于：

(1) 虽然也存在热力不稳定层结，例如K指数、CAPE值等都很大，但是，探空结构表现多为整层饱和(如图 2a)而不是“上干冷、下暖湿”分布;

(2) 热力不稳定的增长主要是由于低空暖湿平流而不是高空冷平流形成的；

(3) 由于高低空都位于槽前，垂直风切变一般表现为水平风速的垂直变化而不是风向上的切变；

(4) 如果降水前0℃、-20℃等特性高度层明显偏高，那么，对流过程一旦开始，形成冰雹的可能性将迅速降低，这是由于对流形成的潜热释放将进一步抬高0℃、-20℃层所在的高度。

5 结语与讨论

强对流天气的形成是一个非常复杂的物理过程。首先，强对流中尺度天气系统酝酿、发生、发展、消亡的物理过程受制于天气尺度的演变和环境大气基本要素的配置结构的影响，一般认为，强对流天气的发生需要以下基本条件：不稳定层结、垂直风切变、初始的抬升触发机制和适当的水汽补充条件，这些基本条件的形成既可能是由天气尺度系统的演变而形成，也可能是由于局地中尺度环流演变而形成，如地形效应、水(海)陆分布、城市效应等。

其次，即使可以预见强对流现象可能发生，或者说，未来大气的演变特征足以满足上述基本条件，要进一步区分强对流发生时的伴随现象或者说做出准确的分类预报，如雷暴大风、冰雹、龙卷或短时强降水依然是非常困难的，因为这些对流过程发生前的环境大气特征并不存在非常明确的物理界限，也就是说，它们发生的阈值区间存在很大的重叠性^[28]。正因如此，预报员大多根据对流云的结构特征，如雷达回波特征来区分强对流现象而实现分类预警。

其三，强对流一旦发生，将剧烈地改变周边大气的温、压、风、湿等基本要素的水平梯度和垂直梯度，形成与环境大气的相互作用，诱发新的雷暴生成，并与原来的雷暴形成强烈的相互影响，进而影响到强对流系统的生消、维持或移动^[29-30]。

本文仅仅涉及到上述三个物理过程中的第一个问题，或者说，我们在这里仅仅讨论了与强对流潜势预报有关的基本概念和基础理论的应用问题。很多预报员对这些概念、理论的认识程度处于“既熟悉、又陌生”的状态，所谓熟悉，是由于预报员们在教科书或很多专著中都有过比较“深入”的接触，而且在实际工作中经常应用它们；所谓陌生，是指对它们的物理含义、应用前提或物理假设以及在天气分析中如何应用并不十分清晰，似是而非，甚至张冠李戴，造成实际业务工作中存在大量的滥用现象。对大气科学基础理论的深刻理解，是天气预报成功与否的基石，是创新的前提。这也正是本文的目的所在。