2. 中国气象局气象干部培训学院,北京 100081;
3. 国家气象中心,北京 100081
2. Training Centre of China Meteorological Administration, Beijing 100081;
3. National Meteorological Centre, Beijing 100081
在《气象》2011年第37卷第2期气象论坛“基础理论和预报实践”[1]中谈到,等熵位涡及其引伸出的平流层干侵入(以后简称干侵入)在预报员中产生了许多违背气象常识的错误概念。但是,要把搞乱的思想“拨乱反正”,需要做“正本清源”的工作。为此,本文从涡度这个源头谈起。首先回顾了为什么需要将涡度引入天气学,然后再介绍为什么在涡度的基础上又引出位涡的概念。其次,回顾平流层干侵入概念的来源,以及它是如何和等熵位涡联系起来的。最后,用一些事实证明,如果误用位涡和干侵入的概念将把天气预报的思路引入歧途。
文中所有问题的讨论都将围绕其天气学意义展开,而不追求数学上所谓的完整性。同时还请读者注意,本文讨论的范围严格限定在天气图上中纬度的大尺度环流系统。因此,不可将相关的概念或结论用于中尺度对流系统和低纬度热带环流系统,因为它们具有完全不同的动力学性质。
1 涡度在天气预报中的积极意义 1.1 涡度和Rossby长波理论将涡度方程引入天气预报是天气学的一个重大转折,这是Rossby对气象科学的巨大历史功绩。在20世纪30年代以前,没有高空天气图,天气预报主要根据海平面气压场分析得出。气压倾向的正或负,是预测天气变化的主要依据,至今西方国家民间还把气压计称为晴雨计。当时的天气学中有大量的内容是对气压场型式的描写和归纳(即天气形势分型)。这种方法由于缺乏对气压形势变化内在机理的认识,谢义炳先生把那一阶段的天气学称为等压线天气学。
那个时代的动力学理论,注意力也同样集中在气压上,用质量连续方程和静力学方程相结合导出的地面气压倾向方程[式(1)]来解释地面气压变化的机理,即水平方向流入和流出单位截面积气柱的空气质量总和决定地面气压的升或降。
在地表平坦的情况下,地面气压倾向方程可写为
| $\frac{{\partial {p_{{z_0}}}}}{{\partial t}} = - \int\limits_{{z_0}}^\infty {g\left( {u\frac{{\partial \rho }}{{\partial x}} + v\frac{{\partial \rho }}{{\partial y}}} \right)} {\rm{d}}z - \int\limits_{{z_0}}^\infty {\rho g} \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right){\rm{d}}z$ | (1) |
式中,各符号为气象常用符号。其中计算密度平流(u∂ρ/∂x+v∂ρ/∂y)和散度(∂u/∂x+∂v/∂y)有关的水平运动分量u和v则由水平运动方程式(2) 决定。
| $\begin{array}{l} \frac{{{\rm{d}}u}}{{{\rm{d}}t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + fv\\ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} - fu \end{array}$ | (2) |
从方程(1) 和(2) 不能求出气压倾向的解析解,但可以计算其数值解。1922年Richardson的数值计算试验表明,由于高低空质量补偿原理,整个气柱的质量收支是个很小的量,而风的观测精度(或尺度代表性)无法满足根据上述方程计算出有实际意义的结果。Richardson数值试验的失败使人们的目光从气压转向了涡度。(注:半个世纪后,原始方程数值预报模式成功地解决了海平面气压数值解的计算问题。)
有了高空天气图以后,Rossby根据高空环流的基本特征,对涡度方程进行了简化,并导出了长波移速公式
| $c = \bar u - \frac{{\beta {L^2}}}{{4{{\rm{\pi }}^2}}}$ | (3) |
揭示了中高纬度西风带上的长波其本质是绝对涡度守恒。式中的Rossby参数(β)及平均西风风速(u)分别反映地球自转涡度平流和相对涡度平流对长波移速的贡献[2]。
1.2 涡度是大尺度环流系统的基本特征Rossby成功提出长波理论的关键有三点:
一是抓住了高空天气系统的基本特征是水平的旋转运动,这正是西方学者总是把天气系统称为大气环流系统(atmospheric circulation systems)的原因[3],因为在流体力学中,涡度就是从环流这个概念引出的(涡度是单位面积的环流)。所以,用涡度这个物理量来表征长波是抓住了问题的本质。需要强调的是,这里所讨论的“涡度”都是指高空天气图上水平环流的涡度,在广义的涡度概念中,它仅仅是三维涡度矢量的垂直分量。但在大尺度环流系统的动力学中,因为大尺度运动是准水平的,即二维的,所以无需考察流体力学或场论中三维涡度矢量的另外两个分量。一些理论气象学者为了追求数学形式上的所谓完整性从三维涡度出发讨论大尺度环流变化机理,从物理上看,恰恰是混淆了大尺度和中尺度的区别,丢掉了尺度这个物理学基本概念。
二是大尺度环流是准水平运动,垂直速度的量级远远小于水平风速,所以在涡度方程的平流项中,只需保留水平平流项。大尺度运动的涡度方程可以简化为
| $\frac{{{{\rm{d}}_h}\left( {\zeta + f} \right)}}{{{\rm{d}}t}} = - fD$ | (4) |
三是根据质量补偿原理,500 hPa等压面接近对流层中部的无辐散层,所以可以略去涡度方程(4) 中的散度项D,从而使方程可以通过引入流函数的方法求解,导出长波公式。
从上面对长波理论的介绍可见,解决物理问题的关键是对物理现象本质的认识,而数学仅仅是解决物理问题的工具。如果把数学作为出发点,就有把问题引入歧途的危险。
2 位涡 2.1 位涡概念的提出要认识位涡的意义,
需要从涡度和散度的关系谈起。从p坐标系简化的涡度方程(4) 可知,涡度虽然代表了水平环流的基本特征,但是涡度的个别变化却取决于数量级更小的散度。所以散度是环流系统发展的根本原因,不可忽略。正由于忽略了散度,Rossby长波理论只能解释长波的移动,而不能解释长波的发生发展。
涡度方程,在本质上只是原始的运动方程的一种变形(微商形式)。散度方程则是运动方程的另一个变形。涡度方程和散度方程加在一起,才和水平运动方程组等价。但是由于大尺度环流的准地转性,散度方程就退化为地转风公式,因此就无从了解散度的产生机理。另一方面,在大尺度运动中,散度比涡度小一个量级(故称为次级环流),而风的观测误差较大,很难准确计算出实际风场的散度。
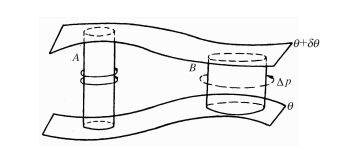
由上可见,散度是大尺度动力学中的一个难点,位涡的概念就是为解决(实际上是回避)涡度方程中的散度问题而提出的。位涡的定义可表述为,一个有限气柱其上下端位于(θ+δθ)和θ面上(图 1),在干绝热的假定下,气柱的平均涡度和气柱上下端的气压差的比值为常数,并称为位涡。位涡的表达式可写为
| $\frac{{({{\bar \zeta }_\theta } + f)}}{{\Delta p}} = {\rm{常数}}$ | (5) |
其中ζθ为(θ+δθ)和θ之间的平均相对涡度。由图 1可见,位涡理论实际上就是用两个固定等熵面之间的厚度Δp来代替散度,Δp为单位面积气柱的质量。在绝热假定下位温守恒,气柱上下端始终保持在两个等熵面上。当等熵面间的厚度Δp减小时,气柱的水平截面积(即水平辐散)增加,涡度减小,位涡保持不变,反之亦然。所以位涡守恒的本质就是涡度方程中辐散导致涡度减小,辐合导致涡度增大,只是散度被隐含在Δp中。
|
图 1 等熵位涡守恒的示意图 (闭合矢线的数目表示气柱的旋转速度) Fig. 1 Schematic illustration of the conservation of isentropic potential vorticity (Curved surface is isentropic surface, and closed vector line denotes vorticity of air column) |
位涡理论给出了在绝热条件下,位涡具有守恒性的特点,它并未涉及气柱长度Δp的变化机理,即辐合辐散的产生机理。这是位涡理论的根本局限性所在。此外,位涡守恒虽然和涡度方程一样表示涡度变化和散度之间的关系,但它并没有说明散度是如何导致涡度变化的物理机理。而在涡度方程[式(4)]中,散度和地转参数f的乘积,揭示出散度是在地转偏向力的作用下转变为涡度的,即辐散流场在地转偏向力的作用下会转换为反气旋式流场。因此位涡的提出虽然在某些方面相对于涡度方程有所进步(如在数学形式上更加简洁),但是在对涡度变化物理机理的认识上却是一个退步。这是在使用位涡概念进行天气分析和诊断时必须有的清醒认识。
2.2 位涡理论的积极意义说到底,位涡是用垂直方向的厚度(即垂直散度,也可称为散度的垂直分量)来代替水平方向的散度。所以,从涡度变化的机理上看,位涡守恒和涡度方程在物理上是等价的,位涡理论并没有增加新的内涵。但是位涡理论还是有其积极意义。
(1) 用得最多的是位涡的守恒性,它可以用来追踪空气运动的轨迹。由于它最简单、很直观,容易“理解”,所以被用得很广泛。但正是由于其直观性,将位涡理论的应用引入歧途的也是守恒性。胡伯威[4]在2003年的文章中就已经指出这一点,但没有详细讨论。本文在后面将集中讨论位涡守恒这个概念是如何在应用中走入歧途的。但究其原因,位涡的守恒性只有在理想的绝热条件下才成立。在一二个小时的短时间内,可以近似认为是绝热的;但对一二天的过程,就不可能是绝热的,位涡也不再守恒。杨大升等[5]在1980年出版的《动力气象学》中早就指出,位涡的守恒性“可用于大尺度运动系统在干绝热情况下的有垂直压缩或伸展(有水平辐散或辐合)时的理论问题解释,但将它应用于天气图分析却受到了一定的限制,因为在一般情况下,很难准确地决定气流的轨迹”。
(2) 在理论上,位涡概念的提出也有积极意义。位温守恒公式中的厚度Δp隐含了位涡概念是一个三度空间的问题,它包含了高低空之间的联系。涡度方程只描写某一层的涡度变化,所以不可能真正揭示环流系统发展的机理。但是位涡理论仅仅是隐含了大气三维结构的重要性,并未具体解决引起气柱压缩或伸长的动力学过程,所以它的理论价值也是很有限的。若想具体揭示斜压扰动发展的机理,要到准地转理论的提出才得到解决。
(3) 位涡的可反演性是一个有用的研究手段。它可以用来考察某一系统与环流背景之间的相互影响,有兴趣的读者可参阅相关文献,此处从简。
3 平流层干侵入 3.1 干侵入的缘起“干侵入”是指平流层的干空气侵入到对流层。这个名词有两层含义,一是空气从平流层进入对流层,故称为“侵入”;二是平流层的特点是水汽非常稀少(小于0.1 g·kg-1),几乎可以忽略,故称为“干侵入”。图 2是关于干侵入的概念模型,它是Danielsen于1964年首先提出来的[6]。这张概念图所表达的思想是,在一个强烈发展的,或发展完好的锋面气旋后方有来自高空平流层空气以扇形辐散的形式下沉到地面冷锋的锋后。实际上Kleinschmidt在1950年已提出了“干侵入”的概念。但一直有不同的观点,对流层顶的4种不同的分析方法就代表了不同的学术观点。

|
图 2 Danielsen[6]的平流层干侵入概念模型 Fig. 2 Conceptual model of stratospheric dry air intrusion from Danielsen[6] |
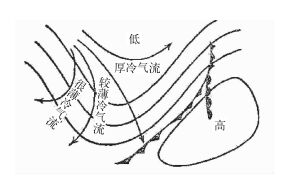
在干侵入的概念模型中,冷空气扇形辐散的下沉形式看似与早年Palmen的锋后冷空气等熵面流线分析的实例一致(图 3),但图 3中的冷空气都来源于对流层下半部,从600~800 hPa下沉到850~950 hPa,而不是来自对流层顶以上。实际上Rossby[7]早就总结了高空槽后的冷空气在冷锋后是浅薄的(图 4)。

|
图 3 Palmen根据等熵面分析得到的锋后冷空气的三维运动 (实线为等压线,单位:hPa;矢线为等熵面上的流线) Fig. 3 Three-dimension cold air motion behind front according to the isentropic analysis made by Palmen (Isobar is solid, unit: hPa; arrow lines are streamlines at the isentropic surface) |
|
图 4 高空槽冷空气的厚度和运动[7] (实线为700 hPa等高线或流线,矢线为冷空气质点的轨迹) Fig. 4 Thickness and motion of cold air in the upper-level trough[7] (Solid lines are height contours or streamlines at 700 hPa, arrow lines are the trajectories of cold air) |
表面上看,Danielsen的概念模型只是对锋后冷空气的来源过分地夸张。但是以科学的观点来看,这种夸张是非常荒谬的。因为,平流层的温度虽然很低(如-60~-50℃),但位温非常高,在300~400 K以上,即平流层空气如果可以下沉到对流层的底部,它的温度将高达零上数十度甚至百度以上。
既然早期的天气分析并没有任何证据表明存在平流层空气侵入到对流层低层的事实,那么是什么原因将位涡理论引导到干侵入这个歧途?这需要从位涡的空间分布及其守恒性和所谓对流层顶断裂(或折叠)现象谈起。
3.2 位涡和位温的关系 3.2.1 位涡和位温的垂直分布及平流层高位涡源位涡在不同的坐标系中有不同的表达形式[8]。在p坐标系中,它可以近似写成如下形式(忽略了斜压项):
| $PV \approx - g\left( {\zeta + f} \right)\frac{{\partial \theta }}{{\partial p}}$ | (6) |
可见,位涡的数值不仅和绝对涡度(ζ+f)有关,而且和位温的垂直分布(∂θ/∂p)有关。为此有必要首先考察位温的垂直剖面图。
图 5为2001年Conaty等[9]给出的1993—1994年冬季3月的纬向平均的位温经向垂直剖面图。由图可见,位温垂直分布的基本特征是随高度增大,特别是平流层,因为温度垂直递减率很小,故位温的垂直梯度非常大,在100 hPa附近位温可高达400 K左右。图中用298和380 K的等位温线(紫色线)分别表示极地气团对流层顶和热带气团对流层顶。50°N以北的极地气团对流层顶较低,在300~400 hPa之间;30°N以南的热带气团对流层顶很高,在150 hPa以上;30°~50°N之间为两个对流层顶之间的断裂带,同时也是极地气团和热带气团之间的过渡带和锋区。在垂直剖面图上,根据等位温线的密集程度很容易把平流层和对流层区别开来。(有关位温、等熵位涡与锋和对流层顶的分析方法,可参阅文献[10]。)

|
图 5 1993—1994年冬季3月平均的位温经向剖面图[9] (图中等位温线间隔为5 K;红色区为风速>35 m·s-1的高空急流,间隔2 m·s-1;紫色线为298和380 K的等位温线,分别代表极地气团的对流层顶和热带气团的对流层顶;蓝色线为等位涡线,0和2.5 PVU分别代表极地气团和热带气团的动力对流层顶) Fig. 5 Meridional cross section of zonally averaged time-mean potential temperature (black contours, interval 5 K) and wind speed (greater than or equal to 35 m·s-1 shaded in red and contoured at a 2 m·s-1 interval) for the Northern Hemisphere. Also shown are the 298 and 380 K isentropes (purple contours), and the 0 and 2.5 PVU surfaces (blue contours). Cross section is based on results from the GEOS GCM for a 1°×1° latitude-longitude grid, the ordinate and abscissa correspond to pressure (hPa) and latitude (°N), and the time-mean refers to the simulated 1993-1994 DJF winter season[9] |
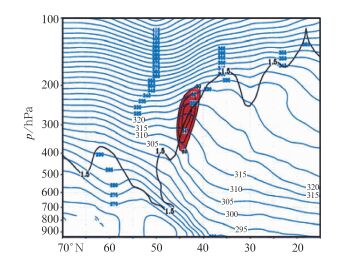
由于位涡和位温垂直梯度成正比,因此平流层的位涡比对流层大一个数量级。图 5中只给出了0和2.5 PVU的两条等位涡线(蓝色),1 PVU为10-6 m2·s-1·K·kg-1。2.5 PVU等位涡线和用位温定义的极地气团对流层顶比较接近,因此也被称为动力对流层顶。其下方对流层中的位涡都小于2.5 PVU。为了进一步了解平流层中位涡的分布,图 6给出了2007年3月初中国一次气旋强烈发展引起的暴雪过程中的位涡垂直分布图[11]。图中平流层中的位涡高达8~10 PVU,而对流层中基本上都在1 PVU以下。

|
图 6 数值模拟的2007年3月4日东北气旋暴雪过程的位涡垂直分布[11] (图中红线为剖面图上的位涡等值线, 单位:PVU;蓝线为1 km高度水平面上的等压线,单位:hPa) Fig. 6 Vertical distribution of PV in the simulated Northeast China cyclone on 4 March 2007[11] (Red lines are PV contours, unit:PUV; blue lines are isobaric lines at 1 km altitude, unit: hPa) |
比较图 5和图 6可以得出结论,位涡的垂直分布特征主要取决于位温的垂直分布。所谓平流层位涡源,实际上是平流层温度随高度变化很小的反映,它与平流层中涡度的大小没有多大关系(注:任意查阅一张100 hPa以上的高空等压面图可知,由于最大的风速层位于对流层顶的下方以及平流层的波动尺度非常大,所以涡度数值一定小于对流层)。
3.2.2 对流层顶的高度及所谓对流层顶的“断裂”或“折叠”如图 5所示,对流层顶的高度和气团的性质有关,极地气团的对流层顶高度很低,大约在300~400 hPa(6~9 km)左右;热带气团的对流层顶很高,大约在200~100 hPa(12~16 km)左右。30°~50°N之间为极地气团和热带气团之间的过渡区,由于冷气团和暖气团的对流层顶高度相差数千米,因此有人把两个气团之间的过渡区称为对流层顶断裂或折叠。而锋就是冷暖气团之间的过渡区,显然,所谓对流层顶断裂或折叠,和锋有着密切的关联。
图 7给出了4种对锋面和对流层顶配置的分析方法,它反映出五十多年前不同的学者对锋面和对流层顶以及两者之间的关系就存在不同的理解。如(a)将对流层顶的断裂表示为对流层顶的折叠;(b)将对流层顶和锋面之间的联系表示为一种模糊的过渡;(c)将对流层顶和锋面表示为相互独立现象,锋面可以穿过对流层顶到达平流层(换言之,平流层中也存在锋面);(d)将对流层顶和锋面表示为同一个面。所谓干侵入,就是由分析方法(d)引伸出来的。即把锋区的上下界及冷暖气团的对流层顶连接成一个漏斗状的物质面,并由此推断平流层的空气通过这个漏斗注入对流层(见图 8)。这就是平流层干侵入的由来。

|
图 7 锋面和对流层顶的各种分析方法 (a) Bjerknes等(1937),(b) Palmen等(1949),(c) Berggren (1952), (d) Reed等(1959) Fig. 7 Schematic diagrams of models used in the past for analyzing upper-level fronts and tropopause (a) Bjerknes et al. (1937), (b) Palmen et al. (1949), (c) Berggren (1952), (d) Reed et al.(1959) |

|
图 8 Danielsen锋面和对流层顶折叠示意图中的平流层空气侵入对流层 (注:此图还含有把锋面看成是由对流层顶折叠而形成的意思,是严重的本末倒置) Fig. 8 Schematic illustration of transverse circulations conductive to upper-level frontogenesis and tropoauase folding |
干侵入论断的基础是把对流层顶和锋看成是固定的物质面,即固定数值的等位温面。但是实际分析早已发现,对流层顶和锋与等位温面只是接近平行而并不重合,且其数值也随时间改变[12]。这是因为对流层顶和锋面的基本性质是温度梯度的不连续,同时实际大气是非绝热的,位温并不守恒。
3.2.3 高空锋区和高位涡异常锋区的基本特征不仅是水平温度梯度大,垂直温度梯度小(甚至是逆温)也是锋区的基本特征。因此,和平流层一样,锋区内的位温垂直梯度也很大。所以,在其他条件接近的情况下,锋区内的位涡大于锋区外,如图 9所示[9]。图中40°~50°N间400 hPa以下倾斜的等位温线密集带是极地气团和热带气团之间的锋区。如果以1.5 PVU位涡等值线作为对流层和平流层的分界,在锋区附近1.5 PVU等值线表现为向下延伸的漏斗状,即所谓“高位涡异常”。从位涡[式(6)]可知,它不过是与锋区逆温的反映。但是在所谓平流层干侵入的概念模型中,把这种从平流层沿锋区下垂的漏斗状高位涡现象想象为它是平流层高位涡的空气在锋区内沿等位温线向下运动的结果(如图 8所示)。
|
图 9 大西洋地区爆发性气旋中沿48°W的垂直剖面[9] (蓝线为等位温线,间隔5 K;黑色粗线为1.5 PVU等位涡线;红色区为风速≥60 m·s-1的急流区,等风速线间隔2 m·s-1) Fig. 9 Meridional cross section along 48°W of potential temperature (blue contours, interval 5 K), wind speed (greater than or equal to 60 m·s-1 shaded in red and contoured at a 2 m·s-1 interval), and the 1.5 PVU surface (black contour) (The results from the GEOS simulation for a 1°×1° latitude-longitude grid at 0000 UTC model day 55[9]) |
干侵入的概念可以说是背离了从Bjerknes到Rossby和Palmen所形成的人们对锋面气旋中冷空气活动的基本认识,因此有必要从物理概念和客观事实两个方面来分析干侵入的谬误或不合理性所在。物理上归纳起来有以下几点:
一是混淆了流线和轨迹的区别。由于锋面是移动的,且移速和风速具有相同的数量级,把流线当作轨迹违背了流体力学的一条基本原理:只有在定常的情况下流线才和轨迹重合。
二是忽视了大尺度环流系统的准水平性,即垂直速度的量级比风速小3个数量级。按照垂直速度的量级100 cm·s-1,24小时内的空气垂直位移大约只有1~2 km。在一天的时间内,锋面的移动距离可达千千米里左右,非绝热过程可引起几度的温度变化,在这个过程中会不断有空气块因为温度的变化而离开等位温面,因此不能把等位温面当作恒定不变的物质面[12]。
三是忘记了位温的物理意义是气块在绝热条件下垂直位移到1000 hPa时的温度。在前面的位温垂直剖面图(图 5)上可见,300 hPa以上的位温值基本上都在310 K以上(200 hPa以上更是高达400 K以上),用摄氏温度表示是37℃甚至127℃以上。也就是说,如果平流层的空气侵入到冷锋后方对流层底时,它将成为温度大大高于夏季地面的最高温度的高温空气。所以干侵入的概念模型(图 2)将冷锋后的空气推断为来自平流层下部或对流层顶是非常荒谬,而应当仅仅理解为垂直方向的空气运动的流线。
归根到底,干侵入的谬误来源于对位温和位涡守恒性的绝对化。正如胡伯威[4]在位涡理论的讨论中所指出的,根据位涡守恒性得出的概念仅仅是一种由“直观地推断”,它并未经过严格的科学论证。下面我们将考察一些文献中已有的轨迹实际计算结果。
3.4 轨迹的实际计算结果如前所述,干侵入的谬误其主要根源在于混淆了流体力学中流线和轨迹这两个基本概念,把图 2或图 8中的流线轻率地当作了轨迹。需知,只有在流场不随时间变化的定常条件下,流线才和轨迹重合,这是流体力学中最基本的常识。在计算机视算技术发展以前,轨迹的计算几乎不可能,因此以Rossby和Palmen为首的芝加哥学派才倡导使用等熵面分析方法。但他们从未把等熵面上的流线当作严格意义上的轨迹,只是用来定性地判定空气块垂直方向的运动方向,如图 3和图 4所示。
典型的干侵入现象都出现在强烈的斜压发展中,如寒潮过程或气旋强烈发展过程,流场随时间的变化非常显著,所以轨迹和流线有很大的差异。干侵入的轻率推断和现代天气学的奠基人Rossby和Palmen根据等熵面分析得到的锋后冷空气来源于对流层下部的结论相矛盾。但是只有实际的轨迹计算结果才能最后证明图 2的干侵入概念模型是错误的。
要获得真正的轨迹必须有高的时间和空间分辨率的三维流场资料。只有有了高分辨率的数值模式输出资料,才有可能计算轨迹。20世纪90年代中尺度数值模拟的大量应用,才开始有爆发性气旋的轨迹计算结果。但是至今在国内外有轨迹计算的文献中(如文献[13]),还没有看到像图 2那样的从平流层底部直达对流下部的干侵入。
王洪庆等[14]在1996年曾经利用中尺度数值模式MM5和可视化软件Vis5D就黄海的一次爆发性气旋过程寻找过干侵入的轨迹,结果只找到了如图 10所示的高空槽后从9 km高度下降到5 km左右的源自对流层顶的气块轨迹。后来张伟等[15]对同一例子研究得到的200 hPa槽后平流层空气的轨迹也未发现到达对流层底部呈反气旋弯曲的轨迹(见图 11),而剖面图上的流线却把200 hPa和地面连接了起来。没有例外地,轨迹计算表明,源自槽后对流层顶附近的干空气轨迹在下沉过程中均逐渐呈气旋式弯曲并转为上升运动,所到达的最低高度在对流层中层附近。轨迹的上述特征,可以根据质量补偿原理和涡度方程得到合乎动力学原理的解释,即与下沉气流相伴随的高空水平辐合引起了气块相对涡度的增加从而导致气块轨迹呈气旋式转变。

|
图 10 1993年6月2日数值模拟的黄海爆发性气旋中冷、暖空气块的三维轨迹(用两组彩色飘带表示,西边的一束来自高空槽后)的自南向北的前视图 (飘带的颜色变化表示轨迹高度的变化,两条水平线的高度分别为9和1.5 km) Fig. 10 View from south of three-dimensional trajectories in the simulated the Yellow Sea explosive cyclone on 2 June 1993 (Two groups of colored ribbons, the west group is from the back of upper-level trough, the different colors in a ribbon denote different height; the two horizontal lines are 9 and 1.5 km altitude, separately) |

|
图 11 (a)与图 10相同,但为三维透视图(蓝色点线为冷空气轨迹,红色点线为暖空气轨迹), (b)为穿过气旋中的垂直剖面图上的流线 (红线为相当位温等值线,填色表示相对湿度,蓝色为干,黄色为湿;图中显示下沉气流和低相对湿度相对应,上升和高相对湿度相对应) Fig. 11 (a) same as Fig. 10, but for 3-dimension perspective view, blue dot line denotes cold air trajectory, red dot line denotes warm air trajectory, and (b) streamline in vertical cross section across the cyclone (Red contours for equivalent potential temperature, color shaded for relative humidity, blue is dry, yellow is moist. It shows that the sinking flow corresponds to low relative humidity, and rising flow to high relative humidity) |
在3.2节位涡和位温关系的讨论中,我们已经在垂直剖面图上(图 6)看到,高位涡确实集中在对流层顶以上,且随高度增加;而对流层的位涡都非常小,在1 PVU以下,以致图中分析不出等位涡线。正是基于上述位涡垂直分布的气候特征,把平流层称为位涡的源,把对流层内大于1.5 PVU(或2.0 PVU)的区域称为位涡的异常。位涡理论则根据守恒性把位涡异常归结为是平流层高位涡源的空气侵入对流层的结果。近年来,这一说法又被用来作为对卫星水汽图像动力学解释的基础。所以,有必要对平流层位涡源和对流层位涡异常这两个现象的天气学本质加以考察。
要弄清平流层位涡源和对流层位涡异常的天气学内涵,必须从位涡的数学表达式出发。从式(6) 可知,位涡是由绝对涡度(ζ+f)和干静力稳定度(∂θ/∂p)两个基本成分组成。将位涡的垂直分布和位温的垂直分布相对照(图 5和图 6),就可以发现平流层密集的等位温线和密集的等位涡线几乎是对应的,可见平流层的高静力稳定度是形成高位涡源的主要原因(在《气象》2012年第1期《气象论坛》栏目的另一篇文章中[10],对此有专门的讨论)。
对流层的位涡异常则和图 5或图 9中从平流层向下延伸的漏斗状的高位涡区和高空锋区密集的等位温线相配合也同样说明静力稳定度是形成锋区内位涡异常的主要原因。应该指出,图 5中对流层顶断裂处附近红色区域所示的高空急流轴的位置表明,锋区高位涡异常区位于急流轴的左侧气旋式的风速切变区,所以急流左侧的正切变涡度对位涡异常也有一定贡献。所以,沿锋区向下延伸的高位涡实际是锋区结构的反映,不应直观地简单推断为是平流层高位涡向对流层侵入的结果。
4.2 等熵位涡图的天气学解释Hoskins把等熵位涡图作为位涡在天气分析和预报中应用最基本的工具。20世纪80年代,在他所主持的Reading大学每周一次当前天气的讨论中,试图用等熵位涡图取代等压面图成为主要的常规天气图。1985年,Hoskins等[16]在英国气象学会季刊上还专门写了一篇名为《等熵位涡图的意义及应用》的文章。
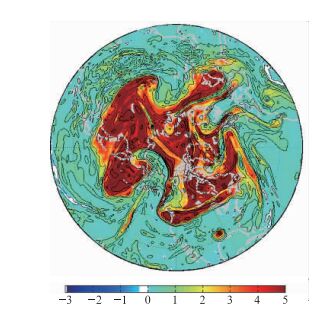
任意一张包括极区在内的中高纬度等熵位涡图都与Hoskins文中给出的图非常相似,它们都可以直观和生动地展示围绕极区附近的扰动,如图 12和图 13所示,这是等熵位涡图的最大优点。图中生动地展示出极区平流层高位涡向中纬度地区移动,而这种位涡扰动的活动又和对流层中的斜压扰动,如长波、阻塞和切断、气旋和反气旋、锋面和高空急流等的活动相伴随。这是位涡理论引起不少人兴趣的主要原因,所以有必要对等熵位涡图的意义进行考察。
|
图 12 2006年2月14日北半球310 K等熵面20°N以北的位涡(填色) Fig. 12 Potential vorticiy (color shaded) to the north of 20°N at 310 K isentropic surface on Feb 14 2006 |
|
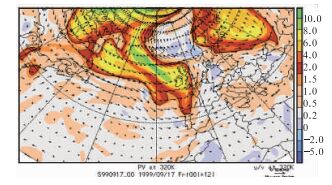
图 13 320 K等熵面上的位涡分布和风矢量 Fig. 13 Potential vorticity (color shaded) and wind at the 320 K isentropic surface |
首先,等熵位涡图是等熵面上的位涡分布图。与等压面高度形势图相类比,它也可以称为等熵面位涡形势图。要了解它的天气学意义,首先需要知道等熵面和等压面有原则上的不同,等熵面不是一个准水平面。从图 5可知,等熵面是自北向南倾斜的面。如300 K的等熵面高度,极地在300 hPa左右,而热带在850 hPa左右。所以等熵面有的部分很低,位于对流层中;有的部分很高,位于在平流层中。
图 12是一张310 K的北半球等熵位涡图,图 13是一张320 K的大西洋地区等熵位涡图。图中的高位涡区都集中在50°N以北的极区和高纬度地区,40°N以南的位涡都非常小,几乎都小于1.5 PVU。从垂直剖面图(图 5、图 6和图 9)上的310和320 K等位温线可知,图 12中50°N以北的地区都在300 hPa以上的平流层中,而40°N以南的地区都在400 hPa以下的对流层中。所以,等熵位涡图中极地和高纬度的高位涡地区都位于平流层中,而中低纬度的低位涡地区则位于对流层中。因此,在等熵位涡图上高位涡区的边界就是平流层和对流层的分界线,即对流层顶的断裂处。
由于对流层顶断裂处和高空锋区紧密相连,所以高位涡区实际上是极地气团活动的区域,因为极地气团的对流层顶很低,所以其等位温面位于平流层中,位涡很大。图 12和图 13等熵面位涡形势的确生动地展示出极地气团南下或北缩(即热带气团北上)的情况。
显然,等熵位涡图的最大优点是可生动地展示高纬度极地气团的活动,所以对地处50°N以北的英国有比较好的分析意义。但是对我国而言,大部分国土位于50°N以南,位涡的数值都非常小,因此其应用受到较大限制。此外还必须懂得,等熵位涡图所给出的是极地气团活动的结果,而不是原因。要认识冷暖气团活动的机理还必须依靠针对斜压扰动发展的准地转动力学理论。
4.3 低空高位涡异常的来源在850或700 hPa低层有时也会出现小范围略高于1.5或2.5 PVU的高位涡现象,如在爆发性气旋中低空有高位涡与高空的高位涡在垂直方向上的“锁相”现象(如图 6)。根据式(6) 不难理解,此时低空高位涡的出现是由于气旋强烈发展导致低空相对涡度急剧增大的结果。数值模拟研究结果表明,气旋强烈发展过程中,位涡在高低空是同时加强的,只是在气旋发展到锢囚阶段时在垂直方向上趋于重合,而不是高空的高位涡侵入低空[11, 14]。
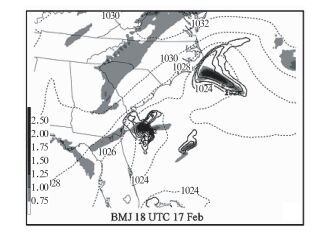
2008年美国“天气和预报”杂志预报员论坛刊登一篇题为“业务预报中的位涡思考:非守恒性的应用”[17]。文中的结论明确指出:数值预报中强降水落区和正位涡异常及水汽输送增强的配置关系,显示出潜热反馈的作用,即由于强降水过程在对流层中高层释放的潜热引起对流层低层等压面高度下降,从而气旋式涡度增加及低空急流增强。图 14为此文中给出的一张30小时数值预报结果。图中900~700 hPa层的位涡和对流性降水的3小时累积雨量的重合清楚地显示出积云对流潜热反馈的作用。
|
图 14 2004年2月16日12 UTC的30小时预报场[17] [阴影区为900~700 hPa层的位涡(灰度, 单位:PVU), 虚线为海平面气压(单位:hPa), 实线为3小时模式预报对流性降水(单位:mm)] Fig. 14 The 30 h forecast valid at 18:00 UTC 17 February 2004 from Workstation Eta BMJ run initialized at 12:00 UTC 16 February 2004 of 900-700 hPa layer potential vorticity (shaded as in legend, unit: PVU), sea level pressure (dashed contours, unit: hPa), and 3 h model forecast of convective precipitation (solid contours, unit: mm)[17] |
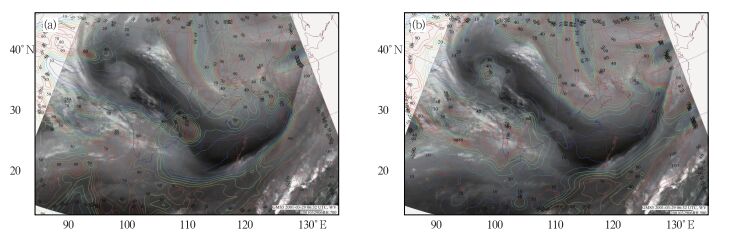
所谓斧形暗区是指卫星水汽图像中与成熟气旋逗点云系相伴随的一个前沿呈光滑弧形的斧状暗区,如图 15所示。由于它的形状和干侵入概念模型(图 2)及等熵位涡图中的位涡异常的形态(如图 12或图 13)有一定程度的相似,因此部分研究者(见文献[18])用平流层位涡源和干侵入作为卫星水汽图像斧形暗区的动力学解释。
|
图 15 2001年3月29日06 UTC的卫星水汽图像中的斧形暗区(也称暗缝)及700 hPa(a)和500 hPa(b)的相对湿度(用细实线表示,间隔10%) Fig. 15 Satellite water vapor images at 06 UTC 29 March 2001 and 700 hPa relative humidity (a) and 500 hPa relative humidity (b) (solid line, interval 10%) |
按照水汽图像的分析原理,暗区应表示对流层中层大气的相对湿度很小,对流层中下层水汽的红外辐射可以穿过中高层大气直接被卫星水汽通道接收,由于低空水汽的温度较高,所以呈现较暗的色调。为此可以考察图 15所给的水汽图像及图中叠加的700或500 hPa相对湿度的分布。不难发现,水汽图像的暗区和相对湿度小于20%的区域几乎完全重合,证明水汽图像的色调主要反映中层大气的相对湿度(注:卫星图像是三维大气的二维显示,所以不可能和某一等压面的相对湿度分布完全重合)。
相对湿度的大小和垂直运动的关系非常密切,下沉绝热增温会使相对湿度迅速减小。例如,从T-logp图分析可知,温度为-10℃的500 hPa饱和湿空气,如果下降到700 hPa,温度会升高到16℃,使相对湿度由100%下降到20%。因此水汽图像的亮温对垂直运动的方向非常敏感,是判断次级环流非常有效的工具。根据作者的经验,水汽图像中大大小小的暗区(或暗缝)及图像的变暗过程与对流层中层(500~700 hPa附近)的下沉运动配合得较好,它符合以水汽图像基本性质为依据的分析原理。
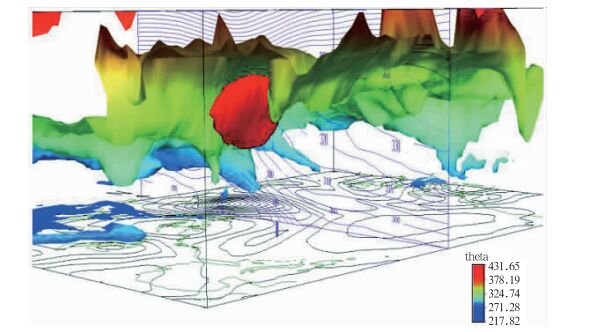
5 总结为了使读者最后对位涡、对流层顶、锋面及所谓的干侵入有一个完整的具体形象,我们给出文献[9]中一个强烈发展气旋位涡分布三维图像(图 16)供读者参考。图中用1.5 PVU的位涡等值面作为对流层顶的三维图像,用沿48°W的位温垂直剖面图(与图 9相同)作为锋面的垂直剖面。由图可见,高位涡都在平流层或对流层顶附近的高空,对流层的中下部位涡都非常小,只有西部靠近地面附近有一片略大于1.5 PVU的区域,但它们并不和高空的大值区相连接。最明显的1.5 PVU等位涡面的下垂现象出现在垂直剖面的锋区上。显然,锋区中密集的等位温线说明,对流层顶下垂仅仅是锋面热力特征在位涡分布上的反映。总之,图 16表明,即使在气旋强烈发展的情况下也不存在平流层干侵入现象。
|
图 16 第55天的动力对流层顶(1.5 PVU等值面)的三维图像[9] (等值面按位温色表着色。红色等值面为风速60 m·s-1,位温的经向垂直剖面图,间隔5 K;海平面气压分布,间隔4 hPa;垂直坐标范围为0.46~16.67 km;蓝色虚线为地面锋线) Fig. 16 Three-dimensional perspective from a southwestern viewpoint of the dynamic tropopause (1.5 PVU surface) with tropopause potential temperature (unit: K) shaded according to legend. Also shown are 60 m·s-1 isosurface of wind speed (red shading), meridional cross section along 48°W of potential temperature (purple contours, interval 5 K), and sea level pressure (contour interval 4 hPa) on lower horizontal plane. Geographical region displayed is the same as in Figs. 9-14; the ordinate corresponds to geometric height ranging between 0.46 and 16.67 km. Perspective is based on results from the GEOS GCM for a 1°×1° latitude-longitude grid at 00:00 UTC model day 55[9] |
本文主要结论如下:
(1) 从大尺度环流看,无论是位涡的三维分布还是气块的三维轨迹,都不存在平流层干侵入的客观证据;
(2) 根据位涡守恒性提出的干侵入概念,是在非定常的情况下混淆了流线和轨迹的原则差异及将守恒性绝对化的基础上作出的错误推断;
(3) 平流层高位涡源是由平流层非常大的位温垂直梯度所决定;
(4) 等熵位涡分析中的位涡分布形势是对流层顶、极地气团、锋面和高空急流形势的综合显示,它仅仅适用于40°~50°N以北的中高纬度地区;
(5) 所谓等熵位涡思考(IPV thinkings)是用守恒性取代斜压大气准地转动力学理论,它只能反映斜压扰动发展的结果,不能说明发展的机理;
(6) 对流层低层的高位涡是潜热反馈的结果;
(7) 水汽图像中的暗区(较高的水汽亮温)与对流层中下层下沉绝热增温产生的的低相对湿度区相对应。
位温和位涡的概念至今已有50~100年的历史,它们的提出无疑是对气象学研究工作的重大贡献,至今仍有非常重要的基础性价值。但是在近50年中,由于将守恒性的绝对化和简单化也出现了将研究和应用(天气预报)导入了歧途的现象,产生与气象学常识背离的看法。作者也曾经在爆发性气旋的研究中讨论过位涡和干侵入问题[11, 14-15]。在撰写此文的过程中,深感科学的发展不是直线前进的,需要我们用求实的态度对不断出现的新观点从原理上和实践上进行检视,无论它们是来自国外还是国内,即使是来自国外名声很大的权威。
位涡的讨论涉及气团、锋、急流和对流层与平流层等天气学的基本概念以及剖面分析、等熵面分析等天气学的基本分析方法。要真正了解等熵位涡的实质,必须首先掌握这些天气学的基本概念和分析方法。作者为此专门撰写了“位温、等熵位涡与锋和对流层顶的分析方法”[10]作为此文的参考。
在结束本文之前还必需申明,本文在讨论位涡问题时没有涉及与强对流有关的所谓干侵入。其原因是:
(1) 对流是中尺度问题,与大尺度环流是物理性质完全不同的两个问题,不能用同一个理论来讨论;
(2) 强对流中的干侵入来源于强风暴研究中发现的一个重要观测事实,在发展旺盛的强对流中存在从云体外向云体内的中层后方入流(Mid-Altitude Rear Inflow),它与下击暴流和阵风锋有密切关系。将中层后方入流称为干侵入是偷换名词;
(3) 中层后方入流是对流风暴中雨水和冰雹强烈下泻而引起的,与锋面扰动强烈发展引起的下沉运动是两种性质完全不同的现象。
为了主题集中,文中没有讨论所谓干侵入和对流高空湍流等的关系。如有必要,今后可专文予以讨论。
致谢:本文来源于和全国各地预报员和培训中心教师(包括Prof. Doswell和Prof. Mass)在轮训期间的讨论。长达两年的讨论使作者逐步加深了对位涡问题的认识,在此对他们表示真诚的感谢。
陶祖钰, 2011. 基础理论与预报实践[J]. 气象, 37(2): 129-135. DOI:10.11898/1001-7313.20110201 |
朱乾根, 林锦瑞, 寿绍文, 2000. 天气学原理与方法(第三版)[M]. 北京: 气象出版社.
|
Palmén E, Newton C W, 1969. Atmospheric Circulation Systems: Their Structure and Physical interpretain[M].
Maryland: Academic Press.
|
胡伯威, 2003. 关于位涡理论及其应用的几点看法[J]. 南京气象学院学报, 26(1): 111-115. |
杨大升, 刘余滨, 刘式适, 1980. 动力气象学[M]. 北京: 气象出版社, 186.
|
Danielsen E K, 1964. Project Springfield Report[M].
Washington D C: Defense Atomic Support Agency, 99.
|
谢义炳, 陈受钧, 肖文俊, 1959. 天气学基础[M]. 北京: 高等教育出版社, 181.
|
周小刚, 柳士俊, 王秀明, 等, 2011. 对气象常用坐标系中位涡形式的探讨[J]. 物理学报, 60(5): 059201(1-7). |
Conaty A L, Jusem J C, Lakacs L, et al, 2001. The structure and evolution of extratropical cyclones, fronts, jey streams, and the tropopause in the GEOS general cirulation[J]. Bulletin of AMS, 82(9): 1853-1867. |
陶祖钰, 郑永光, 2012. 位温、等熵位涡与锋和对流层顶的分析方法[J]. 气象, 38(1): 17-27. DOI:10.7519/j.issn.1000-0526.2012.01.002 |
蔡丽娜, 隋迎玖, 刘大庆, 等, 2009. 一次爆发性气旋引发的罕见暴风雪过程分析[J]. 北京大学学报(自然科学版), 45(4): 693-700. |
顾震潮, 陈雄山, 许有丰, 1958. 锋面假相当位温图和它对中国寒潮冷锋上界变化分析的应用[J]. 气象学报, 29(1): 44-56. DOI:10.11676/qxxb1958.006 |
Mass C F, Schultz D M, 1993. The structure and evoloution of a simulated midlatitude cyclone over land[J]. Mon Wea Rev, 121: 889-917. DOI:10.1175/1520-0493(1993)121<0889:TSAEOA>2.0.CO;2 |
王洪庆, 张焱, 陶祖钰, 等, 1998. 五维大型复杂数据集计算机可视化[J]. 自然科学进展, 8(6): 742-747. |
张伟, 陶祖钰, 胡永云, 等, 2006. 气旋发展中平流层空气干侵入现象分析[J]. 北京大学学报(自然科学版), 42(1): 61-67. |
Hoskins B J, McIntyre M E, Robertson A W, 1985. On the use and significance of isentropic potential vorticity maps[J]. Quart J R Meteor Soc, 111(470): 877-946. DOI:10.1002/qj.49711147002 |
Brennan M J, Lackmann G M, Mahoney K M, 2008. Potential vorticity (PV) thingking in operations: The utility of nonconservation[J]. Weather and Forecasting, 23: 168-182. DOI:10.1175/2007WAF2006044.1 |
桑特里特·乔治夫, 著. 卫星水汽图像和位势涡度场在天气分析和预报中的应用[M]. 方翔, 等译. 北京: 科学出版社, 2008: 78-84.
|
 2012, Vol. 38
2012, Vol. 38 