引言

在《气象》2011年第37卷第2期气象论坛的“基础理论和预报实践”^[1]一文中提到，天气会商中存在把简单问题复杂化的倾向，等熵位涡为其中的一个例子。《气象》编辑部希望专门就此问题作比较系统的讨论，包括位涡问题的缘起、应用及其歧途。在撰写过程中发现要正确理解等熵位涡理论(或等熵位涡思考^[2])，首先需要知道等熵位涡分析的原理和方法，以及与其密切相关的锋、对流层顶、垂直剖面分析等基本概念和原理。所以就决定放下将近完成的位涡问题讨论，于是就先有了此文。

1 位温和位涡分析的意义

位涡理论的应用离不开等熵位涡分析，即在等熵面上分析位涡的空间分布。熵，是个非常抽象的名词，它原是在热力学中提出，在物理学之外的化学、生物学、天文学、信息学、甚至社会学都可使用熵这个抽象概念。学科不同，熵的具体含义也不同。在天气分析中，等熵面分析就是指等位温面分析，因为在绝热和理想气体条件下，熵和位温的对数是线性正比关系，具有一样的守恒性^[3]。但称为等熵面分析反而掩盖了它的具体物理含义，实无此必要。(相关基本概念参见附录1)。

位温，对预报员来说应该不陌生，通俗的讲，它是空气块绝热压缩到1000 hPa时的温度，但在日常天气分析预报中很少分析位温。实际上，每天分析的高空天气图上的等温线就是等位温线。因为高空图是等压面图，从位温公式

$\theta = T{\left( {\frac{{1000}}{p}} \right)^{\frac{{{R_d}}}{{^{{c_{pd}}}}}}}$

可知，等压面上若温度相等，则位温也一定相等，只是两者的数值不相同。

位温主要用在垂直剖面图(以下简称剖面图)的分析上。它是剖面分析的主要内容，因为通过等位温线分析可以非常直观地展示锋面和对流层顶的存在。剖面分析是认识大气热力和动力特征三维结构的基本分析工具。通过垂直剖面图分析，将低空到高空的各层等压面图联系起来。

本文将通过剖面分析介绍位温和位涡的三维分布特点及在剖面图上分析锋面和对流层顶的方法，并进而讨论等熵位涡分析的天气学意义。目的是使读者掌握等熵位涡分析所必需具备的基本概念和方法。

2 剖面图上的位温

图 1给出了一张南北方向的垂直剖面实例。图中红色细点线是等温线，紫色细实线是等位温线。在垂直剖面图上，等温线大致呈水平走向，从南向北缓慢降低，反映气温自南向北逐渐降低。但在中纬度锋区内，等温线的倾斜相当显著，反映锋区内水平温度对比很大。等位温线的走向也是锋区外较平缓，锋区内倾斜，但倾斜的方向和等温线相反，两者接近垂直。其原因是，温度和位温的垂直分布不同。温度是地面高、高空低。图中最高的温度位于低纬度的地面，大于24℃；最低的温度在高空，但也在低纬度，低于-80℃。因为在对流层中，温度随高度递减，低纬度暖气团的对流层顶高，从地面到100 hPa，温度始终随高度递减。

剖面图上位温的分布和温度相反，地面低、高空高。图中最低的位温位于极地的地面，小于272 K(即-1℃左右)；最高的位温也在极地，但在高空，大于400 K(即127℃左右)。其原因是对流层中大气温度的垂直递减率平均为6.5℃·km^-1，小于干绝热递减率9.8℃·km^-1，平流层中垂直递减率更小，甚至随高度不减反增，而极地气团的对流层顶很低，平均只有6~8 km，比热带对流层顶平均的16 km低得多。

3 剖面图上的锋区

锋的基本定义是冷暖气团之间过渡带。所以，锋区是水平温度梯度的集中区，锋区内的温度梯度明显大于锋区外，即锋的基本性质是温度梯度的不连续，而不是温度的不连续。[注：在有些天气学教材中，把锋看成是大气中气象要素(温度、湿度、气压等)的不连续面，但这是一种最简化的抽象，并不符合锋的实际状况。]

在等压面图上，锋区表现为等温线的密集带。在剖面图(图 1)上，锋区表现为倾斜的等温线，它反映了锋区内水平温度梯度大、垂直温度梯度小(甚至逆温)这个基本热力学特征。因此，剖面图定锋的原则是，等温线走向由水平转为倾斜的转折点(也称为折角)来确定锋区上、下界的位置。图 1中黑色粗实线为依据上述原则确定的极锋和副热带锋。需要说明，定锋并没有严格的定量标准，因此具有一定的主观性。锋面分析反映了分析者对大气热力结构的认识，不同人的分析会有所差别。例如图中极锋上界的下端由于等温线的倾斜不太显著所以没有延伸到地面，而是用粗虚线表示它的下端锋区的强度比较弱。此外，冷气团的北部边界由于温度梯度较小，锋区特征不强，故图中用粗点线表示。

剖面图上等位温线在锋区内也表现为倾斜的特征，但由于倾斜的方向和等温线相反，故锋区内等位温线的走向和锋区的走向接近平行。锋区内水平温度梯度大、垂直温度梯度小的热力学特征，在剖面图的位温场上则表现为不仅位温的水平梯度大，而且垂直梯度也很大。从图 1可见，密集而倾斜的等位温线非常直观地表现出了倾斜的锋区的空间形状。这正是在剖面图上分析等位温线的主要目的——凸现锋区。

理论上应该也可以根据位温梯度的不连续来确定锋面的上下界，但等位温线走向的转折不如等温线明显，因此实际定锋时通常不使用等位温线的折角，而是主要参考等位温线的走向来定锋。还需要指出，锋区的上、下界和等位温线只是接近平行，锋面和等位温面并不完全平行。因此，即使在绝热的条件下，锋面也不能看成是物质面。天气学教材中把锋面称为物质面只是一种近似的简化，实际剖面图分析中不可能将锋的上下界分析成与等位温线完全平行。

4 对流层顶分析 4.1 对流层顶在剖面图上的温度特征

对流层和平流层的区别是温度垂直递减率。对流层温度垂直递减率大，平均为6.5℃·km^-1，大气层结稳定度较小，比较容易发生对流，故称为对流层。平流层的垂直递减率很小(平均≤2℃·km^-1，甚至逆温)，故也称为同温层。平流层大气静力稳定度(-∂θ/∂p)很大，非常稳定。对流层中垂直发展旺盛的积雨云到达对流层顶时也会受到抑制，形成平展的云砧。所以，正是因为平流层几乎没有垂直运动，才被称为平流层。

由于温度垂直递减率接近零，所以在剖面图上(见图 1)，平流层的等温线呈上下垂直走向。因此，等温线的折角是在剖面图上确定对流层顶位置的基本原则。图 1中红色粗实线就是根据等温线折角确定的对流层顶。此外，还可以发现对流层顶在剖面图上也表现为温度的最低处，它也是在剖面图上识别对流层顶位置的一条常用的方法，其原因是对流层中温度随高度持续降低，而在平流层中，温度不再降低甚至缓慢增加，所以对流层顶的温度最低。

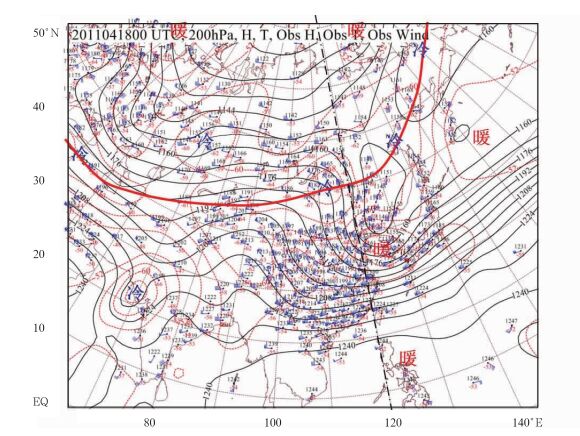
4.2 对流层顶在等压面图上的温度特征

极地对流层顶很低，平均只有6~8 km，热带对流层顶很高可达16 km，所以对流层顶是一个倾斜的面，它和某些高层的等压面图相交。因此，在300~100 hPa等压面图上也存在分析对流层顶的问题。在高空等压面图上，对流层顶处温度最低的特征也非常显著。图 2为与图 1同时刻的200 hPa等压面图，图中红色粗线为对流层顶。它是对流层顶和200 hPa等压面的交线，其北侧为平流层，南侧为对流层。50°N以北的200 hPa等压面位于平流层中，因此显示出北暖南冷的特点。50°N以南位于对流层中，仍为北冷南暖的特点。200 hPa等压面上的对流层顶正好穿过40°~50°N之间的冷区。

对于与对流层顶相交的等压面图，由于平流层中南北温度梯度与对流层相反，环流系统的热力特征完全不同于对流层中。如对流层上部的冷槽、暖脊，在平流层中却表现为暖槽、冷脊。因此需要特别提醒注意，在与对流层顶相交的高空等压面图，如冬季的300 hPa及夏季的200和100 hPa图，都由平流层和对流层两部分组成。属于平流层的部分，温度场中的冷和暖并不代表冷气团或暖气团，如图 2中极地低压和东北切断低压，都与暖中心相配合，但实际上它们都是极地气团上空对流层顶特别低的反映(300 hPa以下，请参阅图 1)。

4.3 对流层顶在剖面图上的位温特征

对流层和平流层的差别在剖面图的等位温线分布上也很突出，平流层中等位温线非常密集，而对流层中则很稀疏(见图 1)。根据等位温线的疏密，一眼就能在剖面图上分辨出平流层和对流层。但是对流层顶和等位温线并不重合，如图 1中用粗点划线表示的310和320 K等位温线和依据温度垂直递减率确定的对流层顶(图中用红色粗实线)，虽然比较接近，但并不重合。因此，将对流层顶看成是物质面也是错误的。这也说明所谓平流层干侵入，从一开始在对流层顶这个基本概念上就存在错误。对流层顶与锋面的性质相似，都是温度梯度的不连续，即垂直温度梯度(也可称为温度垂直递减率或静力稳定度)的不连续。

4.4 对流层顶在剖面图上的位涡特征

剖面图上对流层和平流层的差别，位涡的分布表现得比位温分布更加突出。从图 1可见，对流层中的位涡非常小，基本上都在1.0 PVU以下；对流层顶以上，位涡随高度急剧增加，到100 hPa可以达到10 PVU以上。平流层中等位涡线非常密集，对流层中则稀疏到几乎没有。因此，位涡理论的应用中还提出了所谓动力对流层顶的概念，即根据位涡的数值，将1.5或2.5 PVU作为对流层顶的标志，如图 1中绿色粗虚线所示。显然，它和经典的对流层顶相当接近，不同之处是它将极地气团和热带气团的对流层顶连接起来。但需要说明的是，动力对流层顶的概念并不适合于低纬地区(约15°S~15°N区域)，因为该区域绝对涡度接近于0，从而位涡接近于0。

5 剖面图上的位涡

既然位涡集中在平流层，是平流层和对流层的最大差异，因此弄清楚造成如此巨大差异的原因是十分必要的。为此，我们需要从位涡的定义出发来进行讨论。

位涡不是一个单纯的动力学物理量，它是动力学和热力学混合的一个物理量。为了了解所谓动力对流层顶的真实内涵，有必要分别考察一下决定剖面图上位涡分布的动力因子和热力因子。根据位涡公式

$PV \approx - g\left( {\zeta + f} \right)\frac{{\partial \theta }}{{\partial p}}$

位涡主要是由涡度ζ和位温垂直梯度(-∂θ/∂p)所决定的。由于f是地球自转涡度，它只和纬度有关，所以无需考察。

从图 3给出涡度、位温垂直梯度、位涡的垂直剖面分布看，图中用蓝色实线表示的等涡度线分布和位涡分布(填色)之间几乎没有相似之处。等涡度线以垂直分布为主要特点，而等位涡线则是水平分布为主。涡度分布主要反映各纬度的槽脊分布，如图中最大的正涡度区是40°N附近的切断低压和极地低压，其最大值位于对流层上部的300~400 hPa。而位涡分布则集中在平流层，且越往高空越大。但是用黑色实线表示的位温垂直梯度分布和位涡的分布非常相似，位温梯度也是集中在平流层，且越往高空越大，高位涡中心和位温梯度极大值重合。显然，位涡的垂直分布主要是由热力因子位温垂直梯度决定。正因为热力因子起主要作用，所以根据1.5或2.5 PVU确定的动力对流层顶才和经典对流层顶非常相似，它和“动力”并无多大关系。可见所谓动力对流层顶并无多少动力学的意义，这种提法反而起到了掩盖位涡中热力学意义的负面影响。

6 等位温面上的气压、风和位涡

位涡理论是建立在等熵面分析这个基础之上的。如前所述，等位温面分析就是等熵面分析，主要分析等位温面上的气压、风和位涡，并称为等熵位涡图，但要看懂这类图形，首先需要知道每一张等熵面分析图都是在某一特定位温数值(例如310或320 K等)的位温等值面上的分析。

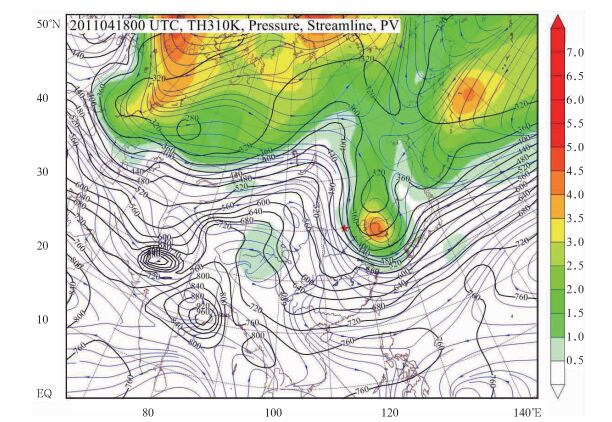
图 4为一张310 K等位温面的分析图，气压、风和位涡的分布分别用等压线、流线和位涡色标表示。下面以图 4为例介绍等熵面分析的基本原理和方法，以认识位涡分析的内在含义。

6.1 气压分析(等位温面的形状)

气压是用来表示等位温面的高度，即用等压线(图中为黑色实线)来表示等位温面的空间形状。等位温面和等压面不同，南北之间的高度差非常大，而等压面接近水平。图 4中最高处的气压为280 hPa，最低处的气压为840甚至960 hPa，所以等位温面不能看作准水平面，而是一个几乎斜穿整个对流层的斜面。等压线越密集，表示等位温面的坡度越大，并通常和锋区相配合。图 4中，40°~50°N间从日本以东的洋面到最西面的黑海，有一条弯曲的等压线密集带，它是极地气团和热带气团之间的过渡带。因为，对照图 1中310 K等位温线可知，50°N以北的等位温面位于极锋北面的极地气团中，温度分布比较均匀，所以等位温面相当平坦，等压线很稀疏；同样，40°N以南的等位温面位于极锋以南的热带气团中，等位温面也相当平坦，等压线稀疏。

由于310 K等位温面横穿过南北两个气团，所以，等位温面上的等压线密集带可以大致反映高空行星锋区及与锋相配合的蜿蜒曲折的高空西风急流。不同的等位温面与锋区和急流的相对位置是不同的，如图 1中310 K靠近极锋和极锋急流，320 K靠近高空副热带锋和副热带急流。等熵面分析中取哪个数值的位温，取决于所要表征的对象。通常选取锋区附近、靠近对流层顶的等位温面，使等位温面上的等压线密集带既可以综合显示气团、锋区、急流的位置，又可以显示对流层顶的位置。换言之，等位温面上的等压线密集带的北侧是极地气团和平流层大气，密集带以南是热带气团和对流层大气。这是阅读等位温面图的第一条原则。

6.2 流线分析

等位温面上的风，采用流线来分析，其目的是通过流线来判别空气垂直运动的方向。这是因为虽然流线只与风向有关，即流线只能代表水平运动的方向，但是，在绝热假定下位温不变，空气块一定沿着等熵面上的流线运动。如果沿流线方向等位温面高度升高(即气压降低)，则有向上的垂直运动；反之，如果沿流线方向等位温面高度降低(即气压升高)，则有向下的垂直运动。这是阅读等位温面图的第二条原则。如图 4中长江以南广大地区的偏北气流，从560 hPa流向760 hPa，说明该地区为下沉的偏北气流。

由于大尺度环流的垂直速度量级只有10^-2 m·s^-1(或10^-3 hPa·s^-1), 比水平风速小3个数量级，所以在常规天气图等压面图上只能分析水平运动，不能分析垂直运动。等位温面图的流线分析解决了这一难题，是天气分析的一个重大进步，也是等位温面分析的主要意义所在。

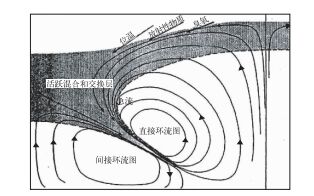
但是，这里要特别强调，等位温面上的流线分析只是定性的判别垂直运动的方向，它绝对不能被当作轨迹。在Danielsen^[4]的概念模型图 5中就是把下沉的流线当作轨迹，从而产生了所谓平流层干侵入的概念。例如上面提到的图 4中长江以南的偏北气流，不能理解为空气块从560 hPa下沉到760 hPa。因为根据垂直速度的量级，从560 hPa下沉到760 hPa高度下降200 hPa需要10⁵ s，即需要约28小时。在这么长的时间里，流线和等位温面都会发生很大的变化^[5]，而在非定常的情况下，流线不等同于轨迹；同时，对于这么长的时间，绝热假定也不再适用，位温不守恒。所以，等熵位涡理论所依据的轨迹，是对等位温面流线分析的误解。

6.3 位涡分析

等位温面上的位涡分析是试图利用位温和位涡这两个量的守恒性结合起来揭示大尺度环流变化机理而提出来的，并试图把等熵位涡图作为业务天气分析和预报的基本工具之一。从图 4可见，1.5 PVU以上的高位涡区都位于与极锋相配合的等压线密集带以北，所以等位温面上的高位涡区其内在的含义就是极地气团的控制区。等位温面上位涡分布形势，反映极地气团的活动情况。例如在50°E，有一股强极地气团正在南下。在120°E，则有一股极地气团已被切断到35°N较低的纬度。在垂直剖面图(图 1)上，我们可以清楚地看到这团被切断的冷气团的空间形状。

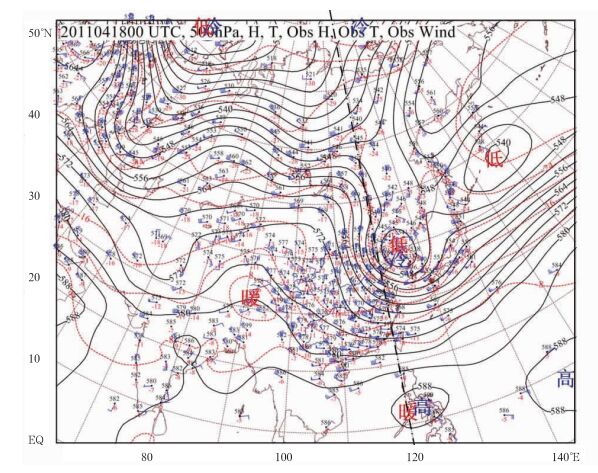
与图 6所给出的日常500 hPa等压面形势图相比，显然图 4的位涡分布所表示的极地气团活动形象更加突出、生动。这可能就是等熵位涡分析得到不少人重视的主要原因^[6]。等熵位涡图上极地气团形象突出的原因是，在热带气团控制区的位涡很小，都在1.0 PVU以下。所以，无论是用等值线还是用色标填充，在极锋以南几乎是一片空白，与极锋以北的高位涡形成非常鲜明的对比。

图 4和图 6的对比表明，在极锋以北，等熵位涡图上的高位涡中心大致和高空图上的涡和槽大致对应，这是因为极地气团上空等压面的高度迅速降低，在高空等压面上表现为低压和槽。但有的高位涡中心(如勘察加半岛以东)，和低涡位置有很大的偏离。其原因是静力稳定度对位涡的分布起了更大的作用。

总之，从等位温面上的气压、流线和位涡分析的内涵可见，等熵位涡图在原理上就是一种将热力和动力结合起来的分析方法，但它最突出的是极地气团的分布，即热力结构直接决定了等熵位涡的分布形势。锋区、急流、对流层顶都是极地气团前沿所伴随的现象，在等熵位涡图上也同时被反映出来。这就是等熵位涡图的天气学意义所在。但是必须懂得，等熵位涡图虽然是气团、锋面、急流、对流层顶的综合反映，但它是一种间接的分析方法，不能代替锋面、急流、对流层顶的直接分析。此外等熵位涡图仅仅给出了极地气团活动的实况，并未给出其动力学机理，因此等压面图结合准地转动力学理论仍是环流形势预报的主要分析工具。

7 等熵位涡分析中应避免的几点误解

等熵面分析是由Rossby在20世纪初引入气团分析和天气分析的。50年代，谢义炳先生回国后大力倡导等熵面分析，并把它作为天气分析的基本方法之一编入天气学教科书。但是，在该节的最后部分专门撰写了一小节“等熵面分析的缺点和限度”，谢义炳指出，等熵面分析是“颇不准确”，“最好不用等熵面分析来判断轨迹”^[3]。为此本节将根据近年来天气分析和预报的现状，提出在进行等熵位涡分析时需要注意避免的几点错误认识。前文所得到的两个基本点是本节讨论的基础：(1) 位涡是由涡度和静力稳定度(即位温垂直梯度)两部分组成，平流层和对流层顶及高空锋区附近的高位涡主要因为温度垂直梯度很小，和涡度的大小无明显的联系；(2) 等熵面就是等位温面，在等熵位涡分析中使用的等位温面都位于和锋区密切相关的对流层顶附近。

需要注意如下几点：

(1) 等位温面不是准水平面，它是与从对流层顶附近到对流层低层多个等压面相交的倾斜的面。

(2) 等位温面上的流线，不是某一个等压面上的水平环流，而是空间的不同高度的水平流线，但可以推测垂直运动的方向(根据该处等位温面的坡度决定)。但是切不可把等位温面上的流线看成是轨迹。

(3) 等位温面上的等压线不同于等压面上的等高线，虽然粗略的印象两者似乎很像。前者仅仅用于表示等位温面的高度，而后者虽然也表示等压面的高度，但其物理内涵是用来表示气压的水平分布。因此，在等压面上可以按地转风关系根据等高线判别风向和风速；但在等位温面上，等压线的分布和风场之间不存在地转风关系。如图 4看起来很像一张对流层上部的高空图，但仔细观察可以发现许多不符合地转风关系的地方，特别是在30°N以南纬度较低的广大地区，气压高的地方并不和反气旋环流相对应，有的地方(如印度北部)甚至相反，为气旋环流。高纬度地区也有同样的情况，如勘察加半岛附近。

比较迷惑人的是，中纬度等压线密集带的流线和等压线基本平行，而且风速也相当大(图中未给出)。其原因是等压线的密集带表示等位温面坡度很陡，所以它和锋区及高空急流相配合。

如果将等位温面上的等压线分析和等压面图上的等温线(见附录2中的500 hPa图)相比较，将会发现两者很相似。不难理解，这是等位温面的基本性质决定的，这里不再做更多的解释。

(4) 等熵位涡分析可用于中高纬度和极区的天气分析，特别是冬季；但不适用于分析中低纬度的天气，特别是夏季的中低纬度，因为只有在极地气团的对流层顶及其上方才有1.5 PVU以上的高位涡。如图 4为春季4月中旬的位涡分析，只有北京附近一个切断的极地气团才有一个高位涡中心，其他中低纬度地区的位涡都非常小。在夏季，极地气团控制的范围将比图 4更加北缩，对50°N以南的地区，基本上没有分析价值(见附录3)。夏季中尺度强降水潜热反馈产生的低空大于1.5 PVU的高位涡是实际大气中位涡非守恒性的结果，与等熵位涡的理念恰恰相反。有关研究结果可参阅相关文献，这里不作详细介绍^[7]。

附录 附录1：相关基本概念的解释 1.1 熵

熵是一个很抽象的物理量。由全国科学技术名词审定委员会审定的熵的定义为：熵是表示物质系统状态的一个物理量(记为S)，它表示该状态可能出现的程度。在热力学中，是用以说明热力学过程不可逆性的一个比较抽象的物理量。孤立体系中实际发生的过程必然要使它的熵增加。

这个定义的表述很抽象，不易理解。熵最初来自物理学的热力学，指热能除以温度所得的商，标志热量转化为功的程度，并由此得名熵。更广义一点，熵在科学技术上用来描述、表征体系统不确定程度或混乱程度，它在不同的学科中，如控制论、概率论、数论、天体物理、生命科学等领域，都各有其具体的定义。如传播学中表示一种情境的不确定性和无组织性。甚至在社会科学也可用熵以借喻人类社会某些状态的程度。熵的应用价值可能主要在于所谓熵增加原理。

大气的可逆绝热过程中熵与位温的对数成线性正比关系，位温和熵在可逆绝热过程中都是守恒的。

1.2 流线和轨迹

某一瞬时, 流体速度场中与各点的风矢量相切的曲线称为流线。流线有以下特点：(1) 流线簇的疏密程度反映了该时刻流场中各点速度的变化；流线越密，速度越大。(2) 当为非恒定流时，流线的形状随时间改变；对于恒定流，流线的形状和位置不随时间而变化。(3) 恒定流时，流线和迹线重合。(4) 一般情况下，流线不能相交，不能折转，只能是一条光滑曲线。

轨迹为某一运动质点在某一时间段内所经历的空间位置所构成的曲线。轨迹线有以下特点：(1) 轨迹线上的每一点的坐标，表示该质点在不同时刻的位置；(2) 轨迹线上每一点的切线方向，表示该质点在不同时刻的运动方向。

流线和轨迹最根本的区别在于，流线是瞬时的，是对流场的描述；轨迹是对流体质点在某一时间段内运动状态的描述。在流体力学中，前者为欧拉分析方法，后者为拉格朗日分析方法。

1.3 连续和不连续

连续和不连续是数学分析中最基本的概念之一。

其文字表述为：对于一定区间上的任意一点，其本身有定义，且其左极限与右极限相等且均存在，则称函数在这一区间上是连续的。

其数学表述为：设函数y=f(x)在点x₀的某个邻域内有定义。如果当自变量Δx趋向于0时, 相应的函数改变量Δy也趋向于0，则称函数y=f(x)在点x₀处连续。只有连续的函数才是可导的(不连续的函数是不可导的，或它的导数是无限大)。

以大气的温度为例，在空间任意一点(x, y, z)都有一个确定的温度数值，所以温度分布函数T=f(x, y, z)是连续的。即使是位于锋面上下界上的任意一点都只有一个温度数值，无论是从冷气团向暖气团方向趋近，还是相反所从暖气团向冷气团方向趋近，都只有一个温度数值。所以，温度分布函数是连续的，是可导的，即可计算出温度的水平梯度，一侧的导数是锋区内的温度梯度，另一侧为气团内的温度梯度。

同样，对流层顶上的任意一点也都只有一个温度数值，无论是从平流层向对流层方向向下趋近，还是相反从对流层向平流层方向向上趋近，都只有一个温度数值。但是对流层顶上任意一点的温度垂直梯度都有两个值。从下向上是对流层的垂直梯度，约6.5 ℃·km^-1；从上向下是平流层的垂直梯度，小于2 ℃·km^-1。

连续这个概念和极限等其他数学分析和微积分的基础知识有密切联系，不一一详述。

1.4 物质面

物质面是指三维流体中由无数个固定质点所组成的面。这是一种理论上想象的面，因为实际上根本无法追踪流体中无数个质点在同一瞬间所处的位置。但是根据某些流体的保守特性(如位温、位涡)来追踪流体质点。例如可以把等位温面当作物质面，因为在绝热过程中位温具有守恒性。但是绝热状态是一种理想状态，实际大气是非绝热的，只有在一个很短的时间内(如数小时)才可以忽略非绝热作用，近似地认为是绝热的。

附录2：

500和700 hPa等压面流线和等温线，供读者用于与等位温面和等压线分布(正文图 4)对比和思考的参考材料。所给图形为2011年4月18日00 UTC。

附录3：

2011年春季4月18日320 K及盛夏7月20日310和320 K等熵面位涡分析，作为参考资料供读者用于与春、夏等熵位涡分析(正文图 4)进行对比和思考。