2. 中国科学院海洋研究所海洋环流与波动重点实验室,青岛 266071;
3. 中国科学院大气物理研究所云降水物理和强风暴实验室,北京 100029;
4. 中国科学院研究生院,北京 100049
2. Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071;
3. Laboratory of Cloud-Precipitation Physics and Severe Storms, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
4. Graduate University of Chinese Academy of Sciences, Beijing 100049
气象预报是经济、社会发展需要和气象科学技术发展的共同产物。从气象预报的诞生到其获得长足进步的今天,人类经历了漫长而艰苦的探索过程。那么在近代甚至千年以前,是怎样进行气象预报的,其间有多少里程碑式的飞跃?随着长期的经验积累以及科技的飞速发展,人们在不断完善大气科学理论体系的同时,气象预报也面临更多新的问题和更大的挑战。今天,广大的社会公众已经习惯于每天通过各种方式获取气象信息,气象预报节目已经成为很多人的生活需求。不过在一定程度上,对于公众来说,气象预报还是带有一种神秘的色彩。
本文首先对气象预报的相关基础知识作简要说明;其次回顾气象预报的发展历史,并介绍当前的气象业务水平及相关研究的进展;然后从初始误差、模式误差、天气与气候的可预报性三个角度分析造成气象预报不准确的原因,并介绍相关的研究领域及研究动态;最后通过阐述集合预报的基本工作原理,讨论如何利用气象预报所提供的信息。
(1) 天气和气候
对于“气象”、“天气”和“气候”的具体含义,可能有人会将这三者混为一谈。所谓气象,一般指大气中各种物理现象(如干湿、晴阴、风雨、冷暖等)及其变化的总称[1]。众所周知,大气是不断变化着的,它在短时间内可以表现出各种状态和过程,而在长时期内又呈现出这些状态和过程出现的规律。于是,人们将这种短时间内影响人类活动的大气状况称为天气,而把某一地区长时期气象要素(温度、降水、风、日照等)的统计状况(平均值、极值、概率等)和天气过程的综合表现定义为气候。比如,谈到我国气候,人们常说:昆明四季如春;长江流域大部分地区四季分明,春、秋温和,夏季炎热,冬季寒冷等等。
(2) 什么是气象预报
通常人们所说的气象预报,用科学的语言是指,把大气作为研究的客体,对某区域未来一定时段内的大气运动状况做出预报。一般地,天气预报和气候预测同属于气象预报的范畴。天气预报按其时效的长短主要包括以下三种:0~12小时的为短时预报;1~2天左右的为短期天气预报;3~15天左右的为中期天气预报(通常在广播与电视里播放的主要是短期与中期天气预报)。月以上到1年的曾被称为长期天气预报。随着混沌现象的揭示,天气预报时效有一定范围,月以上只能做气候预测,所以现在改称短期气候预测。
气候预测是指,对未来某时段(如季节、年际或更长时段)气候发展的可能趋势的描述。气候预测与天气预报的区别在于,后者往往是对短期内某天某一时刻各气象要素的具体状况的预报,而前者则是对某气象要素的统计量(如月平均或季平均气温、降水等)及天气过程的综合情况的长期预测。由于气候有各种时间尺度的变化,也分为月、季度、年际、年代际等。
1 气象预报是怎样做出的?自古以来人类就幻想能控制和驾驭天气和气候。几千年来,人们通过用目力的方式观测天象、物象的变化,编成气象谚语,据以预测未来的天气、气候。那时的气象预报也常和神秘的宗教有关,往往为巫师和祭司所操纵。从17世纪中叶开始,随着水银气压计的发明,科学气象预报的时代终于拉开了序幕,而气象预报真正成为一门科学大约诞生在一个半世纪之前。100多年来,气象科学的先辈们取得了许多光辉的研究成果。气象工作者也已经能够较为准确地预报天气。纵观气象预报发展的历史,大体上可分为4个阶段:(1) 民间技艺,(2) 单站预报,(3) 天气图预报,(4) 数值预报。
1.1 民间技艺我国有关气象知识的记载,可追溯到公元前14世纪的殷代, 如在甲骨卜辞中就发现了天气预报的相关记录(图 1)。图中文字翻译后的意思是:丙子这天举行“立中”仪式,没有风,晴天。不少学者认为“立中”是立表测景,并观风向。在国外[1],从考古发掘出的巴比伦兴盛时期(公元前3000至前300年)的黏土片上发现有许多气象谚语。如有“月有黑晕,本月阴雨”、“云变黑,有来风”等。此后,古希腊学者亚里斯多德将之前的各种气象知识作了系统的总结,大约在公元前340年完成了世界上最早的气象专著——《气象汇论》。

|
图 1 关于中国古代气象预报的记载(摘自《英国所藏甲骨集》) Fig. 1 The historical record on meteorological forecast in China (collection of oraclebones in Britain) |
气象谚语是无数先人智慧的结晶,是根据长期生活实践中发现的自然规律不断总结出来的,其中不少富含深刻的科学道理,因此在一定程度上可预测未来天气、气候情况。此外,气象谚语语言简练、通俗易懂,深受广大农民喜爱,并不断丰富、世代流传。至今仍有许多农村地区的居民愿意相信民间的气象谚语。虽然老百姓未必熟谙其中的科学道理,但据此预测天气,也取得了一定的成功。不过,受当时生产力水平的限制,人们对于真实大气状态和运动的认识是零碎、片面的,甚至是错误的,经过时间检验的气象谚语也是具有明显的地域性和时间性的。
1.2 单站预报16—18世纪是科学革命的时代。1597年,意大利物理、天文学家伽利略发明空气温度表;1643年,E.托里拆利发明气压表。这些仪器以及其他观测仪器的陆续发明,使气压、气温、风速等气象要素实现了定量观测,为逐步组建比较完善的地面气象观测网和近地面层气象要素的日常系统观测提供了物质基础,是气象预报发展史中一次里程碑式的飞跃。
另一方面,传统气象学理论的建立也使气象预报水平上升到新的高度。气象学是一门拥有众多分支的古老学科,以气候学、天气学、动力气象学和大气物理学为主要研究内容。在气象学的理论基础上,随着此后各种科学技术的应用,逐步发展成为一门研究领域更为广泛的综合性学科——大气科学(又称气象科学)。在这一时期[1],信风、大气环流理论的创立以及动力气象学理论基础的形成对大气科学的发展产生了重要的影响。1735年,英国气象学家哈德莱在《关于信风之起因》一文中,首次考虑到地球自转的因素,定性解释了东北信风(北半球)、东南信风(南半球)以及中纬度西风带产生的原因,并创立了大气经圈环流的理论。另外,伴随着经典力学三大定律的发现和微积分学的创立、以及流体力学在气象科学上的应用,动力气象学理论基础初步形成。1755年,在提出反映质量守恒的连续方程后,瑞士数学家、物理学家欧拉进一步提出理想流体动力学方程组,为大气运动方程组的形成奠定了基础。
由于通讯条件的限制,当时人们主要采用分析本站气象要素(地面气压和地面风为主,温度、湿度为辅)时间演变图的方式进行预报(因为天气变化和气压升降关系最为密切,近代许多便携式“晴雨表”就是根据气压计的原理而设计的)。与单纯用气象谚语预报相比,单站预报拥有更多的科学依据,而其基本过程是以气候规律为背景,单站资料为依据,群众经验为线索(图 2)。不过,人们在本站所能观测的天气,和造成天气变化的天气系统相比,只是很小很小的区域,并且天气系统还是不断移动和发展的。从这个角度讲,单站预报天气就犹如“坐井观天”,人们用这种方法来做预报,准确率依然不高。

|
图 2 单站预报的基本步骤 Fig. 2 The main steps of single station forecast |
大气是一个在全球范围内不断发展变化的系统,要掌握大气变化的规律,需要从地面到高空获取大量的气象观测数据和信息。因此,天气图的诞生在大气科学史上具有划时代的意义,同时也是气象预报发展历史中的又一次飞跃。它把一个地点与另一个地点的气象要素有机的联系起来,使人们从“坐井观天”,开始“放眼世界”,并逐渐发展成为气象部门分析和预报天气的重要工具。
1.3.1 一次战争推动天气图预报发展19世纪中叶,英、法和俄国之间爆发的克里米亚战争被称为世界史上的第一次现代化战争。在这次战争中,铁甲船和电报首次在战争中被使用,火车首次被用来补给前线。在气象预报发展史上,这次战争也尤其值得关注。1854年11月14日,风暴的突然降临重创了正在黑海激战的英法联军舰队。通过分析1854年11月12—16日5天的气象资料,巴黎天文台台长勒弗里埃认为,组建气象台站网,用电报迅速收集各站点的气象观测资料,绘制出天气图进行天气预报,损失是可以避免的。根据勒弗里埃的建议,天气图预报的方法在欧洲开始得到推广,并很快普及到世界各地。
图 3是天气分析中常见的地面天气图。图中用各种符号标注的(如三角或半圆)就是通常所说的天气系统。那么,何谓天气系统?100多年前的气象学家给出的解释是“天气系统是各种冷暖气团之间相互作用的系统”,但这仅仅是一个粗略的描述。20世纪20至30年代,以V. Bjerknes(皮叶克尼斯)为首的挪威学派根据地面资料分析提出了气旋、锋面和气团学说,在天气分析和天气预报方法上做出了卓越的贡献。其中,他们将天气系统具体化为锋面、气旋、反气旋等具有一定空间结构和大气运动特征的系统后,使得利用天气图预报天气变成了“看图识字”。天气系统的变化有了空间连续演变的概念,这是天气图预报取得成功的关键。
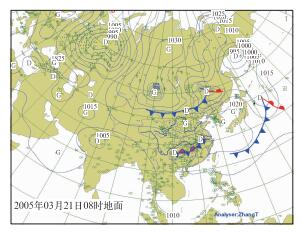
|
图 3 2005年3月21日08时地面天气图(欧亚大陆) Fig. 3 The surface weather chart (Eurasia) at 0800 UTC March 21, 2008 http://www.nmc.gov.cn/publish/observations/weatherchart.htm |
一般来说,天气图分为地面天气图、高空天气图、辅助天气图三大类。天气图的绘制是进行天气图预报的前提。在天气图上,预报员根据各个观测站点的各要素数值,分析出各要素等值线,定出天气系统。其后的过程分两步[1]:
(1) 进行天气形势预报。根据天气过程的发展在一定时间间隔内具有连续性的特点,顺时外推来确定天气系统未来的位置和强度。先从地面图上了解上游大范围天气形势,再结合高空天气图,同一时刻上、下层次配合,了解天气系统的三维空间结构,同时还需判断有无新的天气系统产生。运用天气学和动力气象学的基本原理,根据相关天气系统移动或强度变化的经验预报规则,做出未来天气形势的预报。
(2) 天气形势预报做出后,根据天气形势和当前本站周围气象要素的实际数据再做出具体天气预报。在一定的天气系统控制下,会有一定的天气配合,这是天气形势预报具体天气的依据。不过,天气形势和天气并不是一一对应的。因此,从形势预报过渡到具体的天气预报,主要依靠预报员的分析和判断。预报员在长期预报实践中,将本地区典型的天气事件编成档案并分成类型,根据多年的预报经验并结合档案中最类似的历史个例或天气型,最后做出天气预报。
事实上,这种“外推加经验”的预报方法,在天气形势变化不太大的情况下比较有效,但在发生突然变化时,预报员往往猝不及防而报错。由于制约天气变化的因素很多,很复杂,即使天气形势预报正确,具体到某一地区的天气预报也是十分困难的。
1.3.3 气候预测以统计法为主如同天气预报中的天气系统,气候预测中也有相应的气候系统。不同的是, 气候系统是大气圈与岩石圈、水圈、冰雪圈和生物圈相互作用的系统。这些各不相同的“圈”之间的相互作用可以形成月、季度、年际、年代际以及100年以上时间尺度的气候变化,而把这些气候变化的特征作为研究对象用统计方法进行预测已有近百年的历史。
从19世纪末到20世纪30年代,人们开始考虑各种物理因子如海温、极冰、太阳活动的变化,用简单的统计方法寻找不同要素之间的关系进行气候预测。如果从统计结果中发现某两个先后出现的事件之间的相关性很高,于是就可用前期事件预测后期事件的出现。这一时期的成就是以英国气象学家G. Walker(沃克)关于“世界天气”的研究为代表的。他根据局地气候异常对大气环流变化的依赖关系提出了世界上三大涛动的概念,即北大西洋涛动、北太平洋涛动和南方涛动。这些研究在气候预测研究中具有重要的意义[2]。20世纪60年代,数理统计学的发展为气候预测的进步提供了必要条件。许多学者认为:气候系统变化的规律都隐藏在过去的气候资料序列中;运用各种统计方法发现气候资料中的规律,进而可以预测未来的气候情况。多年的实践证明,用统计学方法做短期气候预测是有一定效果的。不过,统计方法的缺陷在于容易忽略事件背后的某些重要因素而只分析其中部分因子的影响。由此造成用该方法做历史回报拟合率很高,但做实际预测时,准确率常常较低。
1.4 数值预报马克思曾这样认为,一门科学只有在成功地运用数学时,才能达到真正成熟的地步。气象预报的发展也不例外。尽管大气运动是很复杂的,但大气运动始终要遵循某些基本的物理定律,这些物理定律的数学表达式构成了研究大气运动规律的基本方程组。根据V. Bjerknes提出的观点:在一定的初值和边值条件下,通过求解描述大气运动规律的数值模式,可以计算出未来一定时段后的大气状态(图 4)。

|
图 4 数值预报的基本流程 Fig. 4 The basic procedure of numerical forecasting |
图 4中的“初值和边值”是指预报初始时刻对大气状态的一种定量描述,也是进行数值预报的前提。初始条件的生成是以气象观测提供的数据和信息为基础的,而气象观测是对地球大气圈及其密切相关的水圈、冰雪圈、岩石圈、生物圈的物理、化学、生物特征及其变化过程进行系统、连续的观察和测定,并对获得的记录、数据进行整理的过程[3](图 5)。从1928年前苏联莫尔恰诺夫发明无线电探空仪,到探空仪的普遍应用,人们逐渐获得高空气象资料,并对大气的垂直结构有了初步的了解。随后大气遥感技术的发展也极大地推动了气象观测的发展,其中突出的标志是气象雷达与气象卫星的应用:1941年,出现了专门的云雨探测雷达;1960年,美国发射了第一颗气象卫星泰罗斯-1号。迄今,美、欧、前苏联、日本、中国和印度共发射了100多颗气象卫星以获取全球范围的气象资料。随着技术的进步和投入的增加,雷达、气象卫星与自动观测站正逐步成为气象预报以及大气科学研究的强有力的工具,为加速气象事业的整体发展奠定了科技基础。
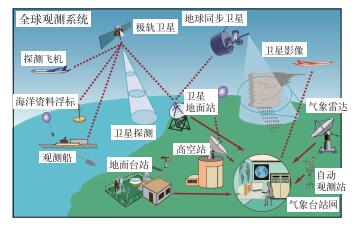
|
图 5 全球观测系统 Fig. 5 The global observing system http://www.wmo.ch/pages/about/purposes_en.html |
数值预报的理论建立是以V. Bjerknes的工作为基础的。他运用牛顿经典力学、流体力学和热力学等物理学理论,制定了研究天气预报的计划,并给出了描写旋转地球大气运动方程组。该方程组是一个非线性偏微分方程组,其变量共有7个:u(纬向风速),v(经向风速),w(垂直风速),T(温度),p(气压),ρ(密度)和q(比湿)。目前人类尚不能给出该方程组的精确解,只能利用数值计算方法将该偏微分方程组离散为计算机可以求解的差分方程组,求其数值解,而围绕这组差分方程组建立起的各种数学模型就是通常所说的数值预报模式(此后简称模式)。在数值计算过程中,模式的空间水平网格距一般在几十千米左右(图 6),垂直层数分布不均(低层密集,高层稀疏);在每个格点都有7个变量描述大气状态,而格点数往往超过1000万个!数值计算的维数是格点数的7倍,因此,求解差分方程组的计算量是惊人的。
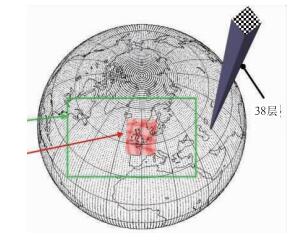
|
图 6 数值预报模式网格 Fig. 6 The grid of numerical forecast model http://plus.maths.org/latestnews/sep-dec04/nwp/index.html |
20世纪初期,英国数学家L. F. Richardson利用数值方法尝试计算天气的变化。在那次计算中,几个人用手摇计算机“摇”了几个月,才求出欧洲地区6个小时天气变化的结果。由于当时缺乏必要的资料和计算机条件,所采用的数值计算方案也存在重大缺陷,试验未能取得成功。后来人们认识到Richardson的失败,主要在于他所得到的大气运动基本方程组的解包含了在计算过程中容易被扩大的快速波(如重力波和声波),以至于掩盖了气象上有意义的扰动。1948年, 美国气象学家Jule G. Charney提出了滤波理论,证明了采用静力平衡和地转平衡近似可以消除重力波和声波。1950年,在世界上第一台电子计算机(ENIAC)诞生5年之后,美国数学家J. von Neuman和Charney等根据简化后的方程(图 7,因为ζφ和Vφ之间满足地转关系,所以式中实际只有一个自由变量)设计的正压(一层)滤波模式[4],首次用电子计算机成功地预报了未来24小时北美地区高空500 hPa的位势高度场。到20世纪70年代,计算机的运算速度已达每秒钟1000万次以上,原来需要1天时间做一次高空流的24小时预报,只要1分钟就可以了。截止2010年5月31日,世界上运行最快的超级计算机,Jaguar-ORNL(美国能源部橡树岭国家实验室)的计算速度每秒达1.75千万亿次。随着电子计算机计算速度与存储能力的提高,数值预报方法在气象预报中发挥着越来越重要的作用。

|
图 7 大气运动基本方程组与正压准地转涡度方程 Fig. 7 The basic system of equations of atmospheric motion and the quasi-geostrophic vorticity equation |
数值预报试验获得成功后,各国都力争早日在业务预报上得到应用。在其后的半个世纪中,数值预报技术不断发展,预报能力持续增强,已逐步成为业务预报的主要手段。当今世界上最先进的两大业务预报系统分别是欧洲中期预报中心(ECMWF)的IFS(Integrated Forecast System)和美国环境预测中心(NCEP)的GFS(Global Forecast System),二者都具备对未来7~9天内全球天气变化概貌做出有效预报的能力。图 8给出了ECMWF对500 hPa重力位势场预报时效性的评估结果(1980—2009年)。由图可见,目前数值天气预报的预报时效已超过了一周。
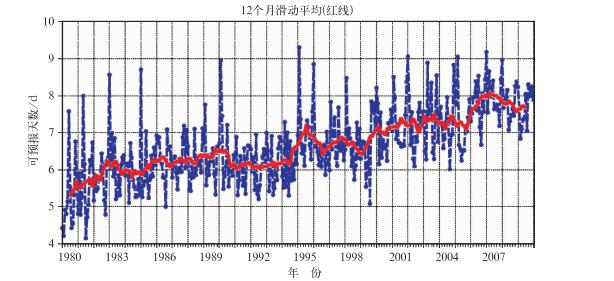
|
图 8 ECMWF对欧洲500 hPa位势场预报时效性的评分 Fig. 8 The ECMWF forecast verification 1200 UTC for 500 hPa geopotential in Europe http://www.ecmwf.int/products/forecasts/d/charts/medium/verification/ |
20世纪80年代以来,由于气候系统的自然振荡和人类活动所引起的全球气候变暖造成了严重的气候灾害,人们越来越认识到气候变化在许多方面深刻地影响着人类的生存和社会的发展。为了应对气候变化的威胁,发展出客观的基于基本物理动力过程的气候预测方法就显得尤为重要。随着人类对气候系统的认识不断增加以及数值天气预报技术的不断成熟,人们在天气预报模式的基础上研发了气候模式并开始运用气候模式进行数值气候预测。如今,气象科学家们对于某些季节到年际气候系统的变化已具有一定的预测技巧。以下将以ENSO现象为例,简要介绍对其数值预测研究的发展情况。
ENSO(厄尔尼诺-南方涛动,El Nino-Southern Oscillation)循环是全球年际气候变化的重要信号。早期的观测发现,南方涛动(热带太平洋东部与西部的气压值呈“跷跷板”式的振荡)与赤道中、东太平洋海温冷暖交替变化的异常表现之间存在密切的联系。这种全球尺度的气候振荡被称为ENSO循环,而厄尔尼诺(El Nino)和拉尼娜分别(La Nina)被称为ENSO循环的暖事件和冷事件。1986年,Cane和Zebiak设计了一个中等复杂程度的海气耦合模式(简称ZC模式),首次成功预报了1986/1987、1991/1992年的El Nino事件。这两次预测的成功,给气象界带来极大的鼓舞。从此,国内外许多学者尝试使用各种复杂程度的气候模式预测ENSO事件。经过二十多年的发展,国际上关于ENSO的理论和数值模拟研究已取得了很大的进步。在近期的研究中,Luo等[5]运用海气耦合全球环流模式进行提前2年的回报试验,显示出较高的预报技巧。
尽管ENSO预测是目前短期气候预测中最为成功的,但当前的气候模式对ENSO的预报技巧具有明显的季节依赖性,同时仍不能精确预报出ENSO事件的强度、空间型式以及ENSO循环过程中SSTA的发展细节等。图 9给出了目前国际上的14个动力预报模式和7个统计预报模式在2009年2月对Nino 3.4区(5°S~5°N,120°~170°W)平均SSTA(海表温度异常, Sea Surface Temperature Anomaly)预报的结果。可见,对于不同的模式,其预报结果之间具有显著的差异,而这也说明,单一模式所提供的确定性预报存在着较大的不确定性。
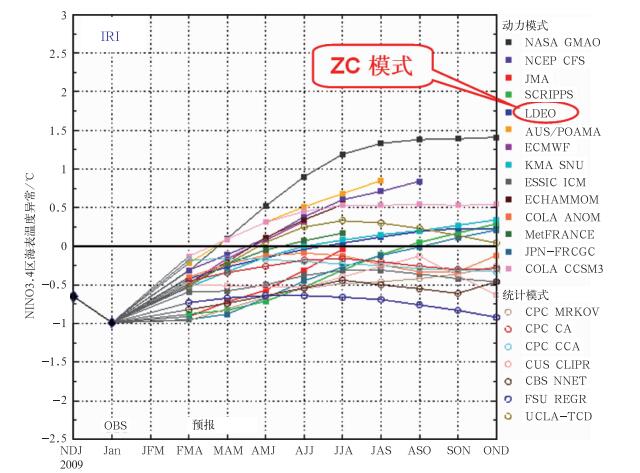
|
图 9 各模式在2009年2月对Nino 3.4区平均SSTA的预报 Fig. 9 The model forecasts for mean SSTA in the Nino 3.4 region from February 2009 http://iri.columbia.edu/climate/ENSO/currentinfo/SST_table.html |
气象预报是一项浩大的系统工程。它是以大气科学理论为基础,以各种大气探测手段为前提,以数值预报为核心,依靠预报员的综合判断分析最终形成的。随着科学技术的不断发展,现代气象预报越来越依靠数值预报的结果,而数值预报水平的高低也已成为一个国家气象现代化水平的重要标志。因此,数值预报结果的不确定性在很大程度上造成了气象预报不准。然而,又是什么原因造成数值预报结果不准?以下将从三个方面(初始误差,模式误差,天气与气候的可预报性)来讨论这个问题。
2.1 初始误差对于数值预报问题,模式初值的质量无疑是至关重要的。由于客观存在的因素,模式的初始条件只是大气的真实状态的一种近似,所以初始误差是永远存在的,它主要包括:
(1) 观测过程中所产生的误差,即观测误差,是完全无法避免的。它主要取决于观测的技术水平、观测方法的正确性,以及所使用仪器的精密程度和客观环境的影响等,比如自动气象站的观测误差(表 1)。同样,利用气象卫星观测时,大气对可见光的散射使得探测出的云顶和地面反照率资料有偏差,由直接观测的红外辐射资料反演云顶和地面温度的过程中也存在误差。不仅如此,利用气象雷达观测时,根据雷达回波强度和降水量的经验关系推测降水量会有误差,特别是远距离探测,误差更大。
|
|
表 1 自动气象站的观测误差 Table 1 Observational errors in automatic weather station http://www.wmo.int/pages/prog/www/IMOP/publications/CIMO-Guide/CIMO_Guide-7th_Edition-2008.html |
这些事实说明在预报过程中,预报员所依据的初始资料是存在一定误差的,甚至是错误的。因此,如何进一步地改善当前观测资料的质量是未来气象预报发展的重要环节之一。相应的,通过持续的技术开发,利用多种手段、多种技术,实现高精度、全方位的定量观测已成为现代气象观测系统发展趋势的主要特征之一[6]。
(2) 常规观测站覆盖不完全。在一些偏远的地区以及大洋区域,观测资料的数量和质量是十分有限的,而在这些区域长时间的增加观测要耗费大量的财力和物力。虽然气象卫星、雷达等遥感技术的应用可以在一定程度上改善这些区域观测资料匮乏的状况,但其数据的质量及观测的强度还不足以应对当前对高影响天气做出实时、精确预报的要求。
针对这一问题,科学家们提出一种被称为目标观测的方法[7]。其基本思想是:为最大限度改善在某一时刻(验证时刻)所关心区域(验证区域)的预报效果,在目标观测时刻将有限的观测资源增加至敏感区(图 10)。所谓敏感区,是指这样的区域,其中的初始误差增长会造成预报准确度的最快下降,而气象工作者则需要在决策时刻根据初始条件及模式动力发展情况将其确定下来。因此,如何寻找敏感区是目标观测的关键所在。目前,许多学者已提出各种确定敏感区的方法,如奇异向量、集合转换卡尔曼滤波和条件非线性最优扰动等[8]。从2003年开始,世界气象组织正在开展一项为期10年的全球观测系统研究和可预报性试验(THORPEX)的计划,其目的在于加速改进灾害性天气的1~3天动力预报和3~15天的概率预报,而这必将进一步促进对目标观测研究的发展。
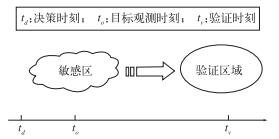
|
图 10 目标观测示意图 Fig. 10 Schematic of adaptive observations |
(3) 各种观测数据的类型及其在空间和时间上的分布往往与模式的配置是不一致的。常规气象观测网的空间分布是不均匀的,在早期的业务预报中,气象工作者通常使用手工的方法将可用的常规资料插值到模式网格点上。另一方面,非常规气象观测系统实施观测的时间可能与数值预报的初始时刻不同,且还要考虑到观测数据的类型与模式变量的一致性。因此,如何处理通过各种观测手段得到的数据,使其能尽量精确客观地描述当前的大气状态,就成为提高数值预报准确性的关键环节之一。近年来,业务数值天气预报中心常使用一种观测资料和短期预报结果的统计结合的方法来产生模式的初始条件,这种方法就是人们越来越熟悉的资料同化[9]。目前,业务预报中,三维、四维变分(3D-Var、4D-Var)方法也被有效应用于同化卫星、雷达等非常规资料。其基本工作流程是:利用之前时刻对当前时刻预报的模式状态以及对模式状态误差的估计,然后根据观测数据对模式状态进行重新分析,接着再进行预报,进而完成预报、分析、再预报的循环过程。近期的许多研究结果表明,集合卡尔曼滤波(EnKF)方法较3D-Var、4D-Var方法具有一定的优势,有可能成为新一代的资料同化技术。目前已有一些业务中心开始将其进行准业务运行,但是不可避免地存在一些棘手的问题,比如集合成员的选取、滤波发散等。针对这些问题,气象学者还需做大量艰苦而细致的工作。
2.2 模式误差模式误差大体可分为三类:
(1) 模式对物理、动力过程描述不准确而产生的误差。例如,大气运动中的湍流过程,小尺度系统的生消机制,在模式中是很难准确描述的。由于大气是一种具有连续运动尺度谱的连续介质,不管模式的分辨率如何高,总有一些小于网格距尺度的运动无法在模式中确切地反映出来(图 11),这种运动过程称为次网格过程(对流、凝结和辐射过程都包含有次网格过程)。一般在模式中,采用了“参数化”的方法来考虑这些过程的影响,即用一种平均过程将次网格的动力和物理过程对网格以上尺度的平均影响表示出来。这种描述与真实次网格过程之间的偏差就成为模式误差的来源之一。

|
图 11 NCEP集合系统中,模式网格内的不同现象 (网格左侧的南北走向的白色区域是卫星遥感的落基山脉山脊上的积雪分布,网格右侧的区域为丹佛市) Fig. 11 A lot of happenings in one grid box of NCEP ensemble system (the north-to-south white area in the left side of the grid box is the snow cover in Rocky Mountains obtained by satellite remote sensing, and the right side of the grid box is the location of Denver) (Source: accessmaps.com) |
(2) 模式“漏掉”某些物理、动力过程而产生的误差。由于人类认识大气运动规律的局限性,一些实际存在的物理、动力过程尚未被人类发现和认识,因而在模式中未能描述。
(3) 数值求解模式不准确造成的计算误差。计算误差来自于模式离散化时离散、谱截断产生的截断误差与计算机的舍入误差。我们知道,求解大气运动方程组需将连续的偏微分方程离散为差分方程。考虑任意函数f(x),将其傅里叶展开,
| $f(x) = \frac{1}{2}{a_0} + \sum\limits_{k = 1}^\infty {({a_k}\cos kx + {b_k}\sin kx)} $ |
取前n项
| ${f_n}(x) = \frac{1}{2}{a_0} + \sum\limits_{k = 1}^\infty {({a_k}\cos kx + {b_k}\sin kx)} $ |
即产生截断误差
| $|f(x) - {f_n}(x)| \le \frac{{\ln (n + \frac{1}{2})}}{{n + \frac{1}{2}}}\max |f'(x)|$ |
舍入误差,指在计算机进行计算时,由于精度有限(16位或32位),原始数据及计算过程中产生的数据的位数超过规定位数进行舍入所产生的误差。Robert在一次北美地区短期预报误差成因问题的分析中发现,预报误差中有38%是由水平截断误差引起的,而这甚至高于次网格物理过程参数化所引起的34%的比例[10]。
最近十多年来,大量的大气科学观测试验加深了人们对大气物理机制的认识,模式物理过程参数化方案也得到进一步的改进,高速度、大容量的巨型计算机及其并行技术的应用使得模式的分辨率和运行模式的计算效率不断提高。目前,全球中期数值预报模式的网格距从早期的几百千米减至几十千米,而区域模式已达到5 km左右,提高了模式对中小尺度天气活动和外强迫(如湍流扩散、辐射传输等)的分辨率以及数值模拟的准确性[11]。不过,地球大气及其与各圈层相互作用的复杂性是超乎人们想象的,模式对于这其中的各种物理过程是难以进行完美描述的。如何让“模式大气”更接近真实大气,仍是一项长远而艰巨的任务。
2.3 天气与气候的可预报性以上讨论了数值预报结果的误差源于初始条件和模式的不准确性。由此出发,人们很容易地想到,如果预报员有了充分准确的模式和数值计算方法,又有了充分准确的气象观测系统,可以对任意长时期的天气或气候情况做出足够准确的预报吗?这就引出了气象科学研究领域的另一个重要方向,即天气与气候的可预报性问题。在数值预报发展初期,Thompson给出了这一问题的经典定义, 即在模式准确而初始资料存在一定误差的条件下,对天气、气候的预报能达到何种水平[12]。不久,E. N. Lorenz在计算机上用他所建立的微分方程组进行关于天气预报的计算时偶然发现[13],输入初始条件的极细微的舍入误差可以引起模拟结果的巨大变化。他用了一个形象的比喻来解释这个发现:一只小小的蝴蝶在巴西的上空扇动翅膀,可能在1个月后的美国德克萨斯州会引起一场风暴。这就是混沌学中著名的“蝴蝶效应”,也是最早描述的混沌现象之一。所谓混沌现象是指在确定性理论描述的系统中, 具有貌似随机或不可预测性质的现象。
对于Lorenz所建立的描述大气运动规律的方程组,用计算机模拟出其解的三维图像,会得到一条自身不重叠或相交的双叶螺旋轨线,常称为“奇怪吸引子”(图 12)。这种结构说明,当模式积分较长的时间后,我们只知道原来扰动的发展会在可能解的统计结果中,但不知道它具体发展到何处,甚至是吸引子的哪个区域。这时,人们对大气状态的确定可能就同掷骰子一样成了随机的。因此,Lorenz认为,即使在模式完美无缺、初始条件近乎完全正确的情况下,大气的可预报性也是有限的,并且这种可预报性大约为两周左右。直到今天,对于天气尺度的系统,国际上依然普遍接受这个可预报时效的理论上限。应当指出,Lorenz的试验结果给出的是“模式大气”的可预报性。然而,在现实情况下,预报员要用不太准确的初始场(其误差远大于舍入误差)和可能存在一定缺陷的模式对未来数天的天气情况做出准确的预报,这本身就是一件非常困难的事情;如果出现了极端天气事件,要报准它则更是难上加难。
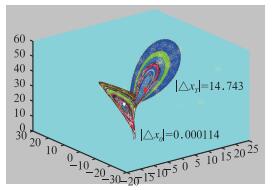
|
图 12 “奇怪吸引子”(Δx0、ΔxT分别表示初始、预报误差) Fig. 12 'Strange Attractor' (the initial/forecast error is denoted by Δx0/ΔxT) |
目前,天气和气候的可预报性研究已经成为当代气象科学研究的前沿热点领域,已经从传统的研究与初始条件误差(模式误差)对应的第一类(第二类)可预报性问题发展为更为广泛的范畴,即研究预报结果不确定性产生的原因和机制,寻找减小不确定性的方法和途径[14]。可预报性研究关注的另一个重要方面是,在目前的科学技术条件下,人类对一些天气、气候事件预报、预测能力的“极限”。这可以使得公众乃至社会不会对气象预报提出不符合科学规律、超越时代的“过分”要求,也可以使气象预报的发展、进步建立在科学、理性的基础之上。
3 如何使用气象预报信息对公众来说,气象预报所提供的信息是整个预报过程中最重要的。上一节介绍了在气象预报中,两种类型的误差始终影响着最后的预报结果,导致了预报误差的形成。因此,对预报结果不确定性的定量估计也是件很有意义的事情。不论是专业气象工作者还是普通公众,在关注气象预报的同时,还应该关注预报误差,其次是逐步学会理解并善用集合预报(概率预报)。
3.1 关注预报误差经常收看天气预报节目的人可能总会听到主持人说“局部有雨”。对此有一个流传很广的笑话:幸亏我们没有住在“局部”这个地方,否则就要天天下雨了。这当然是公众对气象工作者的幽默。责怪天气预报不准确,是一个世界性的现象。在英国国家气象局,工作者对于常规天气要素的24小时定性预报准确率已经达到了86%。这一数字,代表着世界上短期天气预报的最高水平,但同时也意味着还有14%的预报是不够准确的。解决问题的关键就在于如何看待气象预报,如何理性地分析气象预报为什么不准。另一方面,好的气象预报产品,不仅要给出预报结果,还要给出关于预报误差的信息,从而使公众可以更好地使用预报产品。图 13是美国国家飓风预警中心对飓风卡莉(2004年8月13日05时)未来3天登陆以及登陆之后的路径预报和相应的误差分析:黑色圆点是预警中心对飓风卡莉未来1~3天中心位置的预报,而白色区域是未来1~3天卡莉可能出现的区域。显然,除“黑线”标记的地方,在白色范围内的地区也需要做好预防飓风到来的准备。
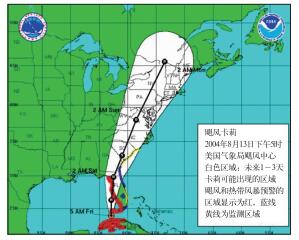
|
图 13 飓风卡莉的预估路径及其可能到达的区域 Fig. 13 The track of hurricane Charley and potential track area http://www.fas.usda.gov/pecad2/highlights/2004/08/cropwatch/index.htm |
上节谈到初始条件与模式总是存在着误差(包括随机误差),而大气运动的不稳定性特别是混沌特性使得从单一初始条件出发的确定性预报不可避免地存在着误差。这些认识导致气象学家思考气象预报的另一种途径:概率预报。这时,初始条件是描述当前大气状态的概率密度分布函数,控制方程是刘维尔随机偏微分方程,给出的结果是将来时刻大气状态的概率密度分布函数。这一思路使得不仅可以考虑初始条件的不确定性,还可以给出预报结果的不确定性。遗憾的是,求解这样的随机偏微分方程,远远超出现在的计算机资源条件,于是集合预报方法应运而生[18]。
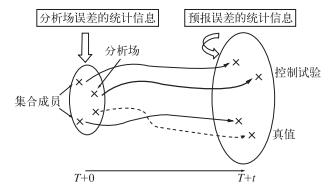
集合预报本质上是近似求解上述随机偏微分方程的一种方法。它通过选取不同初始条件(集合样本)近似描述当前大气状态的概率密度分布,然后运行确定性数值预报模式,得到将来时刻大气状态的概率密度分布的近似估计[19]。与确定性预报不同的是,集合预报所建立的系统(图 14)包含了许多不同的集合成员,每个成员都近似地刻画出了某种随机天气或气候事件的初始状态及其随时间演变发展的过程。在初始T+0时刻,分析场是对初始真实大气状态的最优估计,基于该分析场的确定性预报被称为控制试验(图 14粗实线)。由分析场误差的统计信息(如协方差等),运用一定的扰动生成技术可以得到各集合成员的初始状态[15]。从这些初始状态出发积分到T+t时刻构成了预报结果的集合,然后应用各种统计方法,可以得到预报时刻大气状态的概率密度分布的近似估计。与确定性预报不同的是,据此可以给出该时刻发生各种天气的概率,特别是一些极端天气(或高影响天气)发生的概率。图 15由欧洲中期预报中心(ECMWF)的50个集合成员与控制试验、业务模式的预报结果以及预报终止时刻(1999年12月26日06时)分析场共53张图缩放在一张大图上组成,因图大小形似邮票,常称之为“邮票图”。从图中可以看出,控制试验(左起第1排第1张)和T319业务模式(第1排第2张)都没能预报出低气压中心(分析场,第1排第3张),但部分集合成员却预报出了这一低气压中心。如果凭此结果进行概率预报,则在法国和德国出现风暴的概率大致是20%。当有少数集合成员给出了极端情况时,预报员就应该用概率预报的方式让公众意识到这种极端天气、气候事件发生的可能性。
|
图 14 集合预报的基本构成示意图 Fig. 14 Schematic of the essential components of an ensemble of forecasts |

|
图 15 对发生在1999年12月26日6时法国和德国的“圣诞风暴”的42小时海表气压场预报结果(深色区的气压低于980 hPa)的邮票图[16] Fig. 15 Stamp maps of surface pressure (colored below 980 hPa) for 42 h forecast of the first Christmas storm in French/Germany at 0600 UTC 26 December 1999[16] |
概率预报是集合预报的主要产品。为了了解公众对概率预报的理解,Gigerenzer等[17]曾做过调查,询问了阿姆斯特丹、雅典、柏林、米兰和纽约5个城市的少数居民:降水预报中提到的“明天降水可能性为30%”意味着什么?在纽约,大多数回答者给出了较为标准的气象上的解释,即当天气条件和今天一样的时候,10天有3天的第二天会下雨(至少有迹象);而在欧洲的城市,该解释被判断为最不可能的那个,较多居民的解释则是,明天30%的时间会下雨或者30%的区域会下雨。其实,概率只是一个数学名词,它最直观的意思是指出一件事情发生的可能性。正如降水概率,它不是指降水的时间或地点,而是对降水与否这件事本身的估计。
这种概率预报有什么实际意义呢?事实上,概率预报的目的是,气象部门将具体天气或气候变化的信息提供给用户,用户应该结合实际情况分析利弊,然后作出相应的决策。以一个例子来说明概率预报的优越性,有两种预报:① 明天风力2~3级(确定性预报);② 明天风力4级以下的概率为80%,风力4级以上的概率为20%(概率预报)。假设当风力4级以上时会对某类型的用户造成严重的经济损失,那么对于确定性预报产品,用户不会产生警惕性意识,而对于概率预警产品,一个善于使用概率预报的用户则会考虑是否采取一定的防护措施,因而减少不必要的损失。未来数值预报产品的主要形式将是概率预报,因为它可以量化多时间尺度预报的风险信息,使数值天气、气候预报的经济价值得以体现。另外,随着气象信息与其他圈层甚至人文社会信息的相互融合,会在如公共卫生、环境保护等领域产生有更大附加值的预报产品,而概率预报将在不同对象的预报中发挥重要的作用。
4 结语如今,气象预报已成为一项以数值预报为核心的系统工程,而现代数值预报是在经过气象资料采集、资料同化、数值模式和输出产品的检验等重要环节后,形成从形势预报到气象要素和特殊项目预报的过程。当前,大气探测正在向综合观测系统方向发展,地面观测不断采用先进、成熟的遥测遥感技术,而常规地面观测已实现高度自动化和网络化,高空观测正逐步应用各种更为先进的遥感探测系统。此外,各种数值模式的分辨率越来越高,物理过程越来越完善、复杂;资料同化和分析理论、技术获得了突破性进展,其与数值模式的协调性不断提高,并逐步在业务应用上得到实现;集合预报方法已成为数值预报发展的一个重要方向。放眼未来,随着新的气象科学技术的出现和成熟,多学科交叉融合、全球合作的进一步加强成为大气科学发展的新特征,气象预报将进入一个新时代。
| [1] |
中国大百科全书总编辑委员会《大气科学卷》编辑委员会, 等. 中国大百科全书, 大气科学卷[M]. 北京: 中国大百科全书出版社, 2004.
|
| [2] |
王绍武. 气候预测研究[M]. 北京: 气象出版社, 1996: 1-17.
|
| [3] |
丑纪范, 赵柏林. 中国气象事业发展战略研究-现代气象业务卷[M]. 北京: 气象出版社, 2005: 1-7.
|
| [4] |
Kalnay E. Atmospheric Modeling, Data Assimilation and Predictability[M]. Cambridge: Cambridge University Press, 2003: 1-137.
|
| [5] |
Luo J J, Masson S, and Behera S K. Extended ENSO predictions using a fully coupled ocean-atmosphere model[J]. J Climate, 2008, 21(1): 84-93. DOI:10.1175/2007JCLI1412.1 |
| [6] |
周秀骥, 吴国雄, 郑国光, 等. 中国气象科学技术发展战略研究[J]. 地球科学进展, 2005, 20(3): 261-267. |
| [7] |
Snyder C. Summary of an informal workshop on adaptive observations and FASTEX[J]. Bull Amer Meteor Soc, 1996, 77(5): 953-961. |
| [8] |
Mu M, Zhou F F, and Wang H L. A method for identifying the sensitive areas in targeted observations for tropical cyclone prediction: Conditional nonLinear optimal perturbation[J]. Mon Wea Rev, 2009, 137(5): 1623-1639. DOI:10.1175/2008MWR2640.1 |
| [9] |
Palmer T N, and R Hagedorn. Predictability of Weather and Climate[M]. Cambridge: Cambridge University Press, 2006: 157-180.
|
| [10] |
欧洲中期天气预报中心. 章基嘉等译. 中期天气预报科学基础[M]. 北京: 气象出版社, 1987: 169-176.
|
| [11] |
陈德辉, 薛纪善, 杨学胜, 等. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究[J]. 科学通报, 2008, 53(20): 2396-2407. DOI:10.3321/j.issn:0023-074X.2008.20.002 |
| [12] |
Thompson P D. Uncertainty of initial state as a factor in the predictability of large-scale atmospheric flow patterns[J]. Tellus, 1957, 9: 275-295. |
| [13] |
Lorenz E N. Deterministic nonperiodic flow[J]. J Atmos Sci, 1963, 20(2): 130-141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
| [14] |
Mu M, Duan W S, and Chou J F. Recent advances in predictability studies in China (1999-2002)[J]. Adv Atmos Sci, 2004, 21(3): 437-443. DOI:10.1007/BF02915570 |
| [15] |
Jiang Zhina, and Mu M. A comparison study of the methods of conditional nonlinear optimal perturbations and singular vectors in ensemble prediction[J]. Adv Atmos Sci, 2009, 26(3): 465-470. DOI:10.1007/s00376-009-0465-6 |
| [16] |
Palmer T N, Barkmeijer R, Buizza R, et al. The Future of Ensemble Prediction[J]. ECMWF Newsletter, 2000(No.88, Summer/Autumn). |
| [17] |
Committee on Estimating and Communicating Uncertainty in Weather and Climate Forecast, National Research Council. Completing the Forecast: Characterizing and Communicating Uncertainty for Better Decisions Using Weather and Climate Forecasts[M]. Washington, D.C.: The National Academies Press, 2006: 25.
|
| [18] |
杜钧, 陈静. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 2010, 36(11): 1-11. DOI:10.7519/j.issn.1000-0526.2010.11.001 |
| [19] |
杜钧, 陈静. 单一值预报向概率预报转变的价值:谈谈概率预报的检验和应用[J]. 气象, 2010, 36(12): 10-18. DOI:10.7519/j.issn.1000-0526.2010.12.002 |
 2011, Vol. 37
2011, Vol. 37 