政府间气候变化专门委员会第六次评估报告指出,未来全球升温预计将达到或超过1.5℃(翟盘茂等,2021)。在全球变暖仍将持续的情景下,更频繁、更强盛的极端天气气候事件可能会进一步增多增强(姜彤等,2020;沈贝蓓等, 2021),对人类生存与福祉造成巨大挑战(周佰铨和翟盘茂,2023;周广胜等,2024)。在此背景下,开发与完善气温预报模型显得尤为关键,提供精准预测未来变化,可有效降低极端高温带来的负面后果。
当前气温预报方法主要包括天气图预报、数值天气预报和统计预报(盛春岩等, 2020)。天气图预报依据天气图、气象卫星云图、雷达图等资料推断天气系统的移动与变化(杜钧和钱维宏, 2014);数值天气预报依赖于大量气象观测数据和计算资源(孙全德等, 2019);统计预报则基于概率论和数理统计,通过分析历史预报记录来估计气象灾害发生的概率(杨德全等, 2019)。尽管这些方法在气象预报中广泛应用,但也各自存在局限。例如,天气图预报需要大量人力物力且预报范围受限(钱奇峰等, 2021);数值天气预报要求庞大的计算资源和高精度数据(沈学顺等, 2020);统计预报因其未考虑气象系统的动态演化,无法精确预报极端气象灾害(董颜等, 2020)。
近年来,随着人工智能技术的快速发展,神经网络模型逐步成为气象预报领域的研究焦点(孙健等, 2021)。利用大规模气象观测数据,多层神经网络已实现对气温的非精细化短期预报。例如,Singh and Gill(2014)研究特定气象要素的依赖性,提出了一种基于遗传算法的气温预报模型,但其预报范围仅限于平均、最高和最低气温。段文广等(2012)采用BP神经网络方法,结合时序分析技术学习历史气温序列的变化规律。然而,这些模型在捕捉长期依赖关系、泛化能力以及适用范围方面仍有明显不足。
针对上述问题,本文提出了一种基于稀疏注意力与自适应时序分解的气温预报模型,验证了该模型在“耶拿地区的24 h精细化气温预报”“南京地区的中短期日平均气温预报”以及“多地区单日平均气温预报”方面的有效性和优越性。
1 数据资料 1.1 耶拿气象数据集耶拿气象数据集由德国马克斯普朗克生物地球化学研究所提供,涵盖了2009—2016年的气象记录。这些记录以每10 min一次的频率采集,共计420 551条数据,包含了14种气象要素,如气温、气压、相对湿度和风速等。
1.2 中国地面气候资料日值数据集中国地面气候资料日值数据集由国家气象信息中心提供,涵盖中国752个地面气象观测站1951—2014年的日值数据,包含了最高气压、最低气压、平均气温、最高气温、最低气温、平均风速、降水量等气象要素。
2 方法 2.1 位置与时间信息编码方法(1) 绝对位置编码
绝对位置编码为序列中每个元素赋予一个独特编码,以标明其在序列中的具体位置。尽管注意力机制使得模型能够在处理序列数据时关注各个位置的元素,但其本身无法直接识别位置信息(袁凯等, 2022)。如式(1),通过将正弦和余弦函数的输出融入到气象序列中,为每个位置分配一个唯一编码(Vaswani et al, 2017)。与其他位置编码技术不同,该方法无需依赖神经网络即可得到相关位置信息。
| $ \left\{\begin{array}{l} \mathbf{P E}(\operatorname{pos}, 2 i)=\sin \left(\frac{\text { pos }}{10 \frac{2 i}{d_{\text {model }}}}\right) \\ \mathbf{P E}(\operatorname{pos}, 2 i+1)=\cos \left(\frac{\text { pos }}{10 \frac{2 i}{d_{\text {model }}}}\right) \end{array}\right. $ | (1) |
式中:PE表示绝对位置编码矩阵,pos表示序列位置,i表示编码索引,dmodel表示编码维度。
(2) 时间信息编码
为了挖掘气象数据中时间相关性方面的信息,如式(2),通过对时间数据进行编码并将其与气象序列融合,以提升神经网络在预报气温方面的准确性。编码过程中,首先对时间数据进行归一化处理;随后嵌入函数将其映射至高维空间,确保时间信息与位置信息编码矩阵在维度上匹配。
| $ {\mathbf{T E}}=\text { Embedding }(t) $ | (2) |
式中:t表示气象观测数据的记录时间,TE表示时间信息编码矩阵,Embedding(.)表示嵌入函数。
2.2 自适应时间序列分解方法自适应时间序列分解方法(AdaSTL)根据隐藏状态的动态变化,灵活调整分解效果,解决了传统时间序列分解算法在合理超参数设定上的局限性(Wen et al, 2020)。
首先构建多种不同超参数配置的STL(seasonal and trend decomposition using Loess)单元,并利用可学习矩阵对输入序列进行线性变换式(3);随后,依据神经网络分配的权重式(4),将周期子项和趋势子项分别整合为完整的周期项和趋势项式(5);最后,通过引入多层感知机增强模型对非线性关系的捕捉能力。
| $ S_i, T_i=\operatorname{STL}\left(\theta_i, x \boldsymbol{W}_i\right), \quad i=1, \cdots, k $ | (3) |
| $ \beta_1, \cdots, \beta_k=\operatorname{SoftMax}\left(S_1, \cdots, S_k\right) $ | (4) |
| $ \left\{\begin{array}{l} S=\operatorname{MLP}\left(\sum\limits_{i=1}^k \beta_i \times S_i\right) \\ T=\operatorname{MLP}\left(\sum\limits_{i=1}^k \beta_i \times T_i\right) \end{array}\right. $ | (5) |
式中: x表示被分解的时间序列;W表示可学习矩阵;i表示STL单元编号;θ表示STL超参数;SoftMax(.)函数用于计算权重βi;×表示标量乘法;MLP(.)表示多层感知机;Si和Ti分别表示周期子项和趋势子项,而S和T表示整合后的周期项和趋势项。
2.3 稀疏自注意力机制基于Renyi散度的稀疏自注意力机制, 旨在降低捕捉序列数据间长期依赖关系时无关信息对其带来的干扰,具体如下。
首先将输入序列分别映射为查询矩阵、键矩阵以及值矩阵。随后,通过Renyi散度(van Erven and Harremos, 2014)对查询向量定性,如果该查询的注意力概率分布严重偏离均匀分布,则将其定性为“活性”查询,否则为“惰性”查询。如式(6),将活性查询向量组成稀疏查询矩阵。同时,为了维持与全局注意力矩阵维度一致,利用均值向量对缺失部分进行填充。
| $ \operatorname{SSA}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{SoftMax}\left(\frac{\overline{\boldsymbol{Q}} \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d_{\text {model }}}}\right) \boldsymbol{V} \oplus \operatorname{Mean}(\boldsymbol{V}) $ | (6) |
式中:Q表示查询矩阵,Q表示稀疏查询矩阵,K表示键矩阵,V表示值矩阵;SSA(.)表示稀疏自注意力机制;Mean(.)表示取均值函数;⊕表示向量填充。
3 气温预报模型构建基于稀疏注意力与自适应时序分解的气温预报模型(ATFSAS)的架构如图 1所示。首先,编码器捕获历史气象数据中的长期依赖关系;接着,信息蒸馏模块对特征表示进行去冗余处理;解码器则依据这些经过冗余过滤的编码信息,以分步和分层的方式处理趋势性和周期性分量;最后,将这些分量与近期气温均值相加,实现对未来气温的预报。
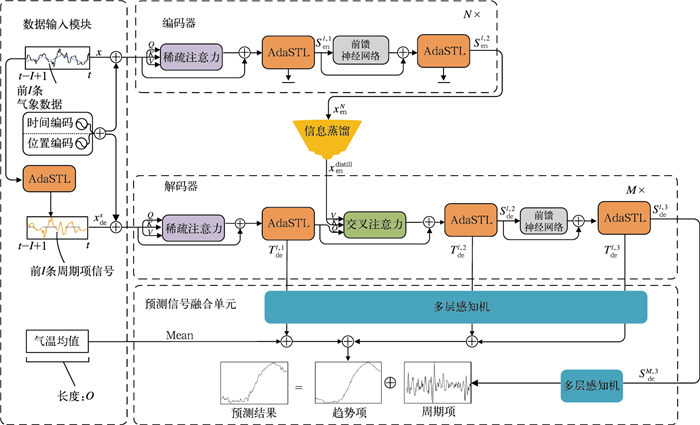
|
图 1 基于稀疏注意力与自适应时序分解的气温预报模型 注:缩写说明:x表示前I条气象数据,对其分解后得到周期项xdes;第l层编码器分解的第i个周期项为Senl, i,第l层解码器分解的第i个趋势项为Tdel, i;近期气温均值为Mean;N与M分别表示编码器与解码器总层数。 Fig. 1 Air temperature forecasting model based on sparse attention and AdaSTL |
将位置信息和时间信息融入编码器与解码器的输入序列中,如式(7)、式(8):
| $ x_{{\rm{en}}}^0 = {\rm{ Linear }}(x) + {\bf{TE}} + {\bf{PE}} $ | (7) |
| $ x_{{\rm{de}}}^0 = {\mathop{\rm Linear}\nolimits} \left({x_{{\rm{de}}}^s} \right) + {\bf{TE}} + {\bf{PE}} $ | (8) |
式中:x和xdes分别表示气象序列与其周期项;PE和TE分别表示位置与时间信息编码矩阵;Linear(.)表示线性映射函数;xen0和xde0分别表示第1层编码器与解码器输入。
3.2 编码器假设编码器共N层,将第l-1层编码器输出作为第l层的输入,以此类推,构成多层编码器结构。第l层编码器概括为xenl=Encoder(xenl-1),具体如式(9)~式(11):
| $ \begin{gathered} S_{\mathrm{en}}^{l, 1}= \\ \operatorname{AdaSTL}\left[\operatorname{SSA}\left(x_{\mathrm{en}}^{l-1} \boldsymbol{W}_Q, x_{\mathrm{en}}^{l-1} \boldsymbol{W}_K, x_{\mathrm{en}}^{l-1} \boldsymbol{W}_V\right)+x_{\mathrm{en}}^{l-1}\right] \end{gathered} $ | (9) |
| $ S_{\mathrm{en}}^{l, 2}=\operatorname{AdaSTL}\left[\mathrm{FFN}\left(S_{\mathrm{en}}^{l, 1}\right)+S_{\mathrm{en}}^{l, 1}\right] $ | (10) |
| $ x_{\mathrm{en}}^l=S_{\mathrm{en}}^{l, 2} $ | (11) |
式中:xenl表示第l层编码器输出;W为可学习矩阵,用以将序列转换为查询矩阵、键矩阵以及值矩阵;编码器层号l=1, …, N;SSA(.)表示稀疏自注意力机制;FFN(.)表示前馈神经网络;AdaSTL(.)表示自适应时序分解。
3.3 信息蒸馏技术信息蒸馏技术旨在消除编码过程中造成的信息冗余,并将其压缩为具有相同语义的紧凑表示。信息蒸馏技术概括为xendistill=Distill(xenN),其中xenN表示最后一层编码器输出(即编码信息),xendistill表示经过冗余过滤后的编码信息,方法如下:
首先通过一维卷积神经网络提取编码信息中的局部特征(陈锦鹏等, 2021),在此过程中,输入序列被视为一维向量,并利用多种卷积核进行处理。其间,卷积输出为特征映射元素,每个元素代表了卷积核在相应位置的响应。为了提升模型的非线性表达能力,在卷积操作后应用ReLU激活函数进行转换,将负值转换为零而保持正值不变(黄骄文等, 2021)。此外,鉴于卷积神经网络主要关注局部特征的提取,引入最大池化层以进行下采样操作,进一步降低编码信息的冗余度。
3.4 解码器解码器在结构上与编码器高度相似,不同之处在于其加入了交叉注意力机制,以捕捉编码信息与解码器输入之间的长期依赖关系,构建一个综合考虑这两种不同序列的特征表示。
假设解码器共有M层,第l层解码器概括为xdel=Docoder(xdel-1, xendistill),其中xendistill表示经过冗余处理的编码信息,xdel-1表示第l-1层解码器输出。首先,通过稀疏自注意力机制来捕获前一层解码器输出序列中的长距离依赖关系。接着,交叉注意力机制将编码与解码过程中的序列相互关联,从而实现高层次的特征表示。其间,AdaSTL单元对各个模块的输出进行时序分解,其中趋势性分量作为气温预报信号的组成部分,而周期性分量传递给下一层解码器,以此方式逐层处理,提高气温预报的准确性。
3.5 气温预报信号融合气温预报信号融合过程如式(12)所示,在此过程中,近期气温均值作为预报结果的初始项,用以缓解偏移现象;趋势性分量由解码器内部的AdaSTL单元逐层、逐步分解得到,有助于减轻震荡反应;而最后一层解码器输出作为周期性分量。通过将这些分解信号与气温均值相加,得到最终的预报结果。
| $ \begin{gathered} \text { Prediction }= \\ \text { Mean }+\operatorname{MLP}\left(S_{\mathrm{de}}^{M, 3}\right)+\sum\limits_{l=1}^M \sum\limits_{i=1}^3 \operatorname{MLP}\left(T_{\mathrm{de}}^{l, i}\right) \end{gathered} $ | (12) |
式中: 解码器层号l=1, …, M,AdaSTL单元编号i=1, 2, 3;MLP(.)表示多层感知机;Mean表示气温均值,Tdel, i表示第l层解码器分解的第i个趋势性分量,SdeM, 3表示第M层解码器分解的第3个周期性分量,Prediction表示预报结果。
4 试验分析 4.1 评价指标本文选择平均绝对误差(MAE)、均方误差(MSE)以及均方根误差(RMSE)作为评价指标。
4.2 基线模型在“24 h精细化气温预报”方面,将ATFSAS与多种方法进行对比, 包括RNN(Shin et al, 2022)、GRU(Subramanian et al, 2022)、LSTM(Gensler et al, 2016)、ConvLSTM(Liu et al, 2017)、Pred RNN(Wang et al, 2017)、Informer(Zhou et al, 2023)以及FEDformer(Zhou et al, 2022)。
在“日平均气温预报”方面,将ATFSAS与ARIMA、GCN-BiLSTM(Miao et al, 2022)、DFN(Xie et al, 2021)以及LSTM(Gensler et al, 2016)进行比较。
4.3 24 h精细化气温预报性能分析 4.3.1 对比结果分析利用“德国耶拿气象数据集”进行24 h气温预报,输入数据为过去48 h气象数据,以预报未来24 h气温变化。
表 1为不同模型在训练集中的拟合情况,分析发现,受限于误差累积、梯度消失问题,RNN的MAE超过了2.5℃,无法完成模型训练任务。而GRU、LSTM及ConvLSTM引入了门控机制策略,有效缓解了梯度相关问题,提高了训练的稳定性。另一方面,基于注意力机制的Informer、FEDformer及ATFSAS模型展现出优异的拟合表现,三者的MAE指标均低于0.94℃,体现了注意力机制在处理时间序列时的有效性。
|
|
表 1 不同模型在训练集中的拟合性能 Table 1 Fitting performance of models on the training set |
表 2为不同模型在测试集中的泛化情况,分析得到,ATFSAS表现出最佳泛化能力,其MAE为1.7108℃。相较于传统神经网络模型(GRU、LSTM及ConvLSTM),ATFSAS分别实现了22.23%、25.29%和19.68%的性能提升。进一步比较基于注意力机制的Informer和FEDformer模型,其泛化性能分别提高了10.89%和7.02%,证明ATFSAS在精细化气温预报方面不仅优于传统模型,同时相比近年提出的方法也同样具有明显优势。
|
|
表 2 不同模型在测试集中的泛化能力 Table 2 Generalization ability of models on the test set |
设定解码器为2层结构,因此气温预报结果由8个分量组成,包括1个周期性分量、1个近期气温平均值,以及6个趋势分量(每层解码器预测3个趋势分量)。
以德国耶拿市2011年1月7日(世界时,下同)气温预报结果融合过程为例(图 2)。最初,预报结果仅表现为一条直线(近期气温均值)。随着周期性分量S和趋势分量T1的加入(图 2b),蓝色曲线(预报值)的走向大体与绿色曲线(实际值)相似,但出现了明显的震荡。随着时间序列分解单元逐步分解隐藏状态,加入趋势分量T1~T5后,预报结果的震荡现象得到缓解,直至最后一个趋势分量T6加入,得到最终的气温预报结果(图 2g)。这一策略从时间序列分解的角度出发,解决了传统模型存在的预测结果偏移、精度不佳,以及泛化性能不足的问题。
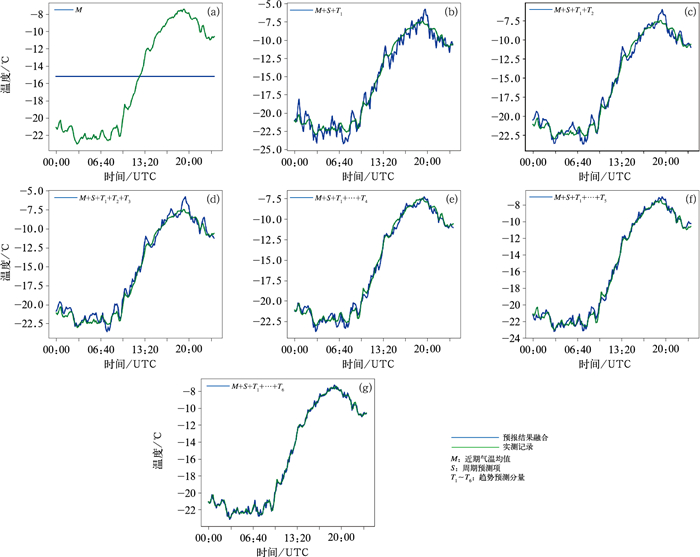
|
图 2 ATFSAS模型对德国耶拿市2011年1月7日气温预报结果的融合过程可视化 Fig. 2 Visualization of the fusion process of air temperature forecasted by ATFSAS in Jena, Germany on 7 January 2011 |
图 3为ATFSAS进行24 h时效的气温预报效果。完整的气温拟合效果图可访问https://zenodo.org/record/8325399获取。总体来看,该模型在精细化气温预报方面表现较好。然而,在不同时间区段的性能表现出一定的差异性。具体来说,在00:00—12:00,预报结果具有较高的准确性。在12:00—18:00,模型受到误差累积等因素的影响,部分结果呈现轻微的偏移和波动现象。此外,尽管ATFSAS在18:00—24:00期间的准确性有所下降,但误差依然被控制在一个相对较小的范围,未观察到逆向趋势预报现象。
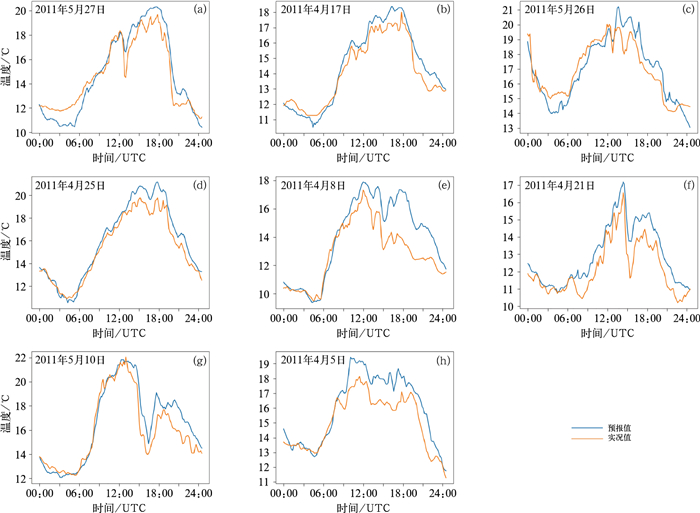
|
图 3 ATFSAS模型对2011年德国耶拿市24 h气温预报与实况对比 Fig. 3 Comparison of 24 h air temperature forecasted by ATFSAS for Jena, Germany with the observation in 2011 |
进一步地,统计了ATFSAS在不同时段的性能表现,如图 4所示,影响性能的主要时间段是16:00—22:00,此期间MAE超过了2.4℃,与图 2表现相符。分析认为,精度下降主要归因于两个方面:首先,数据分布的变化和误差累积导致了神经网络处理时间序列的能力降低(孙健等, 2021);其次,天气突变以及其他与时间相关的因素对预报产生了负面影响(陈鹤等, 2022)。相反,在00:00—10:00期间,其MAE保持在1.3℃以下,表明此期间的预报结果具有较高的可信度。

|
图 4 ATFSAS模型对2011年德国耶拿市气温预报在24 h时效内各时段的平均绝对误差 Fig. 4 Mean absolute error of 24 h air temperature forecasted by ATFSAS in each time interval for Jena, Germany in 2011 |
本节以“中国地面气候资料日值数据集”为数据源,评估了ATFSAS模型在“南京地区的中短期日平均气温预报”和“多地区单日平均气温预报”方面的表现。
4.4.1 中短期日平均气温预报分析选定“南京市”作为研究区域,利用过去30 d的气象数据来预报未来1~14 d的日平均气温。根据表 3,随着预报时效的增长,受限于误差累积,导致所有模型的精度普遍下降。然而,不同模型之间的性能差异显著。具体地,ATFSAS的MAE为2.584℃,相比于统计模型ARIMA,其性能提升了54.98%。与此同时,在与GCN-BiLSTM、DFN和LSTM的比较中,ATFSAS分别实现了14.43%、43.70%和35.56%的提升,表明其在中短期日平均气温预报方面的优越性。
|
|
表 3 不同模型对南京日平均气温的中短期预报性能对比 Table 3 Comparison of daily average air temperature forecasted performance of models in the medium and short terms for Nanjing |
选取哈尔滨、北京、济南、青岛、南京、杭州、广州以及深圳作为研究区域,将各地区前30 d的气象数据作为输入,旨在预报各地区未来1 d的平均气温。
图 5显示了不同模型在各地区的单日平均气温预报性能,最右列总结了不同模型对于所有研究区域日均气温预报的平均性能。结果表明,统计学模型ARIMA的表现依旧不佳。DFN模型因其结构较为简单,虽然性能优于统计学模型,但与其他深度学习模型相比仍有改进空间。相比之下,ATFSAS模型在各地区的单日平均气温预报任务中均展现出最佳性能,平均MAE值达到2.32℃。比较MAE情况,与ARIMA相比,ATFSAS实现了44.42% 的性能提升;与DFN、LSTM和GCN-BiLSTM相比,则分别提升了34.25%、23.66%和10.10%的预报精度(表 4)。此外,图 5也表明,ATFSAS对不同研究地区的预报性能表现保持稳定,没有出现显著波动,展现了其良好的适用性。
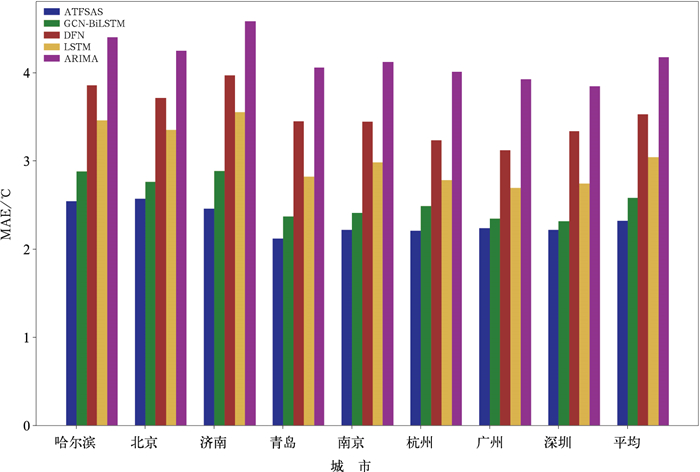
|
图 5 不同模型对中国8个城市单日平均气温的预报性能对比 Fig. 5 Comparison of models' performance in single-day average air temperature forecasted for 8 cities of China |
|
|
表 4 不同模型对中国8个城市单日平均气温的预报性能对比 Table 4 Comparison of single-day average air temperature forecast performance of models for 8 cities of China |
针对传统方法在气温预报中存在精度不足、泛化能力弱以及适用性不佳的问题,提出了一种基于稀疏注意力与自适应时序分解的气温预报模型ATFSAS,主要结论如下:
(1) 稀疏注意力机制有效聚焦于重要序列信息,减少无关信息的干扰,提高了ATFSAS在捕捉气象观测数据之间依赖关系的能力。
(2) 信息蒸馏方法有效减少了编码过程中造成的信息冗余,提高了编码信息的有效性以及解码器处理隐藏状态表示方面的效率。
(3) 通过将多层解码器与自适应时序分解单元相结合,缓解了预报结果的震荡和偏移现象,进一步提高了气温预报精度。
利用ATFSAS模型完成了包括“德国耶拿地区的24 h精细化气温预报”“南京地区的中短期日平均气温预报”以及“多地区单日平均气温预报”方面的可行性试验。结果表明,与传统方法相比,该模型具有较高的气温预报精度以及较广的适用范围。未来工作将致力于解决模型在中长期预报中由于误差累积等因素引起的精度下降问题。
陈鹤, 蔡荣辉, 陈静静, 等, 2022. 基于深度学习方法的气温预报技术应用与评估[J]. 气象, 48(11): 1373-1383. Chen H, Cai R H, Chen J J, et al, 2022. Application and evaluation of temperature forecast based on deep learning method[J]. Meteor Mon, 48(11): 1373-1383 (in Chinese).
|
陈锦鹏, 冯业荣, 蒙伟光, 等, 2021. 基于卷积神经网络的逐时降水预报订正方法研究[J]. 气象, 47(1): 60-70. Chen J P, Feng Y R, Meng W G, et al, 2021. A correction method of hourly precipitation forecast based on convolutional neural network[J]. Meteor Mon, 47(1): 60-70 (in Chinese).
|
董颜, 郭文利, 闵晶晶, 等, 2020. 北京道面温度特征分析和统计预报研究[J]. 气象, 46(5): 716-724. Dong Y, Guo W L, Min J J, et al, 2020. Characteristics of road surface temperature in Beijing and its statistic forecasting model[J]. Meteor Mon, 46(5): 716-724 (in Chinese).
|
杜钧, 钱维宏, 2014. 天气预报的三次跃进[J]. 气象科技进展, 4(6): 13-26. Du J, Qian W H, 2014. Three revolutions in weather forecasting[J]. Adv Meteor Sci Technol, 4(6): 13-26 (in Chinese).
|
段文广, 周晓军, 石永炜, 2012. 数据挖掘技术在精细化温度预报中的应用[J]. 干旱气象, 30(1): 130-135. Duan W G, Zhou X J, Shi Y W, 2012. Application of data mining technique on refined temperature forecast[J]. J Arid Meteor, 30(1): 130-135 (in Chinese).
|
黄骄文, 蔡荣辉, 姚蓉, 等, 2021. 深度学习网络在降水相态判识和预报中的应用[J]. 气象, 47(3): 317-326. Huang J W, Cai R H, Yao R, et al, 2021. Application of deep learning method to discrimination and forecasting of precipitation type[J]. Meteor Mon, 47(3): 317-326 (in Chinese).
|
姜彤, 孙赫敏, 李修仓, 等, 2020. 气候变化对水文循环的影响[J]. 气象, 46(3): 289-300. Jiang T, Sun H M, Li X C, et al, 2020. Impact of climate change on water cycle[J]. Meteor Mon, 46(3): 289-300 (in Chinese).
|
钱奇峰, 王川, 徐雅静, 等, 2021. 一种基于深度学习的台风强度估测技术[J]. 气象, 47(5): 601-608. Qian Q F, Wang C, Xu Y J, et al, 2021. A deep learning technique of typhoon intensity estimation[J]. Meteor Mon, 47(5): 601-608 (in Chinese).
|
沈贝蓓, 宋帅峰, 张丽娟, 等, 2021. 1981—2019年全球气温变化特征[J]. 地理学报, 76(11): 2660-2672. Shen B B, Song S F, Zhang L J, et al, 2021. Changes in global air temperature from 1981 to 2019[J]. Acta Geogr Sin, 76(11): 2660-2672 (in Chinese).
|
沈学顺, 王建捷, 李泽椿, 等, 2020. 中国数值天气预报的自主创新发展[J]. 气象学报, 78(3): 451-476. Shen X S, Wang J J, Li Z C, et al, 2020. China's independent and innovative development of numerical weather prediction[J]. Acta Meteor Sin, 78(3): 451-476 (in Chinese).
|
盛春岩, 范苏丹, 荣艳敏, 等, 2020. 几种气温客观预报方法对比及最优集成预报研究[J]. 气象, 46(10): 1351-1361. Sheng C Y, Fan S D, Rong Y M, et al, 2020. Comparison of several objective methods and optimal consensus forecast study of temperature[J]. Meteor Mon, 46(10): 1351-1361 (in Chinese).
|
孙健, 曹卓, 李恒, 等, 2021. 人工智能技术在数值天气预报中的应用[J]. 应用气象学报, 32(1): 1-11. Sun J, Cao Z, Li H, et al, 2021. Application of artificial intelligence technology to numerical weather prediction[J]. J Appl Meteor Sci, 32(1): 1-11 (in Chinese).
|
孙全德, 焦瑞莉, 夏江江, 等, 2019. 基于机器学习的数值天气预报风速订正研究[J]. 气象, 45(3): 426-436. Sun Q D, Jiao R L, Xia J J, et al, 2019. Adjusting wind speed prediction of numerical weather forecast model based on machine learning methods[J]. Meteor Mon, 45(3): 426-436 (in Chinese).
|
杨德全, 郝日栩, 何健新, 等, 2019. 统计预报方法在海洋预报中的应用研究进展[J]. 海洋信息, 34(2): 1-9. Yang D Q, Hao R X, He J X, et al, 2019. Research progress of statistical forecasting methods in ocean prediction[J]. J Mar Inf Technol Appl, 34(2): 1-9 (in Chinese).
|
袁凯, 李武阶, 李明, 等, 2022. 四种机器深度学习算法对武汉地区雷达回波临近预报的检验和评估[J]. 气象, 48(4): 428-441. Yuan K, Li W J, Li M, et al, 2022. Examination and evaluation of four machine deep learning algorithms for radar echo nowcasting in Wuhan Region[J]. Meteor Mon, 48(4): 428-441 (in Chinese).
|
翟盘茂, 周佰铨, 陈阳, 等, 2021. 气候变化科学方面的几个最新认知[J]. 气候变化研究进展, 17(6): 629-635. Zhai P M, Zhou B Q, Chen Y, et al, 2021. Several new understandings in the climate change science[J]. Climate Change Res, 17(6): 629-635 (in Chinese).
|
周佰铨, 翟盘茂, 2023. 未来的极端天气气候与水文事件预估及其应对[J]. 气象, 49(3): 257-266. Zhou B Q, Zhai P M, 2023. The future projections of extreme weather, climate and water events and strategic responses[J]. Meteor Mon, 49(3): 257-266 (in Chinese).
|
周广胜, 何奇瑾, 宋兴阳, 等, 2024. 气候行动最前线的高标准农田生产气象保障[J]. 气象, 50(3): 265-274. Zhou G S, He Q J, Song X Y, et al, 2024. Meteorological services support for high-standard farmland production at the frontline of climate action[J]. Meteor Mon, 50(3): 265-274 (in Chinese).
|
Gensler A, Henze J, Sick B, et al, 2016. Deep learning for solar power forecasting-an approach using AutoEncoder and LSTM Neural Networks[C]//Proceedings of 2016 IEEE International Conference on Systems, Man, and Cybernetics. Budapest: IEEE: 2858-2865.
|
Liu Y P, Zheng H F, Feng X X, et al, 2017. Short-term traffic flow prediction with Conv-LSTM[C]//Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing. Nanjing: IEEE: 1-6.
|
Miao L Z, Yu D Y, Pang Y Y, et al, 2022. Temperature prediction of Chinese cities based on GCN-BiLSTM[J]. Appl Sci, 12(22): 11833. DOI:10.3390/app122211833
|
Shin M, Hwang S, Kim B, et al, 2022. IoT-Based Intelligent Monitoring System applying RNN[J]. Appl Sci, 12(20): 10421. DOI:10.3390/app122010421
|
Singh S, Gill J, 2014. Temporal weather prediction using back propagation based genetic algorithm technique[J]. Int J Intell Syst Appl, 6(12): 55-61.
|
Subramanian B, Olimov B, Naik S M, et al, 2022. An integrated mediapipe-optimized GRU model for Indian sign language recognition[J]. Scientific Reports, 12(1): 11964. DOI:10.1038/s41598-022-15998-7
|
van Erven T, Harremos P, 2014. Rényi divergence and Kullback-Leibler divergence[J]. IEEE Trans Inf Theory, 60(7): 3797-3820.
|
Vaswani A, Shazeer N, Parmar N, et al, 2017. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc. : 6000-6010.
|
Wang Y B, Long M S, Wang J M, et al, 2017. PredRNN: recurrent neural networks for predictive learning using spatiotemporal LSTMs[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc. : 879-888.
|
Wen Q S, Zhang Z, Li Y, et al, 2020. Fast RobustSTL: efficient and robust seasonal-trend decomposition for time series with complex patterns[C]//Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. California: ACM: 2203-2213.
|
Xie R B, Ling C, Wang Y L, et al, 2021. Deep feedback network for recommendation[C]//Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence. Yokohama: ijcai. org: 349.
|
Zhou H Y, Li J X, Zhang S H, et al, 2023. Expanding the prediction capacity in long sequence time-series forecasting[J]. Artif Intel, 318: 103886.
|
Zhou T, Ma Z Q, Wen Q S, et al, 2022. FEDformer: frequency enhanced decomposed transformer for long-term series forecasting[C]//Proceedings of the 39th International Conference on Machine Learning. Baltimore: PMLR: 27268-27286.
|
 2024, Vol. 50
2024, Vol. 50 
