阵风通常指瞬时极大风速,是风速脉动变化中短期极端情况(全继萍等,2022)。当其大于某一个阈值时,就会对人们的生产生活产生重大影响(Kahl et al, 2021)。阵风的形成机理复杂,不仅与平均风速和边界层湍流有关,还受地表粗糙度和大气稳定度影响,因而是预报难点(Kahl, 2020)。阵风系数法是一种常用且计算简单的阵风预报方法, 即通过计算持续时间内最大风速与其所在时间尺度的平均风速的比值来表征风速脉动强弱,进而估算出最大阵风值(Blaes et al, 2014)。为进一步提升阵风系数法在预报中的准确率,诸多学者也开展不同天气条件下的阵风系数差异研究(Shu et al, 2015;胡波,2017;周福等,2017)。阵风系数法只是反映了地面平均风速与阵风之间的一般联系,并不能完全体现高空气象条件对阵风的影响。研究表明:阵风是大尺度低频结构及强湍流脉动叠加而成的,当地面风速较大时,叠加在平均流动上的脉动不仅包含随机湍流脉动,还会出现边界层上层阵风向下传递的过程(程雪玲等,2016),因此考虑高空的气象条件更有利于阵风的准确预报。欧洲中期天气预报中心(ECMWF)(2016)及胡海川等(2022)在地面10 m风速的基础上,利用可表征湍流及对流作用的高空垂直风速切变,来寻求更为合理与准确的阵风预报。但上述预报方法均基于线性回归且只考虑了高空风速,不足以精准刻画出高空气象条件对于阵风的影响。
近年来,机器学习(深度学习)方法被广泛应用于天气预报之中,并取得较好的预报效果(Rasp and Lerch, 2018;周康辉等,2021;张延彪等,2022)。相比于传统统计学方法,机器学习(深度学习)方法在解决复杂问题中具有明显优势,因此可以将其应用于海上阵风预报之中,以进一步提高海上阵风预报服务能力。利用2021年1—12月ECMWF确定性模式的24 h中低层风、温预报数据及近海浮标实况观测数据,分析可能对海面阵风产生影响的因子,通过将影响机理与机器学习方法相结合的方式(Sheridan,2018)构建我国近海阵风预报模型。利用2022年1—9月数据对构建预报模型进行独立样本检验,验证其在实际应用中的效果。
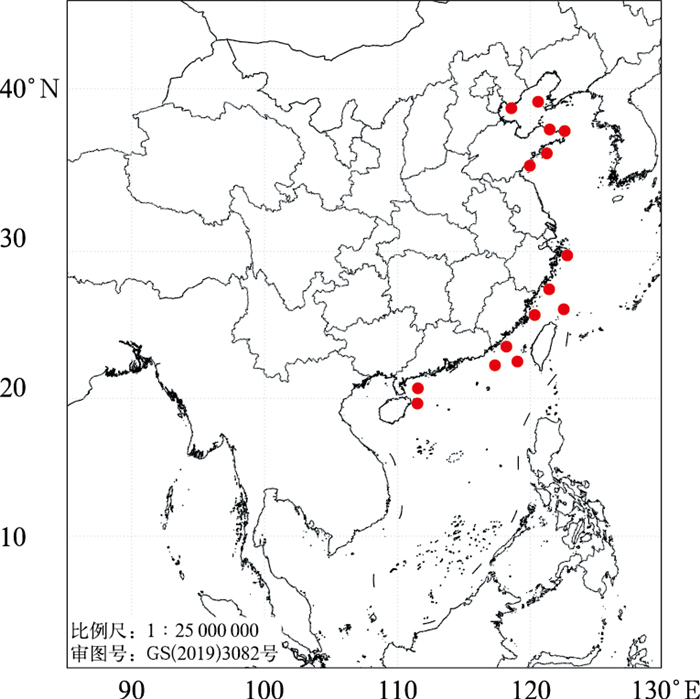
1 资料利用2021年1月至2022年9月中国气象局地面观测数据中小时内最大阵风数据及观测时刻10 m风速数据(保留一位小数);ECMWF确定性模式08时和20时(北京时,下同)起报的24 h预报时效的10 m风速、2 m温度数据,925、850、700和500 hPa的风速及温度预报数据。数值模式中地面预报数据的分辨率均为0.125°×0.125°,高空风速及温度预报数据的分辨率为0.25°×0.25°。海上观测资料稀缺,但下垫面相对均一,降低了阵风预报的复杂程度(Letson et al,2018),因此选取我国近海自北向南15个浮标观测站点统一构建预报模型,站点位置如图 1所示。其中,2021年1—12月数据用于预报模型建立及对比分析,2022年1—9月数据用于独立样本检验。
|
图 1 浮标站点分布 Fig. 1 Distribution of buoy sites |
根据阵风系数的定义,其计算公式如下(杨璐等,2023):
| $ \mathrm{GF}=\frac{\mathrm{Gust}}{W_{10}} $ | (1) |
式中:GF为阵风系数,Gust表示阵风,W10为10 m风速。文中在不同平均风速的划分下采用最小二乘法计算阵风系数,即通过最小误差的平方和来寻求最佳阵风系数,如式(2)所示:
| $ \begin{gathered} \frac{\partial \sum\limits_{i=1}^n\left(\mathrm{Gust}-\mathrm{GF} \times W_{10_i}\right)^2}{\partial \mathrm{GF}}= \\ -2 \sum\limits_{i=1}^n\left(\mathrm{Gust}-\mathrm{GF} \times W_{10_i}\right) W_{10_i}=0 \end{gathered} $ | (2) |
式中n表示不同平均风速下的样本数。
通过对式(2)进行化简,阵风系数可以表示为10 m风速与阵风乘积的和与10 m风速平方和的比值:
| $ \mathrm{GF}=\frac{\sum\limits_{i=1}^n W_{10_i} \times \text { Gust }}{\sum\limits_{i=1}^n W_{10_i}^2} $ | (3) |
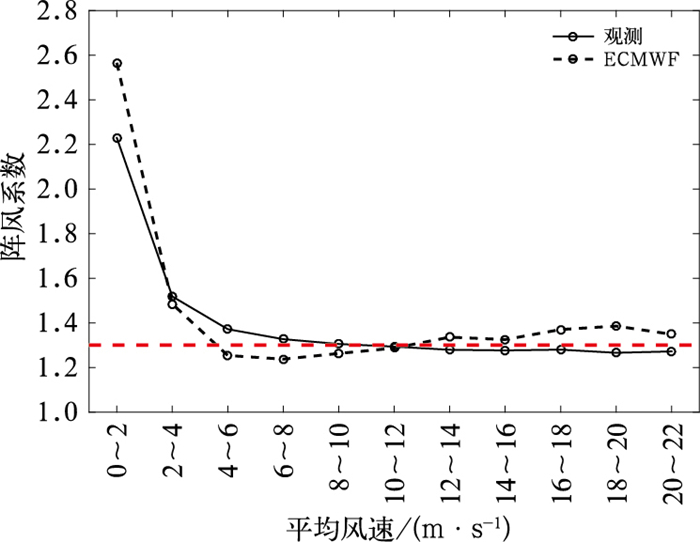
在利用阵风系数进行阵风预报时,所使用的平均风速应为一段时间内的平均(Yu and Chowdhury, 2009),文中利用数值模式预报的10 m风速或观测时刻10 m风速(2 min平均)做近似替代,以便所建立的预报模型能够应用于实际预报之中。如图 2所示,当10 m风速在4~8 m·s-1时,基于数值模式的阵风系数明显小于基于实况观测的阵风系数,当10 m风速大于12 m·s-1时,情况相反。两种阵风系数的差异原因主要是因为ECMWF确定性模式对10 m风速预报具有明显的系统性偏差(胡海川等,2021)。平均风速在16~18 m·s-1时,基于实况观测与基于数值模式的阵风系数分别为1.28、1.37,二者之间0.09的阵风系数差异可导致阵风预报结果相差1.4~1.6 m·s-1。通过对比发现,基于数值模式求解出的阵风系数不仅反映了阵风与10 m风速之间的一般性关系,同时也在一定程度上包含了数值模式的预报偏差特性,因而会对大量级的阵风有更好的预报效果。下文基于ECMWF确定性模式求解出的阵风系数开展相关统计分析工作。
|
图 2 2021年1—12月基于观测和ECMWF确定性模式预报10 m风速的阵风系数 注:红色虚线为阵风系数1.3。 Fig. 2 Gust factor based on observation and ECMWF deterministic model prediction of 10 m wind speed from January to December 2021 |
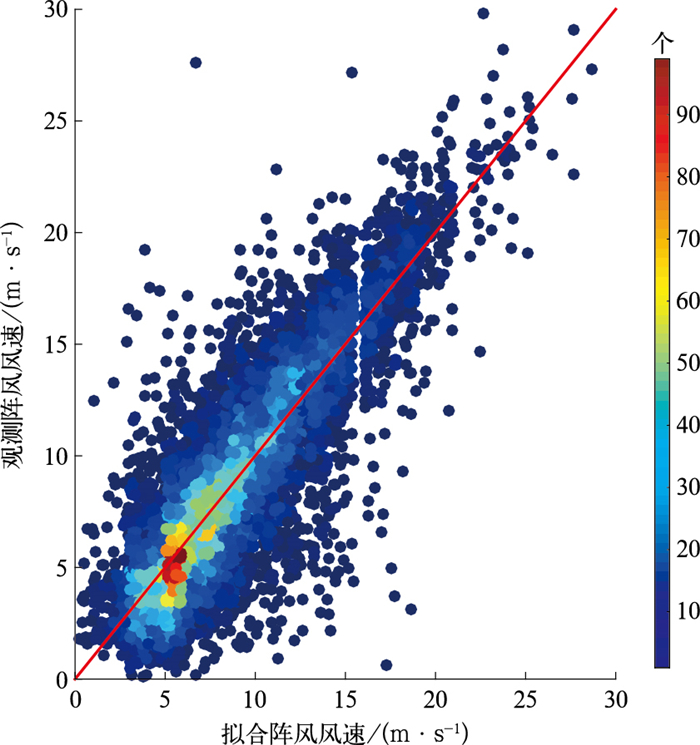
将阵风系数(基于ECMWF确定性模式)回代至2021年1—12月ECMWF数据,分析阵风系数法的拟合结果与阵风观测之间的差异。在阵风系数法拟合结果与阵风观测散点分布图中(图 3),对角线附近散点分布数量最多,表明虽然阵风系数法中仅考虑了10 m风速但却能够对多数的阵风观测具有很好的拟合效果,并且其结果稳定,因此也成为应用较为广泛的阵风预报方法。图 3中,在距对角线较远处仍有部分散点分布,表明在某些情况下,阵风系数法由于明显的高估或低估导致其拟合结果与阵风观测存在较大差异。当阵风观测值较大时,分布在对角线左侧散点数明显高于对角线右侧散点数,即阵风系数法对于大量级阵风的低估明显。造成这种明显差异的主要原因可以分为两类:其一,由于数值模式预报的明显偏差所导致;其二,在部分情况下,单一利用10 m风速不足以准确刻画出阵风,尤其对于大量级阵风。若数值模式对于某一影响系统的位置、强度预报出现明显偏差,无论是阵风系数法或其他阵风预报方法均难以基于单一确定性模式数据生成较为准确的阵风预报结果。在数值模式无明显预报偏差的情况下,如何在阵风系数法的基础上加入高空要素从而提升大量级阵风的预报效果?为此文中进一步分析当阵风系数法的拟合结果与阵风观测存在差异时,其对应的高空要素分布差异。
|
图 3 2021年1—12月阵风观测与阵风系数法拟合结果散点分布 注:散点颜色表示个数,红色实线为对角线。 Fig. 3 Scatter plot of gust observation and gust factor fitting results from January to December 2021 |
在基于天气过程的大风形成机理研究中,通常采用500 hPa及以下的气象要素进行分析(刘香娥和郭学良,2012;盛杰等,2019),同时考虑到受低值系统影响时,1000 hPa高度可能会低于10 m,其要素不具备明确物理意义,因此当阵风系数法拟合结果与阵风观测存在差异时,选取ECMWF确定性模式中的10 m风速(W10)、地面2 m温度(T2),以及925、850、700和500 hPa的风速(W925、W850、W700、W500)及温度(T925、T850、T700、T500)等要素来分析差异原因。
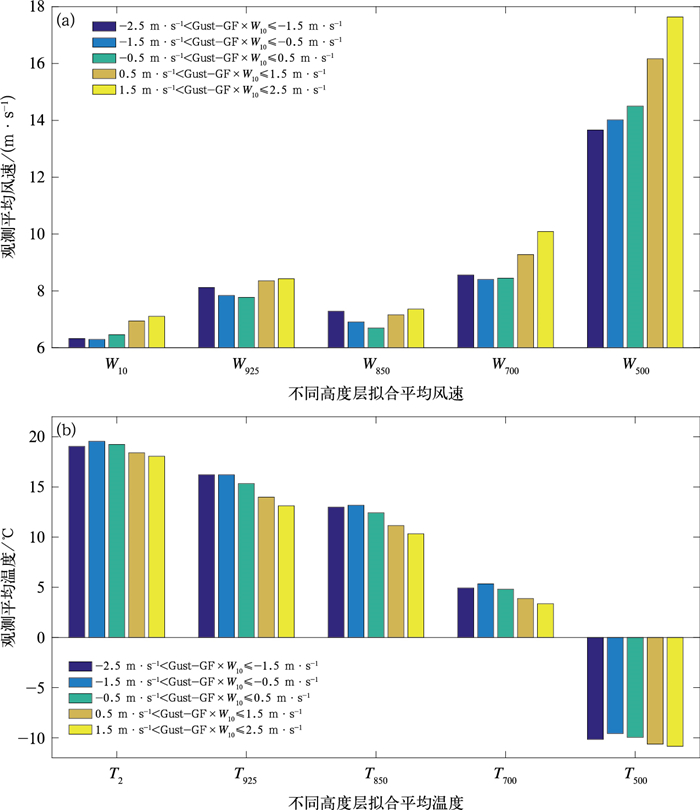
图 4a为阵风系数法拟合结果与阵风观测在不同误差时不同高度层平均的风速。如图所示,当阵风观测减去阵风系数法拟合结果(即Gust-GF×W10)绝对值越大时,即阵风系数法低估程度增加时,所对应的10 m及500 hPa的平均风速也越大;反之,则所对应的10 m及500 hPa风速也越小。当Gust-GF×W10绝对值最小时,即-0.5 m·s-1<Gust-GF×W10≤0.5 m·s-1时,其所对应850 hPa的平均风速为最小值。随着差异增大,850 hPa风速平均值有所增加。对于不同高度层的平均温度而言,随着Gust-GF×W10绝对值的增大,其对应平均温度总体呈现降低的趋势(图 4b)。通过计算阵风与不同高度层的风速、温度值间的简单相关系数(图略),除500 hPa温度与阵风间的相关系数不能够通过水平双侧0.01显著性水平检验外,其余均能够通过。阵风系数法中仅考虑了与阵风相关性最大的10 m风速(相关系数为0.851),忽略了其他高度层风速或温度对阵风不同程度上的影响。
|
图 4 2021年1—12月阵风观测与阵风系法数拟合结果在不同误差下的不同高度层的平均(a)风速和(b)温度 Fig. 4 Average (a) wind speed and (b) temperature at different altitudes under various errors between gust observation and gust factor fitting results from January to December 2021 |
较强的垂直风切变有利于对流天气的发展(何娜等,2020),而对流天气中的下沉气流会影响到地面,使阵风增强(Brasseur,2001)。此外,不同高度层之间的温度差异能够反映出大气的稳定度,可能导致空气的垂直运动,进而影响到阵风。为进一步探究垂直风速变化与垂直温度变化对于阵风系数法拟合结果的影响,首先分别针对垂直方向上的风速及温度数据进行Z-score标准化处理(Manzato,2005),在不改变数据原始分布的基础上使其具有可比较性,标准化处理后的风速或温度值表示其在垂直分布中的相对位置,Z-score计算公式如下:
| $ z(x)=\frac{x-\bar{x}}{\sigma_x} $ | (4) |
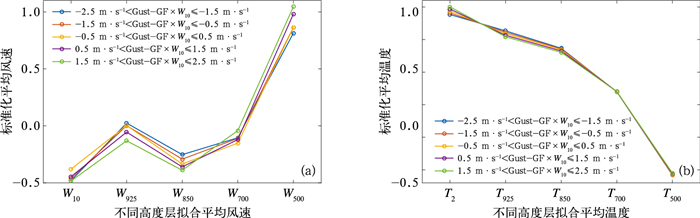
式中:x为数据平均值,σx为数据方差。在不同拟合误差下将标准化后的数据进行平均得到风速及温度的垂直分布(图 5)。如图 5a所示,在不同拟合差异下,500~850 hPa的风速垂直变化(W500-W850)表现出明显的变化规律。W500- W850绝对值越大时,阵风系数法低估的程度越大,即Gust-GF×W10绝对值越大;反之,则高估的程度越大,即Gust-GF×W10绝对值越小。对于温度而言(图 5b),地面2 m至925 hPa的温度变化(T2-T925)在不同拟合差异中表现出一致性的变化规律,即下热上冷的温度分布导致空气垂直运动增强,从而使阵风系数法低估越明显。相反,当T2-T925越小,阵风系数法高估程度越明显。
|
图 5 2021年1—12月阵风观测与阵风系数法拟合结果在不同误差下的标准化平均(a)风速和(b)温度的垂直分布 Fig. 5 Vertical distribution of average standardized (a) wind speed and (b) temperature under various errors between gust observation and gust factor fitting results from January to December 2021 |
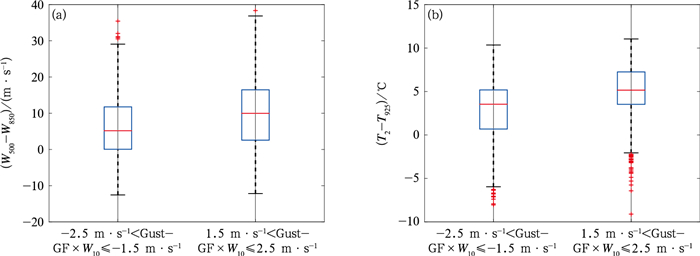
图 6为阵风系数法明显高估(-2.5 m·s-1<Gust-GF×W10≤-1.5 m·s-1)和低估(1.5 m· s-1<Gust-GF×W10≤2.5 m·s-1)时,W500-W850及T2-T925数据分布箱线图。如图所示,在阵风系数法出现明显高估的情况下,W500-W850、T2-T925数据的第25%分位、中位数及第75%分位均要小于阵风系数法低估的情况。阵风系数法出现明显低估时,W500-W850、T2-T925的平均值分别为10.28 m·s-1与4.94℃,而阵风系数法出现明显高估时的平均值分别为6.38 m·s-1与2.82℃。W500-W850、T2-T925同样会对阵风产生影响,导致阵风系数法对阵风的明显高估或低估,通过计算W500-W850、T2-T925与阵风间的相关系数分别为0.113与0.36(通过水平双侧0.01显著性水平检验)。
|
图 6 2021年1—12月不同差异情况下(a)W500-W850,(b)T2-T925数据分布箱线图 注:横线自下而上分别代表最小值、第25%分位数、中位数、第75%分位数及最大值,红色十字表示大于第75%分位数1.5倍四分位差或小于第25%分位数1.5倍四分位差的数值;下同。 Fig. 6 Box plot of (a) W500-W850 and (b) T2-T925 data distribution under various fitting results from January to December 2021 |
阵风系数法预测结果稳定,对大多数阵风具有较好的拟合效果,并且能够降低样本分布不均衡对拟合结果的影响(刘颖和杨轲,2021),因此在阵风系数法预测结果的基础上加入高空要素的信息,以期进一步提高阵风的预报效果。造成我国近海不同海域大风天气过程的主要影响系统有所差异,不同影响系统的高空要素分布及对阵风的影响也有所不同,高空要素信息的加入还可以体现出不同海域阵风预报的差异。通过统计方法能够明确指出不同高度层的风速及温度值、W500-W850、T2-T925对阵风有影响,由于大气运动的高度非线性化,不代表其他层次的风速或温度垂直变化不会对阵风产生影响。研究中选取了5个高度层,共包含10种垂直变化形式,因此也将10种风速垂直变化及温度垂直变化均加入到预测模型中(表 1)。
|
|
表 1 预测模型中不同高度风速及温度的垂直变化 Table 1 Different vertical changes of wind speed and temperature at different altitudes |
利用机器学习方法构建海上阵风预报模型的数学表达式可以写成如下形式:
| $ \text { Gust }=f\left(\mathrm{GF} \times W_{10}, W_i, T_i, \Delta W_k, \Delta T_k\right) $ | (5) |
式中:Wi、Ti分别表示不同高度风速和温度,ΔWk、ΔTk分别表示不同高度的风速及温度变化(表 1),预报因子共计31个。目前决策树、LASSO回归、随机森林等机器学习方法被应用于风速订正(孙全德等,2019;任萍等,2020;韩念霏等,2022),但考虑到本研究中所用于构建预报模型样本较少(共计9309个样本),因此采用更适用于小样本的支持向量机回归(SVR)方法进行预报模型的构建(陈超辉等,2010)。SVR是通过引入核函数将数据映射到高维特征空间,解决在原始空间中线性不可分的问题,将非线性问题转化为线性,并找到具有最小预测误差的超平面机器学习方法,其具有算法简单、计算量小以及易于实现等特点,并且不会出现由于数据维数增加而导致计算量剧增的情况(鞠薇等,2023)。
核函数的选取决定了输出空间到特征空间的映射方式,而核参数的选取直接决定了拟合的精准度及训练速度等性能(高尚等,2013)。常用的核函数有线性核函数、多项式核函数以及高斯核函数等,其中高斯核函数不仅能解决非线性问题,且仅包含一个参数,是被广泛应用的核函数(李清等,2020)。与传统回归模型计算损失的不同,在SVR方法中,当模型输出值与真值之差大于损失距离值后才计算损失,因此在利用SVR进行数据拟合时,除核函数与核参数的确定外,还需要明确损失距离、惩罚系数。在参数的选取问题中,贝叶斯优化方法成为了参数估计领域的重要方法,即通过构造黑箱函数输出的后验概率来寻找函数的最优值,是当前为数不多,具有极好的收敛性理论保证的参数估计方法(李亚茹等,2022)。泛化性是衡量机器学习或深度学习方法的重要指标,即验证其在新的数据中是否能有在训练数据中同样的效果。由于过拟合,导致很多机器学习或深度学习方法在训练数据中能够有很好的表现,而在新的数据中效果较差(沈微微等,2020)。K折交叉验证(K-fold cross-validation)方法是一种被广泛应用于估计泛化误差的方法,通过使用部分数据拟合模型,而另一部分数据来模拟K个训练和测试集,联合K个结果的平均进行泛化误差的估计。结合贝叶斯优化方法与K折交叉验证方法即可以针对预测模型的准确性与稳定性选取出最合适的参数(王宏刚等,2019)。
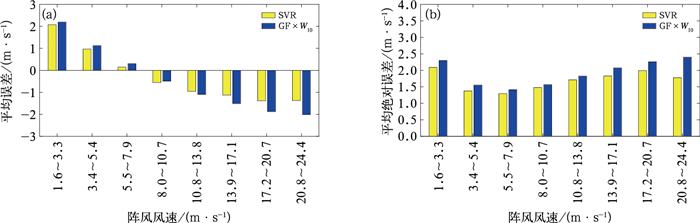
综上所述,利用2021年1—12月数据,选取高斯核函数构建SVR模型。通过贝叶斯优化方法及5折交叉验证法确定损失距离和惩罚系数分别为0.0716和582.8119,高斯核函数参数为36.6715。图 7为利用2021年1—12月阵风系数法与SVR方法在不同风速量级下的平均误差和平均绝对误差。如图 7a所示,除8.0~10.7 m·s-1风速,SVR方法在各个风速级别下的正或负偏差的绝对值均小于阵风系数法,尤其在大级别风速中表现更为明显。表明SVR方法对于大量级阵风预报的偏小程度低于阵风系数法。在平均绝对误差的对比中(图 7b),SVR方法在各个风速级别均小于阵风系数法。平均误差与平均绝对误差的共同改善表明SVR方法能够对不同量级的阵风有更好的刻画。
|
图 7 2021年1—12月SVR方法与阵风系数法的(a)平均误差和(b)平均绝对误差 Fig. 7 Comparison of (a) mean error and (b) mean absolute error of support vector machine regression method and gust factor method from January to December 2021 |
为验证所构建预报模型的实际应用效果,利用2022年1—9月ECMWF确定性模式24 h预报数据对机器学习方法的阵风预报模型进行独立样本的检验。
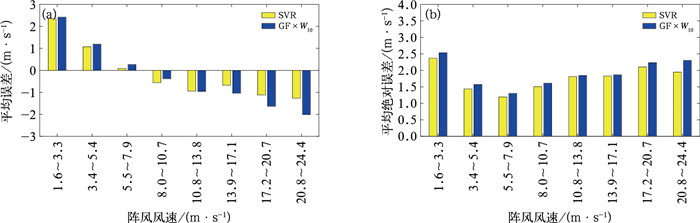
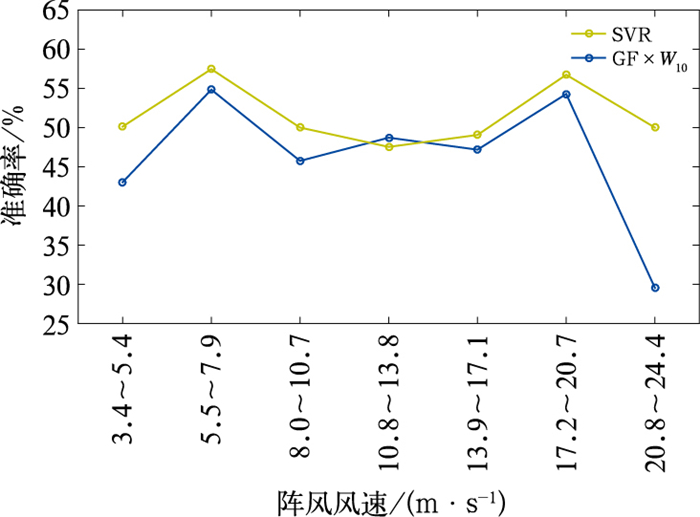
5.1 误差检验图 8为ECMWF确定性模式24 h预报数据的SVR方法、阵风系数法的平均误差和平均绝对误差对比。如图所示,在独立样本的检验中,SVR方法与阵风系数法在不同风速量级下的平均误差及平均绝对误差分布与利用2021年数据的分布基本相同,表明所构建的阵风模型能够对测试数据取得与训练数据较为一致的应用效果。图 9为两种阵风预报方法对于3~9级阵风预报的准确率,由图可见,除10.8~13.8 m·s-1风速外,SVR方法在各级别阵风预报准确率均高于阵风系数法。对于9级阵风,SVR方法的准确率为50%,而阵风系数法为30%。通过上述误差及预报准确率对比表明,SVR方法对我国近海大量级阵风预报效果要优于阵风系数法。
|
图 8 2022年1—9月SVR方法与阵风系数法的(a)平均误差和(b)平均绝对误差 Fig. 8 Comparison of (a) mean error and (b) mean absolute error of support vector machine regression method and gust factor method from January to September 2022 |
|
图 9 2022年1—9月SVR方法和阵风系数法的预报准确率 Fig. 9 Forecast accuracy comparison of support vector machine regression method and gust factor method from January to September 2022 |
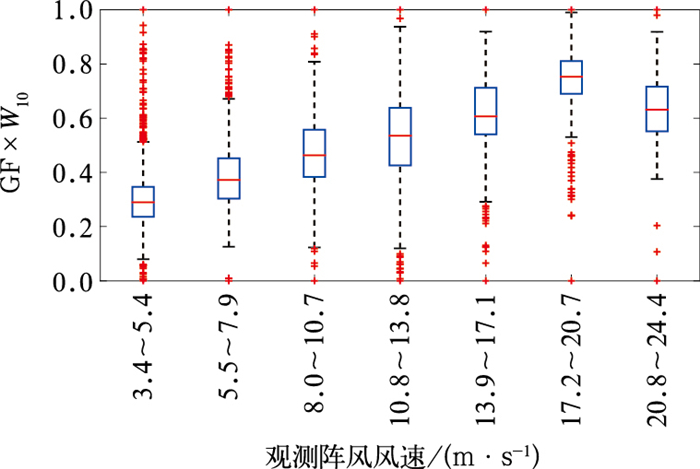
图 10为2022年1—9月阵风实况在3~9级下阵风系数法预报结果分布的箱线图,为便于不同量级风速分布的对比,将阵风系数法预报结果进行归一化处理。如图所示,当实况观测在10.8~13.8 m·s-1时,无论最大值与最小值之间的距离或箱体长度均大于阵风实况在其他级别时的分布,表明出现10.8~13.8 m· s-1阵风时,阵风系数法预报结果的离散度最大。SVR方法的阵风预报是在阵风系数方法基础上加入高空要素信息构建而成,由于阵风系数法对于10.8~ 13.8 m·s-1阵风预报的较大不确定性,因此造成SVR方法对于10.8~13.8 m· s-1级阵风预报准确率(47.5%)略低于阵风系数方法(48.7%)。
|
图 10 2022年1—9月不同阵风观测下阵风系数法预报分布箱线图 注:GF×W10经过归一化处理。 Fig. 10 Box plot of gust forecast results by gust factor method with different observations from January to September 2022 |
研究所建立的阵风预报模型是基于我国近海15个浮标观测站点统一构建而成,虽然其在整体的预报误差及大量级风速预报准确率方面均表现最佳,但仍需验证其是否能够适用于不同海域,尤其是对于大量级阵风的预报效果。因此选取位于我国渤海海峡(站号:54772)、东海南部(站号:58878)及南海北部(站号: 59515)3个浮标观测站点,分别对比SVR方法与阵风系数法对于不同站点全风速(表 2)和8级(17.2 m·s-1)及以上阵风的预报误差(表 3)。如表 2所示,SVR方法对于不同站点全风速预报的负偏差均小于阵风系数法,且平均绝对误差也均小于阵风系数法。由于风速的明显偏态分布,两种阵风预报方法在全风速下的误差对比更多体现为小量级风速预报效果的对比。如表 3所示,SVR方法对于8级及以上阵风预报的负偏差及平均绝对误差也均小于阵风系数法,表明该方法不仅在小量级阵风预报中能有所改善,在大级别阵风中也能取得更好预报效果,具有一定的通用性。
|
|
表 2 2022年1—9月SVR方法、阵风系数法对于不同站点全风速预报平均误差和平均绝对误差(单位: m·s-1) Table 2 Comparison of mean error and mean absolute error by support vector machine regression method and gust factor method for all wind speed at different stations from January to September 2022 (unit: m·s-1) |
|
|
表 3 2022年1—9月SVR方法、阵风系数法对于不同站点17.2 m·s-1及以上阵风平均误差及平均绝对误差(单位: m·s-1) Table 3 Comparison of mean error and mean absolute error by support vector machine regression method and gust factor method for 17.2 m·s-1 and above gusts at different stations from January to September 2022 (unit: m·s-1) |
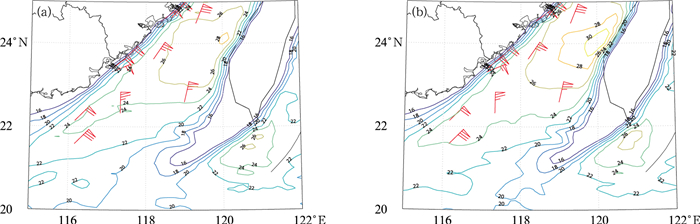
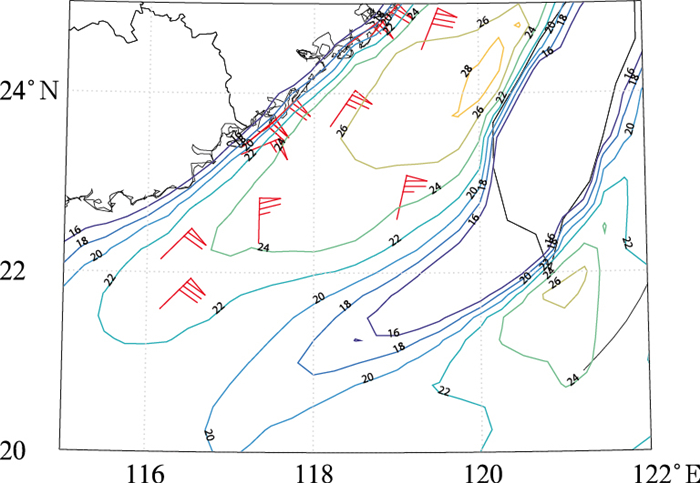
本研究中采用线性插值方法将高空要素数据插值至0.125°×0.125°,将地面及插值后的高空格点数据代入SVR模型中生成0.125°×0.125°格点阵风预报场,以验证其在大风天气过程中的预报效果。受冷空气影响,2022年2月20日08时(北京时,下同),我国台湾海峡、南海东北部海域出现了9~10级阵风。在此次大风天气过程中,SVR方法24 h预报(图 11b)的24 m·s-1及26 m·s-1的大风范围明显大于阵风系数法24 h预报(图 11a),与实况观测更为接近。对于台湾海峡东部海域,阵风系数法仅预报出小范围28 m·s-1阵风,而SVR方法预报出30 m·s-1的阵风。海上观测资料稀缺,为验证SVR方法对于台湾海峡东部海域预报的可信度,对比了2022年2月20日08时ERA5再分析数据中的小时内最大阵风数据(图 12)。如图所示,再分析数据中,台湾海峡东部海域存在着一定范围28 m· s-1的阵风。对于海上的大量级风速,ERA5中的10 m风速存在着较实况明显偏小的情况(渠鸿宇等,2022),而ERA5中的小时内最大阵风数据是在最大10 m风速基础上得到的,因此其可能同样存在着较实况明显偏小的情况,即台湾海峡东部海域有可能存在更大范围28 m·s-1阵风或更大的阵风,SVR方法预报的结果具有一定的可信度。
|
图 11 2022年2月19日08时起报的(a)阵风系数法和(b)SVR方法的10 m风速(等值线,单位:m·s-1)24 h预报 注:红色风羽为2月20日08时阵风观测实况,下同。 Fig. 11 24 h forecast of 10 m wind speed (contour, unit: m·s-1) by (a) gust factor method and (b) support vector machine regression method initiated at 08:00 BT 19 February 2022 |
|
图 12 2022年2月20日08时ERA5再分析数据中的小时内最大阵风风速(等值线,单位:m·s-1) Fig. 12 Hourly maximum gust wind speed (contour, unit: m·s-1) in ERA5 reanalysis data at 08:00 BT 20 February 2022 |
由于数值模式的动力框架、物理参数化、初始场误差、分辨率等因素的影响,数值模式存在着不可避免的预报误差(Toth et al, 2001),在此次大风天气过程中,ECMWF确定性模式24 h预报的10 m风速较实况观测存在有一定偏差(图 13),导致利用阵风系数法的阵风预报出现偏差,但考虑了高空气象要素的SVR方法能够在10 m风速预报出现一定偏差时获得更好的预报效果。

|
图 13 2022年2月19日08时起报的ECMWF确定性模式10 m风速(等值线,单位:m·s-1)24 h预报 Fig. 13 24 h forecast of 10 m wind speed (contour, unit: m·s-1) by ECMWF deterministic model initiated at 08:00 BT 19 February 2022 |
利用2021年1—12月中国气象局地面实况观测数据中小时内极大风数据与ECMWF确定性模式24 h预报数据中的10 m风速、2 m温度,以及925、850、700、500 hPa的风速及温度数据,构建了基于机器学习方法的我国近海阵风预报模型。利用2022年1—9月数据进行独立样本检验,通过与阵风系数法的对比检验,得出以下结论:
(1) 阵风系数法虽然能够对多数阵风有很好的拟合效果,但在部分情况下会出现对阵风明显高估或低估的情况。通过统计分析表明,不同高度层的风速及温度值或其垂直变化均会对阵风产品产生影响。
(2) 在阵风系数法的基础上加入高空气象要素信息,采用支持向量机回归方法构建的我国近海阵风预报模型的预报效果总体上优于阵风系数法。支持向量机回归方法对于9级阵风预报准确率为50%,明显高于阵风系数法的30%,且对于不同海域的大量级风速预报具有较好的效果,能够适用于我国近海的阵风预报。
(3) 在个例对比分析中,虽然ECMWF确定性模式的10 m风速预报与实况存在较大偏差,但考虑了高空要素信息的支持向量机回归模型能够取得较阵风系数法更接近实况的阵风预报结果。
本研究仅基于ECMWF确定性模式的24 h预报数据构建了阵风系数法与机器学习相结合的我国近海阵风预报模型,在今后的工作中可以将该方法拓展到不同预报时效,以实现其在业务预报中的应用。此外,本文中仅利用了不同高度层的风速及温度要素,后期可以加入其他气象要素,如湿度及气压等,采用其他机器学习(深度学习)方法进一步完善该预报模型。虽然预报模型中的因变量为小时内极大风,但是自变量均为数值模式预报的时刻要素值,以及受到样本数据分布的不均衡影响,均会使预报结果与实况观测间存在一定差异,尤其是大量级阵风的预报(Coburn and Pryor, 2022)。因此在实际预报工作中可以考虑利用频率密度匹配等方法对预报结果进行再次修订,以进一步提升海上阵风预报效果。
陈超辉, 李崇银, 谭言科, 等, 2010. 基于交叉验证的多模式超级集合预报方法研究[J]. 气象学报, 68(4): 464-476. Chen C H, Li C Y, Tan Y K, et al, 2010. Research of the multi-model super-ensemble prediction based on cross-validation[J]. Acta Meteor Sin, 68(4): 464-476 (in Chinese). DOI:10.3969/j.issn.1001-7313.2010.04.010
|
程雪玲, 房小怡, 卢俐, 等, 2016. 强风天气下边界层结构特征[J]. 气候与环境研究, 21(1): 99-106. Cheng X L, Fang X Y, Lu L, et al, 2016. The characteristics of boundary layer structure under strong wind weather[J]. Climatic Environ Res, 21(1): 99-106 (in Chinese).
|
高尚, 刘夫成, 于化龙, 2013. 不同准则下的线性支持向量机回归模型[J]. 东南大学学报(自然科学版), 43(Z1): 44-47. Gao S, Liu F C, Yu H L, 2013. Linear support vector machine regression models under different criteria[J]. J Southeast Univ (Nat Sci Ed), 43(Z1): 44-47 (in Chinese).
|
韩念霏, 杨璐, 陈明轩, 等, 2022. 京津冀站点风温湿要素的机器学习订正方法[J]. 应用气象学报, 33(4): 489-500. Han N F, Yang L, Chen M X, et al, 2022. Machine learning correction of wind, temperature and humidity elements in Beijing-Tianjin-Hebei Region[J]. J Appl Meteor Sci, 33(4): 489-500 (in Chinese).
|
何娜, 丁青兰, 俞小鼎, 等, 2020. 北京及周边地区雷暴阵风锋特征统计分析[J]. 气象学报, 78(2): 250-259. He N, Ding Q L, Yu X D, et al, 2020. Statistical analysis of thunderstorm gust front characteristics in Beijing and surrounding areas[J]. Acta Meteor Sin, 78(2): 250-259 (in Chinese).
|
胡波, 2017. 浙江沿海台风阵风系数的影响因子分析[J]. 热带气象学报, 33(6): 841-849. Hu B, 2017. Analysis of gust factor associated with typhoons on Zhejiang Coast[J]. J Trop Meteor, 33(6): 841-849 (in Chinese).
|
胡海川, 刘珺, 林建, 2022. 基于预报方程的我国近海阵风预报[J]. 气象, 48(3): 334-344. Hu H C, Liu J, Lin J, 2022. Application of prediction equation to gust forecasting for Chinese offshore areas[J]. Meteor Mon, 48(3): 334-344 (in Chinese).
|
胡海川, 赵伟, 董林, 2021. 概率密度匹配方法在我国近海海面10m风速预报中的应用[J]. 热带气象学报, 37(1): 91-101. Hu H C, Zhao W, Dong L, 2021. Application of probability density function matching in the offshore 10 m wind speed forecasting in China[J]. J Trop Meteor, 37(1): 91-101 (in Chinese).
|
鞠薇, 鲁昌华, 张玉钧, 等, 2023. 集成学习结合波长选取的有机物红外光谱定量回归方法研究[J]. 光谱学与光谱分析, 43(1): 239-247. Ju W, Lu C H, Zhang Y J, et al, 2023. Research on quantitative regression method of IR spectra of organic compounds based on ensemble learning with wavelength selection[J]. Spectrosc Spect Anal, 43(1): 239-247 (in Chinese).
|
李清, 苏强, 林英, 等, 2020. 基于机器学习的住院患者压力性损伤分析与预测[J]. 同济大学学报(自然科学版), 48(10): 1530-1536. Li Q, Su Q, Lin Y, et al, 2020. Pressure injury analysis and prediction based on machine learning methods[J]. J Tongji Univ (Nat Sci), 48(10): 1530-1536 (in Chinese). DOI:10.11908/j.issn.0253-374x.20096
|
李亚茹, 张宇来, 王佳晨, 2022. 面向超参数估计的贝叶斯优化方法综述[J]. 计算机科学, 49(Z1): 86-92. Li Y R, Zhang Y L, Wang J C, 2022. Survey on Bayesian optimization methods for hyper-parameter tuning[J]. Comput Sci, 49(Z1): 86-92 (in Chinese).
|
刘香娥, 郭学良, 2012. 灾害性大风发生机理与飑线结构特征的个例分析模拟研究[J]. 大气科学, 36(6): 1150-1164. Liu X E, Guo X L, 2012. Analysis and numerical simulation research on severe surface wind formation mechanism and structural characteristics of a squall line case[J]. Chin J Atmos Sci, 36(6): 1150-1164 (in Chinese).
|
刘颖, 杨轲, 2021. 基于深度集成学习的类极度不均衡数据信用欺诈检测算法[J]. 计算机研究与发展, 58(3): 539-547. Liu Y, Yang K, 2021. Credit fraud detection for extremely imbalanced data based on ensemble deep learning[J]. J Comput Res Dev, 58(3): 539-547 (in Chinese).
|
渠鸿宇, 黄彬, 赵伟, 等, 2022. HRCLDAS-V1.0和ERA5海面风场对比评估分析[J]. 热带气象学报, 38(4): 569-579. Qu H Y, Huang B, Zhao W, et al, 2022. Comparison and evaluation of HRCLDAS-V1.0 and ERA5 sea-surface wind fields[J]. J Trop Meteor, 38(4): 569-579 (in Chinese).
|
全继萍, 李青春, 仲跻芹, 等, 2022. "CMA北京模式"中三种不同阵风诊断方案在北京地区大风预报中的评估[J]. 气象学报, 80(1): 108-123. Quan J P, Li Q C, Zhong J Q, et al, 2022. Evaluation of three different gust diagnostic schemes in the CMA-BJ for gale forecasting over Beijing[J]. Acta Meteor Sin, 80(1): 108-123 (in Chinese).
|
任萍, 陈明轩, 曹伟华, 等, 2020. 基于机器学习的复杂地形下短期数值天气预报误差分析与订正[J]. 气象学报, 78(6): 1002-1020. Ren P, Chen M X, Cao W H, et al, 2020. Error analysis and correction of short-term numerical weather prediction under complex terrain based on machine learning[J]. Acta Meteor Sin, 78(6): 1002-1020 (in Chinese).
|
沈微微, 李颖, 杨志豪, 等, 2020. 防止过拟合的属性约简[J]. 计算机应用研究, 37(9): 2665-2668. Shen W W, Li Y, Yang Z H, et al, 2020. Attribute reduction with avoiding overfitting[J]. Appl Res Comput, 37(9): 2665-2668 (in Chinese).
|
盛杰, 郑永光, 沈新勇, 等, 2019. 2018年一次罕见早春飑线大风过程演变和机理分析[J]. 气象, 45(2): 141-154. Sheng J, Zheng Y G, Shen X Y, et al, 2019. Evolution and mechanism of a rare squall line in early spring of 2018[J]. Meteor Mon, 45(2): 141-154 (in Chinese).
|
孙全德, 焦瑞莉, 夏江江, 等, 2019. 基于机器学习的数值天气预报风速订正研究[J]. 气象, 45(3): 426-436. Sun Q D, Jiao R L, Xia J J, et al, 2019. Adjusting wind speed prediction of numerical weather forecast model based on machine learning methods[J]. Meteor Mon, 45(3): 426-436 (in Chinese).
|
王宏刚, 王姗姗, 姚佳, 等, 2019. 基于邻域粗糙集与支持向量机的射频识别系统识别率预测[J]. 计算机集成制造系统, 25(12): 3170-3180. Wang H G, Wang S S, Yao J, et al, 2019. Tag identification rate prediction based on neighborhood rough set and support vector machine[J]. Comput Integr Manuf Syst, 25(12): 3170-3180 (in Chinese).
|
杨璐, 王晓丽, 宋林烨, 等, 2023. 基于阵风系数模型的百米级阵风客观预报算法研究[J]. 气象学报, 81(1): 94-109. Yang L, Wang X L, Song L Y, et al, 2023. An algorithm for objective forecasting of gust winds at 100 m horizontal resolution based on a gust coefficient model[J]. Acta Meteor Sin, 81(1): 94-109 (in Chinese).
|
张延彪, 陈明轩, 韩雷, 等, 2022. 数值天气预报多要素深度学习融合订正方法[J]. 气象学报, 80(1): 153-167. Zhang Y B, Chen M X, Han L, et al, 2022. Multi-element deep learning fusion correction method for numerical weather prediction[J]. Acta Meteor Sin, 80(1): 153-167 (in Chinese).
|
周福, 蒋璐璐, 涂小萍, 等, 2017. 浙江省几种灾害性大风近地面阵风系数特征[J]. 应用气象学报, 28(1): 119-128. Zhou F, Jiang L L, Tu X P, et al, 2017. Near-surface gust factor characteristics in several disastrous winds over Zhejiang Province[J]. J Appl Meteor Sci, 28(1): 119-128 (in Chinese).
|
周康辉, 郑永光, 韩雷, 等, 2021. 机器学习在强对流监测预报中的应用进展[J]. 气象, 47(3): 274-289. Zhou K H, Zheng Y G, Han L, et al, 2021. Advances in application of machine learning to severe convective weather monitoring and forecasting[J]. Meteor Mon, 47(3): 274-289 (in Chinese).
|
Blaes J L, Glenn D A, Hawkins D R, et al, 2014. Developing a dataset of wind gust factors to improve forecasts of wind gusts in tropical cyclones[C]//39th National Weather Association Annual Meeting. Salt Lake City: National Weather Association.
|
Brasseur O, 2001. Development and application of a physical approach to estimating wind gusts[J]. Mon Wea Rev, 129(1): 5-25.
|
Coburn J, Pryor S C, 2022. Do machine learning approaches offer skill improvement for short-term forecasting of wind gust occurrence and magnitude?[J]. Wea Forecasting, 37(5): 525-543.
|
ECMWF, 2016. IFS Documentation CY45R2-Part Ⅳ: physical processes[R]. Reading: ECMWF.
|
Kahl J D W, 2020. Forecasting peak wind gusts using meteorologically stratified gust factors and MOS Guidance[J]. Wea Forecasting, 35(3): 1129-1143.
|
Kahl J D W, Selbig B R, Harris A R, 2021. Meteorologically stratified gust factors for forecasting peak wind gusts across the United States[J]. Bull Amer Meteor Soc, 102(9): E1665-E1671.
|
Letson F, Pryor S C, Barthelmie R J, et al, 2018. Observed gust wind speeds in the coterminous United States, and their relationship to local and regional drivers[J]. J Wind Eng Ind Aerod, 173: 199-209.
|
Manzato A, 2005. The use of sounding-derived indices for a neural network short-term thunderstorm forecast[J]. Wea Forecasting, 20(6): 896-917.
|
Rasp S, Lerch S, 2018. Neural networks for postprocessing ensemble weather forecasts[J]. Mon Wea Rev, 146(11): 3885-3900.
|
Sheridan P, 2018. Current gust forecasting techniques, developments and challenges[J]. Adv Sci Res, 15: 159-172.
|
Shu Z R, Li Q S, He Y C, et al, 2015. Gust factors for tropical cyclone, monsoon and thunderstorm winds[J]. J Wind Eng Ind Aerod, 142: 1-14.
|
Toth Z, Zhu Y J, Marchok T, 2001. The use of ensembles to identify forecasts with small and large uncertainty[J]. Wea Forecasting, 16(4): 463-477.
|
Yu B, Chowdhury A G, 2009. Gust factors and turbulence intensities for the tropical cyclone environment[J]. J Appl Meteor Climatol, 48(3): 534-552.
|
 2024, Vol. 50
2024, Vol. 50 
