2. 杭州市气象局,杭州 310057
2. Hangzhou Meteorological Bureau, Hangzhou 310057
强对流天气主要包括冰雹、雷暴大风、短时强降水和龙卷,一直是天气预报业务中的难点, 其中一大挑战是分类强对流天气预报(郑永光等,2017)。热力和动力物理参数敏感性分析及利用“配料法”,统计分析方法以及高分辨率数值模式进行客观预报方法的研究逐渐成为预报强天气潜势的基础(郑永光等,2015;漆梁波,2015;孙继松和陶祖钰,2012;俞小鼎等,2012;王秀明等,2014)。“配料法”由Doswell Ⅲ et al(1996)提出,该方法物理量意义明确,在强对流的潜势分类预报中得到广泛应用。利用探空数据或数值模式数据计算物理意义明确的对流参数和物理量并作为预报因子,结合基于历史资料获得的统计关系或经验阈值,可以较好地区分强对流天气的类型并进行潜势预报(刘晓璐等,2014;李耀东等,2004;俞小鼎,2011)。周方媛等(2020)利用探空资料计算对流参数及时间变量,采用逐步回归方法建立了分类强对流的潜势预报方程,并提出基于关键对流参数的分级预报方法。雷蕾等(2011)、马淑萍等(2019)、王迪等(2020)、高晓梅等(2018)、樊李苗和俞小鼎(2013;2020)利用探空或者再分析资料计算对流参数和物理参数的变化,通过统计冰雹、雷暴大风和强降水相关性较好的预报因子和阈值,大致可以区分风雹类与强降水天气。曾明剑等(2015)基于中尺度数值模式的对流参数,通过筛选物理量和权重分配得到了分类强对流天气的概率预报。张小玲等(2010)较早基于“配料法”开展了暴雨预报试验;朱月佳等(2019)借鉴“配料法”的思路建立了基于集合预报的对流联合概率预报方法;张华龙等(2021)提出基于显著性和敏感性评价的物理量优选和因子分析法,构建分区短时强降水的概率预报模型, 对区域性短时强降水取得了较好的应用效果;赵渊明和漆梁波(2021)应用动态权重多模式集成方法改进了短时临近定量降水概率预报;田付友等(2024b)设计了融合模糊逻辑方法的分类强对流客观短期概率预报系统,在国家级业务中得到应用。
上述研究侧重于探空或数值模式资料的常规统计方法应用于强对流分类预报。人工智能算法拥有强大的非线性拟合能力,善于处理高维数据信息,可以自动挖掘数据背后的物理关系,而较少地依赖人的经验,在强天气领域展现出较强的预测和学习能力(周康辉等,2021a;McGovern et al, 2017;Han et al, 2017; Lagerquist et al, 2017; Sun et al, 2014)。基于探空数据计算对流指数因子,利用BP神经网络方法应用于闪电潜势预报(陈勇伟等, 2013)和雷暴潜势预报模型建模(赵旭寰等, 2009; 杨仲江等, 2013),取得了较好的预报效果。Manzato(2013)同样利用探空计算的对流指数因子,构建多个神经网络模型,并用集成学习算法,得到更有效的冰雹预报。周康辉等(2021b)基于多源观测数据和高分辨率数值天气预报数据的特性,构建了一个双输入、单输出的深度学习语义分割模型,可较好地实现0~6 h的闪电落区预报。韩丰等(2021)利用探空站的大气层结和对流参数作为特征参数,基于集成学习方法,建立短时强降水事件预报模型,通过使用分段权重损失函数调优,提升模型预报的准确率。朱岩等(2021)利用XGBoost机器学习方法建立基于数值模式预报物理因子的短时强降水预报模型,能较好地描述强降水发生的概率和落区。李文娟等(2018)基于数值模式和随机森林算法建立了分类强对流的潜势预报模型。Herman and Schumacher(2018)利用NOAA全球集合预报系统数据,构建了随机森林模型,能够实现2~3 d的极端降水预报。Zhou et al(2019)将6层卷积神经网络应用于分类强对流的潜势预测,利用NCEP再分析资料计算的超过100个对流指数和物理量,开展强对流天气的分类训练,其分类强对流预报产品已经成为中央气象台强对流天气预报重要的业务参考产品(张小玲等,2018)。
综上所述,基于探空或数值模式的机器学习方法在强对流预报方面表现出良好的应用前景,但是上述研究侧重于人工智能方法的大数据自动建模,模型的可解释性相对较差。将传统“配料法”和机器学习算法融合可能是改进强对流预报的有效方法之一。因此,本文通过构建数值模式资料的机器学习分类和“配料法”的融合方法,探讨提高短时强降水与雷暴大风时空分辨率和预报准确率的方法。
1 数据和方法 1.1 格点化实况分析场数据观测数据来源于华东地区11 300个自动气象观测站点,其中浙江省有1728个,短时强降水实况选用逐小时降水资料,判识标准为小时降水量超过20 mm。雷暴大风实况使用自动观测资料和闪电监测资料进行综合判断,闪电定位仪数据采用最邻近插值方法插值到0.25°×0.25°网格点上,形成小时累计闪电次数网格数据,再采用最邻近插值方法将闪电网格数据插值到观测站点。小时累计闪电次数≥1次并且该时次小时极大风速≥17.2 m· s-1,则判定该自动站出现雷暴大风。站点数据经质量控制后再进行格点化处理,得到短时强降水、雷暴大风的格点分析场数据,分辨率为0.05°×0.05°,数据用于分类强对流的数值模式预报数据的提取和检验。
1.2 数值模式分析场和预测数据数值模式分析场采用NCEP 1°×1°再分析资料,用于构建10年以上的分类强对流机器学习训练集;预报则采用浙江快速更新同化系统(ZJWARRS)数据,空间分辨率为0.03°×0.03°,逐3小时更新,计算得到高时空分辨率的强对流潜势分类预报场。分类强对流逐小时预报模型的构建采用中尺度数值模式CMA-SH9数据。模式统计资料时间段为2019—2021年4—9月,范围为27°~31.5°N、117.5°~123°E。数据处理为等经纬度网格数据,水平分辨率为0.05°×0.05°。本研究中,为了统一数值模式的空间分辨率,采用双线性插值的方法,将不同空间分辨率的数值模式数据均插值至0.05°的空间分辨率,大致相当于5 km。
1.3 方法和步骤融合方法的设计分为三个步骤。
(1) 基于XGBoost机器学习方法实现雷暴大风和短时强降水天气的客观分类和潜在落区预报;
(2) 统计分析中尺度模式预报降水和物理量的最佳空间邻域半径和概率密度分布特征,利用组合最优TS评分提取物理量阈值,构建要素空间邻域“配料”模型;
(3) 对机器学习分类预报结果与“配料”组合因子的二分类(有/无)判别场进行联合判别,最终得到雷暴大风和短时强降水的逐小时确定性预报。
2 基于XGBoost的强对流分类潜势预报模型 2.1 XGBoost的原理XGBoost是当前广泛应用的机器学习算法之一,是由Chen and Guestrin(2016)提出来的一种基于Boosting思想的集成学习算法,是梯度提升迭代决策树(GBDT)的改进,具有防止过拟合、算法效率高、损失计算精确等特点,对稀疏数据的处理能力卓越,其原理是通过弱分类器的迭代计算来实现精确分类。首先将原始数据集分割成多个子数据集,将每个子数据集随机分配给基分类器进行预测,然后将弱分类的结果按照一定的权重进行计算,由模型、参数和目标函数组成。其中,模型是根据给定的输入样本因子预测输出的结果,参数是指最终建立的最优模型对应的系数,而目标函数的优化情况则决定了模型的准确性,目标函数优化得越好,预测结果就越接近真实值。目标函数由两部分组成,如式(1)所示:
| $ \operatorname{Obj}(\theta)=\sum\limits_{i=1}^n L\left(y_i, \hat{y}_l\right)+\sum\limits_{k=1}^K \mathit{Ω}\left(f_k\right) $ | (1) |
式中:右侧第一项代表损失函数,n表示所用的样本数量,yi表示真实值,ŷl表示预测值;右侧第二项是正则化项,用于控制模型的复杂度,防止过拟合,K表示共有K颗决策树,fk表示当前迭代的误差。
XGBoost采用加法训练,即模型的收敛目标不是直接优化整个目标函数,而是分步优化目标函数,如式(2)所示:
| $ \begin{gathered} \hat{y}_i^{(0)}=0 \\ \hat{y}_i^{(1)}=f_1\left(x_i\right)=\hat{y}_i^{(0)}+f_1\left(x_i\right) \\ \hat{y}_i^{(2)}=f_1\left(x_i\right)+f_2\left(x_i\right)=\hat{y}_i^{(1)}+f_2\left(x_i\right) \\ \vdots \\ \hat{y}_i^{(k)}=\sum\limits_{j=1}^k f_j\left(x_i\right)=\hat{y}_i^{(k-1)}+f_k\left(x_i\right) \end{gathered} $ | (2) |
式中:ŷi(k)为第k轮模型预测,ŷi(k-1)为保留前面k-1轮的模型预测,fk(xi)为新加的函数。将式(2)代入式(1),可以得到模型在训练第k棵决策树时的目标函数为:
| $ \operatorname{Obj}(\theta)=\sum\limits_{i=1}^n L\left[y_i, \hat{y}_i{ }^{(k-1)}+f_k\left(x_i\right)\right]+\mathit{Ω}\left(f_k\right) $ | (3) |
其中心思想为不断进行特征分裂生长成树,每次生成的树是一个新函数,用来拟合上次的残差;最后将每个叶节点的计算值相加即为最终的预测值。式(3)中,右侧第一项是损失项。与其他常用的组合预测模型随机森林和梯度提升回归树相比,XGBoost通过列采样和两阶泰勒展开以及正则项,具有更好的性能和良好的拟合能力,并且运行速度比大多数模型都要快。
2.2 机器学习强对流潜势分类模型构建过程 2.2.1 选取预报因子本文将XGBoost机器学习算法应用于强对流的环境场分类。将基于NCEP再分析资料08时(北京时,下同) 分析场计算的若干对流指数和物理量指标作为输入变量,包括水汽因子、热力因子、动力因子、特殊高度层及综合指数等共68类组成预报因子数据集,涵盖了地面至500 hPa的多层次要素,具体参见李文娟等(2018)。通过机器学习的多分类算法,学习不同类型强对流(短时强降水、雷暴大风)环境场的特征差异性,以达到强对流客观分类的目的。
2.2.2 选取目标变量目标变量分为三类,分别是短时强降水、雷暴大风和无强对流天气。以2005—2018年浙江省69个基准站点的监测实况为标准,选取时段为08—20时,考虑到NCEP再分析资料的空间代表性,雷暴大风选取影响范围相对较大的过程,至少三个站点出现8级或以上雷暴大风记为一次过程;短时强降水发生概率远高于雷暴大风过程,因此考虑到多分类训练数据的平衡性,仅选取11个地市级代表站的短时强降水过程,任一个站点出现20 mm·h-1以上降水,记为一次过程。强对流天气往往是相伴产生的,为了取样的平衡性,在分类过程中遵循一定的原则,对于雷暴大风和短时强降水均出现的情况,一般记为雷暴大风过程,但降水强度在50 mm·h-1及以上的极端降水则同时标记为短时强降水和雷暴大风过程;无强对流样本选择余地较大,为了增加与强对流天气的区分度,挑选标准以全省69个基准站无雷暴日和小于10 mm·h-1降水样本为主。由于训练数据对局地性、分散性强对流采样不足,可以通过构建动态学习库的方式,将预报失败的样本重新进入训练库,来弥补局地强对流的训练不足。
最终得到的数据集由1440个样本组成。其中,短时强降水418个,雷暴大风347个,无强对流样本675个。按照近似8∶2的比例随机划分为训练集和测试集:约80%的样本用于建立强对流潜势分类模型,剩余的约20%的样本用于开展独立检验。
2.2.3 模型参数设置模型训练参数的设置有三种:一般参数、提升参数和学习参数,调整的参数主要有每棵树的最大深度、学习率和损失函数以及迭代次数。树深参数设置越大越容易过拟合,默认设置为6;学习率指每个迭代产生的模型的权重,该参数越小计算速度越慢,该参数过大,则有可能无法收敛,默认设置为0.05;解决不同的问题,选择不同的损失函数,该模型选择解决多分类问题的损失函数;最大迭代次数的设置则根据模型的收敛情况进行调整。
2.3 精度评价和重要性因子评价为了客观评测多分类模型的分类效果,利用混淆矩阵和准确率进行模型评价。混淆矩阵是衡量分类模型准确度最直观、计算最简单的方法,具体定义如表 1所示,其中TP表示正类样本中分类正确的数量,FN表示将正类误分为负类的样本数,FP表示将负类错分为正类的样本数,TN表示负类样本中分类正确的样本数。分类正确的样本在样本总数中的占比即为准确率,这是分类器最常用到的评价指标;准确率越高,分类器越好。最后模型在测试集的混合矩阵结果如表 2所示。
|
|
表 1 混淆矩阵 Table 1 Confusion matrix |
|
|
表 2 XGBoost模型预测的混淆矩阵(样本数) Table 2 The confusion matrix of XGBoost model prediction |
由表 2计算可得,XGBoost模型预测准确率达到85.96%,说明模型的整体分类性能较好,有无强对流的分类准确率达到96%,对短时强降水和雷暴大风的分类准确率也达到76%以上,由于强对流往往相伴产生,模型的训练期样本在分类的过程中,会存在混淆的情况,也会导致一定错误率的增加。
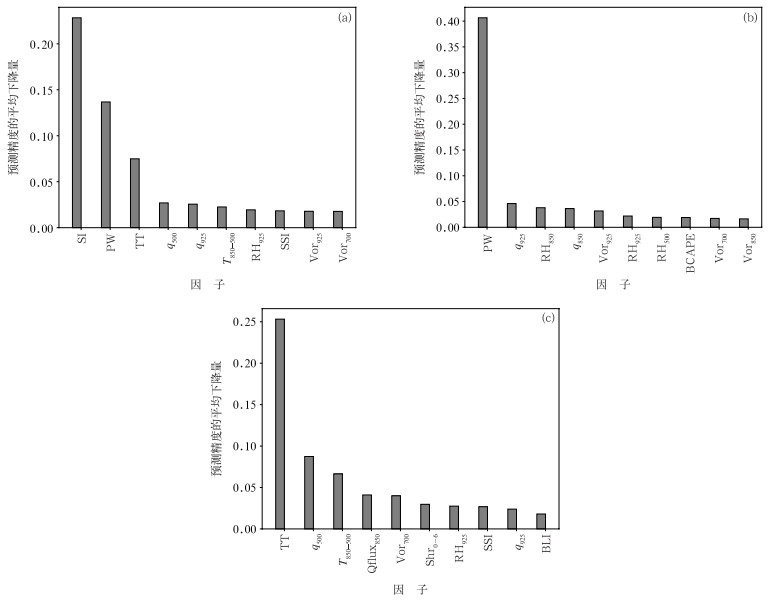
XGBoost算法可通过影响强对流分类因子的重要性排序增加模型的可解释性,数值越大表示越重要。图 1a可见,强对流分类因子的前三项显著高于其他指标,沙氏指数(SI)表征热力不稳定,在有无强对流的分类过程中贡献最高;其次是整层可降水量(PW),是短时强降水分类贡献最为显著的因子;排序第三的是总温度指数(TT),表征大气中的总能量,在雷暴大风分类中贡献显著;其他表征环境高低层温差(T850-500)和中低层水汽含量(比湿q、相对湿度RH)的因子贡献相当。从短时强降水和雷暴大风的分类因子重要性排序可见(图 1b, 1c),短时强降水排序靠前的是PW、q925、RH850和q850等表征中低层水汽条件的因子,其次是925 hPa涡度(Vor925);而雷暴大风与TT、q500、T850-500等因子密切相关,可见机器学习自动筛选的因子和已有的统计结果及主观经验基本相符,通过重要性因子的排序可以一定程度反映模型表征的物理含义。
|
图 1 XGBoost对强对流分类前十位因子重要性排序(a)强对流分类, (b)短时强降水, (c)雷暴大风
注: SI: 沙氏指数 TT: 总温度指数 T850-500: 850 hPa与500 hPa温度差 PW: 整层可降水量 BLI: 最佳抬升指数 RH500、RH850和RH925: 500、850、925 hPa相对湿度 SSI: 风暴强度指数 Qflux850: 850 hPa水汽通量 Vor700、Vor850和Vor925: 700、850、925 hPa涡度 BCAPE: 最佳不稳定能量 Shr0~6: 0~6 km垂直风切变 q500、q850和q925: 500、850、925 hPa比湿 Fig. 1 Importance ranking of the top 10 factors of severe convection classification by XGBoost (a) classification of convective storm, (b) short-time heavy rainfall, (c) thunderstorm gale |
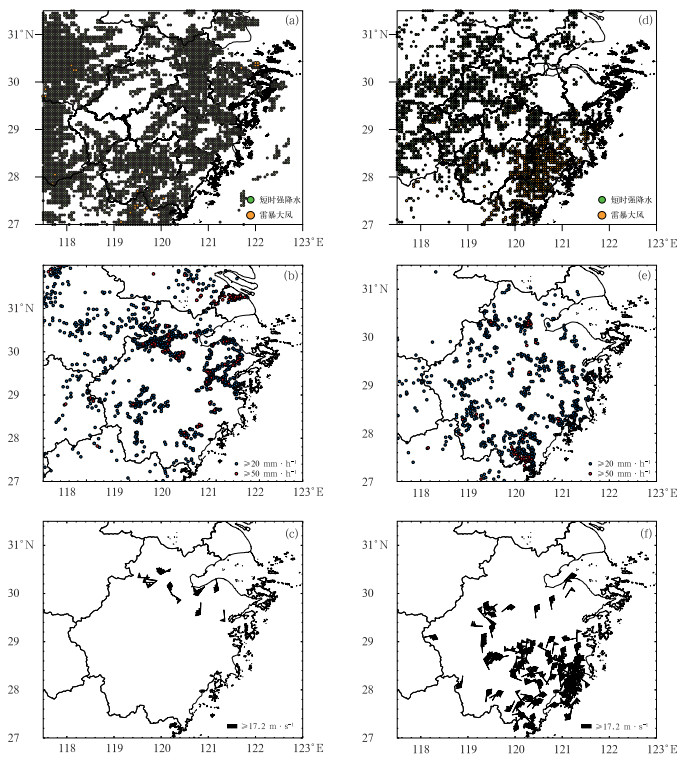
以2023年7月21日和8月7日两次强对流过程为例(图 2),说明机器学习的分类预报实效。2023年7月21日出现了大范围以短时强降水为主的灾害性天气,伴随局地分散性雷暴大风,机器学习分类模型较准确地预报出强对流天气的主要类型和落区,但是对局地分散性大风存在一定的偏差。2023年8月7日是一次大范围混合性的强对流过程,机器学习模型较好地预报出东南沿海及浙南地区的大范围雷暴大风,并且短时强降水的分布和实况也较为吻合,说明机器学习模型对于强对流天气的分类和落区预报具有较好的参考性,尤其是较大范围雷暴大风天气。
|
图 2 2023年(a, b, c)7月21日和(d, e, f)8月7日08—20时(a, d)潜势分类预报和(b, c, e, f)观测的(b, e)短时强降水、(c, f)雷暴大风对比 Fig. 2 Comparison of (a, d) potential classification forecast and (b, c, e, f) the observed (b, e) short-time heavy rainfall and (c, f) thunderstorm gale from 08:00 BT to 20:00 BT on (a, b, c) 21 July and (d, e, f) 7 August 2023 |
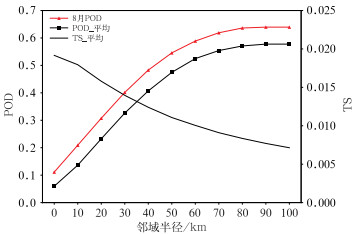
以中尺度模式CMA-SH9为建模分析对象,通过计算2019—2021年4—9月不同邻域空间短时强降水的命中率(POD)和TS,评估模式对短时强降水的空间预报偏差。这里采用点对面的检验方法(田付友等,2015),对于每一个格点上的预报正确与否,是用以该点为中心,搜索从0~100 km(间隔10 km)半径的圆面上是否出现了短时强降水来判别。检验范围为27°~31.5°N、117.5°~123°E, 不包括海上的格点。图 3可见,短时强降水点对点预报的平均POD在0.06左右,而点对面的POD随着邻域半径增加而快速上升,在半径达到50~70 km以后,POD呈缓慢增加或者基本持平的趋势,每个月的演变趋势大致相同,8月的POD相对高于其余月份,最高达到0.6左右。由此说明,CMA-SH9模式对短时强降水的最大预报空间偏差在50~70 km。短时强降水的POD和TS呈反位相,TS最高点对应POD的最低点,由于邻域半径的增加使得命中率增加,同时空报率大幅增加,导致TS呈下降趋势,对于强对流天气等小概率事件,秉着“宁空勿漏”的原则,需要平衡POD和TS两个指标。因此,选取两条曲线的交叉作为平衡点,即约40 km为最佳空间邻域半径,通过空间邻域可以有效提高灾害性天气的命中率。
|
图 3 2019—2021年4—9月短时强降水不同空间邻域半径的POD和TS Fig. 3 Average hit rate and TS of short-time heavy rainfall in different neighborhood radii from April to September of 2019-2021 |
通过XGBoost算法实现了雷暴大风和短时强降水的0~12 h和12~24 h的潜势预报,将潜势预报分割到逐小时,依赖于数值模式逐小时预报要素的释用。下文统计分析2019—2021年4—9月CMA-SH9预报的对流有效位能(CAPE)、整层可降水量(PW)、反射率因子(Z)和小时降水量(R)的概率密度分布特征,以40 km为最大邻域半径提取要素最大值,构建空间要素“配料”模型。
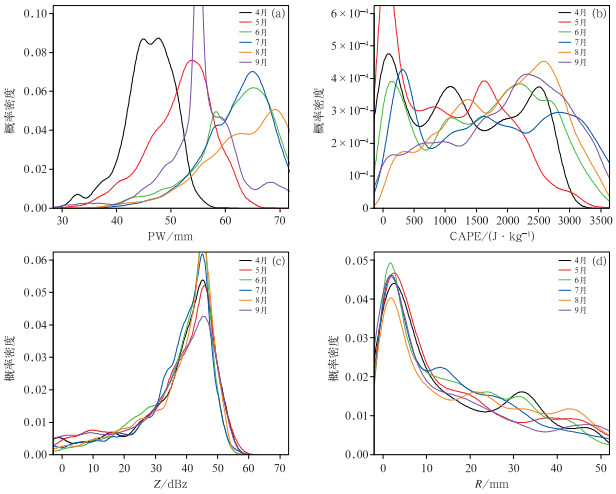
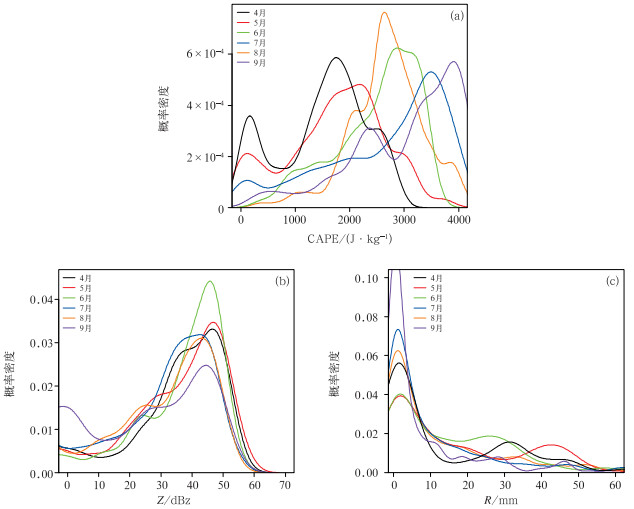
3.2.1 短时强降水对于短时强降水天气,PW的概率密度曲线呈单峰分布特征(图 4a),春季和夏季的重叠区较小,有利于阈值的提取。4月PW峰值在40~50 mm,明显低于其他季节,5月和9月存在较多重叠区,介于50~60 mm,而6—8月离散度较大,峰值在65 mm左右。CAPE逐月均呈现多峰分布特征(图 4b),说明CAPE对于短时强降水的发生并不是充分必要条件,即使低CAPE也易发生短时强降水。Z的分布呈单峰特征(图 4c),峰值在45 dBz,说明对部分短时强降水天气,中尺度模式40 km范围内能够预报出45 dBz左右的回波。R的分布呈单峰为主特征(图 4d),峰值在5 mm左右,但在10 mm以上存在次峰值波动,说明大部分短时强降水的模式预报R明显偏小。
|
图 4 2019—2021年4—9月短时强降水的(a)PW, (b)CAPE, (c)Z, (d)R的概率密度分布 Fig. 4 Probability density distribution of (a) PW, (b) CAPE, (c) Z and (d) R of short-time heavy rainfall from April to September of 2019-2021 |
对于雷暴大风天气,图 5a可见,春季4—5月CAPE呈现双峰特征,峰值介于1500~2000 J·kg-1,而500 J·kg-1以下存在次峰值,原因在于浙江省春季在动力抬升作用下,也容易发生系统性雷暴大风天气,热力作用贡献较小;6—8月CAPE基本呈单峰特征,峰值在2500~3000 J·kg-1,浙江省绝大部分的雷暴大风发生在夏季高CAPE环境下。Z也呈现双峰特征(图 5b),峰值在50 dBz左右,高于短时强降水的峰值(45 dBz),并且分布集中度较低,9月在0 dBz附近存在一个次峰值,说明中尺度模式在雷暴大风发生的40 km范围内没有预报出回波的比例较高。从R的分布(图 5c)可见,主峰值低于5 mm,4—6月在20 mm以上存在次峰值,说明春季预报较强降水可能伴随雷暴大风。
|
图 5 2019—2021年4—9月雷暴大风的(a)CAPE, (b)Z, (c)R的概率密度分布 Fig. 5 Probability density distribution of (a) CAPE, (b) Z and (c) R of thunderstorm gale from April to September of 2019-2021 |
统计可见,模式预报的不同类型强对流的物理量存在季节差异性,尤其是CAPE和PW,并且R预报明显偏弱。因此,针对不同类型的强对流,可以通过将降水和不同物理量要素结合来构建空间邻域要素“配料”模型。下文通过组合最优TS方法提取主要物理量的季节阈值。
3.3 组合最优TS的物理量阈值 3.3.1 小时降水量针对2019—2021年4—9月的短时强降水和雷暴大风过程,点对点输出模式预报R,并分为4个等级(无降水、0.1~5 mm、5.1~15 mm、≥15 mm)统计各量级分布比重(图 6)。对于短时强降水,弱降水(R在5 mm以下)占比明显高于其他量级,平均达到50%,其次是无降水,占比27%,其他量级一般低于15%;对于雷暴大风,无降水占比最高,平均达到65%,其次是弱降水(占比27%),尤其是8月无降水占比达到80%,这是由于夏季在副热带高压环流背景下,多发局地性雷暴大风天气,数值模式的预报能力较为有限。因此,有必要将降水量分级建立强对流的空间“配料”模型。

|
图 6 2019—2021年4—9月(a)短时强降水和(b)雷暴大风不同量级小时降水量的占比 Fig. 6 The proportion of (a) short-time heavy rainfall and (b) thunderstorm gale in different hourly forecast precipitations from April to September of 2019-2021 |
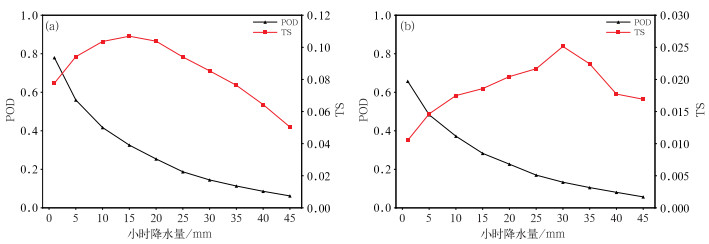
2021年浙江省强对流天气具有多灾种、高频次、高强度的特点,因此,采用2021年CMA-SH9的预报数据分别计算短时强降水、雷暴大风的物理量要素采用不同阈值的评分,分析POD和TS的序列特征,利用两个指标的交叉平衡点计算出要素的最佳阈值。针对R,阈值采用1~45 mm(间隔5 mm)计算POD和TS。
对于短时强降水,图 7a可见,虽然TS的最大值出现在15 mm,但对应的POD快速下降至0.3,TS和POD两条曲线的交叉点在1~5 mm,POD提高到0.7左右;对于雷暴大风,图 7b可见,虽然POD和TS在5 mm左右形成交叉,但雷暴大风命中率不足0.5,而采用1~5 mm的降水阈值,可以使得POD提高到0.6。因此,重点针对弱降水建立配料模型可以显著提高短时强降水的命中率。
|
图 7 2021年(a)短时强降水和(b)雷暴大风不同小时降水量阈值的POD和TS Fig. 7 Hit rate and TS of different hourly precipitation thresholds for (a) short-time heavy rainfall and (b) thunderstorm gale in 2021 |
对于雷暴大风,图 8a可见,TS和POD的曲线同样呈反位相分布,TS最大值对应的POD低于0.4,采用POD和TS两条曲线的交叉点提取阈值,POD可以达到0.5以上,CAPE的逐月阈值差异显著,尤其是春夏季,呈逐月上升的趋势,4月、5月、6月分别为600、1000、2000 J· kg-1,7—8月在2200 J·kg-1,9月在3000 J·kg-1。Z的逐月差异不大,4—9月平均POD和TS的交叉点在35 dBz左右(图 8b),可作为Z的基础阈值,但是TS最高点在45 dBz,因此,下文与模式的对比检验中选取45 dBz作为雷暴大风的判定阈值。
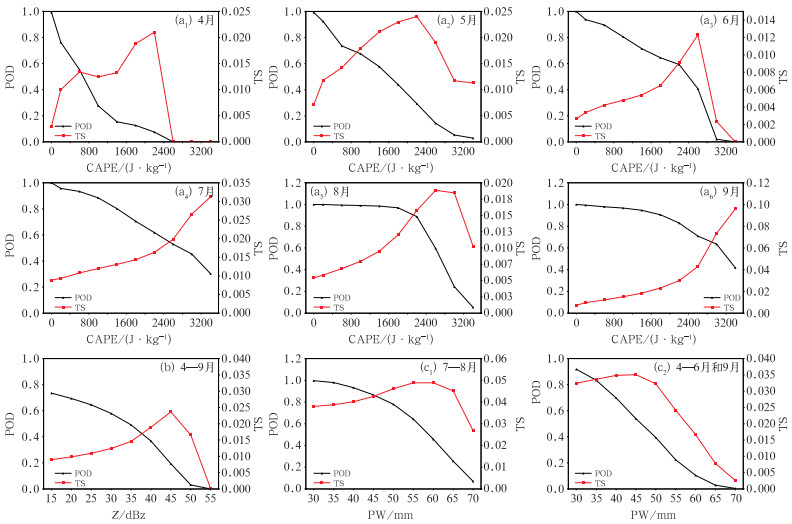
|
图 8 2021年4—9月(a, b)雷暴大风的(a)CAPE, (b)Z和(c)短时强降水的PW不同阈值的POD和TS Fig. 8 Hit rate and TS of different thresholds for (a) CAPE, (b) Z of thunderstorm gale and (c) PW of short-time heavy rainfall from April to September of 2021 |
对于短时强降水,CAPE的季节阈值明显低于雷暴大风的阈值,季节差异也相对较小,4—5月POD和TS的交叉点在200 J·kg-1左右,6月在500 J·kg-1,而7—9月在1100 J·kg-1(图略)。PW是预报短时强降水的重要物理量,春秋季和夏季的阈值差异较大(图 8c),春秋季(4—6月和9月),POD和TS的交叉点在35 mm,而夏季(7—8月),两条曲线的交叉点在45 mm,因此,短时强降水不同季节可设置不同PW阈值。
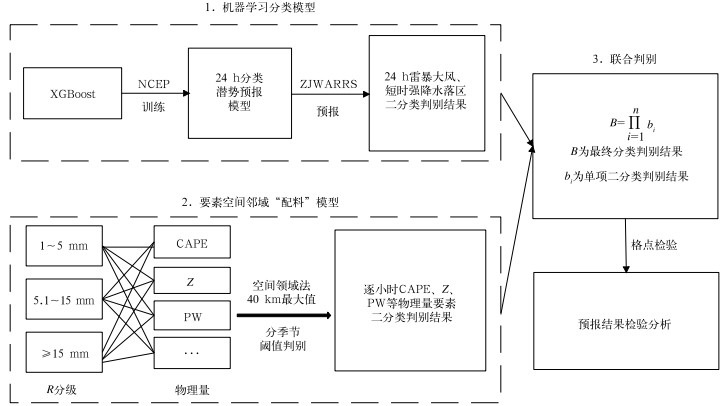
3.4 融合方法的预报模型融合方法构建分类强对流的逐小时预报模型包含三个步骤(图 9):(1)建立机器学习分类潜势预报模型。利用XGBoost算法对雷暴大风和短时强降水的24 h潜在落区进行二分类判别。(2)建立要素空间领域“配料”模型。对R进行分级,加入CAPE、Z、PW等要素形成“配料”组合,对每个分级要素采用组合最优TS方法,预先建立分季节阈值表(表 3)。当前预报时次的要素,应用空间邻域法以40 km半径提取最大值,根据预先建立的阈值表进行二分类判别。(3)联合判别。对机器学习潜势预报落区的二分类判别场、“配料”组合因子的二分类判别场进行联合判别。最终得到逐小时雷暴大风和短时强降水的二分类确定性预报落区。
|
图 9 融合方法的强对流逐小时预报模型流程图 Fig. 9 Flow chart of hourly forecast severe convective model with fusion method |
|
|
表 3 融合方法主要预报要素的季节统计阈值 Table 3 Seasonal statistical threshold for the main forecast elements of fusion method |
强对流预报检验参考国家气象中心“点对面”的检验标准(唐文苑等,2017;田付友等,2015),即对于每一个站点/格点上的各分类预报正确与否,用以该点为中心、40 km为半径的圆面上是否出现了该分类的天气来判别。本文采用格点检验方法,检验范围如1.2节所述, 不包括海上的格点,通过POD和TS评估融合方法建立的分类强对流逐小时预报模型(简称融合方法),并且与CMA-SH9预报结果(简称模式预报)和国家下发指导产品(简称指导产品)进行对比,评估时段为2021—2022年4—9月。指导产品指通过内网定时传输下发的24小时逐小时强对流分类落区预报,空间分辨率0.05°×0.05°,逐3小时更新。
图 10a, 10b是2021—2022年融合方法、模式预报及指导产品的年均对比评分,从中可见,融合方法显著优于模式预报和指导产品,指导产品的评分相对较低,尤其是雷暴大风天气。对于短时强降水,融合方法的POD平均达到0.51,TS为0.15, 而模式预报POD为0.28,TS为0.11,指导产品TS为0.08;对比模式预报, POD改进率为82%,TS改进率为36%。对于雷暴大风,与模式预报的雷达Z(以45 dBz作为大风出现阈值)进行对比,融合方法的POD达到0.37,TS为0.07,而模式预报的POD为0.22,TS为0.03,指导产品的TS仅为0.005;对比模式预报, POD改进率为68%,TS改进率为133%。从2021年4—9月融合方法和模式预报的逐月评分对比(图 10c, 10d)可见,相对模式预报,融合方法的雷暴大风和短时强降水的逐月POD改进显著,短时强降水提高约2倍,TS也有明显的改进,雷暴大风在4月和9月的TS提高3~4倍,9月的TS从0.03提高到0.12。因此,通过三个数据源的对比检验表明,融合方法较模式预报和指导产品的改进显著,尤其是雷暴大风天气, 说明机器学习分类模型对于区分强对流天气类型具有一定的优势。参考国家级12小时强对流潜势主观预报和深度学习客观预报的检验结果(唐文苑等,2017;周康辉等,2021a;田付友等,2024a),雷暴大风的12小时主客观TS在0.05~0.08,而融合方法逐小时预报TS为0.07,与国家级12小时潜势预报的主客观评分接近,说明该方法可以提高雷暴大风的逐小时预报准确性。

|
图 10 (a,b)2021—2022年逐年和(c,d)2021年4—9月逐月的(a,c)短时强降水和(b,d)雷暴大风的逐小时预报POD和TS Fig. 10 Hit rate and TS of (a, c) short-time heavy rainfall and (b, d) thunderstorm gale in (a, b) annual forecast from 2021 to 2022 and (c, d) monthly forecast from April to September 2021 |
虽然雷暴大风TS明显低于短时强降水,但这与风雹类天气发生概率相对较低、局地性和突发性更强、预报难度相对较大有关。同时,并不完备的观测资料也对评分结果有一定程度的影响,雷暴大风天气的判别区分不够严格,也会导致漏报率偏高、TS偏低(唐文苑等,2017)。此外,2022年模式本身的评分结果优于2021年,这种变化同样表现在融合方法中,说明以数值模式释用为基础的算法仍然依赖于数值模式本身的改进。
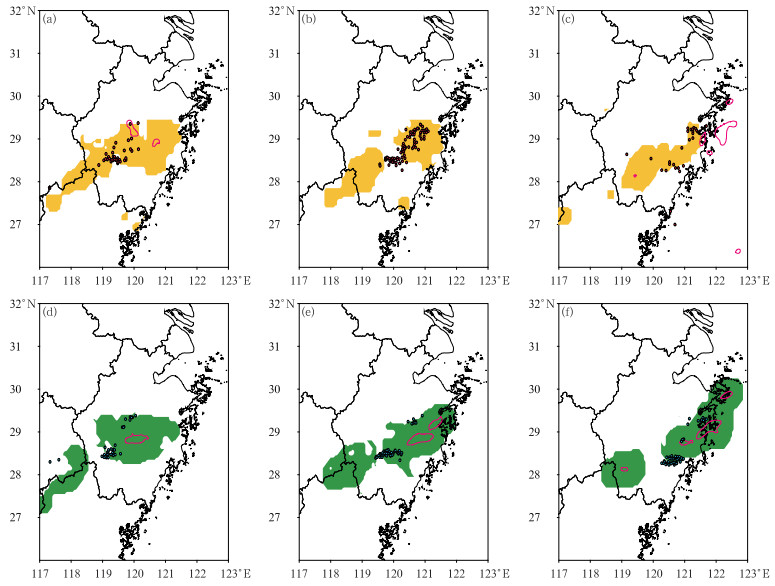
4.2 强对流预报个例检验尽管多数情况下风雹类天气评分较低,但由于导致风雹的天气系统的可预报性不同,不同天气系统下的预报评分差异极大。以2023年3月22日浙江省大范围强对流天气为例,检验融合方法的预报效果。此次过程是一次春季混合性强对流天气,伴随大范围雷暴大风和短时强降水天气,分类潜势预报模型对大风的预测基本准确,短时强降水的逐小时POD为0.56,TS为0.20,雷暴大风POD达到0.64,TS为0.18,显著高于年均TS。从逐小时雷暴大风和短时强降水的融合方法、模式预报及站点观测的叠加(图 11)可见,CMA-SH9较好地预报出短时强降水的分布形态,但是存在明显落区偏差,并且45 dBz以上的回波范围很小,而融合方法能够改善强对流天气的落区预报准确率,漏报明显减小,尤其是雷暴大风天气。但是融合方法仍然存在一定的空报,下一步可引入更多的物理量和动态学习方法研究消空方案。
|
图 11 2023年3月22日14—16时(a, b, c)雷暴大风、(d, e, f)短时强降水的融合方法(橙/绿色填色)、CMA-SH9模式(Z≥45 dBz或R≥20 mm)的落区预报(红色等值线)和自动站监测(彩色圆点) Fig. 11 Fusion method (orange/green shaded), CMA-SH9 (Z≥45 dBz or R≥20 mm) forecast (red contour) and AWS observation (colorful dot) of (a, b, c) thunderstorm gale and (d, e, f) short-time heavy rainfall from 14:00 BT to 16:00 BT 22 March 2023 |
本文提出了一种基于数值模式的XGBoost机器学习客观分类和“配料法”融合的分类强对流预报方法,通过中尺度模式的要素空间邻域和分级“配料”的思路,基于组合最优TS提取物理量季节阈值,建立了雷暴大风和短时强降水的逐小时预报模型。通过CMA-SH9模式的统计分析及模型的对比检验,得到以下结论:
(1) 中尺度模式CMA-SH9对短时强降水存在一定的预报空间偏差,最大空间偏差约为50~70 km,订正后最大命中率约在0.6。模式对短时强降水的预报降水量明显偏低,R在5 mm以下占比最高,平均达到50%。对雷暴大风的预报降水量,无降水占比最高,达到65%,其次是R在5 mm以下。因此,通过模式预报要素的空间邻域和分级“配料”的方法可以显著提高强对流天气的命中率。
(2) 对于短时强降水和雷暴大风,中尺度模式预报物理量的概率密度分布存在季节差异。短时强降水的PW分布集中且季节区分度较大,4月峰值介于40~50 mm,5月和9月介于50~60 mm,而6—8月的峰值在65 mm左右。CAPE呈现多峰特征, 季节差异性较小,低CAPE条件下也易发生短时强降水;雷暴大风的CAPE值季节差异显著,春季呈现双峰特征,峰值介于1500~2000 J·kg-1,500 J· kg-1以下存在次峰值,而夏季呈现单峰特征,峰值在2500~3000 J·kg-1,发生雷暴大风的CAPE显著高于短时强降水。Z呈现单峰特征,雷暴大风的峰值在50 dBz,略高于短时强降水的峰值(45 dBz);雷暴大风和短时强降水的R均呈现单峰分布为主(峰值5 mm左右),并且在10 mm以上存在多个次峰值的特征。
(3) 强对流逐小时预报模型由机器学习客观分类模型和要素空间领域“配料法”融合得到,检验表明,融合方法显著优于模式预报结果和指导产品。2021—2022年短时强降水的命中率平均达到0.51,TS为0.15, 相比模式预报的改进率分别为82%和36%。雷暴大风的命中率达到0.37,TS为0.07,相比模式预报(Z≥45 dBz)的改进率分别达到68%和133%。雷暴大风评分显著优于指导产品,在一定程度上提高了雷暴大风的逐小时预报准确性。
通过算法检验评分,在如何提高强对流天气预报准确率方面,研究中也得到一些启示。由于强对流天气具有时空尺度小、局地性强的特点,TS总体较低,尤其是雷暴大风天气。系统性的雷暴大风天气可预报性相对较强,TS明显较高;而非过程性的、分散局地大风天气,TS远低于前者。如何提高局地突发大风天气的预报评分是模型需要改进的一个难点,下一步可尝试通过预报失败的样本重新训练的动态学习方式和自适应空间邻域半径实现模型的优化,可引入更多物理量和多尺度模式数据来探索消空方案。
陈勇伟, 郑涛, 王汉堃, 等, 2013. 基于BP神经网络模型的雷电潜势预报[J]. 干旱气象, 31(3): 595-601. Chen Y W, Zheng T, Wang H K, et al, 2013. Thunderstorm potential prediction based on back propagation neural network[J]. J Arid Meteor, 31(3): 595-601 (in Chinese).
|
樊李苗, 俞小鼎, 2013. 中国短时强对流天气的若干环境参数特征分析[J]. 高原气象, 32(1): 156-165. Fan L M, Yu X D, 2013. Characteristic analyses on environmental parameters in short-term severe convective weather in China[J]. Plateau Meteor, 32(1): 156-165 (in Chinese).
|
樊李苗, 俞小鼎, 2020. 杭州地区夏季午后雷暴大风环境条件分析[J]. 气象, 46(12): 1621-1632. Fan L M, Yu X D, 2020. Analysis on the environment conditions of afternoon thunderstorm in Hangzhou[J]. Meteor Mon, 46(12): 1621-1632 (in Chinese). DOI:10.7519/j.issn.1000-0526.2020.12.009
|
高晓梅, 俞小鼎, 王令军, 等, 2018. 鲁中地区分类强对流天气环境参量特征分析[J]. 气象学报, 76(2): 196-212. Gao X M, Yu X D, Wang L J, et al, 2018. Characteristics of environmental parameters for classified severe convective weather in central area of Shandong Province[J]. Acta Meteor Sin, 76(2): 196-212 (in Chinese).
|
韩丰, 杨璐, 周楚炫, 等, 2021. 基于探空数据集成学习的短时强降水预报试验[J]. 应用气象学报, 32(2): 188-199. Han F, Yang L, Zhou C X, et al, 2021. An experimental study of the short-time heavy rainfall event forecast based on ensemble learning and sounding data[J]. J Appl Meteor Sci, 32(2): 188-199 (in Chinese).
|
雷蕾, 孙继松, 魏东, 2011. 利用探空资料判别北京地区夏季强对流的天气类别[J]. 气象, 37(2): 136-141. Lei L, Sun J S, Wei D, 2011. Distinguishing the category of the summer convective weather by sounding data in Beijing[J]. Meteor Mon, 37(2): 136-141 (in Chinese). DOI:10.7519/j.issn.1000-0526.2011.2.002
|
李文娟, 赵放, 郦敏杰, 等, 2018. 基于数值预报和随机森林算法的强对流天气分类预报技术[J]. 气象, 44(12): 1555-1564. Li W J, Zhao F, Li M J, et al, 2018. Forecasting and classification of severe convective weather based on numerical forecast and random forest algorithm[J]. Meteor Mon, 44(12): 1555-1564 (in Chinese). DOI:10.7519/j.issn.10000526.2018.12.005
|
李耀东, 刘健文, 高守亭, 2004. 动力和能量参数在强对流天气预报中的应用研究[J]. 气象学报, 62(4): 401-409. Li Y D, Liu J W, Gao S T, 2004. On the progress of application for dynamic and energetic convective parameters associated with severe convective weather forecasting[J]. Acta Meteor Sin, 62(4): 401-409 (in Chinese).
|
刘晓璐, 刘建西, 张世林, 等, 2014. 基于探空资料因子组合分析方法的冰雹预报[J]. 应用气象学报, 25(2): 168-175. Liu X L, Liu J X, Zhang S L, et al, 2014. Hail forecast based on factor combination analysis method and sounding data[J]. J Appl Meteor Sci, 25(2): 168-175 (in Chinese). DOI:10.3969/j.issn.1001-7313.2014.02.006
|
马淑萍, 王秀明, 俞小鼎, 2019. 极端雷暴大风的环境参量特征[J]. 应用气象学报, 30(3): 292-301. Ma S P, Wang X M, Yu X D, 2019. Environmental parameter characteristics of severe wind with extreme thunderstorm[J]. J Appl Meteor Sci, 30(3): 292-301 (in Chinese).
|
漆梁波, 2015. 高分辨率数值模式在强对流天气预警中的业务应用进展[J]. 气象, 41(6): 661-673. Qi L B, 2015. Operational progress of high-resolution numerical model on severe convective weather warning[J]. Meteor Mon, 41(6): 661-673 (in Chinese). DOI:10.7519/j.issn.1000-0526.2015.06.001
|
孙继松, 陶祖钰, 2012. 强对流天气分析与预报中的若干基本问题[J]. 气象, 38(2): 164-173. Sun J S, Tao Z Y, 2012. Some essential issues connected with severe convective weather analysis and forecast[J]. Meteor Mon, 38(2): 164-173 (in Chinese). DOI:10.7519/j.issn.1000-0526.2012.02.004
|
唐文苑, 周庆亮, 刘鑫华, 等, 2017. 国家级强对流天气分类预报检验分析[J]. 气象, 43(1): 67-76. Tang W Y, Zhou Q L, Liu X H, et al, 2017. Analysis on verification of national severe convective weather categorical forecasts[J]. Meteor Mon, 43(1): 67-76 (in Chinese). DOI:10.7519/j.issn.1000-0526.2017.01.007
|
田付友, 郑永光, 坚参扎西, 等, 2024a. .融合物理理解与模糊逻辑的分类强对流客观短期预报系统: (2)表现评估[J]. 气象, 50(6): 649-660. Tian F Y, Zheng Y G, Jiancan Z X, et al, 2024a. Forecasting system for short-term multi-category convective phenomena combining physical understanding and fuzzy logic PartⅡ : performance evaluation[J]. Meteor Mon, 50(6): 649-660 (in Chinese). DOI:10.7519/j.issn.1000-0526.2024.031402
|
田付友, 郑永光, 孙建华, 等, 2024b. 融合物理理解与模糊逻辑的分类强对流客观短期预报系统: (1)系统构成[J]. 气象, 50(5): 521-531. Tian F Y, Zheng Y G, Sun J H, et al, 2024b. Forecasting system for short-term multi-category convective phenomena combining physical understanding and fuzzy logic PartⅠ : system construction[J]. Meteor Mon, 50(5): 521-531 (in Chinese). DOI:10.7519/j.issn.1000-0526.2024.031401
|
田付友, 郑永光, 张涛, 等, 2015. 短时强降水诊断物理量敏感性的点对面检验[J]. 应用气象学报, 26(4): 385-396. Tian F Y, Zheng Y G, Zhang T, et al, 2015. Sensitivity analysis of short-duration heavy rainfall related diagnostic parameters with point-area verification[J]. J Appl Meteor Sci, 26(4): 385-396 (in Chinese).
|
王迪, 牛淑贞, 曾明剑, 等, 2020. 河南省分类强对流环境物理条件特征分析[J]. 气象, 46(5): 618-628. Wang D, Niu S Z, Zeng M J, et al, 2020. Analysis on the characteristics of environmental and physical conditions for the classified severe convections in Henan Province[J]. Meteor Mon, 46(5): 618-628 (in Chinese). DOI:10.7519/j.issn.1000-0526.2020.05.003
|
王秀明, 俞小鼎, 周小刚, 2014. 雷暴潜势预报中几个基本问题的讨论[J]. 气象, 40(4): 389-399. Wang X M, Yu X D, Zhou X G, 2014. Discussion on basical issues of thunderstorm potential forecasting[J]. Meteor Mon, 40(4): 389-399 (in Chinese). DOI:10.7519/j.issn.1000-0526.2014.04.001
|
杨仲江, 蔡波, 刘旸, 2013. 利用双隐层BP网络进行雷暴潜势预报试验——以太原为例[J]. 气象, 39(3): 377-382. Yang Z J, Cai B, Liu Y, 2013. Experimental research on thunderstorm forecasting with double hidden layer BP neural network: case study on Taiyuan[J]. Meteor Mon, 39(3): 377-382 (in Chinese). DOI:10.7519/j.issn.1000-0526.2013.03.013
|
俞小鼎, 2011. 基于构成要素的预报方法——配料法[J]. 气象, 37(8): 913-918. Yu X D, 2011. Ingredients based forecasting methodology[J]. Meteor Mon, 37(8): 913-918 (in Chinese). DOI:10.7519/j.issn.1000-0526.2011.8.001
|
俞小鼎, 周小刚, 王秀明, 2012. 雷暴与强对流临近天气预报技术进展[J]. 气象学报, 70(3): 311-337. Yu X D, Zhou X G, Wang X M, 2012. The advances in the nowcasting techniques on thunderstorms and severe convection[J]. Acta Meteor Sin, 70(3): 311-337 (in Chinese).
|
曾明剑, 王桂臣, 吴海英, 等, 2015. 基于中尺度数值模式的分类强对流天气预报方法研究[J]. 气象学报, 73(5): 868-882. Zeng M J, Wang G C, Wu H Y, et al, 2015. Study of the forecasting method for the classified severe convection weather based on a meso-scale numerical model[J]. Acta Meteor Sin, 73(5): 868-882 (in Chinese).
|
张华龙, 伍志方, 肖柳斯, 等, 2021. 基于因子分析的广东省短时强降水预报模型及其业务试验[J]. 气象学报, 79(1): 15-30. Zhang H L, Wu Z F, Xiao L S, et al, 2021. A probabilistic forecast model of short-time heavy rainfall in Guangdong Province based on factor analysis and its operational experiments[J]. Acta Meteor Sin, 79(1): 15-30 (in Chinese).
|
张小玲, 陶诗言, 孙建华, 2010. 基于"配料"的暴雨预报[J]. 大气科学, 34(4): 754-766. Zhang X L, Tao S Y, Sun J H, 2010. Ingredients- based heavy rainfall forecasting[J]. Chin J Atmos Sci, 34(4): 754-766 (in Chinese).
|
张小玲, 杨波, 盛杰, 等, 2018. 中国强对流天气预报业务发展[J]. 气象科技进展, 8(3): 8-18. Zhang X L, Yang B, Sheng J, et al, 2018. Development of operations on forecasting severe convective weather in China[J]. Adv Meteor Sci Technol, 8(3): 8-18 (in Chinese).
|
赵旭寰, 王振会, 肖稳安, 等, 2009. 神经网络在雷暴预报中的应用初步研究[J]. 热带气象学报, 25(3): 357-360. Zhao X H, Wang Z H, Xiao W A, et al, 2009. A preliminary study of neural network based short-term thunderstorm forecast[J]. J Trop Meteor, 25(3): 357-360 (in Chinese).
|
赵渊明, 漆梁波, 2021. 短时强降水概率预报的多模式集成技术研究[J]. 气象, 47(5): 529-538. Zhao Y M, Qi L B, 2021. Multi-model integration technology for probabilistic forecasting of short-time severe rainfall[J]. Meteor Mon, 47(5): 529-538 (in Chinese). DOI:10.7519/j.issn.1000-0526.2021.05.002
|
郑永光, 陶祖钰, 俞小鼎, 2017. 强对流天气预报的一些基本问题[J]. 气象, 43(6): 641-652. Zheng Y G, Tao Z Y, Yu X D, 2017. Some essential issues of severe convective weather forecasting[J]. Meteor Mon, 43(6): 641-652 (in Chinese). DOI:10.7519/j.issn.1000-0526.2017.06.001
|
郑永光, 周康辉, 盛杰, 等, 2015. 强对流天气监测预报预警技术进展[J]. 应用气象学报, 26(6): 641-657. Zheng Y G, Zhou K H, Sheng J, et al, 2015. Advances in techniques of monitoring, forecasting and warning of severe convective weather[J]. J Appl Meteor Sci, 26(6): 641-657 (in Chinese).
|
周方媛, 戴建华, 陈雷, 2020. 基于关键对流参数分级的强对流潜势预报[J]. 气象科技, 48(2): 229-241. Zhou F Y, Dai J H, Chen L, 2020. Severe convective potential forecast based on key convective parameter classification[J]. Meteor Sci Technol, 48(2): 229-241 (in Chinese).
|
周康辉, 郑永光, 韩雷, 等, 2021a. 机器学习在强对流监测预报中的应用进展[J]. 气象, 47(3): 274-289. Zhou K H, Zheng Y G, Han L, et al, 2021a. Advances in application of machine learning to severe convective weather monitoring and forecasting[J]. Meteor Mon, 47(3): 274-289 (in Chinese). DOI:10.7519/j.issn.1000-0526.2021.03.002
|
周康辉, 郑永光, 王婷波, 2021b. 利用深度学习融合NWP和多源观测数据的闪电落区短时预报方法[J]. 气象学报, 79(1): 1-14. Zhou K H, Zheng Y G, Wang T B, 2021b. Very short-range lightning forecasting with NWP and observation data: a deep learning approach[J]. Acta Meteor Sin, 79(1): 1-14 (in Chinese).
|
朱岩, 翟丹华, 吴志鹏, 等, 2021. 基于XGBoost算法的短时强降水预报方法[J]. 气象科技, 49(3): 406-418. Zhu Y, Zhai D H, Wu Z P, et al, 2021. A method of short-duration heavy rain forecast based on XGBoost algorithm[J]. Meteor Sci Technol, 49(3): 406-418 (in Chinese).
|
朱月佳, 邢蕊, 朱明佳, 等, 2019. 联合概率方法在安徽强对流潜势预报中的应用和检验[J]. 地球科学进展, 34(7): 731-746. Zhu Y J, Xing R, Zhu M J, et al, 2019. Application and verification of joint probability method in potential forecast for severe convective weather in Anhui Province[J]. Adv Earth Sci, 34(7): 731-746 (in Chinese).
|
Chen T, Guestrin C, 2016. XGBoost: a scalable tree boosting system[J]. ACM. DOI:10.1145/2939672.2939785
|
Doswell C A Ⅲ, Brooks H E, Maddox R A, 1996. Flash flood forecasting: an ingredients-based methodology[J]. Wea Forecasting, 11(4): 560-581. DOI:10.1175/1520-0434(1996)011<0560:FFFAIB>2.0.CO;2
|
Han L, Sun J Z, Zhang W, et al, 2017. A machine learning nowcasting method based on real-time reanalysis data[J]. J Geophys Res: Atmos, 122(7): 4038-4051.
|
Herman G R, Schumacher R S, 2018. Money doesn't grow on trees, but forecasts do: forecasting extreme precipitation with random forests[J]. Mon Wea Rev, 146(5): 1571-1600.
|
Lagerquist R, McGovern A, Smith T, 2017. Machine 1earning for real- time prediction of damaging straight-line convective wind[J]. Wea Forecasting, 32(6): 2175-2193.
|
Manzato A, 2013. Hail in northeast Italy: a neural network ensemble forecast using sounding-derived indices[J]. Wea Forecasting, 28(1): 3-28.
|
McGovern A, Elmore K L, Gagne D J Ⅱ, et al, 2017. Using artificial intelligence to improve real-time decision-making for high-impact weather[J]. Bull Amer Meteor Soc, 98(10): 2073-2090.
|
Sun J Z, Xue M, Wilson J W, et al, 2014. Use of NWP for nowcasting convective precipitation: recent progress and challenges[J]. Bull Amer Meteor Soc, 95(3): 409-426.
|
Zhou K H, Zheng Y G, Li B, et al, 2019. Forecasting different types of convective weather: a deep learning approach[J]. J Meteor Res, 33(5): 797-809.
|
 2024, Vol. 50
2024, Vol. 50 