2. 北京市气象台,北京 100089;
3. 国家气象中心,北京 100081;
4. 北京市延庆区气象局,北京 102100
2. Beijing Meteorological Observatory, Beijing 100089;
3. National Meteorological Centre, Beijing 100081;
4. Yanqing District Meteorological Office, Beijing 102100
2022年第24届北京冬奥会和第13届冬残奥会在京举行。在所有比赛项目中,室外雪上项目约占七成,其中延庆赛区承担着高山滑雪和雪车雪橇项目的比赛,由于高山滑雪赛道长、垂直落差大,而且运动员滑行速度快,一旦出现大风,很容易影响赛事正常进行,同时还会对人身安全产生巨大威胁,据新闻报道2018年平昌冬奥会就曾出现过因大风而导致高山滑雪项目推迟的情况。因此,做好冬奥会延庆赛区极大风速的精细化预报尤为重要。
尽管目前数值天气预报准确率在不断提高,但受模式初边界条件以及物理过程参数化方案等多种因素影响,即使采用高分辨率的亚千米网格距,模式仍不可避免地存在一些预报误差(Zhong and Fast, 2003),导致直接应用数值预报结果进行服务会存在很大问题,尤其在地形复杂地区模式预报偏差更为明显(智协飞等,2019),因此,对模式数据进行降尺度是必要的。从全球模式降尺度到区域或局地尺度,大致有动力和统计两种方法,其中统计降尺度是一种可以有效提高预报准确率的常用方法(Tang and Bassill, 2018;杨璐等,2022),经过后处理的预报结果较模式直接输出结果具有更高的可用性(陈豫英等,2006;曾晓青等,2013;de Rooy and Kok, 2004;Plenković et al,2018;申华羽等,2020;Schulz and Lerch, 2022)。在以往的研究中,模式输出统计(MOS)和卡尔曼滤波等方法在降水(孙永刚等,1998)、最高和最低气温(陆如华和何于班,1994;吴启树等,2016)、相对湿度(陈豫英等,2006)以及风速(卢峰本,1998;Cassola and Burlando, 2012)、风向(曾晓青等,2013)等要素预报中得到广泛应用,并取得了良好的应用效果。针对平昌冬奥会气象服务,张玉涛等(2020)采用一阶自适应卡尔曼滤波方法对模式风速进行了偏差订正,使得均方根误差减小到2 m·s-1左右,站点订正改善率达10%~45%;针对克罗地亚复杂的海岸地形,Plenković et al(2018)利用卡尔曼滤波和相似技术相结合的方法设计了10 m风速预报模型,发现该模型对短于一天时间尺度的风的转换预报较为优越。近些年来,随着机器学习算法的兴起,一些非线性处理模型被不断尝试,并在风速等要素预报中表现突出,如钱燕珍等(2012)和Wei(2015)均基于支持向量机算法研发了热带气旋影响时的风速预报模型;胡波(2019)利用BP人工神经网络方法对阵风进行了循环预报试验,发现最佳模型的绝对误差和方差均较对比组模型减小约11%~25%;任萍等(2020)初步研发了基于XGBOOST机器学习且考虑地形特征影响的多模式集成模型,相较于原始预报数据,10 m风速集成误差可降低31.23%~33.22%,10 m风向集成误差可降低4.10%~8.23%;孙全德等(2019)利用三种机器学习算法对华北地区近地面10 m风速的订正效果均优于传统的MOS方法。另外,研究表明, 基于集成学习方法的风速预报模型较单一机器学习模型的改善效果更为明显(韩念霏等,2022)。
山地区域大气流场结构复杂(贾春晖等,2019),当气流遇到山地地形时,流速和流向会发生改变,在动力和热力作用下往往还会形成一些局地环流,即使采用高分辨率数值模式来刻画这些中小尺度现象,也仍然会存在预报能力不足的问题;同时,受山区观测资料缺乏等因素影响,以往针对复杂山区的极大风速预报研究较少,而且缺乏强有力的预报技术支撑。冬奥会延庆赛区位于北京市延庆区海陀山地区,沟壑纵横,地形复杂,不同位置处的风速和风向特征差异明显(王倩倩等,2022;胡艺等,2022),再加上绝大多数数值模式对该地区的地形高度描述存在较大误差,从而导致极大风速预报难度较大。为了充分做好2022年北京冬(残)奥会气象服务保障任务,本文利用优选的ECMWF模式不同高度层要素预报产品以及延庆赛区极大风速观测数据,基于三种不同类型的机器学习算法分别构建赛区不同海拔高度点位的极大风速精细化预报模型,在对比评估预报性能的基础上,进一步基于stacking方法构建了集成学习模型RGL,并评估了较单一模型的改进能力。
1 数据来源及预处理 1.1 数据来源本文所用的数值模式数据为2018—2021年1月1日至3月28日及2022年2月18日ECMWF模式20时(北京时,下同)起报的不同高度层要素预报产品,高度层次包括10 m、900 hPa、850 hPa、800 hPa和700 hPa,要素包括海平面气压、位势高度、温度、相对湿度、水平风速、水平风向和垂直速度,预报时效为72 h,预报间隔为3 h。针对某一点位的模式预报数据,采用最邻近法获取。
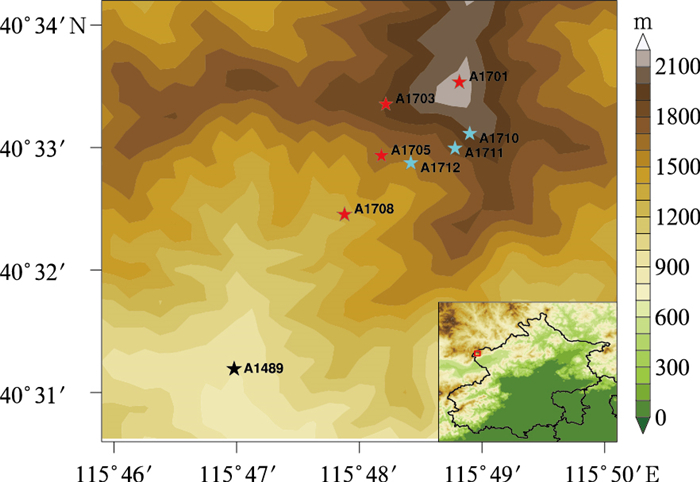
实况数据来源于冬奥会延庆赛区自动气象站2018—2021年1月1日20时至3月31日20时以及2022年2月18日20时至20日20时期间的10 m极大风速观测资料,某一整点的极大风速定义为过去1 h内瞬时风速的最大值。本文选择竞速赛道上的1、3、5、8号站(站号分别为A1701、A1703、A1705、A1708)和竞技赛道上的1、2、3号站(站号分别为A1710、A1711、A1712)以及雪车雪橇赛道上的西大庄科站(站号为A1489)作为研究对象,从站点空间分布及基本信息(表 1, 图 1)可看出,这些站点的分布环境较为复杂,位于山顶的A1701站海拔高度可达2177.5 m,位于山腰的A1708站海拔高度为1289.1 m,而位于山谷的A1489站海拔高度仅为928.0 m,最大垂直落差超过1000 m;另外可看出,有些站点(如A1703、A1710)分布在地形坡度较大的位置,而有些站点(如A1489)则分布在相对平坦的位置。
|
|
表 1 延庆赛区主要自动气象站基本信息 Table 1 Information of main automatic weather stations in Yanqing Competition Zone |
|
图 1 延庆赛区地形海拔高度(填色)和主要自动气象站分布 注:红、青、黑五星符号分别代表高山滑雪竞速赛道、竞技赛道和雪车雪橇赛道上的气象站,右下小图红色矩形为延庆赛区位置。 Fig. 1 Terrain height (colored) of Yanqing Competition Zone and main automatic weather stations |
由于有些观测站位于高海拔地区,当湿度较大且遇到强冷空气时容易出现冻结的情况,从而导致极大风观测有时会出现故障。对于长时间的缺测(3 h以上)时次直接弃用,而对于短时间的缺测,则采用线性插值方法进行数据补全。
为了更好地进行下文中的数据建模,首先对数据中的异常值进行剔除操作,异常数据的确定方法为小于Q1-1.5IQR或大于Q3+1.5IQR的值,其中Q1为下四分位数,Q3为上四分位数,IQR为四分位数间距,是上四分位数Q3与下四分位数Q1之差。
2 机器学习算法介绍 2.1 决策树(DT)决策树(Breiman et al,1984)是一种非参数的监督学习算法,能够从一系列有特征和标签的数据中总结出决策规则,并用树状图的结构来呈现这些规则,该算法因容易理解而被广泛应用于分类和回归问题中,比如降水相态识别(陈双等,2019)。
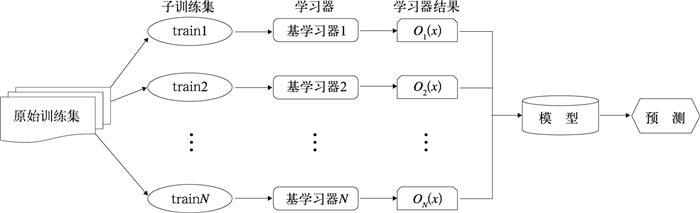
2.2 随机森林(RF)随机森林(Breiman,2001)是机器学习bagging算法族的代表算法之一,在要素预报方面有着广泛的应用(王可心等,2021)。bagging算法可独立构建多个基学习器,且基学习器之间并无强依赖关系。算法具体流程为(图 2):首先,从原始训练集中均匀、有放回地选出多个子训练集;然后,在这些子训练集上分别进行基学习器的训练;最后,将这些基学习器学习结果进行平均以产生最终的模型。由于每个基学习器所采用的数据集都是独立自助采样,从而所有树都互不相同,可以减少模型过拟合。
|
图 2 bagging算法流程图 Fig. 2 Flowchart of bagging algorithm |
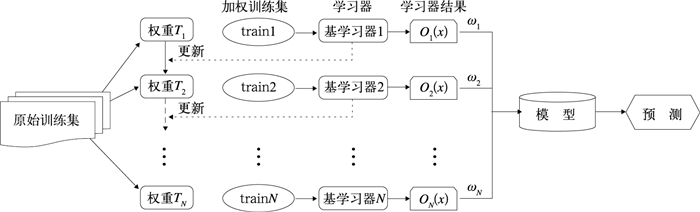
梯度提升决策树(Friedman,2001)是机器学习boosting算法族的代表算法之一。boosting算法的核心思想是在每一次训练时都更加关心预测错误的样例,而下一次迭代的目标就是能够更容易辨别出上一轮预测错误的样例,因此,基学习器之间存在强烈的依赖关系。算法具体流程为(图 3):首先,从原始训练集训练出一个基学习器,再对训练样本分布进行调整,给那些难以预测的样例赋予更大的权重,而易于预测的样例被赋予更小的权重,然后,基于调整后的样本分布来训练下一个基学习器,如此重复进行,直到基学习器数目达到事先指定的值,最后,将这些基学习器学习结果进行加权求和以产生最终的模型。
|
图 3 boosting算法流程图 Fig. 3 Flowchart of boosting algorithm |
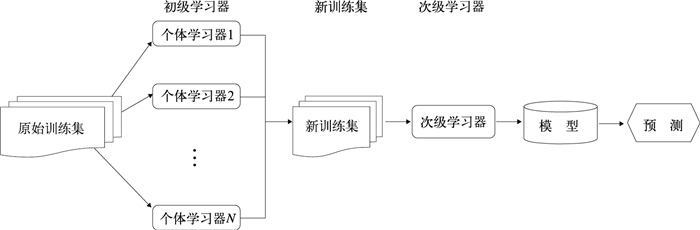
stacking是一种可以组合多个预测模型信息以生成新模型的分层集成学习算法,较单一机器学习模型,可有效提高模型预测结果(韩念霏等,2022)。算法具体流程为(图 4):以两层框架为例,第一层称为初级学习器,第二层称为次级学习器,将所有的初级学习器在原始训练集上进行训练,同时将训练出的结果视为新训练集的某个特征,然后,利用次级学习器在新训练集上进行再训练,次级学习器的输出即为集成模型结果。
|
图 4 stacking算法流程图 Fig. 4 Flowchart of stacking algorithm |
将1.1节数据来源中的数值模式数据及其对应的实况数据划分为训练集和测试集,其中训练集用来构建模型,数据时间段为2018—2020年1—3月,而测试集用于评估模型的预报性能,数据时间段为2021年1—3月,另外,2022年2月18日数据用于对冬奥会期间特定个例的预报性能评估。
3.2 数据标准化由于构建模型的预报因子涉及不同类型的气象要素,量纲之间会存在较大差异,为加快算法利用梯度下降求最优解的收敛速度,将原始数据集标准化处理为均值为0、方差为1的数据集,其公式如下:
| $ y_i=\frac{x_i-\mu}{\sigma} $ | (1) |
式中: μ和σ分别为原始数据集的均值和标准差。
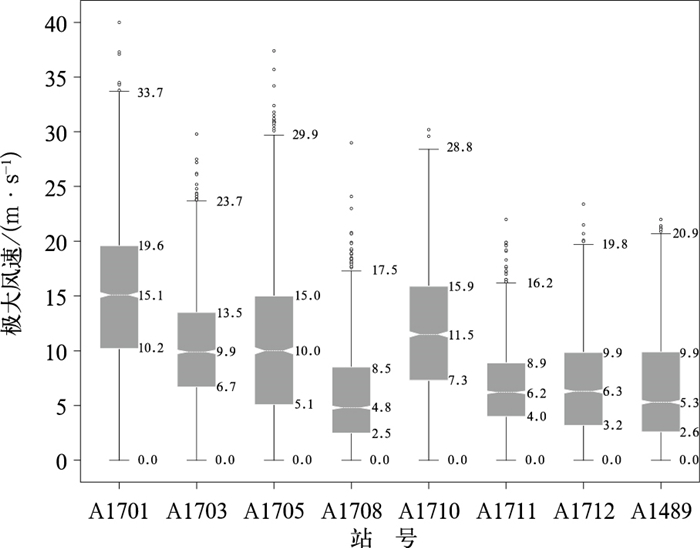
3.3 建模方式图 5为2018—2021年1月1日20时至3月31日20时观测期间8个站点的极大风速统计特征,可以看出,高海拔站A1701、A1703和A1710极大风速的上、下四分位数以及上限值均高于低海拔站A1708、A1712和A1489,针对山顶站A1701,极大风速上限值为33.7 m·s-1,上、下四分位数分别对应19.6 m·s-1和10.2 m·s-1,而山谷站A1489的极大风速上限值以及上、下四分位数分别较A1701站低12.8、9.7和7.6 m·s-1;另外,尽管山腰站A1705和A1711的海拔高度相当,但风速分布却差异较大,A1705站的上四分位数和上限值分别为15.0 m·s-1和29.9 m·s-1,明显高于A1711站,这主要是由于研究期间延庆赛区盛行西北气流,当气流过山顶附近A1701至A1703处的东北—西南向山脊时,A1711站多受西北气流所激发的次级环流影响,以南风居多,且风速相对较小,而A1705站本身位于山脊位置,受山顶附近的山脊影响程度相对较小,导致风速整体较大。可见,各站点的极大风速受海拔高度和周边环境影响显著,这在乌日柴胡等(2019)研究中也有体现。因此,本文针对不同点位进行独立建模。
|
图 5 各站点的极大风速箱线图 注:箱线图中触须的上端和下端分别代表统计最大值和最小值,箱体内三条绕线自下而上分别代表第25%、50%和75%分位值。 Fig. 5 Boxplots of extreme wind speed at each station |
优选预报因子的目的是避免不重要的因子进入预报模型。有些机器学习算法(如决策树)本身具有对特征因子进行打分的机制,而且这些算法对非线性关系的处理较好。在此,本文利用GBDT算法来优选预报因子,该算法是通过特征j在单颗树中的重要度的平均值来衡量其重要性:
| $ \hat{J_j^2}=\frac{1}{M} \sum\limits_{m=1}^M \hat{J_j^2}\left(T_m\right) $ | (2) |
式中M是树的数量。特征j在单棵树中的重要度计算如下:
| $ \widehat{J_j^2}(T)=\sum\limits_{t=1}^{L-1} \hat{i_t^2} f $ | (3) |
式中:f为指示性函数,当Vt=j时,f=1, 否则f=0;L为树的叶子结点数量,L-1为树的非叶子节点数量;Vt是和节点t相关联的特征,节点t分裂之后平方损失的减少值为
针对每个预报点位,将训练集上的ECMWF模式数据及对应的极大风速实况数据分别作为特征向量和标签值输入到GBDT模型,根据模型输出的特征因子重要性排序,同时兼顾到模型在测试集上的预报准确率和计算量,定义各点位最优预报因子的挑选标准为:针对A1701、A1703和A1708站,取重要性不低于0.02的因子,且根据预报经验去掉A1703站因子中的700 hPa和900 hPa的温度,针对其余站点,取重要性不低于0.04的因子,且根据预报经验去掉A1710站因子中的900 hPa温度,最终将各站的预报因子数目均控制在4~5个。
通过表 2可以看出,大多数点位极大风速的最优预报因子均为风速和风向,但不同点位所选用的高度层次存在差异,仅个别站(A1710)还考虑了垂直速度。若以海拔高度1600 m为分界线,该高度以下的3个站(A1708、A1712、A1489)所用的风速层次(10 m、900 hPa和850 hPa)完全一致,但风向层次却各不相同,850 hPa风向为共同因子,随着站点海拔高度升高,其余风向因子的选用层次也相应升高;而对于1600 m高度以上的其余5个站(A1701、A1703、A1705、A1710、A1711),所用的风速层次均包含850 hPa和800 hPa,随着站点海拔高度升高,所考虑的风速层次有升高的趋势,若以A1710站作为参照,该站海拔高度以上的A1701站考虑的是更高层次的700 hPa风速,而该站高度以下的3个站(A1703、A1705、A1711)考虑的则是更低层次的900 hPa风速,对于这5个站所用的风向层次,850 hPa风向为共同因子,随着站点海拔高度升高,其余风向因子的选用层次有降低的趋势。另外注意到,850 hPa风速和风向是所有站中唯一的共同预报因子,这反映出边界层顶附近的气象要素对极大风速预报的重要性。
|
|
表 2 各预报点位极大风速的最优预报因子 Table 2 Best predictors of extreme wind speed at each station |
针对每个预报点位,将优选出的ECMWF模式预报因子数据(表 2)及对应的极大风速实况数据分别作为特征向量和标签值构建DT、RF和GBDT模型;通过对模型性能对比评估,选择其中较为优异的两个模型作为初级学习器,以支持向量机模型(Cortes and Vapnik, 1995)作为次级学习器,基于stacking方法构建集成学习模型RGL。RGL模型的具体构建方法为:选择初级学习器中两个模型之一,将3.1节中的训练集随机划分成4份,以其中3份作为次训练集,剩下1份作为次测试集,在第一次交叉验证后会得到次测试集的预测值,同时可得到3.1节中测试集的预测值。4折交叉验证,即将上述过程进行4次,将4次得到的次测试集的预测值拼接成训练集中的新特征1,其时间段正好为2018—2020年1月1日至3月28日,所对应的新测试集为4次得到的测试集预测值的平均值,时间段为2021年1月1日至3月28日。接着再对另一个模型重复以上步骤得到训练集中的新特征2以及对应的新测试集,最后,在训练集的新特征1、2上,利用支持向量机模型进一步训练即可得到RGL集成学习模型结果。
3.6 模型评估指标本文选用平均绝对误差(MAE)和准确率(Acc)对模型预报性能进行评估,计算公式如下:
| $ \mathrm{MAE}=\frac{1}{N} \sum\limits_{i=1}^N\left|Q_i-Y_i\right| $ | (4) |
| $ \mathrm{Acc}=N_C / N $ | (5) |
式中: Oi和Yi分别为10 m极大风速实况值、模型预报值,NC为|Oi-Yi|≤3 m·s-1的次数,N为样本数。MAE越接近于0,Acc越接近于1,表明模型对10 m极大风速的预报能力越强。
4 模型性能评估 4.1 单一模型评估 4.1.1 总体评估表 3给出了不同模型对测试集上各预报点位在整个预报时效(72 h)内极大风速预报的平均绝对误差和准确率对比情况。从平均绝对误差可看出,针对所有预报点位,GBDT和RF模型的平均绝对误差均要低于DT模型,且以GBDT模型更低,其平均绝对误差在1.56~3.57 m·s-1,较DT模型的改善率介于4.3%~8.7%。一方面,改善率的高低与海拔高度有关,这里选择位置较为重要且代表了不同海拔高度的A1701、A1708和A1489站进行说明,针对山顶站A1701,DT模型的平均绝对误差为3.73 m·s-1,GBDT模型降低至3.57 m·s-1,较DT模型的改善率为4.3%,对于山腰站A1708,DT模型的平均绝对误差为1.65 m·s-1,GBDT模型较DT模型降幅为0.09 m·s-1,改善率为5.5%,对于山谷站A1489,DT模型的平均绝对误差为1.90 m·s-1,GBDT模型较DT模型降低0.16 m· s-1,改善率达8.4%;另一方面,改善率的高低还与周围环境有一定关系,位于山腰的A1703和A1710站海拔高度差不足20 m,但改善率却相差3.7%。从准确率来看,除A1711站外,其余站点的GBDT和RF模型均要高于DT模型,其中,以GBDT模型为最高的站点占75%。
|
|
表 3 不同模型对各点位72 h时效内极大风速预报的平均绝对误差(MAE)(单位:m·s-1)和准确率(Acc) Table 3 MAE (unit: m·s-1) and Acc of extreme wind speed within 72 h lead time predicted by different models at each station |
另外可看出,随着预报点位海拔高度升高,各模型的平均绝对误差有增加的趋势,而准确率有降低的趋势。如果以A1705和A1711站所在的海拔高度1770 m左右为分界线,针对此高度以上的站点A1701、A1703和A1710,各模型的平均绝对误差在2.47~3.73 m·s-1,准确率在0.480~0.673,而对此高度以下的站点A1708、A1712和A1489而言,各模型的平均绝对误差介于1.56~1.91 m·s-1,准确率介于0.769~0.850,这表明,模型预报性能对海拔高度有较强的敏感性,即海拔高度越高的点位,平均绝对误差相应越大,而准确率相应越小,这很可能与海拔高度越高的点位风速越大有关。
为进一步探索风向因子对极大风速预报的影响,本文将每个点位预报因子中的风向因子去掉后重新建模,并与原模型结果进行对比分析。结果(表 3)表明:在去掉风向因子后,绝大多数模型的预报准确率会出现降低,平均绝对误差出现增加,变化幅度最为明显的均为A1705站的RF模型,准确率降幅达0.100,平均绝对误差增幅为0.55 m·s-1。因此,在实际业务中预报极大风速时,除了应该考虑不同层次的风速外,还有必要考虑风向的影响。
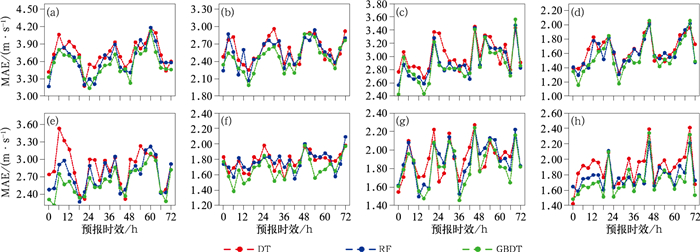
4.1.2 不同预报时效评估图 6为不同模型对测试集上各预报点位极大风速预报的平均绝对误差随预报时效的变化情况,对比可看出,针对每个预报点位,DT、RF和GBDT模型的平均绝对误差值相近,而且随时效的变化趋势也较为一致,尤其是A1701、A1703、A1705、A1708和A1489站,如果以DT模型值为基准,由计算可知,GBDT、RF模型值与其相关系数可高达89%;总体上,各模型的平均绝对误差均以天为周期上下波动,并表现出一定的日变化特征。
|
图 6 不同模型对各点位极大风速预报的平均绝对误差(MAE)随预报时效的变化(a)A1701, (b)A1703, (c)A1705, (d)A1708, (e)A1710, (f)A1711, (g)A1712, (h)A1489 Fig. 6 Variation of MAE with forecasting lead time in extreme wind speed predicted by different models at stations of (a) A1701, (b) A1703, (c) A1705, (d) A1708, (e) A1710, (f) A1711, (g) A1712, and (h) A1489 |
由4.1.1节可知,在整个预报时效上,GBDT模型对各预报点位的平均绝对误差均最小,DT模型均最大,而RF模型介于两者之间。在此重点分析GBDT和DT模型在不同时效上的对比情况,可以看出,针对A1712站,GBDT模型有16个时效的平均绝对误差要低于DT模型,而其余站点,GBDT模型的误差低于DT模型的时效数目均达到20个以上,其中以A1711站最多(24个)。这表明,在逐3 h精细化预报时效上,GBDT模型较DT模型的预报优势也较为明显。
针对GBDT模型,在一定海拔高度以内,日最大平均绝对误差所对应的时刻随站点海拔高度升高有滞后的趋势,针对某一点位而言,不同时效内最大平均绝对误差出现的时刻点基本一致,但达到某一高度后,上述规律变得不明显。对于低海拔站A1705、A1708、A1712和A1489,0~24、24~48和48~72 h内的最大平均绝对误差分别出现在21、45和69 h时效,正好间隔24 h,均对应每日17时;随着站点海拔高度升高,对A1711站预报的最大平均绝对误差分别位于24、48和72 h时效,正好间隔24 h,均对应每日20时;随着海拔高度进一步升高,对A1703站预报的最大平均绝对误差分别位于3、30和51 h时效,对应每日23时或02时;随着海拔高度继续升高,对山顶及附近的站点A1701和A1703预报的最大平均绝对误差分别位于6、39和60 h时效,对应每日02、11和08时。
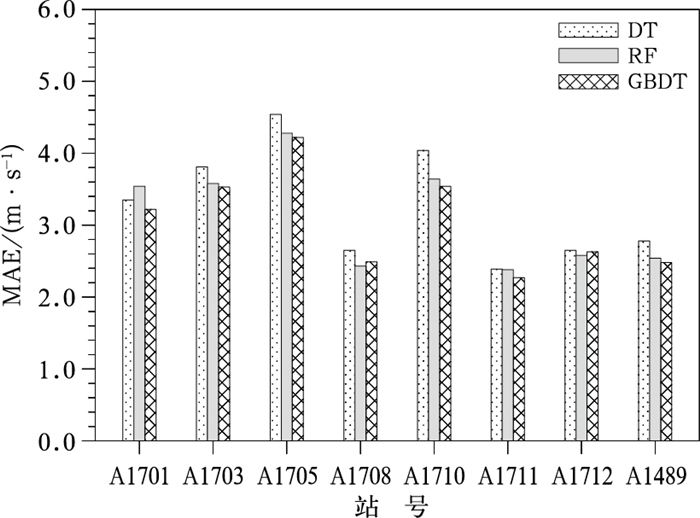
4.1.3 超阈值评估高山滑雪运动对大风较为敏感。图 7给出了不同模型对测试集上各预报点位超阈值极大风速预报的平均绝对误差情况,这里所选取的阈值是由该点位极大风速实况的上四分位数来确定,A1701、A1703、A1705、A1708、A1710、A1711、A1712和A1489站的阈值分别为19.6、13.5、15.0、8.5、15.9、8.9、9.9、9.9 m·s-1。可以看出,针对山顶站A1701,GBDT模型的平均绝对误差最小,为3.22 m·s-1,DT模型有所增大,RF模型进一步增大至3.54 m·s-1,而其余点位的情况则有所不同,DT模型的平均绝对误差均为最大,RF或GBDT模型的误差相对更小,且以GBDT模型为最小的点位居多,比较而言,针对山腰中那些相对低海拔站A1712和A1708,RF模型的平均绝对误差要小于GBDT模型,而对于山腰中的相对高海拔站A1703、A1705、A1710、A1711以及山谷站A1489而言,GBDT模型的平均绝对误差则小于RF模型。A1701站的表现情况之所以与其余点位有所不同,很可能与该点位所处山顶位置有关,该位置海拔最高且较为孤立,受自由大气的影响相对更为明显。综合来看,以GBDT模型的平均绝对误差为最小的站点占75%,可以说,这是一种对延庆赛区超阈值极大风速预报较为优秀的算法模型。
|
图 7 不同模型对各点位超阈值极大风速预报的平均绝对误差(MAE) Fig. 7 MAE in super threshold extreme wind speed at each station predicted by different models |
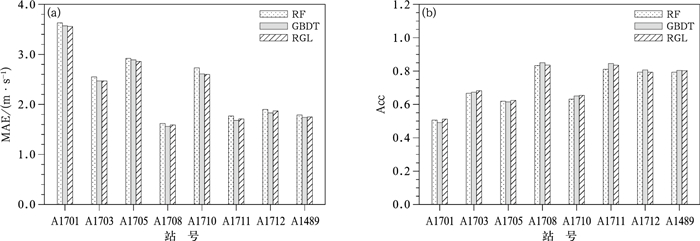
通过集成学习模型RGL与单一模型在测试集上的对比评估(图 8)可以看出,集成模型较单一模型具备一定的改进能力,而且对风速大小表现出较高的敏感性。具体来看,针对极大风速相对较大的高海拔站A1701、A1703、A1705和A1710,集成模型的平均绝对误差较单一模型GBDT和RF均有所降低或与之持平,降低幅度在0.13 m·s-1以内,而准确率较单一模型均有所提高,最大提升幅度为0.022,平均绝对误差和准确率变化幅度最为明显的均为A1710站;而对于极大风速相对较小的低海拔站A1708、A1711、A1712和A1489,集成模型的性能表现介于单一模型RF和GBDT之间,即集成模型的准确率高于或等于RF模型而低于GBDT模型,平均绝对误差高于GBDT模型而低于RF模型。
|
图 8 不同模型对各点位极大风速预报的(a)平均绝对误差(MAE)和(b)准确率(Acc) Fig. 8 (a) MAE and (b) Acc in extreme wind speed at each station predicted by different models |
为了评估集成学习模型在冬奥会保障中的实际应用能力,本文选取了2月19—20日对比赛有较大影响的大风个例进行了检验。
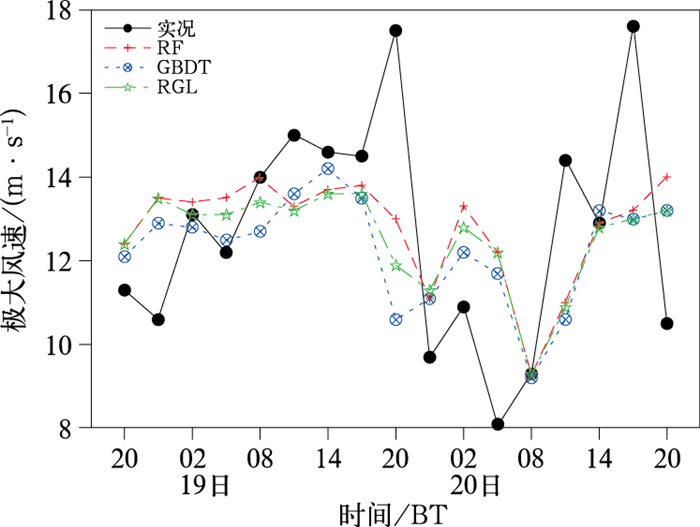
为评估20日上午这个关键时段的风速预报结果,图 9给出了集成模型RGL与单一模型对赛场附近A1712站极大风速的预报与实况对比情况,可以看出,集成模型对20日08时的极大风速预报与实况完全一致,均为9.3 m·s-1,RF和GBDT模型均与集成模型预报效果相当;而对于11时,集成模型的预报值(10.9 m·s-1)较实况偏低3.5 m·s-1,RF模型与集成模型性能相当,GBDT模型预报性能略低,实际上,当时预报员可参考的其他一些客观模型较实况也一致偏低。从另一个角度讲,19日和20日的天气形势总体差异不大,利用19日模型临近误差信息则可以改进20日的预报效果,可以发现,集成模型对18日和19日连续两天夜间(23时至次日05时)风速的预报较实况偏高或与之持平,而对19日白天(08—17时)的风速预报较实况偏低或与之持平。根据19日08时和11时的预报误差(分别为0.6 m·s-1和1.8 m·s-1),可订正得到20日08时和11时的预报值分别为9.9 m·s-1和12.7 m·s-1,与实况偏差均在2 m·s-1以内。可见,在实际应用中,利用模型临近误差信息是必要的。
|
图 9 2022年2月19—20日不同模型对A1712站极大风速的预报和实况对比 Fig. 9 Comparison of extreme wind speed predicted by different models with observations at A1712 Station from 19 to 20 February 2022 |
基于冬奥会延庆赛区极大风速观测数据以及优选的ECMWF模式要素预报产品,利用三种不同类型的机器学习算法(DT、RF和GBDT)分别建立了赛区不同海拔高度点位的10 m极大风速精细化预报模型,在模型对比评估基础上,基于stacking方法构建了集成学习模型RGL,并评估了较单一模型的改进能力。主要得到如下结论:
(1) 延庆赛区各点位极大风速预报的最优预报因子主要集中在不同高度层的风速和风向,个别站还包括垂直速度,若去掉风向预报因子,绝大多数模型的预报准确率会降低,平均绝对误差会增加。这表明:在实际业务中预报极大风速时,除了应该考虑不同层次的风速外,还有必要考虑风向的影响。
(2) 针对延庆赛区不同点位的极大风速预报,基于决策树基学习器集成学习的GBDT和RF模型总体上要优于单一决策树模型DT。从平均绝对误差来看,所有点位的GBDT模型均较RF模型更小,其预报的极大风速平均绝对误差介于1.56~3.57 m· s-1,较DT模型的改善率最高可达8.7%,改善率的高低对海拔高度和周围环境都有较强的敏感性;从准确率来看,绝大多数点位的GBDT模型较RF模型更高。另外,GBDT模型对超阈值极大风速的预报较为优秀。
(3) DT、RF和GBDT模型对延庆赛区极大风速预报的平均绝对误差和准确率均表现出海拔依赖性,即随着预报点位海拔高度升高,平均绝对误差有增加的趋势,而准确率有降低的趋势。随着预报时效增加,各模型的平均绝对误差总体上以天为周期上下波动,且表现出一定的日变化特征。
(4) 与单一机器学习模型相比,基于stacking方法的集成学习模型对延庆赛区的极大风速预报具备一定的改进能力,且以极大风速相对较大的高海拔站改进更为突出,平均绝对误差较单一模型最大可降低0.13 m·s-1,准确率最高可提升0.022。
相关研究成果已集成开发到网页平台,并在2022年冬(残)奥会赛事服务保障中发挥重要作用。该工作仅利用有限的ECMWF模式数据,主要针对冬季复杂山区的极大风速预报模型进行了初步研究,下一步将利用更多的资料进行建模,同时评估模型在不同季节、不同地区的适用性,以期为高质量的精细化预报服务提供参考和依据。
陈双, 谌芸, 何立富, 等, 2019. 我国中东部平原地区临界气温条件下降水相态判别分析[J]. 气象, 45(8): 1037-1051. Chen S, Chen Y, He L F, et al, 2019. Discrimination analysis of snow and rain occurring under critical temperature conditions in central and eastern China[J]. Meteor Mon, 45(8): 1037-1051 (in Chinese).
|
陈豫英, 陈晓光, 马筛艳, 等, 2006. 精细化MOS相对湿度预报方法研究[J]. 气象科技, 34(2): 143-146. Chen Y Y, Chen X G, Ma S Y, et al, 2006. Fine MOS forecasting method of relative humidity[J]. Meteor Sci Technol, 34(2): 143-146 (in Chinese).
|
韩念霏, 杨璐, 陈明轩, 等, 2022. 京津冀站点风温湿要素的机器学习订正方法[J]. 应用气象学报, 33(4): 489-500. Han N F, Yang L, Chen M X, et al, 2022. Machine learning correction of wind, temperature and humidity elements in Beijing-Tianjin-Hebei Region[J]. J Appl Meteor Sci, 33(4): 489-500 (in Chinese).
|
胡波, 2019. 阵风因子与大气边界层要素的关系及预报试验[J]. 气象科技, 47(2): 282-288. Hu B, 2019. Relationship between gust factors and ABL parameters and its prediction test[J]. Meteor Sci Technol, 47(2): 282-288 (in Chinese).
|
胡艺, 符娇兰, 陶亦为, 等, 2022. 冬奥会延庆赛区气象要素分布特征分析[J]. 气象, 48(2): 177-189. Hu Y, Fu J L, Tao Y W, et al, 2022. Characteristics of meteorological elements over Yanqing Area during Winter Olympic Games[J]. Meteor Mon, 48(2): 177-189 (in Chinese).
|
贾春晖, 窦晶晶, 苗世光, 等, 2019. 延庆-张家口地区复杂地形冬季山谷风特征分析[J]. 气象学报, 77(3): 475-488. Jia C H, Dou J J, Miao S G, et al, 2019. Analysis of characteristics of mountain-valley winds in the complex terrain area over Yanqing-Zhangjiakou in the winter[J]. Acta Meteor Sin, 77(3): 475-488 (in Chinese).
|
卢峰本, 1998. 卡尔曼滤波在沿海冬半年风力预报中的应用[J]. 气象, 24(3): 50-53. Lu F B, 1998. The application of Kalman filter to the coastal wind forecast in winter[J]. Meteor Mon, 24(3): 50-53 (in Chinese).
|
陆如华, 何于班, 1994. 卡尔曼滤波方法在天气预报中的应用[J]. 气象, 20(9): 41-43, 40. Lu R H, He Y B, 1994. The application of Kalman filter in weather forecasts[J]. Meteor Mon, 20(9): 41-43, 40 (in Chinese).
|
钱燕珍, 孙军波, 余晖, 等, 2012. 用支持向量机方法做登陆热带气旋站点大风预报[J]. 气象, 38(3): 300-306. Qian Y Z, Sun J B, Yu H, et al, 2012. Application of SVM method to the station strong wind forecast in landfalling tropical cyclones[J]. Meteor Mon, 38(3): 300-306 (in Chinese).
|
任萍, 陈明轩, 曹伟华, 等, 2020. 基于机器学习的复杂地形下短期数值天气预报误差分析与订正[J]. 气象学报, 78(6): 1002-1020. Ren P, Chen M X, Cao W H, et al, 2020. Error analysis and corre- ction of short-term numerical weather prediction under complex terrain based on machine learning[J]. Acta Meteor Sin, 78(6): 1002-1020 (in Chinese).
|
申华羽, 方艳莹, 涂小萍, 等, 2020. ECMWF细网格10 m风预报在浙江沿海的评估与订正[J]. 气象, 46(11): 1485-1494. Shen H Y, Fang Y Y, Tu X P, et al, 2020. Verification of ECMWF 10 m wind forecast for coastal Zhejiang Province[J]. Meteor Mon, 46(11): 1485-1494 (in Chinese).
|
孙全德, 焦瑞莉, 夏江江, 等, 2019. 基于机器学习的数值天气预报风速订正研究[J]. 气象, 45(3): 426-436. Sun Q D, Jiao R L, Xia J J, et al, 2019. Adjusting wind speed prediction of numerical weather forecast model based on machine learning methods[J]. Meteor Mon, 45(3): 426-436 (in Chinese).
|
孙永刚, 李彰俊, 孟雪峰, 等, 1998. 天气动力学组合因子在MOS降水预报中的应用[J]. 气象, 24(2): 27-30. Sun Y G, Li Z J, Meng X F, et al, 1998. The application of composite factors of synoptic dynamics to the MOS precipitation forecasting method[J]. Meteor Mon, 24(2): 27-30 (in Chinese).
|
王可心, 包云轩, 朱承瑛, 等, 2021. 随机森林回归法在冬季路面温度预报中的应用[J]. 气象, 47(1): 82-93. Wang K X, Bao Y X, Zhu C Y, et al, 2021. Forecasts of road surface temperature in winter based on random forests regression[J]. Meteor Mon, 47(1): 82-93 (in Chinese).
|
王倩倩, 权建农, 程志刚, 等, 2022. 2019年冬季北京海陀山局地环流特征及机理分析[J]. 气象学报, 80(1): 93-107. Wang Q Q, Quan J N, Cheng Z G, et al, 2022. Local circulation characteristics and mechanism analysis of Haituo Mountain in Beijing during winter 2019[J]. Acta Meteor Sin, 80(1): 93-107 (in Chinese).
|
吴启树, 韩美, 郭弘, 等, 2016. MOS温度预报中最优训练期方案[J]. 应用气象学报, 27(4): 426-434. Wu Q S, Han M, Guo H, et al, 2016. The optimal training period scheme of MOS temperature forecast[J]. J Appl Meteor Sci, 27(4): 426-434 (in Chinese).
|
乌日柴胡, 王建捷, 孙靖, 等, 2019. 北京山区与平原冬季近地面风的精细观测特征[J]. 气象学报, 77(6): 1107-1123. Wu R, Wang J J, Sun J, et al, 2019. An observational investigation of fine features of near surface winds in winter over Beijing Area[J]. Acta Meteor Sin, 77(6): 1107-1123 (in Chinese).
|
杨璐, 宋林烨, 荆浩, 等, 2022. 复杂地形下高精度风场融合预报订正技术在冬奥会赛区风速预报中的应用研究[J]. 气象, 48(2): 162-176. Yang L, Song L Y, Jing H, et al, 2022. Fusion prediction and correction technique for high-resolution wind field in Winter Olympic Games area under complex terrain[J]. Meteor Mon, 48(2): 162-176 (in Chinese).
|
曾晓青, 赵声蓉, 段云霞, 2013. 基于MOS方法的风向预测方案对比研究[J]. 气象与环境学报, 29(6): 140-144. Zeng X Q, Zhao S R, Duan Y X, 2013. Comparison of wind direction forecast schemes based on MOS method[J]. J Meteor Environ, 29(6): 140-144 (in Chinese).
|
张玉涛, 佟华, 孙健, 2020. 一种偏差订正方法在平昌冬奥会气象预报的应用[J]. 应用气象学报, 31(1): 27-41. Zhang Y T, Tong H, Sun J, 2020. Application of a bias correction method to meteorological forecast for the Pyeongchang Winter Olympic Games[J]. J Appl Meteor Sci, 31(1): 27-41 (in Chinese).
|
智协飞, 吴佩, 俞剑蔚, 等, 2019. GFS模式地形高度偏差对地面2 m气温预报的影响[J]. 大气科学学报, 42(5): 652-659. Zhi X F, Wu P, Yu J W, et al, 2019. Impact of topographic altitude bias of the GFS model on the 2 m air temperature forecast[J]. Trans Atmos Sci, 42(5): 652-659 (in Chinese).
|
Breiman L, Friedman J H, Olshen R A, et al, 1984. Classification and Regression Trees[M].
New York: Chapman and Hall/CRC.
|
Breiman L, 2001. Random forests[J]. Mach Learn, 45(1): 5-32.
|
Cassola F, Burlando M, 2012. Wind speed and wind energy forecast through Kalman filtering of numerical weather prediction model output[J]. Appl Energy, 99: 154-166.
|
Cortes C, Vapnik V, 1995. Support-vector networks[J]. Mach Learn, 20(3): 273-297.
|
de Rooy W C, Kok K, 2004. A combined physical-statistical approach for the downscaling of model wind speed[J]. Wea Forecasting, 19(3): 485-495.
|
Friedman J H, 2001. Greedy function approximation: a gradient boosting machine[J]. Ann Statist, 29(5): 1189-1232.
|
Plenković I O, Monache L D, Horvath K, et al, 2018. Deterministic wind speed predictions with analog-based methods over complex topography[J]. J Appl Meteor Climatol, 57(9): 2047-2070.
|
Schulz B, Lerch S, 2022. Machine learning methods for postprocessing ensemble forecasts of wind gusts: a systematic comparison[J]. Mon Wea Rev, 150(1): 235-257.
|
Tang B H, Bassill N P, 2018. Point downscaling of surface wind speed for forecast applications[J]. J Appl Meteor Climatol, 57(3): 659-674.
|
Wei C C, 2015. Forecasting surface wind speeds over offshore islands near Taiwan during tropical cyclones: comparisons of data-driven algorithms and parametric wind representations[J]. J Geophys Res: Atmos, 120(5): 1826-1847.
|
Zhong S Y, Fast J, 2003. An evaluation of the MM5, RAMS, and Meso- Eta models at subkilometer resolution using VTMX field campaign data in the Salt Lake valley[J]. Mon Wea Rev, 131(7): 1301-1322.
|
 2023, Vol. 49
2023, Vol. 49 