2. 南京信息工程大学, 南京 210044
2. Nanjing University of Information Science and Technology, Nanjing 210044
气象雷达在探测气象目标时,雷达发射出去的电磁波受到路径上气体、降水粒子的吸收和散射,导致了信号的衰减(张培昌等,2001)。波长越短的气象雷达,在探测中信号衰减得越严重,有研究表明,波长较短的X波段雷达,其衰减系数分别是C波段、S波段雷达的7~8倍和10倍以上(Park et al,2005),而X波段雷达的信号衰减问题正是影响其广泛应用的重要因素之一。但与C波段、S波段雷达相比,X波段雷达的体积小、移动方便、造价低,其探测具有更高的时空分辨率,在对冰雹、非降水回波和中气旋等的识别中有着明显的优势(马建立等,2012;夏凡等,2021;苏永彦和刘黎平,2022),能够作为现有业务雷达的补充。对X波段雷达的衰减进行有效的订正是X波段雷达提供准确数据的首要问题。
雷达电磁波在大气路径上的衰减订正是长期研究的问题。Bringi et al(1990)通过对降水粒子散射的数值模拟,认为衰减系数A与差分传播相位常数KDP之间基本上为线性关系,提出了A-KDP的经验公式,这一研究成果被广泛地应用于雷达反射率因子的衰减订正中。Ryzhkov and Zrnic(1995)给出了一种变换系数的方法,Carey et al(2000)讨论了温度、粒子形状等各种因素对C波段雷达衰减的影响,并改进了Ryzhkov的方法,变换系数法对S波段和C波段的衰减订正有较大的改进,但该方法要求降水粒子分布比较均匀,所以仍有一定的局限性。在Testud et al(2000)降水廓线订正法的基础上,Bringi et al(2001)提出了“自适应约束”算法,这种算法利用雷达资料本身,不断调整A-KDP关系中的系数,综合考虑了雨滴谱、粒子形状等因素的影响。肖柳斯等(2021)认为“自适应约束”算法对X波段双偏振相控阵雷达反射率因子有较好订正效果。张林等(2021)对差分传播相移φDP去折叠、抖动和滤波处理后,利用KDP对车载X波段双线偏振雷达进行衰减订正,结果表明反射率因子观测误差得到了改善。李思腾等(2021)研究指出,利用雷达网中不同雷达相互订正的方法对X波段雷达穿透强降水后的回波及探测距离较远的回波有较明显的订正效果。胡志群等(2008)对比了X波段双线偏振雷达不同衰减订正方法后提出Z-KDP综合衰减订正法,认为该方法有稳定的订正效果,并且方法简便易行,订正速度快,能够达到实时运行要求。
本文采用Z-KDP法对X波段雷达反射率因子Z进行衰减订正,分析该方法对于两类不同性质降水回波的订正效果,并利用S波段雷达数据检验衰减订正的准确性。
1 X波段雷达衰减订正方法差分传播相位常数KDP是电磁波在传播过程中单位路径上、水平偏振和垂直偏振电磁波之间的相位变化量,即KDP=[(φHH-φVV)/(2R)] (单位:°·km-1),其中φHH、φVV分别为水平偏振波和垂直偏振波的相位,R表示两种偏振电磁波传播的单程距离。KDP几乎不受雷达定标、衰减和部分阻挡的影响,具有稳定、可靠的特点,被广泛地应用于雷达回波的订正。利用KDP进行订正,考虑的是由非球形粒子组成的雨区反射率因子Z的衰减率系数A(单位:dB·km-1)。Bringi et al(1990)通过散射数值模拟发现,衰减系数A与KDP之间具有线性关系,可表示为
| $ A=\alpha K_{\mathrm{DP}} $ | (1) |
式中:α为与波长有关的常数,本研究将α设置为Matrosov et al(2002)根据场外试验得到的0.22 dB· (°)-1。Z的订正公式为:
| $ Z_{\text {corr }}(r)=Z(r)+2 \int_0^r A(s) \mathrm{d} s $ | (2) |
式中:Z(r)、Zcorr(r)分别为订正前后的反射率因子(单位:dBz), r为探测目标的距离(单位:km),s为径向距离(单位:km), 把式(1)代入式(2),可得:
| $ Z_{\mathrm{corr}}(r)=Z(r)+2 \alpha D \sum\limits_{k=1}^n K_{\mathrm{DP}}(k) $ | (3) |
式中:D为库长(单位:km),n为探测到的库数。在实际的雷达探测数据中,当KDP较小时,易受雷达自身噪声以及其他因素的影响,往往会有较大的误差,会对衰减订正的效果产生很大的影响(赵世颖等, 2015;李喆等,2016),所以不适合作为衰减订正的参考值。本文在KDP≥0.3°·km-1时,用KDP的值进行订正,当KDP<0.3°·km-1时,使用雨滴谱拟合A和Z之间的经验公式做衰减订正,具体订正算法如下:
| $ A=\gamma Z_h^\beta $ | (4) |
式中:Zh=10Z/10 (单位:mm6·m-3), γ和β值基本上不受雨滴形状的影响。这里分别取为:γ=1.37×10-4 dB·km-1·(mm6·mm-3)-1,β=0.78。在订正时,根据KDP值的大小决定用KDP订正还是用Z进行订正。
2 衰减订正效果检验分析 2.1 资料来源及数据预处理本文采用的雷达资料来源于上海市浦东新区气象局位于临港地区的X波段双线偏振多普勒雷达(下称临港X波段雷达)和上海市气象局位于浦东临港地区的S波段双线偏振多普勒雷达(下称南汇S波段雷达)。临港X波段雷达是北京敏视达公司生产的双线偏振多普勒雷达,两部雷达相距20 km左右,雷达天线海拔高度为35 m,选用的雷达资料库长为75 m,波束宽度为1°,仰角为1.5°;南汇S波段双线偏振多普勒雷达是来自美国的WSR-88D雷达,并进行了双线偏振探测功能的升级,雷达天线海拔高度为44 m,选用的雷达资料库长为1000 m,波束宽度为1°,仰角为0.5°和2.4°。
S波段雷达的雨区衰减远小于X波段雷达,适合作为检验X波段雷达衰减订正效果的参考值(Chandrasekar et al,2006)。本文选取南汇S波段雷达的数据作为参考,通过对比分析,检验X波段衰减订正效果。由于两部雷达的位置有所不同,径向分辨率又有明显差异,无法直接建立对应关系,需要对观测数据进行坐标转换和插值处理,将南汇S波段雷达数据插值到临港X波段雷达数据的格点上,构成相同空间位置的观测资料,以便分析衰减订正效果。在构建两部雷达在相同空间的资料时,先将临港X波段雷达资料由极坐标转换为大地坐标,再与南汇S波段雷达的站点位置匹配,计算出南汇S波段雷达在此处对应的极坐标,从而将南汇S波段雷达的数据插值到临港X波段雷达对应的空间格点上。由于雷达数据俯仰分布不均匀,进行坐标转换后,临港X波段雷达格点上不一定能匹配到雷达探测的数据,所以本文采用垂直和水平线性内插(肖艳姣和刘黎平,2006)的计算方法将南汇S波段雷达数据处理到临港X波段雷达的数据格点上,插值示意图见图 1。
|
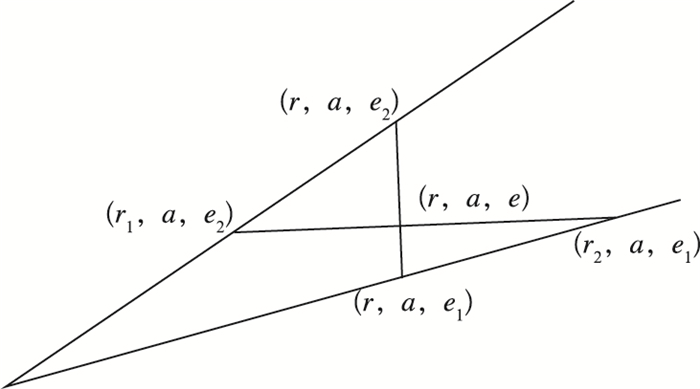
图 1 插值方法示意图 Fig. 1 Schematic diagram of interpolation method |
如图 1所示,(r, a, e2)和(r, a, e1)分别是经过网格点(r, a, e)的垂线与其上下相邻雷达仰角射线的交点, (r1, a, e2), (r2, a, e1)分别是经过网格点(r, a, e)的水平线与其相邻上下仰角射线的交点, 网格点(r, a, e)的分析值fa(r, a, e)可以用这4个点的分析值fa (r, a, e2)、fa (r, a, e1)、fa (r1, a, e2)、fa (r2, a, e1)通过垂直和水平内插得到, 其中这4个点的分析值通过径向和方位的最近邻居法得到:
| $ \begin{gathered} f^a(r, a, e)=\left[w_{e_1} f^a\left(r, a, e_1\right)+w_{e_2} f^a\left(r, a, e_2\right)+\right. \\ \left.w_{r_1} f^a\left(r_1, a, e_2\right)+w_{r_2} f^a\left(r_2, a, e_1\right)\right] / \\ \left(w_{e_1}+w_{e_2}+w_{r_1}+w_{r_2}\right) \end{gathered} $ | (5) |
式中:we1、we2、wr1和wr2分别是给予fa(r, a, e1)、fa(r, a, e2)、fa(r1, a, e2)与fa(r2, a, e1)的内插权重,we1=(e2-e)/(e2-e1),we2=(e-e1)/(e2-e1),wr1=(r2-r)/(r2-r1),wr2=(r-r1)/(r2-r1)。且有r1=rsine/sine2,r2=rsine/sine1。
2.2 订正效果检验为了检验Z-KDP衰减订正方法对对流性降水和稳定性降水回波的订正效果,本文选取2020年9月17日和2021年2月26日两个个例进行分析。其中,2020年9月17日上海出现了对流性降水天气,2021年2月26日白天为大范围的稳定性降水天气。
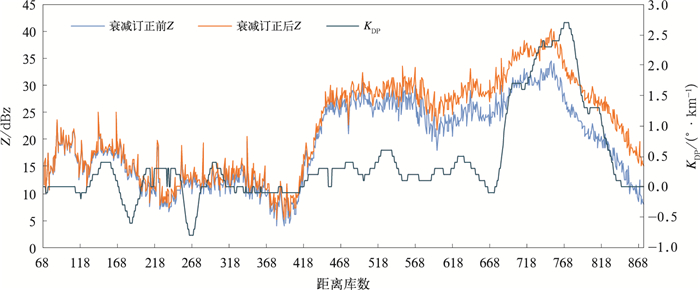
2.2.1 Z、KDP沿径向变化的定量分析2020年9月17日受冷暖空气共同影响,上海出现了对流性降水(雷阵雨)天气,图 2为当日14:04临港X波段雷达衰减订正前、后反射率因子Z及KDP沿径向(方位角269°)的变化折线,这里显示的是有回波区域(第68~第868距离库)的数据。由图可知,反射率因子沿径向大小起伏明显,最大值出现在第750距离库处,订正前为34.5 dBz,经Z-KDP订正到40.3 dBz,这符合对流性降水回波的特点。从KDP沿径向的变化来看,在靠近雷达一侧,由于受各种杂波影响,KDP值变化非常剧烈,且有较大的负值存在,在第350~第437距离库,由于回波强度较弱,KDP的值在正负很小的范围内浮动。在第437距离库之前KDP值均在0.3°·km-1以下,这段距离的KDP值基本没有用到衰减订正中,即在弱回波区用Z进行了衰减订正;在第437距离库之后随着Z值增大,KDP的值增大到0.3°·km-1以上,最大值(2.7°·km-1)出现在第768距离库处,之后随着Z的快速减弱,KDP值也急速减小。在整个强回波区,波束受雨区衰减明显导致信噪比减小,使得KDP的值波动较大,但基本都在0.3°·km-1以上,这段距离库上用KDP进行衰减订正。由于电磁波经过长距离的雨区衰减,距离雷达越远的地方订正值越大,最远处达到了7 dBz左右。
|
图 2 2020年9月17日14:04临港X波段雷达Z和KDP随距离变化(方位角269°) Fig. 2 Variation diagram of Z and KDP of harbor X-band radar with distance (azimuth 269°) at 14:04 BT 17 September 2020 |
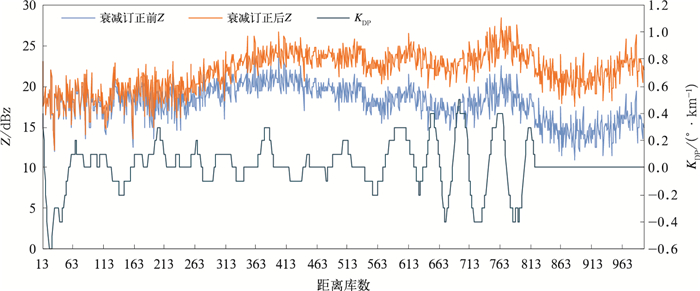
2021年2月26日白天受冷空气影响,上海出现了大范围的小雨天气,图 3为当日12:40临港X波段雷达衰减订正前、后反射率因子Z及KDP沿径向(方位角150°)的变化折线图,这里显示的是有回波区域(第13~第999距离库)的数据。由图可知,Z在整个径向上变化不大,订正前约在15~20 dBz,这符合稳定性降水回波较弱的特点;由于整个径向上KDP值在0°·km-1附近波动,且基本都在0.3°·km-1以下,因此对于稳定性降水回波,基本用Z进行衰减订正。订正结果和对流性降水类似,离雷达越远的地方订正值越大,约为7 dBz,体现了衰减的累积效应。
|
图 3 同图 2,但为2021年2月26日12:40(方位角150°) Fig. 3 Same as Fig. 2, but at 12:40 BT 26 February 2021 (azimuth 150°) |
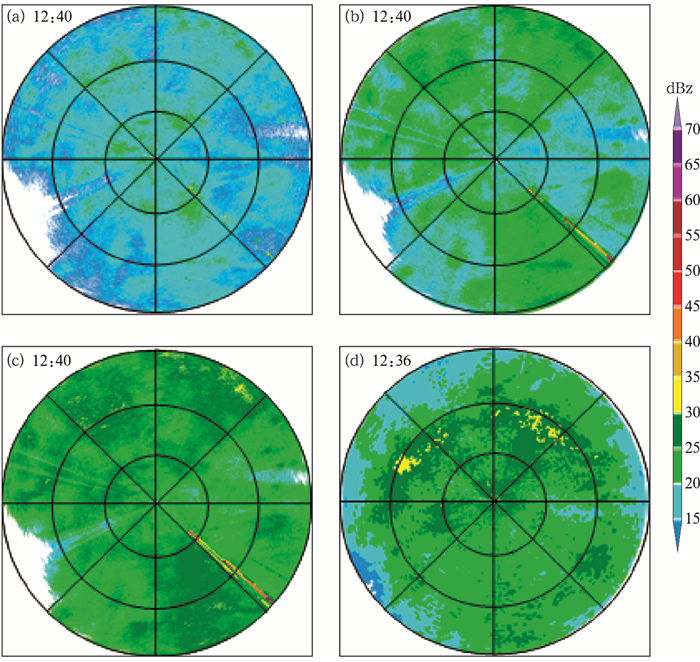
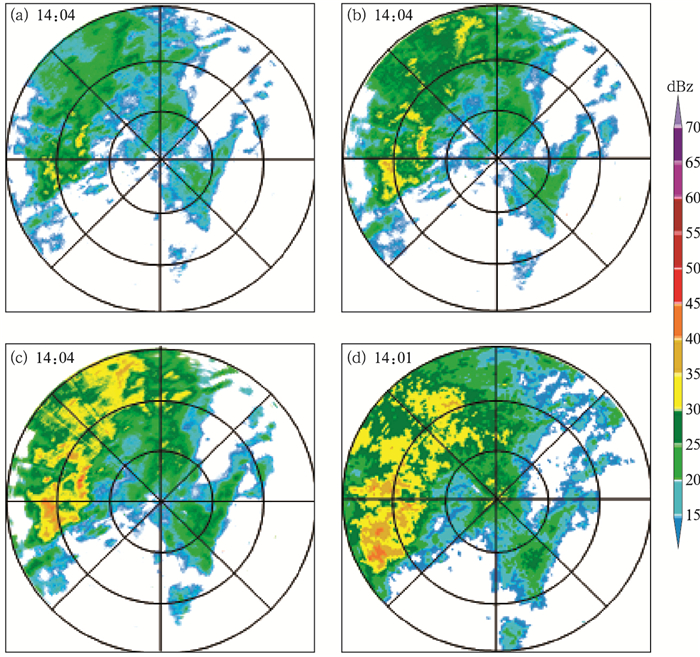
临港X波段雷达探测的径向距离为75 km,图 4和图 5中一个距离圈表示25 km,图 4a,图 5a和图 4b,图 5b分别为利用Z-KDP法进行衰减订正前、后Z的PPI图像,图 4c,图 5c为Z-KDP法进行衰减订正和系统偏差订正后Z的PPI图像,图 4d,图 5d为南汇S波段雷达资料经坐标转换后插值到临港X波段雷达网格上的PPI图像。
|
图 4 2020年9月17日(a)X波段雷达衰减订正前Z,(b)X波段雷达衰减订正后Z,(c)X波段雷达衰减订正+系统偏差后,(d)S波段雷达Z(坐标转换后差值到X波段雷达网格)的反射率因子 Fig. 4 Reflectivity factors of the X-band radar (a) before attenuation correction, (b) after attenuation correction, (c) with both attenuation correction and system bias correction and (d) over the X-band radar grids on 17 September 2020 |
图 4a是2020年9月17日14:04 X波段雷达在1.5°仰角的反射率因子PPI图,可以看出在雷达的西北及偏西方向有大片的层积混合降水回波,强回波区域比较小,图 4b表明,经过Z-KDP订正后的回波值变大、强回波区域增大、回波中心更为明显、反射率因子边缘处弱回波也有所增强,说明衰减影响得到了合理的订正。
与当日14:01 S波段雷达反射率因子(图 4d)相比,衰减订正后的回波强度仍整体偏弱,强回波区面积明显偏小。通过对比X波段雷达附近距离库的雷达反射率与S波段雷达的反射率数值,发现X波段雷达的反射率比S波段雷达偏小约4 dBz。虽然X波段雷达易因雨区衰减,但靠近雷达站的几十个距离库受雨区衰减影响比较小,这个差异应该是由X波段雷达的系统偏差造成的;通过浦东新区气象局和南京大学联合对浦东X波段双偏振天气雷达进行的非固定金属球标定,发现实际探测反射率也偏小4 dBz左右,这同样说明X波段雷达存在系统性偏差。因此有必要对X波段雷达进行系统偏差订正。在Z-KDP衰减订正的同时加上系统偏差值(4 dBz)后(图 4c),可以看出,X波段雷达反射率因子强回波区域和S波段雷达反射率因子强回波分布相接近,两部雷达的反射率因子的最大值基本一致,说明了对X波段雷达反射率因子进行衰减订正和系统偏差订正的必要性。除了系统偏差和衰减订正外,图 4c和4d的回波仍有差异,这是由于两部雷达观测时间没有完全匹配,天线波束宽度(取样体积)及阻挡情况不同、探测高度不同等原因,所以,两部雷达强回波的位置仍有偏差。另外,对比图 4c和4d发现,在225°~315°方位,经过订正后X波段雷达的强回波区面积比S波段雷达的强回波区偏小,说明强降水对X波段雷达的衰减影响没有得到完全订正。
图 5a是2021年2月26日12:40 X波段雷达在1.5°仰角的反射率因子PPI图,整个探测区域内回波强度比较弱。图 5b为经过Z-KDP订正后的反射率因子回波有所增强,在小洋山跨海大桥所在地(133°~134°方位径向上)出现了过度订正的情况。X波段雷达在经过衰减订正和系统偏差订正后(图 5c),最大反射率因子与当日12:36 S波段雷达反射率因子(图 5d)相比,大小基本相当,但面积偏小;当日上午开始有较强冷空气影响上海,零度层高度自北向南逐渐降低,当时零度层高度约为2 km,该高度与X波段雷达1.5°仰角在70 km处的波束高度及S波段雷达2.4°仰角在45 km处波束高度基本一致,这使得X波段雷达最大反射率因子(零度层亮带)出现的位置比S波段雷达的偏北;由于两部雷达探测的目标不完全一致,X波段雷达反射率因子的相对大值区比S波段雷达偏北偏东;在135°~180°方位的X波段雷达反射率因子比S波段雷达反射率因子偏大。经过Z-KDP衰减订正和系统偏差订正后,X波段雷达对于零度层亮带的体现没有S波段雷达明显,且有局部订正过量的情况,但总体上和S波段雷达反射率因子大小基本相当、形态相似,说明该订正方法对稳定性降水也可以适用。
3 结论与讨论X波段雷达的雨区衰减是影响其应用的主要问题之一,为了提高X波段雷达观测资料的质量,本文综合利用Z和KDP对X波段雷达的反射率因子进行了衰减订正。通过和S波段雷达回波的对比分析及非固定金属球定标发现,X波段雷达存在系统偏差,也需要订正。为了验证衰减订正方法的适应性,选取了对流性和稳定性降水个例进行试验,并与S波段雷达反射率因子进行对比分析。得到以下结论:
(1) 相较于S波段雷达,X波段雷达的反射率因子在雨区的中远端存在较大的衰减,必须对其进行衰减订正。
(2) 对X波段雷达反射率因子Z进行衰减订正和系统偏差订正后,对流性和稳定性降水回波与S波段雷达回波均有较高的一致性,说明综合应用Z和KDP对X波段雷达反射率因子Z进行衰减订正的方法具有业务应用价值。
(3) 由于雨区对于X波段雷达的衰减影响,在对流性降水情况下,可能出现强回波区偏小,甚至探测不到强回波后部回波的情况;在稳定性降水情况下,虽然可能会出现局部过量订正的现象,但总体更接近S波段雷达的回波数据。
(4) Z-KDP衰减订正方法可以有效地对X波段双线偏振雷达反射率因子衰减进行订正,由于该方法存在一定的局限性,如在低相关系数、低信噪比等情况下,KDP的使用具有不确定性,为了具有业务应用价值,需要开展不同降水情况下的衰减订正效果评估。
胡志群, 刘黎平, 楚荣忠, 等, 2008. X波段双线偏振雷达不同衰减订正方法对比及其对降水估测影响研究[J]. 气象学报, 66(2): 251-261. Hu Z Q, Liu L P, Chu R Z, et al, 2008. Comparison of different attenuation correction methods and their effects on estimated rainfall using X-band dual linear polarimetric radar[J]. Acta Meteor Sin, 66(2): 251-261 (in Chinese). DOI:10.3321/j.issn:0577-6619.2008.02.011
|
李思腾, 马建立, 陈明轩, 等, 2021. 网络化衰减订正方法在北京X波段网络化雷达中的应用[J]. 气象学报, 79(5): 804-816. Li S T, Ma J L, Chen M X, et al, 2021. The application of network attenuation correction method on the X-band network radar in Beijing[J]. Acta Meteor Sin, 79(5): 804-816 (in Chinese).
|
李喆, 李柏, 赵坤, 等, 2016. 国产双偏振天气雷达差分反射率测量性能分析[J]. 气象科技, 44(6): 855-859, 895. Li Z, Li B, Zhao K, et al, 2016. Measurement performance analysis of differential reflectivity for Dual-polarization weather radar made in China[J]. Meteor Sci Technol, 44(6): 855-859, 895 (in Chinese). DOI:10.3969/j.issn.1671-6345.2016.06.001
|
马建立, 苏德斌, 金永利, 等, 2012. X波段双线性偏振雷达电磁波衰减对冰雹识别的影响[J]. 高原气象, 31(3): 825-835. Ma J L, Su D B, Jin Y L, et al, 2012. The impact of attenuation of X-band dual linear polarimetric radar on hail recognition[J]. Plateau Meteor, 31(3): 825-835 (in Chinese).
|
苏永彦, 刘黎平, 2022. S波段双偏振雷达和X波段相控阵天气雷达中气旋识别结果对比[J]. 气象, 48(2): 229-244. Su Y Y, Liu L P, 2022. Comparison of mesocyclone identification results between S-band dual polarization radar and X-band phased array weather radar[J]. Meteor Mon, 48(2): 229-244 (in Chinese).
|
夏凡, 张乐坚, 张林, 2021. 基于双线偏振参量对北京X波段雷达非降水回波识别方法的研究[J]. 气象, 47(5): 561-572. Xia F, Zhang L J, Zhang L, 2021. Study of recognition algorithm of non-precipitation echo for Beijing X-band radar based on dual polarization parameter[J]. Meteor Mon, 47(5): 561-572 (in Chinese).
|
肖柳斯, 胡东明, 陈生, 等, 2021. X波段双偏振相控阵雷达的衰减订正算法研究[J]. 气象, 47(6): 703-716. Xiao L S, Hu D M, Chen S, et al, 2021. Study on attenuation correction algorithm of X-band dual-polarization phased array radar[J]. Meteor Mon, 47(6): 703-716 (in Chinese).
|
肖艳姣, 刘黎平, 2006. 新一代天气雷达网资料的三维格点化及拼图方法研究[J]. 气象学报, 64(5): 647-657. Xiao Y J, Liu L P, 2006. Study of methods for interpolating data from weather radar network to 3-D grid and mosaics[J]. Acta Meteor Sin, 64(5): 647-657 (in Chinese).
|
张林, 李峰, 冯婉悦, 等, 2021. 移动X波段双线偏振雷达数据质量分析及偏差订正[J]. 气象, 47(3): 337-347. Zhang L, Li F, Feng W Y, et al, 2021. Research of data quality analysis and bias correction on mobile X-band dual-polarization weather radar[J]. Meteor Mon, 47(3): 337-347 (in Chinese).
|
张培昌, 杜秉玉, 戴铁丕, 2001. 雷达气象学[M]. 北京: 气象出版社. Zhang P C, Du B Y, Dai T P, 2001. Radar Meteorology[M].
Beijing: China Meteorological Press (in Chinese).
|
赵世颖, 李柏, 陈晓辉, 等, 2015. 基于交叉-平行法的双偏振雷达差分反射率硬件定标[J]. 气象科技, 43(5): 775-782. Zhao S Y, Li B, Chen X H, et al, 2015. System bias calibration of differential reflectivity for dual polarization radar based on cross and straight measurements[J]. Meteor Sci Technol, 43(5): 775-782 (in Chinese).
|
Bringi V N, Chandrasekar V, Balakrishnan N, et al, 1990. An examination of propagation effects in rainfall on radar measurements at microwave frequencies[J]. J Atmos Oceanic Technol, 7(6): 829-840.
|
Bringi V N, Keenan T D, Chandrasekar V, 2001. Correcting C-band radar reflectivity and differential reflectivity data for rain attenua- tion: a self-consistent method with constraints[J]. IEEE Trans Geosci Remote Sens, 39(9): 1906-1915.
|
Carey L D, Rutledge S A, Ahijevych D A, et al, 2000. Correcting propagation effects in C-band polarimetric radar observations of tropical convection using differential propagation phase[J]. J Appl Meteor, 39(9): 1405-1433.
|
Chandrasekar V, Lim S, Gorgucci E, 2006. Simulation of X-band rainfall observations from S-band radar data[J]. J Atmos Oceanic Technol, 23(9): 1195-1205.
|
Matrosov S Y, Clark K A, Martner B E, et al, 2002. X-band polarimetric radar measurements of rainfall[J]. J Appl Meteor, 41(9): 941-952.
|
Park S G, Bringi V N, Chandrasekar V, et al, 2005. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band.Part Ⅰ: theoretical and empirical basis[J]. J Atmos Oceanic Technol, 22(11): 1621-1632.
|
Ryzhkov A, Zrnic D S, 1995. Precipitation and attenuation measurements at a 10-cm wavelength[J]. J Appl Meteor, 34(10): 2121-2134.
|
Testud J, Le Bouar E, Obligis E, et al, 2000. The rain profiling algorithm applied to polarimetric weather radar[J]. J Atmos Oceanic Technol, 17(3): 332-356.
|
 2023, Vol. 49
2023, Vol. 49