2. 国防科技大学气象海洋学院,长沙 410005
2. College of Meteorology and Oceanology, National University of Defense Technology, Changsha 410005
准确、高时空分辨率的降水信息对于气象水文模式运用、气候研究、城市规划、防汛抗旱等意义重大。天气雷达因探测范围和时空分辨率优势而成为定量测量降水(quantitative precipitation estimation,QPE)的有效手段,但由于降水的垂直变化、亮带现象、微波衰减以及雨滴谱时空变化导致的雷达降水估计关系不够准确等因素的影响,天气雷达降水场与地面降水存在一定偏差(Harrison et al,2000;冯婉悦等,2021)。为减少这种偏差,发展出利用地面雨量计测量结果,对雷达反演的区域降水场进行校准的方法,主要包括平均校准法(Collier,1986;傅德胜和戴铁丕,1991)、最优插值法等(Krajewski,1987;张培昌等,1992;李建通和张培昌,1996;Chumchean et al,2006),以及综合不同方法优势的集成方法和联合分步校准方法(官莉等,2004)。大量研究和业务应用表明,通过将天气雷达与地面测雨传感器数据相融合,能够有效提升降水测量的准确性(Goudenhoofdt and Delobbe, 2009)。
然而,雨量计和天气雷达探测降水的时空代表性差异问题较为严重,使得基于雨量计的天气雷达降水场校准方法的准确性难以进一步提升。雨量计与雷达采样体积差异巨大,差异可达8个量级,导致二者测值一致性较差(Sieck et al,2007;沙修竹等,2019)。雨量计分布稀疏,空间代表性较差,单个雨量计自身测量误差对校准效果的影响很大。因此,为提高降水监测准确度,需要拓展天气雷达和雨量计测量结果的比对时间,或使用与天气雷达更加匹配的地面测雨手段替代雨量计(Krajewski and Smith, 2002)。
近年来,利用无线微波链路(microwave link,ML)实施降水监测受到广泛关注,研究者们建议将已建设的微波链路网络作为天气监测的重要手段,认为其使用衰减与降水的关系(K-R)反演降水更具鲁棒性,且具有微波链路时空分辨率高、分布广泛和无需额外投入的突出优势(Messer et al,2006)。相关研究逐步深入和拓展,将微波链路作为“路径平均雨量计”,能够验证雷达降水估测结果的有效性(Minda and Nakamura, 2005);利用层析(Zinevich et al,2008)、深度学习(Pudashine et al,2020)等方法,微波链路网络能够反演区域降水分布,已在荷兰(Overeem et al,2015)、德国(Graf et al,2020)等国家开展了大范围的应用;微波链路降雨有效衰减的修正模型得以建立(高太长等,2015),应用支持向量机方法能够进一步提升微波链路雨强反演准确性(宋堃等,2015);本地化的微波链路降水估计关系也得到了研究(张鹏等,2021),基于星地链路(earth-space links)能够反演垂直降水场,反演精度随着链路数量的增加而提升(Mercier et al,2015;咸明皓等,2020);另外,在天气雷达衰减订正中引入微波链路测值作为约束也取得了较好效果(Zhang et al,2017;Kim and Kwon, 2020)。这些研究表明,微波链路测得的“线”雨强,具有更好的空间代表性,与雷达探测的时空匹配性更好,有希望解决雨量计的“点”测量和采样稀疏问题,进一步提升雷达定量测量降水的精度。
同时,已建微波链路分布广泛。在我国,无线微波链路除用于移动通信外,还大量应用于广播电视、港航企业、海事管理部门、电力部门以及一些大型企业中,这些部门所属的微波链路往往在某一区域形成了较为密集的微波链路网,非常有利于降水监测。鉴于此,本文开展利用微波链路对天气雷达降水场进行校准的研究。在这方面,目前见诸文献的研究工作仍较少,如Cummingsa et al(2009)利用微波链路反演的路径平均雨强和雨量计雨强,采用平均偏差法计算平均校准因子,对雷达降水场进行校准,结果表明链路对雷达降水场的校准效果至少与雨量计校准方法相当。但该研究中所用方法仍较为基本,且未考虑校准因子随空间位置的变化。因此,本文尝试采用多种方法实现微波链路对雷达降水场的校准,并开展试验验证,分析比较各方法的效果,为进一步提升区域特别是雨量计稀疏地域的定量测量降水能力提供参考。
1 方法 1.1 微波链路和天气雷达反演降水微波链路根据链路路径衰减AML(单位:dB)计算链路路径平均雨强
| $ A_{\mathrm{ML}}=a{\overline{R_{\mathrm{ML}}}}^b L $ | (1) |
式中:L(单位:km)为链路长度,系数a,b随链路频率、极化方式和雨滴谱分布等变化,具体取值可根据国际电信联盟(ITU)建议的ITU_R雨衰模型确定,该模型给出了线极化、频率小于55 GHz条件下系数a和b的取值。例如,当微波链路发射7.7 GHz垂直极化电磁波时
| $ A_{\mathrm{ML}}=0.00395{\overline{R_{\mathrm{ML}}}}^{1.31} \mathrm{~L} $ | (2) |
S波段天气雷达可利用雷达反射率因子Z(单位:mm6·m-3)与雨强R(单位:mm·h-1)的关系反演降水,常用的降水估计关系为:
| $ Z=200 R^{1.6} $ | (3) |
令RML(t)和RR(t)分别为t时刻某位置处微波链路反演的路径平均雨强和天气雷达反演的雨强,则乘性平均校准因子C(t)为
| $ C(t)=\frac{R_{\mathrm{ML}}(t)}{R_{\mathrm{R}}(t)} $ | (4) |
由于微波链路得到的是沿链路路径的平均雨强,当降水估测区域内仅有1条微波链路可用时,若其传输路径对应天气雷达的M个距离库,则t时刻平均校准因子C可由下式得到:
| $ \bar{C}(t)=\frac{R_{\mathrm{ML}}(t)}{(1 / M) \sum\limits_{j=1}^M R_{\mathrm{R} j}(t)} $ | (5) |
当降水估测区域内有N条链路可用时,平均校准因子可由下式计算:
| $ \bar{C}(t)=\frac{1}{N} \sum\limits_{i=1}^N \frac{R_{\mathrm{ML} i}(t)}{\left(1 / M_i\right) \sum\limits_{j=1}^{M_i} R_{{\mathrm{R}}i, j}(t)} $ | (6) |
式中:Mi为第i条链路路径对应的天气雷达距离库数。平均校准因子确定后,将天气雷达降水场各点雨强乘以校准因子,得到校准后的雷达降水场。
1.2.2 卡尔曼滤波校准法将校准因子C(t)视为随机变量,其值可由两个独立估计值C1(t)和C2(t)加权平均得到
| $ C(t)=(1-\omega) C_1(t)+\omega C_2(t) $ | (7) |
式中权重ω的最优选择要使加权平均后的C(t)方差最小,可通过卡尔曼滤波方法实现。由于天气雷达和微波链路测雨在时间上不连续,可对随探测时次k变化的校准因子建立离散形式的状态方程:
| $ C(k+1)=C(k)+W(k) $ | (8) |
以及测量方程:
| $ Y(k)=C(k)+M(k) $ | (9) |
式中:W(k)和M(k)均为均值为零的白噪声,且相互独立。式(8)中C(k)是k时刻校准因子的状态变量,如果雷达和微波链路均测得降水真值,那么校准因子为1,但实际中校准因子并不为1,且随k变化。式(9)中Y(k)根据k时刻微波链路和雷达实测值得到,其值为RML(k)/RR(k),可称其为校准因子测量值,M(k)和W(k)均为高斯白噪声,均值为零,且相互独立。结合它们的协方差估计系统的最优化输出可以得出一组递推公式(张培昌等,2001):
| $ \begin{aligned} \hat{C}(k \mid k)= & \hat{C}(k \mid k-1)+K(k)[Y(k)- \\ & \hat{C}(k \mid k-1)] \end{aligned} $ | (10) |
| $ \hat{C}(k \mid k-1)=\hat{C}(k-1 \mid k-1) $ | (11) |
| $ P(k \mid k-1)=P(k-1)+Q(k-1) $ | (12) |
| $ P(k \mid k)=[1-K(k)] P(k \mid k-1) $ | (13) |
| $ K(k)=P(k \mid k-1) /[P(k \mid k-1)+F(k)] $ | (14) |
方程中:
张培昌等(2001)给出了卡尔曼滤波方程组(10)~(14)的详细解法,其中Q(k)和F(k)可采用自适应滤波算法(赵坤等,2005)得到。求解滤波方程组得出的
由于校准因子具有空间相关性,可使用克里金法得到校准因子的空间分布。对于校准区域内因缺少对应微波链路而无法得到实测校准因子的某个格点,其校准因子C(x, t)可以通过有微波链路的格点处的已知校准因子加权求和得到,如下式(Seo,1998):
| $ C(x, t)=\sum\limits_{i=1}^N \lambda_i C\left(x_i, t\right) $ | (15) |
式中:x为当前格点在校准区域中的序号,N为链路总数,C(xi, t)为第i条微波链路处的校准因子,由于该位置处有微波链路测雨值,故校准因子已知。λi为第i条微波链路处校准因子对于待估计点校准因子的权值,该权值可由变异函数模型确定,可用的模型包括高斯模型、线性模型、指数模型、球面模型等。由于降水的空间连续性,校准因子的空间相关性与格点距离成反比,可采用球面模型计算λi。
1.2.4 变分校准法考虑到降水空间分布的不均一性,可使用变分方法实现对区域中不同的格点进行不同程度的校准。变分校准法(张培昌等,2001)首先将链路位置处的已知校准因子
| $ \sum\limits_i \sum\limits_j[C(i, j)-\widetilde{C}(i, j)]^2 \rightarrow \min $ | (16) |
可通过如下变分模型求取C(i, j)
| $ \begin{gathered} C^*=\min _C \sum\limits_i \sum\limits_j\left\{\alpha\left[(C-\widetilde{C})^2\right]+\right. \\ \left.\beta\left[\left(\frac{\partial}{\partial x} C\right)^2+\left(\frac{\partial}{\partial y} C\right)^2\right]\right\} \end{gathered} $ | (17) |
式中:α为观测权重,β为约束权重,用于过滤校准因子场中的高频噪声。对应欧拉方程为:
| $ \alpha(C-\widetilde{C})-\beta\left(\frac{\partial^2}{\partial x^2} C+\frac{\partial^2}{\partial y^2} C\right)=0 $ | (18) |
将此非线性偏微分方程离散化后,可采用超松弛叠代法求解数值解。本文中权重α在同时有雷达和链路测值处取值为100,否则为0,β取值为64。
1.3 误差分析方法以地面雨量计实测值为真值,计算校准前后雷达降水场的平均误差(ME)、平均绝对误差(MAE)、均方根误差(RMSE),方法如下:
| $ \mathrm{ME}=\frac{1}{N} \sum\limits_{i=1}^N\left(R_{\mathrm{G} i}-R_{\mathrm{R} i}\right) $ | (19) |
| $ \mathrm{MAE}=\frac{1}{N} \sum\limits_{i=1}^N\left|R_{\mathrm{G} i}-R_{\mathrm{R} i}\right| $ | (20) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(R_{\mathrm{G} i}-R_{\mathrm{R} i}\right)^2} $ | (21) |
式中:N为雷达和雨量计匹配格点总数,RGi,RRi分别为某时次某格点处雨量计实测雨强和雷达反演雨强。
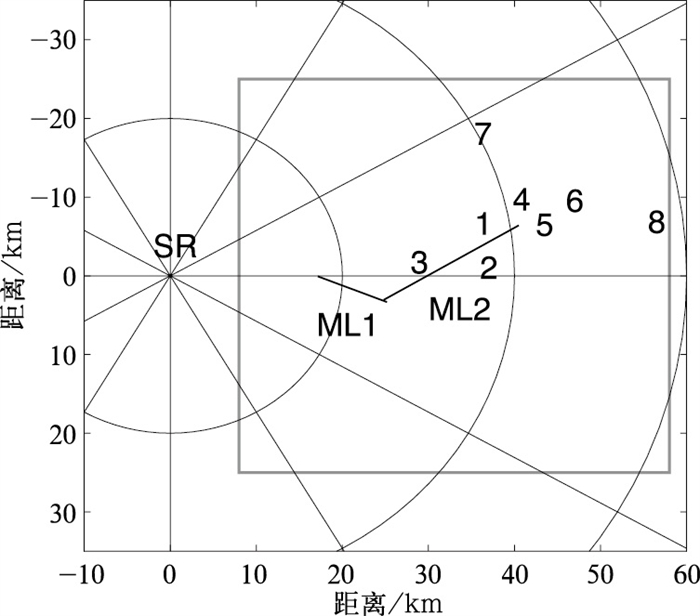
2 试验设备试验设备包括1部S波段天气雷达、8个雨量计和2条微波链路,其中天气雷达为实际业务雷达,2条微波链路均为实际业务用通信链路,设备位置分布如图 1所示。
|
图 1 雷达、链路、雨量计的位置分布 “SR”表示S波段天气雷达,数字1~8代表 8个雨量计,实线“ML1”和“ML2”表示2条微波链路; 方框代表包含链路和雨量计在内的50 km×50 km的正方形校准区域; 距离圈为S波段天气雷达的20 km等距离圈 Fig. 1 Positions of the radar, microwave links and rain gauges The S-band weather radar is indicated by "SR" and the eight rain gauges are indicated by the thick numbers; the two microwave links are indicated by solid lines "ML1" and "ML2"; the square box represents the 50 km×50 km square area of calibration; the circles correspond to S-band radar ranges of 20, 40 and 60 km, respectively |
S波段天气雷达发射频率为2.85 GHz,探测范围为460 km,峰值功率为650 kW,天线高度为138 m,距离库长1000 m,波束宽度为0.99°,进行周期性的体积扫描,每6分钟完成11个仰角层的探测。试验中使用S波段雷达最低仰角(0.5°)层的数据进行降水反演,需首先进行地物消除和滤波处理,以减少地杂波和随机噪声的影响。
两条微波链路均在S波段天气雷达东侧,发射端位置相同,均位于雷达径向距离25 km、方位97°处。链路ML1接收端处在雷达径向距离17 km、方位90°处,海拔高度为126 m。链路ML2接收端位于雷达径向距离41 km、方位81°处,海拔高度为98 m。两条微波链路的发射电磁波频率均为7.7 GHz,垂直极化,发射功率为24.5 dBm,波束宽度为3.5°,发射端和接收端均无天线罩,链路接收功率采集精度均为0.01 dB,采样时间间隔为60 s。通过获取链路接收端自动记录的接收功率,并与链路路径中无降水时的接收功率相比较,可以得到链路路径的雨致衰减量(张鹏等,2021)。微波链路ML1长8.66 km,对应S波段雷达8个距离库,链路ML2长24.05 km,对应S波段雷达17个距离库。
试验所用8个雨量计均为SL3-1型翻斗式雨量计,采样时间间隔为10 min,相对天气雷达和微波链路ML2的位置见表 1。
|
|
表 1 雨量计与天气雷达和微波链路的相对位置 Table 1 The positions of the rain gauges relative to weather radar and microwave link |
在两次实际降水过程中开展了试验,首先由S波段天气雷达利用常用降水估测关系Z=200R1.6反演区域降水分布,同时由两条微波链路基于雨衰关系[式(2)] 反演链路路径平均雨强,然后使用前述四种校准方法,利用微波链路路径平均雨强对雷达降水场进行校准,并与雨量计实测值相比较,结果如下。
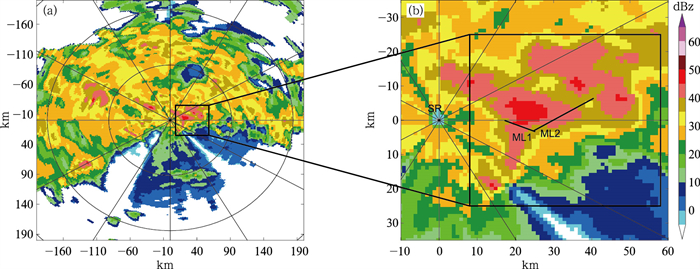
3.1 降水过程Ⅰ:2016年6月1日降水过程2016年6月1日,南京地区经历了一次暴雨过程,降水从08:06—13:00(以下简称降水过程Ⅰ)持续约5 h,将S波段天气雷达进行一次体积扫描的时间(6 min)作为一个时次,此次降水对应50个时次。第9时次(08:54)的雷达回波强度如图 2所示。
|
图 2 2016年6月1日08:54(a)S波段雷达回波强度(仰角0.5°), (b)图 2a中试验区域的放大 粗实线表示微波链路ML1和ML2 Fig. 2 (a) Reflectivity PPI at 0.5° elevation of the S-band radar, (b) the enlarged view of the experimental area in Fig. 2a at 08:54 BT 1 June 2016 Thick solid lines represent microwave links ML1 and ML2, respectively |
本次降水范围广,降水强,部分雨量计测值超过70 mm·h-1,雷达回波分布广,强度大,强中心强度超过50 dBz,整体呈现出混合性降水的特点。在试验区域(图 2b方框区域)内,回波强度大,分布不均匀,对流性降水特点明显。本次降水发展演变很快,试验区域内降水在前14个时次(08:06—09:24)为对流性降水,之后降水强度明显减弱,表现出层状云降水的特点。
(1) 校准因子
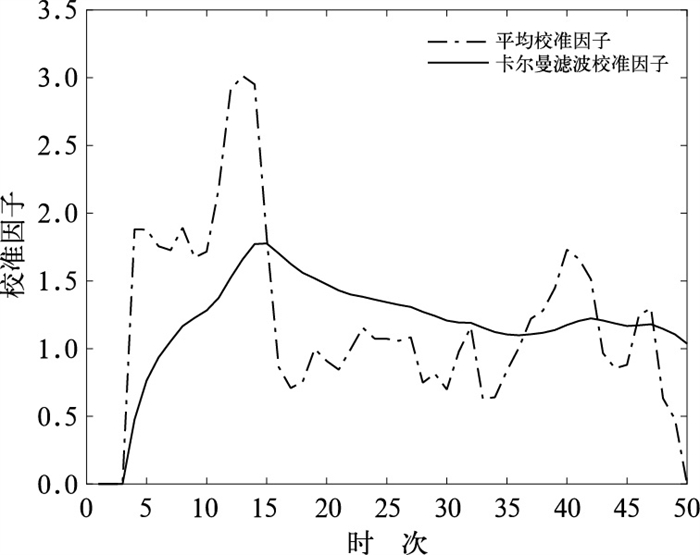
图 3显示了平均校准法和卡尔曼滤波校准法计算得到的校准因子随时次的分布。由图可见,平均校准因子随时间变化较大,部分时段如第13~15时次(09:18—09:30)附近变化剧烈,正好对应降水由对流性降水向层状云降水的转换期,最大校准因子达到3.01,卡尔曼滤波校准因子随时间变化相对平滑,取值也有所降低,最大值为1.77。
|
图 3 2016年6月1日08:06—13:00平均校准法和卡尔曼滤波校准法计算的校准因子 Fig. 3 The calibration factors calculated by the mean calibration method and the Kalman filter calibration method during 08:06-13:00 BT 1 June 2016 |
与平均校准法和卡尔曼滤波校准法不同,克里金校准法和变分校准法得到的校准因子场不仅随时间变化,还随空间位置变化,如图 4所示。
|
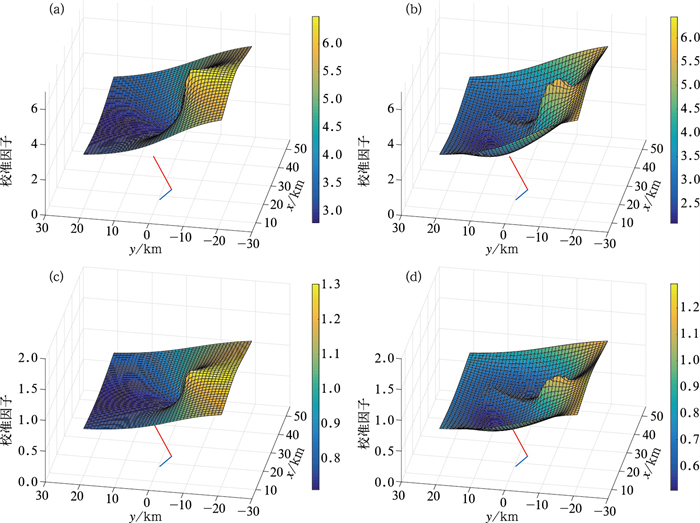
图 4 2016年6月1日08:06—13:00(a, c)克里金校准法以及(b, d)变分校准法在(a, b)第13时次(09:18)和(c, d)第28时次(10:48)得到的校准因子分布 红、蓝实线代表 2条微波链路,下同 Fig. 4 Distribution of the calibration factors calculated by (a, c) the Kriging calibration method, (b, d) the variational calibration method at (a, b) the 13th time point (09:18 BT) and (c, d) the 28th time point (10:48 BT) during 08:06-13:00 BT 1 June 2016 The red and blue lines represent the two microwave links, the same below |
图 4a,4c为克里金校准法在对流性降水阶段的第13时次(09:18)和层状云降水阶段的第28时次(10:48)得到的校准因子场,图 4b,4d为变分校准法在相应时次的校准因子场。图中以S波段雷达为坐标原点,x轴、y轴分别表示东西和南北方向,两条线段代表两条微波链路的位置。可见,两种方法在相同时次的校准因子取值比较接近,变分校准因子场比克里金校准因子场具有更多的空间变化。同时,由于降水的变化,相同方法在不同时次得到的校准因子取值有较大差异,第13时次的校准因子变化范围较大且取值较大(2.0~6.5),而第28时次的校准因子变化范围较小且取值较小(0.5~1.3)。
从校准因子值的变化上看,四种方法得到的校准因子都表现出对流性降水阶段取值较大、层状云降水阶段取值较小且接近于1的特点,说明在对流性强降水阶段,雷达与链路反演的降水差异较大,而在层状云弱降水阶段,二者反演降水差异不大。
(2) 校准结果
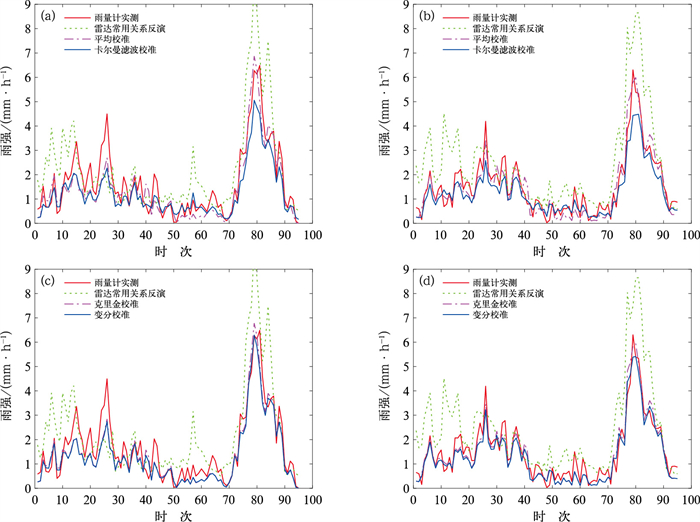
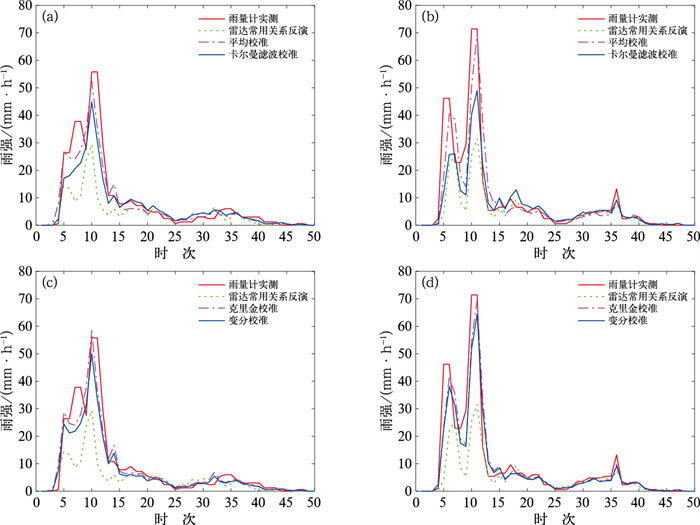
对雷达降水场进行校准,并与雨量计实测雨强进行比较,结果如图 5。图中以不同线型显示了雨量计1和雨量计5位置处的雨量计实测雨强和校准前后雷达反演的雨强随时间的分布。可见,校准前,雷达使用常用降水估计关系反演的降水强度明显低于雨量计实测雨强,对流性降水阶段尤为明显。校准后,雷达反演雨强均得到提升,与雨量计实测值更加接近,不同程度上解决了低估问题。在多数时次,平均校准后的雨强增幅大于卡尔曼滤波校准后的雨强增幅,原因在于卡尔曼滤波校准因子比平均校准因子更加平滑(图 3)。克里金校准后的雨强增幅略高于变分校准,但校准结果基本一致,原因在于试验链路较少,在两条链路位置处得到的平均校准因子,经由克里金校准法和变分校准法“扩散”到整个校准区域,导致克里金和变分校准因子场差异较小(图 4)。
|
图 5 2016年6月1日08:06—13:00(a, b)平均校准法和卡尔曼校准法以及(c, d)克里金校准法和变分校准法在(a, c)雨量计1位置处和(b, d)雨量计5位置处的校准结果 Fig. 5 Calibration results of (a, b) the mean calibration method and the Kalman filter calibration method, (c, d) the Kriging calibration method and the variational calibration method at the position of (a, c) raingauge 1 and (b, d) raingauge 5 during 08:06-13:00 BT 1 June 2016 |
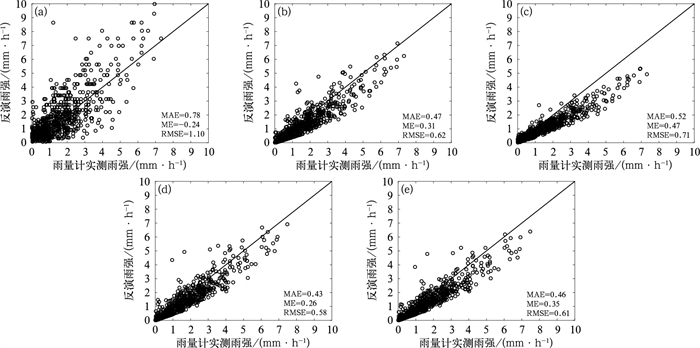
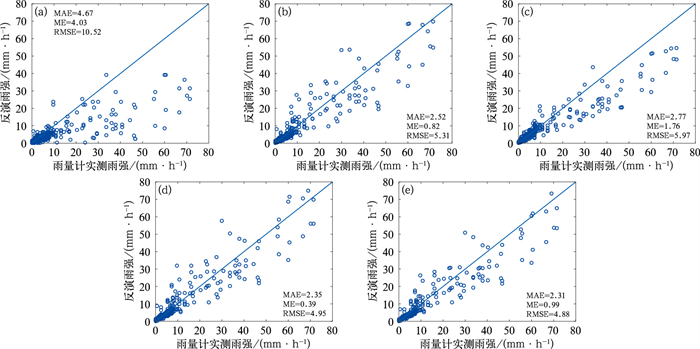
图 6为全部8个雨量计位置处的雨量计实测雨强和雷达反演雨强的散点图,误差统计值也显示在其中。从图 6a可见,与雨量计实测值相比,雷达使用常用降水估计关系反演的雨强存在较大偏差,多数雷达雨强低于雨量计实测雨强,存在明显的降水低估问题。经平均校准(图 6b)、卡尔曼滤波校准(图 6c)、克里金校准(图 6d)和变分校准(图 6e)后,低估问题有所改善,平均校准的改善效果优于卡尔曼滤波校准。克里金校准和变分校准的效果比较接近。
|
图 6 2016年6月1日08:06—13:00雨量计实测雨强与(a)雷达常用降水估计关系反演雨强,(b)平均校准,(c)卡尔曼滤波校准,(d)克里金校准,(e)变分校准后的雷达反演雨强散点图 Fig. 6 Scatter plots of the rain rates measured by rain gauges during 08:06-13:00 BT 1 June 2016 and (a) the radar retrieved rain rates using the default precipitation estimator, calibrated by (b) the mean calibration method, (c) the Kalman filter calibration method, (d) the Kriging calibration method and (e) the variational calibration method |
从图 6中显示的误差统计数值上看,应用各种校准方法后,雷达反演雨强的误差统计值(平均绝对误差MAE、平均误差ME和均方根误差RMSE)均得到明显改善,克里金校准、变分校准、平均校准的效果优于卡尔曼滤波校准方法。
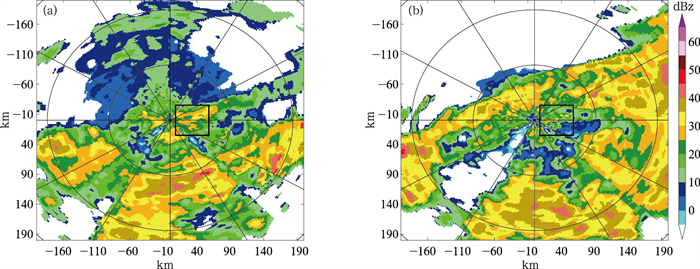
3.2 降水过程Ⅱ:2016年6月12日降水过程南京地区在2016年6月12日发生了一次降水过程,分布范围广,持续时间长,从00:06持续到09:30,将S波段天气雷达进行一次体积扫描的时间(6 min)作为一个时次,共对应95个时次。图 7显示了第6时次(00:36)和第60时次(06:00)的S波段雷达回波强度。
|
图 7 2016年6月12日(a)00:36,(b)06:00的S波段雷达回波强度(仰角0.5°) Fig. 7 Reflectivity PPIs at 0.5° elevation of the S-band radar at (a) 00:36 BT and (b) 06:00 BT 12 June 2016 |
图 7中以S波段雷达为中心,显示了400 km×400 km区域的反射率因子分布,观察降水过程中的S波段雷达回波以及雨量计实测雨强,发现本次降水整体上呈现出混合性强降水的特点。而校准区域(图中以粗实线正方形框表示,50 km×50 km)始终处在强降水的边缘,降水强度较弱且分布不均匀,可以判断校准区域内的降水为对流性弱降水。
(1) 校准因子计算结果
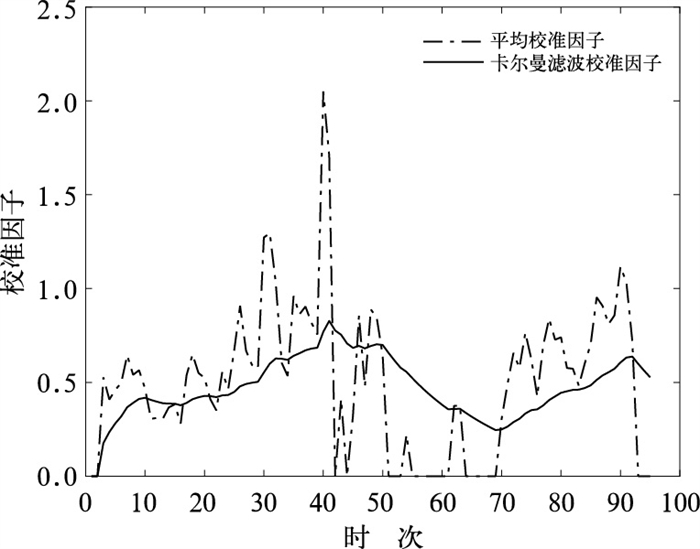
降水过程Ⅱ中的平均校准因子和卡尔曼滤波校准因子随时间的分布如图 8所示。可见,卡尔曼滤波校准因子和平均校准因子在大多数时次都小于1,说明在本次对流性弱降水中,雷达反演的雨强通常高于微波链路反演的雨强,同时也说明,校准后的雨强将低于校准前雨强。与过程Ⅰ相比,平均校准因子随时间变化较大,最大值达到2.0,而卡尔曼滤波校准因子相对平滑,取值有所降低,在所有时次均低于1。
|
图 8 2016年6月12日00:06—09:30平均校准因子和卡尔曼滤波校准因子分布 Fig. 8 Distributions of the mean calibration factors and the Kalman filter calibration factors during 00:06-09:30 BT 12 June 2016 |
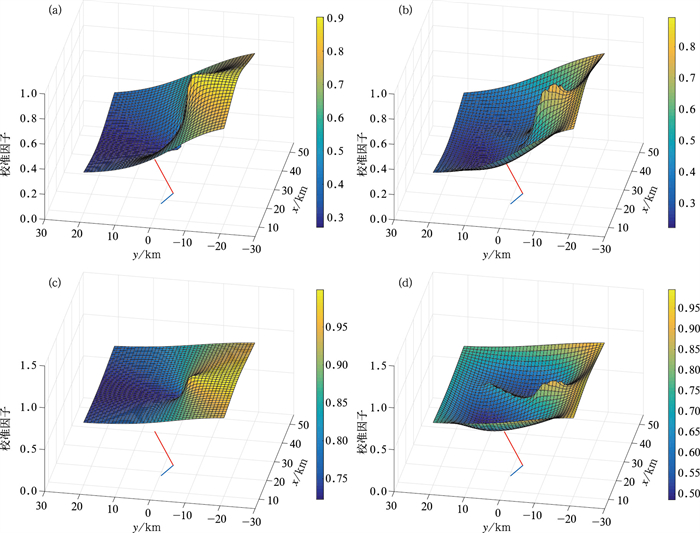
克里金校准法和变分校准法在第12时次(01:12)和第80时次(08:00)的校准因子场如图 9所示。图 9a,9c为克里金校准法在第12时次和第80时次得到的校准因子场,图 9b,9d为变分校准法在相应时次得到的校准因子场。与降水过程Ⅰ中类似,两种方法在相同时次的校准因子取值比较接近,变分校准因子场比克里金校准因子场具有更多的空间变化。同一方法在不同时次得到的校准因子的取值存在较大差异。
|
图 9 2016年6月12日00:06—09:30(a, c)克里金校准法以及(b, d)变分校准法在(a, b)第12时次(01:12)和(c, d)第80时次(08:00)得到的校准因子分布 Fig. 9 Distributions of (a, c) the Kriging calibration factors, (b, d) the variational calibration factors at (a, b) the 12th time point (01:12 BT) and (c, d) the 80th time point (08:00 BT) during 00:06-09:30 BT 12 June 2016 |
(2) 雨强校准结果
使用四种方法计算得到的校准因子,对雷达得到的降水雨强分布进行校准,并与雨量计的实测雨强进行比较,结果如图 10所示。其中,图 10a,10b分别为平均校准和卡尔曼滤波校准方法在雨量计1和雨量计5位置处的校准结果,图 10c,10d分别为克里金校准和变分校准方法在雨量计1和雨量计5位置处的校准结果。可见,不同于降水过程Ⅰ,此过程中雷达使用常用降水估计关系反演的雨强存在明显的高估现象,经四种方法校准后,高估现象均得到有效抑制,校准后的雷达雨强更加接近雨量计实测雨强。克里金校准法与变分校准法的校准结果差异不大。研究中也发现,四种方法在离链路较远的雨量计(如雨量计7、8)位置处也有一定的校准效果,但总体上校准效果不如离链路较近的位置处,特别是在降水时空变化较大时。
图 11为本次降水过程中全部8个雨量计位置处的雨量计实测雨强和雷达反演雨强的散点图。由图 11a可见,与雨量计实测值相比,雷达使用常用降水估计关系[式(3)]反演的雨强存在较大误差,存在明显的高估降水问题。经四种方法校准后,高估问题有所改善。从误差统计数值上看,雷达反演雨强的误差统计值(MAE、ME和RMSE)均比校准前明显降低,平均校准、克里金校准、变分校准的效果优于卡尔曼滤波校准方法。
3.3 两次降水过程综合分析计算了四种方法在两次降水过程(共145个时次)中全部8个雨量计位置处误差统计值,综合分析各种校准方法的效果。为更清晰地分析校准效果,以雷达常用关系反演降水的误差为基准,计算了各校准方法对每种统计误差的优化率(表 2)。例如,若校准前雷达反演雨强的ME为1.2403 mm·h-1,平均校准后为0.4934 mm·h-1,则对ME的优化率为:(1.2403-0.4934)/1.2403×100%=60.22%。
|
|
表 2 四种方法的误差统计 Table 2 Statistics of the errors of the four methods |
可见,四种校准方法均不同程度地降低了各统计误差,说明校准有效。各种方法对ME的改善程度最好,其次是RMSE,最后是MAE(表中加粗数字为对某种统计误差的最高优化率)。具体而言,对统计误差MAE的优化率较高的是克里金校准法(44.57%)、变分校准法(44.56%)和平均校准法(44.37%),对ME的优化率最高的是克里金校准法(75.26%),对RMSE的优化率较高的是变分校准法(52.71%)和克里金校准法(52.26%)。
4 结论本文研究了基于微波链路的天气雷达降水场校准方法,并利用实际业务设备,在两次具有不同特征的实际降水过程中开展了降水校准实验。结论如下:
(1) 通过平均校准法、卡尔曼滤波校准法、克里金校准法和变分校准法,利用2条微波链路,对2500 km2区域的两次降水过程的雷达降水场进行校准,均取得了较好的校准效果,改善了降水过程Ⅰ对流性强降水的低估问题和过程Ⅱ对流性弱降水的高估问题。即使是相对简单的平均校准法,也起到了一定的效果。与校准前相比,校准后的雷达降水场与雨量计实测雨强的一致性得到提升,统计误差得到明显改善,对ME、RMSE和MAE的优化率分别达到75.26%、52.71%和44.57%。
(2) 总体上,克里金校准方法的效果相对较好,变分校准方法和平均校准方法的效果优于卡尔曼滤波校准方法。对统计误差MAE和ME的改善效果最好的均为克里金校准法,对RMSE改善效果最好的是变分校准法。
(3) 平均校准法和卡尔曼滤波校准法得到的校准因子仅随时间变化,不随空间位置变化,而克里金校准法和变分校准法得到的是校准因子场,随时间和空间不同而变化。
由于无线微波链路布设广泛,使用微波链路校准天气雷达降水场不需要额外的投入与建设,使得这种方法具有较为广阔的研究和应用前景,对进一步提升区域降水监测能力具有重要意义。
冯婉悦, 施丽娟, 王智敏, 等, 2021. 雨滴谱仪资料在"温比亚"台风降水估测中的应用探究[J]. 气象, 47(4): 389-397. Feng W Y, Shi L J, Wang Z M, et al, 2021. Application of raindrop disdrometer data in rainfall estimation of Typhoon Rumbia[J]. Meteor Mon, 47(4): 389-397 (in Chinese).
|
傅德胜, 戴铁丕, 1991. 平均订正因子法校准天气雷达测定区域降水量的试验[J]. 气象科学, 11(3): 292-300. Fu D S, Dai T P, 1991. The test of calibrating the weather radar measured precipitation by mean emendation factor method[J]. Sci Meteor Sin, 11(3): 292-300 (in Chinese).
|
高太长, 宋堃, 刘西川, 等, 2015. 基于微波链路的路径雨强反演方法及实验研究[J]. 物理学报, 64(17): 174301. Gao T C, Song K, Liu X C, et al, 2015. Research on the method and experiment of path rainfall intensity inversion using a microwave link[J]. Acta Phys Sin, 64(17): 174301 (in Chinese). DOI:10.7498/aps.64.174301
|
官莉, 王振会, 裴晓芳, 2004. 雷达估测降水集成方法及其效果比较[J]. 气象科学, 24(1): 104-111. Guan L, Wang Z H, Pei X F, 2004. The consensus methods and effects of estimating rainfall using radar[J]. Sci Meteor Sin, 24(1): 104-111 (in Chinese). DOI:10.3969/j.issn.1009-0827.2004.01.013
|
李建通, 张培昌, 1996. 最优插值法用于天气雷达测定区域降水量[J]. 台湾海峡, 15(3): 255-259. Li J T, Zhang P C, 1996. Optimum interpolation method used for measuring regional precipition with weather radar[J]. J Oceanogr Taiwan Strait, 15(3): 255-259 (in Chinese).
|
沙修竹, 丁建芳, 程博, 2019. 地面激光雨滴谱仪反演降水参量的特性探究[J]. 气象, 45(11): 1569-1578. Sha X Z, Ding J F, Cheng B, 2019. Characteristics of precipitation parameters reflected by ground laser raindrop disdrometer[J]. Meteor Mon, 45(11): 1569-1578 (in Chinese). DOI:10.7519/j.issn.1000-0526.2019.11.007
|
宋堃, 高太长, 刘西川, 等, 2015. 基于支持向量机的微波链路雨强反演方法[J]. 物理学报, 64(24): 235-242. Song K, Gao T C, Liu X C, et al, 2015. Method and experiment of rainfall intensity inversion using a microwave link based on support vector machine[J]. Acta Phys Sin, 64(24): 235-242 (in Chinese).
|
咸明皓, 刘西川, 印敏, 等, 2020. 基于星地链路的垂直降雨场反演方法[J]. 物理学报, 69(2): 024301. Xian M H, Liu X C, Yin M, et al, 2020. Inversion of vertical rainfall field based on earth-space links[J]. Acta Phys Sin, 69(2): 024301 (in Chinese).
|
张培昌, 戴铁丕, 伍志芳, 等, 1992. 用变分方法校准数字化天气雷达测定区域降水量基本原理和精度[J]. 大气科学, 16(2): 248-256. Zhang P C, Dai T P, Wu Z F, et al, 1992. Principle and accuracy of adjusting the area precipitation from digital weather radar through variational method[J]. Sci Atmos Sin, 16(2): 248-256 (in Chinese). DOI:10.3878/j.issn.1006-9895.1992.02.13
|
张培昌, 杜秉玉, 戴铁丕, 2001. 雷达气象学[M]. 北京: 气象出版社: 193-196. Zhang P C, Du B Y, Dai T P, 2001. Radar Meteorology[M].
Beijing: Meteorological Press: 193-196 (in Chinese).
|
张鹏, 刘西川, 周则明, 等, 2021. 基于实测雨滴谱数据的微波链路和天气雷达降水估计关系研究[J]. 气象, 47(7): 843-853. Zhang P, Liu X C, Zhou Z M, et al, 2021. Research on precipitation estimators of microwave link and weather radar based on raindrop size distribution data[J]. Meteor Mon, 47(7): 843-853 (in Chinese).
|
赵坤, 葛文忠, 刘国庆, 等, 2005. 在雷达测雨和洪水预报中自适应卡尔曼滤波法的应用[J]. 高原气象, 24(6): 956-965. Zhao K, Ge W Z, Liu G Q, et al, 2005. Application of self-adaptive Kalman filter method to radar rainfall estimation and flood forecasting[J]. Plateau Meteor, 24(6): 956-965 (in Chinese). DOI:10.3321/j.issn:1000-0534.2005.06.016
|
Chumchean S, Seed A, Sharma A, 2006. Correcting of real-time radar rainfall bias using a kalman filtering approach[J]. J Hydrol, 317(1/2): 123-137.
|
Collier C G, 1986. Accuracy of rainfall estimates by radar, part Ⅰ: calibration by telemetering raingauges[J]. J Hydrol, 83(3/4): 207-223.
|
Cummings R J, Upton G J G, Holt A R, et al, 2009. Using microwave links to adjust the radar rainfall field[J]. Adv Water Resour, 32(7): 1003-1010.
|
Goudenhoofdt E, Delobbe L, 2009. Evaluation of radar-gauge merging methods for quantitative precipitation estimates[J]. Hydrol Earth Syst Sci, 13(2): 195-203.
|
Graf M, Chwala C, Polz J, et al, 2020. Rainfall estimation from a German-wide commercial microwave link network: optimized processing and validation for one year of data[J]. Hydrol Earth Syst Sci, 24(6): 2931-2950.
|
Harrison D L, Driscoll S J, Kitchen M, 2000. Improving precipitation estimates from weather radar using quality control and correction techniques[J]. J Meteorol Appl, 7(2): 135-144.
|
Jameson A R, 1991. A comparison of microwave techniques for measuring rainfall[J]. J Appl Meteor, 30(1): 32-54.
|
Kim M S, Kwon B H, 2020. Attenuation correction of X-band radar reflectivity using adjacent multiple microwave links[J]. Remote Sens, 12(13): 2133.
|
Krajewski W F, 1987. Cokriging radar-rainfall and rain gauge data[J]. J Geophys Res Atmos, 92(D8): 9571-9580.
|
Krajewski W F, Smith J A, 2002. Radar hydrology: rainfall estimation[J]. Adv Water Resour, 25(8): 1387-1394.
|
Mercier F, Barthès L, Mallet C, 2015. Estimation of finescale rainfall fields using broadcast TV satellite links and a 4DVAR assimilation method[J]. J Atmos Oceanic Technol, 32(10): 1709-1728.
|
Messer H, Zinevich A, Alpert P, 2006. Environmental monitoring by wireless communication networks[J]. Science, 312(5774): 713.
|
Minda H, Nakamura K, 2005. High temporal resolution path-average rain gauge with 50 GHz band microwave[J]. J Atmos Ocean Technol, 22(2): 165-179.
|
Overeem A, Leijnse H, Uijlenhoet R, 2015. Retrieval algorithm for rainfall mapping from microwave links in a cellular communication network[J]. Atmos Meas Tech Discuss, 8(8): 8191-8230.
|
Pudashine J, Guyot A, Petitjean F, et al, 2020. Deep learning for an improved prediction of rainfall retrievals from commercial microwave links[J]. Water Resour Res, 56(7).
|
Seo D J, 1998. Real-time estimation of rainfall fields using radar rainfall and rain gage data[J]. J Hydrol, 208(1/2): 37-52.
|
Sieck L C, Burges S J, Steiner M, 2007. Challenges in obtaining reliable measurements of point rainfall[J]. Water Res Res, 43(1): 35-42.
|
Zhang P, Liu X C, Li Z M, et al, 2017. Attenuation correction of weather radar reflectivity with arbitrary oriented microwave link[J]. Adv Meteor, 2017: 6124149.
|
Zinevich A, Alpert P, Messer H, 2008. Estimation of rainfall fields using commercial microwave communication networks of variable density[J]. Adv Water Res, 31(11): 1470-1480.
|
 2023, Vol. 49
2023, Vol. 49