引言

风是对多行业生产安全有直接影响的基本气象要素，准确的近地层风速预报对企业提质增效保安全具有重要的作用。随着数值天气预报(numerical weather prediction, NWP)技术的快速发展，基于NWP的风速预报产品越来越多地应用于各行各业的生产决策、重大活动的气象保障中。在港口气象灾害风险评估方面，一些研究采用模式风场预报产品作为驱动，模拟了风暴潮及其增水过程的水位变化，并基于此开展了灾害性天气下港口的气象灾害风险评估(曹越男等，2014；闫丽凤等，2008)。针对易受大风天气影响的重大室外赛事活动，国内外基于不同数值预报产品开展了较多的赛场风速预报及订正技术研究，致力于提高区域模式的风速预报，为重大赛事提供气象保障(王令等，2008；陈超君等，2012；Kiktev et al，2015；杨璐等，2022；邱贵强等，2023；刘郁钰等，2023)。

随着新能源行业的兴起，NWP在风能资源精细化评估和气候模拟中也开始发挥重要作用，国内外在该方向均有大量研究成果与工程实践。一些学者基于数值预报产品研究了我国近海风能资源高分辨率模拟方法，分析了近海风能资源分布状况，部分研究侧重于评估NWP产品在不同区域的风速预报能力，为区域风能模式预报的业务化应用奠定了基础(周荣卫等，2010；何晓凤等，2014；申华羽等，2020)；国外学者也利用NWP产品采用动力降尺度方法或着眼于提高某类天气事件的预报能力来评估局地风能资源(Gioli et al，2014；Storm et al，2009)；还有许多学者分别基于不同NWP产品开展了在各地风能预报中的实践工作(李艳等, 2009; Traiteur et al, 2012; Cheng and Steenburgh, 2015; 刘郁珏等, 2019; Liu et al, 2021)。

虽然现阶段不同的NWP风速产品广泛应用于各行各业并起到了一些效果，但是因NWP的初值准确性、物理过程参数化方案的近似性、求解过程的近似和截断处理、地形与实际情况的偏差等，均会导致近地层风速的预报结果存在较大偏差，为企业用户做决策带来较大的困扰。鉴于这种情况，多位学者开展了基于局地观测数据的预报风速订正技术研究，部分学者利用传统线性方法进行统计订正(常蕊等, 2013; 肖擎曜等，2017)，通过多种试验设计提高了局地风速的预报能力；也有部分学者通过对同一风电场运用多种方法做订正试验，研究传统线性方法和机器学习方法的表现差异(江滢等，2013；Bédard et al，2013)。此外，还有许多学者采用谐波分析、向量机方法、K近邻法、卡尔曼滤波、均生函数法、线性回归法、相似分析法等方法(戚双斌等, 2009; 程兴宏等, 2012; Lin et al, 2015; Zjavka, 2015; 丁煌等, 2013; 张铁军等, 2018; 王彬滨等，2016；王在文等, 2019; 杨程等, 2019)开展了风速预报订正方法研究与应用。这些工作显著减小了预报误差中的系统性偏差，对预报产品精度的提升起到了积极作用，但是对于降低强风时段的预报误差效果有限。

此外，不同的企业生产场景对风速有不同的阈值要求，比如风速超过10 m·s^-1时可能威胁海上施工的作业安全，风速超过25 m·s^-1时部分风力发电机组需要停机等。对特定企业而言，最关注的是影响其生产安全的风速区间内的风速预报能力，当预报风速值接近该阈值时，由于预报不确定性的存在，企业往往最难决策，因此对超过阈值的事件出现与否的预报准确性提出了很高的要求，而对其他风速段预报准确性的要求反而并不那么高。这种情况下，需要面向特定生产场景定义普适性的强风事件，并将这类事件从预报序列中剥离出来有针对性的进行订正，才能更好地将其应用于企业实际生产中。

本文首先基于海上风电安全施工对风速的具体要求，应用滑动平均函数，提出了一种影响海上施工安全的持续性强风事件识别方法，并在充分评估、分析风速预报产品强风预报能力的基础上，结合实况与预报数据，基于所提出的强风识别方法的关键参数，设计了三种预报识别方案，并评估比较了三种预报强风事件，随后基于决策树和一元线性回归方法，分别开展了针对上述强风事件的订正方法研究。

1 资料

本文观测数据源自江苏省南通市如东县近海某风电场激光雷达测风资料(以下简称如东站)，激光雷达安装于该风电场的海上升压站，其距离海平面35 m，选用激光雷达10 m高度层风速观测序列，故观测点距离平均海面的实际高度约为45 m。观测资料采集期为2018年1月1日至12月31日，为了与模式预报输出风速时间对应，提取了每个整点时刻的10 min平均风速观测数据，并对观测风速做极值质量控制、僵值质量控制和均一性检验等，最后根据检验结果剔除了异常值和缺测数据。

本文预报资料来自GDFS(Grid Data Forecast System)(陈笑等, 2018)。GDFS是基于多模式预报产品的集成预报系统(以下简称模式)，其空间分辨率为0.025°×0.025°，时间分辨率为1 h，预报时效为72 h，每天起报2次。该模式基于全国7万多个自动站实时观测资料和ECMWF、CMA-MESO、RMAPS_Wind等多个业务化数值预报系统的预报产品，通过动态误差权重法实现了集成预报。本文直接采用该模式每天08时起报的50 m高度层的前24 h预报风速数据开展研究。鉴于海上的下垫面较光滑，风速的空间变化在一定范围内较小，故未对格点数据做插值，而是直接选用距离观测地点最近的模式格点数据，并将观测资料与该格点的预报数据进行逐时匹配。

2 强风事件的定义与识别方法研究 2.1 强风事件的定义

根据海上施工作业经验，10 m·s^-1是影响施工安全的重要风速阈值，连续超过该阈值的强风过程会导致施工无法进行，因此认为连续几个小时平均风速超过10 m·s^-1即为一次海上安全施工高影响持续性强风事件，通过以下具体流程识别强风事件。

首先对风速序列做滑动窗口为5 h的滑动平均，公式如下：

$ \widehat{x}_i=\frac{\sum\limits_{j=-2}^2 x_{i+j}}{5} $

(1)

式中: $\widehat{x}_i$为经过滑动平均后i时刻的风速，i为时序，i=3, 4, …, n-2，n为样本数；x_i+j为i+j时刻的原始风速，j为时间增减量，j=-2, -1, 0, 1, 2。

对滑动平均后得到的新序列做判断，当风速超过给定风速阈值(针对本文研究的影响海上施工安全的持续性强风事件，观测强风事件阈值为10 m·s^-1)，定义为一个强风时次。当强风时次连续出现大于等于3 h，则记为一次强风事件。第一个强风时次为强风事件的开始时间，最后一个强风时次为结束时间。考虑到两次强风事件相距较近时，小风窗口太短无法完成施工，因此将后一次事件开始时间与前一次事件结束时间的差小于等于3 h的两次强风事件合并为一次强风事件。

2.2 强风事件识别及特征分析

为开展本文研究工作，首先需在风速的观测和预报序列中识别出强风事件，再开展特征分析和后续订正技术研究。

首先严格根据上文定义，从观测数据中进行海上观测强风事件识别，结果显示2018年该海上风电场区域共出现观测强风事件71次，总时长为1374 h，事件平均时长约为19.35 h。

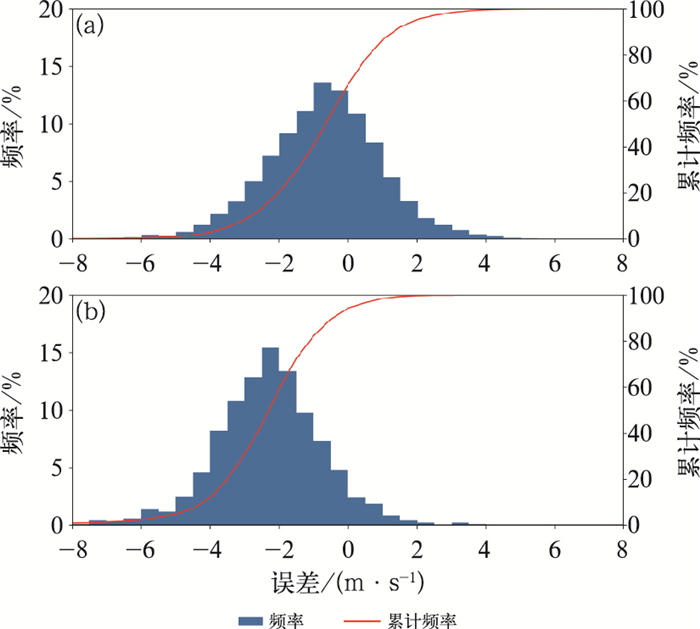
从预报风速序列中识别强风事件时，首先需要了解模式预报风速的基本情况。统计结果显示, 如东站2018年风速观测均值为7.01 m·s^-1，预报均值为6.29 m·s^-1，预报比观测系统性偏小0.72 m·s^-1，预报与观测的相关性较高，相关系数达到0.86，表明预报能较好地反映出实际风速的波动转折。从逐时预报误差的频率和累计频率统计(图 1a)可以看出，如东站预报偏小的频率明显大于预报偏大的频率，预报偏小占67.4%，频率峰值对应的误差范围为偏小0.5~1 m·s^-1，偏小2 m·s^-1以上达20.6%。针对本文研究侧重的强风段，筛选出观测风速大于等于10 m·s^-1的相对强风时次，提取出对应时次的预报，可计算得到强风段误差分布情况(图 1b)，强风段预报偏小频率达94.1%，频率峰值对应的误差范围偏小2~2.5 m·s^-1，且偏小2 m·s^-1以上的达到58.9%，即强风时段预报偏小的情况更为明显。

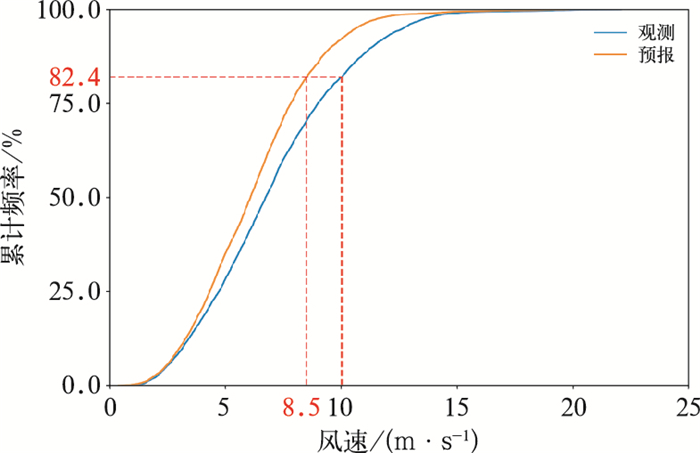
基于模式预报风速总体偏小且强风时段显著偏小的特征，对预报风速序列进行强风事件识别时，开展了三种敏感性识别方案的对比，以得到与实况强风事件匹配度更高的预报强风事件，这对于后续开展订正非常重要。模式阈值方案(以下简称模式法)：基于上文定义的强风事件阈值(10 m·s^-1)和式(1)对预报风速序列进行直接识别，将该方案识别结果称为模式强风事件；消偏阈值方案(以下简称消偏法)：将模式预报的原始风速进行系统性偏差简单订正，即对逐时预报均加上预报与观测的误差均值(0.72 m·s^-1)后，再采用10 m·s^-1阈值和式(1)做强风事件识别，将该方案识别结果称为消偏强风事件；等分位阈值方案(以下简称等分位法)：考虑到观测和预报的强风时段在各自的整个时段内占比是近似的，首先对观测的滑动平均序列由小到大排序，计算出观测阈值10 m·s^-1处的累计频率值(82.4%)，再提取模式预报风速的滑动平均序列由小到大排列后累计频率82.4%处对应风速值(8.5 m·s^-1)，将该值作为预报强风事件阈值(如图 2所示)，再结合式(1)进行强风事件识别，将该方案识别结果称为等分位强风事件。

强风事件评估方法：对持续时间不超过20 h的观测强风事件，其时间范围内任意时刻识别到预报强风事件，则记为一次命中，否则记为一次漏报；若该次观测强风事件持续时间超过20 h，则要求二者的交集时长大于等于5 h才记为一次命中，否则记为一次漏报。将与观测强风事件无交集的预报强风事件记为一次空报。事件命中率定义为命中次数除以观测强风事件总数，以百分率表示。各方案预报与观测事件逐时匹配时长：即预报与观测同为大风事件的时刻累计值。其匹配时长命中率定义为匹配时长除以总的观测大风事件时长(1374 h)。

基于观测强风事件和三种识别方案得到的预报强风事件开展了效果评估，由表 1可见：模式法与观测强风事件的匹配较差，命中事件仅为28次，命中率为39.4%，漏报较多；消偏法将命中率提高到了54.9%；等分位法明显更优，命中事件为54次，相比模式法增加命中26次，命中率提高到76.1%。但是随着命中率的提高，消偏法和等分位法的空报也略有增加：模式法空报为1次，消偏法和等分位法空报分别增加到了8次和9次。从事件总时长来看，模式法、消偏法和等分位法的总时长分别为692、1039和1401 h，与1年内的观测强风事件总时长相比分别表现为偏少682 h、偏少335 h和偏多27 h，等分位法识别的强风事件总时长明显更接近观测。

此外，对各方案预报与观测事件逐时匹配时长对比得出：模式法为625 h，消偏法为911 h，等分位法为1203 h，匹配时长命中率分别为45.5%、66.3%、87.6%，即对观测事件漏报的时长分别为749、463和171 h。而各方案空报事件的时长：模式法为14 h，消偏法为47 h，等分位法为87 h。可见消偏法和等分位法识别的强风事件虽然相比模式法增加了约2 d的空报，但是匹配时长分别增加了约12 d和24 d。

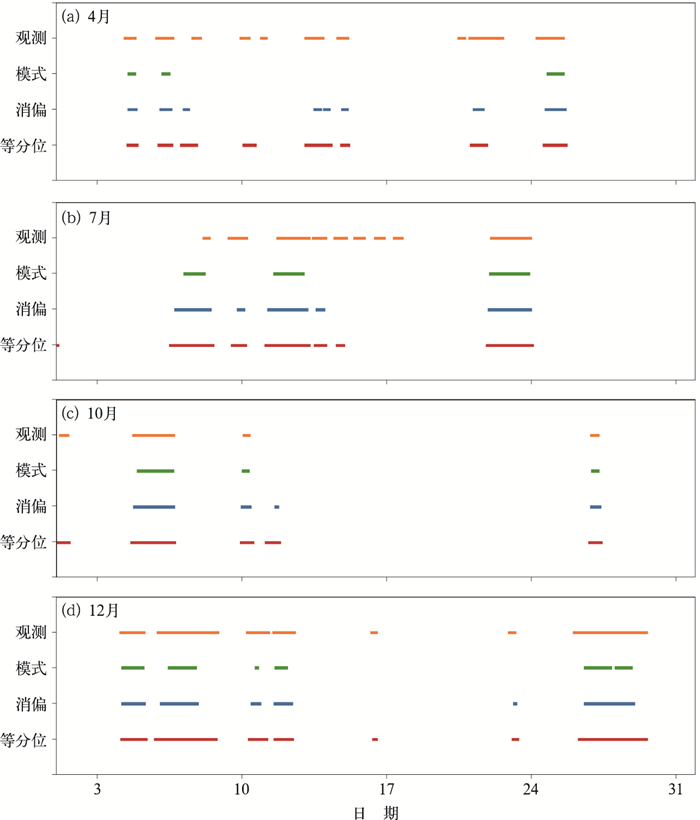
针对各月的强风事件，分析后发现各方案空报和漏报情况在同季节的各月间近似，因此从四个季节中分别选取了季节内观测强风事件最多的月份构成了典型月份(分别为4、7、10、12月)做进一步分析。图 3给出了四个典型月份中，观测强风事件及三种方案得到的预报强风事件的各月分布情况。由图 3可见，虽然消偏法和等分位法识别的预报强风事件会增加少量空报，但是二者能明显减少模式漏报；模式法识别的强风事件时长相对于同期观测普遍偏短，采用消偏法和等分位法识别的预报强风事件时长会更接近观测；消偏法容易漏报影响时间较短的强风事件，而采用等分位法能有效提高这类影响时间较短的强风事件的命中率；并且对比预报和观测的各次事件的起止时间，等分位法基本可以覆盖到各次强风事件的全程。因此等分位法识别的预报强风事件起止时间可为海上施工作业灾害预警的发布和解除提供有效参考。

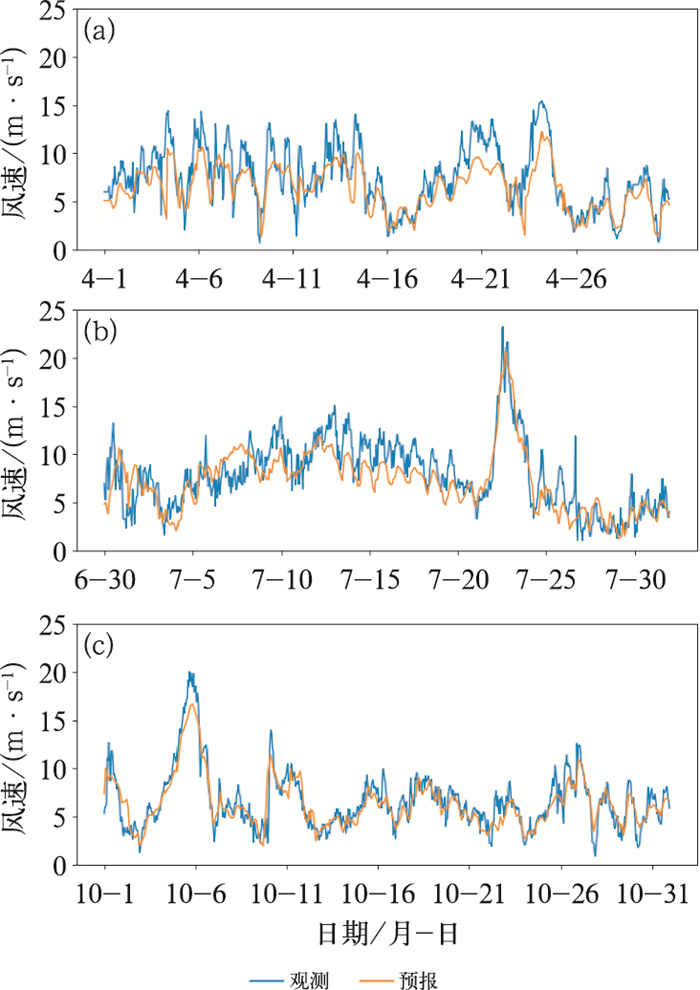
在四个典型月份中7月和10月存在空报事件。图 4b给出了6月30日00时至7月31日23时观测和预报时序，可看到7月1日的空报，是因为6月30日至7月1日模式预报的大风段滞后于观测大风，观测大风段结束于6月30日14时，而预报风速14时才开始高于8 m·s^-1，在采用消偏法和等分位法后，等分位法的预报大风事件开始于12时，命中了观测大风事件的后半段，而消偏法的预报大风事件开始于16时，没有命中大风事件；但是因为预报风速滞后的原因，等分位法预报大风事件的结束时间为7月1日01时，导致了1日的短暂空报。7日的空报则是该段预报与观测反向，表现为预报风速在波峰而观测相对在波谷，预报的相对大风时段提前了一些，导致了预报风速的整体偏大。其中7日的观测平均风速为7.19 m·s^-1，而预报平均为10.23 m·s^-1，预报偏高了3.04 m·s^-1，这导致三个方法均出现了不同时间长度的空报。对10月的观测和预报时序图分析(图 4c)，11日的预报风速非常接近观测风速，预报和观测风速平均分别为8.30 m·s^-1和8.37 m·s^-1，预报风速略偏小，消偏法加上误差均值后风速增加，从而出现了短暂空报，而等分位法因为降低了阈值出现了相对较长的空报。上述两种空报的成因共性不强，且两类空报事件在整个资料时间段内相对较少，因此难以直接通过总结模式风速预报的特征来消除空报。在实际业务运用时，针对此类大风事件，可能需要考虑当前天气型的影响，做人工修正。

消偏法和等分位法预报的强风事件虽能有效增加命中，减少漏报，但是由于模式原始风速预报的固有问题，仍然存在一些强风事件无法被预报出来(如图 3b，7月15—17日的观测强风事件)，且存在一些预报强风事件相对观测强风事件时长偏短的现象(如图 3a，4月20—23日的观测强风事件)。分析对应月份的时序图(图 4a，4b)，可看到上述提到漏报时段的风速预报波动与观测相似，但是峰值风速预报明显偏小，其中4月20日、21日的单日均值分别偏小2.6 m·s^-1和2.9 m·s^-1，7月15日、16日、17日的单日均值分别偏小2.11、2.6和2.12 m·s^-1，这种显著偏小导致了预报事件的时长偏短或漏报的情况。

3 强风事件强度订正方法研究

基于三种预报强风事件识别方案研究的结果分析，运用等分位法识别到的强风事件从开始时间、结束时间、持续时长、命中率、时长匹配等各方面都最接近观测强风事件，其起止时间可为海上施工作业灾害预警的发布和解除提供有效参考。因此，下文基于等分位法识别的预报强风事件开展预报强风事件的强度订正方法研究。

首先根据等分位强风事件的时间段提取观测及模式预报风速数据，并按照事件发生的先后顺序依次重构成新的观测强风序列和预报强风序列(以下简称为强风序列集)。考虑到平均风速是一个连续性的变量，某时刻的风速与其之前和之后时刻的风速均有密切关联，对强风序列集采用如下方法重构样本集：

对强风序列集内某时刻i的观测风速y_i，找到对应时刻前后6 h内(i-6, i-5, …, i, i+1, …, i+6)共13个预报风速构成预报因子集x_i^(k)，其中i=1, 2, …, n为时序(n也为样本总数)；k=1, 2, …, 13为因子序号，k=1时，对应i-6时刻的预报风速，k=13时，对应i+6时刻的预报风速，以此类推。将上述变量合并即可构建出样本集D={(x₁^(k), y₁), (x₂^(k), y₂), …, (x_i^(k), y_i), …, (x_n^(k), y_n)}，其中x_i^(k)=(x_i⁽¹⁾, x_i⁽²⁾, …, x_i⁽¹³⁾)。随后选取样本集前80%时序的数据作为训练样本，剩下的20%时序数据作为独立检验样本，再分别采用了一元线性回归和决策树两种订正方法基于训练样本段构建了订正模型，并用独立检验样本段的数据进行订正和检验。

3.1 一元线性回归

一元线性回归是通过寻找自变量与因变量的最小离差平方和来得到数据最优函数解的方法(黄嘉佑, 2000)。在本研究中，将因变量设置为观测风速y_i，通过对前述样本集x_i^(k)与y_i计算线性相关后，选择相关性最高的x_i⁽⁸⁾(其相关系数为0.72)做为自变量，假定二者存在下述的一元线性统计关系式[式(2)，其为回归理想模型]，利用样本集中的数据对该关系式进行估计，得到的估计方程即为一元线性回归方程[式(3)]。

$ y_i=\beta_0+\beta_1 x_i^{(8)}+e_i $

(2)

$ \widehat{y}_i=b_0+b_1 x_i{ }^{(8)} $

(3)

式中: y_i为i时刻的观测风速，i=1, 2, …, n，n为建模时段样本数，β₀为回归常数，β₁为因子系数，x_i⁽⁸⁾为预报因子，e_i为相互独立的随机变量。$\hat{y}_i$为i时刻的订正风速，b₀和b₁分别为β₀和β₁的估计。

式(3)需要满足使得全部的观测风速与订正风速的离差平方和(Q)达到最小，即：

$ Q=\sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2 $

(4)

将式(3)代入式(4)并展开，根据最小二乘法即可解出方程组的系数。本研究中解出来的一元线性方程如下：

$ \widehat{y}_i=1.119+0.98 x_i{ }^{(8)} $

(5)

3.2 决策树

决策树是一种树结构，是近年来机器学习方法中基本的分类与回归方法。回归决策树主要指CART(classification and regression tree)算法，其由Breiman et al(1984)提出。针对连续值，其是通过误差平方和来度量和划分叶节点的一种算法。算法本质是将样本时段的特征空间根据当前误差平方和最小的条件来划分成左右两个结点，两个结点分别以同一个特征变量的值作条件划分，依次对划分出的每个结点的结果接着进行划分，即得到若干个单元，每一个划分单元有一个特定的输出。在检验时段的数据应用中，只要按照特征将其归到某个单元，便能得到对应的订正输出值。

本研究针对上文中定义的训练数据集D={(x₁^(k), y₁), (x₂^(k), y₂), …，(x_i^(k), y_i), …, (x_n^(k), y_n)}，其中x_i^(k)为不同的特征变量，k的取值为1, 2, 3，…，13，分别表示对应观测时刻往前6 h至往后6 h的预报风速。在决策树CART算法中对上述由所有特征变量组成的特征空间采用遍历当前集合中所有特征变量的所有取值的方法进行划分，根据误差平方和最小化原则选择其中最优的一个作为切分点。如第一轮划分，对训练集中的某一个特征变量x_i^(k)给出一个s值，将x_i^(k)作为切分变量，s作为切分点，即可将D根据s划分为两个区域R₁(k, s)和R₂(k, s)，即R₁(k, s)={(x_i^(k), y_i)|x_i^(k)≤s}, R₂(k, s)={(x_i^(k), y_i)|x_i^(k)>s}。该s的取值要使得当前两个区域的误差平方和最小，即满足式(6)：

$ \mathrm{SE}_k=\min\limits_{k, s}\left[\sum\limits_{R_1(k, s)}\left(y_i-\overline{c_1}\right)^2+\sum\limits_{R_2(k, s)}\left(y_i-\overline{c_2}\right)^2\right] $

(6)

式中: $\overline{c_1} \text {和} \overline{c_2}$分别为R₁(k, s)和R₂(k, s)内y_i的均值，SE_k为以特征变量x_i^(k)为分区时得到的最小误差平方和。对每个特征变量计算SE_k，并记录下对应的切分点s的值，再从所有的SE_k中找出最小的值，即能求得本次划分过程中使式(6)结果最小时的s值和对应的特征变量x_i^(k)，做为当前的最优切分点s和最优切分变量x_i^(k)，同时能根据x_i^(k)和s的取值计算得到确定的$\overline{c_1} \text {和} \overline{c_2}$。此时可将训练集D看作父节点，而R₁(k, s)和R₂(k, s)为其叶子节点，树的深度为一层。随后以R₁(k, s)和R₂(k, s)作为新的训练集分别继续采用上式进行遍历划分求解，不断生成新的叶子节点，直到所有样本切割完或达到给定的树的最大深度。其中，样本切割完的定义为当前叶子节点训练集内的样本个数小于等于给定的最小样本个数，或当前叶子节点的最小误差平方和与进行划分后的最小误差平方和相差不大。这样就生成了一颗回归树，其属于不同特征变量区间范围内(即最后一层叶子节点的样本集内)所对应的均值C，即为决策树模型的订正结果。

在本研究中，最终生成的决策树模型深度为8，最小叶子节点样本个数为1个，第一个根节点以特征变量x_i⁽⁸⁾(订正时刻往后1 h的预报风速)为切分变量，切分点s为13.9 m·s^-1，当x_i⁽⁸⁾>s时，就进入右节点，接着以x_i⁽¹¹⁾ (即订正时刻往后4 h的预报风速)做切分变量，即以切分点s为15.1 m· s^-1做新一轮判断；若x_i⁽⁸⁾≤S，进入左节点，以x_i⁽⁷⁾(即订正时刻的预报风速)为切分变量，即以切分点s为10.4 m·s^-1做新一轮判断。每次判断比较会得到左右两个分支节点，根据当前的判断结果选择对应分支的叶子节点，再根据叶子节点上新的切分变量和切分点继续判断，一直走到底层叶子节点，即可得到该节点样本均值C作为其订正结果。

本文的决策树回归模型其本质可看作是模型根据输入预报的多特征变量的风速与对应的观测风速，总结每一次输入的13个风速预报点的变化曲线与对应观测的特征，通过对各个特征变量的阈值划分将预报风速划分为不同的天气型，并给出了判断不同天气型的逐级关键切分变量和切分点，因此在读入新的预报风速序列时，可根据预报风速值确定对应天气型，最终得到该类天气型下的订正结果。

3.3 两种订正方法性能评估与分析 3.3.1 评估指标

针对两种订正方法在强风事件中订正性能的评估，整体定量评估方面采用平均绝对误差(MAE)、相对误差(RE)、均方根误差(RMSE)三个方法定义检验指标，如式(7)~式(9)：

$ \mathrm{MAE}=\frac{\sum\limits_{i=1}^n\left|\hat{y}_i-y_i\right|}{n} $

(7)

$ \mathrm{RE}=\frac{\sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)}{\sum\limits_{i=1}^n y_i} \times 100 \% $

(8)

$ \text { RMSE }=\sqrt{\frac{\sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2}{n}} $

(9)

式中: y_i和$\widehat{y}_i$分别为观测风速、模式预报(或订正)风速，i为序号，n为样本总数。

3.3.2 综合评价

上述独立检验样本时段包含300个样本，其中观测风速均值为11.91 m·s^-1，模式预报风速均值为10.15 m·s^-1。经过一元线性回归和决策树订正后的风速均值分别为10.98 m·s^-1和11.23 m·s^-1。可见两种订正方法均能有效减少均值误差，使得订正风速均值更接近观测均值。由表 2的模式预报及两种订正方法的风速检验结果可见，MAE从模式预报的1.97 m·s^-1变为1.43 m·s^-1(一元线性回归)和1.31 m·s^-1(决策树)，分别减小了0.54 m·s^-1和0.66 m·s^-1；订正后RE虽然仍然偏小，但是偏小程度明显降低，从模式预报的-14.7% 变为-7.81%(一元线性回归)和-5.71%(决策树); 此外，RMSE也明显减小。无论是从MAE、RE或RMSE来看，经过两种订正方法订正后的风速预报效果相对于模式风速预报效果都有一定提升与改进，其中决策树模型比一元线性回归模型更优。

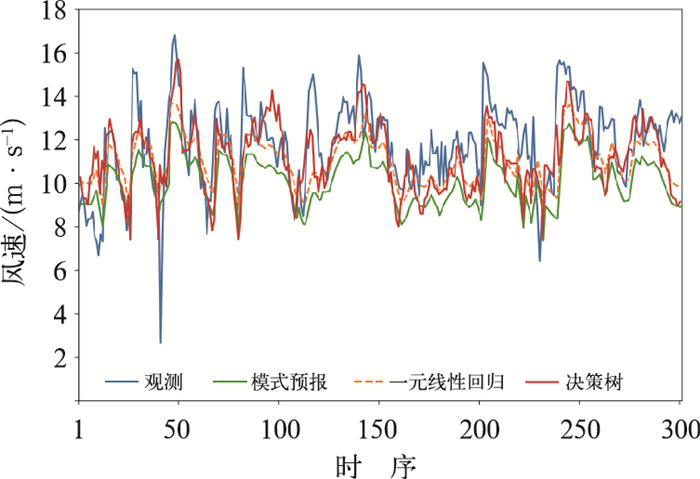
从整个检验样本时段的时序图来看(图 5)，在每个强风事件的波峰处，模式预报的风速均是明显偏小于观测的，经过两种方法订正后，风速均有一定增加，且基本在每个强风事件的波峰处一元线性回归法订正风速的误差均高于决策树订正风速的误差，比观测风速偏小相对较多。

部分波峰处(如序号1~15和94~100)决策树订正后风速偏大于观测，是因为建模样本相对较少，供模型学习分类的历史事件不足，导致一些天气型未学习到，将输入的新时序作为类似于7月12—14日观测出现较长的强风事件中，对预报风速明显偏小的天气型进行订正，导致订正相对实况偏大。

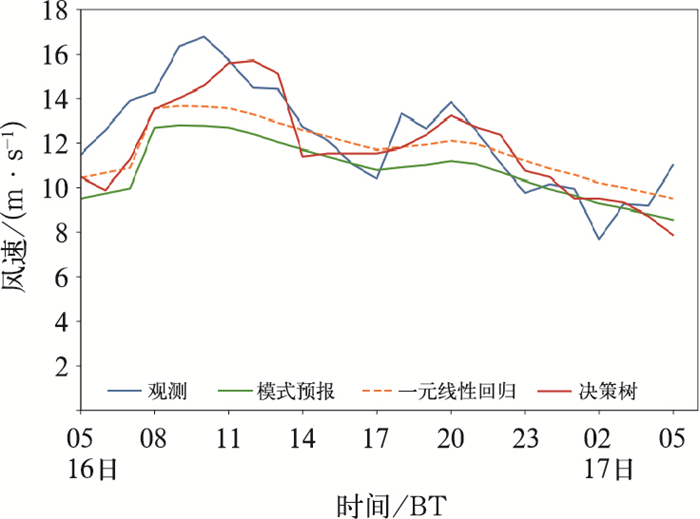
3.3.3 最强强风事件评价

从检验时段中，以观测风速的最大值为条件筛选出了最强强风事件(2018年11月16日05时至17日05时的强风事件)。图 6给出了这次强风事件的时序图，该次强风事件因为东亚大槽东移，地面冷锋南压，带来一股股强冷空气形成大风降温事件。可以看到16日05—10时风速较大，为12~18 m·s^-1，此为该次事件的第一个波峰，随后风速逐渐回落到10 m·s^-1左右再次增大，18—22时为第二个波峰，风速约为12~14 m·s^-1，此后回落到最低7 m·s^-1左右。模式预报出了第一个波峰，但是模式预报的波峰风速明显小于实况，可能是因为该观测站位于近海，从陆地到海洋的下垫面变化使得风力增强，而模式对地形变化的刻画能力不足导致了误差，且模式对第二个波峰几乎没有体现，一元线性回归订正后也仅仅是增加了风速值，整体形态和模式预报一致，没有预报出第二个波峰，而决策树订正后的风速序列能明显看出两个波峰，如上文所述，决策树可看作是通过建模时段输入的预报风速序列学习划分不同天气型，从而根据新的预报风速序列判断对应天气型的过程，此处决策树模型学习到了出现双波峰的天气型，因此增大了第二个波峰处的订正风速，从而订正出第二个波峰。

此外，从这次事件的风速最大值来看：观测风速最大值为16.81 m·s^-1(7级)，模式预报风速为12.82 m·s^-1(6级)，一元线性回归订正风速为13.68 m·s^-1(6级)，决策树订正风速为15.62 m· s^-1(7级)，模式预报和一元线性回归订正的风速均明显低于观测风速，误差分别为3.99 m·s^-1和3.13 m·s^-1，而决策树订正的风速将误差缩小到1.19 m·s^-1。从最大强度和序列形态上看，决策树订正后的风速都更接近观测，适合用作海上施工作业中的强风预警。

在业务化应用时，可以首先对预报风速采用等分位法识别强风事件，若识别到强风事件，则对强风事件对应时间段的预报风速采用上述决策树模型做订正，并替换模式预报的该时间段风速，其余非强风事件时段的预报风速则采用原始模式预报风速。

4 结论与讨论

针对海上施工作业对气象条件的要求，本文定义了一种持续性强风事件识别方法。利用GDFS模式资料，采用实况与预报相结合的方法，设计并比较了三种预报强风识别方案，根据评估结果选出了最优识别方案。在其基础上，采用一元线性回归和决策树方法对预报强风事件的风速序列进行订正，并开展了整体订正效果评估和典型过程订正效果分析，得到了以下结论：

(1) 与原始模式预报相比，消偏法和等分位法均能够有效提高预报强风事件的识别命中率，而等分位阈值方案更优，其识别命中率达到76.1%，匹配时长命中率达87.6%。

(2) 采用消偏法和等分位法均能增加识别强风事件的时长、减少漏报，其中等分位法识别的预报强风时长与观测非常接近，且能明显增加对影响时间较短的观测强风事件的命中率。

(3) 采用等分位法识别的强风事件基本可以覆盖到各次观测强风事件的全程，有利于精准给出强风预警的开始和结束时间。

(4) 一元线性回归和决策树模型都能一定程度上减少强风事件中风速预报的误差，其中决策树相比一元线性回归模型更优。

(5) 从最大强度和序列形态上看，由决策树订正后的风速比一元线性回归订正后的风速更接近实况。

本文研究了海上观测的持续性强风事件特征并分析了模式的预报表现，给出了影响海上施工安全的持续性强风事件的识别方法及基于敏感性参数的预报强风识别方案和预报序列强度的订正方法，有效改进了强风事件预报能力，但仍然存在一些强风事件漏报或预报事件相对观测事件的时长偏短的现象。此外，因为资料时长较短，做决策树订正建模时，数据相对较少且部分天气型未学习到，会导致部分订正偏大，未来可考虑引入风向因子并增加资料时长，根据观测强风事件进行分类，从而归纳不同风向的强风事件，再构建订正模型，尝试进一步降低漏报和减少空报。另外，本文只采用了一个模式对一个海上观测点的数据做研究，得到的预报强风事件识别方案仍有一些局限性。对于其他模式预报，若预报本身与观测风速的相关性太差，可能难以通过上述方法来提高预报强风事件的预报能力。此外，在中国各海域的强风特征也不尽相同，所以识别方法和订正方法有待进一步研究。