2. 武汉中心气象台, 武汉 430074;
3. 湖北省气象信息与技术保障中心, 武汉 43007;
4. 三峡水利枢纽梯级调度通信中心, 湖北 宜昌 443000
2. Wuhan Central Meteorological Observatory, Wuhan 430074;
3. Hubei Meteorological Information and Technology Support Centre, Wuhan 43007;
4. Three Gorges Cascade Dispatch and Communication Center of Hubei Province, Yichang 443000
长江流域水系众多,地形复杂。为满足长江防汛抗洪、水库调度和航运交通等需求,2018年长江流域气象中心从基于气象站点的传统降水预报转向5 km分辨率的精细化网格降水预报发展,预报员通过人机交互的定量降水预报业务平台,基于插值后的高分辨率数值模式降水预报产品进行交互订正。
然而定量降水预报由于影响其时间变化和空间分布的变量太多,被认为是数值模式预报最困难的挑战之一(Golding, 2000; Ebert et al, 2003),使得基于插值后的高分辨率数值模式降水预报产品订正效果充满不确定性。尽管近年来通过持续不断地提升模式空间分辨率、改进数据同化能力、完善数值计算方法和次网格物理过程的参数化方案,数值预报模式的降水预报能力不断上升(Forbes et al, 2015; Malardel et al, 2015),但也造成了模式降水预报的系统性误差不太稳定。各个模式在动力框架、分辨率、初始场、资料同化技术及物理参数化方案等方面存在差异,使得各模式在模拟能力上存在地理差异(智协飞等,2013;范宇恩等,2019), 也在不同降水强度预报上误差各异(陈博宇等,2015;张宏芳等,2014),当然对不同地区不同降水强度的预报性能差异更明显(辛辰和漆梁波,2018; 郝莹等,2019)。
为弥补模式预报缺陷,有必要对数值预报结果进行后处理和订正。Scheuerer and Hamill(2015)指出降水的不连续偏态分布特征和强降水样本的不足,导致降水的统计后处理相比于温度和风速等要素更加复杂。毕宝贵等(2016)指出在实际业务中,为了对海量预报数据中的有效信息进行提取和集成,通常采用定量降水订正与集成技术、概率预报处理技术和统计降尺度技术等方法进行降水预报后处理。由于模式降水预报与实况始终存在一定偏差(王雨和闫之辉,2006;周慧等,2010;熊秋芬,2011;任宏昌, 2017), 智协飞等(2016)、孙靖等(2015)针对不同量级降水进行相应的偏差订正。Ross and Krishnamurti(2005)、陈丽娟等(2005)、赵声蓉(2006)、Cartwright and Krishnamurti(2007)应用超级集合预报技术,对各天气预报中心的模式预报结果进行集成,发现多模式集成预报效果优于单个中心的预报,对平均海平面气压、地面气温等连续变量要素的改进效果较好,但对降水场的改进效果并不理想(智协飞等,2013)。究其原因,该方法过度拟合了某几个样本距平的极大值,使得各模式权重系数不能真实反映模式的预报能力。
综上所述,降水预报的订正需要考虑地理、强度、时效、模式误差等多种因素,所以本文拟对长江流域开展精细分区、分时效、降水量分级的多模式产品动态TS检验,在此基础上建立各分区最优预报方案,对每一个格点通过“邻域择优法”或“点对点择优法”赋值,从而将不同尺度模式的结果进行优势集成,获得0~168 h最优降水预报场,以期为提高流域降水预报准确率以及洪水预报提供技术支撑,为长江大型水库精细化调度和水资源精准开发利用提供参考依据。
1 资料介绍文中使用2018—2020年的全球模式和区域模式降水预报产品,具体为:全球模式采用欧洲中期天气预报中心(ECMWF)、美国国家环境预报中心(NCEP)、中国气象局全球同化预报系统(CMA-GFS)和德国气象局(GERMAN)降水预报产品;区域模式采用中国气象局中尺度天气数值预报系统(CMA-MESO)、中国气象局上海数值预报模式系统(CMA-SH9)降水预报产品。另外,还使用了2018—2020年欧洲中期天气预报中心集合预报概率产品和物理量场预报产品。模式预报产品起报时间为08时(北京时,下同)和20时,预报时效间隔为12 h,并通过距离权重插值法降尺度到5 km分辨率。
实况资料为2018—2020年长江流域723个国家站08时、20时过去12 h降水量观测资料。
雨型判别物理量特征统计使用了2010—2017年58个强降水个例的美国国家环境预报中心(NCEP/NCAR)一日4次的大气再分析资料。
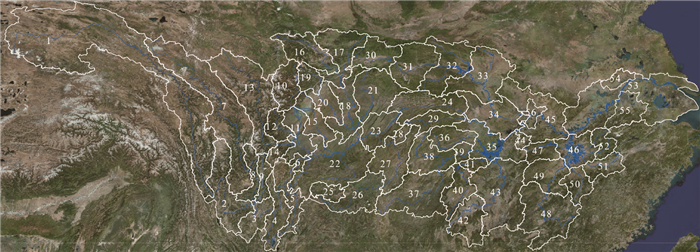
2 长江流域分区方案长江流域大部分地处我国亚热带东南季风和西南季风的影响范围,地势起伏大,水情组成复杂。根据干支流水系分布,长江流域目前有6种分区方式,按子流域的划分方案从粗到细分别为10分区、20分区、28分区、39分区和56分区,其中56分区方案如图 1所示。由于流域内地貌类型多样,造成不同地区降水气候差异较大(周秋雪等,2019),而不同数值模式对各地的降水预报性能差异也较大(智协飞等,2013;陈博宇等,2015;张宏芳等,2014)。因此研究长江流域精细降水预报技术,有必要合理划分子流域区间。本文在长江流域干支流水系56分区的基础上,结合地形特点、水系分布、气候差异和相关部门调度需求,将长江流域分成43个区域(图 2),分区名称见表 1。
|
图 1 长江流域干支流水系56分区示意图 Fig. 1 The 56 divisions of main and tributaries in the Yangtze River Basin branch |

|
图 2 长江流域精细订正预报43分区示意图 Fig. 2 The 43 divisions for fine revised forecast in the Yangtze River Basin |
|
|
表 1 长江流域精细订正预报43分区名称 Table 1 The names of 43 divisions for fine revised forecast in the Yangtze River Basin |
如前文所述,由于模式预报能力不断提升(Forbes et al, 2015; Malardel et al, 2015),在不同年份,同一模式对同一地区的降水预报特点可能会有不同。如果训练期内的降水特征与预报期内的降水特征出现较大差别,训练期方案可能导致对预报期内的降水预报“反订正”(孙靖等,2015),因此训练期须反映近期天气变率的特点。
本文以2018—2020年5月1日至9月30日为预报期构建各模式降水预报样本集,以每个预报日的前14、21、28、35 d为滑动训练期构建各模式降水预报TS评分样本集,还构建了2018—2020年对应时段的实况样本集。
3.2 分区分级模式性能排序将12 h降水量分为4个等级进行检验,分别为小雨(0.1~9.9 mm)、中雨(10~24.9 mm)、大雨(25~49.9 mm)、暴雨(50 mm及以上)。全球模式ECMWF、NCEP、CMA-GFS、GERMAN降水预报产品的检验时效为12~24、24~36、36~48、48~60、60~72、72~84、84~96、96~108、108~120、120~132、132~144、144~156、156~168 h,其中ECMWF、NCEP、CMA-GFS时效较其他模式多168~180 h。区域模式CMA-SH9、CMA-MESO降水预报产品的检验时效为12~24、24~36、36~48、48~60、60~72 h,其中CMA-MESO时效较其他模式多72~84 h。
可见,参与12~72 h检验的模式最多,有6个:ECMWF、NCEP、CMA-GFS、GERMAN、CMA-MESO和CMA-SH9;参与72~84 h检验的有5个: ECMWF、NCEP、CMA-GFS、GERMAN、CMA-MESO;参与84~168 h检验的模式有4个: ECMWF、NCEP、CMA-GFS、GERMAN;参与168~180 h检验的模式有3个: ECMWF、NCEP、CMA-GFS。
首先,开展了2018—2019年汛期(5—9月)各模式在各分区、各量级降水的TS评分检验,建立预报性能基础序列。其次,利用2020年汛期(5—9月)各模式降水预报样本集,计算训练期内各模式在各分区、各分级降水的TS评分,从而按评分高低得到各模式在各分区、分级降水的预报性能序列。若某分区在训练期内的某一量级降水实况样本数为0个,或所有模式针对该量级降水的TS评分为0,则以预报性能基础序列(即2018—2019年各模式的该量级降水TS评分)作为排序依据。
3.3 雨型客观识别法对于不同尺度的降水,全球模式和区域模式的预报能力各有优劣,在分级降水预报性能序列的基础上,通过研究建立物理量阈值,确定全球模式和区域模式选用的优先级。
利用58个强降水个例,按照水汽条件、动力条件、不稳定条件三要素以及特殊环境条件,分别提取水汽及层结特征(可降水量、850 hPa露点温度、700 hPa温度露点差)、动力条件(925 hPa锋生函数、地面3 h变压、700 hPa风速)、不稳定能量(湿对流有效位能CAPE、抬升指数LI、沙氏指数SI和K指数)、降水效率(抬升凝结高度LCL、暖云厚度)等相关物理量做统计分析,分析大尺度和中尺度降水过程期间物理量的异同,凝练了两个主要物理量作为雨型客观识别判据。条件1:LI < 0℃;条件2:CAPE≥477 J·kg-1。当同时符合这两个条件时,认为降水为对流性降水,优先使用区域模式;否则为稳定性降水,优先使用全球模式。
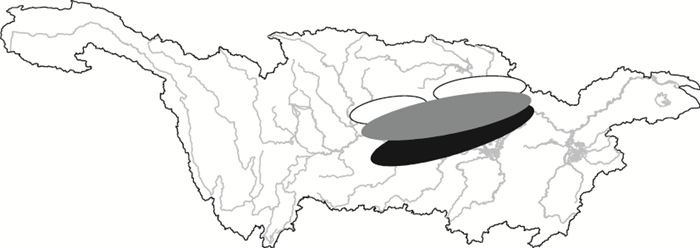
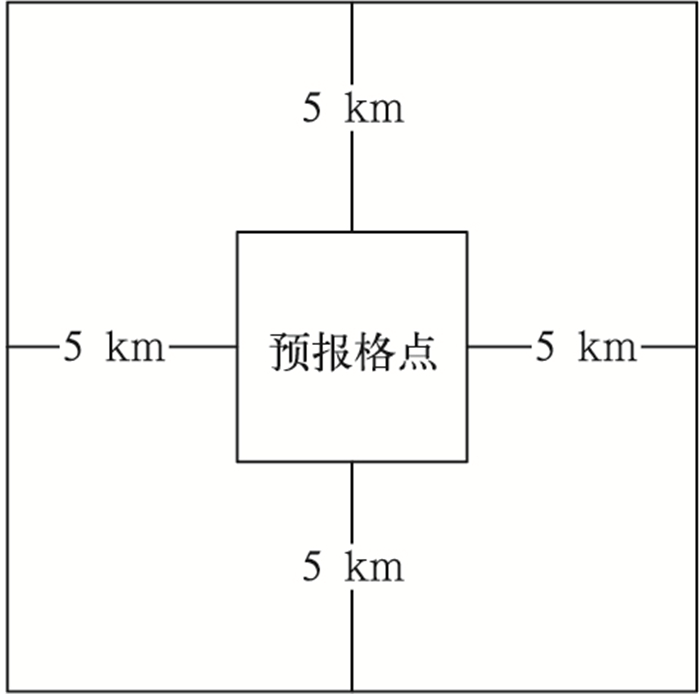
3.4 “邻域择优法”和“点对点择优法”研究表明,ECMWF模式在长江上游流域的降水预报在落区上存在偏差(王海燕等,2017), CMA-GFS存在对流性降水预报较实况偏北或主雨带南侧暖区降水预报不足的偏差特征(宫宇等,2018)。如图 3所示,实际暴雨落区发生在灰色区域的可能性较大,但若严苛地点对点比较模式1和模式2预报的暴雨落区,则易漏掉暴雨重要信号。本文对大雨及以上量级采用“邻域择优法”,以期有效保留各模式的强降水信息。以图 4为例,假设该预报格点所在分区、暴雨量级的模式性能排序前三的为模式a1、模式a2、模式a3,对该格点周围5 km范围内进行搜索,若排序前三模式中有超过两个预报为暴雨,则认为该格点为暴雨量级,并在两个预报暴雨的模式中采信预报性能排序最前、距离该格点最近的模式暴雨值进行赋值。但对中雨、小雨量级,若采用“邻域择优法”则会增加空报率,因此采用“点对点择优法”。
|
图 3 模式a1(白色)和模式a2(黑色)预报暴雨落区及易发生暴雨落区(灰色)的示意图 Fig. 3 Rainstorm forecast area of model a1 (white), model a2 (black) and rainstorm prone area (grey) |
|
图 4 邻域择优法示意图 Fig. 4 Schematic diagram of neighborhood optimization method |
在方案试验评估过程中发现,采用上述思想建立的产品与客观数值模式对比,对大量级降水的预报质量明显提高,对大雨以上量级降水采用“邻域择优法”较“点对点择优法”TS评分提高2%以上。
3.5 降水预报消空方法(1) 基于集合预报概率阈值暴雨消空法
对大量级降水预报采用“邻域择优法”赋值虽然提高了预报的TS评分,但也在一定程度上增加了空报率。研究表明,ECMWF集合预报的集合平均对暴雨存在明显漏报(董全等,2016;陈圣劼等,2019),利用集合预报的这一特性,对2018—2019年长江流域汛期暴雨过程样本进行统计,分析表明,当50 mm以上强降水概率预报小于5%时,暴雨出现概率极低,因此,选取5%作为强降水消空阈值。
(2) 分时段阈值小雨消空法
对于小雨预报,模式预报普遍空报,因此统计分析各模式不同月份的小雨空报率,选取弱降水空报的最佳阈值,作为消空指标。基于不同模式降水预报产品在不同分区的检验结果,得到不同月份各模式在各分区的弱降水阈值,如:检验表明,7—8月ECMWF模式在某分区预报12 h降水量≤0.5 mm时,降水实况一般为0 mm,则ECMWF模式在该分区7—8月的弱降水阈值为0.5 mm。
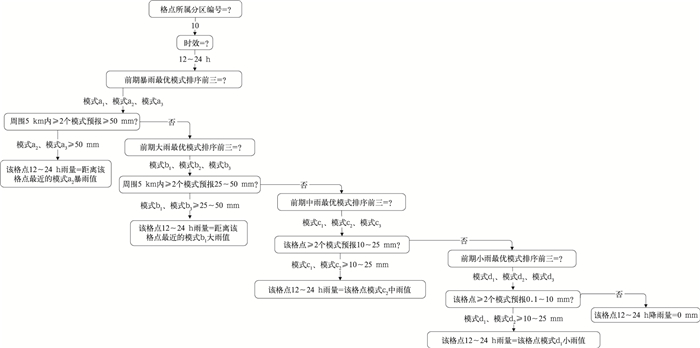
3.6 最优集成思路由于获取数值模式资料的滞后性,集成时采用前12 h起报的数值模式构成该时次的模式集。以20时的12 h降水订正为例,采用数值模式08时起报的12~24 h降水预报数据。最优集成预报的“择优”流程如图 5所示。首先判断该格点50 mm以上的集合预报概率是否大于5%,当大于5%时,判断其所属分区内滑动训练期暴雨最优模式排序,假设排序前三的模式依次为模式a1、模式a2和模式a3,且该格点周围5 km范围内模式a2和模式a3预报该时效有50 mm以上的降水,则认为该格点该时效为暴雨量级。由于模式a2的预报性能优于模式a3,因此采信模式a2的暴雨值赋值该格点。
|
图 5 多模式动态集成预报的“择优”流程图 Fig. 5 Flow chart of multi-mode dynamic integrated forecast |
若该格点周围5 km范围内暴雨排序前三的模式中≤1个模式预报或该时效50 mm以上的集合预报概率小于5%,则认为该格点为暴雨以下量级。假设其所属分区内滑动训练期大雨最优模式排序为模式b1、模式b2和模式b3,则寻找该格点周围5 km内是否有≥2个模式预报大雨,若模式b1和模式b3预报大雨,则采信滑动训练期预报效能较好的模式b1大雨值赋值该格点。若≤1个模式预报大雨,则继续判断该格点是否有≥2个模式预报中雨;若≤1个模式预报中雨,则判断该格点是否有≥2个模式预报小雨,并利用最优模式的小雨消空阈值判断是否需要做消空处理;若≤1个模式预报小雨,则认为该格点无雨。由此获得的0~168 h多模式动态集成降水预报场,称为MDI(multi-model dynamic integration),以预报日前14、21、28、35 d作为滑动训练期产生的多模式动态集成降水预报场分别称为MDI-14、MDI-21、MDI-28、MDI-35。
4 2020年业务应用效果评估 4.1 总体检验2020年MDI产品投入业务应用,在长江流域汛期降水预报服务中取得了良好的应用效果。表 2~表 5分别是2020年5—9月MDI-14、MDI-21、MDI-28、MDI-35、ECMWF、NCEP、CMA-GFS、GERMAN、CMA-MESO、CMA-SH9逐24 h降水预报产品的分级降水TS评分。
|
|
表 2 2020年5—9月MDI及各模式暴雨及以上预报TS评分 Table 2 TS scores of MDI and numerical models' rainstorm forecast from May to September 2020 |
|
|
表 3 2020年5—9月MDI及各模式大雨预报TS评分 Table 3 TS scores of MDI and numerical models' heavy rain forecast from May to September 2020 |
|
|
表 4 2020年5—9月MDI及各模式中雨预报TS评分 Table 4 TS scores of MDI and numerical models' moderate rain forecast from May to September 2020 |
|
|
表 5 2020年5—9月MDI及各模式小雨预报TS评分 Table 5 TS scores of MDI and numerical models' light rain forecast from May to September 2020 |
对暴雨以上量级(表 2),MDI产品TS评分最高,其中MDI-28有6个时效排前二,且在168 h时效排第一;MDI-21有5个时效排前二,且在24、48、120、144 h等4个时效排第一;MDI-14和MDI-35都有4个时效排前二,MDI-14在72 h、168 h排第一,MDI-35在96 h时效排第一。对大雨量级(表 3),MDI产品TS评分仍为最高,其中MDI-28和MDI-35的预报效果较好,有5个时效排前二,其中MDI-28在24、48、96、168 h等4个时效排第一,MDI-35在24 h、72 h等2个时效排第一,另外,MDI-14在120 h、144 h等2个时效排第一。对中雨量级(表 4),MDI产品中MDI-35和MDI-28较模式预报优势明显,有6个时效排前二,其中MDI-35有4个时效排第一。对小雨量级(表 5),MDI产品中MDI-35、MDI-28、MDI-21的预报效果较好,均有6个时效排前二,其中MDI-35有5个时效排第一。
分析各分级降水的空、漏报率(表略)发现,MDI产品对大雨、暴雨及以上的空、漏报率均明显优于模式产品,特别是24 h大雨和暴雨的空、漏报率分别为0.561、0.462和0.521、0.605,远低于模式产品, 对中雨的漏报率也远比模式产品低; 而空报率除在96~168 h的4个时效略高于ECMWF以外,其他时效均低于模式产品。对小雨的空报率,24~72 h小于0.5,低于数值模式预报空报率,96 h之后较模式预报略高;漏报率则相反,24~72 h在0.149~0.174,略高于模式预报,96 h之后漏报率显著降低,在0.1以下,远低于模式预报。
总体来看,MDI产品对大雨及以上降水预报,在TS评分及空、漏报的整体预报效果均较好。MDI-21对24 h、48 h暴雨以上预报效果较好,MDI-28对大雨以上降水预报效果整体较好;对中雨及以下降水,MDI-35预报效果较好,尤其是对小雨采取了分时段阈值消空法有效控制了小雨的空报率。
4.2 24 h分级降水TS检验空间分布对比挑选24 h预报各量级降水TS最高的MDI产品和ECMWF作比较(图 6)。以ECMWF模式为参照,对于暴雨及以上降水预报,MDI-21产品在除金沙江以外长江流域大部地区TS评分达到0.2以上,高于ECMWF模式,特别是在汉江上游、乌江下游、清江、澧水、长江下游等地在0.35以上,且较ECMWF模式高出0.15以上;对于大雨预报,MDI-28产品在流域大部达到0.3左右或以上,且除金沙江上游、嘉陵江上游少数地区外,在流域其他大部地区高于ECMWF模式,其中汉江上游部分地区高出0.1以上;对于中雨预报,MDI-35产品在流域大部地区达到0.32左右或以上,除金沙江上游、汉江上游、陆水、洞庭湖流域部分地区外,流域其他地区均高于ECMWF模式;对于小雨预报,MDI-35产品在大部地区达到0.45以上,金沙江上中游、雅砻江、岷沱江、嘉陵江、长江上游干流等地达到0.55以上,且大部分地区高于ECMWF模式。
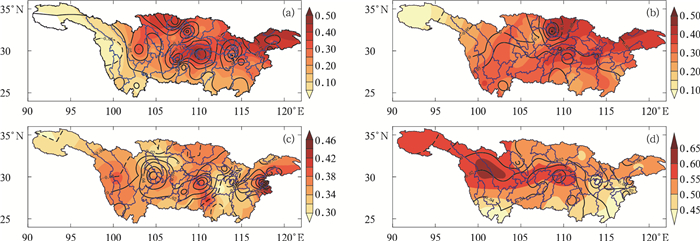
|
图 6 2020年5—9月(a)MDI-21暴雨,(b)MDI-28大雨,(c)MDI-35中雨,(d)MDI-35小雨的预报TS(填色)分布及其与ECMWF对比 (等值线为MDI与ECMWF的TS评分差值,实线为正值,虚线为负值) Fig. 6 TS-score (colored) distribution of (a) MDI-21 rainstorm, (b) MDI-28 heavy rain, (c) MDI-35 moderate rain and (d) MDI-35 light rain from May to September 2020 and its comparison with ECMWF (Contour is the TS-score difference between MDI and ECMWF, solid line is positive, and dotted line is negative) |
可以看出,MDI产品的各级降水预报TS评分在长江流域大部地区较ECMWF模式有很大提高,特别是对大雨及以上量级的降水,在长江上游东部、中下游沿江及以北地区的优势较为明显;对中雨及以下量级的降水,则在长江流域中部和南部地区的优势较为明显。
5 结论与讨论将长江流域划分成43个区域,分别以预报日前14、21、28、35 d作为滑动训练期,基于多种全球和区域模式对每个分区开展分时效、降水分级的滚动TS检验,得到每个分区各时效各量级的模式性能排序。按照暴雨、大雨采用“邻域择优法”,中雨、小雨采用“点对点择优法”的集成思路,输出MDI-14、MDI-21、MDI-28和MDI-35共四种产品。对比分析2020年5—9月MDI及模式降水产品的预报效果,得到以下结论:
(1) 从TS评分来看,MDI产品整体的预报效果较好。对大雨及以上量级降水MDI-28的整体预报效果较好,另外,24 h暴雨及以上降水MDI-21具有较好预报效果。对中雨及以下量级降水MDI-35产品预报效果较好。
(2) 从空、漏报率来看,MDI产品对大雨及以上降水的预报效果最好,可见“邻域择优法”应用在≥25 mm的降水上,并采用基于集合概率预报阈值消空的方法,可以较好地控制空、漏报率。“点对点择优法”应用在<25 mm的降水上还是会造成一定的空报率的增加,而对小雨采取分时段阈值消空法有效降低了小雨的空报率,以此为代价带来的漏报率的增加也有限,整体还是对预报的正确率有正贡献。
(3) 从MDI产品与ECMWF模式的24 h检验结果在长江流域分布情况来看,MDI产品在各量级降水的预报上较ECMWF模式有很大优势,特别是对大雨及以上量级的降水,其在长江上游东部和中下游中部、北部地区表现出较好的预报能力,可为长江流域洪涝灾害防御气象服务提供较好的科技支撑和决策依据。
(4) 最优集成方案能有效提升长江流域降水预报能力,不足之处在于对长江上游金沙江流域预报能力改善效果差。这主要是因为制定分区分级模式性能排序方案时,仅考虑了TS评分这一项检验指标,金沙江上游、雅砻江等地由于观测站点少,限制了对降水分布的细致分析和预报效果的评估。今后还需开展多源降水融合分析格点实况应用, 纳入多种检验方法, 结合天气系统移动、降水季节变化和地形分布特点设计最佳模式集成方案,从而更合理地取众模式之长,找到每一个格点的最佳赋值。
毕宝贵, 代刊, 王毅, 等, 2016. 定量降水预报技术进展[J]. 应用气象学报, 27(5): 534-549. Bi B G, Dai K, Wang Y, et al, 2016. Advances in techniques of quantitative precipitation forecast[J]. J Appl Meteor Sci, 27(5): 534-549 (in Chinese).
|
陈博宇, 代刊, 郭云谦, 2015. 2013年汛期ECMWF集合统计量产品的降水预报检验与分析[J]. 暴雨灾害, 34(1): 64-73. Chen B Y, Dai K, Guo Y Q, 2015. Precipitation verification and analysis of ECMWF ensemble statistic products in 2013 flooding season[J]. Torr Rain Dis, 34(1): 64-73 (in Chinese). DOI:10.3969/j.issn.1004-9045.2015.01.009
|
陈丽娟, 许力, 王永光, 2005. 超级集合思想在汛期降水预测集成中的应用[J]. 气象, 31(5): 52-54. Chen L J, Xu L, Wang Y G, 2005. Application of superensemble to precipitation prediction in China during flood season[J]. Meteor Mon, 31(5): 52-54 (in Chinese). DOI:10.3969/j.issn.1000-0526.2005.05.011
|
陈圣劼, 刘梅, 张涵斌, 等, 2019. 集合预报产品在江苏省暴雨预报中的应用评估[J]. 气象, 45(7): 893-907. Chen S J, Liu M, Zhang H B, et al, 2019. Evaluation on forecasting heavy rainfall over Jiangsu Region using ensemble forecast techniques and products[J]. Meteor Mon, 45(7): 893-907 (in Chinese).
|
董全, 金荣花, 代刊, 等, 2016. ECMWF集合预报和确定性预报对淮河流域暴雨预报的对比分析[J]. 气象, 42(9): 1146-1153. Dong Q, Jin R H, Dai K, et al, 2016. Comparison between ECMWF ensemble and deterministic forecast for heavy rainfall in the Huaihe River Basin of China[J]. Meteor Mon, 42(9): 1146-1153 (in Chinese).
|
范宇恩, 陈静, 邓国, 等, 2019. GRAPES区域集合预报两种侧边界扰动方法对比试验[J]. 气象, 45(12): 1629-1641. Fan Y E, Chen J, Deng G, et al, 2019. Comparison of two lateral boundary perturbation methods in the regional ensemble prediction system of GRAPES[J]. Meteor Mon, 45(12): 1629-1641 (in Chinese). DOI:10.7519/j.issn.1000-0526.2019.12.001
|
宫宇, 代刊, 徐珺, 等, 2018. GRAPES-GFS模式暴雨预报天气学检验特征[J]. 气象, 44(9): 1148-1159. Gong Y, Dai K, Xu J, et al, 2018. Synoptic verification characteristics of operational GRAPES-GFS model heavy rain event forecast[J]. Meteor Mon, 44(9): 1148-1159 (in Chinese).
|
郝莹, 王元, 王皓, 等, 2019. 淮河流域不同时间尺度暴雨的多模式预报性能评估及洪水可预报性探讨[J]. 气象, 45(7): 989-1000. Hao Y, Wang Y, Wang H, et al, 2019. Evaluation of multi-NWPs rainstorm forecasting performance in different time scales in Huaihe River Basin and discussion on flood predictability[J]. Meteor Mon, 45(7): 989-1000 (in Chinese).
|
任宏昌, 2017. 2017年6—8月T639、ECMWF及日本模式中期预报性能检验[J]. 气象, 43(11): 1439-1445. Ren H C, 2017. Performance verification of medium-range forecasts by T639, ECMWF and Japan models from June to August 2017[J]. Meteor Mon, 43(11): 1439-1445 (in Chinese).
|
孙靖, 程光光, 张小玲, 2015. 一种改进的数值预报降水偏差订正方法及应用[J]. 应用气象学报, 26(2): 173-184. Sun J, Cheng G G, Zhang X L, 2015. An improved bias removed method for precipitation prediction and its application[J]. J Appl Meteor Sci, 26(2): 173-184 (in Chinese).
|
王海燕, 田刚, 徐卫立, 等, 2017. ECMWF模式在长江上游流域调度关键期的预报检验评估[J]. 干旱气象, 35(1): 142-147. Wang H Y, Tian G, Xu W L, et al, 2017. Evaluation and inspection of ECMWF model forecast product during dispatch key periods in upper reaches of the Yangtze River Basin[J]. J Arid Meteor, 35(1): 142-147 (in Chinese).
|
王雨, 闫之辉, 2006. 2004年汛期(5~9月)主客观降水预报检验[J]. 热带气象学报, 22(4): 331-339. Wang Y, Yan Z H, 2006. Verification of subjective and objective precipitation forecast in flood season of 2004[J]. J Trop Meteor, 22(4): 331-339 (in Chinese). DOI:10.3969/j.issn.1004-4965.2006.04.004
|
辛辰, 漆梁波, 2018. ECMWF模式对南方春雨期降水预报的检验和分析[J]. 暴雨灾害, 37(4): 383-391. Xin C, Qi L B, 2018. Verification and analysis on precipitation forecast of ECMWF model during spring rain period in South China[J]. Torr Rain Dis, 37(4): 383-391 (in Chinese). DOI:10.3969/j.issn.1004-9045.2018.04.011
|
熊秋芬, 2011. GRAPES_Meso模式的降水格点检验和站点检验分析[J]. 气象, 37(2): 185-193. Xiong Q F, 2011. Verification of GRAPES-Meso precipitation forecasts based on fine-mesh and station datasets[J]. Meteor Mon, 37(2): 185-193 (in Chinese). DOI:10.3969/j.issn.1000-6362.2011.02.006
|
张宏芳, 潘留杰, 杨新, 2014. ECMWF、日本高分辨率模式降水预报能力的对比分析[J]. 气象, 40(4): 424-432. Zhang H F, Pan L J, Yang X, 2014. Comparative analysis of precipitation forecasting capabilities of ECMWF and Japan high-resolution models[J]. Meteor Mon, 40(4): 424-432 (in Chinese). DOI:10.3969/j.issn.1671-1742.2014.04.016
|
赵声蓉, 2006. 多模式温度集成预报[J]. 应用气象学报, 17(1): 52-58. Zhao S R, 2006. Multi-model consensus forecast for temperature[J]. J Appl Meteor Sci, 17(1): 52-58 (in Chinese). DOI:10.3969/j.issn.1001-7313.2006.01.007
|
智协飞, 季晓东, 张璟, 等, 2013. 基于TIGGE资料的地面气温和降水的多模式集成预报[J]. 大气科学学报, 36(3): 257-266. Zhi X F, Ji X D, Zhang J, et al, 2013. Multimodel ensemble forecasts of surface air temperature and precipitation using TIGGE datasets[J]. Trans Atmos Sci, 36(3): 257-266 (in Chinese).
|
智协飞, 王姝苏, 周红梅, 等, 2016. 我国地面降水的分级回归统计降尺度预报研究[J]. 大气科学学报, 39(3): 329-338. Zhi X F, Wang S S, Zhou H M, et al, 2016. Statistical downscaling of precipitation forecasting using categorized rainfall regression[J]. Trans Atmos Sci, 39(3): 329-338 (in Chinese).
|
周慧, 崔应杰, 胡江凯, 等, 2010. T639模式对2008年长江流域重大灾害性降水天气过程预报性能的检验分析[J]. 气象, 36(9): 60-67. Zhou H, Cui Y J, Hu J K, et al, 2010. Validation of 2008 heavy rain events over the Yangtze River Basin forecast by T639 model[J]. Meteor Mon, 36(9): 60-67 (in Chinese).
|
周秋雪, 康岚, 蒋兴文, 等, 2019. 四川盆地边缘山地强降水与海拔的关系[J]. 气象, 45(6): 811-819. Zhou Q X, Kang L, Jiang X W, et al, 2019. Relationship between heavy rainfall and altitude in mountainous areas of Sichuan Basin[J]. Meteor Mon, 45(6): 811-819 (in Chinese).
|
Cartwright T J, Krishnamurti T N, 2007. Warm season mesoscale superensemble precipitation forecasts in the southeastern United States[J]. Wea Forecasting, 22(4): 873-886. DOI:10.1175/WAF1023.1
|
Ebert E E, Damrath U, Wergen W, et al, 2003. The WGNE assessment of short-term quantitative precipitation forecasts[J]. Bull Amer Meteor Soc, 84(4): 481-492. DOI:10.1175/BAMS-84-4-Ebert
|
Forbes R, Haiden T, Magnusson L, 2015. Improvements in IFS forecasts of heavy precipitation[R]. ECMWF Newsletter No. 144: 21-26.
|
Golding B W, 2000. Quantitative precipitation forecasting in the UK[J]. J Hydrol, 239(1-4): 286-305. DOI:10.1016/S0022-1694(00)00354-1
|
Malardel S, Wedi N, Deconinck W, et al, 2015. A new grid for the IFS[R]. ECMWF Newsletter No. 146: 23-28.
|
Ross R S, Krishnamurti T N, 2005. Reduction of forecast error for global numerical weather prediction by the Florida State University (FSU) superensemble[J]. Meteor Atmos Phys, 88(3): 215-235.
|
Scheuerer M, Hamill T M, 2015. Statistical postprocessing of ensemble precipitation forecasts by fitting censored, shifted gamma distributions[J]. Mon Wea Rev, 143(11): 4578-4596. DOI:10.1175/MWR-D-15-0061.1
|
 2022, Vol. 48
2022, Vol. 48 
