引言

大气是高度非线性的混沌系统、数值模式初始场具有不确定性、物理过程参数化方案还不够完善，这几点因素导致单一数值预报存在预报不确定性问题。集合预报技术基于大气非线性运动使得传统的确定性预报向概率预报转变，从而能为用户提供更全面完整的信息(Leith, 1974)。

目前最具代表性的全球集合预报系统(global ensemble prediction system, GEPS)包括美国国家环境与预报中心，欧洲中期天气预报中心和加拿大气象局(Canadian Meteorological Centre, CMC)，这几个中心所采用的初始扰动方法与集合预报结果都有一定差异，国内对集合预报的研究也方兴未艾。田伟红和庄世宇(2008)采用集合变换卡尔曼滤波(ensemble transform Kalman filter, ETKF)方法对我国的GRAPES预报模式做集合预报的扰动，取得一定效果。不同国家的模式在分辨率、参数化方案、资料同化等方面差异明显，各有优劣。所以，如果能将各模式结果组合起来，整合优点，可以减小单个模式的系统误差，多模式集成预报这个概念应运而生。Krishnamurti et al(1999)将多元线性回归方法应用到多模式集成预报之中，这也是最早被提出的超级集合预报方法。经对比分析结果，超级集合预报提高了天气尺度预报和季节尺度气候预测的预报技巧，比单个模式的预报效果优秀。

多模式集成预报在我国的研究与应用虽然起步较晚，但也己取得许多成果。智协飞等(2009)基于TIGGE资料中气温这个物理量，进行不同地区的超级集合预报试验，发现超级集合预报误差比单模式预报减小很多。张涵斌等(2015)也集合了TIGGE下各模式预报资料，得到了西太平洋气旋预报, 效果较好。林春泽等(2009)发展了滑动训练期消除偏差集合平均(running-bias removed ensemble mean, R-BREM)和滑动训练期超级集合预报(running super-ensemble forecast, R-SUP)，训练期每日向后滑动，使得每次预报的都为训练期后一天的日期，降低了季节影响的误差，预报效果优于固定的训练期。在地面气温的延伸期预报中，崔慧慧和智协飞(2013)也证明了多模式集成能够较好地改善单模式预报效果。Zhi et al(2012)研究了2007年北半球夏季地面2 m气温，其结果表明短期的预报(24~72 h)，超级集合的预报效果要远优于单个模式的预报结果，而对于中短期的预报(96~168 h)，超级集合预报也能有效改善集合成员的预报结果。针对集合降水预报订正，目前贝叶斯模式平均和频率匹配订正法业务上较为常用，已有不少研究。针对不同区域降水预报采用分级贝叶斯模式平均改进(Ji et al, 2019；祁海霞等，2020)。频率匹配订正法在集合降水预报订正上，明显消除了大范围小雨空报，提高了晴雨预报准确率，降水落区分布更加合理(智协飞和吕游，2019；李俊等，2015)。Ji et al(2020)还采用基于目标的MODE评估(method for object-based diagnostic evaluation)对多模式降水预报进行集合，所得预报结果优于传统的基于点对点评估的多模式超级集合预报。近年来，人工智能方法在科学计算、回归预测模型上应用较广。应用到多模式集成预报之中的神经网络方法，也显露一定的优势。智协飞等(2020)和Peng et al(2020)利用浅层神经网络、长短期记忆神经网络、自然梯度提升等机器学习方法与传统多模式集成预报方法进行对比，发现LSTM方法对于较长预报时效的地面气温预报改进效果较好，更多改进在我国西北、华北、东北等地区。上述研究均已充分证明了多模式集成预报的相对优越性，可用于业务预报中，更好地提高气象服务水平。

卡尔曼滤波是一种根据观测和预报数据自适应迭代权重系数减小误差的有力工具。它的迭代计算过程较为简单，线性拟合能力较强，对于噪声的处理效果好，因此被广泛应用。然而将卡尔曼滤波应用于多模式集成预报的研究目前并不多，尤其在气象领域。基于卫星降水资料，Krishnamurti et al(2003)采用卡尔曼滤波，对卫星降水资料进行线性拟合，这也是该方法在气象领域中的较早尝试。随后，Rixen et al(2009)、Rixen and Fevreira-Coelho(2007)与Lenartz et al(2010)利用卡尔曼滤波集合各个海洋模式的结果，对48 h海表温度的预报也取得较好效果。智协飞和黄闻(2019)基于TIGGE资料集中多个模式预报的结果，利用卡尔曼滤波方法对气温和降水预报进行多模式集成预报研究，发现该方法对地面2 m气温和短预报时效的降水均有明显改进。智协飞和赵忱(2020)将卡尔曼滤波技术和频率匹配法相结合，对2016年夏季中国区域降水预报进行了订正，发现降水落区预报和降水中心的量级预报效果均比其他多模式集成预报更加准确。近年来，数值模式日益提高了高低层大尺度变量(如500 hPa高度场、地面温度等)的预报准确率。然而，对于风场的预报仍然存在较大误差，并且风场作为一种具有二维变量的要素，除了对各分量进行预报，还需要考察矢量风场纬向和经向分量之间的联系和配合，这也是目前风场预报存在不足的部分原因。He et al(2015)将卡尔曼滤波方法进行扩展变形，将台风位置表示成复数，实部(虚部)表示台风路径的经度(纬度)，在台风路径的多模式集成预报中取得较好效果。这种适用于二维矢量订正的复卡尔曼滤波方法在本文中被应用于风场的预报订正。

卢晔等(2015)分析总结了华东区域风速变化特征。华东地区海岸线绵长，作为我国一大平原地带，不仅地理位置特殊而且人口密集，对风场预报的准确预报对于航空和风能开发都具有重要的意义。本文对2020年1—4月华东区域地面和高空风速的预报资料进行多模式集成预报试验。

1 资料与方法 1.1 资料 1.1.1 模式预报资料

① 欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)风场预报资料(u, v)，地面水平分辨率为0.125°，高空各层水平分辨率为0.25°，逐日起报时间为12: 00 UTC，预报时效为0~72 h，每隔3 h输出一次预报结果。垂直层次主要包括700、850、925、950和1 000 hPa、地面10 m等。时间取2020年1月13日至4月13日。研究区域取20°~40°N、110°~130°E。

② 同期、同区域中国气象局的中尺度数值业务预报系统(CMA-MESO)风场预报资料，各层水平分辨率均为3 km，初始场时间间隔为24 h，逐日起报时间为12: 00 UTC，预报时效为0~72 h，每隔3 h输出一次预报结果。垂直层次主要包括700、750、800、850、900、925、950、975和1 000 hPa、地面10 m等。

③ 同期、同区域美国国家环境预报中心的全球预报系统(Global Forecast System, GFS)风场预报资料，各层水平分辨率均为0.5°，初始场时间间隔为24 h，逐日起报时间为12: 00 UTC，预报时效为0~72 h，每隔3 h输出一次预报结果。垂直层次主要包括700、750、800、850、900、925、950、975和1 000 hPa、地面10 m等。

④ 同期、同区域中国气象局全球预报系统(CMA-GFS)风场预报资料，各层水平分辨率均为0.25°，初始场时间间隔为24 h，逐日起报时间为12: 00 UTC，预报时效为0~72 h，每隔3 h输出一次预报结果。垂直层次主要包括700、800、850、925、975和1 000 hPa、地面10 m等。

1.1.2 再分析资料

用来评估模式预报技巧的观测资料的质量、分辨率、覆盖的地理范围等都应考虑。实测站点资料能更好地反映真实物理量情况，能更加客观地检验多模式集成预报，但是对于格点精度较高的预报资料，观测资料存在不够精细和缺测较多等缺点，容易导致额外的误差。ERA5资料是ECMWF打造的最新一代再分析资料。孟宪贵等(2018)指出，ERA5在其前身ERA-Interim(Uppala et al, 2008)的基础上实现了很大升级，时空分辨率大幅提升，提供的变量增加到240种。所以经过综合考量，本文选择ERA5资料作为评估用“观测”资料。

ERA5再分析资料: 地面10 m水平分辨率为0.125°，高空各层水平分辨率为0.25°，高空垂直层次主要包括700, 750, 800, 850, 925, 950, 975和1 000 hPa等。所取时间和区域同ECMWF预报资料。

1.2 方法 1.2.1 数据预处理

由于各个模式预报资料及观测资料的分辨率并不完全一致，为了得到华东地区更为精细化的气象要素数据，在试验之前需要对数据进行预处理和插值。本文先采用线性插值的方法将各中心预报数据的预报时效统一为0~72 h，各预报时效间隔为1 h。对比后选取最优区域插值方法，将低分辨率的格点预报数据插值到高分辨率的网格上。本文将各模式地面预报值统一插值到0.125°×0.125°经纬网格上，高空预报值插值到0.25°×0.25°经纬网格上。将高空等压面上风速数据插值到等位势高度层(约为0~3 000 gpm，垂直方向间隔为300 gpm)，得到高空非常规层垂直风场。这样处理的目的是能得到水平和垂直方向上高分辨率的风场预报资料，用于民航飞行的气象保障。

得到统一的高时空分辨率风场资料后，再基于均方根误差、距平相关系数等评估方法，采用简单集合平均(ensemble mean, EMN)、消除偏差集合平均、超级集合预报、适用于矢量二维风场订正的复卡尔曼滤波技术等方法对多模式预报数据进行集合。

1.2.2 反距离权重法插值

反距离权重法插值(inverse distance weight, IDW)，是按照目标站点与已有网格点间的距离反比分配权重，距离较近的数据点权重较高，距离较远的数据点分配的权重较小。

$Z=\frac{\sum\limits_{i=1}^{n} Z_{i} / d_{i}^{a}}{\sum\limits_{i=1}^{n} 1 / d_{i}^{a}} $

(1)

式中: Z为目标站点的物理量要素，Z_i为站点i的要素值，n为站点数，d_i为与第i个站点的距离，a为反比例系数(一般取2)。

1.2.3 多模式简单集合平均

多模式简单集合平均(EMN)对参与多模式集成的各模式预报结果进行简单平均。计算公式如下:

$F_{\mathrm{EMN}}=\frac{1}{N} \sum\limits_{i=1}^{N} F_{i} $

(2)

式中: F_EMN为经EMN方法集合后的预报值，N为预报模式的总数，F_i为模式i的预报值。

1.2.4 多模式超级集合预报和消除偏差集合平均

多模式超级集合预报(super-ensemble forecast, SUP)和多模式消除偏差集合平均(bias-removed ensemble mean, BREM)的公式如下所示:

$F_{\mathrm{SUP}}=\bar{O}+\sum\limits_{i=1}^{N} a_{i}\left(F_{i}-\overline{F_{i}}\right) $

(3)

$F_{\mathrm{BREM}}=\bar{O}+\frac{1}{N} \sum\limits_{i=1}^{N}\left(F_{i}-\overline{F_{i}}\right) $

(4)

式中: F_SUP为超级集合预报值，F_BREM为消除偏差集合平均预报值，$ {\bar O}$为观测值在训练期间内的平均，N为参与多模式集成的模式总数，${\bar F} $为模式i在训练期内预报值的平均，a_i为每个模式的权重系数。

本文都采用滑动训练期方法(智协飞等，2009)，即设置一个最优长度的时间段为训练期，逐日向后滑动，这样能根据季节实时更替各模式预报权重，更为准确。

BREM和SUP的方法将整个时间段分成训练期和预报期两部分。本文经过调试，得到最优训练期长度为40 d。采用滑动训练期方法，2020年2月22日至4月13日设为预报期，2020年1月1日至2月21日设为训练期，进行多模式集成试验。例如: 2020年2月22日的多模式集成预报结果就是训练该日前40 d的预报数据。即2020年1月1日至2月21日为训练期，在训练期间计算出各个模式预报效果，在预报期中进行集合。

1.2.5 卡尔曼滤波和复卡尔曼滤波多模式集成方法

卡尔曼滤波不同于常见的线性的多模式集成预报方法，它是一种能够根据每个时次的预报和观测数据，自适应迭代各模式预报的权重系数的非线性方法。然而，即使采用滑动训练期的方法，训练期间的观测值和预测值都是等价的。其实，观测预报的重要性会随着时间的推移而增加，即越接近预报时间，观测预报的重要性就越大。因此，自动调整模态权系数的方法是非常有效的。这种想法与数据同化技术非常相似: 在训练期间，从最佳初始猜测场出发，确定权重系数；在增加新的观测数据和预报数据时，立即调整权重系数；最后，确定权重系数并用于预测。然后当新的预测开始时，新的迭代又开始了。卡尔曼滤波长期以来被证明是消除系统误差的有力工具，在数据同化领域得到了广泛的应用。卡尔曼滤波的优点是可以自动适应模型与观测值之间的差异以及非线性关系下的预测过程。

卡尔曼滤波的公式由预报和分析方程两部分组成。

预报方程:

$ \begin{gathered} \boldsymbol{W}_{t}^{\mathrm{f}}=\boldsymbol{I} \boldsymbol{W}_{t-1}^{\mathrm{a}} \end{gathered} $

(5)

$ \boldsymbol{P}_{t}^{\mathrm{f}}=\boldsymbol{I} \boldsymbol{P}_{t-1}^{\mathrm{a}} \boldsymbol{I}^{\mathrm{T}}+\boldsymbol{Q} $

(6)

分析方程:

$\begin{gathered} \boldsymbol{K}_{t}=\boldsymbol{P}_{t}^{\mathrm{f}} \boldsymbol{H}_{t}^{\mathrm{T}}\left(\boldsymbol{H}_{t} \boldsymbol{P}_{t}^{\mathrm{f}} \boldsymbol{H}_{t}^{\mathrm{T}}+\boldsymbol{R}\right)^{-1} \end{gathered} $

(7)

$ \boldsymbol{W}_{t}^{\mathrm{a}}=\boldsymbol{W}_{t}^{\mathrm{f}}+\boldsymbol{K}_{t}\left(\boldsymbol{Y}_{t}-\boldsymbol{H}_{t} \boldsymbol{W}_{t}^{\mathrm{f}}\right) $

(8)

$ \boldsymbol{P}_{t}^{\mathrm{a}}=\boldsymbol{P}_{t}^{\mathrm{f}}-\boldsymbol{K}_{t} \boldsymbol{H}_{t} \boldsymbol{P}_{t}^{\mathrm{f}} $

(9)

式中: 上标f和a代表预报与分析状态，下标t表示时刻。P为权重误差协方差矩阵，Q与R分别为模式误差协方差矩阵与观测误差协方差矩阵，它们均为对角阵。I代表单位向量，状态向量W代表各个模式在预报期中的权重占比系数，其展开如下式所示:

$ \boldsymbol{W}_{t}=\left(w_{1}^{1}, w_{1}^{2}, \cdots, w_{1}^{M}, w_{2}^{1}, \cdots, w_{N}^{M}\right)_{N M}^{T} $

(10)

式中: N与M分别代表参与的模式个数以及预报范围内的格点总数。这里我们假设，上一步的分析权重W_a可作为下一步的预报权重W_f。

观测算子H特殊排列了各个模式的预报值，Y包含了观测值，式(8)中Y-HW为预报残差，当每一新的起报时次的预报和观测数据输入的时候，Y-HW预报残差会进行更新。卡尔曼增益K类似比例系数，当K趋于0时，权重系数趋于稳定，算法收敛。H的结构如下:

$ \left.\begin{array}{ccccccc} {\boldsymbol{H}_{t}=} \\ f_{1}^{1}(t) & \cdots & 0 & \cdots & f_{N}^{1}(t) & \cdots & 0 \\ \vdots & & \vdots & \cdots & \vdots & & \vdots \\ 0 & \cdots & f_{1}^{M}(t) & \cdots & 0 & \cdots & f_{N}^{M}(t) \end{array}\right)_{M(N M)} $

(11)

式中: f(t)为模式预报。

P内元素之和随着算法迭代将趋近于0，而Q始终保持不变。Q过大易导致算法不稳定，经过多次试验发现Q < 0.01时，最终的预报效果能够达到最优，我们经验性地设Q为0.01，在本文中我们选取训练期间观测值Y的标准差作为R。

水平风场是一种二维矢量场，我们将它分解为纬向风和经向风，某一点的水平风可以简单地表示成复数，实部(虚部)表示纬向风(经向风)。该思路与台风的复卡尔曼滤波方法(augmented complex extended Kalman filter, ACEKF)类似。在ACEKF中，所有的初始矩阵除了观测算子H的长度变为2，宽度扩展了1倍之外，其余向量长度均扩展了1倍，宽度变为2。矩阵E为复卡尔曼滤波中矢量风场复数形式的示意，代表公式中的权重误差协方差矩阵P、模式误差协方差矩阵Q和观测误差协方差矩阵R。

$ E^{\mathrm{exp}}=\left[\begin{array}{cc} E^{\text {real }} & 0 \\ 0 & E^{\text {imag }} \end{array}\right] $

(12)

相应的，预报期中的预报方程为:

$ S_{t}=\sum\limits_{i=1}^{N} w_{i}^{f}(t) f_{i}(t) $

(13)

式中S_t为最终预报结果。

1.3 评估与检验 1.3.1 均方根误差

均方根误差(root mean square error, RMSE)的计算如下:

$R M S E=\left[\frac{1}{N} \sum\limits_{i=1}^{N}\left(F_{i}-O_{i}\right)^{2}\right]^{\frac{1}{2}} $

(14)

式中: N是样本总数，F_i为样本i的预报值，O_i为样本i的观测值。RMSE的数值越小，实测值和预报值的差值越小，表明预报越准确。

1.3.2 距平相关系数

距平相关系数(anomaly correlation coefficient, ACC)的计算如下:

$ A C C=\frac{\sum\limits_{i=1}^{N}\left(F_{i}-\bar{F}\right)\left(O_{i}-\bar{O}\right)}{\sqrt{\sum\limits_{i=1}^{N}\left(F_{i}-\bar{F}\right)^{2} \sum\limits_{i=1}^{N}\left(O_{i}-\bar{O}\right)^{2}}} $

(15)

式中: F_i为样本i的预报值，O_i为样本i的观测值，$ {\bar F}$为各模式在所有样本中预报的平均值，${\bar O} $为与之对应的观测的平均值。ACC是评估模式预报值和观测值的相关性的一个指标，其值越大，则表明模式的预报效果越好。

2 单个模式风速预报的检验评估

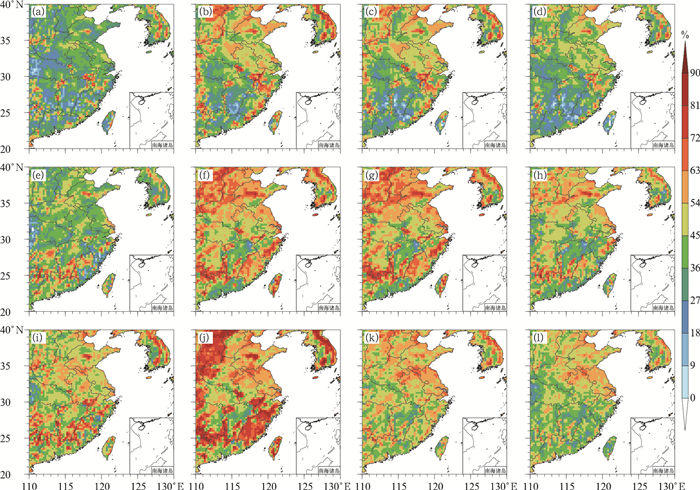
首先以均方根误差为评估指标来对比各个模式的预报效果。如图 1所示，分别计算了4个模式(ECMWF、GFS、CMA-GFS、CMA-MESO)在预报期内华东区域预报时效为24 h、时间平均的地面10 m u、v、全风速预报的均方根误差的地理分布。

在几个单模式中，ECMWF(简称EC)、GFS及CMA-GFS的预报技巧评分较高，其中EC模式预报的误差最小，GFS次之，误差分布表现稳定，CMA-MESO模式的预报技巧较差。误差最小的EC模式在区域分布上RMSE相较于CMA-MESO平均低了1.5 m·s^-1左右。从整个华东地区来看，4个模式对风速预报的误差的地理分布较为一致，大体显示出纬度从低到高RMSE逐渐增加的趋势。山东及广东、福建沿海地区均方根误差较大，长江以南内陆地区均方根误差较小。

EC模式评分表现最好，后续将应用多模式集成技术，将预报技巧最优的单模式与传统的多模式集成、复卡尔曼滤波方法进行对比分析。

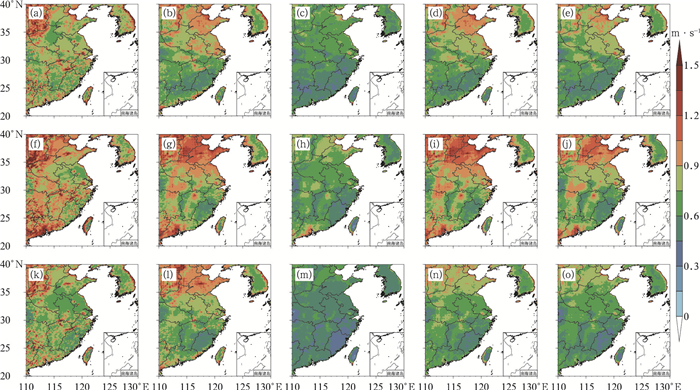
3 多模式风速集成预报结果分析

为更好研究华东地区对精细化风场的预报能力，图 2选取预报期内EMN、BREM、SUP、ACEKF方法及EC模式在预报时效为24 h的地面10 m风速预报的平均RMSE进行比较分析。由图 2可知，EMN、BREM方法预报效果较差，在山东及广东部分地区地面风速RMSE较大，约为1.5 m·s^-1。不等权的多模式集成预报中，SUP方法的预报效果有一定改进，ACEKF预报效果最好，华东地区误差明显减小。

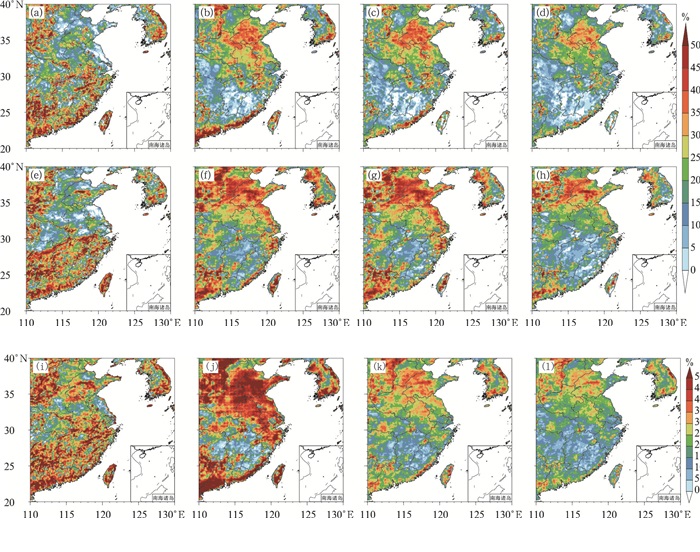
为了进一步讨论ACEKF预报的优越性，我们计算了地面10 m ACEKF预报相较其他多模式集成方法和单模式预报的均方根误差减小的百分比(图 3)。ACEKF相较EMN方法，改进率最高。在广东沿海、福建地区、江淮地区地面风场ACEKF预报改进效果最好，改进率约为40%，华东地区平均地面10 m风速预报RMSE改进率在20%左右。

图 4选取高空具有代表性的几个位势高度层, 对比了300、1 500、2 100、3 000 gpm的预报期内各模式纬向风速24 h预报的平均均方根误差。同地面10 m的结果一样，ACEKF方法预报效果最好，SUP方法次之。ACEKF方法在2 100 gpm高度层上预报均方根误差最大，也与前面机场预报误差的垂直廓线一致。图 5是ACEKF方法较其他多模式集成预报方法和EC单模式预报的均方根误差减小的百分比。以300 gpm为例，华东地区平均预报均方根误差改进率在53%左右，ACEKF对高空风场预报的改进效果要优于地面风场。

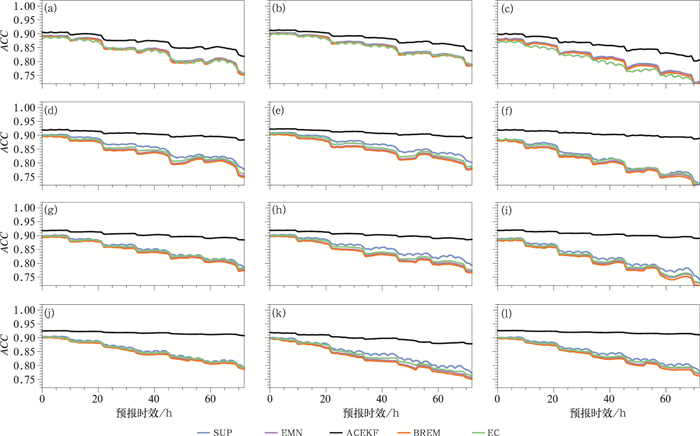
图 6、图 7为预报期内华东地区地面10 m和高空各层风速预报的平均均方根误差和距平相关系数(时间和空间上求平均)，BREM、EMN均方根误差相比于EC预报略高，距平相关系数略低，SUP和EC预报技巧相差无几，ACEKF方法预报效果最优。因区域较小、时间段较短，模式预报总体均方根误差较小、距平相关系数较高。随着预报时效延长，ACEKF方法优势更加明显，预报时效为72 h，ACEKF相比BREM方法，均方根误差约改进1.3 m·s^-1，距平相关系数提高0.1左右。ACEKF方法对高空预报的改进效果优于对地面预报的改进效果。

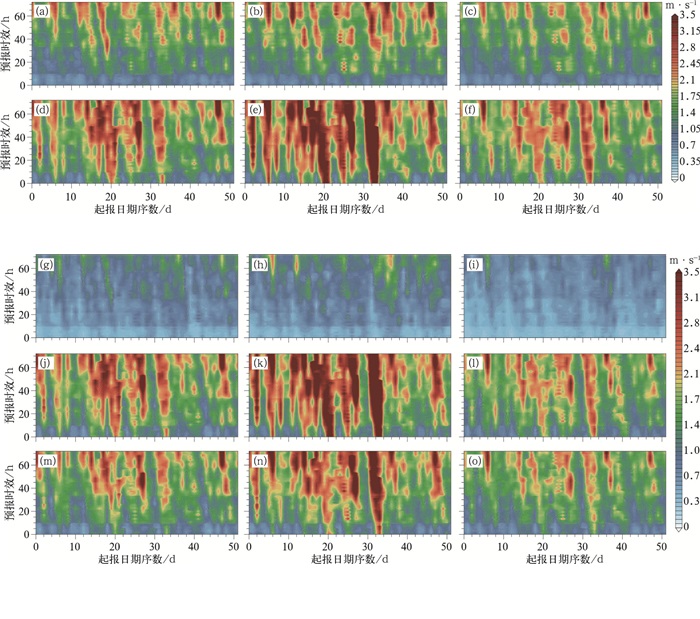
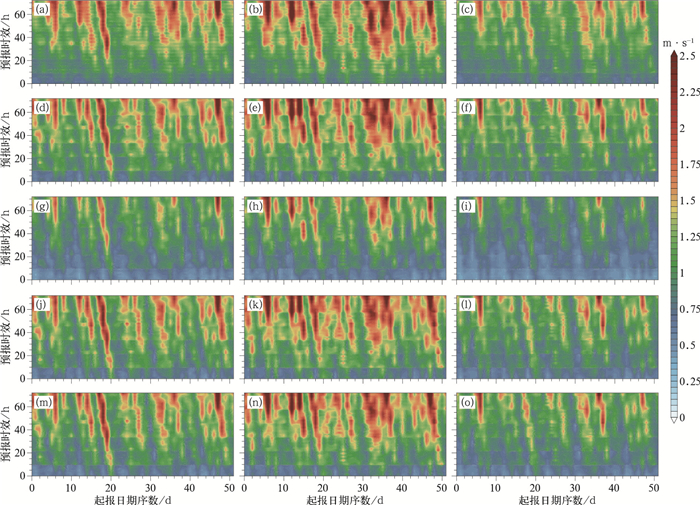
图 8、图 9分别为地面10 m和高空300 gpm 24 h风预报均方根误差随预报时效和起报日的变化。地面24 h风速预报的RMSE基本小于1 m·s^-1，误差随预报时效延长而增长。ACEKF方法对高空300 gpm风预报具有明显改进，比其他多模式集成预报以及EC单模式预报技巧都有很大改进。ACEKF方法对于预报的稳定性也有一定改进。在预报期的第12日，也就是2020年3月4日时模式预报误差比较大，这一天有持续阴雨和大风预警。运用复卡尔曼滤波多模式集成对预报进行集合后对风速预报的改善比较明显。

4 结论与讨论

本文利用简单集合平均、滑动训练期消除偏差集合平均、多模式超级集合预报和复卡尔曼滤波几种方法对EC、GFS、CMA-MESO和CMA-GFS共4个模式预报的0~72 h地面、高空风预报进行多模式集成，得到以下几点结论:

(1) ACEKF能够进一步减小风场预报的误差，提高预报技巧，在纬向风、经向风、全风速预报上均有体现。

(2) 从风场预报结果来看，无论是对地面10 m风预报还是高空风预报，ACEKF对经向风预报的改进效果都要优于纬向风预报，在预报RMSE和ACC上都有反映。

(3) ACEKF对高空风场预报的改进效果要优于地面风场，对高空风速预报的改进率可达53%左右，而对地面风速预报的改进率只有约20%。

(4) 随着预报时效延长，风场预报误差增大，但ACEKF方法对风场预报改进效果更为明显。

致谢：本文的结果是在南京信息工程大学高性能计算中心计算获得的，在此表示由衷感谢！