引言

2012年国家气象中心将基于中尺度数值模式CMA-MESO开发的区域台风模式系统CMA-TYM投入业务运行。近些年来检验表明，该系统120小时内路径强度预报性能接近国际水平，在业务应用中具有重要参考价值。但与此同时，CMA-TYM在进一步提高其预报能力方面遇到了诸多技术难题，一个最主要的困难是如何提高初始台风涡旋质量。虽然存在丰富的、时空密集的卫星探测数据，但受云和降水污染，这些资料并不能被分析系统有效吸收和同化。同时，受限于传统变分同化技术局限性，部分台风探测数据同化反而会对模式预报产生负面影响(Aberson, 2008)。

进入21世纪，一种引入集合预报扰动表达流依赖背景误差协方差的混合变分同化方案被发展起来(Hamill and Snyder, 2000；Lorenc，2003；Etherton and Bishop, 2004；Wang et al，2007；Wang，2010)，相比于传统方案使用气候统计(静态)背景误差参数，混合方案将集合预报扰动引入变分同化系统，显著改善背景误差协方差对实时天气系统描述能力，因而对观测数据信息的提取和传播，更符合实际天气系统分布特征。科学研究(Wang et al，2008a; 2008b；Buehner et al，2010a; 2010b；Zhang and Zhang, 2012; Zhang et al, 2013)和业务应用(Clayton et al, 2013；Bonavita et al, 2012; Wang, 2011; Wang et al, 2013；Kleist and Ide, 2015)都表明，混合变分同化方案会明显提高分析场质量及模式预报水平。随着技术成熟，混合变分同化方案也开始应用于台风模拟研究(Wang, 2011；Hamill et al，2011；Li et al, 2012)取得不错预报效果。

因此，在CMA-TYM 3DVar基础上，本文设计发展了通过三维Alpha控制变量引入集合预报扰动(隐式流依赖背景误差协方差表达)的混合En3DVar同化方案。然后利用单点台风中心气压数据进行测试，验证En3DVar方案对观测信息的提取和传播，是否与集合预报扰动统计的背景误差协方差特征相符合，以及形成的分析增量是否与实际台风环流分布及动力学属性相匹配。最后基于新建立CMA-TYM En3DVar系统进行台风个例试验，来分析其改进台风初始结构方面的能力，以及提高模式路径和强度预报方面的效果。

1 CMA-TYM 3DVar同化系统

CMA-TYM衍生于中国气象局自主研发的新一代全球与区域同化预报系统GRAPES(Global/Regional Assimilation and Prediction System)，是一个全可压非静力有限差分格点模式(薛纪善等，2008；陈德辉等，2012)。水平方向为经纬网格点球面坐标，垂直方向为高度地形追随坐标。主要特点包括：模式预报变量在水平方向采用Arakawa-C跳点格式，垂直方向采用非均匀Charney-Philips跳层格式，时间上采用半隐式-半拉格朗日差分方案。CMA-TYM是一个覆盖西北太平洋、南海和部分东亚大陆的区域台风数值模式系统(张进等，2017；麻素红等，2018; 麻素红，2019；麻素红和陈德辉，2018)。水平分辨率为0.12°，垂直方向为50层，模式层顶约为33 000 m，参考大气采用水平平均廓线。模式物理过程包括(郭云云等，2015；聂皓浩等，2016；郑晓辉等，2016)：包含水汽、雨、雪、云水、云冰、霰的WSM6显式微物理方案、YSU边界层方案、Monin-Obukhov近地面层方案、Goddard短波辐射、RRTM长波辐射，陆面过程采用SLAB热量扩散方案。另外，考虑0.12°分辨率不能完全描述台风对流特征，Meso-SAS积云对流参数化方案(Pan et al, 2014)也考虑在内。

针对CMA-MESO发展的CMA-TYM 3Dvar系统(马旭林等，2009；张华等，2004；庄世宇等，2005；庄照荣等，2006)，其变量水平、垂直分布与模式完全一致。虽然CMA-TYM为非静力模式，预报变量包括水平和垂直风、温度、比湿、无量纲气压(Exner函数)、云水等。但考虑到观测资料属性和变分同化可操作性，3DVar选取水平风(u, v)、位温θ、比湿q、无量纲气压π作为同化分析变量，其中质量场变量：无量纲气压π或位温θ只能二选一(本文选取了无量纲气压π)。

2 混合En3DVar同化方案

以一种简单形式，用权重平均(集合预报扰动统计的和气候统计的背景误差协方差)后的背景误差协方差替换3DVar目标函数中相应项，就可以获得混合En3DVar同化方案直接表达公式：

$ \begin{array}{l} \;\;\;\;J({\mathit{\boldsymbol{x}}^\prime }) = \frac{1}{2}{({\mathit{\boldsymbol{x}}^\prime })^{\rm{T}}}{\left({{\beta _1}\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} + {\beta _2}\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}}} \right)^{ - 1}}{\mathit{\boldsymbol{x}}^\prime } + \\ \frac{1}{2}{[\mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^\prime } + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}[\mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^\prime } + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}} \end{array} $

(1)

其中

$ \begin{array}{l} \;\;\;\;\;\;\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} = \sum\limits_{\tau = 1}^m {\mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }}} {(\mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }})^{\rm{T}}}\\ \mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }} = \frac{1}{{\sqrt {m - 1} }}(\mathit{\boldsymbol{x}}_\tau ^{\rm{e}} - \frac{1}{m}\sum\limits_{\pi = 1}^m {\mathit{\boldsymbol{x}}_\tau ^{\rm{e}})} \\ \;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{x}}^\prime } = \mathit{\boldsymbol{x - }}{\mathit{\boldsymbol{x}}^{\rm{b}}}\\ \;\;\;\;\;\;\;\;\;\;{\beta _1} + {\beta _2} = 1 \end{array} $

(2)

式中：x^b表示分析状态变量x先验估计值(背景场)，x^′为x相对于先验估计的分析增量。y^o代表观测信息向量，对应观测误差协方差矩阵为R。H表示将模式空间分析状态变量转换为观测空间状态变量的观测算子(如卫星辐射传输模式)。$\mathit{\boldsymbol{B}}_{\rm{C}}^{\rm{S}} $表示基于气候(历史)数据统计的背景误差协方差矩阵。$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $表示由m个实时集合预报扰动场统计的背景误差协方差矩阵。系数β₁，β₂分别控制$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $，$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $权重比例(β₁+β₂=1满足混合同化概念性定义)。实际应用中，由于集合成员数m远远小于分析状态变量维数n(m≪n)，因此$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $必然存在抽样误差，典型表现为较远距离格点间出现虚假相关。为保留$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $中那些局地相关真实性统计信息，又能抑制远距离相关虚假性统计信息，Houtekamer and Mitchell(2001)提出对$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $作用一个随物理空间距离增加而单调下降的Schur点积算子C，来实现局地化分析功能。即目标函数表达式改写为：

$ \begin{array}{l} J({\mathit{\boldsymbol{x}}^\prime }) = \frac{1}{2}{(\mathit{\boldsymbol{x}}^\prime)^{\rm{T}}}{({\beta _1}\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} + {\beta _2}\mathit{\boldsymbol{C}} \bullet \mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}})^{ - 1}}\mathit{\boldsymbol{x}}^\prime + \\ \frac{1}{2}{[\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{x}}^\prime + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}[\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{x}}^\prime + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}} \end{array} $

(3)

满足梯度为零目标函数极小化条件：

$ \begin{array}{l} {\nabla _{{x^\prime }}}J\left({{\mathit{\boldsymbol{x}}^\prime }} \right){\rm{ = }}{\left({{\beta _1}\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} + {\beta _2}\mathit{\boldsymbol{C}} \bullet \mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}}} \right)^{ - 1}}{\mathit{\boldsymbol{x}}^\prime } + \\ \;\;\;{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}[\mathit{\boldsymbol{H}}({x^\prime } + {x^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ] = 0}} \end{array} $

(4)

$ \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}^\prime } = \mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^\prime } + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^{\rm{b}}}) $

(5)

分析增量场最优解为：

$ \begin{array}{l} {\mathit{\boldsymbol{x}}^{\begin{array}{*{20}{l}} \prime \end{array}}} = {[{({\beta _1}\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} + {\beta _2}\mathit{\boldsymbol{C}} \bullet \mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}})^{ - 1}} + {\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{H}}]^{ - 1}} \times \\ \;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}[\mathit{\boldsymbol{y}}{\rm{^\circ }} - \mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^{\rm{b}}})] \end{array} $

(6)

尽管可以采用各种形式的梯度下降算法，但上式直接求解仍然面临着超大矩阵$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $表达问题，目前资源条件下无法显式计算。

通过引入扩展控制变量α=(α₁, …, α_m)^T，Lorenc(2003)以一种巧妙方式获得了混合En3DVar同化方案间接表达式：

$ \begin{array}{l} \;\;\;J({\mathit{\boldsymbol{x}}^\prime }_1, \mathit{\boldsymbol{a}}) = \frac{1}{{2{\beta _1}}}{({\mathit{\boldsymbol{x}}^\prime }_1)^{\rm{T}}}{(\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}})^{ - 1}}({\mathit{\boldsymbol{x}}^\prime }_1) + \\ \;\;\;\;\;\;\;\;\;\frac{1}{{2{\beta _2}}}\sum\limits_{\tau = 1}^m ({\mathit{\boldsymbol{a}}_\tau }{)^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}{\mathit{\boldsymbol{a}}_\tau } + \\ \frac{1}{2}{[\mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^\prime } + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}[\mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^\prime } + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}} \end{array} $

(7)

在应用相同局地化矩阵C条件下, 上式与直接表达式(3)是等价的(Wang et al，2007)。式(7)分析增量解为：${\mathit{\boldsymbol{x}}^\prime } = {\mathit{\boldsymbol{x}}^\prime }_1 + \sum\limits_{\tau = 1}^m ({\mathit{\boldsymbol{a}}_\tau } \bullet \mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }}) $。可以看出，由$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $贡献的那部分分析增量实质是集合预报扰动的线性权重组合$\sum\limits_{\tau = 1}^m ({\mathit{\boldsymbol{a}}_\tau } \bullet \mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }}), {\mathit{\boldsymbol{a}}_\tau } $表示第τ个预报扰动场权重系数。在方案具体实现过程中，根据局地化矩阵C将背景误差协方差由全局影响限制为局地影响功能性定义，可定义一个(类)高斯形状三维空间分布函数来模拟完成，通过设置特征长度参数值(Gaspari and Cohn, 1999)就可以将协方差空间相关性截断在特定格点距离范围内。

可以看出，只要选择合适局地化矩阵模拟方法，基于扩展控制变量技术的混合En3DVar方案很容易在传统3DVar方案上融入实现(具体实现细节见下节)。

3 混合En3DVar同化方案实现

在CMA-TYM 3DVar方案实现过程中，为避免超大矩阵$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $求逆运算(马旭林等，2009；张华等，2004；庄世宇等，2005)，采用如下预调节变换技术：根据$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $对称半正定实矩阵属性，将其分解为$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} = \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{U}}^{\rm{T}}} $形式，然后通过引进新控制变量$\mathit{\boldsymbol{v = }}{\mathit{\boldsymbol{U}}^{ - 1}}{\mathit{\boldsymbol{x}}^\prime } $，将目标函数变换为基于υ的表达式：

$ \begin{array}{l} J(\mathit{\boldsymbol{v}}) = \frac{1}{2}{\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{v + }}\frac{1}{2}{[\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{Uv + }}{\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}}^{\rm{T}}} \times \\ \;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{R}}^{ - 1}}[\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{Uv + }}{\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}} \end{array} $

(8)

接下来为消除分析状态变量(π, u, v, q)之间相关，通过物理算子U_p将其变换为互不相关分析变量：流函数ψ、势函数χ^u(与ψ不平衡部分)、π^u(与ψ不平衡部分)、比湿q。然后假设ψ，χ^u，π^u，q自身空间相关结构在水平和垂直方向上具有可分离属性，利用垂直模态映射算子U_v与水平滤波算子U_h的Kronecker积来共同模拟实现。经过上述系列变换，目标函数及其梯度计算就转为对新控制变量υ的迭代求解，分析增量x^′的计算表达式为：${\mathit{\boldsymbol{x}}^\prime } = \mathit{\boldsymbol{Uv = }}{\mathit{\boldsymbol{U}}_{\rm{p}}}{\mathit{\boldsymbol{U}}_{\rm{V}}}{\mathit{\boldsymbol{U}}_{\rm{h}}}\mathit{\boldsymbol{v}} $。

相比于传统3DVar方案，混合En3DVar方案目标函数表达式[式(7)]的求解变量从x^′变成(x₁^′, α)，方程右端增加了关于α集合背景项$\sum\limits_{\tau = 1}^m ({\mathit{\boldsymbol{a}}_\tau }{)^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}{\mathit{\boldsymbol{a}}_\tau } $。可以看出，该增加项与方程右端第一项${({\mathit{\boldsymbol{x}}^\prime })^{\rm{T}}}{(\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}})^{ - 1}}{\mathit{\boldsymbol{x}}^\prime }_1 $有诸多相似之处(同样面临与$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $同维超大矩阵C求逆运算)。因此可以借鉴传统方案中$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} = \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{U}}^{\rm{T}}} $分解形式来模拟构建局地化矩阵C。根据C功能定义，如果假设三维空间局地化函数在所有格点具有相同分布形状，且可以分解为$\mathit{\boldsymbol{C = U}}_{\rm{v}}^{\rm{a}}\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}}{(\mathit{\boldsymbol{U}}_{\rm{v}}^{\rm{a}}\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}})^{\rm{T}}} $形式($\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}}, \mathit{\boldsymbol{U}}_{\rm{v}}^{\rm{a}} $分别代表水平、垂直方向上的局地化算子)，那么通过引进新控制变量$\mathit{\boldsymbol{w = }}{({\mathit{\boldsymbol{w}}_1}, \cdots, {\mathit{\boldsymbol{w}}_m})^{\rm{T}}} $，令${\mathit{\boldsymbol{w}}_\tau } = {(\mathit{\boldsymbol{U}}_{\rm{v}}^{\rm{a}}\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}})^{ - 1}}{\mathit{\boldsymbol{a}}_\tau }, \tau = 1, 2, 3, \cdots, m $，式(7)右端中集合背景项就变换为关于w的项$ \frac{1}{{2{\beta _2}}}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}}$。相应的，目标函数表达式变换为：

$ \begin{array}{l} J(\mathit{\boldsymbol{v}}, \mathit{\boldsymbol{w}}) = \frac{1}{{2{\beta _1}}}{\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{v + }}\frac{1}{{2{\beta _2}}}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w + }}\\ \frac{1}{2}{[\mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^\prime } + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}[\mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^\prime } + {\mathit{\boldsymbol{x}}^{\rm{b}}}) - \mathit{\boldsymbol{y}}{\rm{^\circ ]}} \end{array} $

(9)

x^′的计算表达式为：

$ {\mathit{\boldsymbol{x}}^\prime } = {\mathit{\boldsymbol{U}}_{\rm{p}}}{\mathit{\boldsymbol{U}}_{\rm{v}}}{\mathit{\boldsymbol{U}}_{\rm{h}}}\mathit{\boldsymbol{v + }}\sum\limits_{\tau = 1}^m (\mathit{\boldsymbol{U}}_{\rm{v}}^{\rm{a}}\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}}{\mathit{\boldsymbol{w}}_\tau } \bullet \mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }}) $

(10)

目标函数及其梯度的计算就转换为对新控制变量(υ, w)的迭代求解。

在具体实现过程中，水平方向局地化算子$\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}} $可利用U_h中滤波算法来实现(高斯形状局地化模型)；垂直方向局地化算子$\mathit{\boldsymbol{U}}_{\rm{v}}^{\rm{a}} $可通过先设定一个高斯形状垂直局地化模型，然后利用U_v中正交特征分解算法来实现。最后，通过设定相应水平与垂直局地化特征长度参数值，局地化矩阵C就可以利用$\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}} $与$\mathit{\boldsymbol{U}}_{\rm{v}}^{\rm{a}} $的Kronecker积获得。具体算法步骤为：

1) 读取背景场格点数据x^b及其相关气候背景误差协方差矩阵$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $统计数据；

2) 读取m个集合成员预报扰动值$\mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }}, \tau = 1, 2, 3, \cdots, m $；

3) 读取各种类型观测资料y^o并设定相应观测误差；

4) 计算新息向量：$ \mathit{\boldsymbol{d = y}}{\rm{^\circ - }}\mathit{\boldsymbol{H}}({\mathit{\boldsymbol{x}}^{\rm{b}}})$；

5) 设置分析控制变量(υ, w)迭代初值，其中w由m个向量场${\mathit{\boldsymbol{w}}_1}, {\mathit{\boldsymbol{w}}_2}, \cdots, {\mathit{\boldsymbol{w}}_m} $组成；

6) 计算基于控制变量(υ, w)表达的目标函数值；

a) 计算目标函数中背景项值：$ \frac{1}{{2{\beta _1}}}{\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{v + }}\frac{1}{{2{\beta _2}}}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}}$；

b) 计算增量x^′值：$ {\mathit{\boldsymbol{x}}^\prime } = {\mathit{\boldsymbol{U}}_{\rm{p}}}{\mathit{\boldsymbol{U}}_{\rm{v}}}{\mathit{\boldsymbol{U}}_{\rm{h}}}\mathit{\boldsymbol{v + }}\sum\limits_{\tau = 1}^m (\mathit{\boldsymbol{U}}_{\rm{v}}^{\rm{a}}\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}}{\mathit{\boldsymbol{w}}_\tau } \bullet \mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }})$；

c) 计算目标函数中观测项值：$\frac{1}{2}{(\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}^\prime } - \mathit{\boldsymbol{d}})^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}(\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}^\prime } - \mathit{\boldsymbol{d}}) $；

7) 计算目标函数关于分析控制变量(υ, w)梯度值；

a) 计算目标函数关于υ梯度值：$\frac{1}{{{\beta _1}}}\mathit{\boldsymbol{v + }}{({\mathit{\boldsymbol{U}}_{\rm{h}}})^{\rm{T}}}{({\mathit{\boldsymbol{U}}_{\rm{v}}})^{\rm{T}}}{({\mathit{\boldsymbol{U}}_{\rm{P}}})^{\rm{T}}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}(\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}^\prime } - \mathit{\boldsymbol{d}}) $；

b) 计算目标函数关于w梯度值[${(\mathit{\boldsymbol{U}}_{\rm{e}}^{\rm{a}})^{\rm{T}}} $表示$ \sum\limits_{\tau = 1}^m {\left({{\mathit{\boldsymbol{a}}_\tau } \bullet \mathit{\boldsymbol{x}}_\tau ^{{{\rm{e}}^\prime }}} \right)} $矩阵算子转置]：

$ \frac{1}{{{\beta _2}}}\mathit{\boldsymbol{w + }}{(\mathit{\boldsymbol{U}}_{\rm{h}}^{\rm{a}})^{\rm{T}}}{(\mathit{\boldsymbol{U}}_{\rm{v}}^{\rm{a}})^{\rm{T}}}{(\mathit{\boldsymbol{U}}_{\rm{e}}^{\rm{a}})^{\rm{T}}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}(\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}^\prime } - \mathit{\boldsymbol{d}}) $

8) 基于获得的梯度值，计算梯度下降方向和最优步长，并更新控制变量(υ, w)迭代值。后重复计算目标函数和目标函数梯度值(步骤6和步骤7)，直至达到收敛标准；

9) 计算最终分析值：x^a=x^b+x^′。

计算资源方面，混合En3DVar方案利用的是三维α控制变量，在传统3DVar方案分析状态变量总维数为n前提下，会额外增加n×m维分析状态变量空间，且随着集合预报成员数目m增加，空间还在增大，这对计算资源硬件需求是一个比较大的挑战。不过，在采用并行计算环境下，这个需求会随着并行核增加而变得相应容易满足。

4 集合预报扰动数据来源

本试验所需集合预报扰动场数据，源自96个成员的全球(谱模式)集合预报系统T574-EnKF^*(Whitaker et al, 2008；Wang et al, 2013；Kleist and Ide, 2015)的，通过CMA-TYM积分获得。具体方案为，首先基于T574-EnKF系统输出的分析场集合，利用降尺度技术获得CMA-TYM初值集合。然后，考虑En3DVar分析更多关注台风内中小尺度信息提取和传播，而降尺度形成的初值仅包含全球模式可分辨的(较粗分辨率)天气尺度信息，因此需通过CMA-TYM模式短时间积分，来获得具有中小尺度信息的集合预报场(Pu et al, 2016; Lu et al, 2017)。

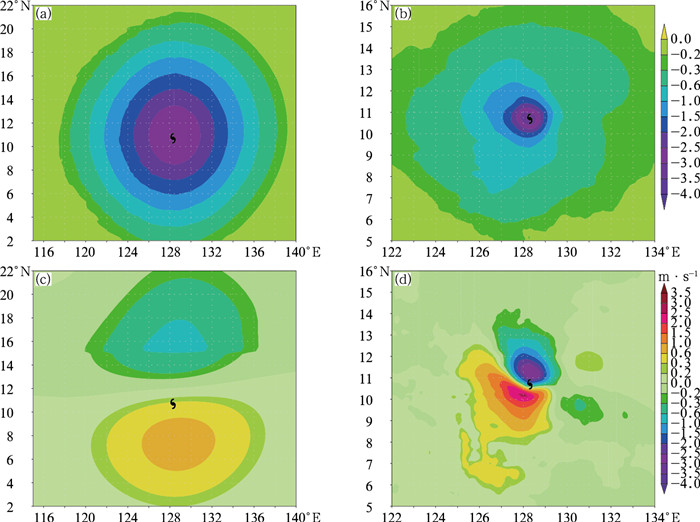
图 1显示的是1306号台风温比亚(Rumbia)形成初期，基于96个集合预报扰动场统计表达的：背景场状态变量π, u, v, q在850 hPa层上误差(集合预报离散度)分布信息。从图中可以看出，各个状态变量误差水平分布范围，具有明显台风环流特征：无量纲气压(图 1a)和风场u(图 1b)、v(图 1c)都显示越靠近台风中心，误差值越大，并且呈现闭合环流形状。很明显，这些状态变量误差分布与模式对台风系统描述能力吻合，台风内部模拟准确程度要远低于外围环流准确程度。同时，图 1d显示的比湿q也符合台风降雨云系分布的螺旋形状(螺旋雨带降水模拟也是常见台风模拟误差来源)。

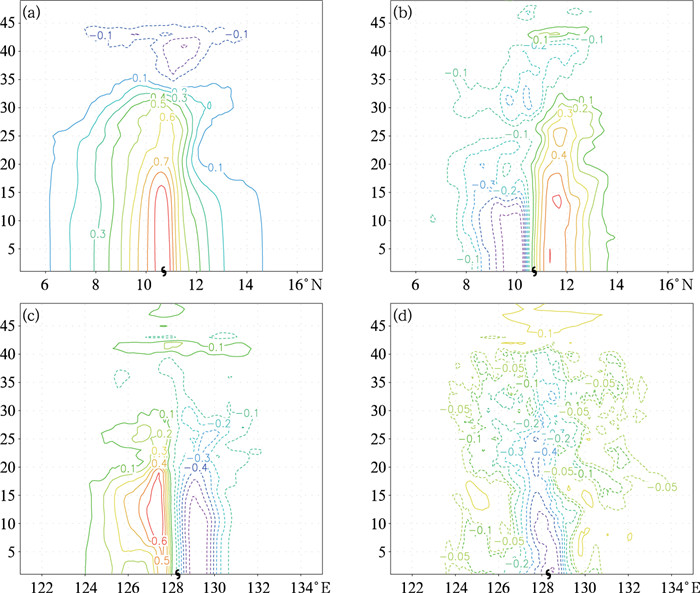
除误差分布信息外，集合预报扰动统计的$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $还有一个巨大优势：隐式包含分析状态变量之间的局地相关，并且这种相关是随着实际天气系统分布区域而不断变化。由于这种相关性通过协方差矩阵非对角线部分体现，维数巨大，难以展示。这里配合即将展开的单点台风中心气压数据试验，选取台风中心气压误差与其他分析状态变量误差在垂直方向(沿台风中心的经、纬向剖面)的统计相关来展示其部分属性，结果如图 2所示。

从图 2中可以看出，在垂直方向上，台风中心气压误差与中低层无量纲气压π误差存在正相关，与高层存在负相关，这与台风环流中低层气旋辐合、高层反气旋辐散结构相吻合。同时台风中心气压误差与风速u, v分量误差在不同象限区域显示着有正有负的相关，并且正负值所在区域与台风风压动力学平衡关系相匹配。

由此可见，相比于传统3DVar方案将$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $假设为均匀、各向同性属性，由集合预报扰动统计表达的$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $矩阵中，分析状态变量误差不仅在台风区域有显著差异，而且这种差异还符合模式对台风系统模拟的精确度分布。同时，状态变量之间误差相关也与台风动力属性相匹配，明显具有表达实时台风系统背景误差分布特征。

5 台风中心气压的单点同化分析

依据前文算法步骤，本文发展实现了混合En-3DVar同化方案。为了验证其合理性和正确性，选取单点台风中心气压数据进行同化测试，并将分析结果和传统3DVar方案进行了对比分析。

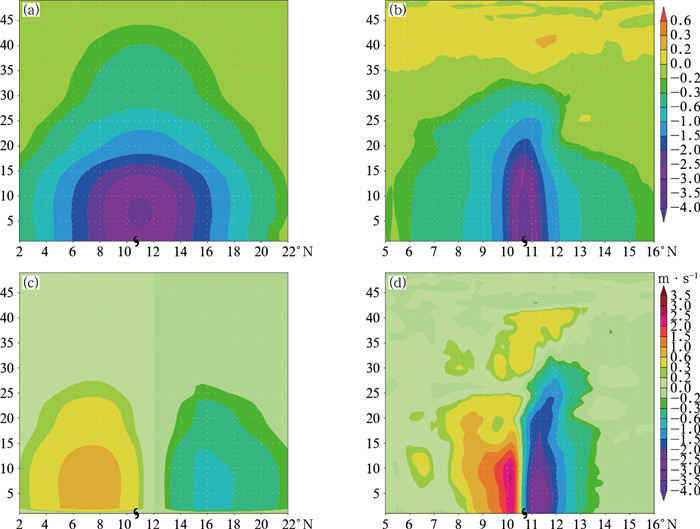
图 3展示了两种同化方案形成π, u增量在模式表面层上对比图。从π来看，混合En3DVar方案分析增量(图 3b)分布范围相对较小，局限于台风环流区域，但数据量级更大(暗示分析后台风气压会变得更深)；而传统3DVar方案分析增量分布范围明显偏大(图 3a)，远超出实际台风环流区域。从u对比来看，混合En3DVar方案分析增量(图 3d)形成了一个气旋性环流分布结构，且非对称特征明显，数值最大能达到±3 m·s^-1；而传统3DVar方案分析增量(图 3c)不但数值偏小(仅在±1 m·s^-1值之内)，而且影响范围也超出了台风环流区域。同样地，从沿台风中心π, u增量垂直剖面对比图中(图 4)也可以看出：相比于传统3DVar方案，混合En3DVar方案分析增量分布区域与实际台风范围更加匹配，且数值较大，尤其在u, v增量上表现明显。除此之外，由于传统3DVar方案$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $中假设气压误差与比湿误差互不相关，气压增量不会引起比湿变化，而混合En3DVar方案引入的$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $，直接表达各个分析变量之间交叉相关，因而气压增量会明显引起比湿增量出现(图略)，这从另外一个侧面也反映出混合En3DVar方案在变量相关属性方面存在明显优势。

从技术层面来说，传统3DVar方案在模拟$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $时，为解决各分析状态变量之间误差相关，施加了物理平衡约束算子，它提取传播的分析增量，主要体现的是模式格点对大气演变描述中最主要贡献天气尺度，如气压场与风场地转或平衡方程形式的物理相关。同时，为解决各个非平衡变量(施加物理约束后)自协方差矩阵维数巨大问题，对其进行了水平均匀，各向同性假设。因而这样条件下模拟的$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $只是一个“平均”天气状态简化体现，很难将其与具体每个实时天气尺度系统联系起来。而混合En3DVar方案吸收的$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $，直接表达了分析状态变量误差的自相关和交叉相关，并且这种相关是利用描述实时天气系统的集合预报成员统计而来，因而在时间、空间分布属性上和背景场表征的天气尺度系统紧密联系在一起。

6 实际观测资料同化效果分析

基于新建立的CMA-TYM En3DVar系统，本文进行了实际观测资料同化试验。试验模式区域范围为5°~49°N、93°~156°E，覆盖部分大陆和太平洋、南海的东南亚地区，水平格点数为531×451。试验时间是2013年6月28日12：00 UTC(1306号台风温比亚生成初期)。试验冷启动数据来自T1148-GSI^*全球数值预报模式系统(提供初始场和侧边界)和T574-EnKF全球集合预报系统(提供集合预报场)。同化所需观测资料来自实时数值预报业务常规观测资料集，包括探空、地面站、洋面浮标和船舶资料、飞机报和云导风、洋面风等。除此之外，由预报员实时分析的台风中心海平面气压也作为常规资料进入了分析同化系统。

En3DVar方案实际应用中，有三个待定参数。一个是$\mathit{\boldsymbol{B}}_{\rm{c}}^{\rm{s}} $(或$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $)的权重系数β₁(或β₂)，参照Wang et al(2013)做法，本文试验选取β₁=0.2。另外两个参数是局地化矩阵C在水平和垂直方向上特征长度(限制观测信息水平和垂直传播范围)。这里垂直方向局地化模型采用是高斯型函数，通过经验正交函数变换实现，即任意两个模式层之间的相关系数定义为：

$ y({k_1}, {k_2}) = {\rm{exp(- }}{{\rm{d}}^2}/{L^2}) $

(11)

式中：d为模式层k₁和k₂的几何距离，L为垂直局地化特征长度。为获得最优取值，本文对100~1 000 km范围内的水平局地化特征长度进行了测试，最终发现在260 km情况下会显示非常合理的分析增量。L也采取了类似的测试确定取值为36。

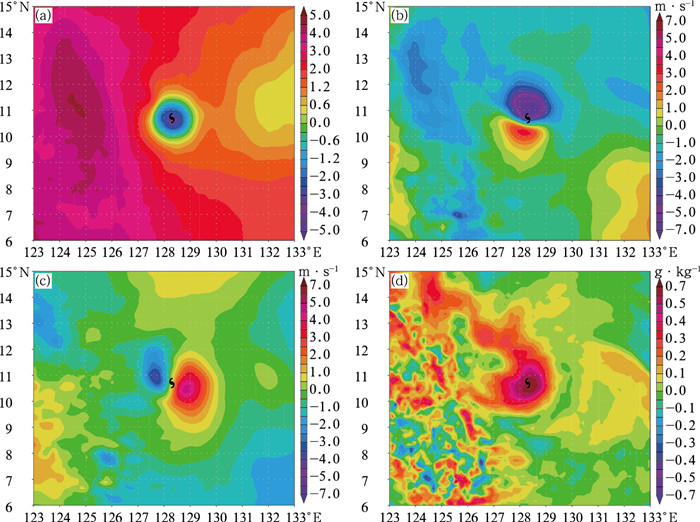
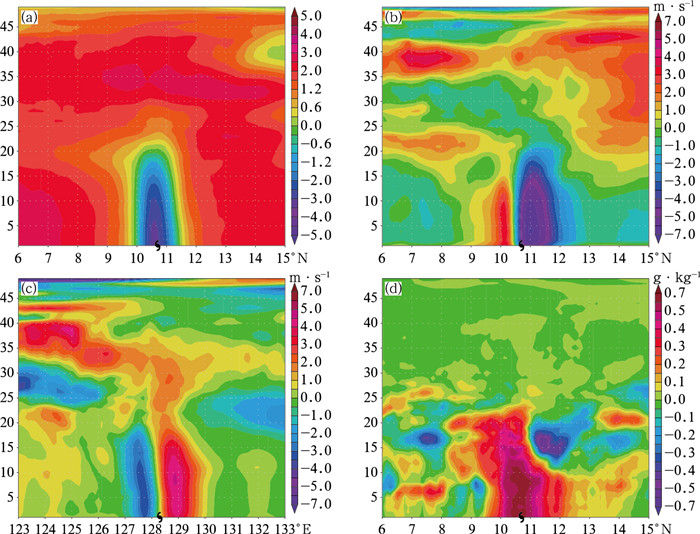
图 5、图 6显示的是En3DVar系统同化观测资料后，状态变量π, u, v, q在水平(地面层)和垂直方向上(沿台风中心经纬向剖面)的增量分布。从π来看，水平方向上(图 5a)在台风中心周围形成一个气压增量负值区；垂直方向上(图 6a)，气压增量呈现中低层有效加深，高层反气旋弱增强的分布形式，匹配台风低层辐合高层辐散的质量场属性。从u，v分析增量来看，图 5b和5c显示在水平方向上，伴随着气压场加深，围绕台风中心形成明显气旋性环流。实际数据显示增量分布并不均匀，东部、北部区域更大一些，呈现明显非对称加深结构。图 6b和6c显示在垂直方向上，u，v分析增量紧密围绕台风中心，且遍布整个中低层，同样非对称特征也非常明显。从湿度q分析增量来看, 水平方向上(图 5d)其分布区域与台风环流螺旋状云系特征紧密匹配, 垂直方向上(图 6d)，在台风中心附近产生的分析增量遍布眼区及周围环流区域(看似“杂乱”的增量分布实际和台风中小尺度对流区域十分吻合)。

诊断结果显示，台风环流区域内仅有中心气压、有限云导风资料被同化吸收。这就说明，台风区域内分析增量都是基于这些观测信息，通过$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $中变量自身相关和交叉相关属性获得(这一点在中下层湿度分析增量上体现的尤其明显)。同时，由于$\mathit{\boldsymbol{P}}_{\rm{e}}^{\rm{f}} $的存在，分析增量的分布范围、数值大小和实际台风动力平衡关系、环流区域也十分匹配。当然，如果集合预报扰动成员不能准确描述背景场台风误差信息，那么同化阶段就不会提取出合理观测资料信息且有效传播出去，因此也不会形成匹配实际台风分布区域和动力学特征的分析增量。

7 台风预报试验

为评估混合En3DVar方案对台风路径强度预报影响，基于CMA-TYM模式系统对1306号台风温比亚进行了预报试验。试验分两种方案进行，一种为3DVar方案，另一种为En3DVar方案，即分别应用3DVar、En3DVar形成的分析场进行模式积分预报。运行方案为，在“温比亚”生命史期间，每天选取00 UTC和12 UTC时刻进行同化分析和预报试验。预报所需数据同样来自全球模式系统T1148-GSI和全球集合预报系统T574-EnKF。

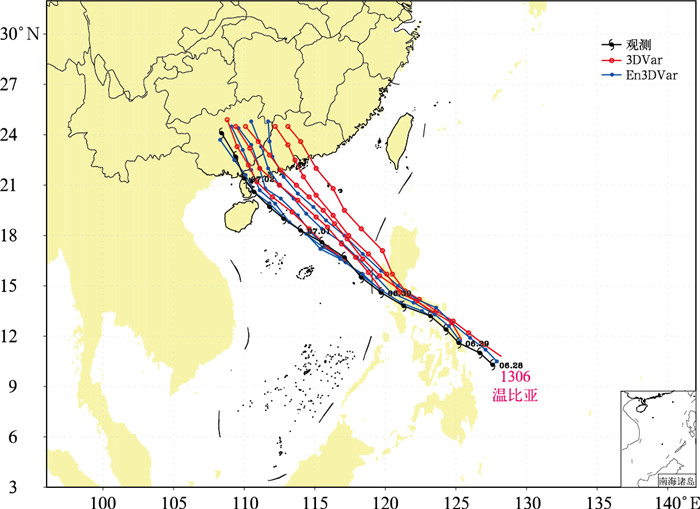
图 7显示在“温比亚”生命史期间，CMA-TYM模式分别应用3DVar系统和混合En3DVar系统产生的预报路径和实际观测路径情况。从图中可以看出，两种方案对36 h内台风路径预报效果差别不大，但是对长时效的48~96 h预报，混合En3DVar方案表现较好，特别在“温比亚”生命史早期几个预报时刻，相比于3DVar方案，混合En3DVar方案产生的预报路径更趋向于实际观测，有效纠正其右偏趋势。而在“温比亚”生命史后期，尽管混合En3DVar方案优势表现的并不如前期那么明显，但是实际检验数据显示，其路径预报还是好于3DVar方案。

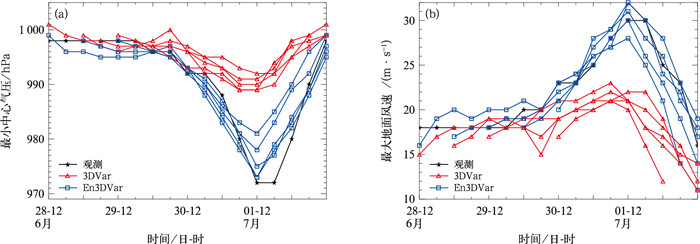
从强度预报检验来看(图 8)，无论是中心气压还是近地面最大风速，混合En3DVar方案产生的预报结果都好于3DVar方案。特别在“温比亚”生成初期，混合En3DVar方案就提前72 h准确预报出其在近海快速增强爆发过程，并且这种表现一直延续贯穿后期所有预报时刻，直至台风登陆消亡。反观3DVar方案，尽管也预报描述出台风后期增强过程，但是这个趋势缓慢且不明显，而且在数据量级(气压与风速大小)上也和实际观测相差甚远。

8 结论与讨论

基于CMA-TYM 3DVar同化系统，本文设计发展了通过三维Alpha控制变量引入集合预报扰动(隐式流依赖背景误差协方差表达)的混合En3DVar同化方案。在匹配现有3DVar方案算法流程的基础上，具有计算高效、易于实现的特点。

单点台风中心气压数据同化测试表明，相比于3DVar方案，混合En3DVar方案形成的气压场分析增量明显分布于台风环流区域内，风场分析增量结构上更加匹配台风动力学特征：数值量级上更大且非对称结构明显。更重要的是，气压分析增量会导致湿度场(比湿)增量的出现(传统3DVar方案假设两者是不相关的)。由此可见，在集合预报扰动统计表达的背景误差协方差能准确表征背景台风误差条件下, 台风内部资料的同化就能够获得与台风环流范围相匹配的分析增量, 并且这些分析增量内部之间的相关平衡符合实时台风动力学特征。

应用常规观测资料的同化试验显示, 混合En3DVar方案能有效提取台风区域内零散观测信息，并且这部分信息会按实时台风特征向周围传播出去，从而影响分析场台风结构、强度变化。这使得通过有限观测资料信息同化改进初始台风涡旋质量成为可能。同时，台风个例预报试验表明，无论是路径还是强度，混合En3DVar产生的预报结果都要明显好于3DVar预报结果。

需要指出的是，混合变分同化方案形成的分析增量实质是多个集合成员预报扰动的线性组合(被限制在集合成员扰动所张的子空间)，其同化效果与集合预报扰动统计表达的背景误差协方差的准确程度密切相关。只要有限集合预报扰动成员能够抓住实时天气系统在模式格点尺度体现的主要误差特征，那么基于其统计所得的误差协方差矩阵就具有实时天气系统的流依赖型表达能力。