2. 北京市气象台, 北京 100089
2. Beijing Meteorological Observatory, Beijing 100089
风的预报是精细化预报产品的重要组成部分,也是政府和公众重点关注的预报要素之一。复杂地形条件下,风场微尺度的高度非均一性特征(刘敏等,2010),对估计潜在风能源生产、建筑发展规范和评估及与潜在大风有关的灾害(杨璐等,2018a;2018b)非常重要。2022年北京冬季奥运会(简称冬奥会)(Chen et al, 2018)举办时间临近,冬奥会雪上项目赛区地处山地,地形比较复杂,而风的预报结果对冬奥会室外赛事至关重要,大风天气可能会导致冬奥会多项赛事及赛事运维服务都受到明显影响。
目前大多数风场预报产品,都来自于区域或全球尺度数值天气预报模式,因其拥有丰富的物理参数化方案,能很好地捕捉中尺度天气事件,模拟气象场的平均状态;但基于动力过程的预报本身存在初始条件偏差和模式自身的不确定性,使得数值模式目前还不具备捕捉大气小尺度特征和微尺度湍流运动能力(Winstral et al, 2017)。复杂地形下风场预报的准确率也一直是风能研究和气象研究领域的难点和重点(程雪玲等,2015;李艳等,2015)。
中国气象局北京快速更新循环数值预报系统(CMA北京模式,CMA-BJ),是目前华北区域的中尺度区域数值预报业务系统,采用快速更新循环同化预报方式运行,以欧洲中期天气预报中心(ECMWF)的全球预报为背景场(以下简称EC)冷启动,同化包括地面、探空、飞机报、地基GPSZTD等在内的观测资料,每3 h滚动更新预报(范水勇等, 2009; 童文雪等, 2018)。CMA-BJ模式输出的近地面风场,是基于模式地形,通过使用有效的(地形)粗糙度和边界层方案,对复杂地形的影响进行参数化设置,但实际上这种参数化方案只是有效模拟了天气尺度系统下的地形拖曳。而在复杂地形下,许多站点位于山区,狭窄峡湾、山谷众多,风场在微尺度上动态及非线性的流动特性(Wood, 2000)都可能对局地风产生极大影响。
目前,使用动力降尺度方法(Lee and Lundquist, 2017;刘郁珏等, 2019)来获取更高分辨率风场产品及风速偏差订正的尝试。虽然在一些特定的个例测试中已取得了一些成功,但由于缺乏批量检验以及计算资源需求过大的原因,对于模式参数方案的特定配置还没有被纳入常规的模式预报框架中(Wagenbrenner et al, 2016),暂时无法满足精细化预报的业务需求。能够捕捉天气系统精细结构信息的高时空分辨率综合气象观测资料、多源实况融合分析技术以及多尺度数值预报模式的快速发展和支撑,为精细化网格预报发展提供了坚实的基础和必要的前提条件(金荣花等,2019)。在模式预报基础上利用实况观测资料进行空间和时间上的统计降尺度和偏差订正(曹勇等,2016; Michelangeli et al, 2009; Curry et al, 2012; 江滢等, 2013; Winstral et al, 2017; 于丽娟等,2017)是非常必要和有效的,而且相比动力降尺度方法计算量更小。但目前基于统计订正的研究主要是针对低海拔到中海拔高度地区的低风速区域,或者只包含少量的高海拔高度地区的大风区域(Huang et al, 2015; Trubilowicz et al, 2016)。而且之前的许多研究都是基于站点的订正(Kirchmeier et al, 2014),但是,基于站点的订正具有空间局限性(Winstral et al, 2017),因此迫切需要基于整个模型网格开展偏差订正(曾晓青等,2019)。
睿图-睿思(RMAPS-RISE)系统(陈康凯等,2020),基于CMA-BJ模式和自动气象站观测资料,利用多源数据融合技术、偏差订正技术(杨璐等,2019;程丛兰等,2019;宋林烨等,2019)及高分辨率地形降尺度技术,可以实现10分钟更新、百米级空间尺度的冬奥会赛区风场临近、短时预报。睿图-睿思风场一方面能够继承CMA-BJ模式完备的参数化方案,将具有中尺度动力特征的初始风场降尺度到更精细的网格点上,并利用松弛迭代算法保持风场的质量守恒,更好地描述复杂地形特征下高分辨率格点流场的动量和能量;另一方面又能够在百米级尺度高精度地形条件下更快地吸收和融合观测资料,显著提升了复杂地形下风场的预报能力。但基于观测资料融合和地形降尺度的偏差订正技术对于风场预报能力的提升主要体现在短时临近预报时效内,6 h以后风场预报基本为地形降尺度后的数值预报结果,预报性能较CMA-BJ模式改进有限。而CMA-BJ模式在复杂地形区域对近地面风速模拟又存在较大系统性偏差,呈现出对平原、山谷风速高估及对山腰、山顶地区风速低估的现象(刘郁珏等, 2019)。Neilley and Hanson(2004)提出消除系统偏差是数值模式释用方法降低整体误差的最有效途径。
本研究综合考虑多源实况融合分析技术与复杂地形下高精度风场偏差订正技术,利用冬奥会山地赛场区域及其周边地区不同海拔高度上收集的133个自动气象站风场实况观测资料与睿图-睿思系统高精度风场预报数据相结合,利用统计偏差订正方法,获取复杂地形下133个站点1~12 h的平均系统偏差,将降尺度后的高分辨率风场利用格点偏差订正系数优化后再作为背景场融合观测资料,以实现复杂地形下不同海拔高度上高精度风场的融合订正优化,更好地捕捉局地地形对山区风场的平均影响。研究包括大量山区站点的大风天气,而且适用于整个冬奥赛区高分辨率格点场的订正。
1 资料文中所发展的统计偏差订正方法将最终应用于睿图-睿思系统冬奥会赛区百米级分辨率10 m风场预报性能的改进。睿图-睿思系统是北京城市气象研究院研发的短时临近融合预报系统,具有快速更新、资料融合、无缝隙、集合集成预报这几个重要特点。睿图-睿思系统以2022年北京冬奥会山地赛场区域及其周边地区(100 km×100 km)作为运算范围,覆盖了张家口崇礼和北京延庆海陀山这两个冬奥会重点高山赛区(图 1),目前已形成了冬奥会重点区域百米级分辨率0~12 h短时临近无缝隙精细分析和预报实时产品,数据格点分辨率为100 m,逐10 min快速更新循环,在2019—2020年冬季冬奥会测试赛和预报员冬训期间提供了支持,尤其为0~3 h的地面2 m温度、10 m风场短时临近预报提供了很好的技术支撑。
|
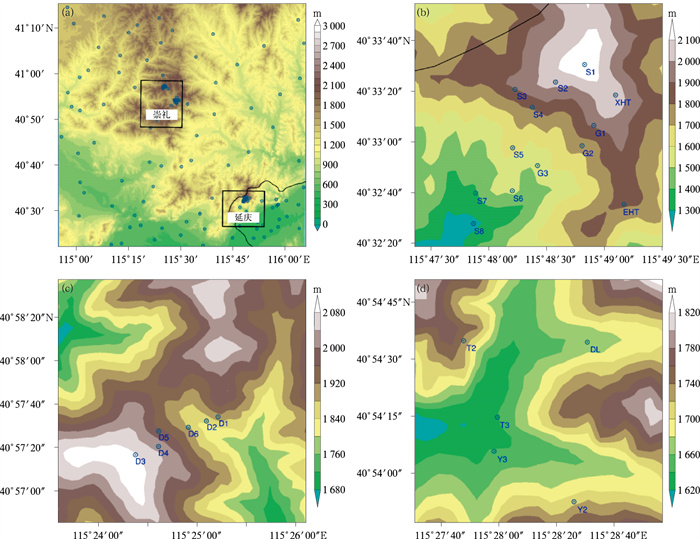
图 1 睿图-睿思系统冬奥会区域(a)、延庆赛区(b)、张家口云顶(c)和古杨树赛区(d) (图中填色为地形高度, 圆圈为赛区自动观测站位置;图 1b中S1~S8表示竞速1~8号站,G1~G3表示竞技1~3号站,XHT和EHT分别表示小海陀和二海陀站;图 1c中D1~D6表示云顶1~6号站;图 1d中Y2~Y3为越野2~3号站,T2~T3为跳台2~3号站,DL为冬两1号站) Fig. 1 The Winter Olympic Games area (a), Yanqing competition area (b), Yunding (c) and Guyangshu (d) competition areas in Zhangjiakou (The shaded area indicates terrain height, circle indicates the position of the automatic weather station; S1-S8, G1-G3, XHT and EHT indicate Jingsu 1-Jingsu 8, Jingji 1-Jingji 3, Xiaohaituo and Erhaituo in Fig. 1b respectively; D1-D6 indicate Yunding 1-Yunding 6 in Fig. 1c; Y2-Y3 indicate Yueye 2-Yueye 3, DL indicates Dongliang 1 in Fig. 1d) |
文中选取的资料包括2020年1—3月睿思系统冬奥赛区高精度风场融合预报订正技术改进前后的2 min平均10 m风场格点预报产品,以及研究范围内参与融合和用于格点偏差订正的133个自动气象站实况观测资料(图 1a),其中包括冬奥会延庆赛区13个和张家口云顶和古杨树赛区11个重点关注站点。自动气象站观测数据虽然精度高、时效性强,但也存在缺测、误测等问题。因此,文中对所用的观测资料进行了质量控制和筛选(窦以文等,2008)。资料质量控制所用的方法是:①缺测检查,剔除冬奥赛区自动气象站点缺测率超过50%的天数(如2月13—15日;2月25—26日);②时间连续性检查,剔除连续性较差(相邻两个时刻风速差大于10 m·s-1,小于0.5 m·s-1;风向变化小于10°)的站点(如2月19日竞速2);③内部一致性检查,剔除同一测站同时测得的参数不一致(风速为0,风向必须为静风;风向为静风时,风速必须为0)的观测值(如2月18日竞速2)(王伯明,2004)。
2 高精度风场偏差订正方案睿思系统风场的准确率一方面依赖于观测资料,另一方面依赖于CMA-BJ模式背景场所提供的风场准确性。风场订正包括两方面:首先利用距离反比插值方法将CMA-BJ模式地形下3 km分辨率的10 m风场产品(数值模式地形高度上的10 m风)插值到睿思更高分辨率和更精细的地形上,通过地形降尺度提升分辨率,用降尺度得到的睿思高精度地形高度上的风速(睿思高分辨率地形高度上的10 m风)去订正CMA-BJ模式本身诊断出的10 m风;然后根据实况观测资料经纬度和海拔高度信息确认观测所在位置,取出对应位置背景场的风速,剔除地形因子及水面阻力等影响以后,用观测场风场值订正背景场值,计算格点场在观测位置的误差。
也就是说,针对每个观测站,都从睿思格点中,找出一个最能代表观测站的格点,与观测站对应值作差,以反映格点数据与观测站数据的差值ΔXk,如式(1)所示:
| $ \Delta {X_k} = X_k^{{\rm{OBS}}} - X_k^{{\rm{ST}}} $ | (1) |
然后利用已知的这些差异,针对睿思系统研究范围内的每个格点,水平距离在12.5 km以内最近的n个站点,将最近n个站点的差值进行加权融合,得到该点与观测站数据的差值。站点的距离越近,其权重越大,其差值的置信度越高。对于睿思的某个格点(i, j), 它与第k个自动气象站的距离为rijk,则第(i, j)个格点的风场差分如式(2)所示:
| $ \Delta X\left({i, j} \right) = \frac{{\sum\limits_{k = 1}^n {\frac{{\Delta {X_k}}}{{r_{ijk}^2}}} }}{{\sum\limits_{k = 1}^n {\frac{1}{{r_{ijk}^2}}} }} $ | (2) |
将风场差分场ΔX(i, j)与CMA-BJ模式预报的风场XSTt0(i, j)相加就可以得到睿思的风场分析场,如式(3)所示:
| $ X_{\mathrm{ANA}}^{t_{0}}(i, j)=X_{\mathrm{ST}}^{t_{0}}(i, j)+\Delta X(i, j) $ | (3) |
但基于观测资料融合和地形降尺度的偏差订正技术对于风场模拟能力的提升主要体现在短时临近预报时效内,风场1~6 h的临近预报模块是基于融合分析场的外推预报和数值模式预报的加权平均,当预报时效ti < 6 h时,风场的计算如式(4)所示:
| $ \begin{aligned} X_{\mathrm{FORC}}^{t_{i}}(i, j)=& f_{\mathrm{T}}\left(t_{i}\right) X_{\mathrm{ANA}}^{t_{0}}(i, j)+\\ & {\left[1-f_{\mathrm{T}}\left(t_{i}\right)\right] X_{\mathrm{ST}}^{t_{i}}(i, j) } \end{aligned} $ | (4) |
式中:XFORCti(i, j)为预报时效为ti时的风场预报值,XSTti(i, j)为第ti预报时效CMA-BJ模式插值到睿思格点上初猜场的值,XANAt0(i, j)为风场分析场值,fT为权重系数,计算方法如式(5)所示:
| $ f_{\mathrm{T}}\left(t_{i}\right)=\max \left\{0, \min \left[1, 1-\left(t_{i}-2\right)\right] / 4\right\} $ | (5) |
从权重系数公式可以得出,ti为0~6 h时,预报中外推预报的权重系数从1线性递减至0。ti=3 h,权重系数降为0.75;如ti=3 h时,睿思预报风场计算公式如式(6)所示:
| $ X_{\mathrm{FORC}}^{t_{3}}(i, j)=0.75 X_{\mathrm{ANA}}^{t_{0}}(i, j)+0.25 X_{\mathrm{ST}}^{t_{3}}(i, j) $ | (6) |
ti=6 h,权重系数衰减为0,所以当ti≥6 h,风场的计算方法如式(7)所示,即6 h及以后风场预报完全表现为CMA-BJ模式降尺度到睿思高分辨率后的结果。
| $ X_{\mathrm{FORC}}^{t_{i}}(i, j)=X_{\mathrm{ST}}^{t_{i}}(i, j) $ | (7) |
研究表明,CMA-BJ模式在复杂地形区域对近地面风速模拟存在较大系统性偏差,呈现出对平原、山谷风速高估及对山腰、山顶地区风速低估的现象(刘郁珏等, 2019)。根据睿思风场的订正原理,若想进一步提升睿思风场的预报性能,可以尝试从提升背景场预报性能入手,假设先消除背景场的系统偏差,再将其作为睿思系统的背景场,对于提升睿思风场预报性能可能会有一些帮助。
而睿思系统包含大量的高海拔地区,不同海拔高度上格点的风速大小不仅受热力影响,在很大程度上还受山谷逆温、复杂地形等因素的影响(刘敏等,2010),如果只针对个别站点计算系统偏差,并不能提升整个网格范围内风场预报的准确率,需要根据不同观测站的位置来具体判断偏差订正系数。所以本研究利用睿思系统冬奥会区域不同海拔高度上收集的133个自动气象站风场实况观测资料与睿思系统高精度风场预报数据相结合,利用统计偏差订正方法,获取复杂地形下睿思系统冬奥会区域133个站点2020年1—3月,每个站点1~12 h的睿思预报平均风速WSRISE与观测平均风速WSOBS的比值,并将其定义为站点偏差系数S10k,如式(8)所示:
| $ {S_{10k}} = \frac{{{{\overline {WS} }_{{\rm{RISE}}}}}}{{{{\overline {WS} }_{{\rm{OBS}}}}}} $ | (8) |
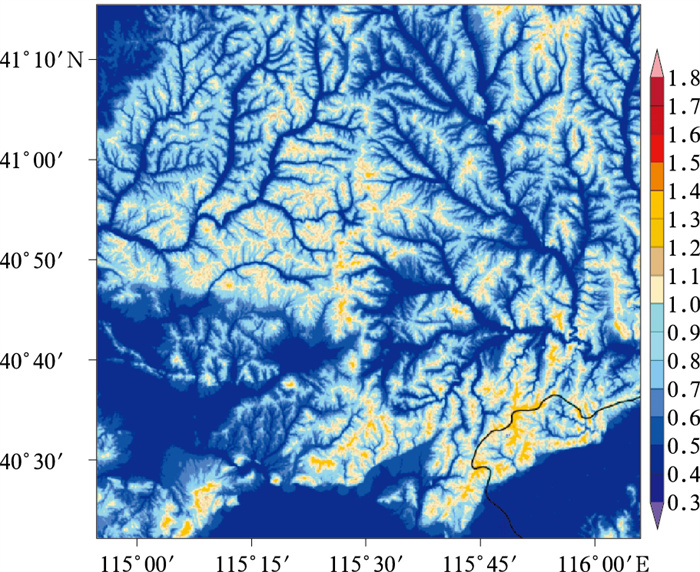
然后将S10k通过距离反比插值方法,插值到睿思高分辨率格点场上,获取格点偏差订正系数C10,如图 2和式(9)所示:
| $ {C_{10}} = \frac{{\sum\limits_{k = 1}^n {\frac{{{S_{10k}}}}{{r_{ijk}^2}}} }}{{\sum\limits_{k = 1}^n {\frac{1}{{r_{ijk}^2}}} }} $ | (9) |
|
图 2 睿图-睿思系统冬奥会区域格点偏差订正系数C10 Fig. 2 Grid point bias correction coefficient C10 in the Winter Olympic Games area of RMAPS-RISE system |
式中rijk与第(i,j)个格点与第k个地面测站的距离。为了最大程度地降低133个观测站点上的系统偏差和预报误差,偏差订正系数插值到格点后,133个站点重新赋值为统计得到的站点偏差订正系数,即这133个站不做插值和平滑处理。如延庆赛区竞速1自动站海拔高度为2 177 m(山顶站),统计得到的偏差订正系数为1.6;竞速5自动站海拔高度为1 669 m(山腰站),统计得到的偏差订正系数为0.99,竞速8自动站海拔高度为1 289 m(山脚站),统计得到的偏差订正系数为0.4,张家口赛区云顶3自动站,海拔高度为2 076 m(山腰站),与竞速1海拔相差100 m,统计得到的偏差订正系数为0.78。最后将降尺度后的高分辨率风场利用偏差订正系数优化之后再作为背景场,利用多源数据融合技术进一步做融合订正,更好地捕捉局地地形对山区风场的影响。订正后的风场预报场计算公式如式(10)所示:
| $ \begin{gathered} X_{\mathrm{FORC}}^{t_{i}}(i, j)=f_{\mathrm{T}}\left(t_{i}\right) X_{\mathrm{ANA}}^{t_{0}}(i, j)+ \\ {\left[1-f_{\mathrm{T}}\left(t_{i}\right)\right] C_{10} X_{\mathrm{ST}}^{t_{\mathrm{T}}}(i, j)} \end{gathered} $ | (10) |
图 3分别给出了2020年1月18日10时冬奥会赛区CMA-BJ模式10 m风场,睿图-短期模式地形降尺度后的10 m风场,睿思系统10 m风场分析场,自动气象站实况观测10 m风场及睿思系统偏差订正前后的10 m风场预报场,其中填色表示风速值大小。对比图 3a和3b可以看出,经过地形降尺度后的CMA-BJ模式风场继承了CMA-BJ模式完备的参数化方案,将具有中尺度动力特征的初始风场(图 3a)降尺度到更精细的网格点上(图 3b),能够更好地描述复杂地形特征下高分辨率格点流场的动量和能量;在次千米级尺度高精度地形条件下进一步融合观测资料后的睿思风场(图 3c),可以在很大程度上弥补山区自动气象站观测网稀疏(图 3d)以及CMA-BJ模式预报产品分辨率不足(图 3a)的缺陷,为冬奥会赛事服务提供更加精细化的风场产品。而经过高精度风场偏差订正后的睿思风场(图 3f),能够进一步消除CMA-BJ模式的系统性偏差,如图 3e红色框区中,偏差订正前,风速相比自动气象站实况风场(图 3d)及睿思风场分析场(图 3d)明显偏大,但经过偏差订正后风速与实况更加吻合,能够更好地捕捉局地地形对山区风场的平均影响。

|
图 3 2020年1月18日10时冬奥会区域CMA-BJ模式直接输出的风场(a),CMA-BJ模式降尺度至睿图-睿思格点上的风场(b),睿图-睿思高精度风场分析场(c),睿图-睿思高精度风场偏差订正前后风场与叠加的风速填色图(e,f)及自动气象站实况风场(d) Fig. 3 Wind field directly output from CMA-BJ model (a), downscaling wind field of CMA-BJ model to RMAPS-RISE grid point (b), high-precision RMAPS-RISE wind analysis field (c), RMAPS-RISE wind field before (e) and after (f) bias correction, and the actual wind field of automatic weather station (d) in Winter Olympic Games area at 10 UTC 18 January 2020 |
利用高精度风场偏差订正技术方案,回算2020年1—3月逐10 min更新、100 m分辨率的睿思风场产品,计算并输出133个自动气象站点上1~12 h预报时效观测平均风速、睿思预报风速平均值、风速平均偏差、风速平均绝对偏差、风速平均绝对误差及均方根误差,与风场技术方案改进前同时期睿思风速预报结果进行对比分析。
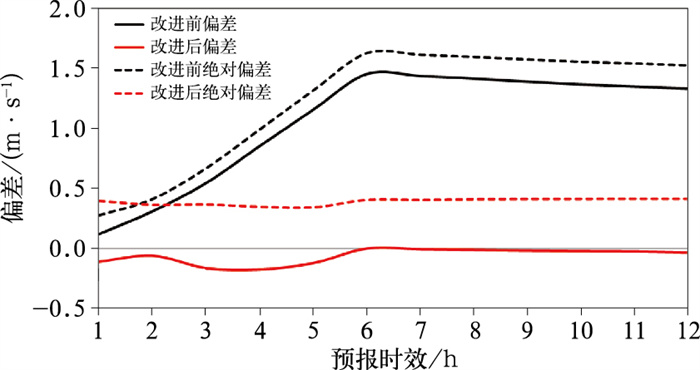
3.1 偏差和绝对偏差图 4给出了睿思系统风场技术方案改进前后所有站点1~12 h风速平均偏差和平均绝对偏差。从图中偏差对比可以看出,改进前2020年1—3月睿思预报风速系统性偏大,1~6 h内偏差随预报时效偏差不断增加,6 h以后,偏差基本维持在1.4 m·s-1左右。经过统计偏差订正后,风速系统性偏差基本消除,1~5 h内,风速系统性略偏小0.1 m·s-1左右;5 h以后,偏差基本为0。从图中绝对偏差对比可以看出,改进后,风速绝对偏差较改进前大幅度降低,12 h以内都维持在0.5 m·s-1以下。
|
图 4 2020年1—3月冬奥会区域所有站点改进前后风速1~12 h偏差(实线) 和绝对偏差(虚线) Fig. 4 The 1-12 h wind speed deviation (solid line) and absolute deviation (dotted line) before (black line) and after (red line) correction at all stations in Winter Olympic Games area from January to March 2020 |
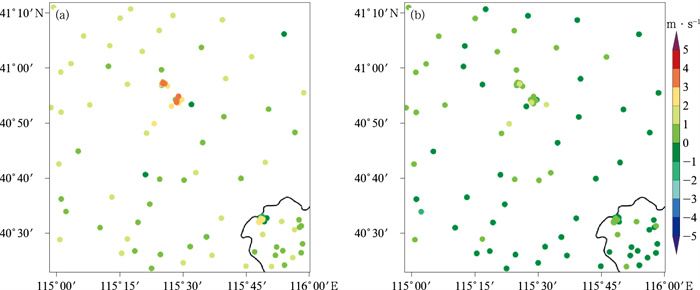
图 5和图 6给出了风场技术方案改进前后睿思区域所有站点、延庆赛区站点及张家口云顶和古杨树赛区站点1~12 h风速平均偏差的空间分布图。从站点偏差的空间分布图可以看出,各个站点平均偏差程度不同,大部分站点表现为系统性偏大,小部分站点表现为系统性偏小,偏差值分布在[-4 m·s-1, 4 m·s-1]区间,如:延庆赛区竞速1睿思预报风场较观测系统性偏小3.1 m·s-1,改进后竞速1系统性偏差降低为1.26 m·s-1;竞速7较观测系统性偏大2.88 m·s-1,改进后降低为0.48 m·s-1;崇礼赛区越野2睿思预报风场较观测系统性偏大2.97 m·s-1,改进后降低为0.46 m·s-1;越野3较观测系统性偏大3.40 m·s-1;改进后降低为1.03 m·s-1。
|
图 5 2020年1—3月冬奥会区域改进前(a)、后(b)所有站点1~12 h风速偏差空间分布 Fig. 5 Spatial distribution of 1-12 h wind speed deviation of all stations before (a) and after (b) correction at all stations in Winter Olympic Games area from January to March 2020 |

|
图 6 2020年1—3月延庆赛区(a,b),张家口云顶(c,d)和古杨树赛区(e,f)各站点改进前(a,c,e)、后(b,d,f)1~12 h风速偏差空间分布 (图中填色为地形高度) Fig. 6 Spatial distribtion of 1-12 h wind speed deviation before (a, c, e) and after (b, d, f) correction in Yanqing competition area (a, b), Yunding (c, d) and Guyangshu (e, f) competition areas in Zhangjiakou from January to March 2020 (Colored area indicates terrain height) |
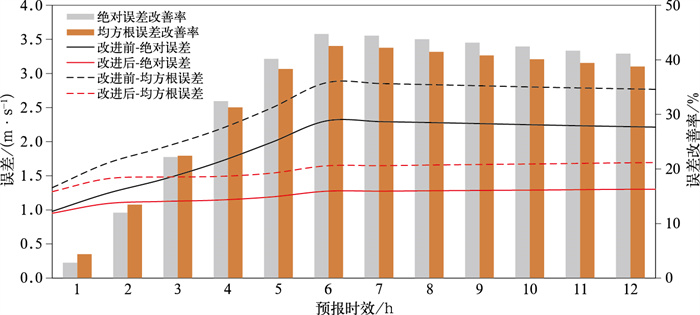
图 7给出了风场技术方案改进前后睿思系统范围内所有站点1~12 h预报风速平均绝对误差、均方根误差以及风速平均绝对误差和均方根误差改善率。从图 7可以看出,风场技术方案改进前风速平均绝对误差和均方根误差在6 h前随预报时效不断增大,12 h以内平均绝对误差在2.5 m·s-1以下,均方根误差在3 m·s-1以下。经过高精度风场统计偏差订正后,风速平均绝对误差和均方根误差降低明显,12 h以内,平均绝对误差降低至1.5 m·s-1以下,均方根误差降低至1.7 m·s-1以下。越临近的时次,风速误差改善率越小,3 h前风速误差改善率在20%以下,6 h以后达40%以上。这也进一步说明,基于观测资料融合和地形降尺度的偏差订正技术对于风场模拟能力的提升主要体现在短时临近预报时效内,越临近的时次,系统性偏差越小,偏差订正效果越不明显。
|
图 7 2020年1—3月冬奥会区域改进前后风速的1~12 h预报平均绝对误差(实线)、均方根误差(虚线)和误差改善率(柱状) (黑线表示改进前,红线表示改进后,灰色和橙色柱状分别表示平均绝对误差、均方根误差的改善率) Fig. 7 The 1-12 h mean absolute error (solid line), root mean square error (dashed line) and improvement rate of wind speed (histogram) before (black) and after (red) correction at all stations in Winter Olympic Games area from January to March 2020 (Gray and orange histograms indicate improvement rates of mean absolute error and root mean square error, respectively) |
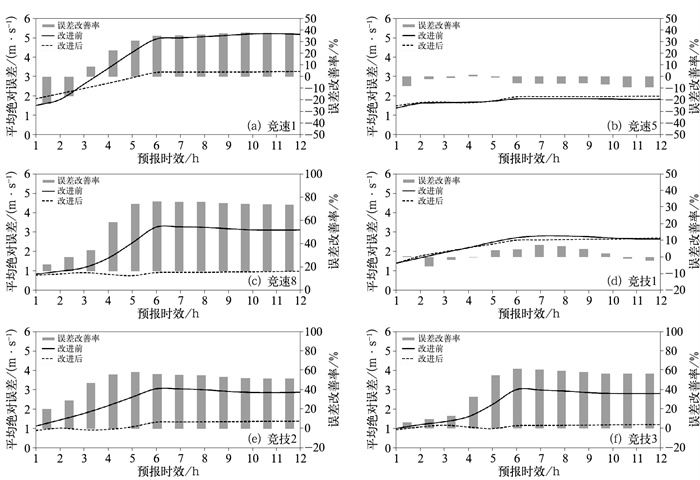
图 8给出了延庆赛区高山滑雪竞速赛道三个站点(竞速1、5、8)和高山滑雪竞技赛道三个站点(竞技1、2、3)的1~12 h风速平均绝对误差和误差改善率。从图中可以看出,竞速5和竞技1,风场技术方案改进前后,平均绝对误差变化不明显。竞速1、8、竞技2和3,经过高精度风场统计偏差订正后,平均绝对误差降低明显,其中竞速1平均绝对误差12 h以内由5 m·s-1降低为3 m·s-1,竞速8、竞技2和3,平均绝对误差12 h以内降低为1 m·s-1以下。
|
图 8 2020年1—3月延庆赛区不同站点改进前后的1~12 h风速平均绝对误差和误差改善率(柱状) (实线表示改进前,虚线表示改进后) Fig. 8 The 1-12 h average absolute error and improvement rate (histogram) of wind speed error before (solid line) and after (dashed line) correction at different stations in Yanqing competition area from January to March 2020 |
延庆赛区高山滑雪竞速1为高海拔山顶站,发生大风的概率较大,而大风事件会严重影响冬奥赛事的决策和赛程安排,所以文中特针对竞速1六级以上和八级以上大风分别对照中国气象局QX/T 229-2014风预报检验方法进行了风速和风向预报评分检验。
表 1给出了竞速1(山顶站)2020年1—3月六级(10.8 m·s-1)以上和八级(17.2 m·s-1)以上大风风速和风向评分。由于高精度风场偏差订正技术方案只针对风速进行调整,所以风场技术方案改进前后对风向无明显影响。从表中可以看出,经过高精度风场统计偏差订正后,对于竞速1,六级以上和八级以上大风风速评分,1~2 h相对技术方案调整前,略有降低(这主要与偏差订正时,偏差订正系数取的是1~12 h平均值,而实际上临近时次由于自动气象站融合订正权重系数较大,系统偏差较后面时次要小很多,所以对于风速比较大的站点,偏差订正以后,1~2 h会造成了一定的负订正效果)。3 h后,六级以上和八级以上大风风速评分都有很大提高。六级以上大风,5 h前,风速评分基本在0.5以上,6 h后,基本接近0.5。八级以上大风,5 h前,风速评分基本在0.5以上,6 h后,基本在0.6以上。
|
|
表 1 竞速1号站2020年1—3月六级以上和八级以上大风风速和风向评分 Table 1 Wind speed and wind direction score of wind scale above 6 and above 8 in Jingsui 1 Station from January to March 2020 |
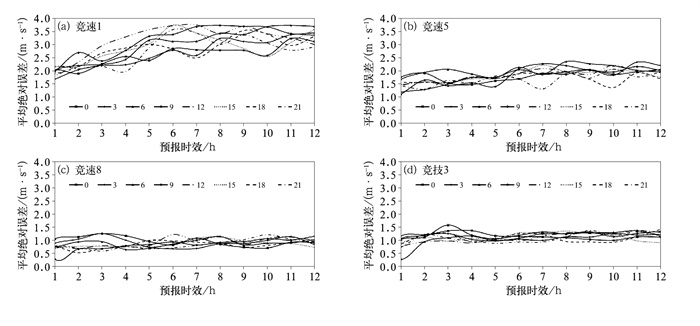
图 9给出了延庆赛区竞速1(山顶站)、竞速5(山腰站)、竞速8(山脚站)及竞技3(山脊站)四个站点00、03、06、09、12、15、18时不同起报时效的平均绝对误差。
|
图 9 2020年1—3月延庆赛区典型站点(竞速1、5、8、竞技3)不同起报时效(00、03、06、09、12、15、18、21 UTC)风速平均绝对误差 Fig. 9 Average absolute error of different starting time (00, 03, 06, 09, 12, 15, 18, 21 UTC) of typical stations (Jingsu 1, 5, 8, Jingji 3) in Yanqing competition area from January to March 2020 |
竞速1为高海拔山顶站,山谷风的方向主要受背景风场影响,白天和夜间均表现为偏西气流,夜间山风更为强盛,风速略大于白天。从竞速1站点不同起报时效平均绝对误差可以看出,不同起报时效平均绝对误差起伏较其他站点略大一些,00时起报的1~12 h预报(白天)平均绝对误差在所有起报时次中最小,12 h以内,平均绝对误差都在3 m·s-1以下;12时起报的1~12 h预报(夜间)平均绝对误差在所有起报时次中最大,误差最大的时刻出现在19时左右(平均绝对误差为3.74 m·s-1)。其他三个站点,竞速5为山腰站,竞速8为山脚站,竞技3为山脊站,不同起报时效平均绝对误差起伏不大,尤其是竞速8和竞技3不同起报时次的12 h预报平均绝对误差都较小,基本在1.3 m·s-1以下。
4 大风个例分析2020年1月18—20日受西北干冷空气影响,延庆赛区出现大风, 云顶山顶降雪,局地短时低能见度现象。竞速1自动站自18日10时开始2 min平均风速超过17.2 m·s-1,八级以上大风一直持续至19日05时;19日06时至20日风力等级一直维持在七级以上。
图 10分别给出了1月18—20日此次大风个例竞速1、5、8,竞技1、2、3睿思风场技术方案改进前后1~12 h风场预报的平均绝对误差。

|
图 10 2020年1月18—20日延庆赛区典型站点睿思风场技术方案改进前后1~12 h预报风场的平均绝对误差 Fig. 10 Average absolute error of 1-12 h forecast wind field before (solid line) and after (dashed line) correction of RISE wind field in Yanqing competition area in 18-20 January 2020 |
从图 10可以看出,风场技术方案改进后,对于冬奥延庆赛区预报重点关注站点,除竞速5,其他站点平均绝对误差都有很大程度的降低,竞速1,12 h以内平均绝对误差从6 m·s-1降低到了3 m·s-1以下;竞技1,平均绝对误差从3.5 m·s-1降低到了2.5 m·s-1以下;竞技2、3和竞速8,平均绝对误差都降低到了1.5 m·s-1以下。
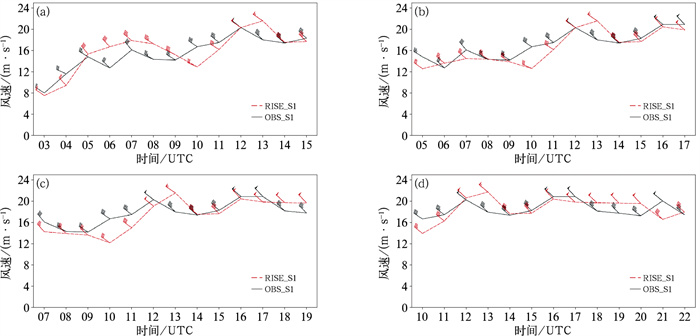
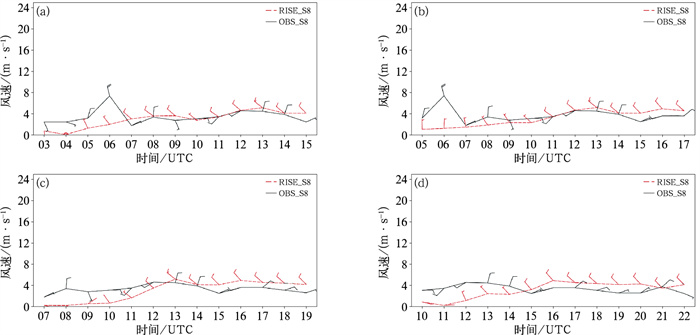
图 11和图 12分别给出了竞速1和竞速8站点1月18日03、05、07、10时不同起报时效睿思0~12 h分析和预报场风场与实况观测风场的时间序列图。从图中可以看出,整体来看,竞速1睿思预报的风向与实况基本吻合,都为西北风,山谷风风向变化本身比较小,风力等级较大,风速大部分时次与实况偏差在2 m·s-1以内,个别时次偏差较大,为3~4 m·s-1。竞速8为山脚站,实况风向基本为北东北或偏南风,而睿思预报风向大都为西北风或北东北风,风向误差相对竞速1号站较大,风力等级相比竞速1小很多,风速与实况比较吻合。
|
图 11 2020年1月18日延庆赛区竞速1站点03时(a),05时(b),07时(c),10时(d)不同起报时效睿思0~12 h分析和预报场风场(黑色) 与实况观测风场(红色)的时间序列 Fig. 11 Time series of 0-12 h RISE analysis and forecast wind field (black) and observed wind field (red) of Jingsu 1 Station in Yanqing competition area at 03 UTC (a), 05 UTC (b), 07 UTC (c) and 10 UTC (d) 18 January 2020 |
|
图 12 同图 11,但为延庆赛区竞速8站点 Fig. 12 Same as Fig. 11, but for Jingsu 8 Station in Yanqing competition area |
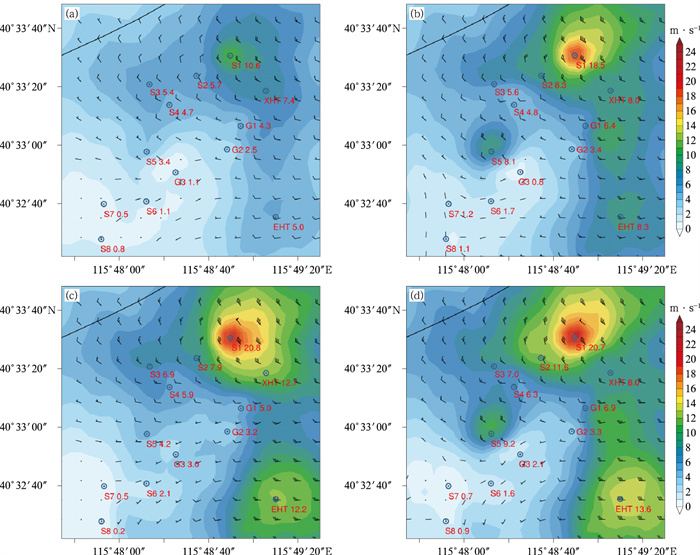
图 13给出了延庆赛区1月18日睿思风场03、05、07、10时格点分析场产品,可用于分析赛区整体的环流形势,图中红色标注的S1~S8表示竞速1~竞速8,G1~G3表示竞技1~3,XHT表示小海坨站,EHT表示二海坨站。从格点分析场可以看到,此次大风个例,受西北干冷空气影响,竞速1山顶站点风向维持为西北风,风速较其他站点明显更大;竞速5山腰站点风向也为偏北风;竞速8山脚站点风速小,大小为1 m·s-1左右,风向为偏南风或偏东风;竞技1山脊站,风向维持为西北偏西风,风速大小为6 m·s-1左右。
|
图 13 延庆赛区2020年1月18日03时(a),05时(b),07时(c),10时(d) 睿思风场格点分析场产品 (图中填色为风速) Fig. 13 Analysis products of RISE wind field with different forecasting times in Yanqing competition area at 03 UTC (a), 05 UTC (b), 07 UTC (c) and 10 UTC (d) 18 January 2020 (Colored area indicates wind speed) |
本文描述了一种综合考虑多源实况融合分析技术与复杂地形下高精度风场偏差订正相结合的方法,利用北京冬奥会山地赛区及其周边地区不同海拔高度上收集的133个自动加密气象站风场实况观测资料与睿图-睿思系统高精度风场预报数据相结合,利用统计偏差订正方法,获取复杂地形下133个站点1~12 h的平均系统偏差,将降尺度后的高分辨率风场利用格点偏差订正系数优化后再作为背景场融合观测资料,以实现复杂地形下不同海拔高度高精度风场的融合订正优化。通过批量对比检验、冬奥赛区站点检验、典型大风个例检验,结果表明:
(1) 本方法极大程度地降低了睿图-睿思高分辨率格点风速预报的系统性偏差和预报误差,12 h内风速平均绝对误差降低率最高达44.7%以上,均方根误差降低率最高达42.5%。延庆赛区,竞速5和竞技1,风场技术方案改进前后,平均绝对误差变化不明显。竞速1、8、竞技2和3,技术方案改进后,平均绝对误差降低明显;其中竞速8、竞技2和3,技术方案改进后,平均绝对误差在12 h预报时效以内基本维持在1 m·s-1以下。
(2) 由于所有站点的偏差订正系数取的都是1~12 h平均值,而不是针对每个预报时效、不同风力等级给出一个偏差订正系数,而实际上睿图-睿思风场预报前2 h受自动气象站融合订正影响比较大,风速偏差要较后面预报时次小很多,所以在偏差订正以后,对于平均风速比较大的站点,如竞速1,在1~2 h会造成一定的负订正效果;另外在不同风力等级区间,不同站点系统性偏差也会有所不同,对于风速预报订正效果也会造成一定影响。因此,后续工作将进一步考虑发展不同站点、不同风力等级、不同预报时效的格点偏差系数统计研究。
(3) 本风场技术方案受制于数值预报背景场的系统性偏差,若更换数值预报背景场,需要重新获取各个站点的偏差订正系数。技术方案经过适当修改,也可用于对更长预报时效或其他要气象素场的偏差订正。
曹勇, 刘凑华, 宗志平, 等, 2016. 国家级格点化定量降水预报系统[J]. 气象, 42(12): 1476-1482. Cao Y, Liu C H, Zong Z P, et al, 2016. State-level gridded quantitative precipitation forecasting system[J]. Meteor Mon, 42(12): 1476-1482 (in Chinese). DOI:10.7519/j.issn.1000-0526.2016.12.005
|
陈康凯, 宋林烨, 杨璐, 等, 2020. 一种基于高斯模糊的复杂地形下高分辨率三维插值方法的研究与试验应用[J]. 高原气象, 39(2): 367-377. Chen K K, Song L Y, Yang L, et al, 2020. Research and application of a three-dimensional interpolation method for high-resolution temperature in complex terrain based on Gaussian fuzzy[J]. Plateau Meteor, 39(2): 367-377 (in Chinese).
|
程丛兰, 陈敏, 陈明轩, 等, 2019. 临近预报的两种高时空分辨率定量降水预报融合算法的对比试验[J]. 气象学报, 77(4): 701-714. Cheng C L, Chen M, Chen M X, et al, 2019. Comparative experiments on two high spatiotemporal resolution blending algorithms for quantitative precipitation nowcasting[J]. Acta Meteor Sin, 77(4): 701-714 (in Chinese).
|
程雪玲, 胡非, 曾庆存, 2015. 复杂地形风场的精细数值模拟[J]. 气候与环境研究, 20(1): 1-10. Cheng X L, Hu F, Zeng Q C, 2015. Refined numerical simulation of complex terrain flow field[J]. Clim Environ Res, 20(1): 1-10 (in Chinese).
|
窦以文, 屈玉贵, 陶士伟, 等, 2008. 北京自动气象站实时数据质量控制应用[J]. 气象, 34(8): 77-81. Dou Y W, Qu Y G, Tao S W, et al, 2008. The application of quality control procedures for real-time data from automatic weather stations[J]. Meteor Mon, 34(8): 77-81 (in Chinese).
|
范水勇, 陈敏, 仲跻芹, 等, 2009. 北京地区高分辨率快速循环同化预报系统性能检验和评估[J]. 暴雨灾害, 28(2): 119-125. Fan S Y, Chen M, Zhong J Q, et al, 2009. Performance tests and evaluations of Beijing local high-resolution rapid update cycle system[J]. Torr Rain Disaster, 28(2): 119-125 (in Chinese). DOI:10.3969/j.issn.1004-9045.2009.02.004
|
江滢, 宋丽莉, 程兴宏, 2013. 风电场风速预报集合订正方法的尝试性研究[J]. 资源科学, 35(3): 673-680. Jiang Y, Song L L, Cheng X H, 2013. An integrated and revised method of forecasting wind speed for wind farms[J]. Resour Sci, 35(3): 673-680 (in Chinese).
|
金荣花, 代刊, 赵瑞霞, 等, 2019. 我国无缝隙精细化网格天气预报技术进展与挑战[J]. 气象, 45(4): 445-457. Jin R H, Dai K, Zhao R X, et al, 2019. Progress and challenge of seamless fine gridded weather forecasting technology in China[J]. Meteor Mon, 45(4): 445-457 (in Chinese).
|
李艳, 成培培, 路屹雄, 等, 2015. 典型复杂地形风能预报的精细化研究[J]. 高原气象, 34(2): 413-425. Li Y, Cheng P P, Lu Y X, et al, 2015. Wind power forecasting over the typical complex terrains[J]. Plateau Meteor, 34(2): 413-425 (in Chinese).
|
刘敏, 孙杰, 杨宏青, 等, 2010. 湖北省不同地形条件下风随高度变化研究[J]. 气象, 36(4): 63-67. Liu M, Sun J, Yang H Q, et al, 2010. The study on wind speed change with height under different terrain conditions in Hubei Province[J]. Meteor Mon, 36(4): 63-67 (in Chinese). DOI:10.3969/j.issn.1006-009X.2010.04.015
|
刘郁珏, 苗世光, 刘磊, 等, 2019. 修正WRF次网格地形方案及其对风速模拟的影响[J]. 应用气象学报, 30(1): 70-81. Liu Y J, Miao S G, Liu L, et al, 2019. Effects of a modified sub-grid-scale terrain parameterization scheme on the simulation of low-layer wind over complex terrain[J]. J Appl Meteor Sci, 30(1): 70-81 (in Chinese).
|
宋林烨, 陈明轩, 程丛兰, 等, 2019. 京津冀夏季雷达定量降水估测的误差统计及定量气候校准[J]. 气象学报, 77(3): 497-515. Song L Y, Chen M X, Cheng C L, et al, 2019. Characteristics of summer QPE error and a climatological correction method over Beijing-Tianjin-Hebei Region[J]. Acta Meteor Sin, 77(3): 497-515 (in Chinese).
|
童文雪, 李刚, 孙娟珍, 2018. 针对对流降水预报的BJ-RUC系统1小时更新循环方案研究[J]. 热带气象学报, 34(2): 177-187. Tong W X, Li G, Sun J Z, 2018. The design of hourly update BJ-RUC system for improving convective precipitation forecasting[J]. J Trop Meteor, 34(2): 177-187 (in Chinese).
|
王伯明, 2004. 基本气象资料质量控制综合判别法的研究[J]. 应用气象学报, 15(S1): 50-59. Wang B M, 2004. A study on synthetic differentiation method for basic meteorological data quality control[J]. J Apply Meteor Sci, 15(S1): 50-59 (in Chinese).
|
杨璐, 陈敏, 陈明轩, 等, 2019. 高时空分辨率三维风场在强对流天气临近预报中的融合应用研究[J]. 气象学报, 77(2): 243-255. Yang L, Chen M, Chen M X, et al, 2019. Fusion of 3D high temporal and spatial resolution wind field and its application in nowcasting of severe convective weather[J]. Acta Meteor Sin, 77(2): 243-255 (in Chinese).
|
杨璐, 陈明轩, 孟金平, 等, 2018a. 北京地区雷暴大风不同生命期内的雷达统计特征及预警提前量分析[J]. 气象, 44(6): 802-813. Yang L, Chen M X, Meng J P, et al, 2018a. Radar statistical characteristics and warning lead analysis of thunderstorm gales in different life periods in Beijing[J]. Meteor Mon, 44(6): 802-813 (in Chinese).
|
杨璐, 韩丰, 陈明轩, 等, 2018b. 基于支持向量机的雷暴大风识别方法[J]. 应用气象学报, 29(6): 680-689. Yang L, Han F, Chen M X, et al, 2018b. Thunderstorm gale identification method based on support vector machine[J]. J Appl Meteor Sci, 29(6): 680-689 (in Chinese).
|
于丽娟, 尹承美, 林应超, 等, 2017. 中国区域近地面风速动力降尺度研究[J]. 干旱气象, 35(1): 23-28, 56. Yu L J, Yin C M, Lin Y C, et al, 2017. Study of dynamical downscaling on near surface wind speed over China[J]. J Arid Meteor, 35(1): 23-28, 56 (in Chinese).
|
曾晓青, 薛峰, 姚莉, 等, 2019. 针对模式风场的格点预报订正方案对比[J]. 应用气象学报, 30(1): 49-60. Zeng X Q, Xue F, Yao L, et al, 2019. Comparative study of different error correction methods on model output wind field[J]. J Appl Meteor Sci, 30(1): 49-60 (in Chinese).
|
Chen M X, Quan J N, Miao S G, et al, 2018. Enhanced weather research and forecasting in support of the Beijing 2022 Winter Olympic and Paralympic Games[J]. WMO Bulletin, 67(2): 58-61.
|
Curry C L, van der Kamp D, Monahan A H, 2012. Statistical downscaling of historical monthly mean winds over a coastal region of complex terrain.I.Predicting wind speed[J]. Climate Dyn, 38(7-8): 1281-1299. DOI:10.1007/s00382-011-1173-3
|
Huang H Y, Capps S B, Huang S C, et al, 2015. Downscaling near-surface wind over complex terrain using a physically-based statistical modeling approach[J]. Climate Dyn, 44(1-2): 529-542. DOI:10.1007/s00382-014-2137-1
|
Kirchmeier M C, Lorenz D J, Vimont D J, 2014. Statistical downscaling of daily wind speed variations[J]. J Appl Meteor Climatol, 53(3): 660-675. DOI:10.1175/JAMC-D-13-0230.1
|
Lee J C Y, Lundquist J K, 2017. Observing and simulating wind-turbine wakes during the evening transition[J]. Bound-Layer Meteor, 164(3): 449-474. DOI:10.1007/s10546-017-0257-y
|
Michelangeli P A, Vrac M, Loukos H, 2009. Probabilistic downscaling approaches: application to wind cumulative distribution functions[J]. Geophys Res Lett, 36(11): L11708. DOI:10.1029/2009GL038401
|
Neilley P, Hanson K A, 2004. Are model output statistics still needed?[C]//20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction. Seattle: Numerical Weather Prediction.
|
Trubilowicz J W, Shea J M, Jost G, et al, 2016. Suitability of North American Regional Reanalysis (NARR) output for hydrologic modelling and analysis in mountainous terrain[J]. Hydrol Process, 30(13): 2332-2347. DOI:10.1002/hyp.10795
|
Wagenbrenner N S, Forthofer J M, Lamb B K, et al, 2016. Downscaling surface wind predictions from numerical weather prediction models in complex terrain with WindNinja[J]. Atmos Chem Phys, 16(8): 5229-5241. DOI:10.5194/acp-16-5229-2016
|
Winstral A, Jonas T, Helbig N, 2017. Statistical downscaling of gridded wind speed data using local topography[J]. J Hydrometeorol, 18(2): 335-348. DOI:10.1175/JHM-D-16-0054.1
|
Wood N, 2000. Wind flow over complex terrain: a historical perspective and the prospect for large-eddy modelling[J]. Bound-Layer Meteor, 96(1): 11-32.
|
 2022, Vol. 48
2022, Vol. 48 
