引言

近年来极端暴雨灾害带来越来越严重的影响及危害。尤其是城市突发极端暴雨积涝及洪涝，造成了巨大的人员伤亡及财产损失，引起了世人的广泛关注(Zhou et al，2013; 孙继松等，2012; 扈海波和张艳莉，2014)。分析此类灾害性天气事件的气象服务过程，对今后遭遇类似事件的风险评估及预判、极端天气气象服务质量提升、应对及降低极端天气灾害风险等，均有借鉴及参考价值。

2012年北京的“7·21”特大暴雨天气过程及其气象服务就是一场典型及值得事后总结分析的服务案例，特别是针对天气预报及预警服务的决策判断的总结分析。因此，本文尝试剖析气象部门在应对极端天气气象服务及决策过程中，探讨在当前预报技术手段及探测条件下，借助决策分析模型，是否可改进气象服务，辅助得出更为贴近实际的预警信号，从而降低灾害风险及损失。

准确的天气预报是灾害性天气预警的重要依据，也是致灾因子强度判断及风险分析的基础(Li et al, 2012; Meyer et al, 2009; Hirschberg et al, 2011; Zhou et al, 2011)。从决策分析的角度来剖析如何应对类似极端暴雨事件的气象服务过程，必须清楚地认识到在现有气象观测及预报技术水准下，很难完全撇除预报不确定性，得到近似完美的天气预报。那么如何依靠这种不确定性天气预报做好灾害性天气气象服务过程中的决策判断及分析，是需要解决的首要难题。本文尝试利用贝叶斯方法，模拟预报员在决策判断前，依据未来天气及气候背景资料，大致估计未来灾害性天气的发生概率，据此判断三类服务方案下(保守、冒险及不确定)可导致的损失期望大小，并按最小期望损失来选择服务方案或者做出决策判断。

以“7·21”事件为个例，模拟在贝叶斯及决策树模型下的决策支持服务及判别过程，揭示在此决策判断情景下，是否可得到最佳决策，这种决策判断能否达到理想的服务效果。当然，灾害性天气服务过程中所遭遇的具体情况可能比事后的模拟过程要复杂得多，数据资料的不确定性会更突出，数据解读会掺杂更多的误导。本文力图真实还原“7·21”的气象服务过程，按照各时间节点上所能得到的资料和情景，并在这类资料上进行基于决策判断的模拟分析。目的是为今后遭遇类似极端天气事件时，提供可借鉴的处理及判断模式。也尽量从预报人员的角度，结合预警信息发布、应急联动及灾害救助过程，分析类似事件中的气象服务决策人员是否有条件得出最佳决策方案，改善气象服务效果。如果能，该怎么做；不能，又怎么去改进决策判断结果。并从这一模式中探索极端天气及气候事件发生时，预报人员怎样才能借助类似贝叶斯方法及决策树模型，给出合理的判断及决策分析，达到最优化决策目的。

1 数据与资料

本项研究运用的主要数据资料有：

(1) 北京地区20个气象站点近60年到30年不等的降水日雨量资料，用于气候背景分析，推算极端降水的累积或超越概率。

(2)“7·21”暴雨当天提前24 h的ECMWF模式(以下简称EC)、JAPAN模式(以下简称JP)和北京Beijing Rapid Update Cycle模式(以下简称BJ_RUC)的数值预报雨量资料。EC(HRES及ENS)资料的起报时间为00 UTC及12 UTC，1 h或3 h更新一次，预报提前量可达+144 h及以上，空间分辨率为9 km。BJ_RUC为3 h快速更新循环同化预报系统，空间分辨率为3 km(D2区域)。JP的预报为有限区域及半球资料，两次初始场时间为00 UTC及12 UTC，空间分辨率为1.25°及2.5°格距。JP资料用作定性分析，不参与模型的计算。而EC及BJ_RUC资料则参与模型的计算分析，其中，研究用距离权重插值将EC的9 km预报雨量降尺度到3 km的风险评估模型网格。

(3)“7·21”当天北京市气象局的短时临近预报系统(BJ_ANC)的定量降水估计(QPE)(6 min、30 min、60 min、3 h、6 h)雨量，以及BJ_ANC的定量降水预报(QPF)(30 min、60 min)雨量。

(4) 北京市气象台提供的“7·21”当天的预报及预警信息发布结果及发布时次，包括预报时刻、预报时间范围、预报雨量结果及实况雨量统计结果、预警时刻、预警提前时间及预警等级等内容。

(5) 在制作洪涝灾害快速风险评估及风险预警结果图件时，使用北京市测绘局2006年提供的1∶5万比例尺的北京市基础地理信息数据。地形因子的计算选用空间分辨率为92 m×92 m的数字高程模型(DEM)。河网密度及不透水地表参数均从北京市基础地理信息数据及卫星资料中提取生成。重点防汛路段及防汛点信息由北京市防汛办提供。评估所用的北京地区人口密度及地均GDP数据来源于北京市2007年统计年鉴并按照空间网格数据计算的要求进行数值离散化处理及应用(扈海波和王迎春，2007)。

(6) 在制作泥石流灾害风险评估图件时，使用北京市地质规划研究所提供的泥石流发育区分布图。该类图件给出了北京地区泥石流的重度、中度、轻度等3~4类的发育区分布结果，该图件的矢量图可与格点雨量资料叠置，用于泥石流风险分析(陈悦丽等，2019)。需要说明的是洪涝和泥石流灾害的风险评估均提供两类灾害对人员的胁迫人数分布结果。

上述资料为从决策支持的角度模拟及分析“7·21”暴雨当天的气象服务过程，以及决策判断提供实况信息和可供分析与判断的计算结果。

2 方法与计算

在气象决策服务及高影响天气灾害防御过程中需要解决两个关键的问题：一是要充分了解高影响天气的致灾能力和危险性状况可能对承灾体带来的冲击和影响，而现实的情况却是对未来天气及其变化情况无法把握或者是存有不确定性因素，这时如何决策；二是必须确认现有的气象服务信息是可信的，如何用这类被认定的，但含有不确定性的信息来实施灾害预警，并用于灾害防御以获取最大防灾效果(期望效益)。前者需要解决的是随机决策下的不确定性判定，后者的决策判断其实是可在最优决策分析基础上，以估算的期望损失来做选择。由于随机决策问题中的自然状态概率体现为未来灾害性天气的出现概率，随机决策方法可用于类似“7·21”特大暴雨那种灾害性天气的预报、灾害防御及应急服务。

2.1 不确定型决策方法

当自然状态的概率无法得知时，常用不确定型决策方法。对于未来高影响天气出现的概率把握不大时，可根据服务对象的基本状况或者对待风险的偏好，采用不确定型决策方法进行服务决策。

气象预报服务在高影响天气过程中首先要确定两种可能出现的基本自然状态，或判定未来天气的风险状况，即未来天气的发展会导致灾害性后果和未来不出现灾害性后果。两种自然状态下预期的益损值见表 1，并定义了三种服务及应急方案。

2.2 确定型决策方法

确定型气象决策服务则是通过天气预报，给出未来天气的变化情况，发布气象服务信息。这其实可采取最大期望值决策法(陈珽，1987；冯俊文，1991)，以损失期望值最小的方案，作为最佳服务方案。

2.3 最优决策分析

需要特别指出的是通常情况下，事件的发生概率P是不确定的。灾害性天气事件的发生概率同样如此，在气象决策服务中可以辅以气候及天气预报结果进行灾害性天气的决策判断。下面通过最优决策判断理论对这个问题进行更深一步的探讨。

假定预测对象Y有两种状态y₀(有灾)和y₁(无灾)，这两类状态的先验概率为P(y₀)和P(y₁)，而且P(y₀)+P(y₁)=1；行动空间中有两种策略行动：a₀预报y₀，a₁预报y₁。假设没有天气预报，这个先验概率只能依据气候预测来获取，或者本身即为气候概率。

假定在y₀出现时，因子x的概率为P(x|y₀)；在y₁出现时，因子x的概率为P(x|y₁)。在因子x出现时做出决策S₀(x)=a₀的概率为δ(S₀|x)；做出决策S₁(x)=a₁的概率为δ(S₁|x)，且由于预报决策只有两种可能，因此，δ(S₀|x)+δ(S₁|x)=1，造成的损失如表 2所示。

根据已知条件，由贝叶斯理论，后验概率为：

$ P({y_0}\left| x \right.) = \frac{{P({y_0})P(x\left| {{y_0})} \right.}}{{P({y_0})P(x\left| {{y_0})} \right. + P({y_1})P(x\left| {{y_1})} \right.}} $

(1)

$ P({y_1}\left| x \right.) = \frac{{P({y_1})P(x\left| {{y_1})} \right.}}{{P({y_0})P(x\left| {{y_0})} \right. + P({y_1})P(x\left| {{y_1})} \right.}} $

(2)

如果

$ L[S(x), {y_i}] = \sum\limits_{i = 0}^1 {{L_{ij}} \bullet \delta ({S_i}\left| {x)} \right.} $

(3)

预测有灾的后验期望损失为：

$ EL({y_0}) = \frac{{L[S(x), {y_0}]P({y_0})P(x\left| {{y_0})} \right.}}{{P({y_0})P(x\left| {{y_0})} \right. + P({y_1})P(x\left| {{y_1})} \right.}} $

(4)

无灾的后验期望损失为：

$ EL({y_1}) = \frac{{L[S(x), {y_1}]P({y_1})P(x\left| {{y_1})} \right.}}{{P({y_0})P(x\left| {{y_0})} \right. + P({y_1})P(x\left| {{y_1})} \right.}} $

(5)

因此，如果后验期望损失中，满足：

$ \begin{array}{c} L[S(x), {y_0}]P({y_0})P(x\left| {{y_0})} \right. \ge \\ L[S(x), {y_1}]P({y_1})P(x\left| {{y_1})} \right. \end{array} $

则应该做出有灾的决策，也就是：

$ \frac{{P(x\left| {{y_1})} \right.}}{{P(x\left| {{y_0})} \right.}} \ge \frac{{L[S(x), {y_0}]P({y_0})}}{{L[S(x), {y_1}]P({y_1})}} $

反之则预测无灾。

这里存在的关键问题是有灾和无灾的风险损失比例$ \frac{{L[S(x), {y_0}]}}{{L[S(x), {y_1}]}}$怎么确定，一般情况下这个比值与具体的行业相关，其中与气象因子越敏感的行业，风险损失比例就越大；其他的先验概率也需要通过历史灾情或者是气候统计得到。

3 “7·21”特大暴雨服务过程的决策分析判断及检验

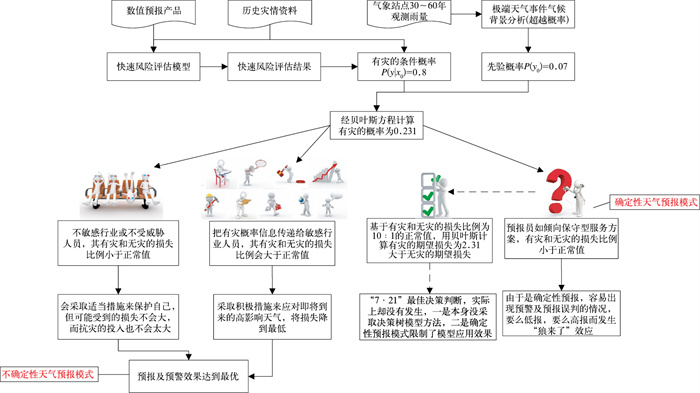
图 1展示“7·21”气象服务决策分析的工作流程及设想示意。高影响天气的气象服务决策分析有必要用快速风险评估结果做决策依据(扈海波等，2013)。再辅以贝叶斯方法可得出有灾条件概率(如“7·21”当天的推断为0.231)或无灾概率。这个计算结果节点其实是气象服务模式选择的一个分界点。如果完全由预报及决策人员根据这个概率值来做判断，并据此发布预报及预警信息，这显然是通常的确定性预报及预警模式。而在高影响天气气象服务过程中，这个概率值如直接传递给公众，可认为是一种不确定性预报及预警模式(Demuth et al, 2009)。图 1的分析认为这种不确定性预警模式既可将灾害损失降到最低，又可避免确定性模式下的“狼来了”效应。反之确定性模式很难做到最优决策效果，因为在不确定性天气情况下，必须做出确定性预报，必须做有灾或无灾的判定。此时倾向于保守型服务方案就在所难免。而不确定性模式下，就不会出现这种难局。将决策的优先权真正交还最终用户后，行业人员可以根据本行业对高影响天气的敏感性做出决策判断及灾害防御对策，将灾害损失减少到最理想状态，同时又减少不必要的恐慌和投入。以下将结合“7·21”个例给出具体的决策过程分析。

3.1 基于贝叶斯方程的“7·21”最优决策判断模型应用实例

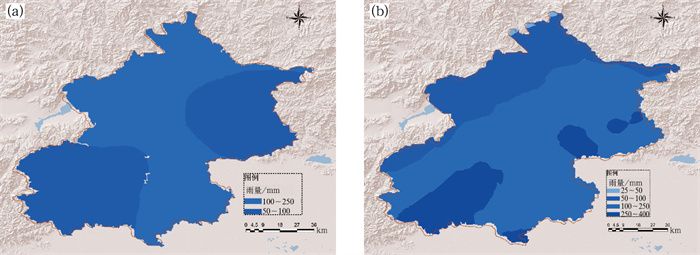
回顾“7·21”的过程预报是：北京地区暴雨，西南部(房山、门头沟、海淀、石景山)、东北部(平谷、密云、怀柔东部、顺义北部)等地降水量将超过100 mm(大暴雨总面积超过北京行政区域面积一半以上)，城区降水时间午后开始(图 2a)。实况是：大暴雨区域(超过100 mm)面积约占北京行政区域面积的2/3，出现西南、东北两个特大暴雨中心(图 2b)。另外，几乎所有数值预报模式(EC，JA，T639，WRF等)的降水预报都一般偏晚6~8 h。主要的原因是：模式预报为锋面降水，其主要过程发生在暖区的低空急流中，而“7·21”当天在地形强迫和低层风辐合的作用下，导致中尺度对流系统(MCS)长时间的“列车效应”的维持和MCS的发展(陈明轩等，2013)，加上中高层水汽垂直输送作用(王婧羽等，2014)，因此产生了连续大强度降水(孙继松等，2012; 俞小鼎，2012; 谌芸等，2012; 孙军等，2012)。“7·21”特大暴雨正常体现了极端天气过程发生及发展的不确定性(Morss et al, 2008)。

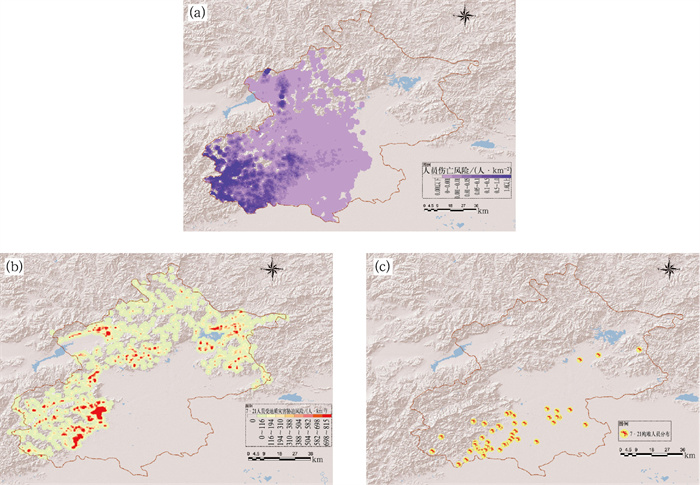
从预报的角度给出图 2a那样的有一定准确度的预报结果是无可厚非的。那么怎么根据这种具有较大不确定性且与实际需求有差距的预报结果进行决策分析，也就是说按照最优决策理论是否首先可以做出有灾或无灾的判定，从而选取最佳服务方案。图 3是根据EC在7月20日提供的未来24 h数值预报结果，按照风险评估模型方法(扈海波等，2013；扈海波和张艳莉，2014；Hu, 2015;Hu et al, 2014; Meyer et al, 2009)，所得到的“7·21”暴雨综合风险及地质灾害风险指数分析结果。从风险评估图上可以看到，“7·21”当天可能的高风险区域集中在北京西南、北部及东北部地区，地质灾害风险区域主要分布在西南、西及北部山区(图 3b)，而实际的受灾殉难人员也主要分布在这些地区(图 3c)。需要指出的是天气预报有很大的不确定性，而风险评估结果同样带有很大的不确定性(Hsu et al, 2012; Merz and Thieken, 2009)。在现有风险管理机制尚未确立之前，预报员也不可能完全靠风险分析及评估结果做决策判定。

除了依据雨量预报进行快速灾害风险评估外(Hu, 2014)。还可参照历史灾情资料，对应这种高影响天气状态，辅助进行有灾或无灾的定性判定。查阅《中国气象灾害大典.北京卷》(谢璞，2005)及相关年份的减灾年鉴，发现北京地区1950—2008年日雨量在100~200 mm的暴雨导致的暴雨洪涝及泥石流灾害事件共有61次之多。也就是说如果北京地区出现如图 2a所示的过程雨量，或出现大面积地区超过100 mm的降水，其发生灾害的可能性会很大，这里暂定为80%的概率值。然后用贝叶斯的最优决策模型来分析，其完整的模型参数计算、取值结果及计算依据参见表 3。此情况下，P(x|y₀)=0.8，P(x|y₁)=0.2。然而，这种预报结果本身具有不确定性，需要进一步推断它的可信度或者说是先验概率是多少，这个先验概率需要根据大量的预报样本(实例)来做出推断。由于这类样本资料不容易收集及整理，这里暂且用“气候概率”来做先验概率。当然实际的先验概率值肯定大于气候概率值。

研究暂用观象台的历史雨量资料，采用对数正态概率分布模型推算出1984年以来其200 mm的超越概率为0.07(0.93的累积概率)(Hu, 2015)。以此从气候背景来定义极端暴雨的先验概率，那么贝叶斯方程的先验概率P(y₀)=0.07;P(y₁)=0.93。根据预报评分标准(Hirschberg et al, 2011；Reynolds et al, 2012)，如果预报的有效性不如气候预测，那么这种预报得分等于零。实际上先验概率多数情况下会比选用的极端降水的气候概率值要高，因为天气预报多数情况下会强于气候预测，而且极端暴雨在气候上毕竟是小概率事件，气候概率值很低。这样，用贝叶斯方程，即式(1)~(5)，可得到“7·21”雨量状况及情景下，可能出现灾害性后果的概率为：

$ P({y_0}\left| x \right.) = 0.231 $

$ P({y_1}\left| x \right.) = 0.769 $

也就是说用贝叶斯方程做判断，得出的概率并不高。主要是因为极端灾害性天气事件的先验概率较低的原因，也就是出现极端暴雨毕竟属于小概率事件。当然实际上要选用的先验概率会比用气候分析的先验概率要高。

决策分析到了这个节点即为图 1所指出的气象服务决策模式选择的关键节点，在此之前的分析及判断属于几乎所有的气象部门都必须有的工作流程，而且分析结果一般无较大差别，其服务效果更多依靠预报准确度。此后，设想如果继续沿用确定性预报模式，就应该做最优决策分析。以下是面对公众气象服务的最优决策分析过程，而行业敏感用户的决策分析与此类似。

在灾害性天气条件下，即便有灾的后验概率远低于无灾的概率，仍应依据期望损失的情况做决策判断。假设有灾和无灾的后验损失比例为:

$ L[S(x), {y_0}]:L[S(x), {y_1}] = 10:1 $

这里暂时这么假定，实际损失情况肯定会复杂很多，而且行业不同，其期望损失是不一样的。因此实际做决策时能否根据这样的损失期望比例做出决策判断就具有很大的不确定性。

依据假定，按照式(4)和式(5)，预测有灾的后验期望损失为EL(y₀)=2.31，而无灾的后验期望损失EL(y₁)=0.769。

显然EL(y₀)>EL(y₁)，根据贝叶斯判定方程式，则应做出有灾的判定，也就是应采取“保守型服务方案”。

3.2 决策树模型判断及敏感性分析

通过以上的贝叶斯方程计算，在“7·21”情景下，根据已有的资料，可得出发生暴雨的概率大致为0.231；但有灾的后验期望损失为2.31，远大于无灾的期望损失。这里用决策树模型，进一步分析服务方案的选取及敏感性。

首先将有灾和无灾的后验期望损失比暂定为10∶1。依据表 1中的预期益损值定义为：

$ {L_{21}} = 1 $

这是保守服务方案中必须投入的益损值，也就是做出有灾判定后，可能后续投入到灾害防御中的人力及物力资源。L₂₁=1，说明即便未来无灾，前期投入的益损值也不会为零。

$ {L_{11}} = 1 + 9k $

式中：L₁₁为未来有灾的情况下的益损值。k(取值范围为0~1)为在采取防护措施的情况下的损失系数，这个值应该属于风险管理的控制范畴，它体现灾害风险的可控及可规避能力。如果风险的可控制及可规避能力较强，那么这个值则小，反之则大。

k=1，说明未采取任何防护措施或防护措施无效。这样L₁₃=10，同时这也是采取冒险型服务方案的后果，即在未来情景为有灾时可能遭受的最大期望益损值。

而L₂₃=0，则是采取冒险型服务方案，但是在没灾的情况下可能的期望益损值，因为没有投入前期灾害防御的人力及物力资源，因此结果显然为零。

那么，在这种情景假设下，“7·21”的保守型气象服务方案(d₁)的期望益损值为

$ EL({{\rm{d}}_1}) = 9k \times 0.231 + 1 $

而对应的冒险型气象服务方案(d₃)的期望易损值为

$ EL({{\rm{d}}_3}) = 10 \times 0.231 + 0 = 2.31 $

要使EL(d₁) < EL(d₃)，即9k×0.175+1 < 2.31, 只要损失系数k < 0.832，那么保守型服务方案(d₁)的期望益损值EL(d₁)就会小于冒险型服务方案(d₃)的期望益损值EL(d₃)。也就是说这种情景下，采取防御措施后只要能达到减免16.8%的灾害损失，那么选择冒险型服务方案(d₂)即为最优决策方案。这个目标对于多数极端暴雨事件的防御来说是很容易达到的。而此时, 不确定型气象服务方案(d₂)越靠近保守型服务方案，期望益损值就越低。

甚至对于面向公众的气象服务或者是公共安全的考量来说，如果选择恰当的服务方案，只要能达到减少人员伤亡的目的，比如采取人口转移措施，将相关人员从危险区域转移到安全区域，从而避免了人员伤亡，那么这种服务效果比数字更有说服力。

4 “7·21”特大暴雨服务过程浅析

本节从时间节点上继续复盘“7·21”特大暴雨气象服务过程，解析最优决策分析的作用及其在气象服务中的切入点，探讨是否有必要及有可能转变现有的确定性预报及预警模式为不确定性模式。

一般灾前2~3 d只能认定“7·21”出现暴雨的大致概率，尚无技术条件确认是一般暴雨还是极端暴雨过程，更难预测该过程的雨量强度是否到达致灾临界条件。受预报技术条件及其服务产品不确定性的限制，这个时段不可能确定暴雨开始时刻、持续时间、雨量强度及分布等信息，也无法做到提前1~3 d的暴雨强度及落区的精准预报。根据决策过程分析，选择“不确定型气象服务方案d₂”是明智的。

而灾前一天，用现有的预报资料及数据可初步给出“7·21”暴雨有可能发生灾害性后果的决策判断。预报人员可在决策树模型的支持下，对未来不确定性天气的预报及预警做出决策分析及判断。其中贝叶斯模型等决策方法有助于给出最优决策。而实际应用中，贝叶斯模型的分析结果还可得到进一步的改进，尤其是先验概率取值的完善。先验概率作为对提前24 h的预报结果(主要是指数值预报结果)不确定性的顾虑，而被引入贝叶斯方程计算中。本文只是暂且用气候背景分析的极端暴雨的超越概率为先验概率。其实预报员完全可运用自己的预报技能及对天气形势的掌握, 技巧性地设置更加合理的先验概率值。另外，还可定量化地对数值预报的不确定性做一定的判断，比如依据模式预报在此类天气形式下的误报、虚报、漏报的情况做统计。通过统计分析，筛选出对应的预报及预警的不确定性信息，获取更合适的先验概率值，用于贝叶斯方程的推算。而且这类不确定性信息可作为天气预报信息提供给公众，而且还应该改变其固有的确定性预报模式为不确定性天气预报及预警模式(Feldman and Ingram, 2009; Zhou et al, 2011)。Hirschberg et al(2011)和Reynolds et al(2012)等NOAA的科学家相继在美国气象学会快报(Bulletin of American Meteorological Society)上撰文指出将确定性天气预报及预警模式转变为不确定性模式，扭转确定性天气预报有可能带来的误导。

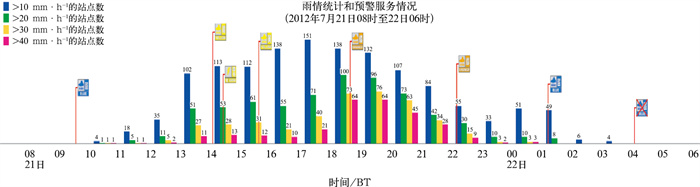
“7·21”特大暴雨当日的气象服务重点是灾害性天气的监测和预警，其预报服务过程见图 4。鉴于预报难度及极端天气发生及发展的不确定性特征，这些服务上的偏差基本在可容纳的误差范围内。但是极端天气事件的气象服务方案不能倾向于“冒险型气象服务方案”。根据贝叶斯模型的分析，这种服务方案在实际有灾前提下所导致的期望损失EL(d₁)是最大的。而决策偏向又受限于天气预报的不确定性，以及预报难度的制约。从图 4可见，在14时发布暴雨黄色预警信号之前，已有11~13个测站相继在2 h内连续出现40 mm·h^-1以上的雨强，在18:30橙色预警发出时，40 mm·h^-1以上雨强的站点已经达到64个。这种雨强对于城市地区来说，几乎肯定会出现城市沥涝。而此时，贝叶斯方程的先验概率值及条件概率值实质上在逼近1.0。如果加以决策模型的判断及模拟，是不难得出有灾的决策判断结果的。

5 结论与讨论

本文将随机决策方法及概念引入到气象服务中，做如下规约：灾害性天气条件下，随机决策所面对的是决策判断服务；决策判断面对未来有灾或无灾两种自然状态；面对决策问题可采取“保守型”d₁、“不确定型(随机)”d₂及“冒险型”d₃等三种行动方案(气象服务方案)。在决策树模型方法基础上给出了不同自然状态下，选取不同服务方案可能产生的期望损益值计算方法及步骤。

随即给出了基于贝叶斯模型的最优决策分析方法，该方法首先根据贝叶斯方程，计算出“有灾”或“无灾”两种自然状态的后验概率，据此估算不同决策方案可导致的期望损失，用于决策判断及选择。最后，基于决策树模型和贝叶斯方法对“7·21”特大暴雨过程的气象决策服务进行了模拟分析。这种事后模拟或“复盘”对改进极端天气条件下的气象服务有一定的参考及指引价值。

研究通过决策模型的模拟及对比“7·21”当天的服务过程，发现尽管在现有天气预报技术条件下，无法完整地对极端天气事件的发生、发展过程进行准确的预报及预警。但如辅以决策判断模型，则有助于给出合理的决策判断，并采取恰当的气象服务方案，可将期望损失降低到合理状态。根据此次的事后模拟分析，这里给出一点经验总结，期望对今后类似事件的发生有所借鉴。

(1) 首先需要注重高影响天气的风险识别及评估工作。在现有数据资料的基础上，用风险评估的结果并结合决策判断模型进行决策及服务取向。当然，灾害风险评估同样会因为预报及评估资料的不确定性，以及不恰当方法运用等因素，造成本身评估结果的不确定性。但是，基于风险评估的风险管理模式本身就是降低灾害风险的唯一及可行的途径，其不确定性可通过天气预报技术及资料准确性的提高加以改进，而风险结果的不确定性同样可作为预警信息的不确定性附加进行发布并加以利用。在决策支持服务中引进灾害风险评估的风险管理模式，并辅以决策分析判断是能达到一定的防灾及减灾效果的。

(2) 从公众需求角度上，“明确、精准、有效”的气象服务信息更乐于被公众接受及认可。但天气预报技术的限制及预报的难度导致天气预报结果与现实情况之间存有一定的偏离，而漏报、虚报、错报现象的时有发生给公众的生产和生活带来相当的困惑，因此提高预报准确率一直是气象部门努力的目标。一方面不能因为虚报可招致公众的不满，而倾向于“冒险型”服务方案。但在高影响天气服务过程中刻意将预警等级人为拔高，也是不可取的。在确定性预报模式下，同样无法兼顾到“保守型”服务效果。这就像一面“双刃剑”，那就是容易招致公众对天气预报及预警的不信任，给未来真正的灾害性天气预警及灾害防御带来极大隐患，也就是“老喊狼来了，而狼又没来”效应。因此建议应急部门主动提升应急等级，将防灾的关口前移，既达到“保守型”服务方案的效果，又消除滥用预警信号给公众带来的混乱。其次则是需要改变现有的确定性天气预报及预警模式为不确定性模式。也就是在高影响天气服务过程中，除了提供预警及预报信息，还应适当提供灾害性天气后果的估测概率，甚至是快速风险评估结果，向公众传递天气预报及预警的不确定性信息。这可明显消弱用确定性预报方式来对付不确定性天气状况可能带来的隐患。而把这些不确定性信息传递给不同的行业用户，此类用户则可根据各自领域或行业应用要求，自行分析各自行业在对应有灾或无灾情况下的损失期望，做出决策判断及选择。而且在天气预报中提供天气不确定性信息的预报，也是国际众多气象学家和资深预报员一直倡导的(AMS, 2008; Morss et al, 2008; Lazo et al, 2009; Demuth et al, 2009; Spiegelhalter et al, 2011; Ash et al, 2014; Carr et al, 2016)。为避免给普通公众造成迷惑，不确定性预报模式可限定在高影响天气气象服务时采用。这样，最终将“确定性气象服务”模式转变为“不确定性气象服务”模式，在灾害性天气的服务过程中达到“保守型服务方案”的减灾效果。