开展气象、气候相关服务及科研工作时,时常需要准确、精细化的栅格气象资料(陈锋等, 2016)。在制作栅格化数据的时候,利用气象观测站的观测数据进行空间插值是一种相对高效的做法。常用的插值算法有反距离权重法(inverse distance weighting,IDW)、样条插值以及普通Kriging法等,这些算法均建立在气象要素空间平滑连续的假设上,主要考虑了空间距离对要素的影响(徐成东等, 2008)。但实际中的气象要素往往还与地形、土地利用等下垫面地理信息有关;同时,受地理位置或者人力物力的影响,气象站的空间密度极不均匀,且难以代表真实的要素空间变化特征(姜晓剑等, 2010),因此获取精度较高的格点化资料存在一定难度(熊敏诠, 2013)。为改善这一状况,国内外相关领域的研究人员开始将地形也考虑到插值过程中,其中PRISM(Parameter-Elevation Regressions on Independent Slopes Model)和Cokriging是两种较为常见的可考虑地形的插值算法。
PRISM是由Daly et al(2002)提出的插值方法。该算法认为局部山地区域内控制气象要素空间分布的最主要因素是高程,但又并非简单的线性相关关系,还受到距离、坡向、坡度、高度等其他地理因子因素的综合影响。Daly et al(2008)利用PRISM对美国1971—2000年的月平均降水和气温进行了插值试验,结果表明PRISM插值得到的数据集质量相比WorldClim和Daymet气候数据集有所提升,但提升幅度与地形的复杂程度有关;朱华忠等(2003)利用PRISM模型结合中国及周边国家气象站点数据,较好地模拟了我国温度和降水的空间分布及季节变化;蒋育昊等(2016;2017)和夏智武等(2016)利用PRISM模型开展了对山地地区的大气湿度、气温、降水的空间插值试验,结果表明PRISM的插值效果较IDW、Kriging、样条插值等方法更好,但当站点密度较低时,PRISM的误差增长较快。
Kriging是一种常用的插值算法(贺芳芳等, 2018),它建立在地理统计学基础上。Cokriging是其考虑地形因素的变异算法:通过在Kriging系统中添加约束项再计算无偏最优解从而完成插值(Hevesi et al, 1992)。当约束项为地形高程时,便实现地形对插值过程结果的影响。Adhikary et al(2017)利用普通Kriging、Cokriging和漂移Kriging算法对澳大利亚地区的降水数据进行了插值试验,结果表明在这几种地质统计学方法中,Cokriging可以得到最好的插值效果;Xu et al(2015)、徐天献等(2010)及吴昌广等(2010)采用Kriging法、反距离权重法和Cokriging进行区域降水插值,表明Cokriging相比另外两种算法在降水的插值中表现更好;刘强和林孝松(2015)利用重庆市台站降水数据进行插值,对比了反距离权重法、Kriging法、样条函数法和Cokriging等四种算法的插值效果,认为Cokriging插值效果最佳;但宋丽琼等(2008)的研究表明,在深圳地区,考虑了海拔的Cokriging插值精度相较普通Kriging法并没有明显提高。
虽然两种算法均能考虑地形,但原理存在较大不同:PRISM建立高程的回归模型,而Cokriging仅将高程作为模型约束项。李月臣等(2014)归纳整理了多个基于站点观测数据的插值方法,但并未做量化比较;Park and Jang(2016)对PRISM和Cokriging法在韩国地区的风速空间插值效果进行了对比,结果表明PRISM方法较优,但这也仅是针对风速的对比结果。目前,国内外的相关研究主要集中在考虑地形的空间插值算法与传统插值算法的对比上,而考虑不同地形插值算法之间的对比还相对缺乏。尤其是针对中国内陆重庆地区的复杂地形区域,PRISM和Cokriging法在进行降水和气温的插值适用性特征方面值得开展进一步研究。
本文利用重庆市2017年区域自动气象站逐月累积降水和月平均气温资料,采用PRISM、Cokri- ging和IDW三种算法进行了插值试验。通过对比三种算法的误差特征,分析并评估其在重庆的插值效果,这对实际业务中选择合适的插值算法能提供重要参考。
1 插值算法介绍 1.1 PRISM插值法PRISM最早由美国气象学家Daly提出,算法通过建立气象要素与地形高程间的一元线性回归方程作为模型的预测方程。方程如式(1)所示。一般求解一元线性方程时,可采用最小二乘法,而PRISM中为了考虑地形的影响,引入了综合权重系数并进行加权线性回归,因此求解如式(2)(Park and Jang, 2016)。
| $ Y=\beta_{1} X+\beta_{2} $ | (1) |
| $ \begin{array}{c} \beta_{1}=\frac{\sum w_{i}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum w_{i}\left(x_{i}-\bar{x}\right)^{2}} \\ \beta_{2}=\bar{y}-\beta_{1} \bar{x} \\ \bar{x}=\frac{\sum w_{i} x_{i}}{\sum w_{i}} \\ \bar{y}=\frac{\sum w_{i} y_{i}}{\sum w_{i}} \end{array} $ | (2) |
式中:X代表地形高程,Y代表插值结果,β1和β2为方程系数;xi、yi和wi分别代表参与插值的每个样本的高程、要素值和对应的综合权重。
为与重庆实际情况相符合,本研究最终使用的综合权重系数计算方程如式(3):
| $ W = {\left({{F_{\rm{d}}}W_{\rm{d}}^2 + {F_{\rm{z}}}W_{\rm{z}}^{\rm{2}}} \right)^{1/2}}{W_{\rm{f}}}{W_{\rm{e}}} $ | (3) |
式中:W代表综合权重,Wd代表距离权重,Wz代表高度权重,Wf代表坡向权重,We为有效地形权重;Fd和Fz分别代表距离权重及高度权重比例。
距离权重的计算如式(4) (Park and Jang, 2016):
| $ W_{\mathrm{d}}=\left\{\begin{array}{ll} 1 & d-r_{\mathrm{m}} \leqslant 0 \\ \min \left[\frac{1}{\left(d-r_{\mathrm{m}}\right)^{a}}, 1\right] & d-r_{\mathrm{m}}>0 \end{array}\right. $ | (4) |
式中:d为样本点到预测格点的距离;rm代表距离阈值;a代表距离权重放大系数,取值通常为2。通过引入距离权重,参与建模的样本点的权重将随其到预测格点的距离而递减。
高度权重的计算如式(5)所示(Park and Jang, 2016):
| $ W_{\mathrm{z}}=\left\{\begin{array}{ll} \frac{1}{\Delta z_{\mathrm{m}}^{b}} & \Delta z \leqslant \Delta z_{\mathrm{m}} \\ \frac{1}{\Delta z^{b}} & \Delta z_{\mathrm{m}} <\Delta z <\Delta z_{\mathrm{x}} \\ 0 & \Delta z \geqslant \Delta z_{\mathrm{x}} \end{array}\right. $ | (5) |
式中:Δz表示样本点与预测格点的高度差;Δzm和Δzx分别表示最小和最大高差阈值;b为高度放大系数,取值通常介于1~2。通过引入高度权重,与预测点高差过大的样本点将获得较小权重。
坡向权重的计算如式(6)(徐成东, 2008):
| $ W_{\mathrm{f}}=\left\{\begin{array}{ll} 1 & |\Delta f| \leqslant 45 \\ \frac{1}{|\Delta f|^{c}} & 45 <|\Delta f| \leqslant 180 \\ \frac{1}{(360-|\Delta f|)^{c}} & 180 <|\Delta f| <315 \\ 1 & |\Delta f| \geqslant 315 \end{array}\right. $ | (6) |
式中:Δf代表样本点与预测格点间的坡向差;c代表坡向放大系数。引入该权重后,与预测格点坡向相近的样本点将获得较大权重。
对复杂地形地区,位于地势平缓区域的格点依然用位于地势复杂区域的样本进行建模,显然并不合理。因此参考Daly et al(2008)的研究引入了有效地形权重。提取有效地形分为如下几步:(1)统计高程数据中每一个栅格点周围半径20 km圆域内最小高程值,得到最小高程基面;(2)在最小高程基面上对每一个栅格点计算半径20 km圆域内像元的平均值以进行平滑;(3)用原始DEM减去平滑后的最小高程基面,得到初始有效地形高度;(4)对初始有效地形高度的每个像元,参照步骤(2)按半径10 km圆域进行平滑,得到最终平滑后的有效地形高度。不断平滑的原因是为了去除一些对气象要素影响不明显的小地形。得到有效地形高度后,需进一步表征平坦地形(2D地形)和复杂地形(3D地形)。因此定义有效地形指数如式(7)。同时,还应考虑有效地形的影响范围。因此继续定义有效距离指数I3a如式(8)所示。最终,根据有效地形指数和有效距离指数,高程的3D指数I3d可定义为式(9)(Daly et al, 2008):
| $ I_{3 \mathrm{c}}=\left\{\begin{array}{lr} 1 & h_{\mathrm{c}} \geqslant h_{3} \\ \frac{h_{\mathrm{c}}-h_{2}}{h_{3}-h_{2}} & h_{2} <h_{\mathrm{c}} <h_{3} \\ 0 & h_{\mathrm{c}} \leqslant h_{2} \end{array}\right. $ | (7) |
式中:hc为有效地形高度;h2和h3分别为2D地形和3D地形阈值,研究中分别设置为50 m和800 m。
| $ I_{3 \mathrm{a}}=\left\{\begin{array}{lr} 1 & h_{\mathrm{a}} \geqslant h_{3} \\ \frac{h_{\mathrm{a}}-h_{2}}{h_{3}-h_{2}} & h_{2} <h_{\mathrm{a}} <h_{3} \\ 0 & h_{\mathrm{a}} \leqslant h_{2} \end{array}\right. $ | (8) |
式中:ha是栅格点周边特定范围内以距离反比为权重的有效地形高度平均值,h2和h3为阈值。
| $ I_{3 \mathrm{d}}=\max \left(I_{3 \mathrm{c}}, I_{3 \mathrm{a}}\right) $ | (9) |
在插值过程中,如果预测站点向相对平坦(3D指数较低)的地区过渡时,应当逐步减少高程对插值结果的影响,使PRISM在地势平缓区域变化为距离权重插值,具体方法如式(10)所示。另外,位于复杂地形区域的样本权重也应随3D指数变化——这就是有效地形权重,其定义如式(11)(Daly, 2002):
| $ \begin{array}{l} \beta_{\text {1new }}=I_{3 \mathrm{d}} \beta_{1} \\ b_{\text {1new }}=I_{3 \mathrm{d}} b_{1} \\ c_{\text {1new }}=I_{3 \mathrm{d}} c_{1} \end{array} $ | (10) |
| $ W_{e}=\left\{\begin{array}{ll} 1 & I_{3 \mathrm{dc}}=1 \\ \frac{1}{\left(100\left|I_{3 \mathrm{dc}}-I_{3 \mathrm{ds}}\right|\right)^{0.5\left(1-I_{3 \mathrm{dc}}\right)}} & 0 \leqslant I_{3 \mathrm{dc}} <1 \end{array}\right. $ | (11) |
式中:I3ds和I3dc分别为气象观测点和插值格点的3D指数。
计算上述各子权重系数后代入式(3)得到综合权重系数,最终代入式(1)、式(2),即可求解PRISM模型并利用高程数据得到任意栅格点的插值结果。另外根据Daly et al(2008),对降水要素进行插值时将对PRISM生成栅格数据进一步做反距离权重平滑,以减少复杂地形导致的降水场空间分布不平滑。
1.2 Cokriging插值法根据地质统计学理论,空间一点处的观测值可理解为随机变量在该处的实现。若随机变量空间变化满足二阶平稳假设,则可利用随机函数理论对特定位置的变量进行无偏估计。Cokriging建立在此理论上,利用统计学知识求解预测样本和次要变量样本的权重,完成对空间某点的预测。考虑单个次要变量的Cokriging方程如式(12)。求解式(12)得到权重a、b,代入式(13)即得到Cokriging预测结果。
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n {{a_i}} \mathit{\boldsymbol{Cov}}\left({{u_i}{u_j}} \right) + \sum\limits_{i = 1}^n {{b_i}} \mathit{\boldsymbol{Cov}}\left({{u_i}{v_j}} \right) + {\mu _1} = }\\ {\mathit{\boldsymbol{Cov}}\left({{u_j}{u_0}} \right)\quad (j = 1, \cdots, n)}\\ {\sum\limits_{i = 1}^n {{a_i}} \mathit{\boldsymbol{Cov}}\left({{u_i}{v_j}} \right) + \sum\limits_{i = 1}^n {{b_i}} \mathit{\boldsymbol{Cov}}\left({{v_i}{v_j}} \right) + {\mu _2} = }\\ {\mathit{\boldsymbol{Cov}}\left({{v_j}{u_0}} \right)\quad (j = 1, \cdots, m)} \end{array} $ | (12) |
式中:a和b分别为预测变量样本和次要变量样本的权重;Cov代表协方差;u和v代表预测变量样本和次要变量样本的数值。
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n {{a_i}} = 1}\\ {\sum\limits_{i = 1}^m {{b_i}} = 0}\\ {{{\tilde u}_0} = \sum\limits_{i = 1}^n {{a_i}} {u_i} + \sum\limits_{i = 1}^n {{b_i}} {v_i}} \end{array} $ | (13) |
求解Cokriging系统的关键在于利用经验协方差函数对空间两点间的协方差进行估计,常用的经验协方差函数模型有指数函数、球面函数、高斯函数、孔穴效应函数等。由于人工对经验函数的参数进行设置存在较大不确定性,研究参考徐武平等(2016)设计了自动拟合方案。即根据观测样本的空间坐标和数值得到协方差与距离的样本对,使用最小二乘法拟合经验协方差函数系数,最终代入Cokriging系统利用高斯消元法求解(Deutsch and Journel, 1992)。
1.3 反距离权重法IDW是一种传统的插值算法,它根据样本点和预测点之间的距离按距离反比计算权重,从而进行插值。
| $ y = \frac{{\sum\limits_{i = 1}^n {\frac{{{x_i}}}{{d_i^a}}} }}{{\sum\limits_{i = 1}^n {\frac{1}{{d_i^a}}} }} $ | (14) |
式中:xi代表样本值,di代表样本到预测格点的距离, y为插值结果,a代表距离权重放大指数。
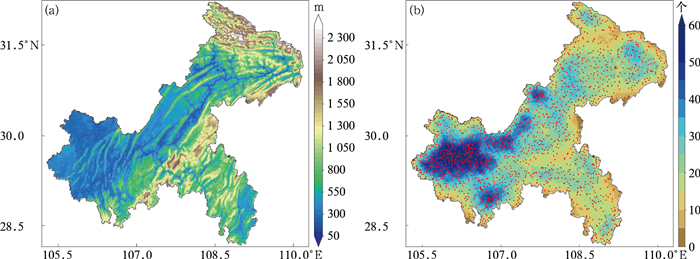
2 资料与试验设计 2.1 资料介绍研究使用的基础地理信息数据为美国国家航空航天局(NASA)提供的Shuttle Radar Topographic Mission (SRTM) 30 m分辨率高程数据(吴昌广等, 2010),使用Arcgis 10.2插值到1 km分辨率。PRISM所需坡向、有效地形等数据均利用Arcgis得到。图 1a为1 km分辨率重庆地区高程分布,可见重庆市地形分布非常复杂,重庆东北部和东南部海拔较高,以山区为主;西部和中部偏北地区地势相对平缓,但也有局部山体分布。
|
图 1 重庆市地理高程分布(a)以及区域自动气象站点(红点)及20 km半径圆域内站点数量(填色)分布(b) Fig. 1 (a) Elevation distribution of Chongqing, (b) automatic weather stations (red points) and number of stations within 20 km radius (shaded area) |
研究所用气象资料来自重庆市气象信息与技术保障中心提供的2017年全市范围内2 024个自动气象站逐日气温和降水资料,并参考前人工作(江志红等, 2018)进行了质量控制,对问题数据采取剔除处理,最后再统计得到逐月累积降水和平均气温。通过质量控制并保证12个月有连续记录的站点共1 761个。图 1b为研究所用站点的空间分布,其中填色为20 km半径圆域内的站点数量。由图 1b可知,重庆市的地面气象站分布密度也极不均匀,绝大部分站点都位于重庆西部地势较为平缓的区域,而重庆东北部和东南部等地形复杂区域站点密度较少,有些局部山区甚至没有站点。
2.2 试验设计为评估PRISM、Cokriging和IDW三种算法在重庆地区的插值效果,研究针对不同数量样本进行了交叉验证试验。为减少随机采样导致站点空间分布不均匀影响插值结果,首先按照一定约束条件挑选1 300个站点,挑选时应当满足:(1)保证每个区(县)都至少有20个观测点;(2)采样结果中包含样本数最少的区(县),其站点数量不得低于各区(县)站点数量平均值的40%;(3)站点数量最多的区县,其站点数量不得超过平均数量的2倍。再由初始1 300个样本按100个逐次递减至200个,得到一共12组样本,后一组样本均从前一组中进行采样,未参与采样的461个站点将作为验证站。由于重庆地区站点空间分布较不均匀,因此插值时使用固定插值半径搜索建模样本并不合适。经试验后,最终确定利用待插栅格点邻近的20个站点作为样本进行建模,如此既能得到较好的插值结果,同时也可兼顾计算效率。利用插值算法得到1 km分辨率栅格后,再经双线性内插到验证站得到要素值,使用平均相对误差(MRE)、平均绝对误差(MAE)和均方根误差(RMSE)作为检验标准。MRE可反映误差相对估计值的大小,MAE可估算预测值可能的误差范围,RMSE则能反映估值的灵敏度和极值效应(李朝奎等, 2007)。MRE、MAE和RMSE的计算公式如式(15)所示。为减少因随机采样造成的不确定性,参考陈锋等(2016)的研究工作,按照前述采样方法进行10次独立采样,得到10组样本并分别进行插值试验及检验,最终统计并对比平均误差。
| $ \begin{array}{*{20}{l}} {MRE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{X_i} - {Y_i}}}{{{Y_i}}}} \right|} }\\ {MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{X_i} - {Y_i}} \right|} }\\ {RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left({{X_i} - {Y_i}} \right)}^2}} } } \end{array} $ | (15) |
图 2为IDW、PRISM和Cokriging三种插值算法使用1 300个样本时的2017年6月平均气温和累积降水插值结果。对比气温的插值,IDW算法(图 2a)由于仅考虑样本与格点间的空间距离,使得在局部地形较复杂的重庆出现大量“牛眼”现象,尤其在重庆东北部和东南部等山地为主的区域更为明显。进一步试验发现,增加或减少插值时的扫面范围并不能有效地改善该现象(图略)。PRISM算法(图 2b)采用了基于高程的回归模型,并没有出现“牛眼”,同时还能清晰地分辨出复杂地形区域山体脉络。另外,由于考虑了有效地形,在重庆西部地势平缓区域,PRISM基于距离权重得到了相对平滑的结果,且仍能分辨出重庆主城区一带的高温中心。Cokriging插值(图 2c)是三种算法中得到结果最平滑的,这是因为经验协方差函数本身只是协方差空间变化的近似,拟合过程不可避免会损失局部细节。但Cokri-ging插值依然能较好地得到气温“西高东低”主要空间分布型。
|
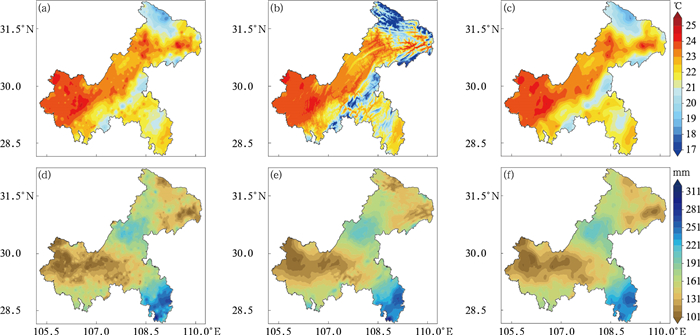
图 2 IDW(a,d)、PRISM(b,e)和Cokriging(c,f)方法使用1 300个样本在2017年6月的平均气温(a,b,c)和累积降水(d,e,f)的插值结果 Fig. 2 Interpolated average temperature (a, b, c) and interpolated cumulation precipitations (d, e, f) in June 2017 by using IDW (a, d), PRISM (b, e) and Cokriging (c, f) methods using 1 300 samples |
对比累积降水的插值结果可知,IDW插值(图 2d)依然得到了大量的“牛眼”,显得非常零乱,但可大致判断重庆西部和东北部降水较少、东南部存在较大降水中心。而PRISM插值(图 2e)由于做了一步反距离权重平滑,使插值结果损失了一些局部细节,但在重庆东南和东北等地形复杂区域,PRISM插值依然能得到较明显的随地形而变化分布的降水。在Cokriging插值中(图 2f),由于经验协方差函数的平滑效果而并未出现“牛眼”,但同时重庆西部地区一些局部降水分布细节也得到保留,这对于气候研究中分析降水空间形态能提供一定帮助。
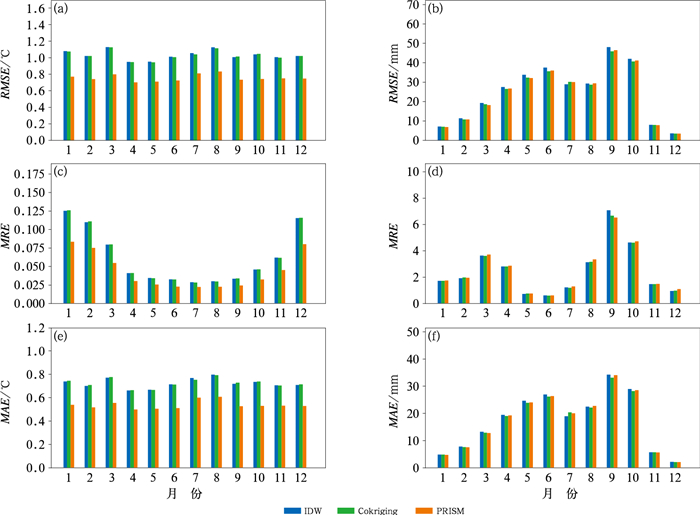
图 3a、3c和3e所示为使用1 300个样本时三种插值算法得到的2017年逐月平均气温误差分布。首先可知,PRISM的三类误差在三种插值算法中都是最小的,年平均RMSE仅有0.75℃;而Cokriging的插值误差与IDW基本相当,均为1.03℃。从平均气温的MRE可知,三种算法均呈现冬季(12月、1—2月)高、夏季(6—8月)低的现象,其中IDW、Cokriging和PRISM在1月(7月)的MRE分别为:0.125(0.029)、0.126(0.028)和0.083(0.022),这说明重庆地区冬季气温的空间分布比夏季更有局地性,插值算法很难把握个别极端气温地区的插值效果。图 3b、3d和3f所示为三种插值算法得到的逐月累积降水误差。根据RMSE变化可知两种考虑了地形的插值算法误差较IDW略小,但优势并不明显。三种算法的累积降水RMSE均表现为从1—12月先呈增长趋势,并在7月和8月突然下降后,又在9—10月突然增加,然后又减小。其中最大RMSE出现在9月,IDW、Cokriging和PRISM的误差分别为48.04、45.84和46.50 mm;最小出现在12月,分别为3.55、3.48和3.45 mm。对比逐月的总降水量(图略)可知,累积降水插值误差的RMSE与当月降水量分布一致,说明降水事件的强弱对插值误差有重要影响。而从MRE分布可知,9月和10月的累积降水插值相对误差明显较高,说明这两个月降水局地性较强,使得空间插值算法将很多降水量级较小的地区也预测为大量级降水。
|
图 3 逐月平均气温(a, c, e)和累积降水(b,d,f)的RMSE(a,b)、MRE(c,d)和MAE(e,f)变化 Fig. 3 Monthly RMSE (a, b), MRE (c, d) and MAE (e, f) of interpolated monthly average temperature (a, c, e) and interpolated accumulated precipitation (b, d, f) |
表 1给出了利用三种插值算法2017年平均气温插值绝对误差与验证站观测值和高程值计算的相关系数。可见高程是气温误差的重要影响因素,IDW和Cokriging算法的插值误差关于高程的相关系数均达到了0.3以上;但PRISM算法将误差与高程的相关系数降到了0.142,说明该算法有效地改善了因地形高度造成的平均气温插值误差。表 2给出了累积降水插值绝对误差与验证站观测和高程的相关系数,可见降水量与误差的相关性已经超过了高程与误差的相关,说明降水插值的误差主要受降水事件本身影响,对重庆这样降水局地性较强的地区,考虑地形的空间插值算法并不一定有优势。
|
|
表 1 三种插值算法平均气温插值误差与验证站观测值和高程的相关系数 Table 1 Correlation coefficients between interpolation errors from the three methods and observation values and elevations |
3.2 不同样本数量对插值的影响
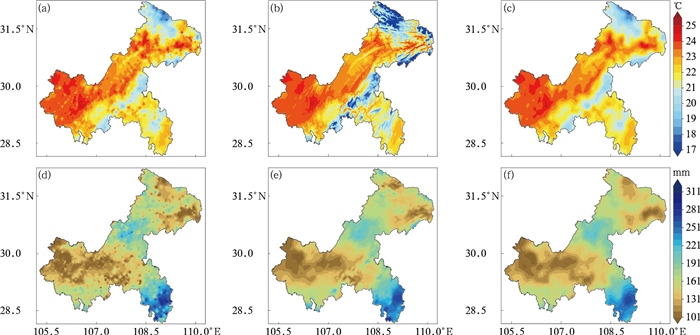
图 4给出了只使用500个样本时各算法在2017年6月的平均气温和累积降水插值结果。与图 2a、2d对比可见,样本减少后IDW插值无论平均气温还是累积降水均损失了一些局部细节,但“牛眼”现象并未得到明显缓解。而PRISM平均气温的插值结果受样本数量的影响较小,仅在个别局部与图 2b存在区别。这是由于PRISM采用了高程回归模型,而插值使用的高程数据并未发生变化。累积降水的变化(图 4e)较平均气温更明显,这可能是由于PRISM算法在降水插值中进行了反距离平滑,因而对样本数量变化更敏感。当采用较少数量样本时,Cokriging插值结果(图 4c、4f)较图 2c、2f明显更加平滑,这可能是由于样本与格点间距离增大,对应了经验协方差函数中较平滑部分所致。
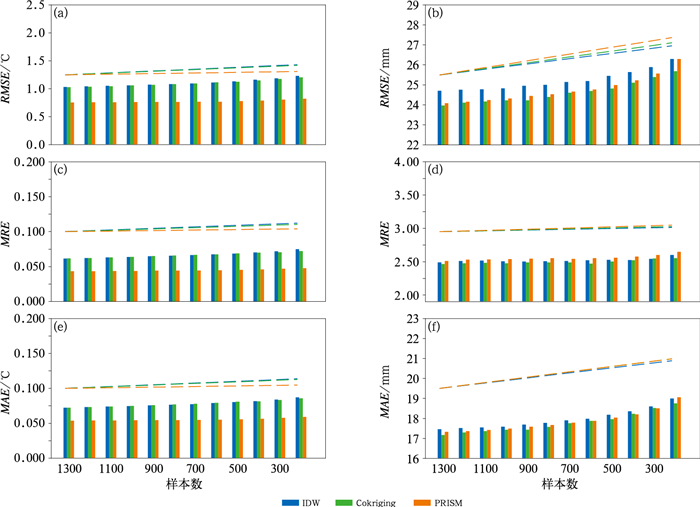
图 5给出了不同样本数量时三种算法2017年月平均气温和累积降水插值的全年平均RMSE、MRE和MAE变化。从图 5a、5c和5e可见,IDW、Cokriging和PRISM的气温插值平均误差均随样本数量减少而递增,三种算法的RMSE斜率分别为0.005 5、0.005 1、0.001 8,以IDW误差斜率最大,PRISM最小。当样本数量低于600个时,IDW法的平均RMSE已经略高于Cokriging,成为误差最大的算法。从累积降水的误差变化可知(图 5b、5d和5f),不管样本数量多少,两种考虑地形的插值算法RMSE均低于IDW的,但PRISM的MRE较另外两种算法更高,且PRISM的误差增长速度较快:RMSE的增长斜率为0.056,明显高于另外两种算法。使用不同数量样本时,PRISM法的误差均高于Cokriging;当只有200个样本时,PRISM的均方根误差达到26.29 mm,已经接近于IDW的误差。这说明进行累积降水插值时,PRISM法受样本数量影响较大,误差随样本数量减少增长较快;当样本数量较少时,采用Cokriging算法可能误差更小。
|
图 5 不同样本数量下三种算法全年平均气温(a, c, e)和累积降水(b,d,f)的RMSE(a,b)、MRE(c,d)和MAE(e,f)变化(虚线为误差增长趋势线) Fig. 5 (a, c, e) Average RMSE (a, b), MRE (c, d) and MAE (e, f) of average temperature using three interpolation methods, (b, d, f) corresponding errors of accumulated precipitation (dashed lines: trendlines) |
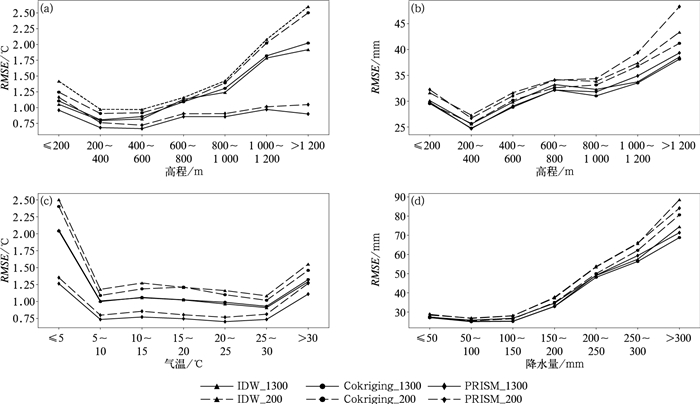
为直观地分析误差的分布情况,图 6给出了各算法采用1 300和200个样本时在不同观测数值和验证站高度等级区间的全年平均RMSE变化。由图 6a可知,三种算法气温插值误差表现为随高度增加先减小后增大,并以Cokriging和IDW误差随海拔升高增加最明显;说明在地势较矮地区和地势较高区域插值误差都偏大,前者可能是受城市热岛或河谷的影响,后者则可能受高海拔地区站点数量较少影响。采用200(1 300)个样本时,IDW、Cokriging和PRISM三种算法在200 m以下地区的气温RMSE分别为:1.42(1.05)、1.25(1.1)和1.16(0.95) ℃;在1 200 m以上地区的RMSE分别为:2.6(1.9)、2.5(2.0)和1.05(0.9) ℃。可见样本数量较少时,Cokriging的误差略低于IDW;而不论样本数量多少,在任意海拔区间PRISM的RMSE都是最低的,且可见PRISM在温度插值中对样本数量的变化并不敏感。另外根据图 6c,三种方法按气温数值分段的误差呈两端高中间低,说明算法对极端气温的插值误差偏大;但依然以PRISM误差最小。
|
图 6 采用1 300个样本(实线)、200个样本(虚线)时,三种算法插值结果在不同高程区间(a,b)和不同观测数值区间(c)平均气温及(d)累积降水的平均RMSE变化(a,c)平均气温,(b,d)累积降水 Fig. 6 RMSE of three interpolation methods using 1 300 (solid line) and 200 (dashed line) samples at different elevations (a, b) and observation values of average temperature (c) and accumulated precipitation (d) (a, c) temperature, (b, d) accumulated precipitation |
图 6b为累积降水插值误差随高度的变化,可见当高度低于200 m时插值误差较高,随后误差减少又随高度递增,并以PRSIM增速较快。采用200(1 300)个样本时,IDW、Cokriging和PRISM三种算法在200 m以下地区的累积降水RMSE分别为:31.6(30.1)、29.5(29.5)和32.2(29.8) mm;在1 200 m以上地区的RMSE分别为:43.3(38.5)、41.2(38.1)和48.3(39.3) mm。根据站点降水与海拔关系(图略),低海拔地区误差较大可能是因局地性强降水较多造成,而高海拔地区的误差可能因样本较少造成。另外,当样本数量较多时,PRISM与Cokriging插值误差接近;而当样本数量较少时,PRISM在高海拔与低海拔地区误差均大于Cokriging。图 6d为降水误差随降水量级的变化,可明显看出误差随降水量级增大而增大。其中当样本数量较少时,Cokriging对大量级降水的插值误差小于另外两个算法。综合图 6b、6d可见,Cokriging算法在对累积降水的空间插值中相对IDW和PRISM有一定优势。
4 结论为评估Cokriging和PRISM两种可考虑地形因素的空间插值算法在重庆地区的插值效果,本文使用重庆市2017年逐月平均气温和累积降水资料,利用IDW、PRISM和Cokriging三种算法进行了插值试验,详细分析对比了其插值误差。根据分析结果,主要结论如下:
(1) PRISM和Cokriging能较好地改善IDW算法插值结果中明显的“牛眼”现象。其中,PRISM的插值结果能较好地表现出局地地形轮廓,对实际气候研究与分析有很大帮助;Cokriging的插值结果相比另外两种算法更加平滑,但依然能保留一些重要的要素局部细节。
(2) 采用1 300个样本时,平均气温的插值误差以PRISM最小,年平均均方根误差仅为0.75℃;累积降水插值效果则以两种考虑地形的算法略优,年平均均方根误差为24 mm左右,略低于IDW。进一步分析表明,PRISM能较好地改善地形对气温插值误差的影响,可将绝对误差与高程的相关系数降低至0.142,另外两种算法均为0.3以上;但对于累积降水,由于局地性较强,误差主要受降水量级影响,两种考虑地形的插值算法并无明显优势。
(3) 采用不同数量样本的插值试验表明,三种算法插值误差均随样本数量减少而递增。气温插值误差以PRISM增长最慢,增长斜率为0.001 8,低于IDW的0.005 5和Cokriging的0.005 1;但PRISM的降水插值误差则为最快,同时各数量样本均以Cokriging误差最小。这说明Cokriging算法在累积降水插值中,尤其当样本数量较少时,具有一定优势。
(4) 对算法在不同样本数值和高度区间的误差分析表明,平均气温插值在低海拔和高海拔地区的误差最大,前者可能是受河谷、城市热岛影响,后者可能是高海拔地区观测样本较少的缘故。PRISM在不同高度区间、不同气温数值区间的误差均为最小,且误差随高度增加的增速较慢。但两种考虑地形的插值算法在降水插值中优势并不明显:Cokri-ging误差略小于另外两种算法;当样本数量较少时,Cokriging的优势相对突出。
综合来看,虽然PRISM和Cokriging同属能考虑地形的插值算法,其插值误差特征却存在较大不同。在重庆地区,PRISM算法的平均气温插值精度较高,受样本数量影响较小;当样本数量较多时,其在累积降水的插值中误差也并不太大。考虑到该算法运算稳定、速度较快,因此相对Cokriging而言是一种适合气象业务工作使用的算法。但在累积降水的插值中,PRISM的误差受样本数量影响较大;样本数量较少时,Cokriging相比PRISM和IDW能有更好的表现。
陈锋, 董美莹, 冀春晓, 2016. 综合分析法在复杂地形气温精细格点化中的应用[J]. 高原气象, 35(5): 1376-1388. Chen F, Dong M Y, Ji C X, 2016. Application of a comprehensive analysis method on hourly surface air temperature interpolation over a complex terrain region[J]. Plateau Meteor, 35(5): 1376-1388 (in Chinese).
|
贺芳芳, 徐卫忠, 周坤, 等, 2018. 基于雷达资料的上海地区暴雨面雨量计算及应用[J]. 气象, 44(7): 944-951. He F F, Xu W Z, Zhou K, et al, 2018. Compution and application of rainstorm surface rainfall based on radar data in Shanghai[J]. Meteor Mon, 44(7): 944-951 (in Chinese).
|
姜晓剑, 刘小军, 黄芬, 等, 2010. 逐日气象要素空间插值方法的比较[J]. 应用生态学报, 21(3): 624-630. Jiang X J, Liu X J, Huang F, et al, 2010. Comparison of spatial interpolation methods for daily meteorological elements[J]. Chin J Appl Ecol, 21(3): 624-630 (in Chinese).
|
蒋育昊, 刘鹏举, 夏智武, 等, 2016. 基于PRISM的山地环境大气湿度的空间插值[J]. 福建农林大学学报(自然科学版), 45(6): 692-699. Jiang Y H, Liu P J, Xia Z W, et al, 2016. Spatial interpolation of humidity over mountain area based on PRISM[J]. J Fujian Agric Forestry Univ (Nat Sic Ed), 45(6): 692-699 (in Chinese).
|
蒋育昊, 刘鹏举, 夏智武, 等, 2017. 站点密度对复杂地形PRISM月降雨空间插值精度的影响[J]. 南京林业大学学报(自然科学版), 41(4): 115-120. Jiang Y H, Liu P J, Xia Z W, et al, 2017. Effects of spatial station density on accuracy of spatial interpolation of monthly rainfall over complex terrain base on PRISM[J]. J Nanjing Forestry Univ (Nat Sci Ed), 41(4): 115-120 (in Chinese).
|
江志红, 祝亚鹏, 马红云, 等, 2018. 同化自动站资料建立三峡地区2014年1月高分辨率温度场的模拟研究[J]. 大气科学学报, 41(3): 289-297. Jiang Z H, Zhu Y P, Ma H Y, et al, 2018. Simulation study of establishment of high resolution temperature field by assimilating automatic station data in the Three Gorges Area in January 2014[J]. Trans Atmos Sci, 41(3): 289-297 (in Chinese).
|
李朝奎, 陈良, 王勇, 2007. 降雨量分布的空间插值方法研究——以美国爱达荷州为例[J]. 矿产与地质, 21(6): 684-687. Li C K, Chen L, Wang Y, 2007. Research on spatial interpolation of rainfall distribution—a case study of Idaho State in the USA[J]. Miner Resour Geology, 21(6): 684-687 (in Chinese). DOI:10.3969/j.issn.1001-5663.2007.06.016
|
李月臣, 何志明, 刘春霞, 2014. 基于站点观测数据的气温空间化方法评述[J]. 地理科学进展, 33(8): 1019-1028. Li Y C, He Z M, Liu C X, 2014. Review on spatial interpolation methods of temperature data from meteorological stations[J]. Prog Geogr, 33(8): 1019-1028 (in Chinese).
|
刘强, 林孝松, 2015. 重庆市降雨空间模拟方法研究[J]. 重庆工商大学学报(自然科学版), 32(10): 28-32. Liu Q, Lin X S, 2015. Study on the method of rainfall spatial simulation in Chongqing[J]. J Chongqing Technol Business Univ (Nat Sci Ed), 32(10): 28-32 (in Chinese).
|
宋丽琼, 田原, 邬伦, 等, 2008. 日降水量的空间插值方法与应用对比分析——以深圳市为例[J]. 地球信息科学学报, 10(5): 566-572. Song L Q, Tian Y, Wu L, et al, 2008. On comparison of spatial interpolation methods of daily rainfall data:a case study of Shenzhen[J]. Geo-Inf Sci, 10(5): 566-572 (in Chinese). DOI:10.3969/j.issn.1560-8999.2008.05.003
|
吴昌广, 林德生, 周志翔, 等, 2010. 三峡库区降水量的空间插值方法及时空分布[J]. 长江流域资源与环境, 19(7): 752-758. Wu C G, Lin D S, Zhou Z X, et al, 2010. Spatial interpolation methods and temporal spatial distribution of precipitation in the Three Gorges Reservoir Area[J]. Resour Environ Yangtze Basin, 19(7): 752-758 (in Chinese).
|
夏智武, 刘鹏举, 陈增威, 等, 2016. 山地环境日气温PRISM空间插值研究[J]. 北京林业大学学报, 38(1): 83-90. Xia Z W, Liu P J, Chen Z W, et al, 2016. Spatial interpolation of daily air temperature in mountain area based on PRISM[J]. J Beijing Forestry Univ, 38(1): 83-90 (in Chinese).
|
熊敏诠, 2013. 滑动窗口的普通克立格方法在降水量插值中的应用[J]. 气象, 39(4): 486-493. Xiong M Q, 2013. Application of the moving window ordinary Kriging method in precipitation interpolation[J]. Meteor Mon, 39(4): 486-493 (in Chinese). DOI:10.3969/j.issn.1000-6362.2013.04.017
|
徐成东, 2008.基于线性加权回归模型的降水量空间插值方法研究[D].郑州: 河南大学. Xu C D, 2008.Research on the spatial interpolation for precipitation data using weighted linear regression model[D].Zhengzhou: Henan University(in Chinese).
|
徐成东, 孔云峰, 仝文伟, 2008. 线性加权回归模型的高原山地区域降水空间插值研究[J]. 地球信息科学学报, 10(1): 14-19. Xu C D, Kong Y F, Tong W W, 2008. A weighted linear regression model for precipitation spatial interpolation in altiplano and mountain area[J]. Geo-Inf Sci, 10(1): 14-19 (in Chinese). DOI:10.3969/j.issn.1560-8999.2008.01.003
|
徐天献, 王玉宽, 傅斌, 2010. 四川省降水空间分布的插值分析[J]. 人民长江, 41(10): 9-12. Xu T X, Wang Y K, Fu B, 2010. Interpolation analysis of precipitation spatial distribution in Sichuan Province[J]. Yangtze River, 41(10): 9-12 (in Chinese). DOI:10.3969/j.issn.1001-4179.2010.10.003
|
徐武平, 邱峰, 徐爱萍, 2016. 空间数据插值的自动化方法研究[J]. 武汉大学学报·信息科学版, 41(4): 498-502. Xu W P, Qiu F, Xu A P, 2016. Automatic method of Kriging interpolation of spatial data[J]. Geo Inf Sci Wuhan Univ, 41(4): 498-502 (in Chinese).
|
朱华忠, 罗天祥, Daly C, 2003. 中国高分辨率温度和降水模拟数据的验证[J]. 地理研究, 22(3): 349-359. Zhu H Z, Luo T X, Daly C, 2003. Validation of simulated grid data sets of China's temperature and precipitation with high spatial resolution[J]. Geogr Res, 22(3): 349-359 (in Chinese). DOI:10.3321/j.issn:1000-0585.2003.03.011
|
Adhikary S K, Muttil N, Yilmaz A G, 2017. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments[J]. Hydrol Process, 31(12): 2143-2161. DOI:10.1002/hyp.11163
|
Daly C, 2002.Variable influence of terrain on precipitation patterns: Delineation and use of effective terrain height in PRISM[EB/OL].Oregon State University: 7.http://www.prism.oregonstate.edu/documents/pubs/2002_influenceTerrain_daly.pdf.
|
Daly C, Gibson W P, Taylor G H, et al, 2002. A knowledge-based approach to the statistical mapping of climate[J]. Climate Res, 22: 99-113. DOI:10.3354/cr022099
|
Daly C, Halbleib M, Smith J I, et al, 2008. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States[J]. Int J Climatol, 28(15): 2031-2064. DOI:10.1002/joc.1688
|
Deutsch C V, Journel A G, 1992. GSLIB Geostatistical Software Library and User's Guide[M].
New York: Oxford University Press.
|
Hevesi J A, Istok J D, Flint A L, 1992. Precipitation estimation in mountainous terrain using multivariate geostatistics.Part Ⅰ:structural analysis[J]. J Appl Meteor, 31(7): 661-676. DOI:10.1175/1520-0450(1992)031<0661:PEIMTU>2.0.CO;2
|
Park J, Jang D H, 2016. Application of MK-PRISM for interpolation of wind speed and comparison with co-Kriging in South Korea[J]. GISci Remote Sens, 53(4): 421-443. DOI:10.1080/15481603.2016.1192373
|
Xu W B, Zou Y J, Zhang G P, et al, 2015. A comparison among spatial interpolation techniques for daily rainfall data in Sichuan Province, China[J]. Int J Climatol, 35(10): 2898-2907. DOI:10.1002/joc.4180
|
 2020, Vol. 46
2020, Vol. 46