引言

在气象业务中，延伸期预报涵盖10~30 d预报时效，它介于中短期预报和短期气候预测的预报缝隙中，科研和预报难度均较大。但从社会发展和经济建设的需求出发，人们希望得到这种更长预报时效的精细化预报。

由于数值模式初始场的不确定性及其对大气的近似处理，加之大气本身是存在随机性的非线性系统(Lorenz，1963；丑纪范，1990)，数值模式不可避免地存在预报偏差(任宏利和丑纪范，2005；Cui et al，2012)。运用一些统计后处理方法并结合集合预报可以对模式预报的不确定性和系统偏差予以订正，对提升预报性能有很大帮助(Hamill and Whita-ker，2007；Cui et al，2012)。结合大气动力学和统计学方法来处理数值模式预报产品的模式输出统计(model output statistics，MOS)法由Glahn and Lowry(1972)提出以来得到广泛应用(刘还珠等，2004；Taylor and Leslie, 2005)。陈豫英等(2011)将MOS方法用于预报宁夏未来40 d逐候的平均气温，研究显示预报效果较模式直接输出有显著提高。然而该方法需要较长时间的资料训练统计模型，在当前数值预报模型频繁更新的情况下应用效果已不能达到最优(佟华等，2014)。因此，众多采用较短时间的模式结果就能进行误差订正的技术方法不断涌现。研究指出，卡尔曼滤波的订正方法对集合预报的中短期温度预报订正效果显著(马清等，2008；李莉等，2011；邱学兴等，2012)。Cui et al(2012)和Guan et al(2015)的研究表明，结合格点分析场应用基于卡尔曼滤波的衰减平均偏差估计法也能有效提高模式对1~16 d地面温度预报的准确率。崔慧慧和智协飞(2013)探索了运用多模式集成的方法对延伸期10~15 d天气过程的气温预报进行订正的可行性。此外，美国环境预报中心运用再预报数据的历史偏差进行延伸期逐周温度预报订正，也取得了较好的预报效果(Guan et al，2019)。

上述研究在延伸期温度的天气过程预报方面做了较好的尝试，并探索了将中短期订正技术应用于较长时间尺度的可能性。然而，在中国延伸期逐日温度预报的订正效果尚不明确。同时，受实际业务预报中的数据储备和时效所限，某些订正方法并不一定能较好地应用于产品研发。滑动平均误差订正是一种基于近期模式预报误差对未来模式预报值进行订正的方法(Stensrud and Yussouf, 2005；Cheng and Steenburgh, 2007；曾晓青等，2019；薛谌彬等，2019)，该方法在国家级业务部门的中短期温度预报中有较好的应用效果(董全等，2012)。本文尝试将该方法推广至延伸期订正预报，探究其适用性。此外，用于美国周气温预报的历史偏差订正方法是否能本地化用于我国精细化逐日预报也有待验证。因此，本文将以ECMWF数值模式为例，采用这两种方法对延伸期逐日2 m温度预报的偏差订正展开研究，探索改善ECMWF模式在中国区域延伸期温度预报效果的订正技术，以支撑日常预报业务需求。

1 资料和方法

使用2015年2月11日至2018年12月31日ECMWF模式集合预报08时起报的240~360 h时效地面2 m温度预报和中国2 093个站日平均气温观测资料，运用滑动平均误差订正和历史偏差订正两种模式误差订正方法对温度的集合平均预报进行偏差订正。其中，ECMWF模式集合预报数据的时空分辨率分别为12 h和0.5°×0.5°，预报区域为0°~55°N、70°~150°E。由于资料分辨率有限，取当日08时和20时的温度预报平均值近似为日平均温度预报。采用双线性插值方法将格点数据插值到站点上进行误差订正。

选用平均绝对误差(MAE)、系统偏差(SB)和预报准确率(TT_k)对预报产品质量进行检验评估。

$ MAE = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{T_{{m_i}}} - {T_{{o_i}}}} \right|} $

$ SB = \frac{1}{N}\sum\limits_{i = 1}^N {\left({{T_{{m_i}}} - {T_{{o_i}}}} \right)} $

式中：T_m和T_o分别为模式预报温度和实况观测值。

式中：N_ri和N_fi分别是预报正确的站数和预报的总站数，温度预报绝对误差≤2℃即为预报正确。

$ T T_{k}=\frac{N_{I_{i}}}{N_{i_{i}}} \times 100 \% $

文中试用滑动平均误差订正和历史偏差订正两种方法探索11~15 d逐日温度预报订正效果。滑动平均误差订正方法是根据数值模式近N日的平均预报误差ΔT_t, 对数值模式第t日起报的未来第d日温度预报进行订正:

$ \Delta {T_i} = \frac{1}{N}\sum\limits_{i = 1}^N {\left({{T_{{m_1} - {\alpha _2}}} - {T_{{r_{ - 1}}}}} \right)} $

式中，N为滑动训练期的长度，T_mt-i-d和T_ot-i分别是模式第t-i-d日预报的未来第d日的温度和第t-i日的台站观测气温实况。温度订正预报为模式预报温度减去模式的平均预报误差，即T_t=T_mt-ΔT_t。历史偏差订正方法主要基于2015—2017年的ECMWF逐日集合预报资料估算平均的模式预报偏差(集合平均预报值与台站实况观测的差值)进行订正。订正后的温度预报为模式预报减去当日模式预报偏差值。

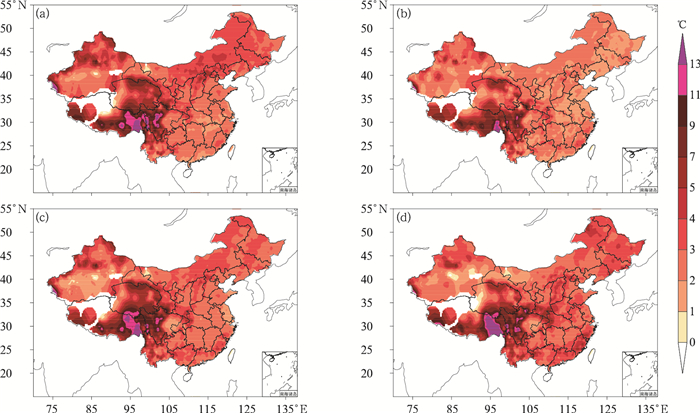
2 模式误差分析

图 1是结合台站观测资料和ECMWF模式集合预报历史数据，估算的该模式对中国不同季节延伸期逐日2 m平均温度预报的平均绝对误差。以第11 d的预报为例可知，模式对中国江淮、江南、西南地区东部等地的延伸期日平均温度的预报误差绝对值相对较小，在1~3℃左右，在华北、东北地区和华南等地的误差略大。误差最大的区域在新疆北部、西北地区中东部、西藏大部及川西高原等地，误差可达5~10℃，其中西藏东部局地可达11℃及以上。不同季节的误差空间分布较类似，夏季的预报误差明显小于其他三个季节，这可能与夏季冷空气过程较少、日变温较其他季节偏小有关。第12~14 d的预报误差空间分布与图 1相似，随着预报时效的延长，误差略有加大(图略)。

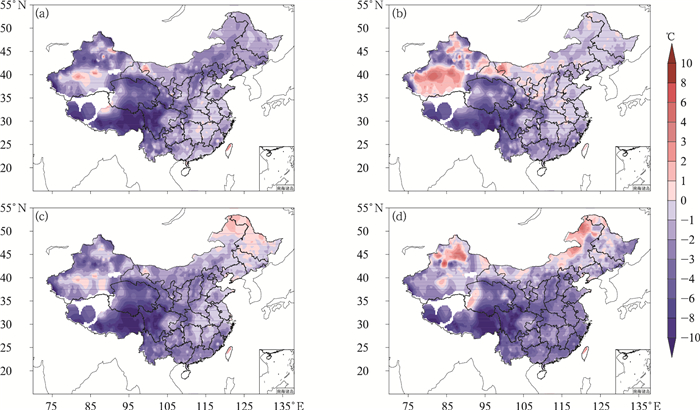
从2015—2017年ECMWF模式预报的系统偏差来看，模式预报的温度在中国大部均较实况偏低，特别是在青海、甘肃南部、西藏和川西高原等地，模式预报较实况偏低3℃以上(图 2)。江汉、江淮、江南等地在各季节的预报偏差均较小，平均系统偏差在-2~-1℃左右。此外，在夏季的南疆盆地高温区，模式预报的温度较实况偏高1~4℃左右。冬季，在新疆北部和内蒙古东北部也存在温度预报偏高的现象，说明冬季在上述地区模式可能存在冷空气强度预报偏弱或回温幅度预报偏高等问题。与平均绝对误差相似，整体而言，中国中东部地区的温度预报系统偏差在夏季最小。

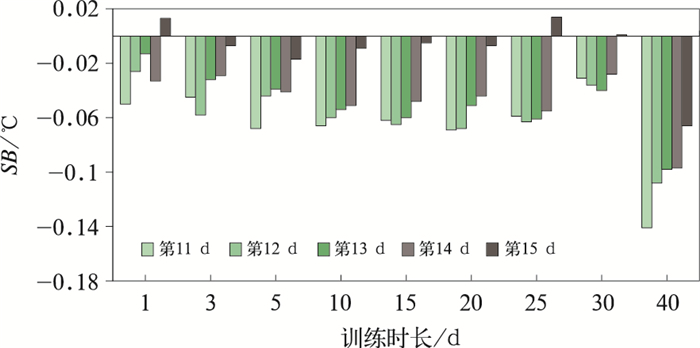
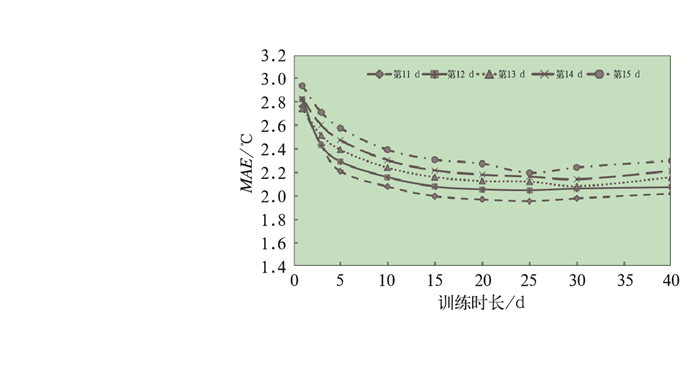
3 滑动训练期预报误差分析

在国家级气象部门温度预报业务中，滑动平均误差订正方法使用2~3 d作为误差滑动训练长度。为了选取适用于预报订正的延伸期逐日温度预报的滑动训练期，利用2015—2017年集合预报数据分别从1~40 d挑选滑动训练时长进行模式逐日温度预报订正试验，检验分析其平均绝对误差和系统偏差值。经对比分析发现，无论选用多少天用于滑动平均误差订正，订正后的预报效果均优于订正前(图 3)。订正前模式预报的平均绝对误差为2.8~3.8℃，订正后上述误差明显减小，说明该方法对延伸期逐日温度预报有一定的订正效果。对于11~15 d的预报，滑动训练期在10 d内时，随着训练期的延长，平均绝对误差迅速减小。超过10 d后，平均绝对误差减速变缓，至25~30 d达到最小值。另一方面，相较于订正前全国平均的温度预报明显低于实况观测2.2~3.8℃，订正后的平均温度系统偏差显著减小。除选用40 d作为滑动训练期的订正后预报系统偏差相对略大外，其他训练时长的系统偏差差异并不明显(图 4)。在各试验训练期中，不同时效的预报系统偏差整体较小的有1、3和30 d。

综合上述检验结果可知，在延伸期逐日温度预报上应用滑动平均误差订正技术时，25~30 d是较优的滑动训练期长度。

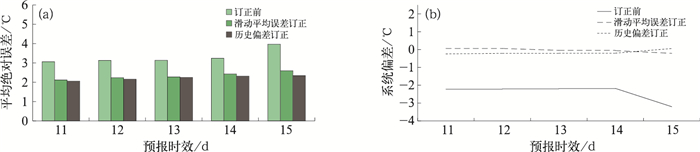
4 预报订正结果分析

基于前文研究结果，本文选取30 d作为滑动训练期应用滑动平均误差订正技术，同时运用历史偏差订正方法，对2018年的ECMWF模式延伸期逐日温度预报进行了订正。检验发现，上述两种订正方法对延伸期逐日平均温度均有较好的订正效果。订正前模式对11~15 d逐日平均温度预报的平均绝对误差为3.1~4.0℃，误差随着时效的延长增加。运用滑动平均误差订正技术订正后的预报平均绝对误差均控制在2.6℃以内；历史偏差订正方法订正后的为2.0~2.3℃，随着时效的延长，其预报效果相较于滑动平均误差订正产品的优势更明显(图 5a)。订正前模式在各时效预报的系统偏差均较实况偏低2.2~3.2℃，而两种订正预报的系统偏差均在-0.3~0.3℃(图 5b)。在11~15 d预报时效的前期，滑动平均误差订正产品的预报相对于实况偏高，随后转为偏低，而历史偏差订正产品的预报则相反，大部分时效以预报偏低为主，后转为较实况偏高。

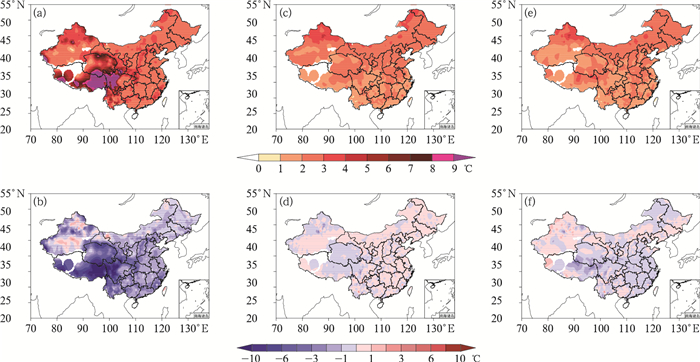
从空间分布上看，两种订正方法对西北地区中东部、西南地区等地的误差订正最为显著，这些地区也是模式预报误差较大的区域。以第11 d的预报为例(图 6)，订正前的模式预报中2018年日平均温度的平均绝对误差在青藏高原及青海北部超过5℃，特别是在青藏高原东部和川西高原，误差更为明显。订正后在上述大部地区的预报平均绝对误差为1~3℃，相对于订正前误差明显减小。在中国中东部地区，两种预报订正方法在南方的订正效果优于北方。随着预报时效的延长，温度预报的平均绝对误差在全国大部均有所升高。历史偏差订正预报的误差增长率低于滑动平均订正预报，特别是在四川盆地、云南和华南东南部沿海地区，在第15 d的平均绝地误差仍低于2℃(图略)。从系统偏差的角度也能看出两种方法对延伸期日平均温度的订正效果十分显著。订正前, 模式预报相对于实况存在预报偏低的问题，几乎在全国各地均存在(图 6b)，在高原地区和中国西北部地区这一偏差更为明显。订正后，年平均的系统偏差在全国大部明显减少至1℃以内。在新疆北部、青藏高原中东部、川西高原等地，订正后的系统偏差略高。

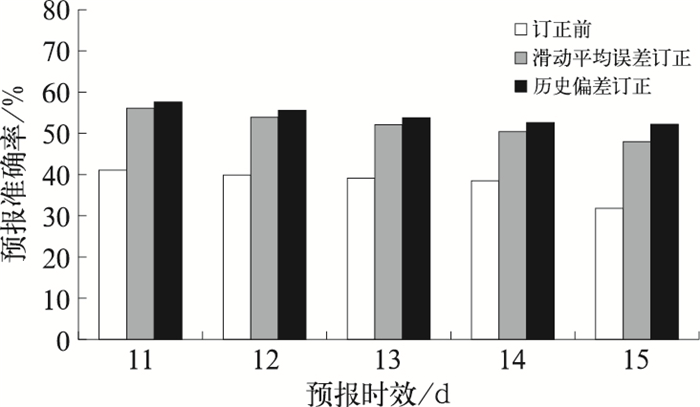
此外订正前后温度的预报准确率差别，同样体现出两种温度预报订正方法对11~15 d延伸期模式日平均温度预报的改进(图 7)。订正前，温度预报在上述延伸期时效的预报准确率几乎均在40%以下，而订正后则基本均达到50%以上。相对于订正前的模式预报，订正后的预报准确率的提升超过30%，在第15 d预报时效更达到50%~60%。此外，应用历史偏差订正方法处理后的温度预报准确率较滑动平均误差订正结果高1%~4%。

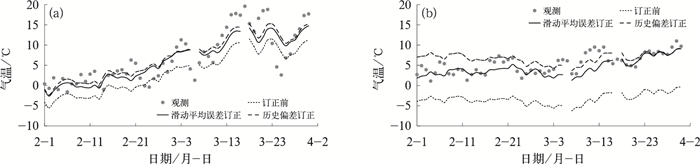
从单站的逐日温度序列(图 8)可以进一步看出，订正后的延伸期时效温度预报的系统性偏差有一定改善。以2018年2—3月北京和拉萨的温度预报为例，两种订正方法均较好地修正了模式预报较实况明显偏低的问题，订正后的预报值与实况观测更为接近，具有较好参考性。由于滑动平均误差订正和历史偏差订正方法的优势是对系统性误差的订正，因此，模式对变温幅度及变温时间的预报偏差无法有效修正。例如，在2月中旬前期、3月上旬前期和下旬北京出现了三次冷空气过程，模式明显低估了其降温幅度，订正后的预报同样存在类似问题。

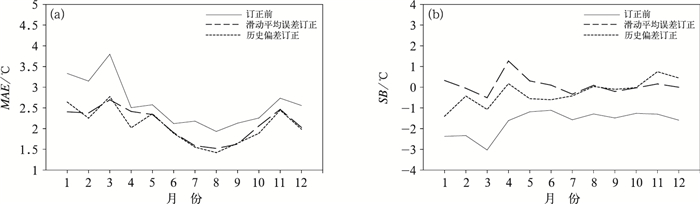
对比订正前后中国中东部(105°E以东)地区温度预报误差的逐月变化可知，两种订正预报的误差全年各月均小于订正前的模式预报，且在1—3月的订正效果尤为明显(图 9a)。在6—10月，订正后的温度预报平均绝对误差基本在2℃以内，表现出较好的参考性。1—5月和11—12月的误差较大，是由于在该时段受冷空气影响，我国中东部温度波动较大，从而延伸期时效逐日预报的难度明显加大。但两种订正方法均能较好地订正模式预报温度偏低的问题(图 9b)，有一定的参考性。历史偏差订正预报较实况偏低的问题主要出现在上半年，随着月份的推进，该订正预报由较实况偏低逐渐转为略偏高。

综上所述，本文研究的两种订正方法对延伸期11~15 d ECMWF模式逐日温度的预报均有较好的订正能力。比较而言，历史偏差订正方法的订正效果略优于滑动平均误差订正方法。

5 结论和讨论

本文研究了滑动平均误差订正方法应用于延伸期逐日预报时的最优滑动训练期长度。在此基础上采用该方法和历史偏差订正方法对延伸期11~15 d ECMWF模式日平均温度预报进行了误差订正，并对2018年的订正预报进行检验分析。主要研究结果如下。

(1) 采用滑动平均误差订正方法改进延伸期模式逐日温度预报时，25~30 d是最优的滑动训练期长度。

(2) 滑动平均误差订正方法和历史偏差订正方法均能有效订正延伸期模式逐日温度预报误差。订正后的平均绝对误差由订正前的3.1~4.0℃减少至2.0~2.6℃，系统偏差由订正前的-3.2~-2.2℃减至-0.3~0.3℃，预报准确率提升30%以上。两种方法均可修正模式温度预报较实况明显偏低的问题。随着时效的延长，历史偏差订正方法相对于滑动平均误差订正方法的优势逐渐显现。

(3) 两种订正方法在全年各月份均有正的预报订正技巧，1—3月预报订正效果尤为明显。在6—10月，订正后的温度预报平均绝对误差基本在2℃以内，具有较好的参考性。采用两种订正方法制作的延伸期逐日精细化订正预报可以为预报员日常业务提供一定的参考，以满足当前迫切的服务需求。

(4) 两种订正方法能修正模式温度预报的系统性偏差，但无法订正模式对变温时间的预报误差。利用动力-统计相结合的方法进行数值模式预报产品的解释应用可能是实现延伸期气象要素预报时间偏差订正的有效途径。

目前国外主流气象中心的延伸期预报产品多以客观化和概率化相结合的方式展现。相对而言，我国决策者和公众对概率预报的接受程度还比较低。从本文研究也可看出，在不同的季节，预报的准确率差异较大，可信度不一样。因此，需要进一步发展我国的延伸期精细化概率预报技术，推广气象概率预报理念。

致谢：感谢国家气象中心唐健和宫宇给本文的修改完善提供了宝贵的建议和意见。