随着互联网的快速发展,政府和公众获取气象信息的渠道已经从电视、短信等传统媒体过渡到新兴互联网时代,智能手机的出现更是让公众对任意地理位置气象产品的及时性、准确性提出了更迫切的需求。为了更好地满足社会需求,完善气象预报产品结构,同时推进精细化气象格点预报业务与技术的发展,需要对高时空分辨率的预报技术进行研究(矫梅燕,2010),快速制作出更精准的预报产品。
大气是一个混沌系统,由于模拟大气的数值模式初值场的不确定性、模式自身存在的缺陷,造成了模式预报产品的不确定性和不准确性。即使数值模式发展至今,系统误差依然存在。闵晶晶(2014)、魏东等(2010)对BJ-RUC系统地面要素预报进行评估, 结果表明模式预报产品系统误差依然存在。张萌等(2018)对GRAPES_GFS模式进行了详细的系统误差评估,这些研究表明,伴随着数值模式的发展,模式预报产品的误差虽有减小,但仍未消除。Klein et al(1959)提出的完全预报法(perfect prognostic,PP)以及Glahn and Lowry(1972)提出的模式输出统计法(model output statistics,MOS)是目前业务中数值预报误差订正的主要方法。Marzban(2003)利用非线性神经网络方法对区域模式的温度输出进行后处理,使得多种预报评分都有所提高。之后很多学者利用线性和非线性预报方法对数值模式预报产品进行订正(曾晓青等, 2009;曾晓青, 2010),黄治勇等(2011)利用灰色预测模式对温度预报进行修正,在湖北不同地区的高低温预报上都有订正效果。罗聪等(2012)基于GRAPES模式预报结果,利用最新的气象观测要素对数值模式预报的结果进行订正,表明对温度预报能力有明显改进。白永清等(2013)分时建立MOS方程能够有效降低夜间的预报误差,将实况最高气温引人卡尔曼滤波方程能提高预报准确率。王婧等(2015)在对比多种订正方法后认为采用滑动双权重平均法得到的2 m温度预报效果最好。
从这些研究中可以看出,数值模式预报产品经过站点统计建模订正后,误差都得到减小,站点订正方法具有正技巧效果。但以上研究都是利用数值模式预报产品与同时刻站点实况建立统计关系进行站点订正预报。目前国家气象中心正开展5 km气象要素格点化预报业务,随着格点化预报技术发展,一日2次的站点预报已远远不能满足业务要求,另外,高分辨率模式预报产品在时效上和准确率上又很难支撑目前业务发展。同时,国内高频次、高时空分辨率的格点多元融合产品(grid multi-source observed merging product)已经开始出现。为了快速获得更精准的格点预报产品,使用高频次的温度格点多元融合产品,采用8种不同的误差订正方案,对欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)发布的模式2 m温度预报产品进行滚动订正预报试验,并对订正前后的预报结果进行检验分析,找出最优订正方案。
1 数据和预报方案 1.1 数据2 m温度模式预报产品采用ECMWF细网格模式产品(以下简称EC),模式起报时间是08时(北京时,下同),范围是0~60°N、70°~140°E,时间分辨率为3 h,预报时效为0~48 h,空间分辨为0.125°×0.125°。2 m温度格点多元融合产品(以下简称GOBS)选用国家气象信息中心的高分辨率陆面数据同化系统(High Resolution China Meteorological Administration Land Data Assimilation System,HRCLDAS)产生的温度格点多元融合产品(张涛等, 2014;韩帅等, 2017;2018),范围是0~60°N、70°~140°E,时间分辨率为1 h,空间分辨为0.05°×0.05°。1 h的2 m温度站点观测数据来自国家级2400个地面气象观测站。研究中的订正场空间分辨率为0.05°×0.05°,需要先采用双线性插值法将EC的2 m温度预报产品插值成空间分辨率为0.05°×0.05°的模式直接输出数据(direct model output,DMO)。所有数据样本时间均从2017年1月1日至9月1日中截取。
1.2 预报方案采用区域数值模式和同化方法对中国区域进行降尺度逐时订正是比较不错的选择之一,但要产生高分辨、高时效性的预报产品, 将会受计算资源和区域模式预报不确定性的很大制约,短期内无法解决。为了在有限资源下获得高质量预报场,利用GOBS来修正预报场的统计建模滚动订正法成为重要手段。滚动误差订正即在获得t时刻的GOBS后,及时对未来t+n(n=1, 2, …,24 h)时刻的预报场进行误差修订。为了得到误差小、准确率高的预报产品,研究采用8种误差订正方案进行回报模拟对比试验,所有方案如下:
方案1:简单误差订正(bias correction,BC),首先根据式1求出t时刻GOBS与DMO预报场的误差Et,然后将误差订正到t+n时刻的DMO预报场式(2),得到最终订正场。
| $ \boldsymbol{E}_{t}=\boldsymbol{O}_{t}-\boldsymbol{Y}_{t} $ | (1) |
| $ \mathit{\boldsymbol{Y}}_{t + n}^\prime = {\mathit{\boldsymbol{Y}}_{t + n}} + {E_t} $ | (2) |
方案2:加权误差订正(weight bias correction,WBC),由于误差Et对临近的预报场影响最大,随着预报时效的延长,影响逐渐减弱,需要用一个权重来调节,将权重调节的误差订正到t+n时刻的DMO式(3),得到最终订正场。权重根据过去30 d预报检验结果进行人工调整得到。
| $ \mathit{\boldsymbol{Y}}_{t + n}^\prime = {\mathit{\boldsymbol{Y}}_{t + n}} + W{\mathit{\boldsymbol{E}}_t} $ | (3) |
方案3:误差回归订正(bias regression correction,BRC),由于很多格点误差变化很大,特别是陆地区域,预计权重方案订正效果有限,采用最小二乘回归的思路对t时刻的误差与t+n时刻的预报误差进行建模式(4),得到回归模型,根据模型进行预报,得到订正场。
| $ \boldsymbol{Y}_{t+n}^{\prime}=\boldsymbol{Y}_{t+n}+b_{0}+b_{1} \boldsymbol{E}_{t} $ | (4) |
方案4:DMO回归订正(DMO regression correction,DRC),根据MOS思想,由于同时刻的模式预报产品对最终订正场有决定性作用,同时与方案3进行对比,采用最小二乘回归的思路对t+n时刻的DMO预报场与t+n时刻的GOBS进行回归建模式(5),得到回归模型,根据模型进行预报,得到订正场。
| $ \mathit{\boldsymbol{Y}}_{t + n}^\prime = {b_1}{\mathit{\boldsymbol{Y}}_{t + n}} + {b_0} $ | (5) |
方案5:双因子回归订正(two-predictor regression correction,TPRC),考虑到t时刻的误差与t+n时刻的DMO预报场都与t+n时刻的GOBS有很强的相关性,将t时刻的误差与t+n时刻的DMO预报场都作为预报因子,与t+n时刻的GOBS进行回归建模式(6),得到回归模型,根据模型进行预报,得到订正场。
| $ \mathit{\boldsymbol{Y}}_{t + n}^\prime = {b_1}{\mathit{\boldsymbol{Y}}_{t + n}} + {b_2}{\mathit{\boldsymbol{E}}_t} + {b_0} $ | (6) |
方案3~方案5中的模型建立完成后,模型不随时间而变化。在模型样本不足的情况下,模型有可能不能很好地适应新因子的变化,为了获得更好的预报结果,将采用滑动建模的方式更新模型。
方案6:滑动误差回归订正(sliding bias regression correction,SBRC)、方案7:滑动DMO回归订正(sliding DMO regression correction,SDRC)、方案8:滑动双因子回归订正(sliding two-predictor regression correction,STPRC)分别与方案3~方案5相对应,订正方案均一致,区别是方案6~方案8中的模型是随预报时间滑动建模。以上8种订正方案对比见表 1。
|
|
表 1 8种订正方案综括 Table 1 Comparison of 8 correction methods |
式中,Ot是t时刻的GOBS,Yt和Yt+n分别是t和t+n时刻的DMO, Et是t时刻的GOBS与DMO的误差,Y ′t+n是t+n时刻的订正场。W是权重系数,取[0, 1]。b0、b1、b2是利用最小二乘法建立的模型系数。
检验方案采用平均绝对误差(MAE)和准确率(A):
| $ M A E=\frac{1}{m} \sum\limits_{1}^{m}\left|\boldsymbol{O}_{t+n}-\boldsymbol{Y}_{t+n}^{\prime}\right|_{i} $ | (7) |
| $ A=\frac{h}{m} $ | (8) |
式中,m是样本总数;h是绝对误差在指定数值以内的样本数;MAE是m个预报样本与GOBS样本的平均绝对误差;Ot+n是t+n时刻的GOBS;A是m个样本绝对误差在2℃以内的准确率,同时,A也是温度误差在[0, 1]、(1, 2]、(2, 4]、(4, 8]、(8, 12]℃的频率统计结果。
2 试验与分析为了全面测试预报方案,试验选择两个时间段进行回报模拟,试验1选择2017年1月1—31日的31 d作为模型样本,以2017年2月1—28日的28 d作为预报样本。试验2选择2017年6月1—30日的30 d作为模型样本,以2017年7月1—31日的31 d作为预报样本,方案6、7、8的模型样本为每个预报日期前31 d(吴启树等,2016)的滑动样本。试验1代表了冷季情况,试验2代表了暖季情况。方案2中的权重是通过前期检验人工调整而得到的权重分布,权重序列为U型曲线,调整后的权重分别为0.98、0.90、0.8、0.7、0.6、0.6、0.7、0.8,不同起报时间权重略有调整,但趋势和形状不变。业务中DMO在08时的4~5 h后才能获得,6 h之后的预报场才真正有实际预报作用,15 h后20时的新预报场将产生,因此两次试验针对08时后6 h(14时起报)、12 h(20时起报)分别进行未来3~24 h(预报时间间隔3 h)的滚动订正研究将更有意义。
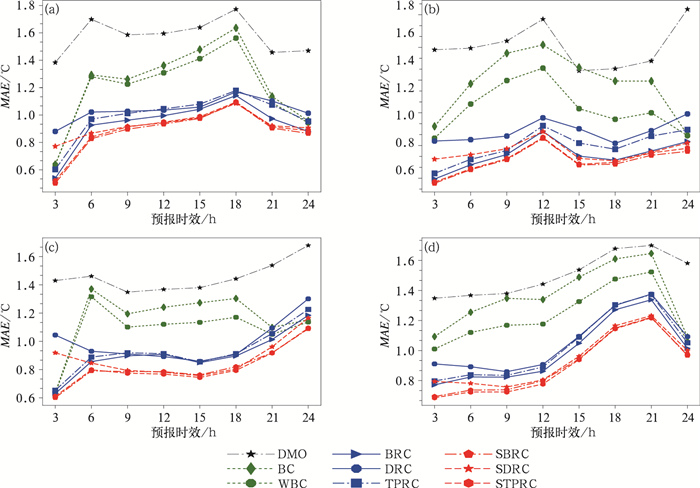
图 1、2、3都是试验1和试验2的格点对格点检验图,即订正场的每个格点与同时刻GOBS中对应格点的检验情况。图 1是试验1和试验2的14和20时起报的8种订正方案订正场的MAE检验,DMO的MAE在1.4~1.8℃。方案1对两次滚动的3 h预报都有明显的订正效果,MAE减小幅度在0.4~0.8℃,随着预报时效延长,订正变得不稳定,在试验1(20时起报)中,15 h的订正结果MAE比DMO偏大。方案2比方案1的订正效果要好,3 h订正的MAE与方案1基本一致,3~24 h订正变得更加稳定,避免了订正后出现MAE比DMO大的情况。方案3的订正效果比较明显,多个预报时效的平均MAE(average MAE for multiple forecast times,AMAE)整体比DMO分别减小了0.64、0.67、0.55、0.51℃(图 1)。基于DMO的全格点建模(方案4)也有很好的订正效果,但订正效果不如方案1~方案3好,特别是3和6 h的订正效果比方案3差很多。说明起报时刻的误差场对短时预报效果有很强的影响。基于误差和DMO的双因子模型(方案5)同时考虑了两个重要影响因子,两次试验的总体预报效果都要好于方案1、方案2、方案4,方案5的AMAE比DMO分别减小了0.59、0.61、0.53℃、0.48℃(图 1)。方案6~方案8的格点MAE检验结果要全面优于方案3~方案5,试验1中方案8的14和20时起报的AMAE分别为0.89和0.92℃,略高于方案6的0.88和0.91℃,试验2中方案8的14和20时起报的AMAE分别为0.81和0.90℃,分别略低于方案6的0.82和0.91℃。可以看出,方案6和方案8是所有方案中预报效果最好的。
|
图 1 试验1(a, b)和试验2(c, d)中14时(a,c)和20时(b,d)起报的8种订正场的MAE格点检验对比 Fig. 1 Comparison of average grid MAE for 8 corrected results forecasted at 14:00 BT (a, c) and 20:00 BT (b, d) in Test 1 (a, b) and Test 2 (c, d) |
|
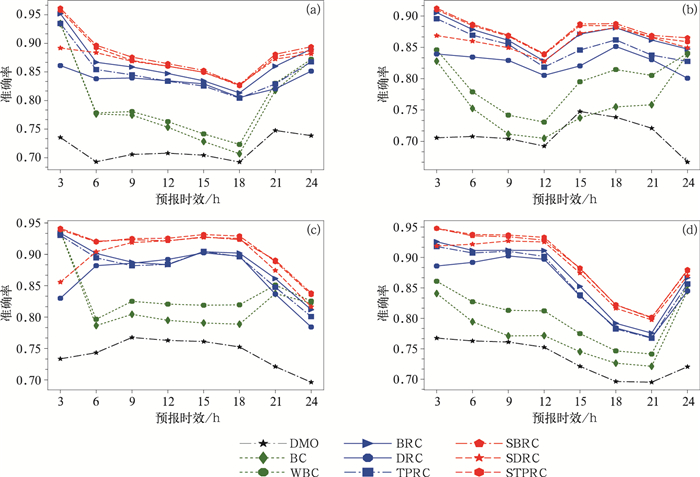
图 2 试验1(a, b)和试验2(c, d)中14时(a,c)和20时(b, d)起报的8种订正场的准确率站点检验对比 Fig. 2 Comparison of hit rate for 8 corrected results forecasted at 14:00 BT (a, c) and 20:00 BT (b, d) in Test 1 (a, b) and Test 2 (c, d) |
|
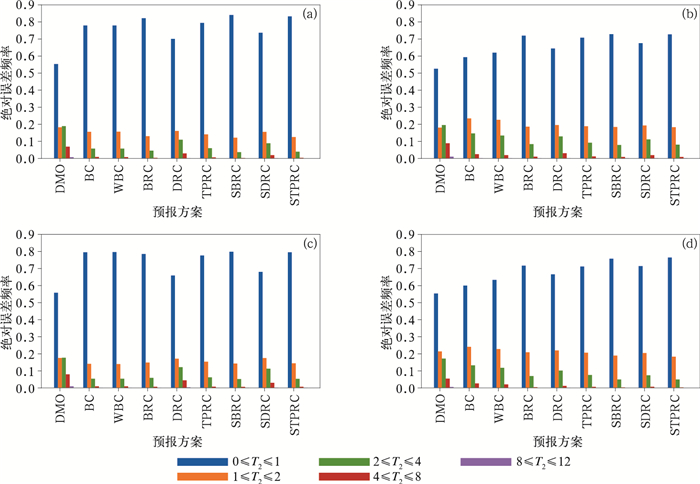
图 3 试验1(a, b)和试验2(c, d)中14时(a,c)和20时(b,d)起报的8种订正场的3 h格点绝对误差频率分布 (T2为2 m温度误差,下同) Fig. 3 The 3 h grid absolute error frequency distribution of the 8 corrected results forecasted at 14:00 BT (a, c) and 20:00 BT (b, d) in Test 1 (a, b) and Test 2 (c, d) (T2 is absolute error of 2 m temperature) |
MAE从一个角度反映了不同方案的预报效果好坏,但仅验证MAE还不能完全反映预报方案的优劣,为了更全面地分析不同方案的订正效果,还需要综合准确率、误差频率分布分析。图 2是试验1和试验2的14和20时起报的8种订正方案订正场的平均准确率检验。图 2中DMO的多个预报时效的平均准确率(average hit rate for multiple forecast times,AHIT)分别为0.72、0.71、0.74、0.73(图 2)。方案1订正后14时起报的AHIT提升到0.8以上, 20时起报的AHIT提升到0.76以上。方案2比方案1的部分时效准确率更高。方案3的AHIT比方案1和方案2又有本质提升,试验1和试验2的AHIT分别达到0.87和0.89。方案4的AHIT虽然总体比方案1和方案2好,但在14时起报的两次试验中,3和6 h订正结果的平均准确率低于方案1、方案2和方案3。方案5虽然比方案4的准确率要高,但是仍然没有方案3的好。方案6、方案7、方案8的准确率在两次试验中都得分最高,方案6和方案8的AHIT都在0.88之上,其中3、6和9 h准确率几乎都在0.9以上。同样两次试验中,方案6和方案8是所有方案中预报效果最好的。
图 3是试验1和试验2中14和20时起报的8种订正方案的3 h订正场的误差频率分布检验。从图中可以看出,方案1~方案8均有明显的订正效果,同样,方案3、方案6、方案8的订正效果最好,试验1(14时起报)中,DMO的4~12℃绝对误差频率是7.6%, 使用三种方案3、方案6和方案8订正后,频率分别减小到0.3%、0.21%、0.29%;试验2 (14时起报)中,DMO的4~12℃绝对误差频率是8.9%, 使用方案3、方案6和方案8订正后,频率分别减小到0.72%、0.68%、0.72%。DMO经过方案1、方案2、方案4、方案5、方案7订正后误差大值区的频率都有不同程度降低,两次试验中方案4和方案7的频率降低幅度最小。可以看出,方案3、方案6和方案8对大值误差的减小效果是非常明显的。同时表明,作为预报模型因子的起报时刻误差场对预报误差大值的减小具有非常好的正技巧作用。
图 4给出了试验1中14时起报的8种预报结果的3 h格点订正场MAE空间分布,DMO的误差主要集中在陆地,特别是青藏高原、缅甸地区,印度北部地区以及蒙古高原、天山山脉、台湾岛等地区。经过方案1~方案8订正后,上述地区的MAE得到很大幅度的减小。方案4和方案7在西伯利亚地区和太行山脉的订正效果不如其他方案。特别是西伯利亚地区MAE大值区域没有得到很好的减小。而方案3和方案5比前几种方案订正更有效,特别是能很好地减小西伯利亚地区和太行山脉的MAE,但在云贵高原和黄土高原仍然有相对周围地区较大的MAE。方案6和方案8的订正效果最明显,将云贵高原和黄土高原的MAE再次减小,使得订正后整个区域的MAE基本在2℃以下。

|
图 4 试验1中14时起报的DMO(a)和8种订正场(b~i)的3 h格点MAE分布 Fig. 4 The grid MAE distribution of DMO and 3 h corrected field forecasted at 14:00 BT in Test 1 (a) DMO, (b-i) 8 corrected fields |
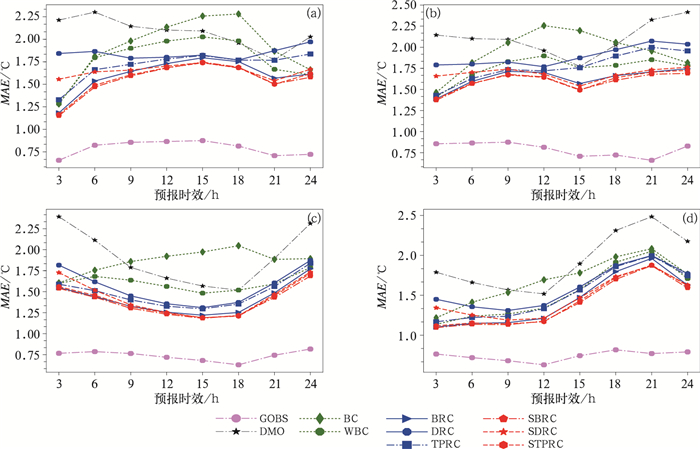
为了综合反映订正方案的优劣,除了对各方案的订正场进行格点检验以外,研究还使用双线性插值方法将GOBS和订正场插值到国家级2400个地面气象站,与同时刻的站点实况进行对比和检验,分析格点订正后的预报结果对站点预报的影响。图 5是在试验1和试验2中,将GOBS和8种订正场插值到站点位置,并与站点实况进行检验的MAE对比图。从两次试验看,GOBS的AMAE在0.75~0.8℃,DMO的在1.9~2.1℃。可以看出GOBS与站点实况是比较接近的。方案1订正后,试验1中14和20时起报的AMAE分别减小到1.91和1.96℃,试验2则分别减小到1.87和1.68℃。方案2在此基础上略有提高,经方案3订正后预报效果得到本质提高,试验1中14和20时起报的AMAE分别减小到1.60和1.64℃,试验2则分别减小到1.41和1.44℃。方案5的订正效果比方案3略差,方案4比方案3和方案5的订正效果都要差。方案6和方案8的检验评分依然取得了最好的成绩,试验1中方案6的14和20时起报的AMAE分别减小到1.55和1.59℃,试验2则分别减小到1.38和1.39℃,两次试验中使用方案6相对DMO的误差分别降低了25%和28%。试验1中方案8的14和20时起报的AMAE分别减小到1.56和1.61℃,试验2均减小到1.40℃,两次试验中使用方案8相对DMO的误差分别降低了25%和27%。
|
图 5 试验1(a, b)和试验2(c, d)中14时(a, c)和20时(b, d)起报的8种订正场以及GOBS的MAE站点检验对比 Fig. 5 Comparison of average site MAE for GOBS and 8 corrected results forecasted at 14:00 BT (a, c) and 20:00 BT (b, d) in Test 1 (a, b) and Test 2 (c, d) |
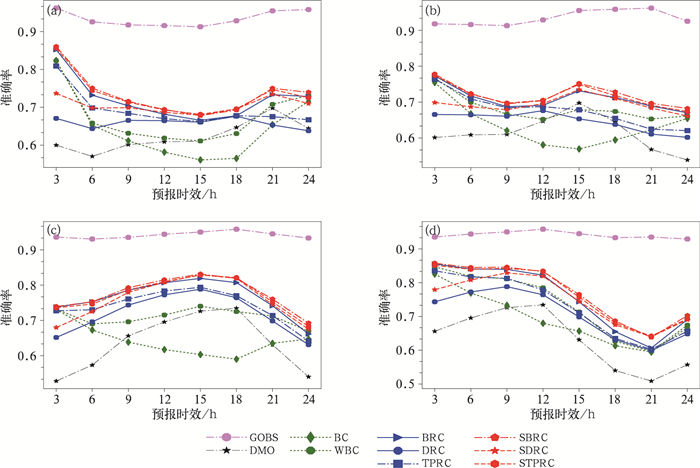
图 6是试验1和试验2中14和20时起报的8种订正方案的订正场及GOBS与站点实况观测的MAE检验。由图可见,插值到站点后,预报准确率比格点检验的准确率有所降低。两次试验中GOBS的准确率都在0.9以上,同样说明了GOBS产品与站点实况观测温度的变化比较一致,误差较小。在两次试验中,方案1在9~18 h的订正结果准确率出现了负技巧,比DMO准确率要低。方案2很好地解决了这一现象,甚至比用方案3的预报结果要好。从3 h准确率检验结果看,方案1和方案2的准确率与方案6和方案8的基本一致,说明使用起报时刻的误差场,仅简单订正后,依然对站点短时预报准确率具有很大的提升作用。
|
图 6 试验1(a, b)和试验2(c, d)中14时(a, c)和20时(b, d)起报的8种订正场以及GOBS的准确率站点检验对比 Fig. 6 Comparison of hit rate for GOBS and 8 corrected results forecasted from 14:00 BT (a, c) and 20:00 BT (b, d) in Test 1 (a, b) and Test 2 (c, d) |
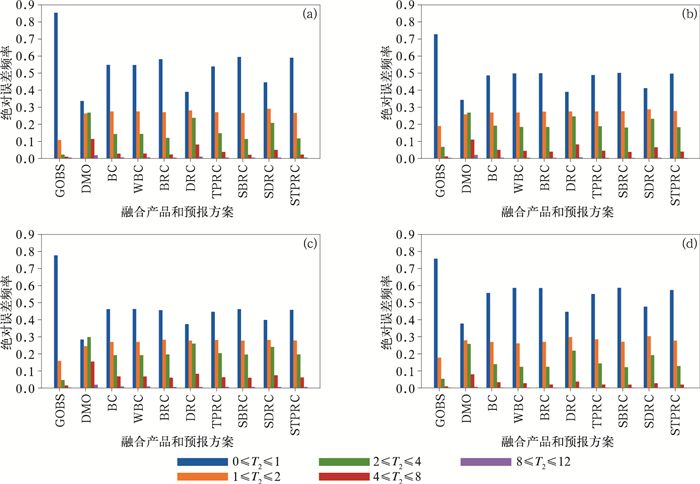
图 7给出了两次试验的全国站点3 h订正场和GOBS的绝对误差频率分布统计情况,试验1(14时起报)中GOBS中4~12℃的绝对误差频率是1.6%, 相应DMO绝对误差频率是13.2%, 使用方案3、方案6和方案8订正后,频率分别减小到2.8%、2.6%、2.7%,试验2(14时起报)中,GOBS中4~12℃的绝对误差频率是1.7%, DMO绝对误差频率是17.4%, 使用方案3、方案6和方案8订正后,频率分别减小到6.5%、6.5%、6.8%。试验1和试验2中20时起报的8种方案的绝对误差频率分布保持了与14时起报结果的同样规律。可以看出,方案3、方案6和方案8对DMO订正后,可使站点预报大值误差大幅减小,表明起报时刻的误差场起到了订正的关键作用。
|
图 7 试验1(a, b)和试验2(c, d)中14时(a, c)和20时(b, d)起报的8种订正场以及GOBS的3 h站点绝对误差频率分布 Fig. 7 The GOBS and site absolute error frequency distribution of the 8 corrected results forecasted at 14:00 BT (a, c) and 20:00 BT (b, d) in Test 1 (a, b) and Test 2 (c, d) |
随着格点化预报业务发展,格点预报产品变得越来越重要。研究使用HRCLDAS业务系统产生的温度格点多元融合产品作为格点实况数据,采用8种不同的误差订正方案,对ECMWF模式的2 m温度预报产品进行滚动订正试验,并对订正前后的预报结果进行格点和站点的综合检验分析,分析结论如下:
(1) 根据两次试验的格点检验情况看,方案1~方案8都对DMO预报场有订正作用,随着预报时效延长,方案1的订正效果会不稳定,出现负订正技巧,方案2是对方案1的有效改进,但不如方案3和方案5的订正效果明显,方案6和方案8的滑动订正法是所有方案中最好的,格点检验中方案6和方案8的8个预报时效MAE基本都在1℃以下, 3、6和9 h格点准确率均在0.9以上。
(2) 根据两次试验的站点检验情况看,GOBS与站点实况是比较接近的,GOBS的AMAE在0.75~0.8℃,准确率均在0.9以上,说明GOBS产品能很好地反映站点温度的变化情况。方案3、方案6和方案8是几种方案中较优的,其中方案6评分最好,3种方案对DMO订正后,可使站点预报大值误差大幅减小。
(3) 总体来说,无论是从格点预报还是站点预报检验结果来看,采用方案6和方案8的订正效果最优,从3、6 h的短时预报检验评分看,方案6检验评分略微高于方案8,表明起报时刻的误差场预报模型因子比数值模式因子在短期订正预报中扮演着更为重要的角色。
白永清, 林春泽, 陈正洪, 等, 2013. 基于LAPS分析的WRF模式逐时气温精细化预报释用[J]. 气象, 39(4): 460-465. Bai Y Q, Lin C Z, Chen Z H, et al, 2013. Product interpretation of refined hourly temperature based on the assimilation of WRF model in LAPS[J]. Meteor Mon, 39(4): 460-465 (in Chinese). |
韩帅, 师春香, 姜立鹏, 等, 2017. CLDAS土壤湿度模拟结果及评估[J]. 应用气象学报, 28(3): 369-378. Han S, Shi C X, Jiang L P, et al, 2017. The simulation and evaluation of soil moisture based on CLDAS[J]. J Appl Meteor Sci, 28(3): 369-378 (in Chinese). |
韩帅, 师春香, 姜志伟, 等, 2018. CMA高分辨率陆面数据同化系统(HRCLDAS-V1.0)研发及进展[J]. 气象科技进展, 8(1): 102-108, 116. Han S, Shi C X, Jiang Z W, et al, 2018. Development and progress of high resolution CMA land surface data assimilation system[J]. Adv Meteor Sci Technol, 8(1): 102-108, 116 (in Chinese). |
黄治勇, 张文, 陈璇, 等, 2011. 湖北省乡镇温度预报方法初探[J]. 气象, 37(12): 1578-1583. Huang Z Y, Zhang W, Chen X, et al, 2011. The study of township temperature forecast in Hubei Province[J]. Meteor Mon, 37(12): 1578-1583 (in Chinese). DOI:10.7519/j.issn.1000-0526.2011.12.015 |
矫梅燕, 2010. 天气业务的现代化发展[J]. 气象, 36(7): 1-4. Jiao M Y, 2010. Modernization process of weather forecast[J]. Meteor Mon, 36(7): 1-4 (in Chinese). |
罗聪, 曾沁, 高亭亭, 等, 2012. 精细化逐时滚动温度预报方法及检验[J]. 热带气象学报, 28(4): 552-556. Luo C, Zeng Q, Gao T T, et al, 2012. Research of seamless hourly updated forecast of temperature and verification[J]. J Trop Meteor, 28(4): 552-556 (in Chinese). DOI:10.3969/j.issn.1004-4965.2012.04.014 |
闵晶晶, 2014. BJ-RUC系统模式地面气象要素预报效果评估[J]. 应用气象学报, 25(3): 265-273. Min J J, 2014. Evaluation on surface meteorological element forecast by Beijing rapid update cycle system[J]. J Appl Meteor Sci, 25(3): 265-273 (in Chinese). DOI:10.3969/j.issn.1001-7313.2014.03.002 |
王婧, 徐枝芳, 范广洲, 等, 2015. GRAPES_RAFS系统2m温度偏差订正方法研究[J]. 气象, 41(6): 719-726. Wang J, Xu Z F, Fan G Z, et al, 2015. Study on bias correction for the 2 m temperature forecast of GRAPES_RAFS[J]. Meteor Mon, 41(6): 719-726 (in Chinese). |
魏东, 尤凤春, 范水勇, 等, 2010. 北京快速更新循环预报系统(BJ-RUC)模式探空质量评估分析[J]. 气象, 36(8): 72-80. Wei D, You F C, Fan S Y, et al, 2010. Assessment and analysis of sounding information obtained from Beijing Rapid Update Cycle Forecast System[J]. Meteor Mon, 36(8): 72-80 (in Chinese). |
吴启树, 韩美, 郭弘, 等, 2016. MOS温度预报中最优训练期方案[J]. 应用气象学报, 27(4): 426-434. Wu Q S, Han M, Guo H, et al, 2016. The optimal training period scheme of MOS temperature forecast[J]. J Appl Meteor Sci, 27(4): 426-434 (in Chinese). |
曾晓青, 2010.模式输出统计技术在局地中短期天气预报中的研究与应用[D].兰州: 兰州大学. Zeng X Q, 2010.Research of model output statistics technique and its application in short-term and medium-term local weather forecast[D].Lanzhou: Lanzhou University(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10730-2010132095.htm |
曾晓青, 王式功, 刘还珠, 等, 2009. 统计降尺度方法在青海省冬季最低温度预测中的应用[J]. 高原气象, 28(6): 1471-1477. Zeng X Q, Wang S G, Liu H Z, et al, 2009. Application of statistical downscaling in minimum temperature prediction over Qinghai Province in winter[J]. Plateau Meteor, 28(6): 1471-1477 (in Chinese). |
张萌, 于海鹏, 黄建平, 等, 2018. GRAPES_GFS2.0模式系统误差评估[J]. 应用气象学报, 29(5): 571-583. Zhang M, Yu H P, Huang J P, et al, 2018. Assessment on systematic errors of GRAPES_GFS 2.0[J]. J Appl Meteor Sci, 29(5): 571-583 (in Chinese). |
张涛, 苗春生, 王新, 2014. LAPS与STMAS地面气温融合效果对比试验[J]. 高原气象, 33(3): 743-752. Zhang T, Miao C S, Wang X, 2014. Comparison tests of the integration effect of surface temperature by LAPS and STMAS[J]. Plateau Meteor, 33(3): 743-752 (in Chinese). |
Glahn H R, Lowry D A, 1972. The use of model output statistics (MOS) in objective weather forecasting[J]. J Appl Meteor, 11(8): 1203-1211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2
|
Klein W H, Lewis B M, Enger I, 1959. Objective prediction of five-day mean temperatures during winter[J]. J Meteor, 16(6): 672-682. DOI:10.1175/1520-0469(1959)016<0672:OPOFDM>2.0.CO;2
|
Marzban C, 2003. Neural networks for postprocessing model output:ARPS[J]. Mon Wea Rev, 131(6): 1103-1111. DOI:10.1175/1520-0493(2003)131<1103:NNFPMO>2.0.CO;2
|
 2019, Vol. 45
2019, Vol. 45 