引言

随着社会经济的发展和科技的不断进步，人民群众对天气预报的准确率和精细化程度提出了越来越高的要求。2 m温度是天气预报中最重要的气象要素之一，提高其预报准确率也是天气预报的重要工作之一。尽管高分辨率数值预报技术的快速发展对中小尺度天气的预报能力不断提高，也为天气预报提供了丰富的客观预报产品，但是由于数值模式的初始场存在误差、模式物理过程的不完美以及大气的混沌性，数值预报存在不可避免的系统性误差。为了减小模式误差和提高预报准确率，一方面可以通过资料同化来改善初始场(王学忠等，2003；托亚等，2003；盛春岩等，2006；官元红等，2014；薛谌彬等，2017)，优化模式的辐射过程、微物理过程、边界层方案、积云对流过程、陆面过程等物理过程参数化方案(陈德辉等，1996；刘还珠等，1998；陈静等，2003；黄安宁等，2008；徐道生等，2014；陈海山和孙照渤，2004a；2004b；2005)等途径来提高数值模式的准确度；另一方面可以利用误差订正技术对数值预报产品进行解释应用(杨松等，2003；赵声蓉，2006；段文广等，2012；王敏等，2012；王丹等，2016；吴启树等，2016)，以降低高分辨率模式中的相对误差可能导致的模式低命中率和高虚假预警率(Mass et al, 2002)。前者需要深入研究数值模式和大气物理过程，难度较高；后者采用数理统计的方法，相对而言简单些。国内学者在模式误差订正方面做了很多相关工作。马清等(2008)利用滞后平均降低误差尺度的自适应误差订正法(类似卡尔曼滤波)对多个国家的区域集合预报模式2 m温度预报做订正，订正后温度预报的各项检验指标都显示出不同程度的改善，对短期预报订正效果较好。李佰平和智协飞(2012)采用一元线性回归、多元线性回归、单时效消除偏差和多时效消除偏差平均的订正方法，对ECMWF模式地面气温预报进行订正。结果表明，四种订正方法都能有效地减小地面气温多个时效预报的误差，改进幅度约为1℃。马旭林等(2015)针对集合预报存在的偏差和集合离散度通常偏小的问题，在卡尔曼滤波递减平均的一阶矩和二阶矩偏差订正方案的基础上发展了综合偏差订正方案，有效地融合了一阶矩和二阶矩订正的优势，对集合平均偏差和离散度具有良好的订正效果，能够改善集合预报的整体质量。王婧等(2015)采用平均法、双权重平均法、滑动平均法和滑动双权重平均法分别对GRAPES_RAFS系统的2 m温度预报产品进行偏差订正，订正后的平均误差大部地区减小到-1~1℃，均方根误差大部地区降低到2.5℃以内，其中订正效果最好的是滑动双权重平均法，全国平均误差大部分在-0.5~0.5℃，不超过-1~1℃的范围。

ECMWF是欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts)的中期天气预报数值模式，国内对T639、ECMWF和日本高分辨率模式预报性能对比后发现(尹姗，2016；张峰，2016；张夏琨，2017)，ECMWF对亚洲中高纬环流形势、西太平洋副热带高压、850 hPa温度变化趋势预报具有较高的预报水平，对中短期天气预报具有重要的指导意义。目前，国内科研业务工作者在数值模式检验评估方面做过很多研究，但是对ECMWF高分辨率模式的2 m温度预报误差订正工作开展较少。为了减小高分辨率数值模式的预报误差，提高模式的释用能力，本文在Xu et al(2013)、王婧等(2015)等工作基础上，进一步采用动态滑动双权重平均法和空间误差逐步订正法，对ECMWF高分辨率模式的2 m最高和最低温度预报进行误差分析和订正，并对订正前后的结果进行检验和对比，从而确定最佳订正方案以改善ECMWF高分辨率模式的2 m温度预报，以期能为模式温度预报释用和精细化气象要素客观预报提供技术支撑。

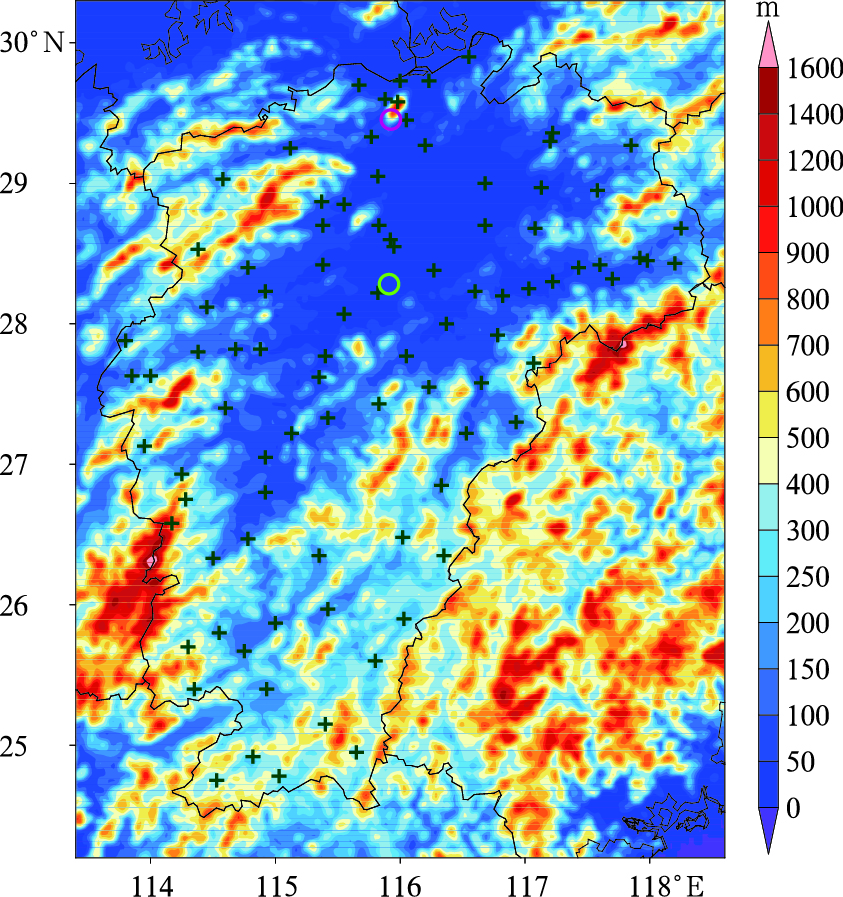
1 资料和方法 1.1 资料

本文采用的资料是ECMWF 2016年5月1日至2017年5月1日的2 m最高和最低温度预报产品，分辨率为0.125°×0.125°，模式预报起始时间为每天12时(世界时，下同)，对预报时效为24、48、72、96、120、144和168 h内的2 m温度进行检验。实况资料为江西省91个县级站(图 1)对应的同时期最高和最低温度观测资料。江西省地形较为复杂，除北部较为平坦外，东西南部三面环山，中部丘陵起伏，全省成为一个整体向鄱阳湖倾斜而往北开口的巨大盆地，如图 1所示。ECMWF高分辨率模式预报具有稳定的预报质量和较高的预报准确率，为了尽量减小地形的影响，本文采用双线性插值方法将模式输出的2 m温度格点预报场插值到站点，以此来订正站点温度预报，并与站点的观测值进行对比，统计分析温度的预报误差。

1.2 订正和检验方法 1.2.1 动态滑动双权重平均订正法

本文采用的滑动双权重平均订正与Xu et al(2013)的方法类似，不同之处在于本文的滑动订正周期是动态调整的，而不是固定不变的。订正方法公式如下：

$ T_{i, t}^{a}=T_{i, t}^{b}+T_{i, t}^{o -b} $

(1)

$ \begin{align} & T_{i, t}^{o-b}=M_{i, t}^{o-b}+ \\ & \frac{\sum\limits_{j=1}^{n}{\left[ \left(T_{i, j, t}^{o}-T_{i, j, t}^{b} \right)-M_{i, t}^{o -b} \right]}{{\left[ 1-{{\left(\omega _{i, j, t}^{o -b} \right)}^{2}} \right]}^{2}}}{\sum\limits_{j=1}^{n}{{{\left[ 1-{{\left(\omega _{i, j, t}^{o -b} \right)}^{2}} \right]}^{2}}}} \\ \end{align} $

(2)

式中，$T_{i, t}^{a}$为第i个测站在预报时效t (t=24, 48, 72, 96, 120, 144, 168 h)订正后的温度，$T_{i, t}^{b}$为模式插值到测站的温度，$T_{i, t}^{o}$为测站的观测温度，$T_{i, t}^{o-b}$为订正项，是两个权重之和，$M_{i, t}^{o-b}$为第i个测站$\left(T_{i, j, t}^{o}-T_{i, j, t}^{b} \right)$的中位数，n为滑动订正周期(n=3, 4, 5, …, 20 d)。$\omega_{i, j, t}^{o-b}$为权重项：

$ \omega _{i, j, t}^{o-b}=\frac{\left(T_{i, j, t}^{o}-T_{i, j, t}^{b} \right)-M_{i, t}^{o-b}}{7.5\times D_{i, t}^{o-b}} $

(3)

式中，$D_{i, t}^{o-b}$是$\left|\left(T_{i, j, t}^{o}-T_{i, j, t}^{b}\right)-M_{i, t}^{o-b}\right|$的中位数。当$\omega _{i, t}^{o-b}>1\ $时，取$\omega _{i, t}^{o-b}=1$；当$\omega _{i,t}^{o-b}<-1$时，取$\omega _{i, t}^{o-b}=1$。

动态滑动双权重平均订正法的滑动订正周期n是不固定的，订正时首先根据前n天的模式预报和观测值计算出订正量，然后对当前预报场进行订正，以此类推，计算出2016年5月1日至2017年5月1日订正后的预报场，本文将分别对用不同滑动周期订正后的温度预报进行误差分析，以确定最佳的滑动订正周期。

1.2.2 空间误差逐步订正法

考虑到上述动态滑动双权重平均订正是对每个测站分别进行的，订正后的温度在空间分布上可能会出现差异较大的情况，比如，高山站观测到的气温经常比周围测站的要明显低，因此，本文又提出了空间误差逐步订正法来消除这种空间上的不连续性。首先考虑预报时效t时刻，在目标测站i附近搜索最邻近的m个测站(本文取m=5)，根据这m个测站与目标测站i的空间位置关系，将这m个测站的温度值用Cressman插值方法(Cressman, 1959)得到参考温度$T_{i, t}^{p}$，公式如下：

$ T_{i, t}^{\rho }=\frac{\sum\limits_{j=1}^{m}{{{w}_{j}}}{{T}_{i, j, t}}}{\sum\limits_{j=1}^{m}{{{w}_{j}}}} $

(4)

式中w_j为权重项：

$ {{w}_{j}}=\left\{ \begin{matrix} \frac{R_{j}^{2}-D_{j}^{2}}{R_{j}^{2}+D_{j}^{2}}, & {{D}_{j}}<{{R}_{j}} \\ 0, & {{D}_{j}}\ge {{R}_{j}} \\ \end{matrix} \right. $

(5)

式中，R_j是影响半径，D_j是周围测站与目标测站的距离。

在滑动订正周期n内每个测站的实况温度与周围m个测站插值到站点的参考温度偏差的平均值记为$\bar{T}_{i, t}^{o}$：

$ \bar{T}_{i, t}^{o}=\sum\limits_{j=1}^{n}{\left(T_{i, j, t}^{o}-T_{i, j, t}^{op} \right)} $

(6)

式中$T_{i, j, t}^{o p}$是将实况温度$T_{i, j, t}^{o}$代入到式(4)得到的温度。那么，考虑了空间误差的温度订正值可以写成以下形式：

$ T_{i, t}^{a}=(1-\alpha)T_{i, t}^{b}+\alpha \left(T_{i, t}^{bp}+\bar{T}_{i, t}^{o} \right) $

(7)

式中，$T_{i, j, t}^{b p}$是将预报温度$T_{i, j, t}^{b}$代入到式(4)得到的温度，α为订正系数，本文取α=0.2。式(7)的目的是将预报温度在空间上的误差逐步向观测误差靠近，采用迭代方法逐步逼近空间观测误差$T_{i, t}^{o}$就能得到订正后的温度值。具体计算过程中，先由式(7)计算得到$T_{i, t}^{a(1)}$，判断是否收敛，如果不收敛，将$T_{i, t}^{a(1)}$作为模式预报值代入式(7)再次计算得到$T_{i, t}^{a(2)}$，直到收敛为止。收敛条件为：

$ \max \left| T_{i, t}^{a(k)}-T_{i, t}^{a(k-1)} \right|<\varepsilon $

(8)

本文取ε=0.1℃。

1.2.3 误差分析方法

本文采用平均误差(ADEV)、均方根误差(RMSE)和预报准确率(ACC)来进行检验分析。公式如下所示：

$ ADEV=\frac{1}{n}\sum\limits_{i=1}^{n}{\left(T_{i}^{a}-T_{i}^{o} \right)} $

(9)

$ RMSE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{{{\left(T_{i}^{a}-T_{i}^{0} \right)}^{2}}}} $

(10)

$ ACC=\frac{{{N}_{c}}}{{{N}_{t}}} $

(11)

式中，N_c和N_t分别为预报误差的绝对值≤2℃的站数和预报总站数。

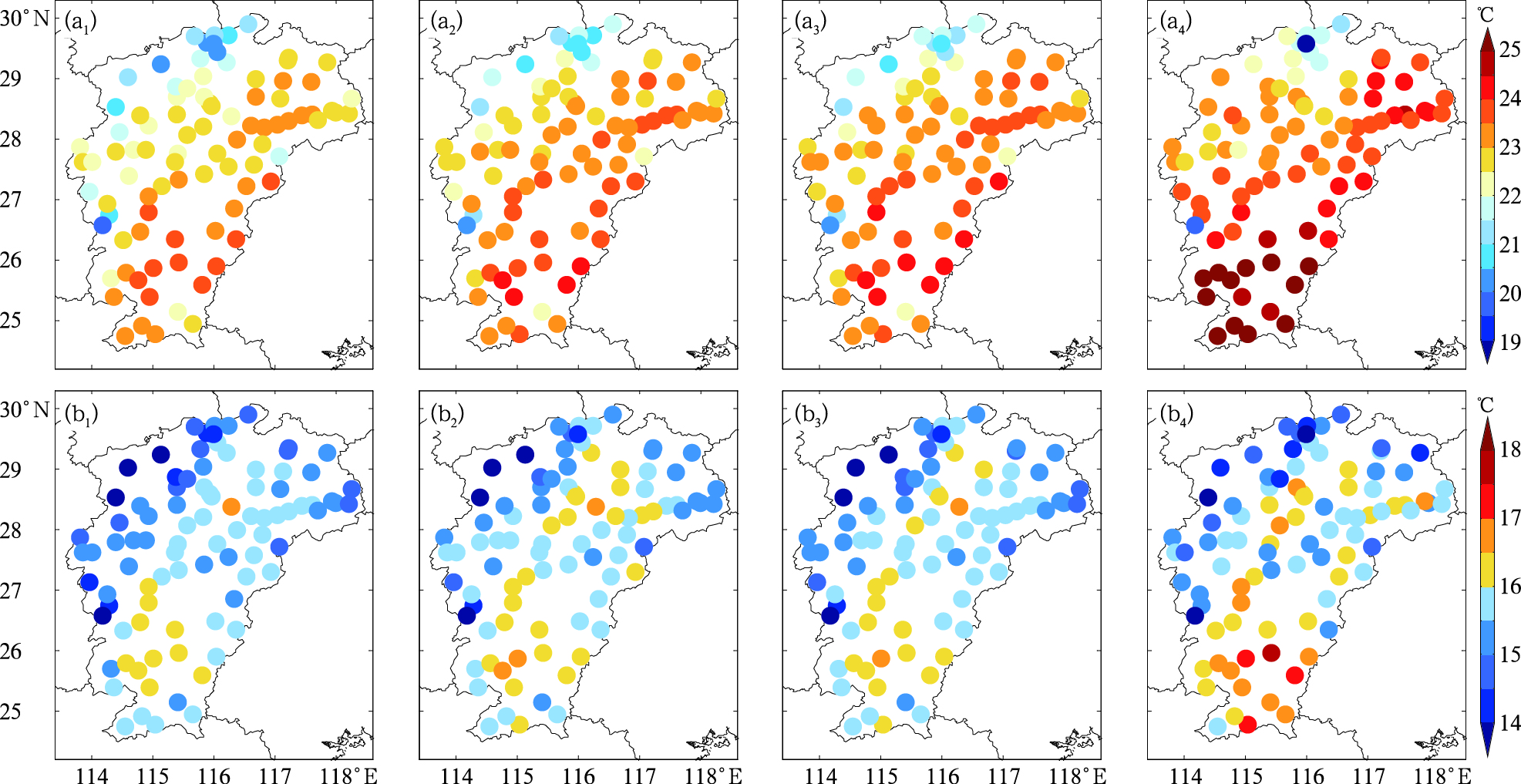
2 模式温度误差与订正方案 2.1 模式温度预报误差分析

本文首先通过对ECMWF高分辨率2016年5月1日至2017年5月1日的预报时效分别为24、48、72、96、120、144和168 h内的2 m最高和最低温度预报产品和江西省91个县级站对应的最高和最低温度观测值进行检验评估，分析了模式2 m温度的预报性能和相对于实况的空间分布(图 2)。结合图 1的地形和观测站地理分布可以发现，ECMWF模式的最高、最低温度能够很好地表现出温度随地形分布的特征。相对于实况而言，模式温度的空间分布表现出显著的系统性偏差，以24 h预报为例(图 2a₁)，江西西北部的最高温度仅在21℃左右，而实况在23℃左右；江西南部的最高温度在23.5℃左右，而实况在25℃左右；其他地方的最高温度较实况也偏低。随着预报时效的延长(图 2a₂，2a₃)，偏低的程度有所改善。整体而言，ECMWF模式的最高温度较实况偏低。模式最低温度也有类似的结果，江西北部和中部的最低温度和实况较接近，而南部的最低温度在16℃左右，而实况在17℃左右。

为了进一步印证上述分析，本文通过计算模式24~168 h不同预报时效的2 m温度预报与实况的ADEV和RMSE后发现(表 1)，模式所有预报时效的最高和最低温度整体上比实况低，最高温度较明显，24 h的ADEV达-1.02℃。最高和最低温度的RMSE随着预报时效的增加而增加，两者在168 h达到最大值，分别为3.39和2.24℃。通过对比还可以发现，最低温度RMSE的最大值比最高温度RMSE的最小值还要低。由此可见，模式的最低温度预报比最高温度要可靠，这是符合常理的。因此，总体而言，ECMWF模式对江西地区的2 m温度预报误差是具有系统性的，可以通过误差订正方法来进行调整改善以满足业务需求。

2.2 订正试验方案

为了检验和评估1.2节所述的动态滑动双权重平均订正和空间误差逐步订正方法对温度预报的订正效果，本文设计了六组订正试验方案：(1)cntl：不订正，ECMWF模式直接输出；(2)mbw05：滑动双权重平均订正，滑动订正周期为5 d；(3)mbw10：滑动双权重平均订正，滑动订正周期为10 d；(4)mbw15：滑动双权重平均订正，滑动订正周期为15 d；(5)mbw20：滑动双权重平均订正，滑动订正周期为20 d；(6)final：在试验(5)的基础上，再用空间误差逐步订正法订正。试验(2)~(5)的目的是考察不同滑动订正周期n对温度预报订正的影响，以确定最佳滑动订正周期n，试验(6)的目的是考察在进行滑动双权重平均订正后，空间误差逐步订正法的进一步订正效果。

3 订正结果分析

图 3为订正前后ECMWF高分辨率模式2016年5月1日至2017年5月1日期间2 m最高和最低温度24~168 h预报时效年平均的ADEV和RMSE、24 h预报时效月平均的ADEV和RMSE分布。对于最高温度(图 3a, 3b, 3e, 3f)，订正前的2 m最高温度年ADEV普遍为负值，24 h达-1.02℃，而经过订正后的误差明显减小，24~168 h预报时效内控制在0.2℃以内，24~72 h预报时效内控制在0.1℃以内(图 3a)。RMSE分布表明，滑动双权重平均订正法在24~72 h预报时效内RMSE都比订正前的小，订正效果较好，24和48 h分别控制在1.9和2.3℃以内，而72 h以后滑动订正周期为5、10、15 d订正方法的RMSE逐渐大于订正前的，订正效果变差，而滑动订正周期为20 d和考虑了空间误差的逐步订正法在168 h预报时效依然比订正前的小，但订正幅度越来越小(图 3b)。这表明：(1)较长的滑动订正周期对模式温度预报有更好的订正效果，采用滑动订正周期20 d是比较理想的；(2)空间误差逐步订正法能进一步提高滑动双权重平均订正法的预报订正质量。试验final的RMSE在所有试验中是最小的，24、48、72 h的RMSE分别从订正前的2.26、2.45、2.61降低到1.81、2.12、2.36，减小幅度为0.45、0.33、0.25，误差相对于订正前减小19.9%、13.5%、9.6%，且48 h的RMSE低于订正前模式24 h的预报，72 h的RMSE低于订正前模式48 h的预报。2 m最低温度的ADEV(图 3c)和RMSE(图 3d)也有类似的结果，24~168 h预报时效内经过各误差订正方法订正后的ADEV控制在-0.2~0℃，效果较好。误差订正方法对于RMSE也有改进，试验final的改进幅度最大，24、48、72 h的RMSE分别从订正前的1.49、1.54、1.60降低到1.29、1.37、1.48，减小幅度为0.20、0.17、0.12，误差相对于订正前减小13.4%、11.0%、7.5%，略低于对最高温度的订正效果。同时注意到72 h的2 m最低温度RMSE低于订正前模式24 h的预报，96 h的RMSE低于订正前模式72 h的预报。总的来说，采用滑动双权重平均订正法和空间误差逐步订正法的综合订正技术(试验final)能较好地订正模式2 m最高和最低温度的系统性误差。

逐月平均的24 h预报时效最高温度ADEV(图 3e)显示，在6—9月ECMWF模式的最高温度比实况偏低幅度较大，其中8月的误差达-1.9℃，RMSE在6—9月也较大，达到2.5℃。经过订正后的ADEV明显减小，误差订正方法对6—9月ECMWF模式最高温度有持续订正能力，对应的RMSE(图 3f)也是逐月减小的，8月的RMSE几乎是全年最低的，仅1.5℃。值得注意的是，由于滑动双权重平均订正法是根据前n天的模式预报和观测值计算出订正量对当前预报场进行的订正，因此一定程度上存在滞后性，9月ECMWF模式最高温度与实况的偏差约为-1.5℃，而在10月，ECMWF模式预报比实况偏低幅度明显减小(图 3e)，偏差为-0.7℃，因此滑动双权重平均订正法对于10月的温度订正可能过度，经过滑动订正周期为5、10、15、20 d的订正后，ADEV(图 3e)呈现出递增的趋势，试验mbw20的误差最大，而经过空间误差逐步订正后误差减小，同样，在RMSE图上(图 3f)，10月的仅采用滑动双权重平均订正法订正后的RMSE与订正前的非常接近，订正效果不太好，在经过空间误差逐步订正后，RMSE减小，因此空间误差逐步订正法能一定程度地改善订正效果。2月和3月也有类似的结果，这可能跟季节过渡期间温度日变化偏大和冬季冷空气降温天气过程有关。对于逐月平均的24 h预报时效最低温度(图 3g)，ECMWF模式的预报偏差较小，仅1月的偏差在-0.65℃，其他月份都在-0.5~0℃；RMSE(图 3h)，夏、秋两季的明显比冬、春两季的小，经过订正后，7月的RMSE最小，约1 ℃。值得一提的是，图 3g中，2月滑动双权重平均订正法的订正效果并不理想，而空间误差逐步订正法的订正幅度最大，订正效果较明显。

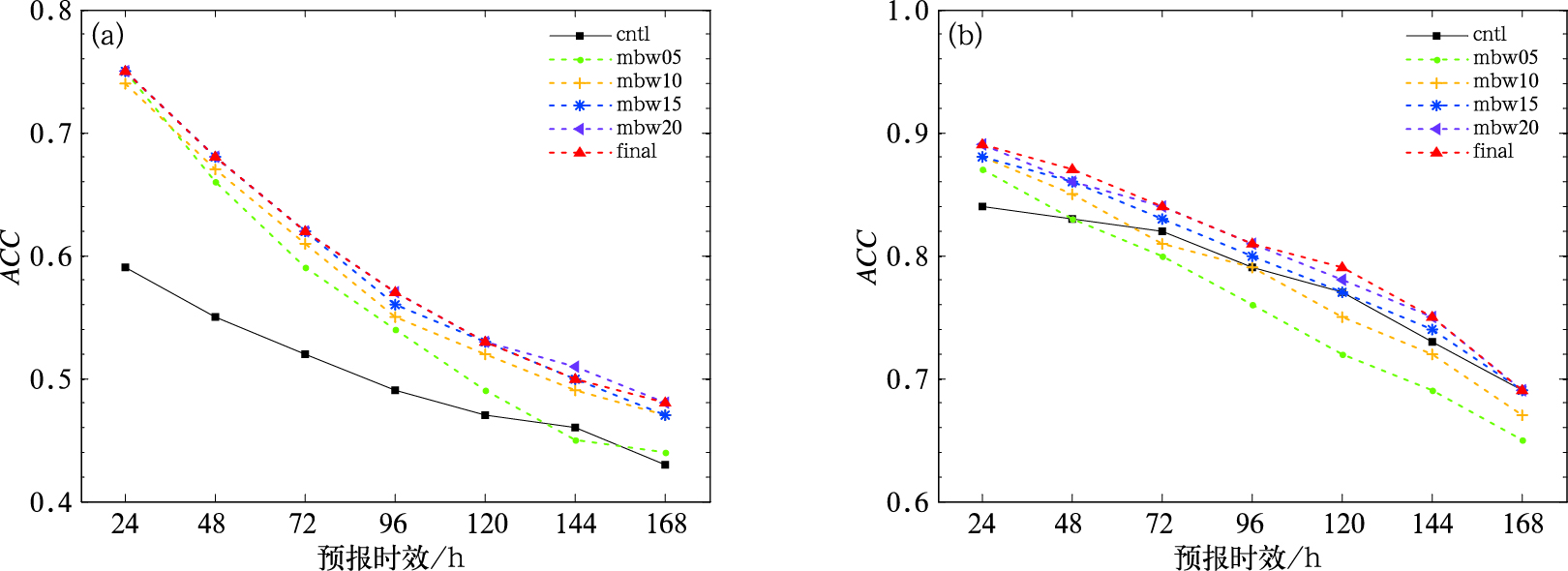
为了检验和评估上述订正方法在业务中的实际应用效果，本文进一步计算了六组试验预报误差≤2℃的准确率(图 4)以评估误差订正方法的订正技巧，发现经过误差订正方法订正后的预报准确率整体上优于订正前。对于最高温度(图 4a)而言，几乎所有订正方法的预报准确率比ECMWF模式的高，有显著正的订正技巧，24 h的预报准确率最高为0.75，随着预报时效的增加逐渐减小，72 h仍在0.6以上，试验mbw05、mbw10、mbw15和mbw20的结果表明，预报准确率随着滑动订正周期n的增加而增加，但增加的幅度越来越有限，n为20 d时预报准确率是比较满意的，同时可以兼顾业务运行效率，试验final的结果和试验mbw20非常接近，预报准确率最高，相对原ECMWF预报，24、48、72、96 h预报准确率分别从0.59、0.55、0.52、0.49提高到0.75、0.68、0.62、0.57，提高幅度为0.16、0.13、0.10、0.08，大幅度提高了预报准确率，且订正后72 h的准确率大于订正前模式24 h的准确率。对于最低温度(图 4b)而言，由于ECMWF模式对最低温度的系统性误差较小，具有较高的预报质量，24 h预报准确率达0.84，48~168 h预报时效的预报准确率在0.7以上，所以订正方法的预报准确率提高相对有限，甚至试验mbw05和mbw10在72 h以后是负的订正技巧，但预报准确率随滑动订正周期的变化趋势和最高温度的是一致的，滑动订正周期为20 d时为最佳，而考虑了空间误差的逐步订正(试验final)能够进一步提升最低温度的预报质量，相对于ECMWF预报，24、48、72、96 h最低温度预报准确率分别从0.84、0.83、0.82、0.79提高到0.89、0.87、0.85、0.81，提高幅度为0.05、0.04、0.03、0.02，与最高温度类似的结果是订正后72 h的准确率大于订正前模式24 h的准确率，较好地订正了模式误差，在六组试验里是最优的。因此，综合考虑这六组试验方案对模式最高温度和最低温度的订正效果，本文最终采用试验final的方案作为最佳试验方案，即综合了滑动双权重平均订正法(n=20 d)和空间误差逐步订正法的订正技巧。

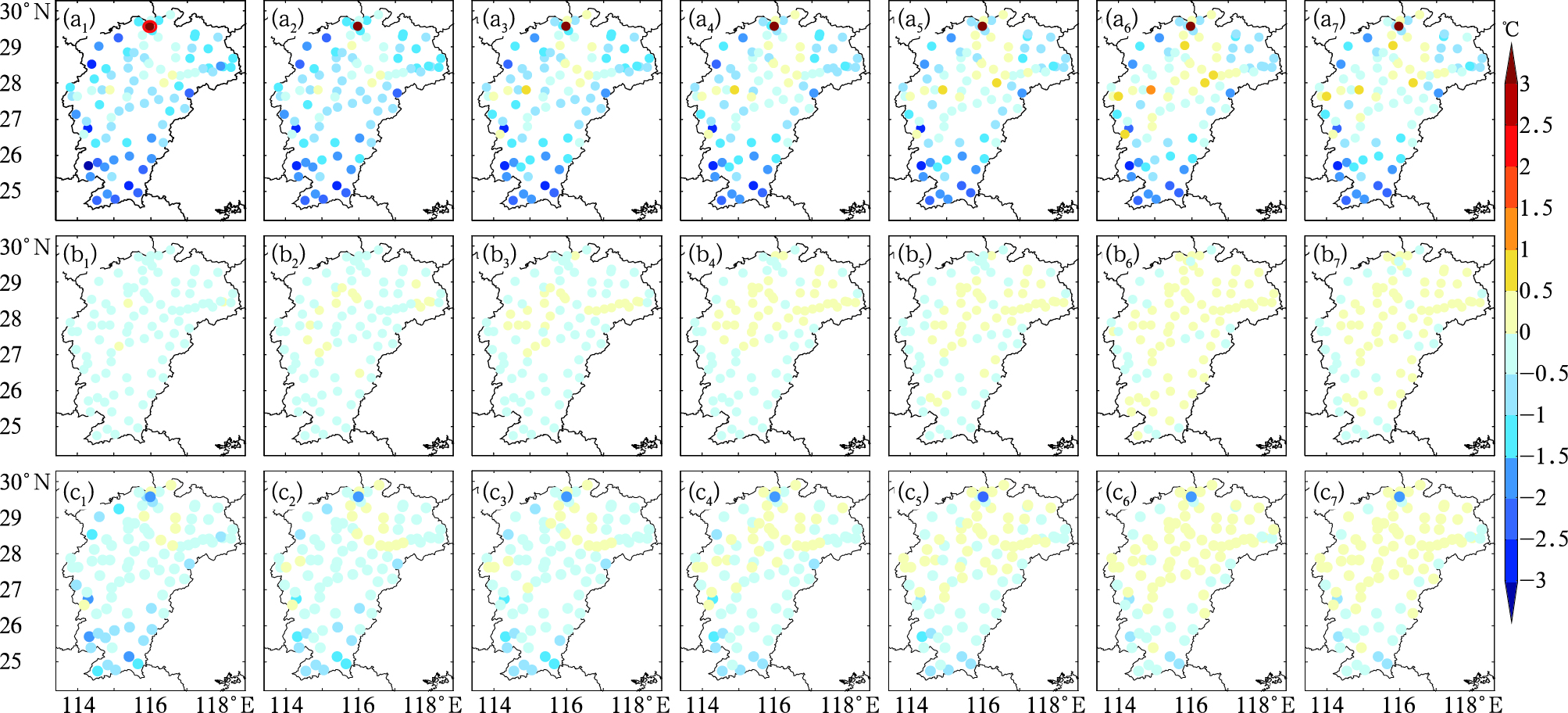
图 5给出了采用试验final方案订正前后2 m最高温度在24~168 h预报时效的ADEV和RMSE空间分布。可以发现，订正前江西西北部和南部的最高温度平均偏差普遍在-2℃左右，其他地区在-1.5~0.5℃(图 5a₁~5a₇)，山区和丘陵地区平均偏差明显高于平原地区，订正后的所有站点对平均偏差控制在±0.5℃之内(图 5b₁~5b₇)，与观测更为接近。RMSE(图 5c₁~5c₇)，订正后与订正前的偏差在24~96 h预报时效内大部分在-1.0~0.5℃，江西西北部和南部部分海拔较高的站点在-2.0~-1.5℃，误差有较明显改善，120 h预报时效以后订正效果不太明显，但对于高山站(例如庐山站)而言，24~120 h预报时效内订正后的RMSE始终是减小的。整体而言，订正后的误差在空间分布上是较均匀的，并没有因为地形和南北纬度差异影响出现分布不均的现象。2 m最低温度订正前后的误差空间分布也有类似的特征(图略)。结果总体上表明，经过滑动双权重平均订正法和空间误差逐步订正法综合订正后，很好地改善了站点温度的预报质量。

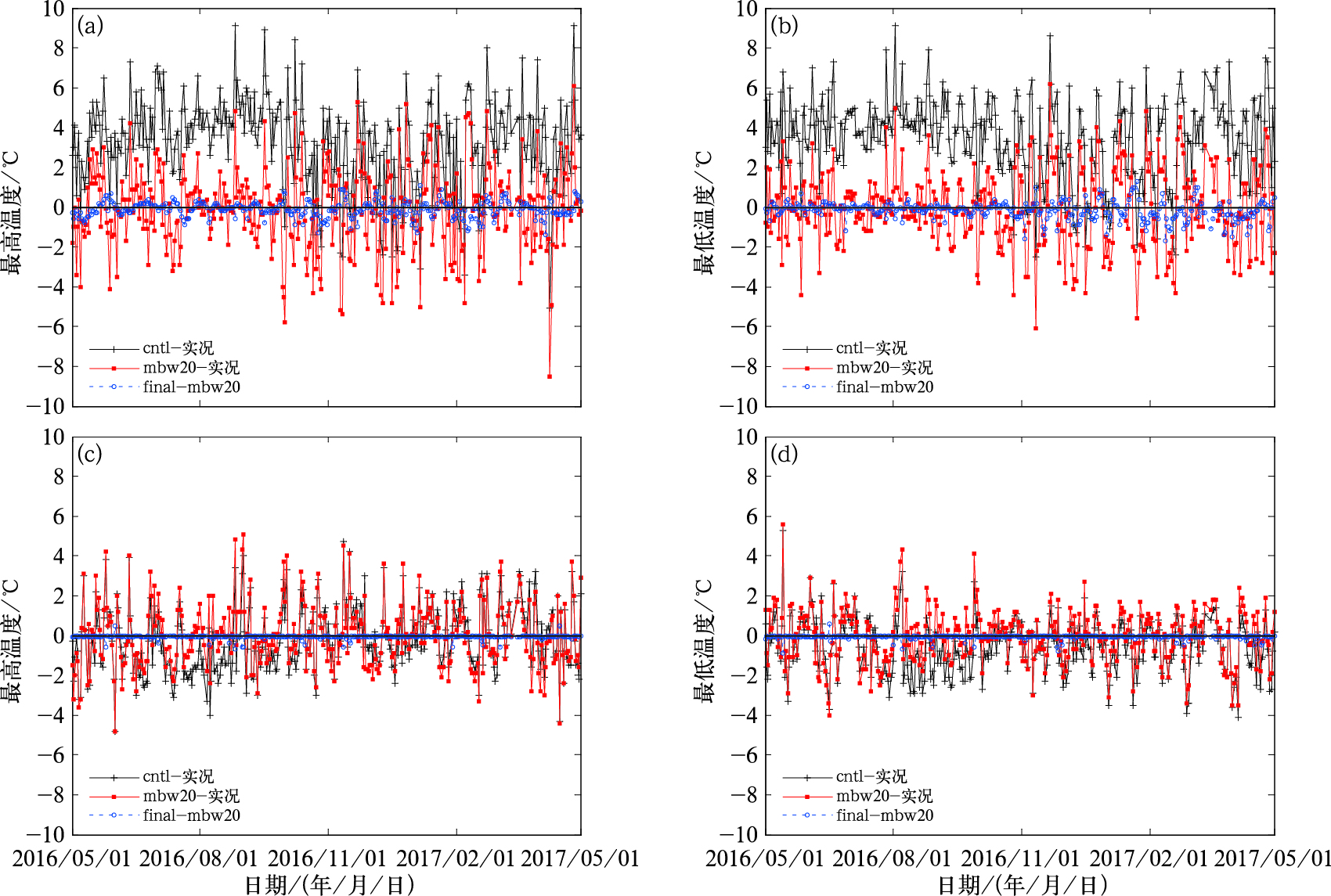
上述分析了滑动双权重平均订正法和空间误差逐步订正法对模式温度预报的平均订正效果，并不能代表单站的订正作用，尤其是那些受地形作用影响较大的高山站，因此，本文选取具有代表性的高山站——庐山站(位置在图 1中的紫色圆圈标注，观测站高度1164.5 m)和平原站——南昌县站(位置在图 1中的浅绿色圆圈标注)24 h预报时效最高和最低温度订正前后与实况进行对比(图 6)，以进一步分析订正方法对高山站和平原站的订正效果，其中订正后的数据来自于试验mbw20和试验final，试验final-试验mbw20表示空间误差逐步订正法的订正量。对于庐山站(图 6a, 6b)，模式的最高和最低温度存在普遍偏高的现象，在夏季6—9月尤为明显，最高和最低温度偏差普遍在3~6℃，最高偏差可达9℃，并且这种偏差在其他预报时效(图略)变化很小，一方面说明ECMWF模式的稳定性较高，另一方面说明模式存在的系统性也是稳定的，可以通过偏差订正消除。经过订正后(红色线)，最高和最低温度与实况的偏差曲线在0线附近振荡，特别是在7—9月偏差较小，大部分在2℃以内，跟实况有很好的一致性。空间误差逐步订正法的订正量(蓝色线)在±1℃之内，跟订正后的偏差(红色线)呈现一定的负相关，表明有正的订正效果。注意到，订正前后温度偏差的离散程度在5—9月较小，而在其他月份较大，表明该综合订正方法可能无法改变模式预报误差的离散程度，因此具有一定的局限性，需要今后做进一步研究。对于南昌县站(图 6c, 6d)，平原站的温度预报相对于高山站的平稳很多，订正后的最高、最低温度偏差大部分在±2℃以内。该测站在7—10月ECMWF模式存在较明显的系统误差，模式最高和最低温度比实况偏低2℃左右，经过滑动双权重平均订正法后偏差得到较好地订正。空间误差逐步订正法对偏差较大的预报有一定的订正，但总体上订正量较小，基本上在±0.5℃以内，大部分时间接近于0℃，表明该方法对平原站的订正作用较小。

4 结论和讨论

本文通过对ECMWF高分辨率2016年5月1日至2017年5月1日24~168 h预报时效内的2 m最高和最低温度预报产品和江西省91个县级站相应观测值进行检验评估，分析了ECMWF模式2 m温度的预报性能和相对于实况的空间分布。然后采用滑动双权重平均订正法和空间误差逐步订正法对模式温度预报进行偏差订正，并对订正前后的结果进行检验分析，主要结论如下：

(1) 结合江西省地形和观测站地理分布发现，ECMWF模式的最高、最低温度能够很好地表现出温度随地形分布的特征。整体而言，ECMWF模式在江西省的温度预报比实况偏低，最高温度尤为明显，模式温度的空间分布表现出显著的系统性偏差，且偏差在不同预报时效是稳定的，订正ECMWF模式温度具有可行性。

(2) RMSE分布表明，滑动双权重平均订正法中较长的滑动订正周期对模式温度预报有更好的订正效果，采用滑动订正周期20 d是比较理想的。空间误差逐步订正法能进一步提高滑动双权重平均订正法的预报订正质量，RMSE在所有试验中最小，24、48、72 h最高温度的RMSE相对于订正前分别减小19.9%、13.5%、9.6%，且48 h的RMSE低于订正前模式24 h的预报，72 h的RMSE低于订正前模式48 h的预报；24、48、72 h最低温度的RMSE相对于订正前分别减小13.4%、11.0%、7.5%，且72 h的RMSE低于订正前模式24 h的预报，96 h的RMSE低于订正前模式72 h的预报。滑动双权重平均订正法具有持续的订正能力，但在季节过渡期间订正效果可能并不理想，经过空间误差逐步订正后订正幅度较大，效果较明显，因此结合空间误差逐步订正法能一定程度地提高订正作用。总的来说，采用滑动双权重平均订正法和空间误差逐步订正法的综合订正技术能较好地订正模式2 m最高温度和最低温度的系统性误差。

(3) 温度的预报准确率总体上表明，经过综合订正技术后，很好地改善了站点温度的预报质量，在6组试验里是最优的。模式最高温度经过订正后，相对原ECMWF预报，24、48、72、96 h预报准确率分别从0.59、0.55、0.52、0.49提高到0.75、0.68、0.62、0.57，提高幅度为0.16、0.13、0.10、0.08，大幅度提高了预报准确率。对模式最低温度的订正相对有限，24、48、72、96 h预报准确率分别从0.84、0.83、0.82、0.79提高到0.89、0.87、0.85、0.81，提高幅度为0.05、0.04、0.03、0.02。订正后72 h最高温度和最低温度的预报准确率都大于订正前模式24 h的准确率。24~168 h预报时效的ADEV和RMSE空间分布同样表明经过综合订正技术订正后江西西北部和南部山区和丘陵地区的误差有明显改善，且误差在空间分布上是较均匀的，并没有因为地形和南北纬度差异影响出现分布不均的现象。

(4) 对于高山站而言，经过订正后的最高和最低温度基本和实况吻合，特别是在7—9月偏差较小，大部分在2℃以内，跟实况有很好的一致性。空间误差逐步订正法的订正量在±1℃之内，与滑动双权重平均订正后的偏差呈现一定的负相关，表明有正的订正效果。对于平原站而言，平原站的温度预报相对于高山站的平稳很多，订正后的最高、最低温度偏差大部分在±2℃以内，空间误差逐步订正法对偏差较大的预报有一定的订正，但总体上订正量较小，对平原站的订正作用较小。另外，从偏差的离散度来看，该综合订正方法可能无法改变模式预报误差的离散程度，因此具有一定的局限性，需要今后做进一步研究。