引言

强降水作为气象灾害的重要诱因之一，已经成为中国多数城市和地区一种严重的致灾因子，容易诱发城市内涝、泥石流和山体滑坡等灾害，造成严重的财产损失和人员伤亡。近年来，在甘肃河东地区(以下简称河东地区)短时强降水造成的灾害非常严重，如2010年7月7—8日舟曲和2012年5月10日定西由短时强降水分别引起的泥石流和暴洪都造成了严重的人员伤亡和财产损失(曲晓波等，2010；杨小银等，2013；张之贤等，2013)。

国内较多的气象学者通过逐小时降水数据对强降水的变化特征、环流分型等方面进行了研究(白晓平等，2016；陈元昭等，2016；杨波等，2016；伍红雨等，2017；李强等，2017；董旭光等，2017；王丛梅等，2017；杨萍等，2017)。以上研究在强降水的日变化、年际变化、强度变化等特征变化方面取得了显著成果，但对强降水发生概率的探讨较少。Kim et al(2012)指出强降水持续时间、过程雨量和降水强度是描述强降水的重要指标，因此国内外学者通过建立强降水持续时间与过程雨量的二元Copula分布函数分析强降水的发生概率(De Michele and Salvadori, 2003；Zhang and Singh, 2007；Vandenberghe et al，2011；张强等，2011；曹伟华等，2016)。Copula方法还被用于干旱(张玉虎等，2014；刘晓云等，2015；Rauf and Zeephongsekul, 2014)、水文(周念清等，2014；郭爱军等，2015)等多个领域。在参考借鉴上述研究的基础上，本文采用1960—2014年河东地区逐分钟降水资料细致分析了强降水频次的时空分布特征，构建强降水持续时间和过程雨量的二元Copula函数，并基于该函数分析了强降水的发生概率。希望研究结果能够进一步加强对该地区强降水的认识，从而供预报业务参考。

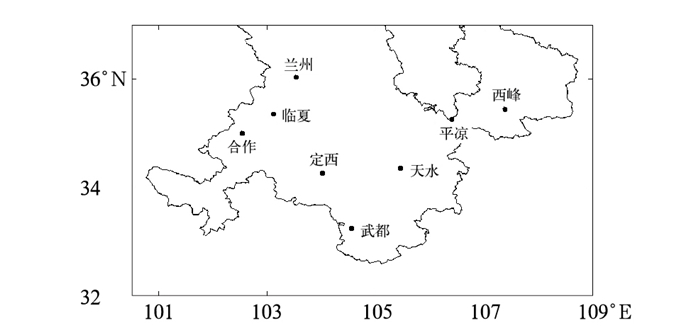
1 使用资料和方法介绍 1.1 使用资料

使用资料为1960—2014年兰州、临夏、合作、定西、武都、天水、平凉和西峰逐分钟降水资料(图 1)。本文定义一次强降水事件为过程雨量≥10 mm，雨强≥5 mm·h^-1，连续1 h无降水视为一次降水过程结束。按照持续时间将(0, 1] h划分为超短历时强降水，(0, 3] h划分为短历时强降水，(3, 6] h划分为较长历时强降水，＞6 h划分为长历时强降水。按照降水量将(10，25]、(25，50]、>50 mm分别划分为中雨、大雨和暴雨及以上量级强降水。地理上将兰州、临夏、合作划分为甘肃省中部地区，将武都、天水、定西划分为陇南地区，将平凉、西峰划分为陇东地区。需要说明的是定西使用资料为定西市岷县站资料，平凉使用资料为平凉市崆峒站资料。

1.2 方法介绍

研究主要讨论河东地区强降水频次的时空分布特征和强降水发生概率，使用常规统计分析、Kendall秩相关系数分析、正态分析和墨西哥帽小波分析等方法研究强降水频次的时空分布特征，通过构建最优Copula函数并基于该函数分析强降水发生概率。Copula函数介绍参见曹伟华等(2016)。构建最优Copula函数，分为两个步骤：(1)分别建立强降水过程雨量和持续时间的边缘分布函数。目前强降水中广泛采用的分布函数有指数、广义极值、伽玛、对数正态、韦伯、广义帕累托分布(Vandenberghe et al，2011；Rauf and Zeephongsekul, 2014；曹伟华等，2016)等。采用EasyFit统计分布拟合软件(包含上述提到的6种分布函数在内的61种分布函数)对各站强降水持续时间、过程雨量进行拟合并根据K-S检验选择最优分布函数，表 1给出拟合结果。在表 1中P值表示实际样本分布和拟合分布之间的差异性，P值越大差异性越小，当P=1时表示两组数据基本相同，D值是K-S检验的统计量，用于检验拟合分布函数假定是否成立，即在假定的显著性水平检验区间和样本数量下得出D值，然后计算实际样本与拟合样本的最大离差，若最大离差小于D值，则说明在该显著性水平检验下假定成立，反之则不成立。(2)建立边缘分布函数后需要选择合适的Copula函数来描述各致灾因子的联合分布。一般气象上常用的Copula函数为二元Archimedean Copula函数族，其成员分别为Gumbel Copula、Clayton Copula、Frank Copula(公式、参数范围参见曹伟华等，2016)。选用这3种Copula函数作为候选，通过极大似然估计确定Copula函数参数值，并通过CvM检验对候选Copula函数进行拟合优度检验，以挑选最优Copula函数。拟合结果如表 2所示：合作最优Copula函数为Clayton Copula，其余站为Frank Copula(在0.01显著性水平检验下)。P值越小说明该Copula函数越不适于用来拟合目标站点数据。

2 结果分析 2.1 强降水频次时空分布特征 2.1.1 强降水频次、持续时间、过程雨量

如表 3所示，河东地区近55年来平均强降水频次为1.64次/(a·站)，逐年来看，0.5~2.5次·站^-1的年份占87%，大于3.0次·站^-1的年份仅占4%，平均持续时间为2.88 h，平均过程雨量为23.4 mm。其中2010年7月发生在平凉的一次强降水持续时间最长为30.88 h，过程雨量最大为169.4 mm。河东地区强降水持续时间与过雨量为明显的正相关，Kendall秩相关系数达到0.54，基于这种较高的相关性，为后续采用Copula函数进行发生概率研究奠定了基础。

从过程雨量统计概率分布可以看出(图 2a)，随着过程雨量的增加，河东地区强降水发生概率迅速减小；过程雨量在10~15 mm概率为38.7%，15~20 mm时迅速减小至19.4%，20~25 mm占12.9%；中雨量级强降水发生的概率占71%，大雨量级强降水占22.6%，暴雨以上量级强降水仅占6.4%。

从持续时间统计概率分布可以看出(图 2b)，随着持续时间的增加，河东地区强降水发生概率先增加后减小；持续时间在1.5~2 h概率最高，占18.7%，1.0~1.5 h次之，占16.4%，0.5~1.0 h和2.0~2.5 h相当，均占11%左右；超短历时强降水占13.4%，短历时强降水占67.6%，较长历时强降水占24.2%，长历时强降水占8.0%；超过12 h的概率仅为0.8%。综合来看河东地区强降水以中雨量级、短历时为主。

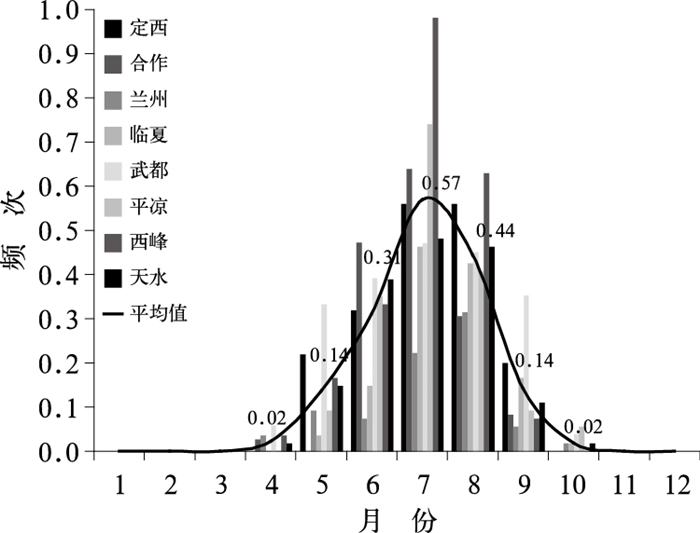
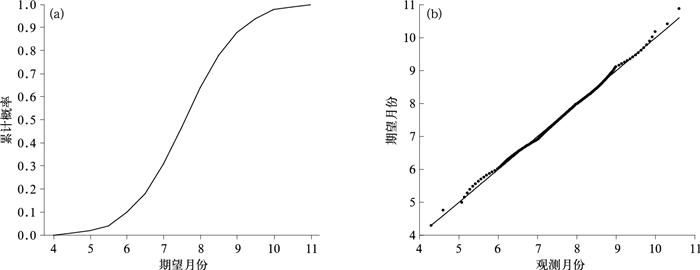
2.1.2 强降水频次月变化特征

如图 3所示，强降水频次从4月开始至10月结束，5月增多到0.14次，占9%，6月快速增加为0.31次，占19%，至7月达到峰值为0.57次，占35%，8月回落为0.44次，占27%，进入9月迅速减少为0.14次，占9%。99%的强降水发生在汛期(4—9月)，6—8月最集中(1.32次)，占到了强降水的81%，近55年来只有平凉在10月出现过一次强降水。对强降水频次月变化进行正态分布检验发现(图 4a)，其服从数学期望为7.59、方差为1.20的正态分布(在0.01显著性水平下通过K-S检验，临界值为0.127；D值为0.03，P值为1)，偏度系数为-0.140，峰度系数为-0.145，表明相对于标准正态分布其概率密度峰值略微偏右(峰值出现在7月并且8月概率要大于6月)且偏低。从Q-Q图(图 4b)可以看出，6月初至8月底更加遵循正态分布。

2.1.3 强降水频次周期变化

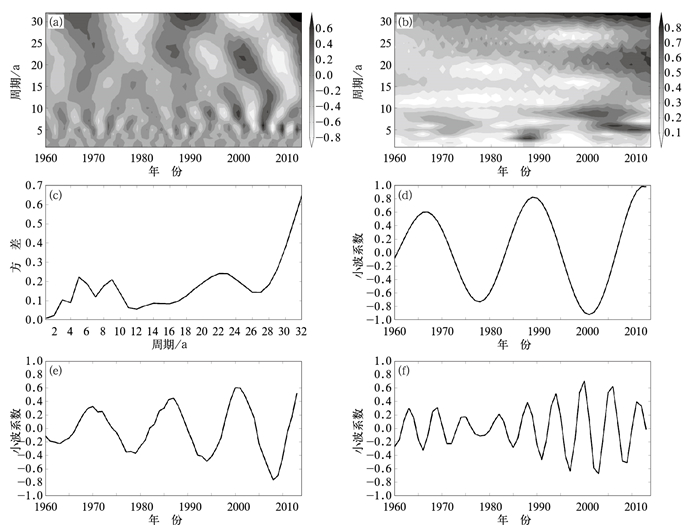
图 5a为墨西哥帽小波系数实部，由图可见河东地区近55年来强降水频次存在着18~32、4~10 a的特征时间尺度区间，同时在整个时间尺度上出现了3个偏多中心以及2个偏少中心，分别为1968、1988、2012、1976和2003年，此外强降水频次的变化趋势在这2个区间上都在加快，从图 5d~5f中可以看到振幅都在增强。图 5b为小波系数模值，由图可见28~32 a特征时间尺度模值较大，尤其是1975年以后，准20 a和4~10 a的特征时间尺度在1995年以后显著增加，表明对应时间段内周期性变化显著。进一步由小波方差图(图 5c)可以看出，存在着4个较为明显的峰值，从大到小依次为32、22、9和5 a特征时间尺度，分别对应图 5d~5f小波系数的周期性变化(5 a特征时间尺度图略去)，32、22、9、5 a特征时间尺度对应的河东地区强降水频次的周期变化分别为22~23、13~15 a的年代际变化和5~7、3~4 a的年际变化，周期变化显著，振幅增强。需要说明的是为了考虑小波分析的边界效应问题，对原始数据序列头尾增加了5 a的对称延伸。

2.2 基于Copula函数的强降水发生概率分析

深入研究河东地区强降水发生概率特征，能够提升该区域应对强降水灾害风险的能力。基于Copula函数分析强降水发生概率，包括两方面内容：(1)计算强降水持续时间和过程雨量的联合概率密度函数，以此分析强降水的分布类型以及概率密度。例如出现较大过程雨量的强降水，尤其是较短持续时间强降水的联合概率密度值，其值越高则代表发生概率越强。(2)重现期是一种量化致灾因子发生概率的指标，而重现期对应的过程雨量是城市排水规划设计的重要依据，为城市防灾工程设计和制定应急措施提供依据，对于城市灾害风险评估和管理具有重要意义。一般情况下某一过程雨量对应的重现期以及某一重现期对应的过程雨量都是在一个固定的持续时间内，例如：最大雨量对应的重现期，默认的规定了持续时间为24 h，又人为地将一场可能的强降水过程分为两段(08—08时或20—20时)；在城市暴雨公式编制中对重现期的统计也没有考虑具体的持续时间。因此考虑不同持续时间下的有条件重现和过程雨量能够更加精细地刻画强降水的发生概率，这两个致灾因子的发生概率指标更加科学合理，能解决强降水造成的诸如城市内涝、山洪、泥石流、洪水等灾害中涉及时间的具体问题。有无条件重现期定义如下：

(1) 无条件重现期：定义为大于等于一定过程雨量的强降水平均出现的时间间隔，可表示为：

$ {T_{\rm{w}}} = {\tau _t}/[1 - G(r)] $

(1)

式中，T_w表示无条件重现期，τ_t表示强降水平均时间间隔，以西峰为例，53 a里共出现120次强降水，则τ_t=53/120=0.412次·a^-1，G(r)为过程雨量的分布函数。

(2) 有条件重现期(简称为条件重现期)：定义为在一定持续时间内过程雨量超过一定阈值的强降水平均出现的时间间隔。通过边缘分布函数和二元Copula函数构建条件概率表达式[见式(2)]进而计算条件重现期[见式(3)]。

$ \begin{array}{*{20}{c}} {P(R \ge r|T \le t) = 1 - H(t, r)/F(t) = }\\ {1 - C(F(t), G(r))/F(T)} \end{array} $

(2)

$\begin{array}{l} {T_y} = {\tau _t}/P(R \ge r|R \le t) = \;\;\;\;\;\\ \;\;\;\;\;\;\;\;\;{\tau _t}/[1 - C(F(t), G(r)/F(t)] \end{array} $

(3)

式中，P为持续时间小于某阈值(t)、过程雨量大于某阈值(r)的强降水条件概率，C为相同情况下Copula联合密度分布函数，F为持续时间分布函数，T_y为条件概率下的条件重现期。

2.2.1 强降水联合概率密度分析

基于选定的最优Copula函数，分析河东地区8站过程雨量与持续时间的联合概率密度分布(图 6)，各站联合概率密度分布均不相同，共同特征为中间部分(中间持续时间段、中间过程雨量)和短历时、中雨以上的概率密度较低。从概率密度峰值来看，合作为单峰分布，主要集中在过程雨量 < 15 mm、持续时间 < 1.5 h，峰值高达16%。其余7站为双峰分布，一个峰值均出现在过程雨量 < 13 mm、持续时间 < 1.5 h，其中临夏概率密度峰值为5.9%，其余6站在4%左右；另一个峰值出现在较长降水历时、较大过程雨量，例如兰州出现在过程雨量 > 35 mm、持续时间 > 4 h，峰值为4.2%。对相同承灾体而言，较短持续时间、较大过程雨量的强降水造成的危害性最大，以持续时间 < 6 h、过程雨量 > 50 mm为例，从大到小分别为平凉、西峰、天水、武都、定西、兰州、临夏，其中平凉最高概率密度为3.5%，合作最低，不足1.5%。

2.2.2 强降水条件重现期分析

计算特定过程雨量[(25, 50] mm]下不同持续时间的条件重现期(表略)发现：条件重现期随着降水历时的增加而迅速减小，随着过程雨量的增加而迅速增大，短历时强降水条件重现期的变化剧烈，较长历时强降水条件重现期变化相对平稳；以过程雨量 > 50 mm为例：超短历时强降水发生的可能性极小，条件重现期均在百年以上；短历时强降水条件重现期在几十至百年之间，其中西峰最低为18.9 a，平凉次之为28 a；较长历时强降水和长历时强降水(分别对应暴雨蓝色和暴雨橙色预警)：河东地区条件重现期平均值为15、11 a；陇东地区最短，约为10、8 a，陇南地区和中部地区相当，分别为16、12 a；西峰最短，分别为9、8 a，平凉、天水次之，武都最长，分别为21、17 a。

河东地区各站不同持续时间、条件重现期下强降水的过程雨量(表 4)，过程雨量随着持续时间的增加而增大，较短持续时间内增加更迅速，6 h以后增幅极小，随着条件重现期的增加而增大，较短条件重现期内增加更迅速，20年以后增加幅度较小；以兰州为例：5年条件重现期下，持续时间在3 h(0 < t≤3)、6 h(0 < t≤6)、12 h(0 < t≤12)的强降水过程雨量分别为24.0、30.6、33.3 mm；10 a条件重现期下，分别为31.6、41.6、45.7 mm；20 a条件重现期下，分别为41.0、54.0、58.9 mm；30 a条件重现期下，分别为47.2、61.6、67.0 mm。以20 a条件重现期、12 h持续时间为例，各站过程雨量均达到暴雨，除平凉最大为118.8 mm以外，其余站相差不大，对应的陇东地区过程雨量最大，陇南和中部地区相当。

通过Copula函数计算各站强降水联合概率密度分布、条件重现以及不同持续时间下的过程雨量的强降水发生概率分析，强降水发生概率从大到小依次为平凉、西峰、天水、定西、武都、临夏、兰州和合作，对应的陇东发生概率最大，陇南次之，中部地区最小。

3 结论

利用1960—2014年兰州、临夏、合作、定西、武都、天水、平凉和西峰气象观测站逐分钟降水资料，开展两方面的研究，第一是使用统计分析、Kendall秩相关系数分析、正态分析、墨西哥帽小波分析方法分析河东地区强降水频次的时空分布特征，第二是通过构建最优Copula函数并基于该函数来分析强降水发生概率，得到以下结果：

(1) 近55年来强降水频次为1.64次/(a·站)，平均持续时间为2.88 h，平均过程雨量为23.4 mm，以短时、中雨组合型强降水为主，同时超短时强降水占13.4%，由于持续时间短，这类强降水会导致更高的气象灾害风险，需要密切关注。

(2) 强降水主要发生在汛期(4—9月)，6—8月最集中占81%，频次的月变化服从数学期望7.59、方差1.20的正态分布；墨西哥帽小波分析表明强降水频次有着显著的22~23 a和13~15 a的年代际和3~7 a的年际变化。

(3) 基于Copula函数的强降水发生概率分析表明：河东地区各站强降水的发生概率从大到小依次为平凉、西峰、天水、定西、武都、临夏、兰州和合作，对应的陇东发生概率最大，陇南次之，中部地区最小。