2. .中国科学院大气物理研究所,北京 100029;
3. 北京大学,北京 100871;
4. 中国气象科学研究院灾害天气国家重点实验室,北京 100081
2. Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. Peking University, Beijing 100871;
4. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
提高风速的精细化预报水平是很多行业对精细化天气预报服务的需求。例如,对风速的精确预测是风电场风能预测的基础(张颖超等,2016;叶小岭等,2017),目前对风的精准预报水平不高在一定程度上制约了风力发电的发展,做好对风速的精确预报有助于高效利用风能这种可再生资源。又如,北京2022年冬季奥运会赛区地面风场是冬季奥运会组委会十分关注的气象条件之一(张治国等,2017),基于赛场赛道风速的预测才能对雪上项目的进行、基础设施(如缆车的使用)等提前做风险评估和应对准备。
目前风速预测方法大致可分为物理方法和统计方法。物理方法,如数值天气预报,主要考虑到影响风场的物理因素(如地形特征、气压和环境温度等)及其间的物理相互作用规律来对风场进行预测。这类方法需要对实际物理过程有清晰的认识和重现能力,但由于模式的物理参数化方案的不完善和很多参数的不确定性等,使得对近地面风场的预报存在较大的误差。统计方法通常利用大量历史数据来构建预测的统计模型,包括传统统计方法(Erdem and Shi, 2011;Ren et al,2016;胡海川等,2017)和机器学习方法(Li and Shi, 2010;杨薛明等,2016;López et al,2018;Wang et al,2018)。实践表明,现有单一模型很难准确地进行局地风速预测。近年来一些学者尝试基于机器学习方法对数值天气预报模式结果进行订正,达到对风速的精细化预报。传统的订正模型大多采用线性方法(肖擎曜等,2017),不足以捕捉风速变化中隐藏的非线性特征。基于机器学习方法的订正模型则能捕捉非线性风速变化,在风速预报上表现出良好的性能,例如针对风速预报订正的人工神经网络(孙军波等,2010;Zjavka,2015;邓华等,2018)、支持向量机(戚双斌等,2009;孔令彬等,2014)、随机森林(Lin et al,2015)等方法。
本文采用目前较为常用的三种机器学习(LASSO回归、随机森林和深度学习)以及MOS方法(经典天气预报的统计订正方法),对ECMWF数值天气预报模式预测的近地面(10 m)风速进行订正。首先基于ECMWF模式计算所得的各种要素特征进行特征选择,即通过机器学习算法自适应地获得相关要素特征集,再以选择的特征集进行机器学习建模,对ECMWF预测的未来1~15 d华北地区逐日格点风速进行订正。以此评估各订正方法的能力,为实现风速的精细化预报提供新的方法思路。
1 数据与方法 1.1 数据本文采用的数据来源于欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)网站公开的数值模式输出数据。数据包括逐日00时(对应北京时间为08时)的分析场(0时刻场)和24~360 h(逐日)的预报场。时间范围为2012年1月至2016年12月,空间范围为38°~43°N、113°~119°E(华北地区),空间分辨率为0.5°×0.5°。ECMWF模式输出数据共包括23个气象要素场(表 1)。
|
|
表 1 ECMWF数值预报23个气象要素场 Table 1 Twenty-three meteorological element fields of ECMWF numerical prediction |
首先将10 m纬向风分量(U)和10 m经向风分量(V)合成为10 m风速(W),合成公式如下:
| $ W = \sqrt {{U^2} + {V^2}} {\rm{ }} $ | (1) |
故现在共有24个要素。本研究将采用研究时段内模式0时刻10 m风速的分析场作为标记(机器学习算法中的真值),将ECMWF预测的对应标记所处时刻的所有24个气象要素作为机器学习算法的输入,以此构建机器学习风速订正模型。
1.2 方法 1.2.1 MOS预报方法MOS方法是在数值天气预报模式的预报产品和相应时次的预报对象间建立统计关系(预报方程)(吴启树等,2016)。本文以ECMWF数值预报模式在某一预报时效的风速的预报场和与其对应的分析场建立一元线性回归方程:
| $ {S_i} = a + b{F_i} $ | (2) |
式中,Si为第i时刻回归订正值,Fi为该时刻模式预报值,a为常数项,b为回归系数(采用最小二乘法求解)。用得到的回归方程对所有时效的风速进行订正。
1.2.2 LASSO回归LASSO(least absolute shrinkage and selection operator)回归通过构造一个惩罚函数得到一个较为精炼的模型,使得它压缩一些系数,同时设定一些系数为0。因此保留了子集收缩的优点,是一种处理具有复共线性数据的有偏估计。LASSO回归通过放弃最小二乘法的无偏性,以损失部分信息和降低精度为代价获得回归系数更为符合实际、更可靠的回归方法。
在本文风速预测中,给定有m个气象因素(特征)的特征向量x=(x1, x2, …, xm),其中xi为x在第i个特征上的取值,通过m个气象特征的线性组合来进行预测风速,即公式如下:
| $ f\left({{\rm{ }}\mathit{\boldsymbol{x}}{\rm{ }}} \right) = {w_1}{x_1} + {w_2}{x_2} + \ldots + {w_m}{x_m} $ | (3) |
式中w=(w1, w2, …, wm)是气象特征的权重。
损失函数定义为
| $ loss\left({{\rm{ }}\mathit{\boldsymbol{w}}{\rm{ }}} \right) = \parallel f\left({{\rm{ }}\mathit{\boldsymbol{x}}{\rm{ }}} \right) - y{\parallel ^2} + \alpha \parallel {\rm{ }}\mathit{\boldsymbol{w}}\parallel $ | (4) |
式中,y表示风速实测值,α‖ w‖是正则化项,不仅有助于降低过拟合风险,还具有特征选择的作用(周志华,2016)。通过对loss(w)进行求最小值,模型学习得到w,从而LASSO回归模型得以确定。
1.2.3 随机森林随机森林(random forest)算法是由多个决策树集成的,在进行随机森林过程中,其输出值是随机森林中所有决策树结果的平均值。
在本文风速预测中,就是以气象要素建立特征向量作为输入,以该特征向量对应的风速大小作为预测结果,通过训练样本进行拟合得到预测模型的过程(李丽辉等,2017)。随机森林建模过程如下:
(1) 定义风速预测训练集合Xi→Yi。其中,Yi为随机森林预测模型中的真实值,映射为资料中第i个样本的风速实值;Xi为资料中第i个样本的气象要素取值所建立的特征向量,以{Ii1, Ii2, …Iin}→Xi表示第i个样本的n个影响因子。
(2) 在确定了训练集的基础上,建立单棵回归决策树。通过训练样本中的特征向量X和其对应的真实值Y,对分裂变量和分裂值进行搜索,回归决策树将整个向量空间分为m个分区{ R1, R2, …, Rm}。对于其中任意分区可以映射为模型Cm,通过某个特征的取值将向量空间分为两部分,表达式为
| $ \mathit{\boldsymbol{R}}{_1}\left({j, s} \right) = \{ {\rm{ }}\mathit{\boldsymbol{I}}{\rm{ }}|{I_j} \le s\} $ | (5) |
| $ \mathit{\boldsymbol{R}}{_2}\left({j, s} \right) = \{ {\rm{ }}\mathit{\boldsymbol{I}}{\rm{ }}|{I_j} > s\} $ | (6) |
式中,j代表一个影响因子,s代表进行分裂时的值。进行向量空间分裂变量和分裂值搜索的目标函数为
| $ \begin{array}{l} z:\mathop {{\rm{min}}}\limits_{j, s} {\rm{ }}[\mathop {{\rm{min}}}\limits_{{c_1}} \sum\limits_{{x_i} \in {R_1}\left({j, s} \right)} {} {\rm{ }}{({y_i} - {c_1})^2} + \\ \mathop {{\rm{min}}}\limits_{{c_2}} \sum\limits_{{x_i} \in {R_2}\left({j, s} \right)} {} {\rm{ }}{({y_i} - {c_2})^2}] \end{array} $ | (7) |
式中,z为风速实值的最小方差;yi为第i个样本的风速实值;xi为第i个样本的影响因子向量的对应值;c1为第一部分风速实值均值;c2为第二部分风速实值均值。
(3) 在单棵决策树的构建基础上,构建整个随机森林。生成的随机森林是多元非线性回归分析模型,随机森林预测值是所有决策树预测值的平均值。
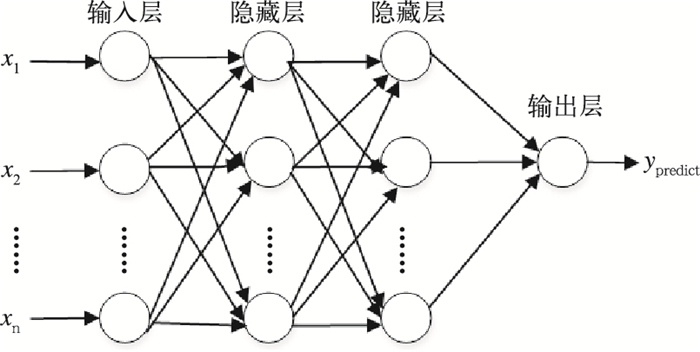
1.2.4 深度学习深度学习是含有多个神经元层的深层神经网络。深度学习基本模型如图 1所示,深度学习是由输入层、隐藏层和输出层三部分组成,隐藏层可以包含很多层。相对比于浅层学习,深度学习显然在计算层次上更为复杂。在模型训练方面,深度学习采用反向传播算法。反向传播算法的核心思想是求导的链式法则,常被用来求解神经网络中的最优化问题。输入层神经元个数等于样本的特征量,隐藏层的层数、隐藏层的神经元数、学习率等参数,是通过大量的训练与验证而确定。
|
图 1 深度学习基本模型 Fig. 1 The basic model of deep learning |
结合图 1和本文研究内容,由于本文构建的是回归模型,故输出层不设激活函数,即将第四个隐藏层的输出数据加权平均后直接输出。公式如下:
| $ \mathit{\boldsymbol{y}}{^{(1)}} = {\rm{ }}\mathit{\boldsymbol{W}}{^{(1)}}\mathit{\boldsymbol{x}}{\rm{ }} + {\rm{ }}\mathit{\boldsymbol{b}}{^{(1)}} $ | (8) |
| $ \mathit{\boldsymbol{y}}{^{(2)}} = {\rm{ }}\mathit{\boldsymbol{W}}{^{(2)}}{\varphi _1}({\rm{ }}{\mathit{\boldsymbol{y}}^{(1)}}) + {\rm{ }}\mathit{\boldsymbol{b}}{^{(2)}} $ | (9) |
| $ \mathit{\boldsymbol{y}}{^{(3)}} = {\rm{ }}\mathit{\boldsymbol{W}}{^{(3)}}{\varphi _2}({\rm{ }}{\mathit{\boldsymbol{y}}^{(2)}}) + {\rm{ }}\mathit{\boldsymbol{b}}{^{(3)}} $ | (10) |
| $ {\mathit{\boldsymbol{y}}^{(4)}} = {\rm{ }}\mathit{\boldsymbol{W}}{^{(4)}}{\varphi _3}({\rm{ }}{\mathit{\boldsymbol{y}}^{(3)}}) + \mathit{\boldsymbol{b}}{^{(4)}} $ | (11) |
| $ {\mathit{\boldsymbol{y}}_{{\rm{predict}}}} = \mathit{\boldsymbol{W}}{^{(5)}}{\varphi _4}({\rm{ }}{\mathit{\boldsymbol{y}}^{(4)}}) + {\rm{ }}\mathit{\boldsymbol{b}}{^{(5)}} $ | (12) |
式中,x是有气象要素组成的特征向量,是输入层的输入信号。y (i)为第i个隐藏层的输入信号,W(i)为第i-1层到第i层的连接权重,b(i)为第i-1层到第i层的连接偏差,φi为第i个隐层的激活函数。ypredict(风速预测值)为输出层的输出信号。隐层神经元输出的激活函数采用ReLU函数,它的数学表达式如下:
| $ \varphi \left(z \right) = {\rm{max}}\left({0, z} \right) $ | (13) |
优化算法采用Adam算法,该算法是随机梯度下降算法的扩展式,它对超参数的选择相当鲁棒。
1.2.5 检验方法均方根误差(root mean square error,RMSE)是风速预报中最常用的性能度量指标,均方根误差越小,风速整体预报就越准确。公式如下:
| $ RMSE\left({f;D} \right) = \sqrt {\frac{1}{K}\sum\limits_{k = 1{\rm{ }}}^K {{{[f({\rm{ }}\mathit{\boldsymbol{X}}{_k}) - {y_k}]}^2}} } $ | (14) |
式中,f为算法模型,D为数据集,K为数据集D的样本总数,Xk为第k个样本的输入,yk为第k个样本的标记。
风速预报准确率(Fa)是风速预报绝对偏差不大于1 m·s-1的百分率,公式如下:
| $ {F_a} = {\rm{ }}\frac{{{N_r}}}{{{N_f}}} \times 100\% $ | (15) |
式中,Nr为风速预测值与分析场风速值之差不大于1 m·s-1的样本数,Nf为预报的样本数。
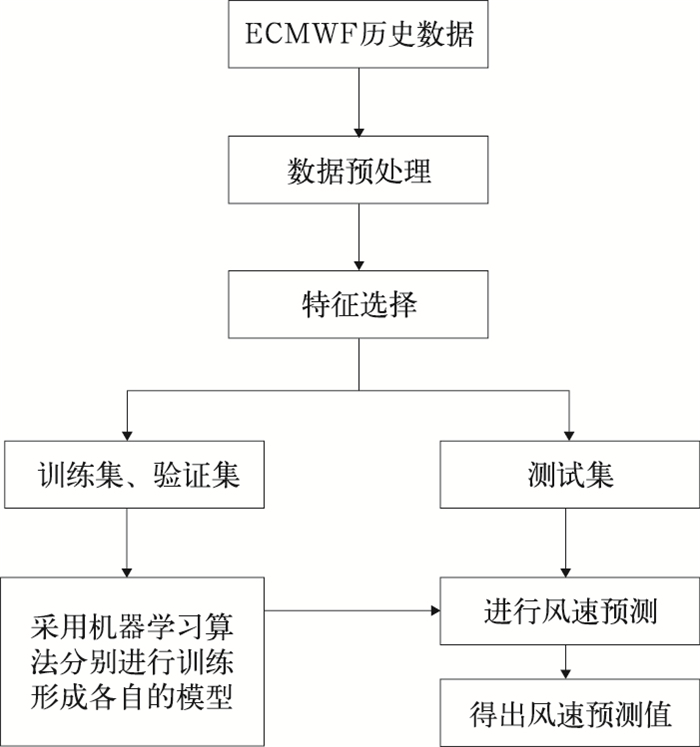
2 预测模型构建将数据分为三部分:训练集、验证集和测试集。训练集和验证集用于确定预测模型,测试集进行实际预测。从2012年1月至2015年12月ECMWF预报数据中随机抽取85%作为训练集,剩下15%作为验证集;2016年1—12月ECMWF预报数据作为测试集。基于机器学习的风速预测模型流程图如图 2所示。
|
图 2 机器学习风速预测流程图 Fig. 2 Flow chart of machine learning predicting wind speed |
(1) 数据预处理。针对数据矩阵中的空值和乱码进行处理,也对整体数据进行拆分和采样等操作。同时,对各要素数据进行标准化处理,不仅避免训练时由于各要素数值小而贡献小的问题(袁翀等,2016),而且提高运算速率。本文预报时效为24~360 h(时效间隔为24 h)的预报场数据分别对应未来第1~15 d(间隔为1 d)的分析场数据;数据集为2012年1月至2016年12月一共有1827 d;华北地区(38°~43°N、113°~119°E)模式预报数据,水平分辨率为0.5°×0.5°的网格,共计143个格点;因此每个预报时效的原始数据集由一个大小为1827×143个样本组成,每个样本有24个特征。
(2) 特征选择。从输入的原始数据(共24个特征)中,利用LASSO回归算法提取出对10 m风速有影响的气象要素特征集。结果详见第3节。
(3) 将选择选出的特征组合成新的输入数据,采用机器学习算法(LASSO回归、随机森林和深度学习)分别进行训练形成模型。
(4) 将测试集数据输入到已训练好的模型中,输出即为订正后的风速数据,评估预测模型的准确性。
3 特征选择特征选择是从原始特征中选择出一些最有效特征以降低数据集维度的过程,学习任务的难度会有所降低,涉及的计算和存储开销会减少,学习得到模型的可解释性也会提高。常见的特征选择法有过滤式选择、包裹式选择和嵌入式选择。过滤式选择过程与后续学习器无关。从最终学习器性能来看,包裹式特征选择比过滤式特征选择更好,但包裹式特征选择计算开销大(周志华,2016)。本文是基于LASSO回归的嵌入式选择法进行特征选择,LASSO回归的学习方法是其特征选择过程与学习器训练过程融为一体,两者在同一个优化过程中完成,并且LASSO回归计算效率高。
结合1.2.2节,使用LASSO模型后,由于加入了正则化因子α‖ w‖,不显著的变量被收缩为0。随着惩罚力度的加强(超参数α变大),越来越多的变量会被收缩为0。LASSO不仅可以降低过拟合风险,还具有稀疏作用(韩耀风等,2017)。
以预报时效为216 h为例,如图 3所示,基于LASSO模型对测试集的风速预测,横坐标特征的数目是通过调节LASSO模型中超参数α的大小来控制,纵坐标是RMSE。当LASSO筛选出10个特征时,就足以将RMSE降低到平稳的边界。为了检验这10个特征(10 m纬向风分量、10 m经向风分量、10 m风速、积雪深度水当量、地表净热辐射、地面气压、地面感热通量、最高净热辐射、总柱水汽量和海陆)选择结果的稳健性,分别采用随机森林和深度学习算法进行风速预测。并把ECMWF风速预测(EC)、输入24个特征的随机森林风速预测(RF-all)、输入选择出这10个特征的随机森林风速预测(RF-select)、输入24个特征的深度学习风速预测(DL-all)和输入选择出这10个特征的深度学习风速预测(DL-select)。图 4显示,随机森林和深度学习算法的预测性能明显优于ECMWF;并且RF-select的RMSE基本等于RF-all,DL-select的RMSE基本等于DL-all,充分证明LASSO能够筛选出对风速有关的主要特征。

|
图 3 基于LASSO模型的风速预测 Fig. 3 Wind speed forecast based on LASSO model |

|
图 4 特征选择前后的风速预测对比 Fig. 4 Comparison of wind speed prediction before and after feature selection |
按照上例特征选择方法对所有时效(24~360 h逐24 h)进行特征选择。选择结果如表 2和表 3所示,表中的数值是各预报时效中特征权重。特征对风速预测的影响程度与特征权重的大小成正比,即某个特征的权重越大说明这个特征对风速预测的影响就越大。对预报时效24~360 h中的平均权重由大到小依次特征排列为:10 m风速、海陆、地表净热辐射、积雪深度水当量、地面气压、10 m纬向风分量、10 m经向风分量、最高净热辐射、地面感热通量、总柱水汽量、2 m露点温度、降雪水当量、平均海平面气压、总云量。在以上对风速预测有影响的特征中:(1)10 m风速的权重随着预报时效的增加而减小;(2)海陆、地表净热辐射、积雪深度水当量、地面气压、地面感热通量的权重是随着预报时效的增加而增大的;(3)10 m纬向风分量、10 m经向风分量、最高净热辐射、总柱水汽量、2 m露点温度、降雪水当量、平均海平面气压、总云量的权重与预报时效的增加没有明显的相关关系。
|
|
表 2 各预报时效中特征权重分布(预报时效为24~192 h) Table 2 Distribution of feature weights in each forecast period (forecast lead-time is 24-192 h) |
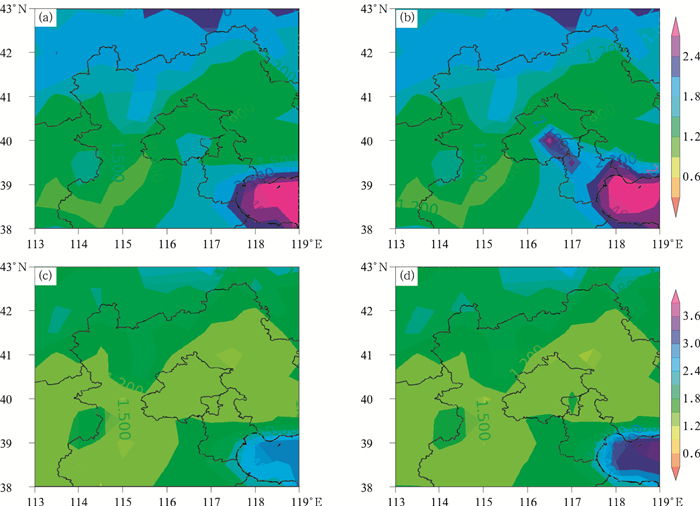
风是一个二维矢量,即10 m风速由10 m纬向风分量和10 m经向风分量组成。ECMWF预测的10 m纬向风分量、10 m经向风分量和10 m风速,显然与分析场风速相关。当太阳福射在地球表面上后,地表会向大气支出热量(地表净热辐射和最高净热辐射),地表的空气受热膨胀变轻而往上升。热空气上升后,造成气压分布不均,低温的冷空气横向流入,这种空气的流动就产生了风。地表感热通量是由于湍流运动从地面向大气传输的热量通量,一般地风速越大,感热通量越大(阳坤等,2010)。当阳光照向地球表面上时,云、地面积雪从中吸收一部分热辐射,所以云和地面积雪的分布会影响地表热量分布。2 m露点温度和总柱水汽量是衡量空气湿度的重要指标,风是表征大气运动的变量,湿度的分布因大气的运动而改变,在数值预报中,风会引起湿度场的迅速改变(陶祖钰等,2016)。海陆是区分陆地和海洋的重要特征,因海洋和陆地受热不均匀造成地面与海平面气压不同,从而在海岸附近形成的一种有日变化的风系。以预报时效为216 h为例对海陆因素的影响进行进一步的对比分析,它们的区域预测RMSE空间分布如图 5所示,去掉海陆后,海域及沿海地区的RMSE明显上升,说明海陆对风速预测确实有重要作用,从一定程度上反映了使用LASSO方法进行特征选择的合理性。
|
图 5 去掉海陆因素前后的风速预测空间分布(单位:m·s-1) (a)基于随机森林的订正(有海陆因素),(b)基于随机森林的订正(没有海陆因素),(c)基于深度学习的订正(有海陆因素),(d)基于深度学习的订正(没有海陆因素) Fig. 5 Prediction of spatial distribution of wind speed before and after removing the land-sea mask (unit: m·s-1) (a)correction based on random forest (with land-sea mask), (b) correction based on random forest (without land-sea mask), (c) correction based on deep learning (with land-sea mask), (d) correction based on deep learning (without land-sea mask) |
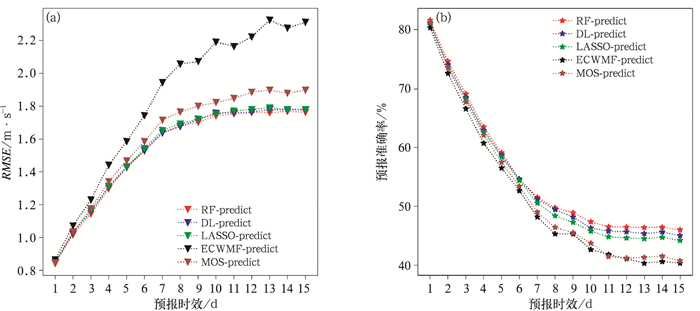
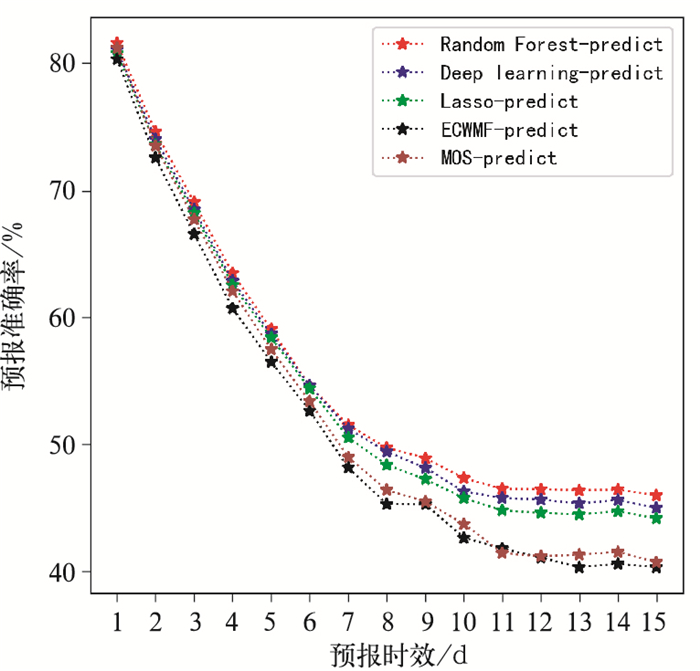
分别采用机器学习(LASSO回归、随机森林和深度学习)和MOS方法,对华北地区进行风速格点预测,预报时效为24~360 h(时效间隔为24 h)。并结合ECMWF分析场对预报能力进行客观检验。在测试集进行测试,对每个预测时效(样本量360×143个)计算RMSE和精准度,结果如图 6所示:机器学习、MOS法和ECMWF的预报精度都在随着预报时效的增加而下降;MOS方法和机器学习的预报效果优于ECMWF,并且在未来第8~15 d,MOS方法和机器学习方法预报效果明显优于ECMWF;在未来第1~5 d,机器学习方法略优于MOS方法,在未来第6~15 d,机器学习方法明显优于MOS方法。总之,机器学习对ECMWF在不同时效的10 m风速预报有不同程度的订正,尤其对未来第8~15 d有明显的订正。
|
图 6 ECMWF、三种机器学习模型、MOS在预报时效上的预测效果 (a)RMSE,(b)预报准确率 Fig. 6 Comparison of ECMWF, three machine learning models and MOS prediction (a)RMSE, (b)forcast accuracy |
分别采用LASSO回归、随机森林、深度学习和MOS方法,对华北地区进行风速格点预测,预报时效为24~360 h(时效间隔为24 h)。并结合ECMWF分析场对预报能力进行客观检验。在测试集进行测试,分别对预报时效为72、192和312 h中的每个格点(样本量360个)计算RMSE,结果如图 7所示:随着预报时效的增加,机器学习、MOS法和ECMWF在各格点预测的误差都呈逐渐上升趋势;机器学习和MOS法在格点上对ECMWF都有不同程度订正;机器学习在北京地区的预测精度优于其他地区;ECMWF和MOS法对海域预测较差,机器学习明显改善了对海域及沿海地区预测的精度;总之,机器学习对ECMWF在不同区域的10 m风速预报有不同程度的订正,尤其对海域及其沿海地区有明显的订正。
|
图 7 ECMWF(a)、MOS(b)、LASSO(c)、深度学习(d)和随机森林(e)在区域上的72 h(a1,b1,c1,d1,e1)、192 h(a2,b2,c2,d2,e2)、312 h(a3,b3,c3,d3,e3)预测结果(RMSE,单位:m·s-1) Fig. 7 ECMWF (a), MOS (b), LASSO (c), deep learning (d) and random forest (e) prediction results (RMSE) distribution in area (unit: m·s-1) (a1, b1, c1, d1, e1) 72 h, (a2, b2, c2, d2, e2) 192 h, (a3, b3, c3, d3, e3) 312 h |
本文基于机器学习方法针对数值天气预报模式ECMWF预测的10 m风速进行了订正。较之于传统MOS订正方法,本研究中机器学习模型构建中综合考虑了多种气象要素特征,获得了更完善的风速订正模型。结果表明,机器学习对不同时效的10 m风速预报有不同程度的订正,随着预报时效的增加,订正的力度越来越大。尤其是LASSO回归算法不仅提高了风速订正的准确性,还在特征选择上表现非常出色;特征选择降低机器学习任务的难度,减少了计算和存储开销,从而优化了学习模型。研究表明,对10 m风速预测有影响的特征主要(按平均权重由大到小排序)是10 m风速、海陆、地表净热辐射、积雪深度水当量、地面气压、10 m纬向风分量、10 m经向风分量、最高净热辐射、地面感热通量、总柱水汽量、2 m露点温度、降雪水当量、平均海平面气压、总云量。通过机器学习算法自适应获得的气象要素特征集从一定程度上也有助于加深对以往建立的风速预测物理模型所使用的气象要素组合的认识。
邓华, 张颖超, 顾荣, 等, 2018. 基于PCA-RBF的风电场短期风速订正方法研究[J]. 气象科技, 46(1): 10-15. Deng H, Zhang Y C, Gu R, et al, 2018. Research on Short-term wind speed correction method of wind farm based on PCA-RBF[J]. Meteor Sci Tech, 46(1): 10-15 (in Chinese). |
韩耀风, 覃文锋, 陈炜, 等, 2017. adaptive LASSO logistic回归模型应用于老年人养老意愿影响因素研究的探讨[J]. 中国卫生统计, 34(1): 18-22. Han Y F, Qin W F, Chen W, et al, 2017. Study on the application of adaptive LASSO logistic regression model to the influencing factors of the elderly's willingness to support the elderly[J]. Chin J Health Statis, 34(1): 18-22 (in Chinese). |
胡海川, 黄彬, 魏晓琳, 2017. 我国近海洋面10 m风速集合预报客观订正方法[J]. 气象, 43(7): 856-862. Hu H C, Huang B, Wei X L, 2017. An objective correction method for the ensemble prediction of 10 m wind speed near the ocean surface in China[J]. Meteor Mon, 43(7): 856-862 (in Chinese). |
孔令彬, 赵艳茹, 王聚杰, 等, 2014. 基于支持向量机风速订正方法的研究[J]. 西南大学学报(自然科学版), 36(5): 194-200. Kong L B, Zhao Y R, Wang J J, et al, 2014. Research on wind speed correction method based on support vector machine[J]. Southwest Univ(Nat Sci), 36(5): 194-200 (in Chinese). |
李丽辉, 朱建生, 强丽霞, 等, 2017. 基于随机森林回归算法的高速铁路短期客流预测研究[J]. 铁道运输与经济, 39(9): 12-16. Li L H, Zhu J S, Qiang L X, et al, 2017. Research on short-term passenger flow forecasting of high-speed railway based on random forest regression algorithm[J]. Rail Way Transport and Economy, 39(9): 12-16 (in Chinese). |
戚双斌, 王维庆, 张新燕, 2009. 基于支持向量机的风速与风功率预测方法研究[J]. 华东电力, 37(9): 1600-1603. Qi S B, Wang W Q, Zhang X Y, et al, 2009. Research on wind speed and wind power prediction based on support vector machine[J]. East China Electric Power, 37(9): 1600-1603 (in Chinese). DOI:10.3969/j.issn.1001-9529.2009.09.045 |
孙军波, 钱燕珍, 陈佩燕, 等, 2010. 登陆台风站点大风预报的人工神经网络方法[J]. 气象, 36(9): 81-86. Sun J B, Qian Y Z, Chen P Y, et al, 2010. Artificial neural network method for landing typhoon site gale forecast[J]. Meteor Mon, 36(9): 81-86 (in Chinese). |
陶祖钰, 范俊红, 李开元, 等, 2016. 谈谈气象要素(压、温、湿、风)的物理意义和预报应用价值[J]. 气象科技进展, 6(5): 59-64. Tao Z Y, Fan J H, Li K Y, et al, 2016. Talk about the physical meaning and forecasting application value of meteorological elements (pressure, temperature, humidity, wind)[J]. Adv Meteor Sci Technol, 6(5): 59-64 (in Chinese). |
吴启树, 韩美, 郭弘, 等, 2016. MOS温度预报中最优训练期方案[J]. 应用气象学报, 27(4): 426-434. Wu Q S, Han M, Guo H, et al, 2016. Optimal training period scheme in MOS temperature prediction[J]. J Appl Meteor, 27(4): 426-434 (in Chinese). |
肖擎曜, 胡非, 范绍佳, 等, 2017. 风能数值预报的模式输出统计(MOS)研究[J]. 资源科学, 39(1): 116-124. Xiao Q Y, Hu F, Fan S J, et al, 2017. Model output statistics (MOS) of wind energy numerical prediction[J]. Res Sci, 39(1): 116-124 (in Chinese). |
阳坤, 郭晓峰, 武炳义, 2010. 青藏高原地表感热通量的近期变化趋势[J]. 中国科学:地球科学, 40(7): 923-932. Yang K, Guo X F, Wu B Y, 2010. Recent changes in surface sensible heat flux over the Qinghai-Tibet Plateau[J]. Sci China:Earth Sci, 40(7): 923-932 (in Chinese). |
杨薛明, 边继飞, 朱霄珣, 等, 2016. 基于最大熵混沌时间序列的支持向量机短期风速预测模型研究[J]. 太阳能学报, 37(9): 2173-2179. Yang X M, Bian J F, Zhu X X, et al, 2016. Research on short-term wind speed prediction model of support vector machine based on maximum entropy chaotic time series[J]. Acta Energiae Solaris Sin, 37(9): 2173-2179 (in Chinese). DOI:10.3969/j.issn.0254-0096.2016.09.001 |
叶小岭, 顾荣, 邓华, 等, 2017. 基于WRF模式和PSO-LSSVM的风电场短期风速订正[J]. 电力系统保护与控制, 45(22): 48-54. Ye X L, Gu R, Deng H, et al, 2017. Short-term wind speed correction of wind farm based on WRF mode and PSO-LSSVM[J]. Power System Protection and Control, 45(22): 48-54 (in Chinese). DOI:10.7667/PSPC161827 |
袁翀, 戚佳金, 王文霞, 等, 2016. 采用正则化极限学习机的短期风速预测[J]. 电网与清洁能源, 32(11): 62-68. Yuan C, Qi J J, Wang W X, et al, 2016. Short-term wind speed prediction using regularized limit learning machine[J]. Power System and Clean Energy, 32(11): 62-68 (in Chinese). DOI:10.3969/j.issn.1674-3814.2016.11.011 |
张颖超, 肖寅, 邓华, 2016. 基于ELM的风电场短期风速订正技术研究[J]. 气象, 42(4): 466-471. Zhang Y C, Xiao Y, Deng H, 2016. Research on short-term wind speed correction technology of wind farm based on ELM[J]. Meteor Mon, 42(4): 466-471 (in Chinese). |
张治国, 崔炜, 白雪涛, 等, 2017. 第24届冬奥会海坨山赛区近两年冬季地面风场特征[J]. 干旱气象, 35(3): 433-438. Zhang Z G, Cui W, Bai X T, et al, 2017. Characteristics of ground wind field in the winter of Haishu Mountain in the 24th Winter Olympic Games[J]. Arid Meteor, 35(3): 433-438 (in Chinese). |
周志华, 2016. 机器学习[M]. 北京: 清华大学出版社: 248-261. Zhou Z H, 2016. Machine Learning[M]. Beijing: Tsinghua University Press: 248-261 (in Chinese). |
Erdem E, Shi J, 2011. ARMA based approaches for forecasting the tuple of wind speed and direction[J]. Appl Energy, 88(4): 1405-1414. DOI:10.1016/j.apenergy.2010.10.031
|
Li G, Shi J, 2010. On comparing three artificial neural networks for wind speed forecasting[J]. Appl Energy, 87(7): 2313-2320. DOI:10.1016/j.apenergy.2009.12.013
|
Lin Y J, Kruger U, Zhang J P, et al, 2015. Seasonal analysis and prediction of wind energy using random forests and arx model structures[J]. IEEE Trans Control Syst Technol, 23(5): 1994-2002. DOI:10.1109/TCST.2015.2389031
|
López E, Valle C, Allende H, et al, 2018. Wind power forecasting based on echo state networks and long short-term memory[J]. Energies, 11(3): 526. DOI:10.3390/en11030526
|
Ren Y, Suganthan P N, Srikanth N, 2016. A novel empirical mode decomposition with support vector regression for wind speed forecasting[J]. IEEE Trans Neural Netw Learn Sys, 27(8): 1793-1798. DOI:10.1109/TNNLS.2014.2351391
|
Wang J J, Wang Y F, Li Y N, 2018. A novel hybrid strategy using three-phase feature extraction and a weighted regularized extreme learning machine for multi-step ahead wind speed prediction[J]. Energies, 11(2): 321. DOI:10.3390/en11020321
|
Zjavka L, 2015. Wind speed forecast correction models using polynomial neural networks[J]. Renew Energy, 83: 998-1006. DOI:10.1016/j.renene.2015.04.054
|
 2019, Vol. 45
2019, Vol. 45 
