短时强降水是指短时间内出现的强度较大的降水,是由中小尺度对流系统造成的一种重要的强对流天气。短时强降水具有突发性和局地性强、生命史短、灾害重等特点。随着经济和技术的发展,政府和公众对短时强降水短时临近预报预警准确率和精细化水平的需求越来越高;但由于其发生发展十分迅速,对其落区和时效的预报预警一直都是预报业务中的难点。
虽然世界气象组织2005年定义的临近预报则拓展为0~6 h的天气预报;但我国气象预报业务中,短时预报是指0~12 h以内的天气预报,临近预报是0~2 h的天气预报。对流风暴和降水的0~2 h临近预报技术主要包括外推预报、经验预报(或者称为“专家预报”)。当前,国内外业务上应用的短时临近预报技术主要是基于雷达及卫星等资料的外推,但由于缺乏对强对流天气系统的发生、发展和消亡的物理机制描述,预报时效超过1 h以上的预报准确率大大降低,因此,更长时效的强对流天气系统预报采用数值模式预报在原理上应当优于简单的外推(陈葆德等,2013)。目前国内外的强对流天气的短时预报更多依赖于快速更新或者集合的高时空分辨率中尺度数值模式系统, 其中降水的客观短时预报技术主要思路是将外推预报和高分辨率数值预报结果相融合(Wilson et al, 1998;2010; Walser et al, 2004;俞小鼎等,2012;郑永光等,2015):1~3 h预报需要融合雷达外推和数值预报,3~6 h预报以数值预报为主(俞小鼎等,2012),而6~12 h几乎完全依赖数值预报或者利用统计等后处理手段对其订正和释用。
近年来,随着高分辨率中尺度模式的准确率和分辨率的不断提高,研究和业务使用表明,高分辨率模式将在强对流天气预报及预警中发挥越来越重要的作用。但是高分辨率模式本身存在的诸多“不完美”,进而会局限其在业务预报中的作用,这些局限主要源于初边界条件、同化技术、模式物理过程、模式适用性(漆梁波,2015)、降水系统的可预报性、中尺度观测网布局和数值模式本身(Sun et al, 2014)等方面。因此对高分辨率模式产品应用的一个重要的方面就是模式产品后处理技术,基于高分辨率模式预报发展更精细化的、准确率更高的强对流直观预报产品(比如小时降水量、雷达反射率因子、最大阵风等)提供给预报员,是有效快捷地发挥高分辨率模式性能的重要途径,也是未来对高分辨率模式预报应用的方向。
在短时临近预报时效内,模式预报误差很大程度上是由于初始分析场的不确定性造成的,集合预报技术在减小预报不确定性,提高模式预报技巧上已经得到了成功的应用和发展(Krishnamurti et al, 1999; Cartwright and Krishnamurti, 2007; Zhi et al, 2012)。时间滞后集合订正预报技术最先由Hoffman and Kalnay (1983)应用于中长期预报。近年来,许多研究人员已经开始将此技术用于短期时效预报,其原因之一就是短期预报的误差重要来源归咎于初始场的不确定性,而该技术可以解释为通过一系列不同的初始扰动条件得到的一组预报结果,各成员为不同起报时间、不同预报时效对同一时间点的模式预报结果,其作用与通过不同的初始场扰动获得的集合成员效果相似。此外,采用该方法进行模式资料后处理,不需要对数据进行过于复杂的计算,不会占用过多的计算资源,是一种高效节能的计算方案。这方面的工作,国内外的相关研究工作已经积累了一些经验。李佰平和智协飞(2012)基于欧洲中期天气预报中心(ECMWF)模式,采用多元线性回归和多时效消除偏差平均方法建立单一模式的多时效集成订正预报,有效地减小了地面温度的预报误差。Lu et al(2007)、Mittermaier(2007)、Yuan et al(2009)分别基于美国RUC(Rapid Update Cycle)模式、英国UM(Unified Model)模式、MM5(第五代中尺度模式)和WRF(Weather Research and Forecasting)模式的预报构建了单一模式或多模式时间滞后集合预报,并采用集合平均、集合最大值以及集合概率值获取6 h累积降水确定性预报及概率预报场。他们的结果表明时间滞后方法可以有效降低高分辨率模式的漏报率,提高模式的预报质量,尤其是针对漏报问题更为突出的高影响天气。傅娜等(2013)基于华东中尺度快速更新同化系统,仅仅使用时间滞后集合平均和集合概率方法分别得到了小时降水量及概率预报,并发现小-大雨量级集合平均降水预报优于各集合成员,但集合平均暴雨预报不如部分集合成员。
GRAPES-RAFS是基于中国气象局新一代全球/区域多尺度统一的同化与数值预报系统(Global/Regional Assimilation and Prediction System, GRAPES)的中尺度快速分析数值预报系统。在GRAPES-RAFS模式预报基础上,本文通过时间滞后的集合方法构建多个集合成员,使用平均TS评分值计算相应预报成员权重系数的方法建立预报方程,并采用频率匹配订正方法进行降水量级订正,从而得到订正的逐小时降水预报,以提升GRAPES-RAFS预报的应用水平并为降水短时业务预报提供客观技术产品支撑。
1 GRAPES-RAFS模式简介中尺度数值模式快速分析预报系统已经在国外先进的强对流业务中心(如美国的SPC/NCEP)证明是在强对流短时预报预警业务(0~12 h)中最有力预报工具。GRAPES-RAFS系统每天冷启动两次(08和20时,北京时,下同)后,每隔3 h在前一次模式场基础上进行快速三维变分更新同化,同化分析的背景场资料包括探空(气压、湿度)、飞机报资料(温度、风场)、地面资料(气压、湿度)、船舶资料(气压、风场、湿度)、雷达VAD风场(通过速度方位显示算法反演获得的某高度平面上的平均风向、风速)、FY-2E云导风等资料(徐枝芳等,2013;黄丽萍等,2017),之后开始计算0~30 h逐小时预报。模式预报产品水平分辨率为0.1°×0.1°,每天运行8次(3 h为周期),起报时间分别为02、05、08、11、14、17、20和23时。实际业务中产品可保证在起报时间后4 h以内提供至服务器,供预报员调用。
2 时间滞后集合和频率匹配订正方法 2.1 时间滞后集合方法虽然GRAPES-RAFS模式预报具备分辨大气中的中小尺度对流活动的能力,但其本身不可避免的具有一些不足。使用高频次的非常规观测资料对模式初值进行不断更新同化,可以得到更精准的模式初值,提高中尺度预报系统的预报准确率,但也带来了模式初始变量不协调而引发的初始平衡问题与误差累积问题,需要通过模式积分一段时间之后才能达到新的平衡,一般称这个过程为平衡调整(spin-up)过程(陈葆德等,2013)。时间滞后集合预报方法综合考虑不同起报时间不同预报时效对同一时间点的模式预报结果,选取不同的权重系数经过计算获得订正后的小时降水量预报值,可以有效地改善由于模式“spin-up”以及短时临近预报时效内初始分析场的不确定性带来的预报误差。此外,从主观预报角度出发,由于模式总在不断地调整更新中,通常预报员会主观对比不同起报时间预报场对所关注的时间点的预报准确度来剔除预报效果较差的预报成员,保留具有预报优势的成员,通过时间滞后集合预报计算,提供直接的订正降水预报产品,可以为预报员节约时间成本,提高预报效率。
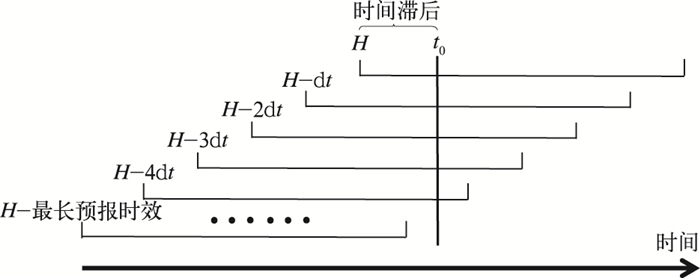
时间滞后集合预报的核心是基于快速更新同化系统构建集合成员,每一次循环更新将产生高频次的预报场,贡献新的集合成员,这一过程并不占用额外的计算机资源,成为一种经济实用的集合预报方案。基于GRAPES-RAFS模式,以24 h预报时效为限,选取间隔3 h起报的预报场构造集合成员,图 1为当前时刻H的时间滞后集合成员构成示意图。
|
图 1 时间滞后集合预报成员构造示意图 Fig. 1 Schematic diagram of the construction of time-lagged ensemble members |
对于当前时刻H,t0时刻的预报场集合成员总数N计算公式如下:
| $N = {\rm{INT}}\left[ {\frac{{\max\;forecast\;projection - lead\;time}}{{\mathit{model\;initial\;interval}\left({{\rm{d}}\mathit{t}} \right)}}} \right] + 1 $ |
式中,N为集合成员总数,INT为取整的运算符,max forecast projection为可选的模式预报的最长预报时效,lead time为预报时刻对于当前时刻H的预报时效,model initial interval(dt)为模式的预报时间间隔。对于GRAPES-RAFS模式,本文中的集合预报成员预报时效限制在24 h范围内,因此max forecast projection为24 h,模式起报间隔时间dt为3 h,因此,集合成员数
为了尽量发挥预报性能较好成员的作用,如何评估各集合成员的预报性能从而赋予不同的权重系数就成为影响最终集合订正预报效果的重要因素。以前的研究(Lu et al,2007;Mittermaier,2007;Yuan et al,2009;傅娜等,2013)多是针对6 h及其以上的累积降水量场进行订正,获得的是集合平均的累积降水量的预报和概率预报,没有不同成员预报能力的评估,也没有对小时降水量进行订正,因此,本文基于GRAPES-RAFS模式的不同起报时间的小时降水量预报效果的评估结果来确定不同成员权重系数以获取最终集合预报结果。
权重系数的计算参考美国风暴预报中心(SPC)业务检验方法(Hitchens and Brooks, 2012;2014),选用基于站点的“点对面”TS评分标准,即以评分站点为中心,40 km为半径的范围内自动站监测到的最大小时降水量为该评分站点的检验实况降水量(唐文苑等,2017),同时,采用三角线性插值的方法将模式格点预报插值到评分站点上,获取预报降水量,形成基于评分站的实况与预报一一对应的数据序列,以此统计二维列联表中预报正确站数、空报站数及漏报站数并计算TS评分值。采用的降水数据为经过质控的我国28400个自动站观测的小时降水量资料。
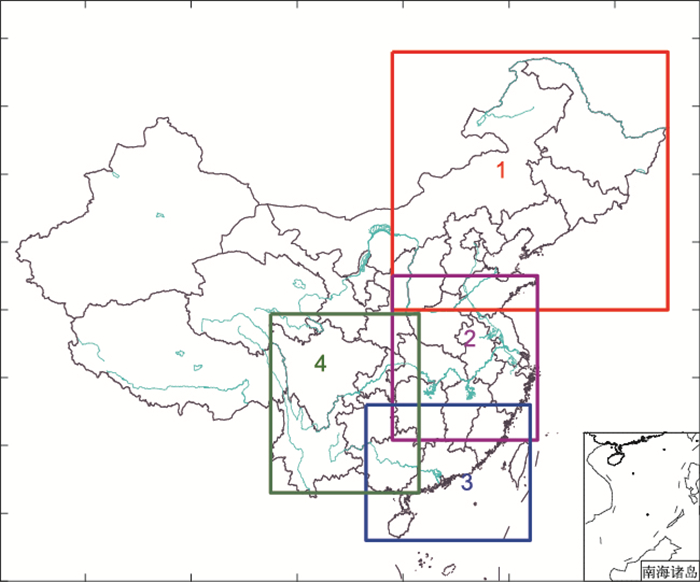
考虑模式对不同区域的预报性能有所差别,将我国中东部划分为北方、西南、华南及中东部大部地区等4个区域(图 2)。由于模式预报资料的获取较起报时间滞后3~4 h,以起报时间之后4 h的降水场为评分计算的实况场,分别计算每个区域落到站点上的时间滞后集合成员平均TS评分值,区域范围内评分高则该成员的权重系数大。4个区域外的预报值不做调整,选取最临近时次预报场替代,4个区域中相互重合区域的格点降水值取平均值。格点降水值P通过式(1)计算获得。
|
图 2 区域划分示意图 (图中标注数字代表不同区域) Fig. 2 Schematic diagram of region division (Numbers represent different regions) |
| $P = {W_1}{P_1} + {W_2}{P_2} + {W_3}{P_3} + \cdots + {W_\mathit{i}}{P_i} $ | (1) |
式中Pi为第i个成员的格点降水值。权重系数为
| ${W_\mathit{i}} = \frac{{T{S_\mathit{i}}}}{{\sum\limits_{i = 1}^N {T{S_i}} }} $ |
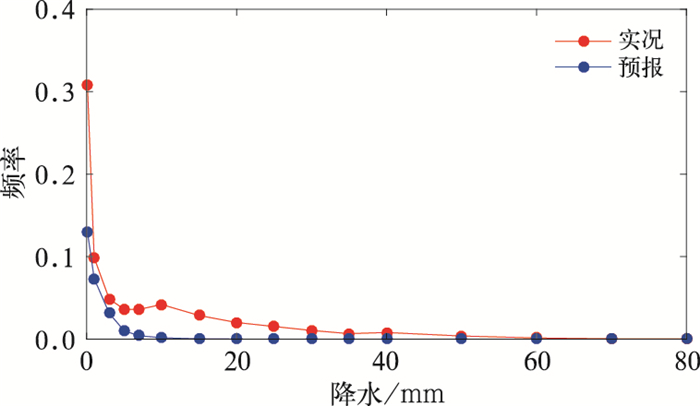
通过统计预报和实况前期在不同阈值条件下降水出现的频率发现(图 3),对于GRAPES-RAFS模式,普遍存在小时降水量预报偏弱的问题。本文采用频率匹配订正法(Zhu and Luo, 2015; 李俊等,2014)对时间滞后集合预报结果再进行降水量级订正,即针对某一阈值,假定它在预报中出现的频率应该同实况中出现的频率一致,那么预报的降水量值应该寻求适当的系数以订正到同实况一致频率的降水量上,通过该方法可有效改善模式在降水量级上的预报偏差。
|
图 3 2017年8月1日11—23时2区GRAPES-RAFS模式与实况降水频率对比 Fig. 3 Comparison of GRAPES-RAFS model and observed precipitation frequency in the second section during 11:00-23:00 BT 1 August 2017 |
对全国范围内的中东部分为4个区域分别进行统计,以当前业务中选定的标准评分站(全国范围内共2410个)为基础,将经过质量控制的我国28400个自动站实况小时降水通过“点对面”的资料处理方法,获取整理后的2410站实况降水量,同时通过三角线性插值法将集合预报场插值到评分站上,采用对各区域内站点统计方式计算降水频率,共统计了0.1、1、3、5、7、10、15、20、25、30、35、40、50、60、70、80 mm 16个阈值的频率分布。预报和实况降水频率的计算方法如下:
| ${F_{频j}} = \frac{{\sum\limits_{i = 1}^{i = N} {{B_{ij}}} }}{{\sum\limits_{i = 1}^{i = N} {{A_{ij}}} }} $ |
式中,F频j为区域内某个阈值降水的平均频率,Bij为某个阈值降水出现的总站数,j代表某个降水阈值,Aij为区域内的站数,i为滑动的时间窗区(李俊等,2014)。
Zhu and Luo(2015)指出滑动窗区时长的选择可以根据实际情况以及方法实现的效果而定。为了满足实际业务中对产品时效性的要求,同时考虑需要有足够的样本总数才具有统计的意义,并且能够尽量实时反映不同集合成员的预报能力,本文采用的频率匹配订正历史样本的时间窗区为最近过去12 h。
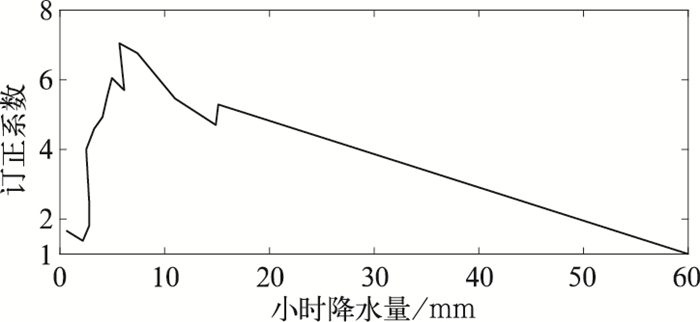
以图 3为例,最新的模式预报资料起报时间为2017年8月1日23时,计算得到2区8月1日11—23时模式和实况的降水量频率分布(有实况资料的列入计算范围,没有实况的摒弃),在相同频率下,模式预报的降水量基本上都小于实况,表明预报与模式相比有明显的干偏差。计算不同阈值下相同频率的模式与实况降水量之比,得到一组降水阈值与对应订正系数的序列,考虑到降水过程存在强弱变化,因此该序列中降水阈值的最大值会存在差异,以60 mm为降水量的最终订正上限,相应的订正系数定为1,获取最终的降水阈值与订正系数序列。根据以上计算的这组各阈值上的订正系数,采用最邻近插值的方法获得对任何降水量的订正系数,用该订正系数乘以对应格点的预报值。以起报时间为8月1日23时为例,使用8月1日11—23时模式和实况的降水量资料得到的8月1日23时起报2区预报场订正系数随小时累积降水量变化曲线(图 4)。
|
图 4 2017年8月1日23时2区订正系数随小时累积降水量变化 Fig. 4 Curve of corrected coefficient with hourly accumulated precipitation in the second section at 23:00 BT 1 August 2017 |
预报结果检验所用观测数据同前文中为了得到不同成员权重系数所计算TS评分所用数据相同。检验方法除了考虑使用传统的TS评分方法外,为了更进一步评价本文方法的预报性能,采用了新型的检验方法——FSS(fractions skill score,分数技巧评分)检验。
3.1 TS检验针对具有高分辨率的中尺度预报系统,传统的观测与预报“点对点”检验方法并不适用,采用前述的“点对面”TS评分方案(唐文苑等,2017)来检验评估订正后的预报结果。
检验阈值的选取也将影响检验结果是否科学可靠,由于GRAPES-RAFS模式存在对降水预报偏弱的系统性偏差,分别选取各区域范围内实况及预报场的第75百分位数作为对应的检验阈值;而对于进行频率匹配订正后的降水预报,主要考察该方法是否可以减小模式对降水量级偏小的系统性偏差,检验阈值选取上没有使用百分位数,而是选定统一的检验阈值。
评分站点选取全国范围内包括基准、基本和一般天气站在内的2410个站点(均为中国气象局观测业务考核的站点)。TS评分计算方法如下:
| $TS = \frac{{NA}}{{NA + NB + NC}} $ |
式中,NA为预报正确的站(次)数,NB为空报站(次)数,NC为漏报站(次)数。
3.2 FSS检验许多研究表明,由于中尺度模式预报能够再现中尺度对流系统的结构和演变特征,模式水平分辨率的提高有利于定量降水预报准确率的提高。尽管如此,相比降水强度和降水形态,对于降水位置预报的差异仍是中尺度模式预报的主要误差来源(Ebert and McBride 2000).通常情况下,中尺度模式预报的降水系统会比实况时间上有若干个小时的偏差,空间距离上有几十千米的偏差(Bernardet et al, 2000)。
模糊检验法通过比较预报和观测场中对应的邻(临)近区域(时间)内的特征,当检验对象预报值相对于实况在空间或时间上有位移偏差时,模糊检验方法仍能反映出预报系统的优劣。FSS方法属于模糊检验方法中的一种,最初由Robert and Lean(2008)提出。首先通过计算给定半径范围的窗区中心格点的概率值(图 5),即超过一定阈值q的格点总数占窗口区总格点数的比值,将预报场和实况场转化为格点概率分布场。

|
图 5 预报及观测格点概率值计算方案示意图 (图中阴影表示降水量超过给定阈值的格点;邻域半径为3个格点,中心格点概率值为6/25) Fig. 5 Schematic diagram of calculation scheme for probability values of forecast and observation points (shaded grids: precipitation exceeds a given threshold; The adjacent radius is set to be 3 grids, and the probability value of the center grid point is 6/25) |
通过式(2)获得给定半径和阈值的FSS评分。
| $FSS = 1 - \frac{{\frac{1}{N}\sum\limits_N {{{\left({{P_{\rm{f}}} - {P_{\rm{o}}}} \right)}^2}} }}{{\frac{1}{N}\left[ {\sum\limits_N {P_{\rm{f}}^2 + \sum\limits_N {P_{\rm{o}}^2} } } \right]}} $ | (2) |
式中,Pf为窗区内预报概率值,Po轴为窗区内观测概率值,N为评分区域内邻域窗区的数量。FSS分值范围为0~1,0为预报与实况邻域窗区内事件发生频率完全不匹配,1为预报与实况邻域窗区内事件发生频率一致。当邻域窗区大小从1(模式格点分辨率)最大增加至2n-1(n为窗区沿长轴方向的格点数)时,FSS趋向于1。在给定的阈值条件下,通过改变窗区的大小,可以获取一系列的FSS评分值。以窗区大小为横坐标,FSS值为纵坐标即可得到FSS随窗区大小变化的曲线。对比不同的预报系统,当FSS变化曲线越接近左上角,即在越小的窗区内越接近1,说明该系统的预报效果越好。对比不同的预报系统,当FSS变化曲线越接近左上角,即在越小的窗区内越接近1,说明该系统的预报效果越好(唐文苑等,2018)。本文使用三角线性插值的方法将站点实况降水量插值到与模式一致的网格点上,然后将邻域窗区大小从1个格点以奇数递增至21个格点,获得FSS评分值随窗区大小的变化曲线。
4 结果及分析 4.1 TS评分采用“点对面”的TS评分方法分区域对2017年8—9月小时降水量时间滞后集合订正预报及模式最新时次的预报(其起报时间为图 1中的当前时刻H)进行对比分析。采用预报场及相应的实况场各区域内的第75百分位数作为检验阈值进行检验。
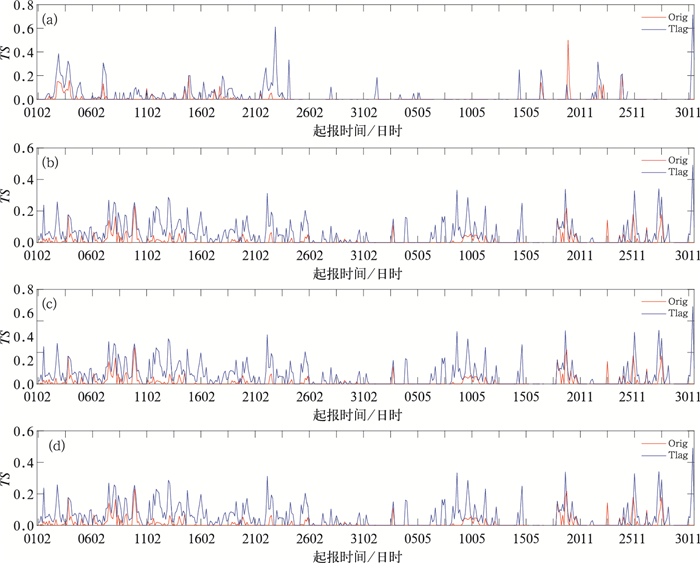
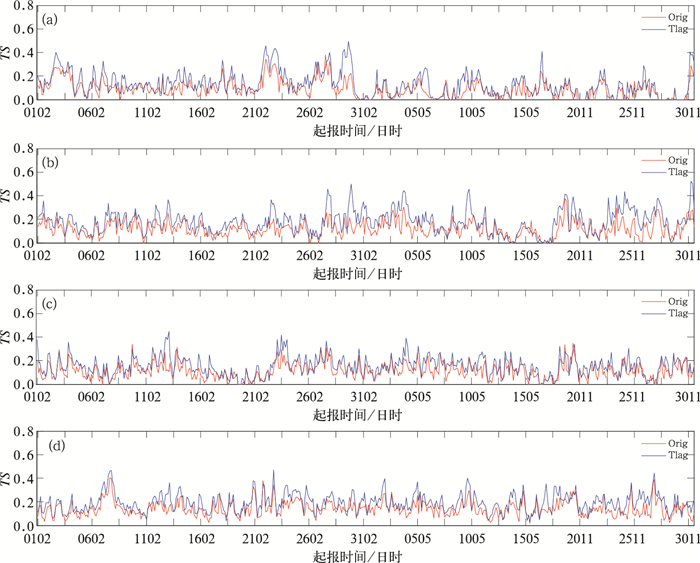
图 6是8—9月逐日逐个预报时次6 h时效模式最新时次预报与集合订正后的预报TS评分对比。整体上看,经过时间滞后集合订正后的预报评分显著高于模式最新时次预报,其他时效预报评分对比结果与6 h时效结果类似(图略)。
|
图 6 2017年8月1日至9月30日逐日间隔3 h起报6 h时效时间滞后集合订正(蓝线)与模式最新时次预报(红线)分区域TS评分曲线图(a)1区,(b)2区,(c)3区,(d)4区 Fig. 6 TS score for the 3 h runs, 6 h forecasts derived from the time-lagged ensemble (blue line) and the up-to-date forecasts (red line) from 1 August to 30 September 2017 (a) Zone 1, (b) Zone 2, (c) Zone 3, (d) Zone 4 |
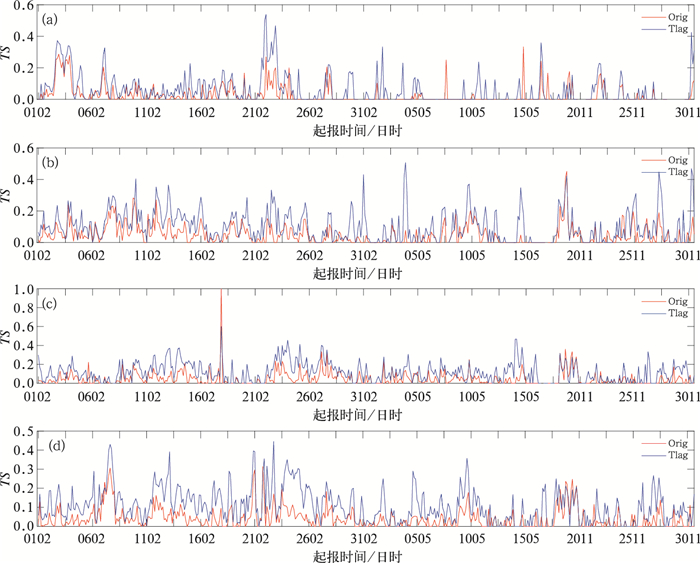
对进一步使用了频率匹配订正法的时间滞后集合降水预报进行了TS评分检验,分别采用了小时降水量5和10 mm这两个统一的检验阈值。图 7是5 mm以上量级降水的TS评分曲线对比图。由图可见,经过量级订正后整体上TS评分有了显著提高,对于降水频率更高,降水强度更大的南方(3、4区)订正后的效果更明显。10 mm阈值的评分结果对比(图 8)显示,频率匹配订正方法的优势更为凸显。
|
图 7 2017年8月1日至9月30日逐日间隔3 h起报6 h时效频率匹配量级订正(蓝线)与模式最新时次预报(红线)分区域TS评分(阈值:5 mm)曲线图(a)1区,(b)2区,(c)3区,(d)4区 Fig. 7 TS score (threshold: 5 mm) for the 3 h runs, 6 h forecasts derived from the frequency matching correction (blue line) and the up-to-date forecasts (red line) from 1 August to 30 September 2017 (a) Zone 1, (b) Zone 2, (c) Zone 3, (d) Zone 4 |
需要说明的是,尽管整体上经过量级订正后降水预报评分提高,但在一些特殊个例中,偶尔也会出现经过订正后评分下降的情况,如在8月17日23时起报6 h时效预报华南区域5 mm阈值评分中(图 7c),模式降水TS评分值达到1,而经过量级订正后评分约为0.6,这主要是由于该时刻整体上降水强度弱、范围小的缘故,该区域评分站中只有3个站点降水超过阈值,而原始模式5 mm以上量级降水落区位置与实况吻合,经过量级订正后,华南区域中一些分散的小范围弱降水区降水量级有所增加,达到5 mm阈值之上,造成一定的空报,导致订正后的评分比模式最新时次预报低。同时,在评分阈值增加的情况下(图 8),评分曲线中,出现多处TS评分为0或是无效值的窗区,这主要是因为小时雨量10 mm以上量级降水出现的几率低,并且位置更难把握造成的,这个特点在降水偏少的东北华北(1区)更显著。
通过集合成员数计算公式
|
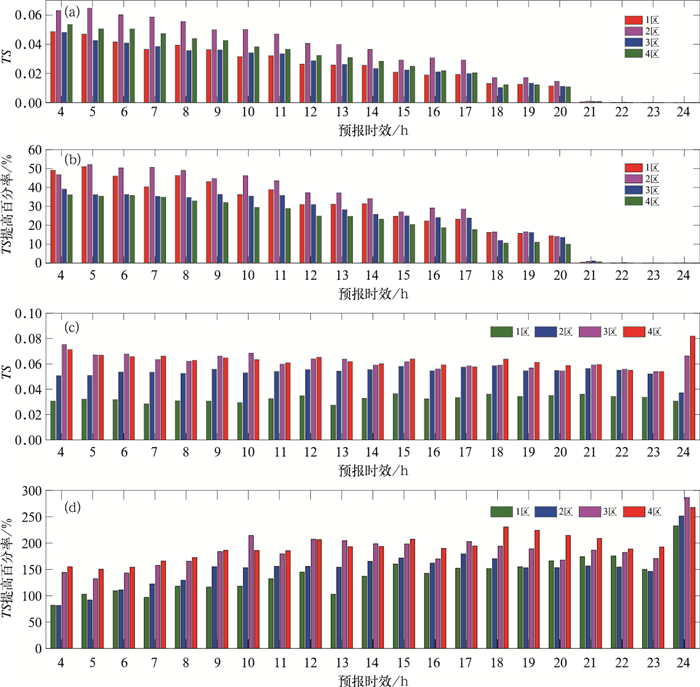
图 9 2017年8月1日至9月30日间隔3 h起报1~24 h时效时间滞后集合预报与模式最新时次预报以第75百分位为阈值TS评分差(a)及TS评分提高百分率(b)、频率匹配量级订正与模式最新时次预报5 mm阈值TS评分差(c)及TS评分提高百分率(d) Fig. 9 Difference of TS score (a) and the percentage increase (b) between the time-lagged ensemble and the up-to-date forecasts for the 3 h runs, 1-24 h forecasts (threshold: the 75th percentile), and difference of TS score (c) and the percentage increase (d) between the frequency matching correction and the up-to-date forecasts for the 3 h runs, 1-24 h forecasts (threshold: 5 mm)from 1 August to 30 September 2017 |
下面评估进一步应用频率匹配订正法对降水量级订正后的预报效果(图 9c,9d)。对于5 mm以上量级降水,模式最新时次预报4个区域平均TS评分在0.025~0.039,集合和降水量级订正后平均评分在0.058~0.098,评分提高百分率在127.6%~186.4%。不同时效对比,评分提高的幅度差异不大。从评分提高百分率上看,量级订正的效果显著,各个区域百分率提高基本在100%以上。同时,频率匹配订正方法在降水频率更高、强度更大的江南南部、华南、西南地区(3区、4区)取得的效果更好,而在降水频率较低、强度较弱的东北、华北(1区)订正效果表现略差。
4.2 个例评估2017年8月22日午后至23日凌晨,受到500 hPa高空槽及副热带高压外围暖湿气流输送影响,河北、北京等地出现了明显的短时强降水过程,小时雨量达20~50 mm。雷达组合反射率因子拼图演变显示(图略),22日15时,较强回波在河北中西部开始发展并且向东北方向移动,之后逐渐发展加强,17:30出现回波强度>55 dBz的团状回波,形成“列车效应”,导致河北中部偏西地区出现持续的强降水。23日04—05时,形成长度约200 km的西南—东北向的准线性回波带,导致北京顺义、密云等地多个站点出现短时强降水,河北满城、易县、北京城区、顺义、密云等地12 h累计降水量超过50~70 mm,局地超过80 mm。
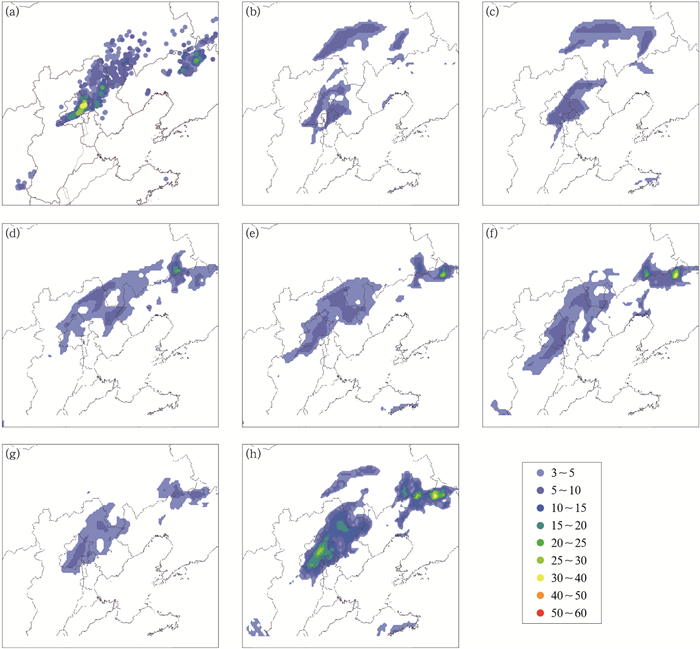
选取北京降水最强时段进行预报效果评估分析(图 10)。小时降水量监测实况显示(图 10a),23日05时,降水主体呈现西南—东北走向的带状分布,主要降水中心位于北京西北部;同时次降水中心位于河北兴隆至承德一带,最大小时降水量在10~20 mm,局地超过20 mm。对比模式预报情况,整体上模式预报降水量级偏小,最大小时降水量各时次预报均低于10 mm;对雨带位置的把握上,最新时次的预报(22日23时及22日20时)并没有表现出优势,天津北部存在空报的问题;22日17时起报12 h时效预报对于降水主体的位置、形态、量级上均表现出明显的偏差;而对于预报时效更长的15及18 h时效,在雨带位置、形态上更接近于实况。通过使用时间滞后集合方法后,虽然降水量级上仍然存在偏小的问题,但降水主体的位置、形态基本与实况吻合,同时经过降水量级偏差订正后,北京东北部的强降水中心小时降水量达到25~30 mm,与实况接近。可见,经过集合和订正后,预报质量明显提高,具有较高的参考价值。
|
图 10 2017年8月23日05时降水实况(a),GRAPES-RAFS模式2017年8月22日23时起报6 h时效降水预报(b),GRAPES-RAFS模式2017年8月22日20时起报9 h时效降水预报(c),GRAPES-RAFS模式2017年8月22日17时起报12 h时效降水预报(d),GRAPES-RAFS模式2017年8月22日14时起报15 h时效降水预报(e),GRAPES-RAFS模式2017年8月22日11时起报18 h时效降水预报(f),经过时间滞后集合运算订正后的小时降水量(g),经过量级订正后的小时降水量(h) Fig. 10 Precipitation observation at 05:00 BT 23 August 2017 (a), 6 h forecasts from GRAPES-RAFS initialized at 23:00 BT 22 August 2017 (b), 9 h forecasts from GRAPES-RAFS initialized at 20:00 BT 22 August 2017 (c), 12 h forecasts from GRAPES-RAFS initialized at 17:00 BT 22 August 2017 (d), 15 h forecasts from GRAPES-RAFS initialized at 14:00 BT 22 August 2017 (e), 18 h forecasts from GRAPES-RAFS initialized at 11:00 BT 22 August 2017 (f), after time-lagged ensemble correction (g), after frequency matching correction (h) |
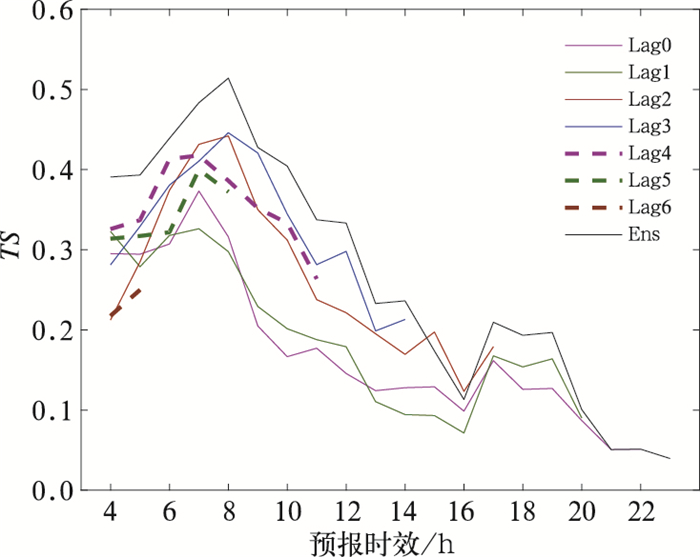
使用TS评分评估22日23时起报4—23 h预报时效内各集合成员(Lag0-6,Lag0为最新时次的预报,Lag6为时效最长的预报;以23时起报4 h时效的预报场为例,Lag0表示22日23时起报4 h时效的模式最新时次预报,Lag1表示22日20时起报7 h时效的模式最新时次预报,以此类推,Lag6表示22日05时起报22 h时效的模式最新时次预报)与集合订正预报结果(Ens)(图 11)。整体上,经过时间滞后集合订正后,各预报时效预报TS评分都高于单一成员,同时对于此次过程,预报员参考最临近的预报(Lag0)并不是最好的选择,Lag0-1预报评分整体上低于其他成员,集合方法为预报员自动挑选最优的预报成员,表现最为出色。虽然GRAPES-RAFS快速更新同化系统采用的是热启动技术,一定程度上缩短了模式的自适应过程,“spin-up”的影响也会在很大程度上得到抑制,但当前版本的GRAPES-RAFS热启动快速更新同化的可用资料有限,同时当前三维雷达反射率组网拼图资料是通过云分析模块并非是同化模块进入模式系统,这些都有可能影响热启动技术的效果,应该引起模式开发者和使用者的注意。
|
图 11 2017年8月22日23时起报4~23 h时效预报TS评分对比 Fig. 11 TS scores for 4-23 h forecasts initialized at 23:00 BT 22 August 2017 |
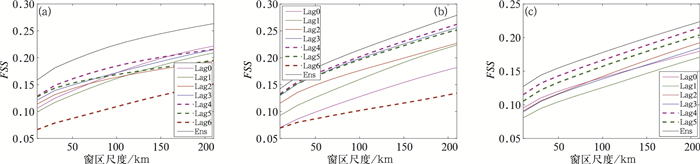
图 12显示各集合成员及订正后的集合预报的FSS曲线图。阈值选取检验区间内第75百分位数降水量,横坐标表示检验的空间尺度,从1个格点(即模式原始分辨率,约10 km)递增至21个格点(约210 km)。如前所述,FSS检验考察的是不同尺度大小的邻域窗区内预报与实况事件发生概率值的匹配程度,评分值越高,该尺度大小的窗区内预报和实况的发生概率越接近,预报效果越好。检验结果显示,无论在那个尺度上,集合订正后的预报评分均高于单一成员,同时,与TS评分结论一致。对各成员进行对比来看,评分最高的成员并不是最临近的预报场,Lag4的预报效果最好。
|
图 12 2017年8月22日23时起报4 h(a),5 h(b),6 h(c)时效预报FSS评分对比 Fig. 12 FSS scores for 4 h (a), 5 h (b), 6 h (c) forecasts initialized at 23:00 BT 22 August 2017 |
本文基于快速更新同化的中尺度数值模式系统GRAPES-RAFS逐时降水预报(分辨率为0.1°×0.1°),通过时间滞后集合方法构建多个集合成员,使用平均TS评分值计算对应预报成员的权重系数建立预报方程,进一步采用频率匹配订正法进行降水量级订正,获得最终集合的逐时降水量预报。本文对使用该方法的2017年8—9月的逐日和典型个例预报结果进行评估分析表明:
(1) 经过时间滞后集合订正后的TS评分明显高于模式最新时次预报。不同预报时效对比,随预报时效的延长,订正效果减弱,这可能是由于各时效预报集合成员数不同造成的,集合成员数越多,评分提高的幅度和百分率越高。不同区域的TS评分提高幅度有明显的差异,时间滞后集合预报对我国中东部(包括黄淮、江淮、江南地区)的小时降水量订正效果最好。
(2) 进一步应用频率匹配订正方法显著改善了模式对于小时降水量预报偏弱的问题,与模式最新时次预报相比,各个区域TS评分百分率提高基本在100%以上。频率匹配订正方法在降水频率更高、强度更大的江南南部、华南、西南地区取得的效果更好,而在降水频率较低、强度较弱的东北、华北订正效果表现相对略差。
(3) 对2017年8月22日午后至23日凌晨河北、北京等地发生的中小尺度强降水过程预报评估分析表明,经过时间滞后集合订正后,各预报时效预报TS评分高于单一成员。同时,对于此次过程,预报员参考最临近的预报并不是最好的选择,集合方法为预报员自动挑选最优的预报成员,表现最为优异。经过本文的方法订正后,大大提高了对强降水系统位置、形态及降水量级的预报水平。
目前,本文给出的时间滞后集合预报技术只是基于单一模式针对小时降水量进行集合订正,下一步将开展基于多模式的时间滞后集合订正预报研究以纳入更多的中尺度模式预报,并将试验集合概率预报,或者应用于雷达反射率因子预报,以进一步提高对小时降水量和中小尺度对流系统的客观短时预报能力。
陈葆德, 王晓峰, 李泓, 等, 2013. 快速更新同化预报的关键技术综述[J]. 气象科技进展, 3(2): 29-35. Chen B D, Wang X F, Li H, et al, 2013. An overview of the key techniques in rapid refresh assimilation and forecast[J]. Adv Meteor Sci Tech, 3(2): 29-35 (in Chinese). |
傅娜, 陈葆德, 谭燕, 等, 2013. 基于快速更新同化的滞后短时集合预报试验及检验[J]. 气象, 39(10): 1247-1256. Fu N, Chen B D, Tan Y, et al, 2013. Time-lag ensemble forecasting experiment and evaluation based on SMB-WARR[J]. Meteor Mon, 39(10): 1247-1256 (in Chinese). DOI:10.7519/j.issn.1000-0526.2013.10.002 |
黄丽萍, 陈德辉, 邓莲堂, 等, 2017. GRAPES_Meso V4.0主要技术改进和预报效果检验[J]. 应用气象学报, 28(1): 25-37. Huang L P, Chen D H, Deng L T, et al, 2017. Main technical improvements of GRAPES Meso V4.0 and verification[J]. J Appl Meteor Sci, 28(1): 25-37 (in Chinese). |
李佰平, 智协飞, 2012. ECMWF模式地面气温预报的四种误差订正方法的比较研究[J]. 气象, 38(8): 897-902. Li B P, Zhi X F, 2012. Comparative study of four correction schemes of the ECMWF surface temperature forecasts[J]. Meteor Mon, 38(8): 897-902 (in Chinese). |
李俊, 杜钧, 陈超君, 2014. 降水偏差订正的频率(或面积)匹配方法介绍和分析[J]. 气象, 40(5): 580-588. Li J, Du J, Chen C J, 2014. Introduction and analysis to frequency or area matching method applied to precipitation forecast bias correction[J]. Meteor Mon, 40(5): 580-588 (in Chinese). |
漆梁波, 2015. 高分辨率数值模式在强对流天气预警中的业务应用进展[J]. 气象, 41(6): 661-673. Qi L B, 2015. Operational progress of high-resolution numerical model on severe convective weather warning[J]. Meteor Mon, 41(6): 661-673 (in Chinese). |
唐文苑, 周庆亮, 刘鑫华, 等, 2017. 国家级强对流天气分类预报检验分析[J]. 气象, 43(1): 67-76. Tang W Y, Zhou Q L, Liu X H, et al, 2017. Anlyisis on verification of national severe convective weather categorical forecasts[J]. Meteor Mon, 43(1): 67-76 (in Chinese). |
唐文苑, 郑永光, 张小雯, 2018. 基于FSS的高分辨率模式华北对流预报能力评估[J]. 应用气象学报, 29(5): 513-523. Tang W Y, Zheng Y G, Zhang X W, 2018. FSS-based evaluation of convective weather forecasts in North China from high resolution modes[J]. J Appl Meteor Sci, 29(5): 513-523 (in Chinese). |
徐枝芳, 郝民, 朱立娟, 等, 2013. GRAPES_RAFS系统研发[J]. 气象, 39(4): 466-477. Xu Z F, Hao M, Zhu L J, et al, 2013. On the research and development of GRAPES_RAFS[J]. Meteor Mon, 39(4): 466-477 (in Chinese). DOI:10.3969/j.issn.1674-7097.2013.04.009 |
俞小鼎, 周小刚, 王秀明, 2012. 雷暴与强对流临近天气预报技术进展[J]. 气象学报, 70(3): 311-337. Yu X D, Zhou X G, Wang X M, 2012. The advances in the nowcasting techniques on thunderstorms and severe convection[J]. Acta Meteor Sin, 70(3): 311-337 (in Chinese). DOI:10.3969/j.issn.1004-4965.2012.03.003 |
郑永光, 周康辉, 盛杰, 等, 2015. 强对流天气监测预报预警技术进展[J]. 应用气象学报, 26(6): 641-657. Zheng Y G, Zhou K H, Sheng J, et al, 2015. Advances in techniques of monitoring, forecasting and warning of severe convective weather[J]. J Appl Meteor Sci, 26(6): 641-657 (in Chinese). |
Bernardet L R, Grasso L D, Nachamkin J E, et al, 2000. Simulating convective events using a high-resolution mesoscale model[J]. J Geophys Res, 105(D11): 14963-14982. DOI:10.1029/2000JD900100
|
Cartwright T J, Krishnamurti T N, 2007. Warm season mesoscale superensemble precipitation forecasts in the southeastern United States[J]. Wea Forecasting, 22(4): 873-886. DOI:10.1175/WAF1023.1
|
Ebert E E, McBride J L, 2000. Verification of precipitation in weather systems:determination of systematic errors[J]. J Hydrol, 239(1/2/3/4): 179-202.
|
Hitchens N M, Brooks H E, 2012. Evaluation of the storm prediction center's day 1 convective outlooks[J]. Wea Forecasting, 27(6): 1580-1585. DOI:10.1175/WAF-D-12-00061.1
|
Hitchens N M, Brooks H E, 2014. Evaluation of the storm prediction Center's convective outlooks from day 3 through day 1[J]. Wea Forecasting, 29(5): 1134-1142. DOI:10.1175/WAF-D-13-00132.1
|
Hoffman R N, Kalnay E, 1983. Lagged average forecasting, an alternative to Monte Carlo forecasting[J]. Tellus A, 35(2): 100-118. DOI:10.3402/tellusa.v35i2.11425
|
Krishnamurti T N, Kishtawal C M, LaRow T E, et al, 1999. Improved weather and seasonal climate forecasts from multimodel superensemble[J]. Science, 285(5433): 1548-1550. DOI:10.1126/science.285.5433.1548
|
Lu C G, Yuan H L, Schwartz B E, et al, 2007. Short-range numerical weather prediction using time-lagged ensembles[J]. Wea Forecasting, 22(3): 580-595. DOI:10.1175/WAF999.1
|
Mittermaier M P, 2007. Improving short-range high-resolution model precipitation forecast skill using time-lagged ensembles[J]. Quart J Roy Meteor Soc, 133(627): 1487-1500. DOI:10.1002/qj.135
|
Roberts N M, Lean H W, 2008. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events[J]. Mon Wea Rev, 136(1): 78-97. DOI:10.1175/2007MWR2123.1
|
Sun J Z, Xue M, Wilson J W, et al, 2014. Use of NWP for nowcasting convective precipitation:recent progress and challenges[J]. Bull Amer Meteor Soc, 95(3): 409-426. DOI:10.1175/BAMS-D-11-00263.1
|
Walser A, Lüthi D, Schär C, 2004. Predictability of precipitation in a cloud-resolving model[J]. Mon Wea Rev, 132(2): 560-577. DOI:10.1175/1520-0493(2004)132<0560:POPIAC>2.0.CO;2
|
Wilson J W, Crook N A, Mueller C K, et a1, 1998. Nowcasting thunderstorms:a status report[J]. Bull Amer Meteor Soc, 79(10): 2079-2100. DOI:10.1175/1520-0477(1998)079<2079:NTASR>2.0.CO;2
|
Wilson J W, Feng Y R, Chen M, et al, 2010. Nowcasting challenges during the Beijing Olympics:successes, failures, and implications for future nowcasting systems[J]. Wea Forecasting, 25(6): 1691-1714. DOI:10.1175/2010WAF2222417.1
|
Yuan H L, Lu C G, McGinley J A, et al, 2009. Evaluation of short-range quantitative precipitation forecasts from a time-lagged multimodel ensemble[J]. Wea Forecasting, 24(1): 18-38.
|
Zhi X F, Qi H X, Bai Y Q, et al, 2012. A comparison of three kinds of multimodel ensemble forecast techniques based on the TIGGE data[J]. Acta Meteor Sin, 26(1): 41-51.
|
Zhu Y J, Luo Y, 2015. Precipitation calibration based on the frequency-matching method[J]. Wea Forecasting, 30(5): 1109-1124. DOI:10.1175/WAF-D-13-00049.1
|
 2019, Vol. 45
2019, Vol. 45