极大风是指在规定时间内最大风速的瞬时值,地面气象观测中规定以3 s的平均值来反映风的瞬时值。由于风速脉动成因复杂,并且缺乏足够观测实况和成因分析(董双林,2001),因此极大风的预报一直是预报中的难点问题。极大风的客观预报方法主要可分为基于统计的预报方法和基于物理过程的预报方法。在统计预报方法中,阵风系数法是一种最为常用且简便的方法,即通过计算持续时间内极大风与其所在时间尺度的平均风速的比值来表征风速脉动强弱,进而估算出极大风(Ahmed, 1994;Paulsen and Schroeder, 2005;Shu et al, 2015;胡波,2016;周福等,2017;Letson et al, 2018)。基于统计的极大风客观预报方法中还有回归方法(赵金霞等, 2014)、多模式集成方法(曾瑾瑜等, 2015)、神经网络方法(Kretzschmar et al, 2004)以及经验相似方法(胡波等, 2014)等。阵风估计(wind gust estimate, WGE)方法是一种完全基于物理过程的阵风预报方法,认为阵风是由于边界层中空气块湍流动能的垂直分量克服浮力后,偏转向下到达地面后形成的(Brasseur, 2001)。WGE方法不仅考虑了平均风和大气湍流结构,还提供了可能出现阵风量级范围,因此有大量学者基于WGE方法的阵风模型进行预报试验(Adams, 2004;Pinto et al, 2009;Ágústsson and Ólafsson, 2009;Chan et al, 2011)。基于统计的预报方法和基于物理过程预报方法各有优劣(Brasseur, 2001),将两者进行结合可以有效地提高极大风的预报准确率(Patlakas et al, 2017)。
目前欧洲中期天气预报中心(ECMWF)集合预报数据中6 h内极大风预报产品仅包含风速,是在10 m风速的基础上考虑湍流和对流作用计算得到(Beljaars, 1987;Bechtold and Bidlot, 2009)。公式如下:
| $ F_{\text {gust }}=F_{10}+C_{\text {ugn }} u_{*}+C_{\text {conv }} \max \left(0, U_{850}-U_{950}\right) $ | (1) |
式中,Fgust为10 m阵风风速,F10为水平风速,Cugnu*为湍流作用造成的阵风,Cconvmax(0, U850-U950)为对流作用造成的阵风,一般取Cugn=7.71,Cconv=0.6。由于模式不可避免的系统性误差和经验参数的适用性问题,数值模式中的极大风预报产品并不能完全满足预报需求,因此需要对其进行相应的订正,提高极大风的预报准确率。
海上极大风直接影响到船舶航行和海上生产作业,但海上观测资料少,极大风的订正工作开展相对较少。胡海川等(2017)利用我国沿海代表站点观测数据和集合预报10 m风场数据进行误差统计分析,并将这种统计误差应用于我国近海,建立了基于集合预报数据的我国近海海域10 m风速客观订正方法。本文采用相似的思路,利用代表站点对集合预报中极大风的预报误差特性进行统计分析,并结合实况观测中极大风出现的频率建立基于集合预报数据的海上极大风客观订正方法。
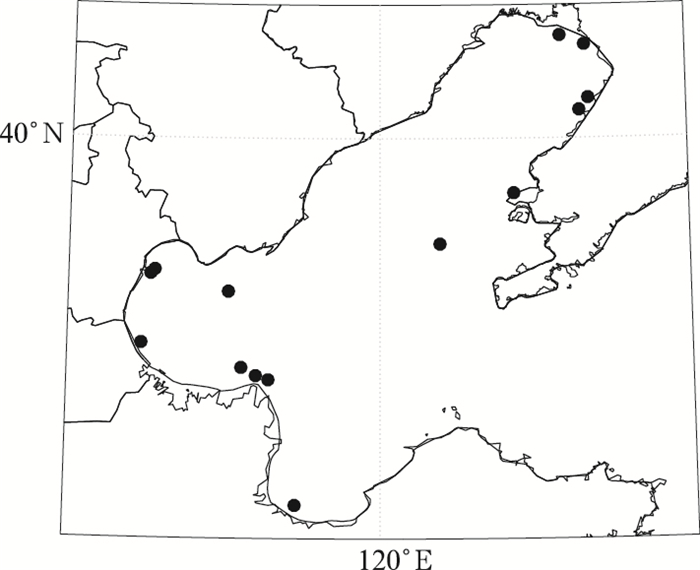
1 资料本文利用2015年2月至2018年2月中国气象局地面气象常规观测资料中逐小时极大风数据以及欧洲中期天气预报中心集合预报中6 h内极大风预报数据(成员数为51,分辨率为0.5°×0.5°,预报时效为6~78 h,间隔为6 h)。其中2015年2月至2017年2月的极大风预报数据用于误差特征分析,2017年3月至2018年2月的极大风预报数据用于订正效果检验分析。本文针对渤海海域进行预报试验,检验中所使用代表站点见图 1。
|
图 1 渤海代表站点分布 Fig. 1 Distribution of observation stations over Bohai Sea |
离散度是表征集合预报不确定性的重要参数,可以由某一个预报成员与其余成员的均方根误差之和构成,公式如下:
| $ S P_{\text {RMSE }}=\underbrace{\frac{\frac{1}{N(N-1)}}{2} \sum\limits_{i} \sum\limits_{j} \sqrt{\left(X_{i}-X_{j}\right)^{2}}}_{i<j} $ | (2) |
式中,N表示集合预报成员总数,Xi、Xj分别表示第i、j个成员的预报值。不同于由偏离某一标准值(集合平均、众数等)的均方根误差所构成的离散度,式(2)将每一个预报成员均作为一个中心,即使极端成员也具有相同权重(彭相瑜等,2014)。
集合预报的均方根误差计算公式如下:
| $ R M S E=\frac{1}{N} \sum\limits_{i=1}^{N} \sqrt{\left(x_{i}-y\right)^{2}} $ | (3) |
式中,i表示第i个成员,y为观测实况,N表示集合预报成员个数。
一般情况下,集合预报离散度越小,预报误差和不确定性小;离散度越大,预报误差和不确定性大。通过计算2015年2月至2017年2月集合预报中极大风预报产品在6~78 h的平均离散度与平均预报误差可以看出(图 2),离散度与预报误差随预报时效的增加而增大,但在各个预报时效离散度均明显小于预报误差,表明集合预报中极大风预报产品总体呈现出“欠离散”状态,离散度大小与预报准确与否关系不明显。

|
图 2 2015年2月至2017年2月ECMWF集合预报中极大风预报产品在6~78 h预报时效的平均离散度与平均均方根误差 Fig. 2 Average spread and RMSE of ECMWF ensemble extreme wind forecast at 6-78 h lead time from February 2015 to February 2017 |
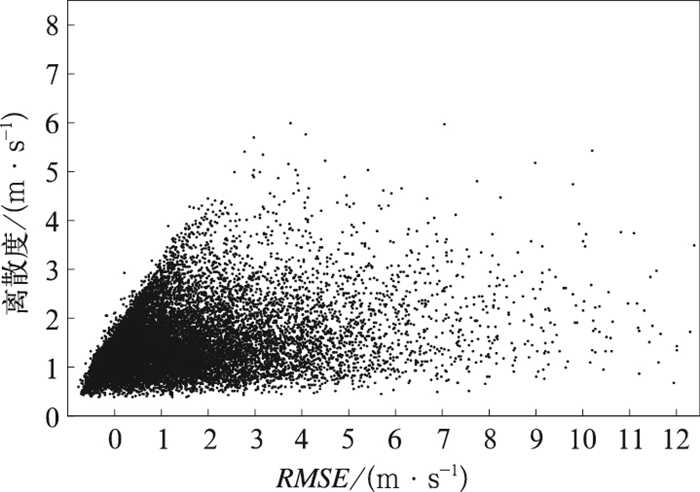
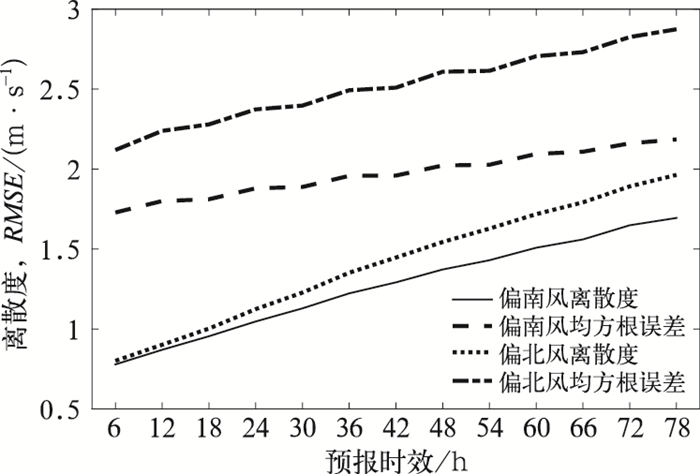
图 3为2015年2月至2017年2月48 h预报时效离散度与均方根误差的散点图。从图 3可以看出,均方根误差较小时存在着大量离散度较大的情况,均方根误差较大时也对应着大量离散度较小的情况。无论是对于小量级风速预报的不确定,或是对于大量级风速预报的能力所限,集合预报极大风预报产品的离散度大小并不能为极大风的准确预报提供太多的指示意义。在6~78 h预报时效中的其余预报时效情况基本相同(图略)。在偏南、偏北极大风情况下离散度均明显小于预报误差,但在偏南风情况下,预报误差要略小于偏北风的情况,并且离散度与预报误差的对应关系相对较好(图 4)。由于渤海海域的大风以偏北风为主(韩永清等,2015),在很大程度上会增加预报误差,因此并不能说明ECMWF集合预报中极大风预报产品对于偏南风的预报效果好于偏北风。
|
图 3 2015年2月至2017年2月ECMWF集合预报中极大风产品48 h预报时效离散度与均方根误差 Fig. 3 Spread and RMSE of ECMWF ensemble extreme wind forecast at 48 h lead time from February 2015 to February 2017 |
|
图 4 2015年2月至2017年2月ECMWF集合预报中极大风产品在6~78 h预报时效偏南极大风、偏北极大风下平均离散度与平均均方根误差 Fig. 4 Average spread and RMSE of ECMWF ensemble extreme wind forecast for the winds from south and north at 6-78 h lead time from February 2015 to February 2017 |
通过对上述离散度与均方根误差的统计分析,无法单纯通过集合预报各个成员预报值集中与否来选取出更为可信的预报结果,同时也无法明确判别出极大风预报对于偏南、偏北风预报效果的优劣。
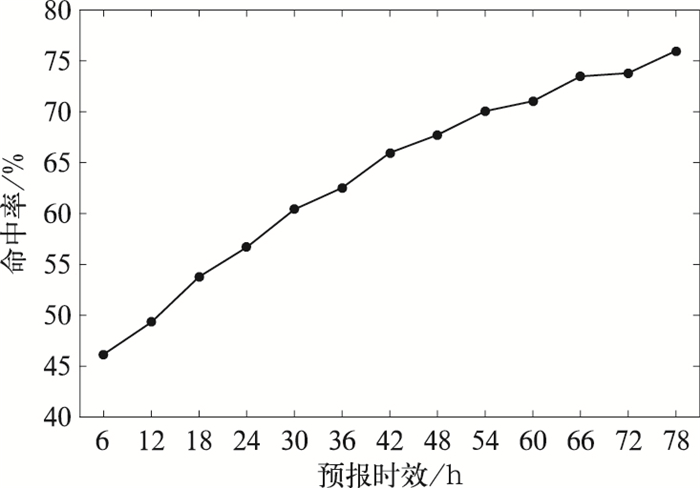
2.2 预报命中率图 5为2015年2月至2017年2月ECMWF集合预报中极大风产品在不同预报时效中能够预报出实况的概率。从图 5可以看出,在6 h预报时效中,集合预报各个预报成员所预报的极大风速范围能够包含实况的概率仅有45%。随着预报时效的增加,集合预报的命中率不断增加,在78 h预报时效,有75%的实况在集合预报各个成员所预报的范围之内。由于集合预报对于极大风的预报能力有限,在6~78 h预报时效内,仅能预报出部分实况风速,有近25%~55%的实况风速是无法预报出的,因此需要对集合预报的极大风产品进行相应的订正,才能使得预报结果与实况更为接近。另外,在时效较短时,离散度小,命中率也小;随着时效的增加,命中率有明显提高,而离散度也随之增大,因此也增加了从集合预报各个预报成员的预报结果中选取最为可信的预报结果的难度。
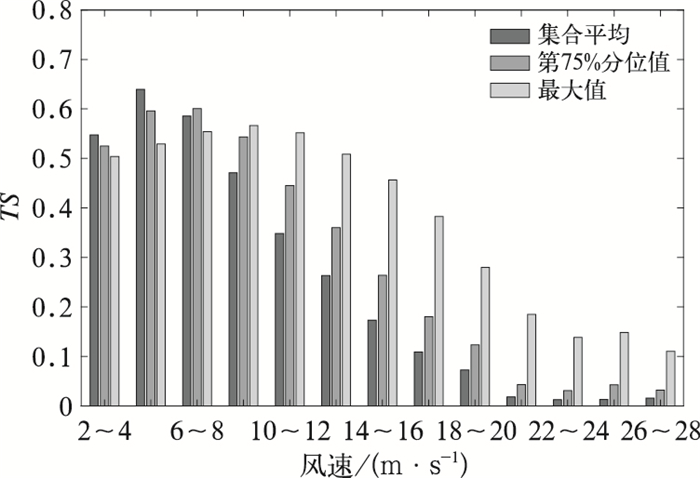
2.3 统计量分析图 6给出了2015年2月至2017年2月ECMWF集合预报中极大风产品的集合平均、第75%分位值、最大值在不同量级划分下6~78 h预报时效的平均TS评分。集合平均对6 m·s-1以下的风速预报效果最好,随着风速增大,预报效果明显下降,对于20 m·s-1以上的风速,集合平均预报的TS评分不足0.02。对于10 m·s-1以上的风速,最大值TS评分要明显高于集合平均和第75%分位值。第75%分位值的预报效果总体上介于集合平均与最大值之间。
|
图 6 2015年2月至2017年2月ECMWF集合预报中极大风预报产品集合平均、第75%分位值、最大值在6~78 h预报时效的平均TS评分 Fig. 6 Mean TS score on the average, 75th percentile and maximum of ECMWF ensemble extreme wind forecast at 6-78 h lead time from February 2015 to February 2017 |
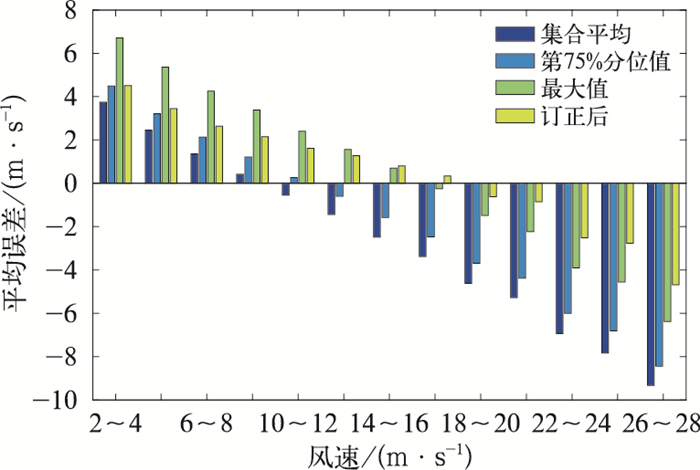
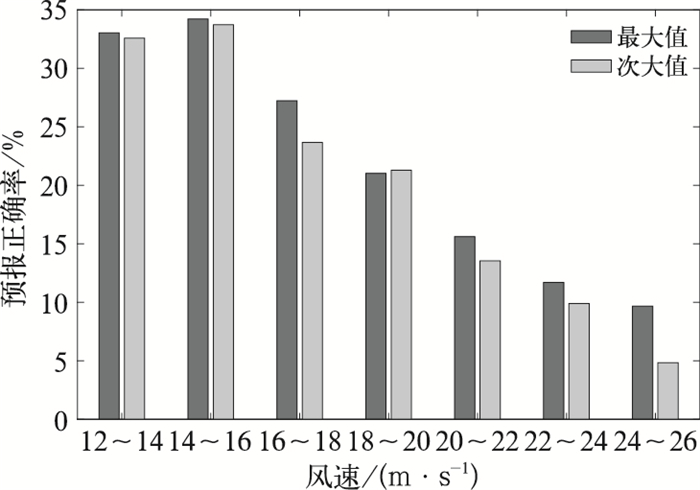
对于大量级风速,最大值预报效果要明显优于集合平均与第75分位值的原因主要有两个:(1)ECMWF集合预报中的极大风预报产品对于大量级风速的预报总体偏小。如表 1所示,对于16 m·s-1以上风速,最大值在各个预报时效内平均误差均为负值,随着风速量级的增加,预报偏小程度明显增加,22 m·s-1以上风速预报偏小达2.5 m·s-1以上。最大值是51个成员中最大的预报值,因此最大值对于大量级风速的预报效果要优于其他统计量。(2)在ECMWF集合预报的极大风产品中存在着最大值“跳跃”的现象,即在较大量级风速的预报中,存在着最大值要明显大于次大值的情况,并且最大值与实况更为接近。如若最大值与次大值差异不明显,两者对于大量级风速的预报准确率应基本相当。为验证最大值的“跳跃”现象,计算了2015年2月至2017年2月ECMWF集合预报中极大风预报产品的最大值与次大值在6~78 h预报时效的平均预报准确率(图 7)。从图 7中可以看出,对16 m·s-1以上的风速,最大值的预报准确率均要明显高于次大值,表明最大值在大量级风速的预报中存在明显的“跳跃”现象,并且对大量级风速的预报有着更为重要的指示意义。
|
|
表 1 2015年2月至2017年2月ECMWF集合预报中极大风预报产品不同风速下最大值在6~78 h预报时效的平均误差(单位:m·s-1) Table 1 Mean error on the maximum of ECMWF ensemble extreme wind forecast at different wind speeds at 6-78 h lead time from February 2015 to February 2017 (unit: m·s-1) |
|
图 7 2015年2月至2017年2月ECMWF集合预报中极大风预报最大值与次大值在6~78 h预报时效的平均预报正确率 Fig. 7 Average accuracy on the maximum and sub-maximum of the ECMWF ensemble extreme wind forecast at 6-78 h lead time from February 2015 to February 2017 |
集合平均保留了可预报性高的信息,其预报稳定,但仅对小量级风速预报效果好;最大值对于大量级风速预报的指示意义大,但对小量级风速容易造成空报,同时对于更大量级的风速预报仍偏小;第75%分位值预报效果介于两者之间,可以平衡集合平均预报偏弱和最大值空报过多的情况。因此本文在集合平均、第75%分位值、最大值预报特性的基础上,考虑不同量级风速出现历史频率对集合预报的极大风预报进行订正,以期取得更为可靠的预报信息。
首先分别计算在不同预报时效集合平均、第75%分位值、最大值出现不同预报值时所对应出现实况的概率。以集合平均为例,在48 h预报时效中(表 2),当集合平均值在6~8、8~10、10~12 m·s-1时,实况出现6~8、8~10、10~12 m·s-1的概率最大,分别达到38%、31%、25%。当集合平均值在12~14、14~16、16~18 m·s-1时,集合平均已表现出略有偏小的情况,出现最大概率的实况分别为14~16、16~18、18~20 m·s-1,相应概率为23%、22%、21%。当集合平均值在18~20 m·s-1时,集合平均明显偏小,出现最大概率的实况为22~24 m·s-1,概率为23%。单一的统计量存在着较大的不确定性,为保证预报结果的稳定性、准确性,对集合平均、第75%分位值、最大值在不同预报时效不同预报值时所对应出现不同实况概率进行平均,因而生成一组新的可能出现不同量级风速实况的概率数据。
|
|
表 2 2015年2月至2017年2月ECMWF集合预报中极大风产品集合平均48 h预报时效的不同预报值对应出现实况的概率(单位:%) Table 2 Average probability on the maximum of ECMWF ensemble extreme wind forecast at 48 h lead time from February 2015 to February 2017 (unit: %) |
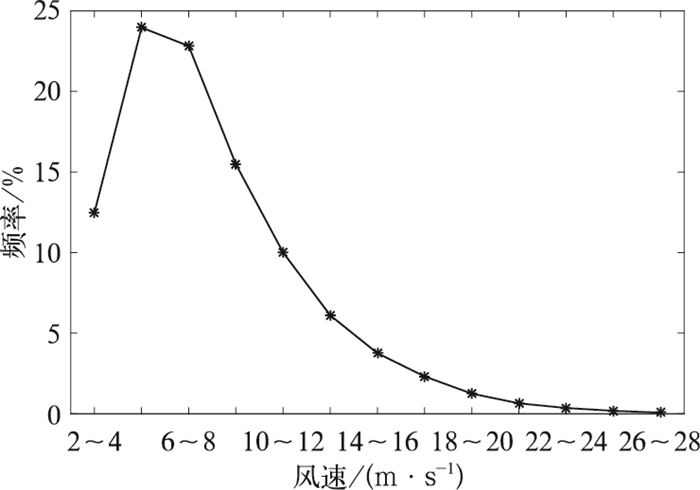
不同风速量级所出现历史频率(图 8)不同,4~6 m·s-1风速出现的频率接近24%,随着风级增大,出现频率明显降低,20 m·s-1以上风速出现频率不足1%,26 m·s-1以上风速出现的频率不足0.6%。小量级风速预报出现的概率较高,但小量级风速出现的历史频率本身较大;大量级风速预报概率尽管较低,但其出现的历史频率较小。为了消除不同量级风速出现频率对预报概率的影响,使不同量级风速预报对应的实况概率更具有可比较性,将集合平均、第75%分位值、最大值预报可能出现不同风速量级实况的概率平均后再除以对应量级的历史频率,得到预报可能出现实况的概率相对于历史频率的比值,并选取比值最大时对应的风速区间来代表最有可能出现的实况风速区间。将集合平均、第75%分位值、最大值的预报结果进行平均并加上其所对应的平均误差,从而得到最终订正结果,公式如下:
|
图 8 2015年2月至2017年2月不同量级风速出现频率 Fig. 8 Frequency of different magnitude wind speeds from February 2015 to February 2017 |
| $ m=\max \left[\frac{1}{3}\left(P_{1(a, i)}+P_{2(b, i)}+P_{3(c, i)}\right) / P_{i}\right] $ | (4) |
| $ \begin{aligned} y=&\left[\left(x_{1}+e_{1(a, \mathrm{Vm})}\right)+\left(x_{2}+e_{2(b, \mathrm{Vm})}\right)+\right.\\ &\left.\left(x_{3}+e_{3(c, \mathrm{Vm})}\right)\right] / 3 \end{aligned} $ | (5) |
式中,m表示预报可能出现实况的概率相对于历史频率的最大比值,P1(a, i)、P2(b, i)、P3(c, i)表示集合平均、第75%分位值、最大值分别预报在a、b、c区间时对应出现的不同实况概率,Pi表示不同量级风速出现的历史概率。x1、x2、x3分别表示集合平均、第75%分位值、最大值的预报结果,Vm表示最有可能出现实况的区间,e1(a, Vm)、e2(b, Vm)、e3(c, Vm)分别表示集合平均、第75%分位值、最大值预报分别在a、b、c区间时对应实况出现在Vm区间时的平均误差。
由于所统计的实况观测资料时间序列较短,因此本文中并未分季节进行订正。为了避免小概率事件的干扰,将集合平均、第75%分位值、最大值出现不同预报值时所对应出现实况的概率低于5%的情况进行剔除。
4 结果检验利用上述方法对2017年3月至2018年2月的ECMWF集合预报中极大风预报产品进行订正,并对比检验订正前后的预报效果(图 9,图 10)。
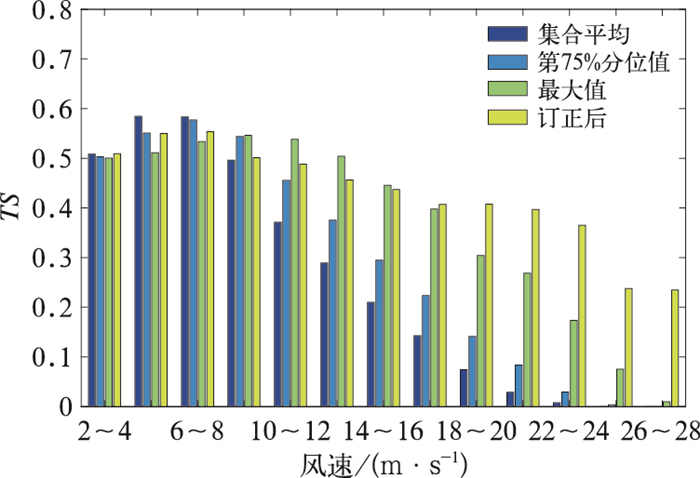
|
图 9 2017年3月至2018年2月ECMWF集合预报中极大风预报产品在6~78 h预报时效的集合平均、第75%分位值、最大值以及订正后的平均TS评分 Fig. 9 Average TS scores, 75th percentile and maximum of ECMWF ensemble extreme wind forecast and revised wind speed at 6-78 h lead time from March 2017 to February 2018 |
对于2~4 m·s-1的风速,订正后风速预报效果与集合平均、第75%分位值、最大值预报基本一致(图 9)。4~6、6~8 m·s-1的风速,订正后的预报效果要优于最大值,但略差于集合平均效果。10~12、12~14、14~16 m·s-1的风速,订正后的预报效果要好于集合平均、第75%分位值,但略差于最大值。16 m·s-1以上的风速,订正后的预报效果要明显好于最大值,尤其对于26~28 m·s-1的大风预报,订正后的预报有更多的参考意义。图 10为订正前后6~78 h预报时效平均误差的对比,对于10 m·s-1以下的风速,订正后预报的平均误差要高于集合平均、第75%分位值,但小于最大值。对于10~16 m·s-1的风速,集合平均、第75%分位值已经表现出预报偏小,订正后的预报与最大值表现为预报偏大,且订正后预报的平均误差要小于或接近于最大值。对于16 m·s-1以上的风速,订正后预报的偏小程度明显低于集合平均、第75%分位值、最大值,与实况风速更为接近。
受冷空气影响,2018年2月23日20时至24日02时,渤海出现大范围9~10级(20.8~28.4 m·s-1)的极大风。对此次的渤海海域大风天气,集合预报21日08时的66 h预报及22日08时42 h预报的最大值并未预报出渤海偏南海域的10级大风(24.5~28.4 m·s-1)(图 11a和11b)。订正后的66和42 h预报在渤海偏南海域预报出10级大风,虽然10级风速带的范围较实况偏小,但较集合预报最大值更接近实况观测。此外,订正后预报未对渤海偏北海域8~9级风(17.2~24.4 m·s-1)造成明显空报(图 11c和11d)。
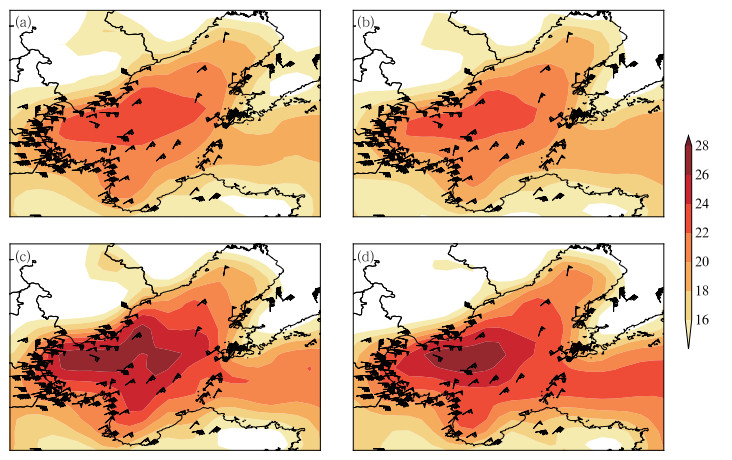
|
图 11 2018年2月23日20时至24日02时6 h内极大风观测实况(风向杆)及21日08时66 h时效(a, c)、22日08时42 h时效(b, d)6 h极大风预报(a, b)和订正结果(c, d)(填色,单位:m·s-1) Fig. 11 Extreme wind observation (wind barb) during 6 h from 20:00 BT 23 to 02:00 BT 24 February 2018 and 6 h extreme wind forecast (a, b) and correction (c, d) (shaded area, unit: m·s-1) at 66 h lead time at 08:00 BT 21 (a, c) and 42 h lead time at 08:00 BT 22 February 2018 (b, d) |
本文利用中国气象局地面气象常规观测资料中逐小时极大风数据及ECMWF集合预报中6 h极大风预报数据,在极大风预报误差特征分析的基础上,建立了基于集合预报的极大风客观订正方法。具体结论如下:
(1) ECMWF集合预报中极大风产品的离散度明显偏小于均方根误差,各预报成员预报结果集中与否并不能反映预报可信度;在较短预报时效内,极大风产品能够预报出实况的概率较低,随预报时效增加,预报概率明显增加。但由于离散度随预报时效增加而增大,因此很难直接通过集合预报选取最为可信的预报结果。
(2) ECMWF集合预报中极大风产品对较大量级风速预报整体偏小。集合平均对小量级风速预报稳定;最大值存在“跳跃性”,对大量级风速预报效果相对较好,但容易空报。
(3) 基于集合预报的极大风客观订正方法综合考虑不同量级风速发生的历史频率及集合平均、第75%分位值、最大值的预报概率和预报误差,其预报结果稳定,对极大风有较好的预报效果,对大风天气过程的预报有重要的参考价值。
董双林, 2001. 中国的阵风极值及其统计研究[J]. 气象学报, 59(3): 327-333. Dong S L, 2001. Gust extremes in China and its statistical study[J]. Acta Meteor Sin, 59(3): 327-333 (in Chinese).
|
韩永清, 郭俊建, 张少林, 等, 2015. 环渤海区域强风的特征及变化分析[J]. 海洋预报, 32(6): 26-33. Han Y Q, Guo J J, Zhang S L, et al, 2015. Characteristics and variation analysis of the strong gale around Bohai Sea Region[J]. Mar Forecasts, 32(6): 26-33 (in Chinese).
|
胡波, 2016. 一种概率方法在沿海海岛台风阵风预报中的应用试验[J]. 气象科技, 44(2): 246-251. Hu B, 2016. Application test of a probability method in forecasting coastal gusts of tropical cyclones in Zhejiang[J]. Meteor Sci Technol, 44(2): 246-251 (in Chinese). DOI:10.3969/j.issn.1671-6345.2016.02.013
|
胡波, 杜惠良, 俞燎霓, 等, 2014. 一种经验相似方法在沿海海岛阵风预报中的应用[J]. 海洋预报, 31(3): 37-44. Hu B, Du H L, Yu L N, et al, 2014. Application of an empirical similar statistic downscaling method in extreme wind forecast[J]. Mar Forecasts, 31(3): 37-44 (in Chinese).
|
胡海川, 黄彬, 魏晓琳, 2017. 我国近海洋面10 m风速集合预报客观订正方法[J]. 气象, 43(7): 856-862. Hu H C, Huang B, Wei X L, 2017. Objective correction method of ensemble forecast of 10 m winds on Chinese offshore[J]. Meteor Mon, 43(7): 856-862 (in Chinese).
|
彭相瑜, 代刊, 金荣花, 等, 2014. 欧洲中心集合预报在中国区域中期时效离散度预报技巧关系分析[J]. 气象, 40(7): 777-786. Peng X Y, Dai K, Jin R H, et al, 2014. Analysis of spread-skill relations using the ECMWF ensemble prediction in medium-term period over China[J]. Meteor Mon, 40(7): 777-786 (in Chinese).
|
曾瑾瑜, 刘爱鸣, 高珊, 等, 2015. 福建省沿海冬半年东北大风的数值预报释用方法研究[J]. 海洋预报, 32(5): 61-68. Zeng J Y, Liu A M, Gao S, et al, 2015. Study on interpretation of numerical prediction method on northeast winds along the coast of Fujian Province in winter half year[J]. Mar Forecasts, 32(5): 61-68 (in Chinese).
|
赵金霞, 曲平, 何志强, 等, 2014. 渤海湾大风的特征及其预报[J]. 气象科技, 42(5): 847-851. Zhao J X, Qu P, He Z Q, et al, 2014. Characteristics and forecasting of strong wind gusts in Bohai Bay[J]. Meteor Sci Technol, 42(5): 847-851 (in Chinese). DOI:10.3969/j.issn.1671-6345.2014.05.022
|
周福, 蒋璐璐, 涂小萍, 等, 2017. 浙江省几种灾害性大风近地面阵风系数特征[J]. 应用气象学报, 28(1): 119-128. Zhou F, Jiang L L, Tu X P, et al, 2017. Near-surface gust factor characteristics in several disastrous winds over Zhejiang Province[J]. J Appl Meteor Sci, 28(1): 119-128 (in Chinese).
|
Adams N, 2004. A numerical modeling study of the weather in east Antarctica and the surrounding southern ocean[J]. Wea Forecasting, 19(4): 653-672. DOI:10.1175/1520-0434(2004)019<0653:ANMSOT>2.0.CO;2
|
Ágústsson H, Ólafsson H, 2009. Forecasting wind gusts in complex terrain[J]. Meteor Atmos Phys, 103(1/2/3/4): 173-185.
|
Ahmed S, 1994. Gust factors within frontal depressions at Rio, Greece[J]. Meteor Appl, 1(3): 205-208.
|
Bechtold P, Bidlot J R, 2009.Parametrization of convective gusts[R].ECMWF Newsletter No.119.ECMWF: 15-18.
|
Beljaars A C M, 1987. The influence of sampling and filtering on measured wind gusts[J]. J Atmos Oceanic Technol, 4(4): 613-626. DOI:10.1175/1520-0426(1987)004<0613:TIOSAF>2.0.CO;2
|
Brasseur O, 2001. Development and application of a physical approach to estimating wind gusts[J]. Mon Wea Rev, 129(1): 5-25. DOI:10.1175/1520-0493(2001)129<0005:DAAOAP>2.0.CO;2
|
Chan P W, Lam C C, Cheung P, 2011. Numerical simulation of wind gusts in intense convective weather and terrain-disrupted airflow[J]. Atmósfera, 24(3): 287-309.
|
Kretzschmar R, Eckert P, Cattani D, et al, 2004. Neural network classifiers for local wind prediction[J]. J Appl Meteor, 43(5): 727-738. DOI:10.1175/2057.1
|
Letson F, Pryor S C, Barthelmie R J, et al, 2018. Observed gust wind speeds in the coterminous United States, and their relationship to local and regional drivers[J]. J Wind Eng Ind Aerod, 173: 199-209. DOI:10.1016/j.jweia.2017.12.008
|
Patlakas P, Drakaki E, Galanis G, et al, 2017. Wind gust estimation by combining a numerical weather prediction model and statistical post-processing[J]. Energy Proced, 125: 190-198.
|
Paulsen B M, Schroeder J L, 2005. An examination of tropical and extratropical gust factors and the associated wind speed histograms[J]. J Appl Meteor, 44(2): 270-280. DOI:10.1175/JAM2199.1
|
Pinto J G, Neuhaus C P, Krüger A, et al, 2009. Assessment of the wind gust estimate method in mesoscale modelling of storm events over West Germany[J]. Meteor Z, 18(5): 495-506. DOI:10.1127/0941-2948/2009/0402
|
Shu Z R, Li Q S, He Y C, et al, 2015. Gust factors for tropical cyclone, monsoon and thunderstorm winds[J]. J Wind Eng Ind Aerod, 142: 1-14. DOI:10.1016/j.jweia.2015.02.003
|
 2019, Vol. 45
2019, Vol. 45