2. 南京信息工程大学气象灾害预报预警与评估协同创新中心,南京 210044
2. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing 210044
随着人类的发展和全球经济的快速提高,化石类燃料日益枯竭,寻求清洁可再生能源迫在眉睫。风能作为清洁可再生能源,不仅能够缓解能源的过度开发问题,在环境保护方面也有着突出优势(王美琳等,2010)。在风力发电中,风速具有很大的随机性、间接性,而风机出力与风速的三次方近似成正比,因而风电输出功率具有较大的不稳定性和不可控性,成为制约风电发展的最根本原因,对电网的稳定和安全产生很大影响(李艳等,2015)。因此风速预测的准确性是风电功率预测极其重要的关键因素。
中尺度数值模式是风速预测的重要手段之一,其中WRF模式(Weather Research and Forecasting Model)最为常见。邓国卫等(2010)运用新一代中尺度WRF模式对酒泉部分地区进行了风场的数值模拟,发现WRF模式对复杂地形条件下的风场具有较好的模拟能力,也能较好地模拟出地形对风速的影响。但现阶段WRF模式仍受物理参数化方案不完善、地形不够精确等因素的影响,导致预报结果误差较大,而较小的风速误差就可能带来较大的风电功率误差(常俊等,2015;王益柏等,2014;方艳莹等,2012;许杨等,2013)。在WRF模式中,边界层方案、近地面层方案、陆面过程方案等各参数化方案配置选择,都会对风速模拟的性能和效果产生影响,其中边界层方案的选择,直接决定了边界层内大气运动遵从的物理规律,对低层风场的模拟有重要影响。另外风场的湍流现象会对风电机组的运行性能有不利影响,需要特别关注,而湍流过程需要边界层参数化方案来描述,不同的边界层参数化方案都有其侧重的优势,可使用不同的边界层参数化方案来弥补其局限性。因此,在应用WRF模式进行风速预报的模拟研究中,必须选择合适的边界层参数化方案。
在边界层参数化方案的选取研究中,贵志成等(2014)对比研究了WRF模式中五种不同边界层参数化方案对东亚夏季风气候的模拟效果。结果表明:WRF模式对各边界层参数化方案均较为敏感,采用不同的边界层参数化方案对模拟区域内的夏季气象要素均可产生明显影响,需合理选取边界层参数化方案。穆清晨等(2017)选取MYJ、YSU、ACM2三种边界层参数化方案模拟贵州某复杂地形条件下的近地层风以检验风速模拟性能。结果表明,在中国西南复杂山地地形条件下,ACM2方案对近地层70 m高度风速的模拟效果优于其余两种方案,对风向的模拟三种方案结果相近。Deng et al(2017)选择WRF/YSU/Noah方案对中国内蒙古高原地区进行风速模拟,发现YSU方案对风电场风速预报精度较高,预报效果较好。从以上的研究可以看出,预报研究主要集中在应用WRF模式对研究区域做不同边界层参数化方案模拟,研究参数化方案的不同对复杂地形风速模拟的影响,分析变化规律。其中不同参数化方案在不同区域有不同表现,但针对某一研究区域,总能将模式调整到最佳状态。
在复杂地形地区,由于各因素的影响,不同位置风速有一定的差异。比如复杂地形会使大气边界层流动产生绕流、涡流甚至回流发生,有明显的湍流特性,使得每一点上的速度、方向等物理特性随机涨落(黄林宏等,2016;朱向东,2016)。因此,当采用单一边界层参数化方案预报风速时,即使与某地区结合最好的参数化方案很有可能在其他地区完全不适用,没有普遍的适用方案。而集成预报方法则为解决这单一的确定性预报存在的不确定问题提供了一条新的途径。
在集成预报风速的模拟研究中,薛禹胜等(2015)提出针对中尺度数值模式,各模型可由相同NWP模式的不同的变量构成,各模型的预测结果越接近,则不确定性越小。蔡子颖等(2017)基于WRF模式采用四种边界层方案模拟2015年全年天津地区细颗粒物质量浓度演变趋势,并构建多种边界层方案的预报模型。结果表明,多种边界层方案的预报可以减小预报的相对误差和均方根误差,提高预报能力,是一种可以提升预报能力的有效手段。从以上的研究中可以看出,集成预报把不同的预报模型对某一气象要素的多种预报结果综合在一起,从而得到一个优于单一方案预报的预报结果。但目前集成预报方法在对降水、污染物等要素方面的研究较多,对风速的预报研究较少,还有待进一步探讨。因此,可采用多种边界层参数化方案来集成预报风速、风向等气象数据,以此得到更好的预报结果。
本文基于WRF模式,采用多种边界层方案预报70 m高度处的风速、风向等气象要素,分析各单一边界层参数化方案预报的风速与测风塔实测风速的误差;再将多种边界层参数化方案预报的风速及相应的实测风速数据,应用随机森林算法建立集成预报模型,对风电场的风速进行预报,并与测风塔实测风速数据进行对比分析,分析集成预报可行性及优势。
1 资料与方法 1.1 风电场及资料选取本文选取重庆某风电场为研究对象,风电场为东北—西南向的长条形风场,测风塔所在区域的地形比较复杂,如图 1所示。观测数据选取9011斗路口梁子测风塔70 m高度处采集的2011年全年的风速、风向等气象数据,数据质量检验结果显示,由于各因素的影响,在观测年内,风塔的测风数据存在一定缺失,有效数据完整率为88.03%。经过传统质量控制,明显的粗大误差被剔除,再选取同期观测时段内,采用比值法进行订正,订正后总体观测数据完整率在93.7%,能够满足风能资源评估的要求。预报数据以六种不同边界层参数化方案2011年全年的WRF数据作为实验资料,时间分辨率为10 min。选取2011年4、7、10、1月数据作为春、夏、秋、冬四季度的代表数据及选取这4个月的数据作为全年的代表数据进行模拟效果的研究分析,研究时段数据通过完整性及合理性检验。
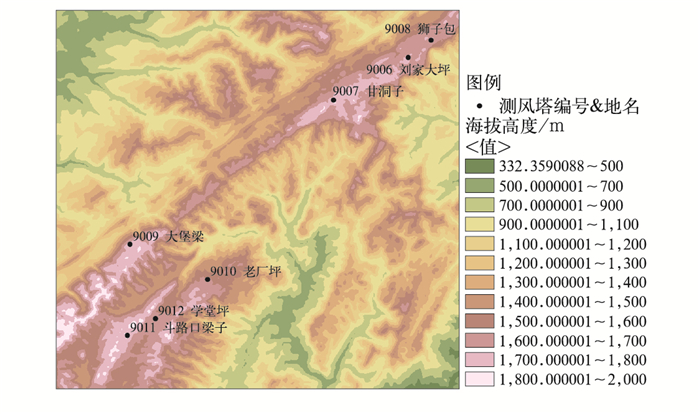
|
图 1 风电场地形图 Fig. 1 Topographic map of wind power plant |
为了符合电网的要求,短期风电功率预测选择对未来72 h的数据进行预测。在训练数据和测试数据的选取上,本研究选取了三种:一是对全年的代表数据进行试验分析,即将每个季度的最后72 h,共12 d 1728组数据作为测试数据,每个季度的其他天数数据作为训练数据;二是分别对每个季度的代表月数据进行试验分析,即将每个季度的最后72 h,共3 d 432组数据作为测试数据,该季度的其它天数数据作为训练数据;三是为了检验预报的有效性和长效性,随机选取一个月共30 d数据作为测试数据,其余数据作为训练数据。为了避免单次训练结果的偶然性,分别对模型进行10次训练,取10次预测结果的平均值作为最终的预测结果。通过误差评价指标来评价预测效果。
1.2 WRF模式WRF是新一代的中尺度数值模式,已被广泛应用于天气系统、气候变化和空气污染等研究和业务预报中(段旭等,2011)。预报区域如图 2所示,本文选用的WRF模式(3.8.1版本)方案设计如下:采用三重嵌套网格,网格数分别为50×60、55×52、67×64,水平网格分辨率分别为27、9、3 km,网格中心点位于29.788°N、108.227°E。采用全球1°×1°,6 h一次的GFS预报场资料作为WRF模式的初始场和侧边界条件。WRF模式参数化方案选择为:微物理过程方案为WSM6类冰雹方案,长波辐射为RRTM方案,短波辐射为Dudhia方案,陆面过程采用Noah陆面过程方案,积云参数化方案第一及第二重模拟区域选用浅对流Kain-Fritsch(new Eta)方案,而最内层区域分辨率能够解析积云对流过程,因此不进行积云参数化。模拟时段为2011年全年,每10 min输出一次模拟结果。在WRF模式后处理系统的数据提取部分,采用双线性插值法(许建伟和高艳红,2014;李得勤等,2012),将格点数据做到测风塔所在位置,提取风速、风向等气象要素。
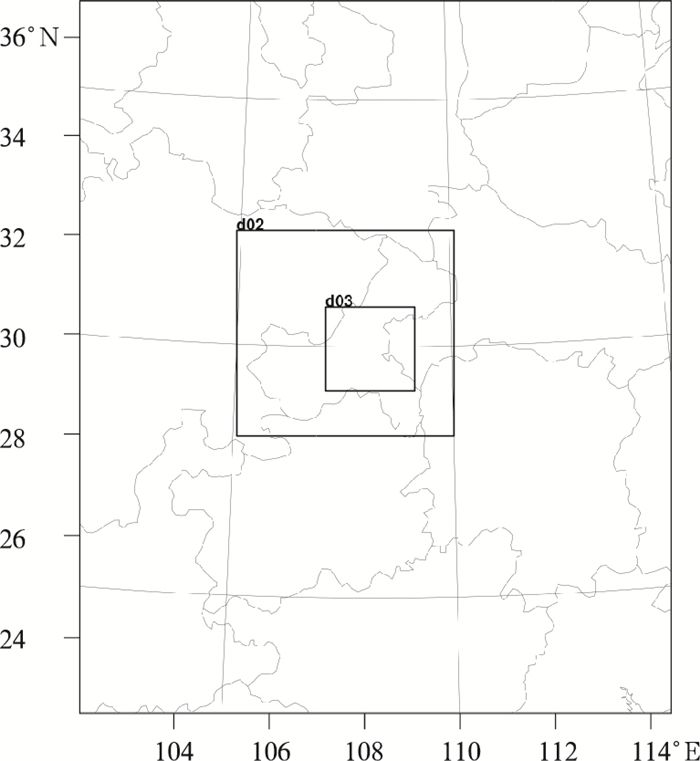
|
图 2 WRF模式模拟区域示意图 Fig. 2 The simulation areas of WRF model |
选取六种边界层参数化方案如下:YSU方案(Hong et al,2006)、ACM2方案(Pleim,2007)、QNSE方案、MYNN2.5方案(Sukoriansky et al,2005)、MYJ方案(Janjić,1994)、BouLac(Bougeault and Lacarrere, 1989)方案。在WRF模式中,每一个使用的边界层参数化方案都有相应的近地面层方案,具有一定的匹配关系,六种组合试验方案设置见表 1。
|
|
表 1 模拟试验方案设计 Table 1 Summary of different simulation schemes |
采用随机森林算法建立集成预报模型,对风电场的风速进行预报。随机森林是通过集成学习的思想将多棵树集成的一种算法,它的基本单元是决策树,是一种比较新的机器学习模型。2001年Breiman(2001a)把分类树组合成随机森林,即在变量(列)和数据(行)的使用上进行随机化,生成很多分类树,再汇总分类树的结果。随机森林在运算量没有显著提高的前提下提高了预测精度,对缺失数据和非平衡的数据比较稳健,可以很好地预测多达几千个解释变量的作用(Breiman,2001b),被誉为当前最好的算法之一。
随机森林由LeoBreiman提出,通过自助法(bootstrap)重采样技术,从原始训练样本集N中有放回地重复随机抽取k个样本生成新的训练样本集合,然后根据自助样本集生成k个分类树组成随机森林,新数据的分类结果按分类树投票多少形成的分数而定。其实质是对决策树算法的一种改进,将多个决策树合并在一起,每棵树的建立依赖于一个独立抽取的样本,森林中的每棵树具有相同的分布,分类误差取决于每一棵树的分类能力和它们之间的相关性。一般情况下,随机森林随机地生成几百个至几千个分类树,然后选择重复程度最高的树作为最终结果(李欣海,2013)。
具体实现过程如下:
(1) 原始训练集为N,应用bootstrap法有放回地随机抽取k个新的自助样本集,并由此构建k棵分类树,每次未被抽到的样本组成了k个袋外数据;(2)设有mall个变量,则在每一棵树的每个节点处随机抽取mtry个变量(mtry n mall),然后在mtry中选择一个最具有分类能力的变量,变量分类的阈值通过检查每一个分类点确定;(3)每棵树最大限度地生长,不做任何修剪;(4)将生成的多棵分类树组成随机森林,用随机森林分类器对新的数据进行判别与分类。
随机森林容易实现、计算开销小,在很多现实任务中展现出强大的性能,为“代表集成学习技术水平的方法”。优点如下:(1)在数据集上表现良好,两个随机性的引入,使得随机森林不容易陷入过拟合;(2)在当前的很多数据集上,相对其他算法有着很大的优势,两个随机性的引入,使得随机森林具有很好的抗噪声能力;(3)它能够处理很高维度的数据,并且不用做特征选择,对数据集的适应能力强:既能处理离散型数据,也能处理连续型数据,数据集无需规范化;(4)训练速度快,可以得到变量重要性排序,能够检测到变量间的互相影响等。
图 3为本文技术路线图。基于WRF模式,选取六种不同边界层参数化方案预报风速、风向等气象数据,分析各单一方案预报的风速与测风塔实测风速数据的误差;再将多种边界层参数化方案预报的风速及相应的实测风速数据,应用随机森林算法建立集成预报模型,对风电场的风速进行预报,并分析预报风速与测风塔实测风速数据的误差,研究集成预报方法可行性及优势。
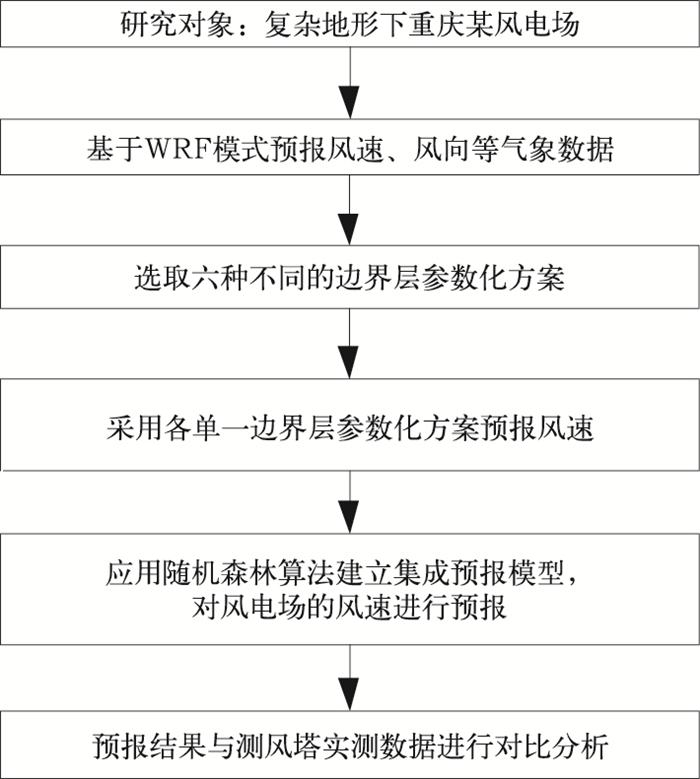
|
图 3 技术路线图 Fig. 3 Technical roadmap in the paper |
风速预测的准确性对风电功率预测的准确性有着非常重要的影响,常用的预测效果评价指标有很多种,本文选用平均绝对误差(MAE)、均方根误差(RMSE)、相对平均绝对误差(rMAE)以及相对均方根误差(rRMSE)误差指标对风电场的短期风速预测结果进行评价。各个误差指标的计算公式如下所示:
(1) 平均绝对误差(MAE)
| $ MAE = \frac{1}{N}\sum\limits_{i = 1}^N {} |\frac{{y_i^ * - {y_i}}}{{{y_i}}}| $ |
(2) 均方根误差(RMSE)
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {} {\rm{ }}{{(y_i^ * - {y_i})}^2}} $ |
(3) 相对平均绝对误差(rMAE)
| $ rMAE = \left\{ {\frac{{\frac{1}{N}\sum\limits_{i = 1}^N {} {\rm{ }}|y_i^ * - {y_i}|}}{{\frac{1}{N}\sum\limits_{i = 1}^N {{y_i}} }}} \right\} \times 100\% $ |
(4) 相对均方根误差(rRMSE)
| $ rRMSE = \left\{ {\frac{{\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {} {{(y_i^ * - {y_i})}^2}} }}{{\frac{1}{N}\sum\limits_{i = 1}^N {} {\rm{ }}{y_i}}}} \right\} \times 100\% $ |
式中,N表示样本序列的长度;yi*是第i个样本的预测值,yi是第i个样本的观测值。
2 基于WRF模式的风速预报 2.1 风电场风速特性风电场测风塔70 m高度处风速数据分布如图 4所示,由图可知,风速主要集中在2~9 m·s-1,风能分布较为集中。月平均得到的风速日变化曲线如图 5所示,由图可知:白天风速偏小,夜晚风速偏大。03—17时,风速呈下降趋势;17时到次日03时,风速呈明显的上升趋势。

|
图 4 测风塔70 m高度处风速数据分布 Fig. 4 Wind speed data distribution at 70 m height of wind tower |
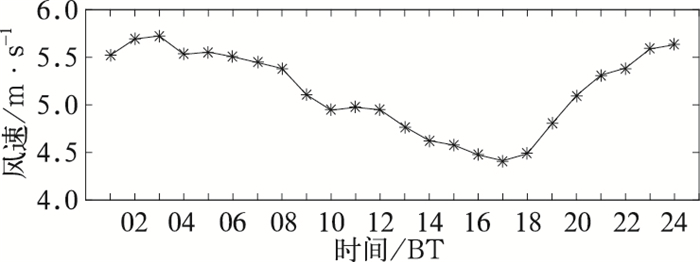
|
图 5 测风塔70m高度处风速日变化 Fig. 5 Diurnal variation of wind speed at 70 m height of wind tower |
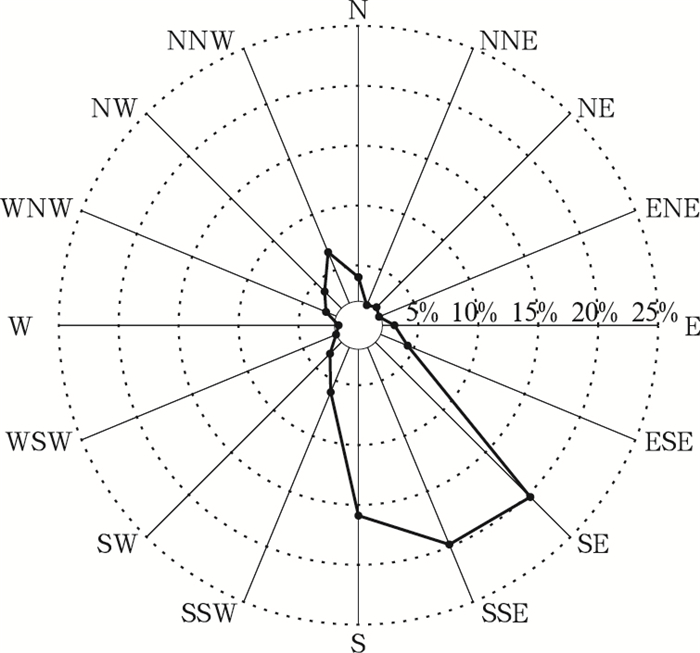
测风塔处实测风向玫瑰图如图 6所示。实测风速主要分布在SE—S范围内,主风向为SSE或SE,风向较集中在主风向上,与当地的气候特征相符合。由风速数据分布和实测风向玫瑰图可知,该处风向较为稳定,风能分布较为集中,适合风力发电。
|
图 6 测风塔实测风向玫瑰图 Fig. 6 Wind rose diagram of wind data measured from wind tower |
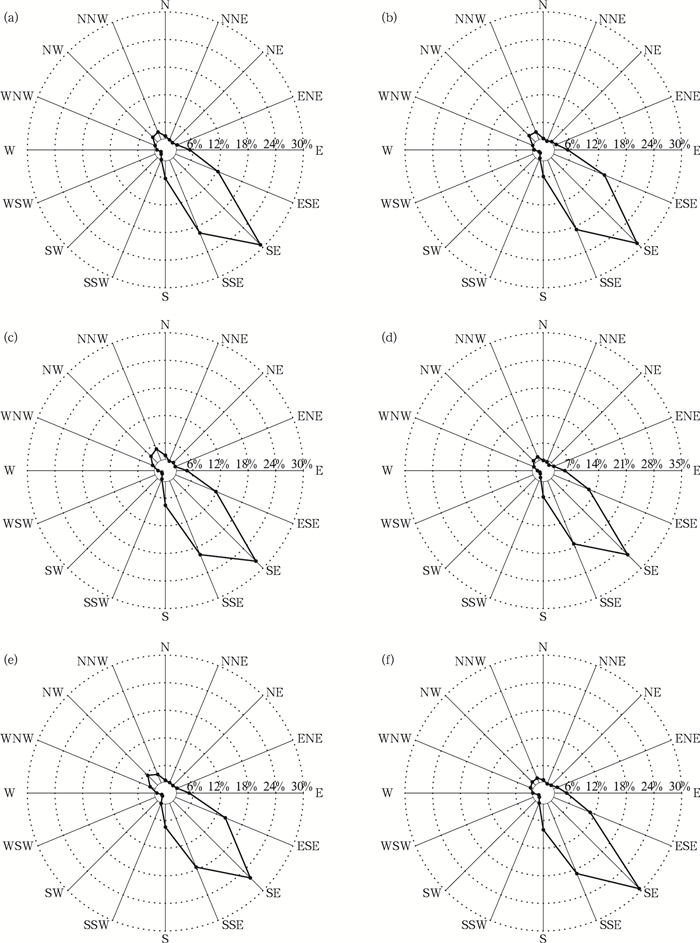
六种单一边界层方案预测风向玫瑰图分布如图 7所示。风速都集中分布在ESE—SSE范围内,主风向为SE。六种边界层方案预测的风向分布略有差异,说明不同边界层参数化方案侧重点不同,采用不同的边界层方案,对风速、风向的模拟效果具有一定的差异性。预报的风向分布与测风塔实测的风向分布也略有差异,但有较好的一致性,说明WRF模式预报数据能较好地反映所研究区域的风速、风向等气象要素特征,证明在复杂地形条件下利用WRF模式预报风电场短期风速是可行的。
|
图 7 方案0(a)、方案1(b)、方案2(c)、方案3(d)、方案4(e)、方案5(f)预测风向玫瑰图 Fig. 7 Wind rose diagrams of (a) Scheme 0, (b) Scheme 1, (c) Scheme 2, (d) Scheme 3, (e) Scheme 4, and (f) Scheme 5 |
表 2为六种边界层方案WRF模式预报风速与测风塔70 m高度处实测风速数据的误差分析。由表 2可知,对于全年代表数据,六种边界层方案预报的风速MAE在2.70~3.19 m·s-1,平均值为2.89 m·s-1;RMSE在3.23~3.81 m·s-1,平均值为3.47 m·s-1;rMAE在43.84%~51.67%,平均值为46.90%;rRMSE在52.46%~61.83%,平均值为56.34%。rRMSE和rMAE都较大,误差较大的是方案3和方案5,误差最小的是方案4。分析可知:六种边界层方案对风速的预报效果略有差异,其中方案4预报风速效果最好,当需要采用单一方案预报风速时,可以选择方案4作为模式模拟的最佳模拟方案。
|
|
表 2 WRF模式单一边界层方案预报风速与实测风速误差分析 Table 2 Error analysis of predicted wind speed by each single boundary layer scheme of WRF model and observed wind speed |
再分别对春、夏、秋、冬四组数据进行误差分析,由表 2可知,春季采用方案0预报风速效果最好,方案2效果最差;夏季和秋季采用方案2预报风速效果最好,方案5效果最差;冬季采用方案4预报风速效果最好,方案5效果最差。由此发现,对于不同的时间段,模式模拟的最佳模拟方案不尽相同,在应用WRF模式进行风速预报的模拟研究中,要根据具体情况选择合适的边界层参数化方案,每种参数化方案侧重点不同,且在不同情况下有不同表现,但针对某一研究对象,可以将模式调整到最佳状态。
但由表格数据分析可知,当采用单一边界层参数化方案预报风速时,即使得到该条件下最佳的边界层参数化方案很有可能在其他情况下完全不适用。比如方案2在夏季预报效果最好,但在春季预报效果却最差,得不到普遍的适用方案。另外由表格数据分析知,即使采用单一最佳的边界层参数化方案预报风速,其预报风速相比测风塔实测风速的误差仍较大。因此,仅采用单一边界层方案预报风速的效果不能满足要求,应采用多种边界层参数化方案来集成预报风速,以此来提高WRF模式预报风速的准确率。
2.3 集成预报风速误差分析如表 3所示,对集成预报风速与测风塔实测风速数据进行误差分析,发现应用随机森林算法建立集成预报模型,采用六种边界层参数化方案集成预报风速时,各误差指标明显减小。比如对于全年代表数据,采用随机森林法建立模型的时间约为159.23 s,预报时间约为0.32 s,预报的风速MAE降低了约1.1 m·s-1,RMSE降低了约1.2 m·s-1,rMAE降低了约18%,rRMSE降低了约20%,预报效果得到明显提高。另外对于春夏秋冬四组数据,采用随机森林法建立模型的时间约为11.69 s,预报时间约为0.096 s,结果发现除了夏季集成预报的风速MAE为1.7950 m·s-1,而方案2预报的风速MAE为1.7373 m·s-1,集成预报的风速效果略差于单一最佳的边界层方案预报的风速效果之外,其余季节的风速预报精度均得到了较好的提高,尤其秋季的风速预报效果提高最为明显,MAE降低了约2.1 m·s-1,RMSE降低了约2.4 m·s-1,rMAE降低了约39%,rRMSE降低了约41%。而且对于夏季来说,集成预报的风速相对于另外五种边界层方案的风速预报效果都要好,若根据RMSE指标分析,集成预报的风速比单一最佳的边界层方案预报风速效果要好。总体分析来说,采用多种边界层参数化方案来集成预报风速方法,可以有效提高WRF模式预报风速的准确率。
|
|
表 3 集成预报风速与实测风速误差分析 Table 3 Error analysis of integrated wind speed prediction and observed wind speed |
此外,对于春夏秋冬和全年代表五组数据,每组数据根据评价指标选择两种预报效果最差的边界层参数化方案来集成预报风速,具体结果如表 3所示。分析发现除了夏季采用方案0和方案5来集成预报风速时,其风速的预报效果没有单一最佳的边界层方案2的预报效果好,但比其他五种边界层方案预报的风速效果都要好之外,其余四组数据的预报结果都比单一最佳的边界层方案预报的风速效果要好。因此,总的分析来说,一般情况下任意选择两种边界层参数化方案来集成预报风速时,其预报结果都比单一最佳的边界层参数化方案预报的风速效果要好。
甚至采用集成预报方式中最初级的等权集成预报方法,对于春季和全年代表数据来说,其预报效果也比单一最佳的边界层方案预报的风速效果要稍好。说明采用集成预报方法能更准确地反映所研究区域风速、风向等气象要素特征,提高了风速预报的精度。因此,在基于WRF模式预报风速时,应采用集成预报方法进行风速预报。
另外,对比分析发现,采用等权集成预报方法,对于夏秋冬三组数据来说,风速的预报效果反而变差。且对比采用等权和随机森林算法集成预报的风速预报结果时,可以发现采用随机森林算法集成预报后的风速误差明显减小。比如对于全年代表数据来说,两者对比发现,预报风速MAE下降了38.33%、RMSE下降了35.21%。说明当选择采用多种边界层参数化方案来集成预报风速时,可应用一些机器学习算法来建立集成预报模型,对风电场的风速进行预报,以此得到更准确的预报风速。
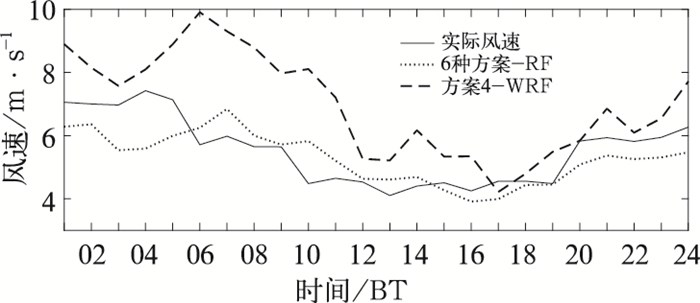
如图 8所示,对于全年代表数据,将实测风速、单一最佳边界层方案(方案4)预报风速和随机森林算法集成预报风速数据进行对比分析。从图中可以看出,采用单一最佳边界层方案预报的风速效果并不理想,而采用随机森林算法集成预报的风速更接近测风塔实测风速数据,预测效果较好。因此,由图形分析可知,在基于WRF模式进行风电场短期风速预测时,应采用集成预报方法来预报风速,得到更准确的风速,提高风速预测的精度。
|
图 8 实测风速和预报风速日变化曲线图 Fig. 8 Diurnal variation of the prediction of wind speed and the observed wind speed |
为了检验预报的有效性和长效性,随机选取一个月30 d数据作为测试数据,其余数据作为训练数据。采用集成预报风速方法,对一个月风速进行逐日逐10 min预报检验,并与实测风速数据进行对比分析,其中采用随机森林法建立模型的时间约为108.44 s,预报时间约为0.62 s,误差结果具体如表 4所示。对比分析发现,当采用单一边界层参数化方案预报风速时,方案1效果最好,方案3和方案5较差;当采用集成预报方式时,不管是等权还是随机森林算法,其风速的预报效果都比采用单一最佳的边界层参数化方案要好;且对比采用等权和随机森林算法集成预报的风速结果时,可以清楚地发现采用随机森林算法集成预报的风速误差比采用等权的风速误差明显减小,预报效果提高较明显,说明在建立集成预报模型时,随机森林算法具有较大的优势。
|
|
表 4 单一边界层方案预报风速与集成预报风速对比分析 Table 4 Comparison and analysis of predicted wind speed by each single boundary layer scheme and integrated wind speed prediction |
本文以复杂地形下某风场为研究对象,试验资料为斗路口梁子测风塔70 m高度处实测数据和六种边界层参数化方案WRF模式预报数据。将多种边界层方案预报的风速及相应的实测风速数据,应用随机森林算法建立集成预报模型,对风电场的风速进行预报研究。主要结论如下:
(1) 不管选取何种单一边界层方案,WRF模式对风速、风向等气象要素都有着较好的预报效果。因此,在复杂地形条件下应用WRF模式预报风电场短期风速是可行的。
(2) 当采用单一边界层方案预报风速时,通过衡量各评价指标,可得到适合于该研究区域单一最佳的边界层参数化方案。但从单一方案预报的风速与测风塔实测风速数据的误差分析可知,采用WRF模式单一方案预报的风速数据误差较大,必须要进一步进行预报研究,得到更为准确的风速。
(3) 采用多种边界层参数化方案来集成预报风速,预报的风速各误差指标均明显减小,预报精度明显提高。且即使选取预报效果最差的两种边界层参数化方案来集成预报风速,其预报结果也比单一最佳的边界层参数化方案预报的风速效果要好。因此,在风电场的短期风速预报研究中,应采用集成预报方法来预报风速,从而提高风速预报的精度。
(4) 对于复杂地形条件下,本文提出采用多种边界层参数化方案来集成预报风速的方法,应用随机森林算法建立集成预报模型,对风电场的风速进行预报研究,得到了较好的风速预报效果。但如何得到最优的集成预报方式,得到更好的风速预报效果,是下一步研究的重点。
蔡子颖, 姚青, 韩素芹, 等, 2017. 基于多种边界层方案的天津PM2.5集合预报试验[J]. 应用气象学报, 28(5): 611-620. Cai Z Y, Yao Q, Han S Q, et al, 2017. Ensemble forecast experiments of PM2.5 based on multiple boundary layer schemes in Tianjin[J]. J Appl Meteor Sci, 28(5): 611-620 (in Chinese). |
常俊, 彭新东, 范广洲, 等, 2015. 结合历史资料的数值天气预报误差订正[J]. 气象学报, 73(2): 341-354. Chang J, Peng X D, Fan G Z, et al, 2015. Error correction of numerical weather prediction with historical data[J]. Acta Meteor Sinica, 73(2): 341-354 (in Chinese). |
邓国卫, 高晓清, 惠小英, 等, 2010. 酒泉地区风能资源开发优势度分析[J]. 高原气象, 29(6): 1634-1640. Deng G W, Gao X Q, Hui X Y, et al, 2010. Analysis on advantage degree of wind energy resource development in Jiuquan Region[J]. Plateau Meteor, 29(6): 1634-1640 (in Chinese). |
段旭, 王曼, 陈新梅, 等, 2011. 中尺度WRF数值模式系统本地化业务试验[J]. 气象, 37(1): 39-47. Duan X, Wang M, Chen X M, et al, 2011. Localization of operational experiment on the WRF mesoscale numerical modeling system[J]. Meteor Mon, 37(1): 39-47 (in Chinese). |
方艳莹, 徐海明, 朱蓉, 等, 2012. 基于WRF和CFD软件结合的风能资源数值模拟试验研究[J]. 气象, 38(11): 1378-1389. Fang Y Y, Xu H M, Zhu R, et al, 2012. Study on numerical simulation of wind energy resources based on WRF and CFD models[J]. Meteor Mon, 38(11): 1378-1389 (in Chinese). |
贵志成, 郑益群, 曾新民, 等, 2014. 不同边界层参数化方案对东亚夏季风气候模拟的对比研究[J]. 气象科学, 34(6): 638-646. Gui Z C, Zheng Y Q, Zeng X M, et al, 2014. Impact of different planetary boundary layer parameterizations on summer monsoonal climate simulation in East Asia[J]. J Meteor Sci, 34(6): 638-646 (in Chinese). |
黄林宏, 宋丽莉, 李刚, 等, 2016. IEC的风机选型参数估算方法在中国的适用性研究[J]. 气象, 42(12): 1522-1530. Huang L H, Song L L, Li G, et al, 2016. Applicability of estimation methods of IEC WTGS selecting parameters in China[J]. Meteor Mon, 42(12): 1522-1530 (in Chinese). DOI:10.7519/j.issn.1000-0526.2016.12.010 |
李得勤, 陈力强, 周晓珊, 等, 2012. 风电场风速降尺度预报方法对比分析[J]. 气象与环境学报, 28(6): 25-31. Li D Q, Chen L Q, Zhou X S, et al, 2012. Comparison analysis of downscaling forecast methods on wind speed in wind power field[J]. J Meteor Environ, 28(6): 25-31 (in Chinese). |
李欣海, 2013. 随机森林模型在分类与回归分析中的应用[J]. 应用昆虫学报, 50(4): 1190-1197. Li X H, 2013. Using "random forest" for classification and regression[J]. Chinese J Appl Entomol, 50(4): 1190-1197 (in Chinese). |
李艳, 成培培, 路屹雄, 等, 2015. 典型复杂地形风能预报的精细化研究[J]. 高原气象, 34(2): 413-425. Li Y, Cheng P P, Lu Y X, et al, 2015. Wind power forecasting over the typical complex terrains[J]. Plateau Meteor, 34(2): 413-425 (in Chinese). |
穆清晨, 王咏薇, 邵凯, 等, 2017. 山地复杂条件下三种边界层参数化方案对近地层风模拟精度初步评估分析[J]. 资源科学, 39(7): 1349-1360. Mu Q C, Wang Y W, Shao K, et al, 2017. Three planetary boundary layer parameterization schemes for the preliminary evaluation of near surface wind simulation accuracy over complex terrain[J]. Resources Sci, 39(7): 1349-1360 (in Chinese). |
王美琳, 罗勇, 周荣卫, 2010. WindSim软件在复杂地形风电场风能资源评估中的应用[J]. 气象, 36(2): 113-119. Wang M L, Luo Y, Zhou R W, 2010. Application of WindSim to wind energy resource assessment of complex terrain in China[J]. Meteor Mon, 36(2): 113-119 (in Chinese). |
王益柏, 梅娜, 范磊, 等, 2014. WRF模式对2013年1月华北一次大雾的数值对比试验[J]. 气象, 40(12): 1522-1529. Wang Y B, Mei N, Fan L, et al, 2014. Comparative experiments of WRF simulation on a fog event of January 2013 in North China[J]. Meteor Mon, 40(12): 1522-1529 (in Chinese). DOI:10.7519/j.issn.1000-0526.2014.12.011 |
许建伟, 高艳红, 2014. WRF模式对夏季黑河流域气温和降水的模拟及检验[J]. 高原气象, 33(4): 937-946. Xu J W, Gao Y H, 2014. Validation of summer surface air temperature and precipitation simulation over Heihe River Basin[J]. Plateau Meteor, 33(4): 937-946 (in Chinese). |
许杨, 陈正洪, 杨宏青, 等, 2013. 风电场风电功率短期预报方法比较[J]. 应用气象学报, 24(5): 625-630. Xu Y, Chen Z H, Yang H Q, et al, 2013. Comparison of short-term forecast method of wind power in wind farm[J]. J Appl Meteor Sci, 24(5): 625-630 (in Chinese). DOI:10.3969/j.issn.1001-7313.2013.05.012 |
薛禹胜, 郁琛, 赵俊华, 等, 2015. 关于短期及超短期风电功率预测的评述[J]. 电力系统自动化, 39(6): 141-151. Xue Y S, Yu C, Zhao J H, et al, 2015. A review on short-term and ultra-short-term wind power prediction[J]. Automation of Electric Power Systems, 39(6): 141-151 (in Chinese). |
朱向东, 2016.基于CFD的复杂地形风电场微观选址技术研究[D].昆明: 昆明理工大学: 1-27. Zhu X D, 2016.Technical study on wind power plant micro location of complex terrain based on CFD[D].Kunming University of Science and Technology: 1-27(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10674-1016195655.htm |
Bougeault P, Lacarrere P, 1989. Parameterization of orography-induced turbulence in a meso-β scale model[J]. Mon Wea Rev, 117(8): 1872-1890. DOI:10.1175/1520-0493(1989)117<1872:POOITI>2.0.CO;2
|
Breiman L, 2001a. Random forests[J]. Mach Learn, 45(1): 5-32.
|
Breiman L, 2001b. Statistical modeling:the two cultures[J]. Stat Sci, 16(3): 199-215.
|
Deng H, Li Y, Zhang Y C, et al, 2017. Prediction of hub height winds over the plateau terrain by using WRF/YSU/Noah and statistical forecast[J]. Earth Sci Res J, 21(1): 37-43.
|
Hong S Y, Noh Y, Dudhia J, 2006. A new vertical diffusion package with an explicit treatment of entrainment processes[J]. Mon Wea Rev, 134(9): 2318-2341. DOI:10.1175/MWR3199.1
|
Janjić Z I, 1994. The step-mountain eta coordinate model:Further developments of the convection, viscous sublayer, and turbulence closure schemes[J]. Mon Wea Rev, 122(5): 927-945. DOI:10.1175/1520-0493(1994)122<0927:TSMECM>2.0.CO;2
|
Pleim J E, 2007. A combined local and nonlocal closure model for the atmospheric boundary layer.Part Ⅰ:Model description and testing[J]. J Appl Meteor Clim, 46(9): 1383-1395. DOI:10.1175/JAM2539.1
|
Sukoriansky S, Galperin B, Perov V, 2005. Application of a new spectral theory of stably stratified turbulence to the atmospheric boundary layer over sea ice[J]. Bound-Lay Meteor, 117(2): 231-257. DOI:10.1007/s10546-004-6848-4
|
 2019, Vol. 45
2019, Vol. 45 