2. 内蒙古自治区气象台,呼和浩特 010051
2. Inner Mongolia Autonomous Regional Meteorological Observatory, Hohhot 010051
由于单一的数值预报存在较强的不确定性,目前的天气预报思想逐渐由确定性预报转变为概率预报,Epstein(1969)和Leith(1974)提出的集合预报方法为概率预报提供了有效的途径。集合预报技术的应用可以为用户提供更全面完整的信息,提高业务预报技巧(Toth and Kalney, 1993;1997;Molteni et al,1996;Houtekamer et al,1996)。目前,为了提高暴雨等中尺度强对流天气预报准确率,国内外开始专注于中尺度区域集合预报技术的研究(Sindic-Rancic et al,1998;智协飞等,2015a),区域集合预报也在世界各国的一些业务单位得到了发展和应用(Du et al,1997;Marsigli et al,2005;Frogner et al,2006;Bowler et al,2008;邓国等,2010)。
区域集合预报扰动方法的相关研究主要依据中尺度数值模拟的若干不确定性来源开展(智协飞等,2015b;赵鸣,2008;Posselt and Vukicevic, 2010;Vie et al,2011)。发展合理的模式扰动方法,是区域集合预报技术的研究重点之一(陈静等,2003)。目前集合预报主要的模式扰动方法有如下几种:(1)通过一个模式不同的物理过程参数化方案组合来体现模式物理过程的不确定性(Houtekamer et al,1996)。(2)在模式中引入随机参数化方案来体现大气运动方程数值求解过程中所存在的不确定性(Buizza et al,1999;Lin and Neelin, 2000;任志杰等,2011;谭宁等,2013)。(3)采用多模式集成的方法来体现模式物理过程和动力过程的不确定性(Krishnamurti et al,1999;Zhi et al,2012)。区域集合预报中,模式物理过程对中尺度环流的发展和演变起到十分重要的作用,包括触发局地强对流、传输能量和动量等(Stensrud and Fritsch, 1994),因此物理过程扰动可以为高分辨率集合预报提供有价值的预报信息(陈静等,2003;2006)。国内外一些典型的区域集合预报模式扰动以多物理过程组合(Stensrud et al,2000)、随机物理过程倾向方案(stochastically perturbed parameterization tendencies,SPPT)(Li et al,2008;Bouttier et al,2012)和随机动能后向散射方法(stochastic kinetic energy backscatter,SKEB)(Shutts,2005;Berner et al,2009;Bowler et al,2009)为主。国内区域集合预报模式扰动方法研究更多的是采用多物理过程组合(谭燕和陈德辉,2007;谭燕和陈葆德,2014;张涵斌等,2014a;2014b;黄红艳等,2016),初步研究了随机物理过程扰动方法,中国气象局数值预报中心正在基于GRAPES区域集合预报系统开展SPPT相关工作(袁月等,2016),并表明SPPT方法能有效提高集合预报离散度。李俊等(2015)研究表明SPPT方案能有效改善对流尺度集合预报效果,但其产生的集合离散度相比多物理方案或多模式技术仍偏小。
作为一项随机模式扰动技术,SKEB方法由于考虑了模式动能守恒的特点,已经在国际上受到研究者的重视。英国气象局MOGREPS系统最初采用随机物理过程扰动为区域集合提供模式扰动(Bowler et al,2008),随后模式物理过程扰动升级为SKEB方案(Bowler et al,2009),升级后有效提高了区域集合预报的离散度和预报技巧。Berner et al(2009)试验了SKEB方法,并与多物理过程组合方法进行了对比(Berner et al,2011),结果表明SKEB方法总体上优于多物理过程组合,并指出同时考虑SKEB和多物理过程组合来代表模式不确定性的方案效果最优。Duda et al(2016)在4 km水平分辨率中,将SKEB扰动方案与多物理扰动结合构建了一种混合模式扰动,研究表明多物理扰动叠加随机扰动的方案显著改善了集合成员的分级概率评分,在构建风暴尺度集合预报的模式扰动中具有重要的潜在使用价值。可以看出,目前区域集合预报模式扰动,对提高集合离散度以及概率预报技巧有显著作用,而国内外均已取得了不错的成果,其中随机物理过程扰动方法如SPPT、SKEB在国外的应用较广泛,而国内应用较多的还是多物理过程组合,对随机物理过程扰动技术的数理基础、应用方式还缺乏认识。本文尝试将SKEB方法引入华北区域集合预报中,探索该方法的适用性以及试验合理的SKEB扰动振幅,并在此基础上将SKEB与多物理过程相耦合,发展一种适用于华北区域集合预报的混合模式扰动方法。通过本研究可以寻找代表华北区域数值预报模式不确定性的新途径,以期改善华北区域集合预报模式扰动应用的效果,另外本研究结果也可为国内区域集合预报系统的改进提供参考。
1 试验系统和方法介绍 1.1 试验系统介绍本文试验采用WRF模式V3.5版构建了区域集合预报系统(WRF based regional ensemble forecast system,WRF-REPS),该系统模式区域设置为水平分辨率6 km,垂直层数为51层模式面,模拟区域范围35.5°~46.5°N、107.2°~123.3°E(图略),覆盖华北大部分区域,共有274×209个格点。该集合预报系统包括一个控制预报和20个扰动成员预报共21个集合成员,采用的背景场及侧边界条件为NCEP全球集合预报资料(Global Ensemble Forecast System, GEFS),集合成员21个,分辨率为1°×1°。本文试验时段为2017年5月1—31日连续一个月,每天从1200 UTC开始起报,模式预报时效48 h。集合预报试验等压面要素检验采用GFS分析场,降水检验采用国家气象信息中心整编的中国2500个台站的实况降水。
1.2 SKEB方法介绍SKEB是一种较为典型的随机物理过程扰动方法,其基本思想是:模式积分过程的一部分不确定性来源于截断尺度附近的湍流耗散过程,因此通过随机动能扰动将参数化的次网格动能重新补偿到模式的湍流中(Shutts,2005)。在ECMWF全球集合预报中,SKEB假定了时间和空间不变的动能耗散率(Berner et al,2009),对于有限区域集合预报系统而言,由于其基于格点模式(如WRF)构建,因此需要构建某一时刻t格点空间x,y的随机动能扰动源。我们基于流函数和温度的耗散来获得流函数扰动和温度扰动(Berner et al,2011),如对于流函数扰动:
| $ \Psi '\left({x, y, t} \right) = rD\left({x, y, t} \right)\psi '\left({x, y, t} \right) $ | (1) |
式中,D(x, y, t)为局地瞬时耗散率,ψ'(x, y, t)为局地二维流函数(扰动)强迫型,r为后向散射率参数,通过对流函数强迫型ψ'(x, y, t)进行谱空间展开,可以得到二维傅里叶空间中的流函数强迫型,以及相应的经向纬向风扰动为:
| $ \psi '\left({x, y, t} \right) = \mathop \sum \limits_{k = - K/2}^{K/2} \mathop \sum \limits_{l = - L/2}^{L/2} \psi {'_{k, l}}\left(t \right){e^{2\pi i(kx/X + ly/Y)}} $ | (2) |
| $ \begin{array}{l} u'\left({x, y, t} \right) = - \frac{{\partial \psi '\left({x, y, t} \right)}}{{\partial y}}\\ \;\;\; = - \frac{{2\pi i}}{Y}\mathop \sum \limits_{k = - K/2}^{K/2} \mathop \sum \limits_{l = - L/2}^{L/2} l\psi {'_{k, l}}\left(t \right){e^{2\pi i(kx/X + ly/Y)}} \end{array} $ | (3) |
| $ \begin{array}{l} v'\left({x, y, t} \right) = - \frac{{\partial \psi '\left({x, y, t} \right)}}{{\partial x}}\\ \;\;\; = - \frac{{2\pi i}}{X}\mathop \sum \limits_{k = - K/2}^{K/2} \mathop \sum \limits_{l = - L/2}^{L/2} k\psi {'_{k, l}}\left(t \right){e^{2\pi i(kx/X + ly/Y)}} \end{array} $ | (4) |
式中,k、l分别代表x和y方向上的波数(x方向波数共K+1个,y方向波数共L+1个),t代表时间,并通过对每个波数进行一阶自回归过程转化来描述流函数强迫的时间变化。流函数强迫引起不同模式积分步长的动能谱变化,从而起到动能补偿(扰动)的作用。
Shutts(2005)指出动能总耗散率D(x, y, t)来源于三方面的贡献:深对流、数值耗散以及重力波拖曳,Berner et al(2009)指出水平扩散过程导致的能量耗散足以表示动能总耗散,因此引入一个简化的假定,即用时空固定的耗散率(D)来表示动能总耗散。当D为常数,可以计算出流函数扰动ψ'。根据Shutts(2005),次网格过程的能量不仅应补偿给动能(即u,v),而且应该补偿给温度,因此采用与流函数扰动计算相类似的方法来计算温度扰动,并将温度扰动加到模式积分方程中。
为了解SKEB方法的作用特征,本文进行敏感性试验,验证不同流函数与温度扰动幅度设置下的SKEB扰动预报与未扰动预报的差异,从而了解SKEB扰动方法对单模式预报的影响,并探索流函数和温度较为合理的扰动振幅(即流函数和温度对应的动能耗散率大小)。设计了五组试验,分别为:(1)控制试验(CN,即不加入任何SKEB扰动的单模式预报);(2)水平扰动幅度采用缺省值的SKEB试验(AMPL1.0);(3)水平扰动幅度减半的SKEB试验(AMPL0.5);(4)水平扰动幅度加倍的SKEB试验(AMPL2.0);(2)~(4)组试验随机型一致,扰动幅度不一致,扰动的垂直结构上下一致,以观察水平扰动振幅对预报的影响;(5)引入垂直随机型扰动试验(PV,即水平扰动振幅采用缺省设置,对扰动的垂直结构采用上下不一致的设置)。不同试验方案配置如表 1。
|
|
表 1 SEKB引入单模式预报试验方案配置 Table 1 Configuration of SKEB method of single model forecast |
为了与SKEB方案进行对比,并构建SKEB-多物理过程组合相耦合的混合模式扰动方案,本文试验也引入多物理过程组合方法。多物理过程组合方法通过一个模式不同的物理过程参数化方案选项组合来体现模式物理过程的不确定性(Houtekamer et al,1996)。由于该方法简便易行,因此应用较为广泛。但是构建多物理过程组合,需要不断的试验调试,以确保所有采用不同物理过程组合的成员都能正常积分,并且在特定的试验时段内没有明显较差的成员。考虑到本文试验中模式分辨率为6 km,未开启积云对流参数化方案,因此采用微物理过程、长波/短波辐射以及边界层方案的不同选项进行组合来构建不同成员的物理过程参数化方案配置,如表 2。
|
|
表 2 不同成员多物理过程组合参数化方案配置 Table 2 Configuration of multi-physics combination for different members |
为了更好地展示1.2节中五组试验结果的差异,了解SKEB扰动对单模式预报的影响,本文通过其中(2)~(5)组SKEB扰动试验和第(1)组控制试验的均方根离差来分析SKEB扰动带来的预报变化。设一个扰动预报二维场(mx×my个格点)和控制预报二维场的均方根离差(RMS-difference)为:
| $ RMS - {\rm{difference}} = \sqrt {\frac{{\mathop \sum \limits_{j = 1}^{my} \mathop \sum \limits_{i = 1}^{mx} {{(F_{ij}^{{\rm{per}}} - F_{ij}^{{\rm{cn}}})}^2}}}{{mx \times my}}} $ | (5) |
式中,Fijper指某一格点(i,j)上的扰动预报,Fijcn为对应格点上的控制试验预报。图 1给出了不同SKEB扰动试验与控制试验的预报均方根离差随预报时效的演变。可以看出,对于0~6 h时效预报,几组扰动试验与控制试验的离差较为类似,离差增长均较快;6 h之后,不同设置的SKEB扰动预报开始表现出与控制试验不同的离差,其中双倍SKEB扰动幅度(AMPL2.0)有助于提高离差,而减半SKEB扰动幅度(AMPL0.5)表现出较小的离差,垂直结构扰动(PV)则对离差增长帮助不大,有时甚至不如AMPL0.5,如30 h预报时效的500 hPa高度以及18 h预报时效的500 hPa风的U分量(图 1c)。对于较长的预报时效(如30 h之后),各扰动试验与控制试验的离差基本不再增长。

|
图 1 不同SKEB扰动试验与控制试验的预报均方根离差随预报时效的演变 (a)Z500, (b)T850, (c)U500 Fig. 1 RMS-difference of SKEB perturbation forecast and control forecast as a function of forecast lead time (a) Z500, (b) T850, (c) U500 |
图 2给出了不同SKEB扰动试验与控制试验30 h预报时效的500 hPa纬向风的差异,同时给出了控制试验500 hPa高度场的等高线。可以看出,不管是哪一组扰动试验,产生的纬向风扰动离差形态均比较类似,与天气流型相对应,各组试验离差最大值位于槽前,扰动量级可达4 m·s-1以上,说明SKEB方法可以有效产生依赖天气流型的扰动模态。从扰动量级来看,减半(图 2b)/加倍(图 2c)SKEB扰动幅度可以有效减小/增加扰动最大值,且保持扰动模态的流依赖结构;而垂直扰动的增加(图 2d)试验的离差总体形态与未增加垂直扰动的试验结果类似,甚至有些区域扰动量级有所减少,这可能是由于SKEB方法通过扰动模式的动力和温度场来反馈到物理过程倾向中,垂直方向的扰动有可能使得动力场产生了较大的不协调,动力调整过程会损失一定的能量,导致模式积分过程中与控制试验的离差增长反而不如垂直方向随机型一致的扰动方案。

|
图 2 不同SKEB扰动试验与控制试验30 h预报时效的500 hPa纬向风差异的水平分布(阴影,单位:m·s-1),以及控制试验500 hPa高度场等高线(单位:gpm) (a)AMPL1.0, (b)AMPL0.5, (c)AMPL2.0, (d)PV Fig. 2 Horizontal distribution of 500 hPa zonal wind difference (shaded area, unit: m·s-1) between multiple SKEB perturbation forecast and control forecast at 30 h forecast lead time, with the 500 hPa geopotential height (unit: gpm) of control forecast given as line in each plot (a) AMPL1.0, (b) AMPL0.5, (c) AMPL2.0, (d) PV |
SKEB方法的作用方式是通过动能扰动来影响次网格物理过程,因此对几种方案进行动能谱分析来更好地了解SKEB方法的作用原理。定义某个格点的动能(kinetic energy,KE)为:
| $ KE = \frac{1}{2}[{u^2}\left({i, j, k} \right) + {v^2}\left({i, j, k} \right)] $ | (6) |
式中,u,v分别为水平纬向风和径向风;i,j,k分别是格点的水平与垂直维数。图 3为6 h预报时效的500 hPa上SKEB扰动方案及控制试验的动能谱,以及SKEB方案与动能谱之差。从5种方案动能谱(图 3a)可以看出,各个方案从长波(波数1,对应波长1781 km)到短波(波数207,对应波长12 km)的动能逐渐减小,4种SKEB扰动方案的动能谱分布与控制试验相比有波动,但是总体上较为一致,这说明SKEB扰动的引入整体上不会增加或者减少模式积分过程中的动能,而是通过对流函数注入“扰动”来对原动能产生影响。而不同的扰动幅度对动能谱的影响有所差异;从图 3b可以看出,几种SKEB与控制试验的动能谱之差有正有负,说明引入SKEB扰动之后,在某些波段可以增加动能,而在另外一些波段则减小动能,其中加倍SKEB扰动振幅(AMPL2.0)对控制试验动能的改变幅度略大。需要注意的是,引入垂直扰动(PV)则对动能的改变幅度明显不如前几种方案。对于短波,几种SKEB方法对动能的改变则越来越小。以上分析说明增加SKEB扰动,对于原模式积分的总动能不会产生较大影响,只会对不同波段的动能产生扰动,因此当SKEB方法引入集合预报时,不会凭空增加(或者减少)某些成员的总体动能,维持各集合成员动能的“等同性”。

|
图 3 6 h预报时效的500 hPa动能谱分析 (a)SKEB扰动方案及控制试验的动能谱,(b)不同SKEB方案与控制试验动能谱之差 Fig. 3 Kinetic energy spectral distribution evaluated at 500 hPa in 6 h lead time of simulation (a) kinetic energy spectral of SKEB schemes and control test, (b) differences in kinetic energy spectral of different SKEB schemes and control test |
在进行了SKEB方法扰动振幅的敏感性试验之后,通过进一步尝试对SKEB引入区域集合预报进行试验,发现当扰动振幅较小则会导致集合离散度过低,而扰动振幅太大则会使得离散度过高,甚至有超过均方根误差的情况出现(图略),而引入垂直扰动试验也显示垂直扰动并未对离散度增长有所帮助。综合比较之后,确认AMPL2.0可以为区域集合预报获得较为适宜的离散度-均方根误差关系,因此在下文试验中的SKEB扰动振幅设置均与AMPL2.0一致。
3 基于SKEB与多物理过程的混合模式扰动方法试验 3.1 混合模式扰动方法的构建目前国内较主流的模式扰动方法依然是多物理过程组合,毫无疑问多物理过程对改进区域集合预报有一定效果,但是若要进一步提高区域集合预报效果,多物理过程组合则难以具备更大的改进空间。对于模式不确定性而言,多物理过程与随机物理过程扰动的搭配是否可以更好地体现模式误差中系统性和随机性的误差,提高预报效果?本节尝试将多物理过程组合方法与SKEB方法相耦合,构建混合模式扰动方案,并与单独的SKEB和多物理过程组合进行比较试验。
本节设计了三组集合预报试验,第一组为SKEB试验,仅采用SKEB扰动,其中20个扰动成员随机种子为1~20;第二组为多物理过程组合方案(multi-physics,MPHY),不同物理过程的组合搭配方案如表 1所示;第三组为组合混合扰动的方案,多物理过程也基于表 1构建,同时对于不同的成员,采用与试验(1)一致的随机种子构建SKEB随机扰动。三组试验的初值扰动均由Breeding(Toth and Kalnay, 1993;1997)提供(表 3),试验时段为2017年5月1—31日连续一个月。
|
|
表 3 三组集合预报试验设置 Table 3 Three ensemble forecast settings |
当集合扰动能够更好地把握误差的快速增长方向的情况下扰动更容易增长(Toth and Kalnay, 1993;1997)。首先对三组试验扰动增长特征进行分析。图 4为三种集合方案12、48 h预报时效的纬向风和温度扰动绝对值的垂直廓线分布。由图 4可以看出,对于风的u分量扰动,12 h预报时效的SKEB方案要优于MPHY方案(图 4a),如SKEB方案扰动最大层次可达3.2 m·s-1,而MPHY方案仅为3 m·s-1;48 h预报时效(图 4b)SKEB方案依然占优,尤其是在模式高层和低层优势较为明显,而SKEB-MPHY方案的表现均优于SKEB方案以及MPHY方案。对于温度扰动,12 h预报时效(图 4c)的SKEB方案和MPHY方案扰动大小各有优劣,其中,在模式低层SKEB扰动呈现出一定的收敛特征,因此地表温度预报是欠离散的;48 h预报时效(图 4d)的SKEB温度扰动在低层依然是欠离散状态,仅为0.8 K,而MPHY扰动可达1 K,而混合了两种扰动的SKEB-MPHY方案,在低层具有较好的离散度,可达1.08 K。以上研究表明,对于不同层次、不同要素的扰动而言,SKEB方案与MPHY方案的扰动增长各有优劣;而SKEB-MPHY方案始终是扰动增长最好的方案。

|
图 4 SKEB,MPHY以及SKEB-MPHY三种集合方案12 h(a, c)和48 h(b, d)预报时效的(a, b)纬向风扰动和(c, d)温度扰动绝对值的垂直廓线分布 Fig. 4 The vertical profile distribution of absolute perturbation values for SKEB, MPHY and SKEB-MPHY (a) U wind at 12 h, (b) U wind at 48 h, (c) T at 12 h, (d) T at 48 h |
为了进一步验证三种模式扰动方案在区域集合预报中的表现,采用若干概率预报检验指标计算了试验时段内的检验结果,包括集合平均均方根误差和离散度、连续等级概率评分(CRPS),以及离群值评分(Outliers)。
图 5a~5c给出了三种方案一个月平均的500 hPa纬向风速(U500)、850 hPa纬向风速(U850)以及850 hPa温度预报(T850)的集合平均均方根误差和集合离散度。对于U预报,不管是高空(U500,图 5a)还是低空(U850,图 5b)SKEB方法离散度在各个预报时效均大于MPHY,均方根误差相对于MPHY也略有减小,如30 h预报时效的U850预报误差SKEB明显小于MPHY(图 5b);对于T850预报,SKEB与MPHY相比,无论是离散度还是均方根误差均差于MPHY,说明SKEB方法对于低层温度预报效果不够好。图中列出的所有变量,SKEB-MPHY方案均显示出较好的误差-离散度关系,其离散度相对于SKEB和MPHY方案均有了明显提高,而其均方根误差则是三种方案中最小的,对于其他等压面要素,SKEB-MPHY方案也显示出了明显优势,不再赘述。以上分析表明SKEB与多物理过程相结合构建模式扰动可以显著改善集合离散度的增长,提高集合预报质量。
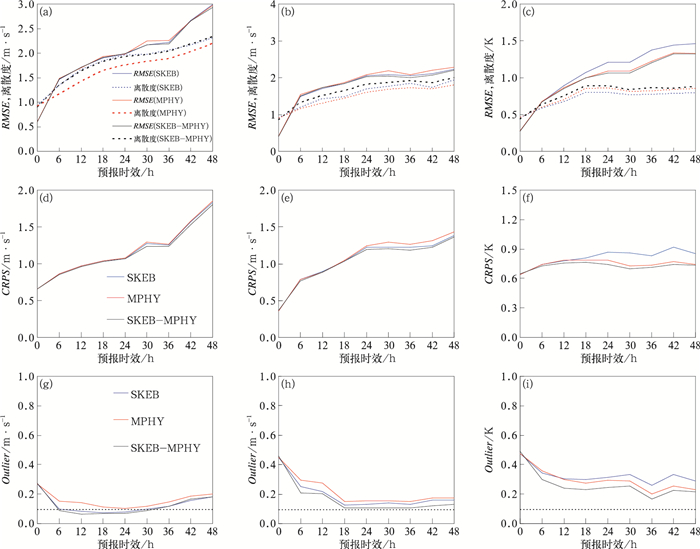
|
图 5 SKEB,MPHY和SKEB-MPHY三种集合方案概率预报检验结果 (a, b, c)U500,U850,T850的均方根误差和离散度, (d, e, f)U500,U850,T850的CRPS评分,(g, h, i)U500,U850,T850的Outlier评分 (虚线为最优离群值) Fig. 5 Ensemble verification results for SKEB, MPHY and SKEB-MPHY (a, b, c) RMSE of ensemble mean and spread for U500, U850 and T850 respectively, (d, e, f) CRPS for U500, U850 and T850, respectively, (g, h, i) percentage of Outliers for U500, U850 and T850, respectively (dashed line: the optimal outlier) |
CRPS评分能够定量比较预报累计分布概率与观测累计分布概率距离差异(Hersbach,2000)。该评分值是负定向的,0值的CRPS意味着最好的预报,值越高表示集合预报系统的概率预报性能越差。图 5d~5f给出了三组集合试验U500,T850以及U850的CRPS评分。由图可以看出对于不同变量,SKEB和MPHY两种方案各有优劣,而SKEB-MPHY方法在各个预报时效的CRPS值均小于SKEB和MPHY方法,说明SKEB-MPHY方法的概率预报技巧最优。
离群值是衡量集合预报可靠性的一种方法,指代观测落在集合成员外的频率。一个较为可靠的集合预报具有较小的离群值(Wang et al,2011),对于可靠性较高的包含21个集合成员的集合来说,其最优离群值为2/22。图 5g~5i为三种方案不同要素的离群值(其中虚线给出了最优离群值)可以看出,SKEB和MPHY两种方案各有优劣,如对于T850(图 5i)SKEB的离群值较高,说明SKEB对低层温度概率预报效果有限,对于U850,SKEB方法则要优于MPHY。与上文类似,离群值检验指标最优的集合依然是SKEB-MPHY方案。对于图中列出的所有变量,SKEB-MPHY方案具有更小的离群值,说明观测更容易落在SKEB-MPHY集合区间中。
通过以上分析可以看出,与单独采用SKEB以及MPHY模式扰动的集合预报结果相比,经过两者相结合的SKEB-MPHY模式扰动方案集合预报效果更好,对不同预报时效以及不同要素,改进程度各不相同。总体而言,两种模式扰动相结合之后的集合预报结果能够提供更优的概率预报。对其他等压面变量的检验(图略)也可以支持这个结论。
3.4 降水预报结果分析本节对SKEB,MPHY和SKEB-MPHY三种集合方案的降水预报效果进行分析,研究了2017年夏季一次典型的降水个例。三种方案均从2017年5月21日1200 UTC起报。
图 6给出了集合模拟区域观测的2017年5月22日0600 UTC的6 h累计降水量>13 mm降水实况分布以及相应的两种集合方案>13 mm降水的概率预报结果。可以看出该降水个例主要在华北地区呈东北—西南向分布,其中22日0600 UTC的6 h累计降水(图 6a)在北京东南部地区较大,可达25 mm以上。
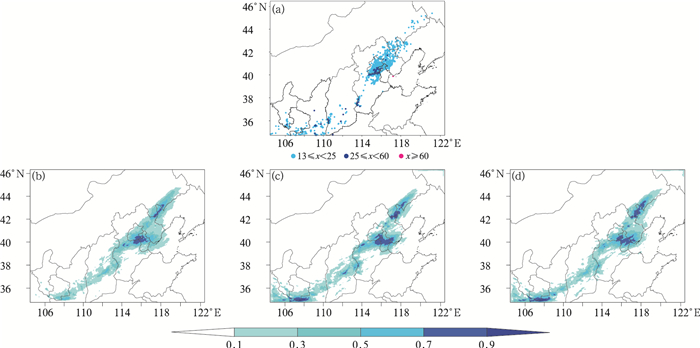
|
图 6 集合模拟区域2017年5月22日0600 UTC的6 h累计降水大于13 mm的值 (a)实况, (b)SKEB方案,(c)MPHY方案,(d)SKEB-MPHY方案 Fig. 6 The 6 h accumulated precipitation with value over 13 mm at 0600 UTC 22 May 2017 (a) obsevation, (b) SKEB, (c) MPHY, (d) SKEB-MPHY |
图 6b~6d给出了SKEB,MPHY和SKEB-MPHY集合的2017年5月22日0600 UTC的6 h累计>13 mm降水概率预报。对于该时段降水,SKEB集合降水的大雨概率分布(图 6b)对北京东南的强降水中心预报较好,给出了很强的指示信号;MPHY集合降水的大雨概率分布(图 6c)与实况相比有所偏差,其中,对北京西北部的强降水区域,MPHY集合概率预报没有给出很好的指示,存在明显的漏报,而天津北部地区明显偏强,降水概率达到70%以上,相对于实况表现出一定的空报,说明MPHY方案成员预报降水落区不够准确,存在一定的偏移;SKEB-MPHY集合概率预报(图 6d)有了一定的改善,在北京西北地区增强了预报概率,与实况对应更好,而对天津北部的空报概率则有一定减少,但依然存在空报现象。
采用两种概率预报检验指标来评估两种集合扰动方案的降水预报能力:相对作用特征面积(area of relative operating characteristic,AROC)以及brier score (BS)评分,这两种方法均适用于评估降水的概率预报能力。AROC指代某一事件在某阈值下的命中率和假警报率的相对关系。AROC值较高,说明命中率高,概率预报具有较好的技巧(段明铿等, 2009)。BS评分旨在评估某一事件预报的概率以及观测出现的频率之间的差异,其值为0~1,越小说明概率预报越准确。图 7a~7c给出了两种方案2017年5月一个月检验时段内逐6 h降水AROC评分,预报时效为48 h。对于小雨(>0.1 mm,图 7a)和中雨(>4 mm,图 7b)量级,三种集合方案各有优劣,其中SKEB-MPHY方案始终处于中间或者最优的水平,对于大雨量级(>13 mm,图 7c)降水预报,在所有预报时效,SKEB-MPHY方案均显示出较好的表现,18 h预报时效之前其效果仅次于SKEB方案,优于MPHY方案,如18 h预报时效SKEB和SKEB-MPHY方案评分为0.82,而MPHY方案评分为0.78,18 h预报时效之后SKEB-MPHY方案为评分最高的方案。图 7d~7f给出了36 h预报时效内三种方案降水预报的BS评分。从图中可以看出,对小雨、中雨量级,三种方案的BS评分在各个预报时效内也是各有优劣,SKEB方案在18 h的小雨量级预报和30 h的中雨量级预报效果较好,其他时段三种方案相差不大,对于大雨量级(图 7f)的6~30 h时效降水,SKEB、SKEB-MPHY均显示出优于MPHY的评分效果。
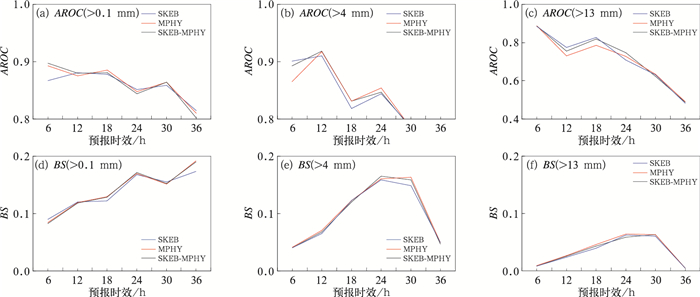
|
图 7 逐6 h累计降水不同阈值ROC面积(AROC,a, b, c)和Brier Score(BS,d, e, f)随预报时效变化 (a, d)小雨(>0.1 mm), (b, e)中雨(>4 mm), (c, f)大雨(>13 mm) Fig. 7 The area of ROC (a, b, c) and Brier Score (d, e, f) for every 6 h accumulated precipitation for different thresholds as a function of forecast lead time (a, d) light rain (>0.1 mm), (b, e) moderate rain (>4 mm), (c, f) heavy rain (>13 mm) |
以上降水个例分析及降水概率预报统计结果表明,SKEB方法的引入能够保持与多物理过程组合相当或者稍好的降水概率预报技巧,对强降水的预报改进较为明显,因此耦合了SKEB与多物理过程组合的混合模式扰动方法在降水预报方面具有较好的应用前景。
4 结论与讨论本文基于WRF模式,利用GEFS全球集合预报资料驱动构建了区域集合预报系统,试验了随机动能后向散射方法(SKEB)在区域集合预报系统中的应用效果,并与多物理过程组合进行对比,在此基础上设计了SKEB与多物理过程组合相结合的混合模式物理过程扰动方法。进行了一个月的批量试验,对扰动特征进行了分析,对概率预报效果进行了检验,并对试验时段内的典型降水个例模拟效果进行了分析,得到以下几点结论:
(1) SKEB方法通过流函数及温度耗散率来对模式积分产生影响,且耗散率大小与预报离差正相关;垂直结构扰动不利于预报离差的发展;SKEB扰动在0~6 h预报时效增长最快,且能够对天气流型的特征有响应。
(2) SKEB、多物理过程组合以及混合模式扰动方法的对比试验表明,对于高空动力场预报,采用SKEB模式扰动比多物理过程组合方法的集合扰动的增长更快,而对于低层温度预报,SKEB扰动方法扰动增长则不如多物理过程组合,而混合模式扰动方法相对于单独SKEB和多物理过程组合而言,均有明显改进,扰动增长能力最强;集合预报检验效果也表明采用混合模式扰动方法的集合预报评分效果较好。
(3) 对典型降水个例试验结果表明,在多物理过程组合的基础上引入SKEB方案的混合物理过程扰动方法相较于仅采用多物理过程组合的模式扰动方法,其降水预报效果能够保持大致相当的水平,SKEB以及混合模式扰动方法对大雨预报有所改进。
本文试验结果说明SKEB方法应用于区域集合预报具有很强的可行性,且具有扰动振幅可调、设置简便的特性,而综合考虑SKEB和多物理过程组合相耦合的方法具有较好的表现,对区域集合预报系统的构建具有很大的应用潜力。对于SKEB模式扰动技术而言,提高模式低层的离散度增长能力也许是今后对其进行改进的方面之一。另外本文试验时段为一个月,今后需要更多的试验来验证文中所介绍方案的普遍适用性。
陈静, 矫梅燕, 龚建东, 等, 2006. 非绝热物理过程对北京暴雨数值预报不确定性影响[J]. 应用气象学报, 17(S1): 18-27. Chen J, Jiao M Y, Gong J D, et al, 2006. The impact of diabatic physics on the uncertainty of heavy rainfall ensemble simulations in Beijing[J]. J Appl Meteor Sci, 17(S1): 18-27 (in Chinese). |
陈静, 薛纪善, 颜宏, 2003. 华南中尺度暴雨数值预报的不确定性与集合预报试验[J]. 气象学报, 61(4): 432-446. Chen J, Xue J S, Yan H, 2003. The uncertainty of mesoscale numerical prediction of South China heavy rain and the ensemble simulations[J]. Acta Meteor Sinica, 61(4): 432-446 (in Chinese). DOI:10.3321/j.issn:0577-6619.2003.04.005 |
邓国, 龚建东, 邓莲堂, 等, 2010. 国家级区域集合预报系统研发和性能检验[J]. 应用气象学报, 21(5): 513-523. Deng G, Gong J D, Deng L T, et al, 2010. Development of mesoscale ensemble pre-dication system at National Meteorological Center[J]. J Appl Meteor Sci, 21(5): 513-523 (in Chinese). DOI:10.3969/j.issn.1001-7313.2010.05.001 |
段明铿, 王盘兴, 吴洪宝, 等, 2009. 夏季亚欧中高纬度环流的集合预报效果检验[J]. 应用气象学报, 20(1): 56-61. Duan M K, Wang P X, Wu H B, et al, 2009. The ensemble forecasting verification on the summer eurasian middle high latitude circulation[J]. J Appl Meter Sci, 20(1): 56-61 (in Chinese). DOI:10.3969/j.issn.1001-7313.2009.01.007 |
黄红艳, 齐琳琳, 刘健文, 等, 2016. 多物理ETKF在暴雨集合预报中的初步应用[J]. 大气科学, 40(4): 657-668. Huang H Y, Qi L L, Liu J W, et al, 2016. Preliminary application of a multi-physical ensemble transform Kalman filter in precipitation ensemble prediction[J]. Chinese J Atmos Sci, 40(4): 657-668 (in Chinese). |
李俊, 杜钧, 刘羽, 2015. 北京"7.21"特大暴雨不同集合预报方案的对比试验[J]. 气象学报, 73(1): 50-71. Li J, Du J, Liu Y, 2015. A comparison of initial condition, multi-physics and stochastic physics-based ensembles in predicting Beijing "7.21" excessive storm rain event[J]. Acta Meteor Sinica, 73(1): 50-71 (in Chinese). |
任志杰, 陈静, 田华, 2011. T213全球集合预报系统物理过程随机扰动方法研究[J]. 气象, 37(9): 1049-1059. Ren Z J, Chen J, Tian H, 2011. Research on T213 Ensemble Prediction System stochastic physics perturbation[J]. Meteor Mon, 37(9): 1049-1059 (in Chinese). |
谭宁, 陈静, 田华, 2013. 两种模式随机扰动方案比较及扰动传播分析[J]. 气象, 39(5): 543-555. Tan N, Chen J, Tian H, 2013. Comparision between two global model stochastic perturbation schemes and analysis of perturbation propagation[J]. Meteor Mon, 39(5): 543-555 (in Chinese). DOI:10.3969/j.issn.1671-1742.2013.05.016 |
谭燕, 陈葆德, 2014. 多种扰动组合的热带气旋路径集合预报技术研究[J]. 高原气象, 33(4): 1012-1021. Tan Y, Chen B D, 2014. Study of multiple perturb tropical cyclone ensemble forecast[J]. Plateau Meteor, 33(4): 1012-1021 (in Chinese). |
谭燕, 陈德辉, 2007. 基于非静力模式物理扰动的中尺度集合预报试验[J]. 应用气象学报, 18(3): 386-406. Tan Y, Chen D H, 2007. Mesoscale ensemble forecasts on physical perturbation using a non-hydrostatic model[J]. J Appl Meter Sci, 18(3): 386-406 (in Chinese). |
袁月, 李晓莉, 陈静, 等, 2016. GRAPES区域集合预报系统模式不确定性的随机扰动技术研究[J]. 气象, 42(10): 1161-1175. Yuan Y, Li X L, Chen J, et al, 2016. Stochastic parameterization toward model uncertainty for the GRAPES mesoscale ensemble prediction system[J]. Meteor Mon, 42(10): 1161-1175 (in Chinese). DOI:10.7519/j.issn.1000-0526.2016.10.001 |
张涵斌, 陈静, 智协飞, 等, 2014a. 基于GRAPES_Meso的集合预报扰动方案设计与比较[J]. 大气科学学报, 37(3): 276-284. Zhang H B, Chen J, Zhi X F, et al, 2014a. Design and comparison of perturbation schemes for GRAPES_Meso based ensemble forecast[J]. Trans Atmos Sci, 37(3): 276-284 (in Chinese). |
张涵斌, 陈静, 智协飞, 等, 2014b. GRAPES区域集合预报系统应用研究[J]. 气象, 40(9): 1076-1087. Zhang H B, Chen J, Zhi X F, et al, 2014b. Study on the application of GRAPES regional ensemble prediction system[J]. Meteor Mon, 40(9): 1076-1087 (in Chinese). |
赵鸣, 2008. 边界层和陆面过程对中国暴雨影响研究的进展[J]. 暴雨灾害, 27(2): 186-190. Zhao M, 2008. A review of the research on the effects of boundary layer and land surface process on heavy rain in China[J]. Torrential Rain Disasters, 27(2): 186-190 (in Chinese). DOI:10.3969/j.issn.1004-9045.2008.02.016 |
智协飞, 孙晶, 周文友, 2015a. 2009年夏季西太平洋台风的集合预报和多模式集成预报试验[J]. 大气科学学报, 38(5): 633-640. Zhi X F, Sun J, Zhou W Y, 2015a. Ensemble and multimodel ensemble forecasts of Western Pacific typhoons during summer 2009[J]. Trans Atmos Sci, 38(5): 633-640 (in Chinese). |
智协飞, 朱寿鹏, 孙晶, 等, 2015b. 基于BGM与ETKF的台风"苏拉"(1209)集合预报的对比试验Ⅰ:路径预报[J]. 大气科学学报, 38(6): 776-784. Zhi X F, Zhu S P, Sun J, et al, 2015b. Comparative experiments of ensemble forecasting of Typhoon Saola(1209)based on BGM and ETKF, Part Ⅰ:track forecast[J]. Trans Atmos Sci, 38(6): 776-784 (in Chinese). |
Berner J, Ha S Y, Hacker J P, et al, 2011. Model uncertainty in a mesoscale ensemble prediction system:stochastic versus multiphy-sics representations[J]. Mon Wea Rev, 139(6): 1972-1995. DOI:10.1175/2010MWR3595.1
|
Berner J, Shutts G J, Leutbecher M, et al, 2009. A spectral stochastic kinetic energy backscatter scheme and its impact on flow-dependent predictability in the ECMWF ensemble prediction system[J]. J Atmos Sci, 66(3): 603-626. DOI:10.1175/2008JAS2677.1
|
Bouttier F, Vié B, Nuissier O, et al, 2012. Impact of stochastic phy-sics in a convection-permitting ensemble[J]. Mon Wea Rev, 140(11): 3706-3721. DOI:10.1175/MWR-D-12-00031.1
|
Bowler N E, Arribas A, Mylne K R, et al, 2008. The MOGREPS short-range ensemble prediction system[J]. Quart J Roy Meteor Soc, 134(632): 703-722. DOI:10.1002/(ISSN)1477-870X
|
Bowler N E, Arribas A, Sarah E, et al, 2009. The local ETKF and SKEB:upgrades to the MOGREPS short-range ensemble prediction system[J]. Quart J Roy Meteor Soc, 135(640): 767-776. DOI:10.1002/qj.v135:640
|
Buizza R, Miller M, Palmer T N, 1999. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system[J]. Quart J Roy Meteor Soc, 125(560): 2887-2908. DOI:10.1002/qj.49712556006
|
Du J, Mullen S L, Sanders F, 1997. Short-range ensemble forecasting of quantitative precipitation[J]. Mon Wea Rev, 125(10): 2427-2459. DOI:10.1175/1520-0493(1997)125<2427:SREFOQ>2.0.CO;2
|
Duda J D, Wang X G, Kong F Y, et al, 2016. Impact of a stochastic kinetic energy backscatter scheme on warm season convection-allowing ensemble forecasts[J]. Mon Wea Rev, 144(5): 1887-1908. DOI:10.1175/MWR-D-15-0092.1
|
Epstein E S, 1969. Stochastic dynamic prediction[J]. Tellus, 21(6): 739-759. DOI:10.3402/tellusa.v21i6.10143
|
Frogner I L, Haakenstad H, Iversen T, 2006. Limited-area ensemble predictions at the Norwegian Meteorological Institute[J]. Quart J Roy Meteor Soc, 132(621): 2785-2808. DOI:10.1256/qj.04.178
|
Hersbach H, 2000. Decomposition of the continuous ranked probabi-lity score for ensemble prediction systems[J]. Wea Forecasting, 15(5): 559-570. DOI:10.1175/1520-0434(2000)015<0559:DOTCRP>2.0.CO;2
|
Houtekamer P L, Lefaivre L, Derome J, et al, 1996. A system simulation approach to ensemble prediction[J]. Mon Wea Rev, 124(6): 1225-1242. DOI:10.1175/1520-0493(1996)124<1225:ASSATE>2.0.CO;2
|
Krishnamurti T N, Kishtawal C M, LaRow T E, et al, 1999. Improved weather and seasonal climate forecasts from multimodel superensemble[J]. Science, 285(5433): 1548-1550. DOI:10.1126/science.285.5433.1548
|
Leith C E, 1974. Theoretical skill of Monte Carlo forecasts[J]. Mon Wea Rev, 102(6): 409-418. DOI:10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2
|
Li X L, Charron M, Spacek L, et al, 2008. A regional ensemble prediction system based on moist targeted singular vectors and stochastic parameter perturbations[J]. Mon Wea Rev, 136(2): 443-462. DOI:10.1175/2007MWR2109.1
|
Lin J W B, Neelin J D, 2000. Influence of a stochastic moist convective parameterization on tropical climate variability[J]. Geophys Res Lett, 27(22): 3691-3694. DOI:10.1029/2000GL011964
|
Marsigli C, Boccanera F, Montani A, et al, 2005. The COSMO-LEPS mesoscale ensemble system:validation of the methodology and verification[J]. Nonlin Processes Geophys, 12(4): 527-536. DOI:10.5194/npg-12-527-2005
|
Molteni F, Buizza R, Palmer T N, et al, 1996. The ECMWF ensemble prediction system:methodology and validation[J]. Quart J Roy Meteor Soc, 122(529): 73-119. DOI:10.1002/(ISSN)1477-870X
|
Posselt D J, Vukicevic T, 2010. Robust characterization of model physics uncertainty for simulations of deep moist convection[J]. Mon Wea Rev, 138(5): 1513-1535. DOI:10.1175/2009MWR3094.1
|
Shutts G, 2005. A kinetic energy backscatter algorithm for use in ensemble prediction systems[J]. Quart J Roy Meteor Soc, 131(612): 3079-3102. DOI:10.1256/qj.04.106
|
Sindic-Rancic G, Toth Z, Kalnay E, 1998.Storm scale ensemble experiments with the ARPS model preliminary results[C]//Proceedings of the 12th Conference on Numerical Weather Prediction.Phoenix, Arizona: American Meteorological Society: 279-280.
|
Stensrud D J, Bao J W, Warner T T, 2000. Using initial condition and model physics perturbations in short-range ensemble simulations of mesoscale convective systems[J]. Mon Wea Rev, 128(7): 2077-2107. DOI:10.1175/1520-0493(2000)128<2077:UICAMP>2.0.CO;2
|
Stensrud D J, Fritsch J M, 1994. Mesoscale convective systems in weakly forced large-scale environments.Part Ⅱ:Generation of a mesoscale initial condition[J]. Mon Wea Rev, 122(9): 2068-2083. DOI:10.1175/1520-0493(1994)122<2068:MCSIWF>2.0.CO;2
|
Toth Z, Kalnay E, 1993. Ensemble forecasting at NMC:The generation of perturbations[J]. Bull Amer Meteor Soc, 74(12): 2317-2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2
|
Toth Z, Kalnay E, 1997. Ensemble forecasting at NCEP and the breeding method[J]. Mon Wea Rev, 125(12): 3297-3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2
|
Vie B, Nuissier O, Ducrocq V, 2011. Cloud-resolving ensemble simulations of Mediterranean heavy precipitating events:uncertainty on initial conditions and lateral boundary conditions[J]. Mon Wea Rev, 139(2): 403-423. DOI:10.1175/2010MWR3487.1
|
Wang Y, Bellus M, Wittmann C, et al, 2011. The Central Euro-pean limited-area ensemble forecasting system:ALADIN-LAEF[J]. Quart J Roy Meteor Soc, 137(655): 483-502. DOI:10.1002/qj.v137.655
|
Zhi X F, Qi H X, Bai Y Q, et al, 2012. A comparison of three kinds of multimodel ensemble forecast techniques based on the TIGGE data[J]. Acta Meteor Sinica, 26(1): 41-51. DOI:10.1007/s13351-012-0104-5
|
 2019, Vol. 45
2019, Vol. 45 