引言

中国幅员辽阔，丰富的风资源主要分布在地形复杂的北部山区和地形平坦的沿海地区，这些资源丰富的区域在早期的风电场建设中已经进行了大规模开发。随着风能利用技术的进步，新型高轮毂、长叶片的风力机具有启动风速小、风能利用率高的特点，使原本不具有开发价值的中国东南部低风速地区的风能资源也具有了开发价值。在风电场选址时普遍采用计算流体力学(CFD)软件进行复杂地形风能资源评估，为风机的合理排布提供依据。由于不同的垂直风速廓线输入导致的CFD计算结果差异很大，怎样确定不同大气稳定度条件下的垂直风廓线及其相应的湍流通量参数，是进行风电场风能资源CFD数值模拟的关键问题，因此研究不同下垫面、不同大气稳定度下的近地层风切变指数变得尤为重要。

19世纪60和70年代美国在平原地区开展了Kansas和Minnesota试验(Kaimal and Wyngaard, 1990)，使用32 m观测塔、系留气球和三维声学风速仪，在此试验结果基础上，得到了至今还被广泛应用的近地层风速廓线关系(Businger et al，1971)。随后的一些研究并未在近地层风速廓线理论上有所突破，多注重于实践应用。Dimitrov et al(2015)利用两个观测站60~200 m高度的多年的高频风速观测数据，验证了风切变预测可以用于风机设计时的风载荷同化，并且提出了一种适用于平坦地形的风切变模型。我国早期对风切变的研究主要是在大气扩散方面，自20世纪80年代以来开展了几次大规模的大气边界层观测试验，结合国外的一些经验，得出了制定地方大气污染物排放标准的技术方法：用Pasquill稳定法分类法将大气稳定度分为强不稳定、不稳定、弱不稳定、中性、较稳定和稳定六个等级，并给出了各种稳定度条件下的风切变指数值，为推算城市和乡村两种平坦地形下垫面的高层风速提供了参考。近年来，随着风电行业的发展，国世友等(2008)利用1999年1、4、7、10月木兰县蒙古山风电厂的逐时梯度风观测资料，考虑了不同的大气稳定度，选用风廓线幂指数律公式对风机高度(40、50 m)月平均风速和月极端风速进行了模拟，模拟值与观测值相当；刘敏等(2010)利用黄冈龙感湖、大悟仙居顶和钟祥华山观70 m测风塔1年的完整测风资料，在风廓线幂指数律公式基础上用最小二乘法拟合、线性分析等，对不同地形条件下风速切变指数的日变化、季节变化、年变化以及不同时段的变化特征进行了分析；李雁等(2012)用中国风能资源专业观测网2009年5—10月的梯度风观测数据和风廓线指数律，分析了全国近地层风切变特征；龚强等(2015)利用辽宁省26座测风塔的梯度风观测数据，研究了辽宁省近地层风切变特征；张双益和胡非(2017)使用激光雷达在吉林某风电场的观测数据，研究了风切变的日变化规律，大的风切变提升了风电机组的功率，减小了输出功率的离散性，降低了风-电转化过程中的不确定性。除此之外，张文龙等(2014)、郑淋淋和孙建华(2016)和张建军等(2016)分别研究了风切变对雷暴新生地点、中尺度对流系统强度和组织结构、飑线组织化过程的影响。

前人的研究取得了一定的成果，但是结论的普适性还有待进一步探讨。为了满足当前我国低风速风能资源开发和大型风电机组设计对进一步认识近地层风特性的需求，本文采用国家气候中心2009—2011年内蒙古锡林浩特市、河北黄骅市、江西湖口县和星子县的100 m铁塔大气湍流观测试验数据，分析不同下垫面、不同稳定度条件下的近地层风切变指数的变化情况，并与2016—2017年荷兰Cabauw大气研究试验场的213 m测风塔观测数据(www.cesar-database.nl)进行对比研究，为低风速风能资源开发的可行性研究、风机的适用性、风机设计、风机的运行维护等提供参考。

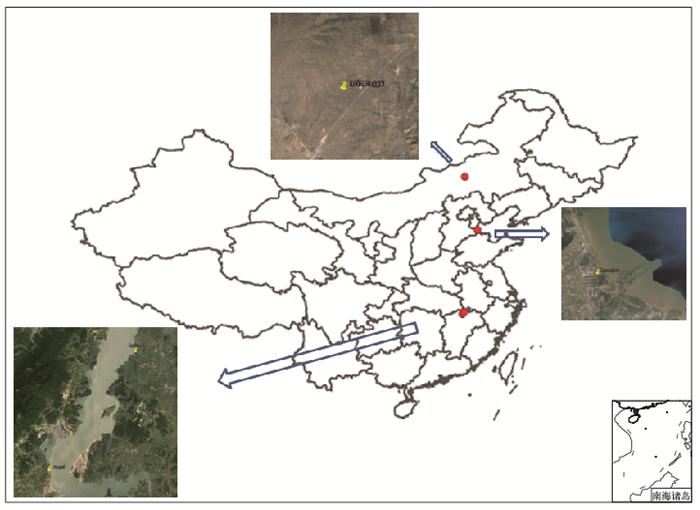
1 观测场地及资料处理 1.1 观测场地特点与观测仪器

2009—2011年期间，在全国风能资源详查项目的支持下，国家气候中心分别在内蒙古锡林浩特市、河北黄骅市、江西鄱阳湖地区进行了为期1年以上的近地层大气湍流观测试验。图 1为4个100 m测风塔位置(圆点)及其周边地形(方图)。内蒙古锡林浩特测风塔(44.12°N、116.30°E)周边地形高度变化平缓，海拔高度整体在1100 m以上。锡林浩特测风塔高100 m，所处位置海拔高度1159 m，其西部和西北部地势稍高一点，约有3°~6°的缓坡。下垫面为草原，夏季草高可达30~40 cm，覆盖率约70%~80%，冬季有高度5 cm左右的枯草。河北黄骅测风塔(38.33°N、117.67°E)周边地形高度变化平缓，NNE—SSN方向是渤海，其他方向为农田和居民区，测风塔距离最近的海岸线约1500 m，下垫面为养虾池，一年四季变化不大。江西两座测风塔，北边的是湖口测风塔(29.60°N、116.20°E)，其西侧距离鄱阳湖仅100 m，南边的是星子测风塔(29.37°N、116.01°E)，其东侧距离鄱阳湖大约500 m，两座测风塔的下垫面几乎一致，均为复杂山地，地面常年覆盖有低矮的植被。依据上述特点，本文用锡林浩特观测场代表内陆简单地形；黄骅观测场代表沿海平坦地形；鄱阳湖观测场代表内陆复杂地形。

本文使用的资料时段为锡林浩特2009年5月至2010年4月、黄骅2009年9月至2010年8月、湖口2011年1—12月和星子2010年11月至2011年10月，观测仪器相同，观测包括平均量梯度观测和湍流通量梯度观测。风速、温度和湿度的平均量观测仪器均采用江苏省无线电科学研究所生产的ZQZ-TF风速风向传感器和空气温度传感器，观测高度分别为10、30、50、70和100 m。10 m高度的湍流通量观测采用美国Campbell公司生产的CSAT3三维超声风温仪，声程为120 mm，换能器直径为6.4 mm，最大采样频率为60 Hz，量程为30 m·s^-1，本文三维超声风温仪采样频率为20 Hz。详细情况见表 1。

凯撒天文台位于荷兰的西部(51.971°N、4.927°E)，在城市平均海平面的0.7 m以下。西北偏西方向距离北海超过50 km的，测风塔周边是开阔牧场。Cesar站点用于大气中的长期变化趋势监测、大气和陆地表面过程的气候建模研究以及航天观测的验证。本文使用的资料时段为2016年4月至2017年3月观测的10 min的数据，气象要素包括风速、风向、湿度、气压、摩擦速度、潜热通量等，观测高度分别为10、20、40、80、140和200 m。

1.2 资料处理 1.2.1 基本质量控制

考虑到受仪器故障、检修或者天气因素以及供电等的影响会出现数据缺测和异常的情况，本文首先对观测资料进行了如下质量控制：

(1) 剔除水平风速±20 m·s^-1，垂直风速±10 m·s^-1，温度±50℃以外不符合物理常识的数据和不符合一般气候统计特征的数据。

(2) 剔除大于5倍方差的数据。

(3) 剔除由于传感器上的水汽凝结等原因导致的数据接收系统和数据传输系统产生的一些随机脉冲。将|X_i+2-X_i|>5σ的值视为随机脉冲进行剔除，其中X为时间序列，σ为方差。

(4) 剔除风速小于1 m·s^-1的静风数据。

1.2.2 旋转坐标

为了分析计算方便，将坐标系的x轴旋转到主导风向，使y方向的平均速度v为0，按照右手螺旋法则建立坐标系，旋转时用湍流梯度观测得到的瞬时u，v，w三个方向的风速乘以旋转矩阵，见式(1)，其中u，v分别为u，v的平均值，旋转后x方向的风速为u₁，y方向的风速为v₁，其满足$\overline {{v_1}} = 0$，z方向的风速为w₁。

$ \begin{array}{l} \left( {\begin{array}{*{20}{c}} u&v&w \end{array}} \right)\left[ {\begin{array}{*{20}{c}} {\frac{{\overline u }}{{\sqrt {{{\overline u }^2} + {{\overline v }^2}} }}}&{\frac{{ - \overline v }}{{\sqrt {{{\overline u }^2} + {{\overline v }^2}} }}}&0\\ {\frac{{\overline v }}{{\sqrt {{{\overline u }^2} + {{\overline v }^2}} }}}&{\frac{{\overline u }}{{\sqrt {{{\overline u }^2} + {{\overline v }^2}} }}}&0\\ 0&0&1 \end{array}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {\left( {{u_1}} \right)}&{\left( {{v_1}} \right)}&{\left( {{w_1}} \right)} \end{array} \end{array} $

(1)

为了消除仪器安装不水平导致的误差，可以通过坐标旋转使平均垂直速度w为0。用式(1)中得到的u₁，v₁，w₁三个方向的风速乘以旋转矩阵，见式(2)，旋转后x方向的风速为u₂，y方向的风速v₂，其满足$\overline {{v_2}} = 0$，z方向的风速为w₂，其满足$\overline {{w_2}} = 0$。

$ \begin{array}{l} \left( {\begin{array}{*{20}{c}} {{u_1}}&{{v_1}}&{{w_1}} \end{array}} \right)\left[ {\begin{array}{*{20}{c}} {\frac{{\overline u }}{{\sqrt {{{\overline u }^2} + {{\overline w }^2}} }}}&0&{\frac{{ - \overline w }}{{\sqrt {{{\overline u }^2} + {{\overline w }^2}} }}}\\ 0&1&0\\ {\frac{{\overline w }}{{\sqrt {{{\overline u }^2} + {{\overline w }^2}} }}}&0&{\frac{{\overline u }}{{\sqrt {{{\overline u }^2} + {{\overline w }^2}} }}} \end{array}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {\left( {{u_2}} \right)}&{\left( {{v_2}} \right)}&{\left( {{w_2}} \right)} \end{array} \end{array} $

(2)

2 近地层大气稳定度日变化特征

大气稳定度是与风切变相关一个要素，经常用于研究不同稳定度条件下风切变对风力机载荷影响。一直以来，工程上都只计算中性大气层结下的风廓线，这是因为在风能发展的初始阶段，为了开发丰富的风资源，必须寻找大风区，而大风区相应的中性大气层结比例较高，为了计算简便，节约计算时间和成本，通常假设大气是中性状态进行计算。随着风能利用技术的进步，使原本不具有开发价值的中国东南部低风速地区的风能资源也具有了开发价值，人们越来越意识到在条件许可的情况下，必须对不同稳定度条件分别进行精细化计算(郭凤霞等，2010；齐冰等，2012；金莉莉等，2016)。

根据Monin and Obukhov(1954)近地层相似理论，

$ 长度尺度:L = - \frac{{u_*^3}}{{k\frac{g}{T}\overline {w'T'} }} $

(3)

$ 速度尺度:{u_{\rm{*}}}{\rm{ = }}{\left( {{{\overline {u'w'} }^2} + {{\overline {v'w'} }^2}} \right)^{\frac{1}{4}}} $

(4)

$ 温度尺度:{T_*} = - \frac{{\overline {w'T'} }}{{{u_*}}} $

(5)

式中，速度尺度(u_*)即摩擦速度；长度尺度即Monin-Obukhov长度L(以下简称L)；u′，v′，w′和T′分别为三维风速脉动和温度脉动；k是Karman常数(取0.4)；g是重力加速度；T为平均温度；z是观测高度。

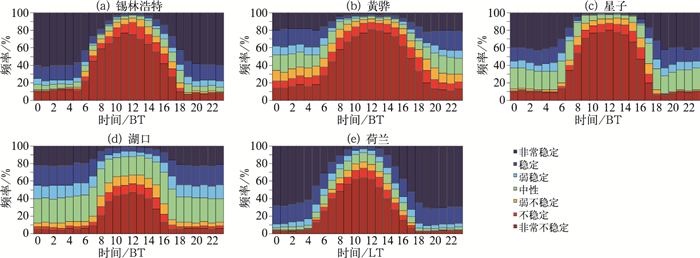
表 2为观测试验期间采用上述公式计算得到的锡林浩特、黄骅、星子、湖口和荷兰10 m高度1年的L值的分布情况，其中稳定度分类参照Gryning et al(2007)和Peña(2009)等的研究, 这是由于国内对于大气稳定分类，一般参考大气污染物排放标准(国家技术监督局和国家环境保护局, 1992)中的Pasquill稳定度分类法，该标准的观测场地为平坦开阔地形，而风机设立的位置常常在复杂地形，且欧洲风能在世界上处于领先地位，故本文采用欧洲的分类标准。可以看出，5个测风塔所处位置的大气稳定度的变化差异很大，锡林浩特非常不稳定和非常稳定层结出现的概率都在30%以上，稳定层结占12%，其余各稳定度出现频率相当；黄骅非常不稳定层结出现概率最高，为41%，其次是非常稳定、稳定和中性层结，都在10%以上，其余各稳定度出现频率相差不大；星子非常不稳定、中性和非常稳定层结出现的概率较高，都在20%以上，其次是稳定层结，而不稳定、弱不稳定、弱稳定层结出现概率相对较低；湖口中性层结概率最高，达到了30%，且稳定层结所占比例大于不稳定层结；荷兰非常不稳定层结出现的概率达到了40%，稳定层结概率占16%，非常不稳定层结概率占23%，其余各稳定度出现频率相当。图 2为不同稳定度分布随时间的变化，一般而言，白天尤其是午间，由于太阳辐射强，地面升温快，大气运动剧烈，不稳定层结比例增加；而在夜间，稳定层结所占比例较大。锡林浩特属于内陆缓坡下垫面，受动力和热力作用的影响较小，所以基本符合经典相似理论描述的大气稳定度的日变化规律。黄骅地势虽然平坦，距海岸线1.5 km，会受到局地海陆环流的作用，陆地上的大气与海洋上的大气交换使得夜间大气层结就没有锡林浩特那么稳定。星子所处地形为复杂的山地，距离鄱阳湖水面水平距离约500 m，地形的动力作用和局地的湖陆环流都会对测风塔观测有影响，所以夜间中性大气层结出现的比例相对较多；湖口地形比星子简单，且距离鄱阳湖更近，大约100 m，局地的湖陆环流对测风塔影响更大，中性大气所占比例最多。荷兰与锡林浩特较为接近，属于内陆平坦地形，受动力和热力作用的影响小，所以夜间稳定层结比锡林浩特有所增加。

3 近地层风切变指数特征

风切变指数是用来描述近地层风速的垂直分布的，它主要取决于下垫面特征和大气层结状态。目前的风机都在往高塔架、长叶片的方向发展，上下层风切变过大，容易使叶片受力不均，塔架的负荷增加，会减短风机寿命。另外，在使用计算流体力学软件模拟风场运动的时候，也需要设定风速垂直廓线作为初始边界条件进行计算。而根据GB/T 18451.1-2012(中华人民共和国国家质量监督检验检疫总局和中国国家标准化管理委员会，2012)，在风机设计时，为了用参考风速推算轮毂高度的风速，假设风切变指数为0.2，是否能满足我国的复杂情况？因此研究不同下垫面、不同稳定度下的风切变指数十分重要。

风速垂直廓线的幂律公式为：

$ {v_2} = {v_1}{\left( {\frac{{{z_2}}}{{{z_1}}}} \right)^\alpha } $

(6)

式中，α是风切变指数，v₂是高度z₂的风速，v₁是高度z₁的风速。

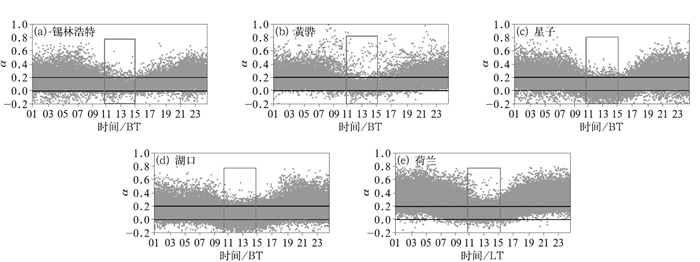
图 3是整体风切变指数α随时间的变化图。图上横坐标是一天24 h，纵坐标是根据10~100 m风速拟合的整体风切变指数α值。可以看出，在白天尤其是午间的时候，由于太阳辐射强，地面升温快，大气上下层混合均匀，锡林浩特、黄骅、星子、湖口和荷兰的整体风切变指数α出现大值的概率低；在夜间大气层结稳定的状态下，整体风切变指数α出现大值的概率大，且α>0.2存在一定比例。

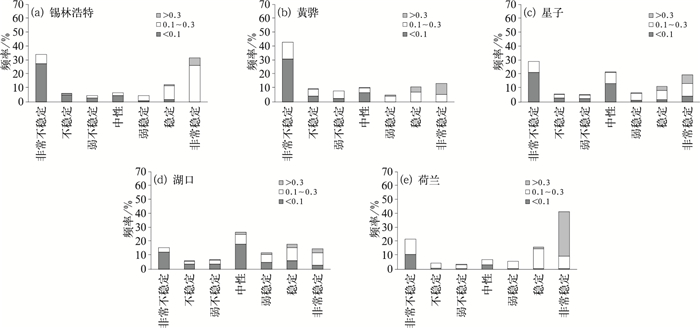
图 4是不同稳定度下整体风切变指数α的频率分布图。图中横坐标是大气稳定度，从左到右依次是非常不稳定、不稳定、弱不稳定、中性、弱稳定、稳定和非常稳定；纵坐标是10~100 m风速拟合的整体风切变指数α的频率。可以看出，锡林浩特整体风切变指数α在非常不稳定和非常稳定状态下的频率最高；黄骅整体风切变指数α在非常不稳定状态的频率最高，其他各稳定度下的频率相当；星子整体风切变指数α在非常不稳定、中性、稳定、非常稳定状态下的频率较高；湖口整体风切变指数α在中性层结时频率最高，总体上稳定层结所占比例高于不稳定层结；荷兰整体风切变指数α在非常不稳定和非常稳定状态下的频率最高。锡林浩特属于内陆丘陵平坦地形，整体风切变指数α>0.3的比例为7%，α>0.5的比例为0.6%，大多出现在非常稳定的状态下，整体风切变指数α相对较小；黄骅沿海地区整体风切变指数α>0.3的概率较高为15%，α>0.5的比例为2%，这是因为黄骅地形平坦，大气层结越稳定，整体风切变指数α越容易出现大值；星子和湖口虽然都处于内陆湖沿岸的山地，但星子地形更为复杂，在局地地形作用下，过山气流加速，大于0.3的整体风切变指数频率为12%，α>0.5的比例为1.3%，而湖口受地形作用小，受局地湖陆环流影响更大，因此大于0.3的整体风切变指数值出现频率少于星子为10%，α>0.5的比例为1.2%；荷兰地势最为平坦，在非常稳定条件下出现整体风切变指数α>0.3的概率最大，α>0.5的比例能达到3.9%。说明研究不同下垫面、不同稳定度下的风切变指数α是很有必要的。

整体风切变指数α < 0.3时，也会发生局部切变远大于0.3的情况。表 3是挑选出10~100 m整体风切变指数α < 0.3的数据，分别统计的相邻两个高度层的分层风切变指数α>0.3的频率百分比。锡林浩特是平坦丘陵地形，分层风切变指数α>0.4的频率为2.95%；黄骅比锡林浩特地形平坦，分层风切变指数α>0.4的频率高于锡林浩特；星子的地形复杂，位于庐山大地形的东南侧，且位于鄱阳湖边，同时受到局地动力产生的气流加速和热对流作用，分层风切变指数α>0.4的频率高达10.4%；湖口也在鄱阳湖边，但距离水面更近，四周几乎被水环绕，受局地热交换影响较大，地形作用相对较小，分层风切变指数α>0.4的频率为3.37%；荷兰地形与锡林浩特相似，但更为平坦，分层风切变指数α>0.4的频率为3.22%。如果在星子这样的复杂地形建设风电场，需要注意选择合适的风机。

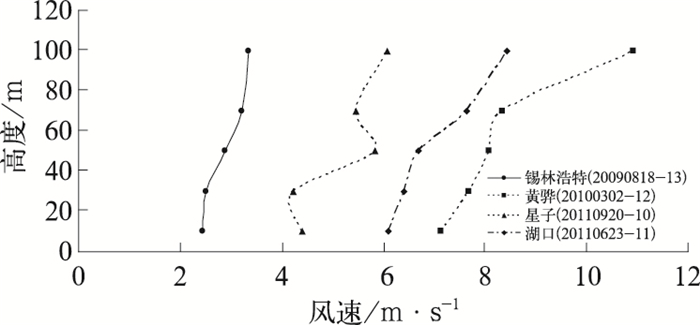
图 5是在4个100 m塔的观测数据中挑选出典型的10~100 m整体风切变指数α < 0.3但分层风切变指数α>0.3的个例。图中锡林浩特10~30 m分层风切变指数是0.02，30~50 m分层风切变指数是0.27，50~70 m分层风切变指数是0.33，70~100 m分层风切变指数是0.12；黄骅10~30 m分层风切变指数是0.07，30~50 m分层风切变指数是0.1，50~70 m分层风切变指数是0.1，70~100 m分层风切变指数是0.75；星子10~30 m分层风切变指数是-0.04，30~50 m分层风切变指数是0.64，50~70 m分层风切变指数是-0.1，70~100 m分层风切变指数是0.31；湖口10~30 m分层风切变指数是0.04，30~50 m分层风切变指数是0.09，50~70 m分层风切变指数是0.39，70~100 m分层风切变指数是0.28。也就是说即使整体风切变指数α < 0.3，分层风切变指数α会有远大于0.3的情况，说明在风机设计时仅考虑整体风切变指数是不够的，分层风切变指数过大仍会对风机造成一定影响。此外也表明，在复杂地形条件下，风速垂直变化是无法用一个单调函数来描述的，最好能够分层考虑。

4 风切变指数分类的应用前景

在风机设计标准GB/T 18451.1-2012中，为了用参考风速推算轮毂高度的风速，假设风切变指数为0.2。除了风力发电机的抗风设计与架设高度，大气污染物扩散能力、桥梁、高楼、电视塔等高大建筑的风压和风振计算分析均与近地层垂直风廓线密切相关。目前的大部分观测达不到90 m，而风机的轮毂高度能高达140 m，假设有70 m高度的观测风速，在不同下垫面、不同大气稳定度条件下，选用不同的风切变指数推算100 m高度的风速，误差究竟有多大呢？

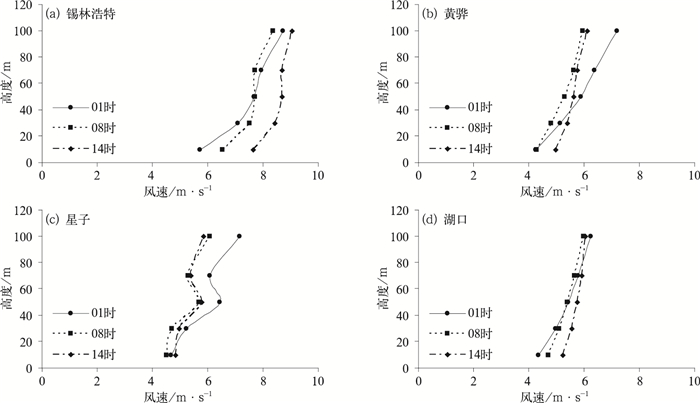
图 6是4个测风塔在01、08、14时的年平均风速随高度变化情况，内蒙古的风速垂直廓线在10~70 m基本能用一个单调函数描述，但是70~100 m有风加速；黄骅地形平坦，基本满足风切变指数的日变化规律：夜间切变指数小，白天切变指数大；星子是复杂的山地，风速垂直廓线变化多端，难以用单调函数描述；湖口地形相对简单，且距离水面很近，受局地环流的影响，其风速垂直廓线的切变指数很小。

表 4是使用10 m高度的各稳定度下的平均风速推算的100 m高度风速与实测风速对比，计算时选取了不同的风切变指数α，第一种方法是按照风机设计标准中假设风切变指数α为0.2，第二种方法是根据10~70 m的观测数据拟合得出的不同稳定度条件下的风切变指数α，可以看出不管在哪个地区，根据10~70 m的观测数据拟合得出的不同稳定度条件下的风切变指数α推算的100 m高度风速与实测风速都更为接近，比直接用0.2推算更为合理。

5 结论

本文根据复杂地形微尺度数值模拟的需要，通过分析内蒙古草原、河北沿海和江西鄱阳湖大气湍流梯度观测试验数据，研究了不同稳定度条件下的近地层大气风速垂直分布特征，主要结论如下：

(1) 内陆简单地形基本符合经典相似理论描述的大气稳定度的日变化规律；沿海平坦地形会受到局地海陆环流的作用，陆地上的大气与海洋上的大气交换使得夜间大气稳定层结出现频率相对较低；内陆复杂地形受到局地地形的动力作用和局地的湖陆环流作用，夜间中性大气层结出现的比例相对较多。

(2) 内陆简单地形整体风切变指数α>0.3的情况出现在稳定和非常稳定的状态下，整体风切变指数α相对较小；沿海平坦地形大气层结越稳定，整体风切变指数α的高值出现频率越高；星子和湖口虽然都处于内陆湖沿岸的山地，但星子地形更为复杂，在局地地形作用下，过山气流加速，大于0.3的整体风切变指数出现频率高，而湖口受局地湖陆环流影响更大，因此大于0.3的整体风切变指数值出现频率略低。

(3) 内陆简单地形相邻两层之间出现风切变指数>0.4的频率为2.95%；沿海平坦地形分层风切变指数>0.4的频率略高，为4.2%；星子的地形复杂，位于庐山大地形的东南侧，且位于鄱阳湖边，同时受到动力和热力作用，分层风切变指数α>0.4的频率高达10.04%；湖口也在鄱阳湖边，但受热力作用影响更大，分层风切变指数α>0.4的频率为3.37%。对于星子这样的复杂地形，在风机设计和风电场风机选型时仅考虑叶轮直径范围内整体风切变指数是不够的，也要考虑到局部风切变大的因素。

(4) 按照风机设计标准中假设风切变指数α为0.2一般会过高地估计轮毂高度的风速，说明现有的标准不能满足我国的需求，若有条件，尤其是在复杂地形下，还是要增加不同高度的风、温观测，求出实际不同稳定度下的风切变指数进行推算风廓线的变化情况，进一步精确计算结果，为低风速风能资源开发的可行性研究、风机的适用性、风机设计、风机的运行维护等提供参考。