引言

600 hPa以下出现的窄而强的气流称为低空急流(朱乾根, 2007)。低空急流与强对流天气的形成有着密切的关系，它可以为强降水输送充足的水汽并提供动力条件(孙淑清, 1979)，是预报强对流天气的重要依据。因此，自20世纪30年代低空急流这一概念被提出起便受到人们的广泛关注。王东阡等(2016)使用温度资料和再分析资料分析指出了低空急流对中国梅雨期雨量和雨期时长的影响。冯文等(2015)指出了低空急流对中国海南后汛期特大暴雨的促进作用。李进等(2015)利用ECMWF的全球再分析资料指出了高低空急流耦合对暴雨发生的重要作用。Higgins et al(1997)和Weaver and Nigam(2008)分别利用高分辨率再分析资料研究了美国大平原地区低空急流对夏季降水和水汽输送的作用。Qian et al(2004)和Zhao(2012)也分别利用中尺度模式研究了中国梅雨期强降水发生过程中潜热释放和低空急流的相互作用以及局地地形对低空急流的调制作用。

气象业务中，低空急流通常借助MICAPS平台人机交互绘制，效率低且易受主观因素影响。对此，金宏忆等(2008)从多普勒雷达径向速度图入手尝试进行低空急流的自动识别；王毅等(2013)基于ECMWF模式细网格风场资料，使用归并算法提取急流轴并进行多项式拟合，将低空急流自动识别出来。基于以上方法识别出的低空急流轴或者受雷达探测范围所限，仅能识别出低空急流的小局部，或者仅适于方向平缓的急流类型。

中国境内的低空急流主要以偏南向急流为主，存在方向缓变(或不变)及方向急变两种类型，通常会延绵上千甚至几千千米。基于探空站风场信息(850 hPa)，本文提出一种能适应不同类型低空急流自动识别算法。该算法首先利用传递闭包聚类法形成满足风向条件的探空站聚类，每个子聚类与一个急流的全部或局部相关联。然后在每个子类中提取急流轴关键点，归纳出局部急流区域连接规则，给出全部关键点的平滑急流轴自动绘制方法。

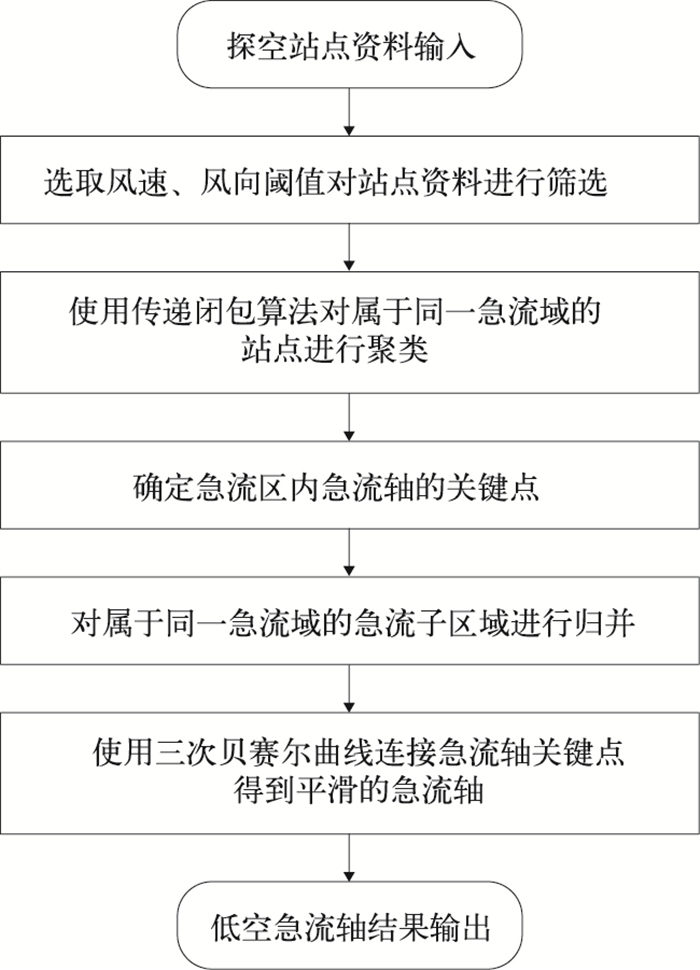
1 低空急流自动识别算法

低空急流的分布特点一定会得到多个测站的数据支持，这些测站点虽非均匀布局，但它们覆盖的区域形同急流分布，同时，各站数据受到风速和风向的一致性或相似性制约。本文提出的从点(各测站)到面(急流域)、再到线(急流轴)的低空急流自动识别算法流程主要思想如图 1所示。

1.1 探空站数据筛选

面对全部境内探空站，仅有一部分探空站能联合给出低空急流的可用信息，它们之间满足以下约束条件：

(1) 在850 hPa等压面上，连续两个以上测站风速超过12 m·s^-1。

(2) 中国境内的低空急流主要以偏南风急流为主。

用满足以上条件的探空站勾勒出大风区，并在大风区的几何中心分析低空急流轴。为此，设探空站筛选条件为：

(风速≥α₁)∪(风向=南风±α₂)

为了更加完整地体现水汽输送路径，对南部沿海地区将阈值α₁略微降低到10 m·s^-1，其余设为12 m·s^-1；另外设α₂≤90°。

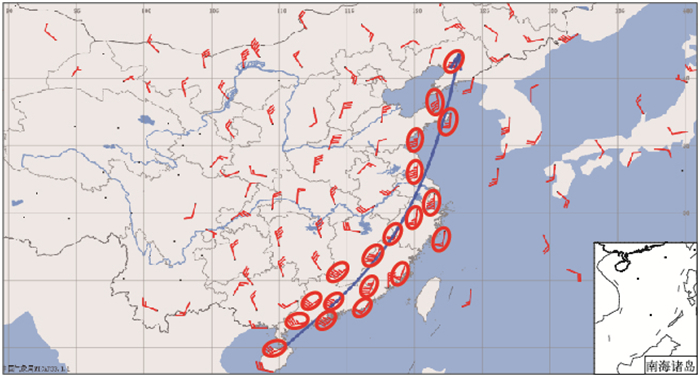
1.2 急流区聚类

急流区是狭长的带状，我们称同属这样的带状区域的探空站为一个聚类。例如在图 2中西南方向的急流轴周边，有19个探空站(图 2中用椭圆标记的站点)位于由此急流所代表的带状区域内。不难分析出，在这19个探空站中，相邻探空站风向相近，而相距较远(例如区域两端)处探空站风向已相差甚远。因此，最常用的K均值聚类法没有能力将它们聚成一类；再者，在一个较大的范围内，是否存在低空急流，存在几条低空急流是未知的，这就使得很多以聚类数为先验的聚类算法失去了前提条件。

传递闭包聚类的主要思想是基于两两样本间的相似性来决定某样本是否具有进入当前子类的资格(Rosen, 2006; 陈显强, 2004)。通过选择合适的相似性度量及其使用规则，一个样本属于哪一类，仅需计算该样本与其相邻样本的相似度，并被带入符合相似性度量阈值的相邻样本所属的一类。显然这种聚类思想符合急流区域内探空站间风向的渐变关系特点。

1.2.1 传递闭包聚类算法

经过筛选，得到满足风向、风速要求的探空站P₁, P₂, P₃, …, P_n。

定义P_i和P_j间的相似性度量θ(i, j)和D(i, j)。其中θ(i, j)表示P_i、P_j坐标连线与这两探空站风向平均值的角度差。D(i, j)表示P_i、P_j两探空站间的距离。

定义布尔关系矩阵R_n×n=[r_ij]_n×n，其中r_ij非0即1。

设布尔矩阵A_n×n=[a_ij]_n×n和布尔矩阵B_n×n=[b_ij]_n×n，定义这两个布尔矩阵的积运算为C_n×n=A_n×n×B_n×n=[c_ij]_n×n，其中c_ij=∨_k=1ⁿ(a_ik∧b_kj)。特别的，A_n×n与自身的布尔积称为二次布尔幂，记作A_n×n^[2]。

传递闭包聚类算法步骤如下：

步骤1：生成一个布尔矩阵R_n×n=[r_ij]_n×n。在P_i、P_j均为东南风或者均为西南风的前提下，对给定阈值δ和d，若θ(i, j)≤δ且D(i, j)≤d，则令r_ij=1；否则，令r_ij=0。

步骤2：对布尔矩阵R_n×n=[r_ij]_n×n执行p(p为整数，p≥2)次布尔幂运算得到R_n×n^[p]。若R_n×n^[p]为全1矩阵或R_n×n^[p]=R_n×n^[p-1]，聚类结束。否则令p→p+1，重复执行步骤2。

步骤3：分析R_n×n^[p]，若某一行中标记为1的元素大于两个，则认为该行中所有标记为1的探空站组成一个有效聚类，提取所有有效聚类，将其中风向为东南风的探空站聚类记作Ω_ek(k=1, 2, 3, …, m)，风向为西南风的探空站聚类记作Ω_wk(k=1, 2, 3, …, n)。

图 3为对2009年7月23日08时数据执行传递闭包聚类算法后得到的结果。其中，矩阵R的维度n=8，表明数据筛选后满足风向风速条件的探空站有8个，对这8个探空站生成的布尔矩阵进行3次布尔幂运算后变为全1矩阵，因此8个探空站构成一个聚类，即图 3b中用椭圆标记的站点。图中还给出了这个聚类区外包椭圆及其长轴。在此称聚类区外包椭圆的长轴为该区域的主方向，并称长轴明显大于短轴的情形为主方向显著。可以看出，经传递闭包得到的图 3聚类区域的主方向显著且与探空站风向趋于一致，这是相似性度量θ(i, j)和D(i, j)对探空站的距离约束以及探空站相对位置与风向之间约束的联合反应。

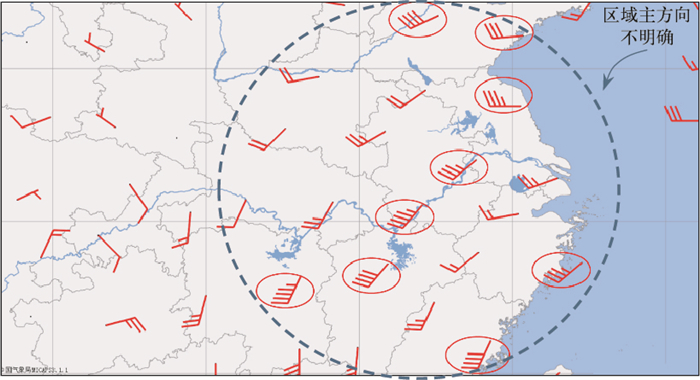
在聚类过程中为了尽可能找到支持急流的探空站，需要适当将阈值δ、d条件放宽，这可能会导致聚到一起的探空站区域主方向不十分显著的情形。例如对2009年7月20日08时数据进行聚类的结果(图 4)中，探空站风向均为西南方向，但9个探空站的外包椭圆趋于圆形，主方向不显著，这样会给之后准确定位急流轴带来困难。为此，对聚类结果再次执行传递闭包聚类算法。

1.2.2 二次传递闭包聚类算法

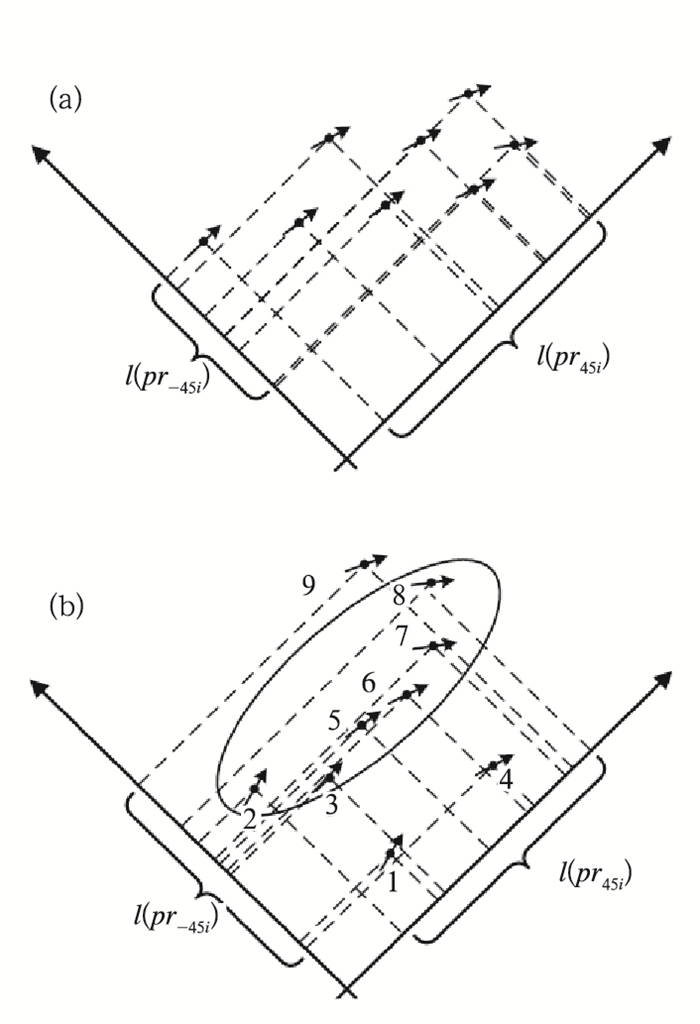
仅保留图 3b和图 4中需聚类处理的探空站得到图 5a和5b。将这些探空站分别在±45°方向上投影，不难发现，图 5a所示的聚类集较理想(探空站分布主方向显著且与风向趋于一致)，其l(pr_45i)=γ₁l(pr_-45i)且γ₁往往大于1.5；图 5b给出的聚类集不甚理想(探空站分布主方向不显著)，其l(pr_45i)≈l(pr_-45i)。设这种不理想聚类集中，实际存在着密集站点子集合(见图 5b椭圆内的站点)，由它们形成的子区域，其主方向与风向一致。从分布上看，这些密集站点之间关系较为紧密，而其他站点与这些站点之间的关系则较为松散，导致这一现象的原因在于进行首次传递闭包聚类时，所选择的相似性度量阈值δ和d较为宽松。为此，可以当l(pr_-45i)约等于甚至小于l(pr_45i)的情形出现之后，收紧阈值δ、d，对该局部区域进行再次传递闭包聚类，将首次聚类给出的大风区分解成若干个关系紧密的子域，并保留其中站点数最多、最能反映急流趋势的那个子域。

算法步骤如下：

步骤1：假设Ω_i为第i个聚类，P_ij(j=1, 2, 3, …, n)为Ω中的第j个探空站。P_ij在45°方向上投影长度记为pr_45ij，P_ij在-45°方向上投影长度记为pr_-45ij，则l(pr_45i)=max{pr_45ij-pr_45ik}，l(pr_-45i)=max{pr_-45ij-pr_-45ik}(j, k=1, 2, 3, …, n且j≠k)。并以此计算$\gamma {\rm{ = }}\frac{{l\left( {\mathit{p}{\mathit{r}_{{\rm{45}}\mathit{i}}}} \right)}}{{l\left( {\mathit{p}{\mathit{r}_{{\rm{ - 45}}\mathit{i}}}} \right)}}$

步骤2：给定γ₁=1.5。若Ω_i∈Ω_ek，当$\gamma > \frac{1}{{{\gamma _1}}}$时，执行步骤3，否则算法结束；若Ω_i∈Ω_wk，当γ<γ₁时，执行步骤3，否则算法结束。

步骤3：对于P_ij(j=1, 2, 3, …, n)∈Ω，给定新的阈值δ_new，重新进行传递闭包聚类，得到针对Ω_i的二次聚类结果Ω_i1, Ω_i2, Ω_i3, …, Ω_in。

步骤4：选择Ω_i1, Ω_i2, Ω_i3, …, Ω_in中站点数最多的子类代替原来的第Ω_i类。

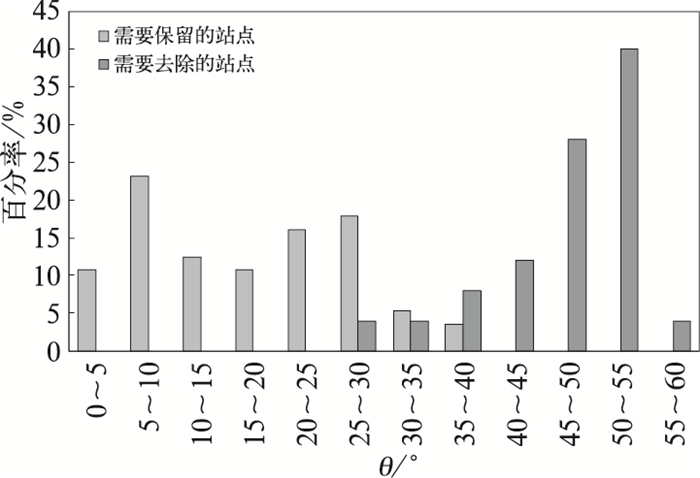
为确定二次传递闭包聚类时相似性度量θ的收紧程度，选用2009年3—8月全部数据执行首次传递闭包聚类算法，筛选出所有聚类区域主方向不显著的聚类结果，将其中的所有探空站进行“保留”和“去除”的人工标注。并计算“保留”类站点的θ和“去除”类站点的θ，形成θ的统计分布(图 6)。可以看出，“保留”类站点间的θ值主要分布在0°~30°，且分布较为均匀。而“去除”类站点间的θ值集中分布在40°~55°。所以用于二次聚类的θ的阈值δ_new可选在30°~40°。图 7a为对图 4的9个站点在δ_new =30°、d=600 km条件下进行二次传递闭包聚类的结果。对比图 4可以看出，图 7a中剔除了首次聚类中较为松散的8、9、1、4号站点，使二次聚类给出的探空站分布主方向与其风向趋于一致。从布尔矩阵R_9×9可以看出，因为阈值的收紧，切断了6号探空站与8、1号探空站的关系，继而剔除了9和4号探空站。

1.3 提取绘制急流轴的关键点

二次传递闭包聚类后，得到若干组沿风向呈带状分布的探空站点集合，急流轴应从它们中间穿过。由于探空站地理位置分布的不均匀性，不宜采用简单的取中法。下面给出一种根据站点数量及站点之间相对关系确定急流轴关键点的算法。算法步骤如下：

步骤1：假设Ω_i为第i个聚类，P_ij(j=1, 2, 3, …, n)∈Ω_i。若Ω_i∈Ω_ek，将P_ij按照pr_-45ij(j=1, 2, 3, …, n)由小到大进行排序；若Ω_i∈Ω_wk，将P_ij按照pr_45ij(j=1, 2, 3, …, n)由小到大排序。当n=2时执行步骤2，n=3时执行步骤3，否则执行步骤4。

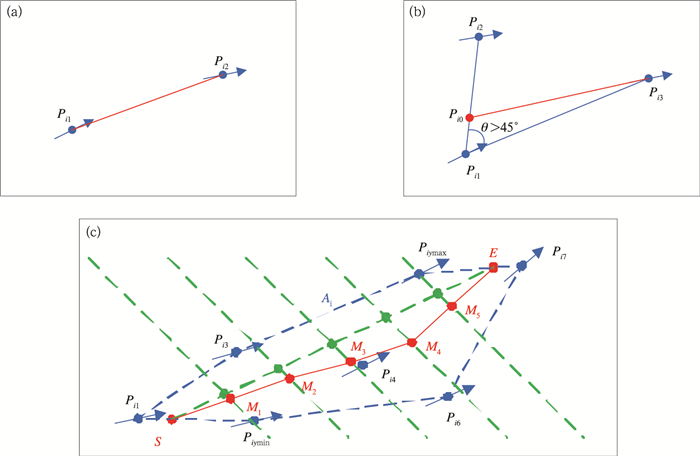
步骤2：直接将P_i1、P_i2作为第Ω_i类中轴的关键点，如图 8a所示。

步骤3：若P_i1P_i2与P_i1P_i3的夹角大于45°，则将P_i1、P_i2的加权中点P_i0与P_i3一起作为第Ω_i类中轴的关键点，如图 8b所示；若P_i1P_i3与P_i2P_i3的夹角大于45°，则将P_i2、P_i3的加权中点P_i4与P_i1一起作为第Ω_i类中轴的关键点；除此之外，则直接将P_i1、P_i3作为第Ω_i类中轴的关键点。

步骤4：

(1) 求取P_i1, P_i2, P_i3, …, P_in(n≥4)的凸包(Graham, 1972)，记作A_i。

(2) P_i1, P_i2, P_i3, …, P_in中纬度最大的站点记作P_iymax，纬度最小的站点记作P_iymin。取P_iymin与P_i1的加权中点S作为第Ω_i类中轴起始关键点；取P_iymax与P_in的加权中点E作为第Ω_i类中轴的终止关键点。

(3) 将线段SE五等分，等分点分别记为Q₁, Q₂, Q₃, Q₄。若Ω_i∈Ω_ek，则分别过Q_i(i=1, 2, 3, 4)做正北偏东45°的直线；若Ω_i∈Ω_wk，则分别过Q_i(i=1, 2, 3, 4)做正北偏西45°的直线。直线分别交A_i于Q_i1、Q_i2，记Q_i1、Q_i2的中点为M_i(i=1, 2, 3, 4)。

(4) 将S, M₁, M₂, M₃, M₄, E作为第Ω_i类中轴的关键点，如图 8c所示。算法结束。

按照以上步骤，分别找到Ω_ek(k=1, 2, 3, …, m)中每一子类的中轴L_ek(k=1, 2, 3, …, m)的关键点，及Ω_wk(k=1, 2, 3, …, n)中每一子类的中轴L_wk(k=1, 2, 3, …, n)的关键点。

1.4 急流轴关键点归并

行进过程中方向发生较大改变的低空急流下的探空站，一般会被传递闭包算法至少聚成两个子类(参见图 9)，因此需要将原本属于一条急流轴但又不属于一个聚类子集的关键点进行合并。

首先定义不同聚类子集的连接规则：设两个聚类子集区域中轴为L₁和L₂，记L₁中的最后一个关键点为L_1n，L₂中的第一个关键点为L₂₁。计算L_1n、L₂₁的距离d_l1n, l₂₁，若d_l1n, l₂₁≤δ，则认为L₁、L₂同属一个急流区，将L₁和L₂的关键点集合的并集作为新的关键点集合，并在连接处以l_1n、l₂₁的中点代替两点作平滑处理。若d_l1n, l₂₁>δ，则在沿L₁方向±15°、半径δ的范围内搜索是否存在满足本急流轴风向条件，但风速略小的探空站点。若存在，则将该站点作为关键点加入L₁，并按照上述连接规则判断并归并两关键点集，否则不进行关键点集的归并。

急流轴关键点归并算法步骤如下：

步骤1：取L_ei∈L_ek(k=1, 2, 3, …, m)，依次判断L_ei与L_wj∈L_wk(k=1, 2, 3, …, n)是否满足上述归并规则。若满足，则将L_ei与L_wj的关键点归并，记作L_k，并从L_ek中删除L_ei，从L_wk中删除L_wj。否则将L_ei记作L_k，并从L_ek中删除L_ei，对L_wk不作处理。执行此步骤直到各L_ek均为空集。

步骤2：若L_wk(k=1, 2, 3, …, n)为空集，则结束算法，L_k(k=1, 2, 3, …)即为所求；否则取L_wj∈L_wk(k=1, 2, 3, …, n)，依次判断L_wj与L_k是否满足上述连接规则，若满足，则将L_wj与L_k归并以代替之前的L_k，并从L_wk中删除L_wj。否则将L_wj记作新的L_k，并从L_wk中删除L_wj。进行此步骤直到各L_wk均为空集。L_k(k=1, 2, 3, …)即为所求。

1.5 急流轴平滑

经过以上步骤，得到低空急流轴L_k(k=1, 2, 3, …)的一系列关键点。为使低空急流轴展现为一条光滑的曲线，用三次贝塞尔曲线将L_k(k=1, 2, 3, …)中的关键点平滑地连接起来(王家润等, 2010)。

图 10给出了基于2009年7月20日08时数据的平滑急流轴。

2 算法应用

本算法基于Visual Studio 2015平台使用C++编程语言实现，输入数据为MICAPS第2类数据中的850 hPa探空站风场信息，输出为低空急流轴的经纬度坐标。在Intel i5-4590硬件平台下整个算法运行平均耗时0.0249 s。

使用2009年3月12日至8月27日及2012年5月31日至12月18日08—20时中的291组数据对算法的准确性和鲁棒性进行测试。并将测试结果交予气象专家核实，若识别结果与人工分析结果一致则定义为准确检出；若识别结果与人工分析结果不完全一致但自动识别结果能大致反映低空急流趋势，则定义为偏差；若自动识别存在低空急流但人工分析不存在低空急流，则认为空报；若人工分析存在低空急流但本算法并未识别出，则认为漏报。在上述291组数据中，有位于中国地区的低空急流139处，准确检测出132处，有偏差的为4处，漏报3处，空报0处，检出率达到97.84%，准确击中率为94.96%(表 1)。

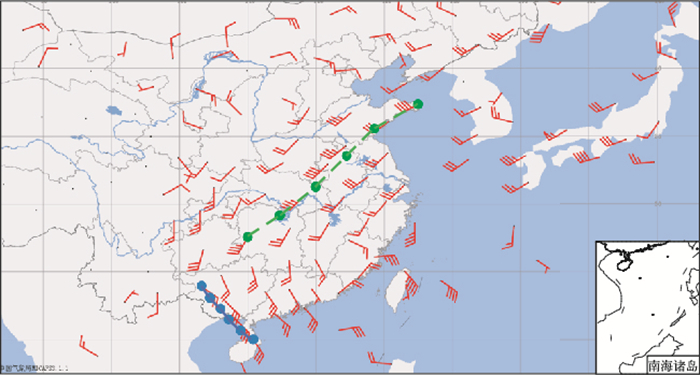
图 11给出了一组低空急流轴识别结果示例，其中图 11a为识别并绘制出的单一风向的低空急流轴，位置准确，形状自然。图 11b为风向发生改变的低空急流轴，位置准确，在连接处曲线平滑，没有明显连接痕迹。图 11c为4例低空急流识别发生偏差的典型代表，其特征为：一块区域中，同时存在风向临界于东南风与西南风之间的站点。这样会对传递闭包聚类时的风向划分带来影响。从而影响急流轴的起止位。造成以距离为度量的急流轴关键点归并算法失效，导致在同一区域内识别出多条急流轴。但此种情况并不会使识别出的急流轴过于偏离急流区域的中轴，识别出的多条急流轴仍能大致反映急流的形态和位置。图 11d为3例漏报的典型代表，其特征为：发生漏报的低空急流长度较短(由3个探空站组成)，且发生风向改变。造成漏报的原因为：对于风向发生改变的低空急流，本算法首先按不同风向进行聚类，再将其关键点进行归并。发生漏报的低空急流虽然总探空站数满足低空急流要求(大于2个探空站)，但按风向聚类时却由于属于每个风向的站点数过少而不满足条件，最终导致漏报。

3 结论与讨论

本文根据低空急流定义及其特点，首先，以相邻探空站位置分布与其风向的一致性关系为依据，对探空站进行传递闭包聚类分析，得到多个聚类子集。针对同属一个聚类子集但分布不均的探空站，提出探空站凸包法，得到基于这些探空站的一片区域，并对该区域求取满足风向约束的关键点。针对急流行进过程中可能产生的风向改变的情形，提出一种距离约束下的急流轴关键点归并算法，最后选用贝塞尔曲线模型实现基于关键点的低空急流的自动绘制。

经对291组数据检验，结果经人工核实，得出以下结论：

(1) 算法中的两次传递闭包聚类可以在最大程度上识别出急流完整路径的基础上，圈定急流的准确区域范围，达到较为完整和准确地反映水汽输送路径的目的。

(2) 算法同时适用于单一风向的低空急流和方向发生改变的低空急流的自动识别，算法鲁棒性强。

(3) 绘制出的急流轴均处于急流区域的中轴位置且表现为光滑的曲线，与手工绘制的结果相符。

(4) 在291组数据中，准确检出139例低空急流中的132例，准确击中率达到94.96%，未发现空报。

(5) 本算法使用C++语言实现，便于编译成库文件以提供给气象部门进行业务应用。同时本算法适用性较强，稍作改动亦可用于格点数据中的低空急流的识别。

本文的算法还存在一些缺陷，(1)当支持方向急转型急流的探空站过少时，会出现漏检。(2)当在一个区域内满足风向条件的探空站过于密集但同时存在两类风向子集时，可能出现急流轴关键点归并算法失效或在同一区域识别出多条急流轴的情况。这需要在更大规模样本的支持下，发现问题的规律，对本文方法进行改进和补充。