2. 国家卫星气象中心,北京 100081
2. National Satellite Meteorological Centre, Beijing 100081
向外长波辐射(outgoing longwave radiation,OLR)是地球大气系统在大气顶向外空辐射出去的热辐射通量,是地球大气系统能量平衡的参量之一,在气候模式中是一个重要的输出参量。从20世纪60年代气象卫星问世以来,对OLR的观测一直延续至今,各种仪器、各种反演方法被设计和研究出来用以从卫星获取对地球上不同地区的OLR观测(Wark et al,1962;Jacobowitz et al,1979;Gube,1982;Jacobowitz and Tighe, 1984;Green and Wielicke, 1997;Loeb et al,2001;吴晓和白文广,2017; 吴晓,2011),如搭载在NOAA、NIMBUS卫星上的ERB仪器,AQUA、TERRA卫星上的CERES仪器,均通过宽波段通道观测地球OLR,而NOAA的AVHRR仪器、GOES的VISSR、METEOSAT的SEVIRI和FY-2的VISSR、FY-3的VIRR等仪器均通过其窄波段的红外通道观测由反演模式估算得到区域或全球OLR。在种类繁多的各卫星OLR产品中,历史最长、应用最广的是NOAA系列卫星AVHRR仪器的全球OLR产品,其处理方法是经典的AVHRR窗区通道5亮温-通量等效辐射温度(TB5-TF)反演模式,Gruber(1997)通过辐射传输模拟和统计回归,建立了TB5-TF的回归关系,Ohring et al(1984)根据Nimbus-7卫星上宽波段通道的辐射率和窗区通道亮温匹配数据,又建立TB5-TF的经验关系式,这一经验模式NESDIS(National Environmental Satellite Data and Information Service)处理NOAA/AVHRR的OLR产品达40多年。而我国的FY-3极轨气象卫星,因其星载VIRR仪器与AVHRR近似,也采用了TB5-TF模型反演处理FY-3/VIRR的OLR产品(吴晓和鄢俊洁,2011),但无论NOAA/AVHRR还是FY-3/VIRR,其OLR产品与国际最先进的CERES仪器OLR观测产品相比,都存在-10 W·m-2的系统负偏差,NESDIS的原因在于模式建立过程中匹配数据源的定标处理有误,FY-3则是由于模式建立过程中辐射传输计算软件精度不够(吴晓,1998),吸收系数过于老化。鉴于这一原因,我们采用了美国最新逐线辐射传输模型计算软件(line-by-line radiative transfer model, LBLRTM),重新模拟大气廓线的大气顶光谱辐射率和OLR,基于模拟数据重新建立了FY-3A,3B,3C卫星VIRR仪器的OLR反演模式,以期解决VIRR OLR产品10 W·m-2负偏差的问题。本文就是关于新的FY-3B/VIRR OLR反演模式的建立及应用情况的详细介绍。
1 建立FY-3B/VIRR仪器OLR反演模式 1.1 红外辐射传输计算 1.1.1 LBLRTM软件及大气顶红外辐射传输计算方程LBLRTM是美国在21世纪初开发的软件,其融入了国际最新吸收带试验数据,光谱分辨率为0.01 cm-1,是继LOWTRAN和MORTRAN之后精度更高的辐射传输模型计算软件,其计算准确度达99.5%(Clough et al,2005),LBLRTM通过如下红外辐射传输方程计算大气顶的射出辐射率。
| $ \begin{array}{l} {I_v}({z_{\rm{t}}}, \theta, \phi) = {\varepsilon _v}{B_v}({T_{\rm{S}}}){\tau _v}({z_{\rm{t}}}, 0;\theta, \phi) + \\ \;\;\;\;\;\int_0^{{z_t}} {{B_v}\left({z'} \right)\frac{{\partial {\tau _v}({z_{\rm{t}}}, z';\theta, \phi)}}{{\partial z'}}{\rm{d}}\mathit{z'} + } \\ \;\;\;\;(1 - {\varepsilon _v})\tau _v^2({z_{\rm{t}}}, 0;\theta, \phi)\int_0^{{z_t}} {{B_v}\left({z'} \right) \times } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial {\tau _v}({z_{\rm{t}}}, z';\theta, \phi)}}{{\tau _v^2({z_{\rm{t}}}, z';\theta, \phi)\partial z'}}{\rm{d}}\mathit{z'} \end{array} $ | (1) |
| $ {B_v}({T_{\rm{S}}}) = \frac{{{c_1}{v^3}}}{{{{\rm{e}}^{{c_2}v/{T_{\rm{S}}}}} - 1.0}} $ | (2) |
式中,Iv(zt,θ,ϕ)是大气顶射出辐射率[单位:mW·m-2·sr-1·(cm-1)-1],TS是地表温度(单位:K),εv是地表光谱比辐射率,B是普朗克函数,c1和c2是辐射常数,v是波数(单位:cm-1),τv是单色透过率,θ是当地天顶角,ϕ是方位角,zt是大气顶高度。
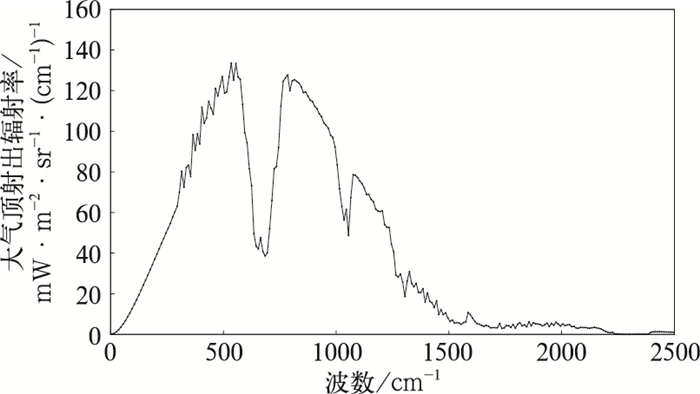
1.1.2 大气廓线的射出辐射率光谱模拟由2010年ECMWF资料整理出代表全球各种天气状况的2521条大气廓线,每条廓线分为101层,内容为温度、水汽混合比、O3体积混合比、地面温度、地面气压等,将廓线输入到LBLRTM软件中,得到了2521条廓线的大气顶射出辐射率光谱,图 1是一条廓线的辐射率光谱。
|
图 1 洋面晴空大气廓线大气顶光谱辐射率 (地面温度TS=299.25 K,地面气压pS=1012 hPa) Fig. 1 Simulated radiances at TOA for a clear-sky atmospheric profile over ocean (surface temperature TS=299.25 K, surface pressure pS=1012 hPa) |
整理廓线的光谱数据,由式(3)计算大气顶0~+∞ cm-1波段的总波段射出辐射率,
| $ I({z_{\rm{t}}}, \theta) = \int_0^\infty {{I_v}({z_{\rm{t}}}, \theta){\rm{d}}\mathit{v}} $ | (3) |
式中I(zt, θ)为总波段射出辐射率,整理时,将式(3)的上限取为2500 cm-1,因为地球发射的小于4 μm(即波数≥2500 cm-1)的红外辐射信号已很弱,每一条廓线OLR由如下方程计算(Wark et al,1962):
| $ OLR = 2\pi \int_0^{\frac{\pi }{2}} {I\left({{z_{\rm{t}}}, \theta } \right){\rm{sin}}\theta {\rm{cos}}\theta {\rm{d}}\theta } $ | (4) |
通过对2521条廓线的统计分析,I(zt,θ)具有如下临边变暗关系:
| $ I({z_{\rm{t}}}, \theta) = I({z_{\rm{t}}}, 0)(1 + a\theta + b{\theta ^2} + c{\theta ^3}) $ | (5) |
| $ \gamma = \frac{{\frac{{I({z_{\rm{t}}}, \theta)}}{{I({z_{\rm{t}}}, 0)}} - 1}}{{a\theta + b{\theta ^2} + c{\theta ^3}}} = \alpha + \beta I({z_{\rm{t}}}, 0) $ | (6) |
式中a,b,c,α,β是经验回归系数,将式(5)和式(6)代入式(4)得到:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;OLR = I({z_{\rm{t}}}, 0)[A + CI({z_{\rm{t}}}, 0)]\\ A = 2\pi \int_0^{\frac{\pi }{2}} {\left[ {1 + \alpha\left({a\theta + b{\theta ^2} + c{\theta ^3}} \right)} \right]{\rm{sin}}\theta {\rm{cos}}\theta {\rm{d}}\theta } \\ \;\;\;\;C = 2\pi \int_0^{\frac{\pi }{2}} {\beta \left({a\theta + b{\theta ^2} + c{\theta ^3}} \right){\rm{sin}}\theta {\rm{cos}}\theta {\rm{d}}\theta } \end{array} $ | (7) |
每条廓线的FY-3B/VIRR仪器通道5辐射率,可由辐射率与光谱响应函数的卷积计算得到,如下:
| $ {I_5}\left(\theta \right) = \frac{{\int_{{v_1}}^{{v_2}} {{I_v}({z_{\rm{t}}}, \theta)f\left(v \right){\rm{d}}\mathit{v}} }}{{\int_{{v_1}}^{{v_2}} {f\left(v \right){\rm{d}}\mathit{v}} }} $ | (8) |
式中,f(v)是通道5光谱响应函数,I5是VIRR通道5辐射率,v1和v2是通道响应的起始波数,通道5亮度温度TB5进一步由普朗克公式的反函数得到:
| $ {T_{{\rm{B5}}}} = \frac{{{c_2}{v_0}}}{{{\rm{ln}}[\frac{{{c_1}v_0^3}}{{{I_5}\left(0 \right)}} + 1.0]}} $ | (9) |
式中v0是通道中心波数。每条廓线的通量等效亮度温度TF为
| $ {T_{\rm{F}}} = {\left({\frac{{OLR}}{\sigma }} \right)^{\frac{1}{4}}} $ | (10) |
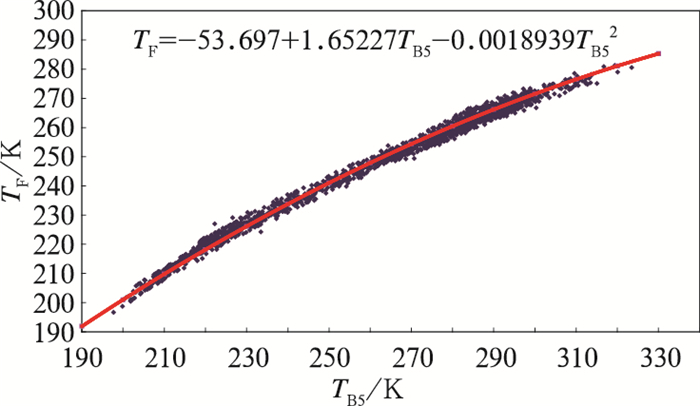
式中σ是斯蒂芬-玻尔兹曼常数,如此分别得到2521条廓线的TB5和TF,图 2是TB5和TF的回归关系,由图得出:
| $ {T_{\rm{F}}} = A + B{T_{{\rm{B5}}}} + CT_{{\rm{B5}}}^2 $ | (11) |
|
图 2 2521条廓线的FY-3B/VIRR通道5亮温与通量等效辐射温度的回归关系 Fig. 2 Regression relationship between FY-3B/VIRR Channel 5 brightness temperature and flux equivalent temperature of 2521 global atmospheric profiles |
式中,A,B,C是统计回归系数。
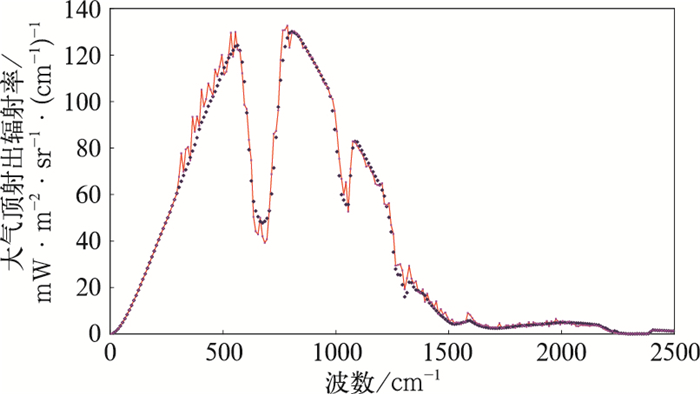
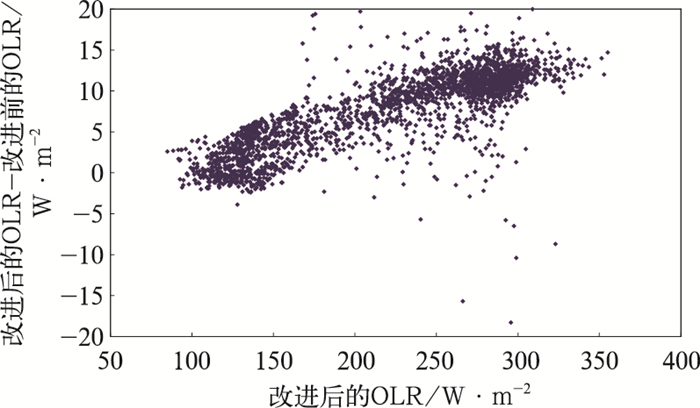
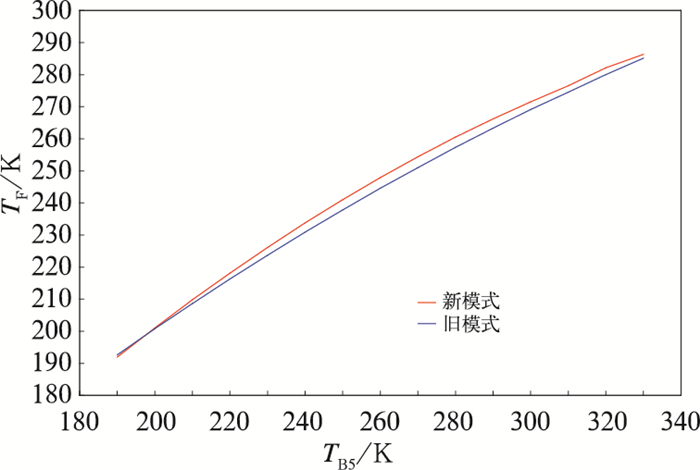
2 新旧模式的对比FY-3B/VIRR的新旧OLR反演模型相同,但由于采用了不同的辐射传输计算软件,对大气顶辐射率光谱及OLR的模拟数据不尽相同,由此建立的模式系数也不同,图 3是一条廓线新老两种软件计算出的射出辐射率光谱分布,可见两者有明显差别,尤其在水汽转动吸收带;图 4是新旧软件的OLR差值图,可见LBLRTM模拟的OLR系统偏高于旧软件,这使得有可能从理论模式上解释FY-3B/VIRR OLR业务反演模式得到的产品系统偏低于CERES观测OLR产品10 W·m-2的现象,新旧模式的回归系数分别为:A=-53.69, B=1.65227, C=-0.0018939(新); A=10.5, B=1.1333, C=-0.000917 (旧);图 5是新旧两种模式TB5-TF关系曲线对比图,图中新模式的TF偏高于旧模式2~3 K。
|
图 3 两种辐射传输计算软件计算的一条廓线大气顶射出辐射率光谱 (红色:LBLRTM,蓝色:旧软件) Fig. 3 Simulated radiances at TOA for a clear-sky atmospheric profile with LBLRTM and radiative transfer calculation softwares (red: LBLRTM, blue: old software) |
|
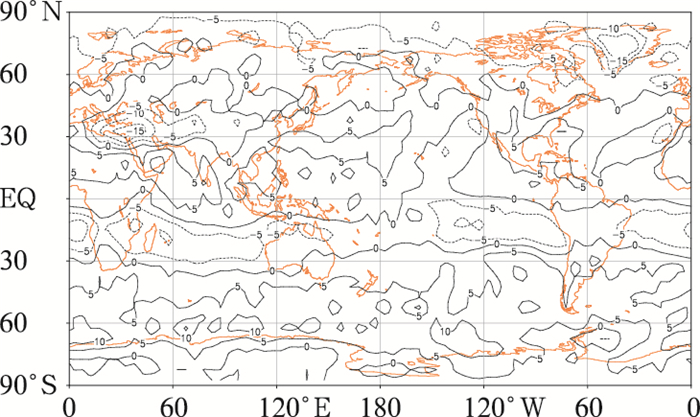
图 4 LBLRTM与旧软件对2521条大气廓线模拟OLR的差值图 Fig. 4 The OLR simulated with LBLRTM minus the OLR calculated by old software for 2521 atmospheric profiles |
|
图 5 新旧两种TB5-TF模式关系曲线对比图 Fig. 5 The TB5-TF regression curves of the new and old models |
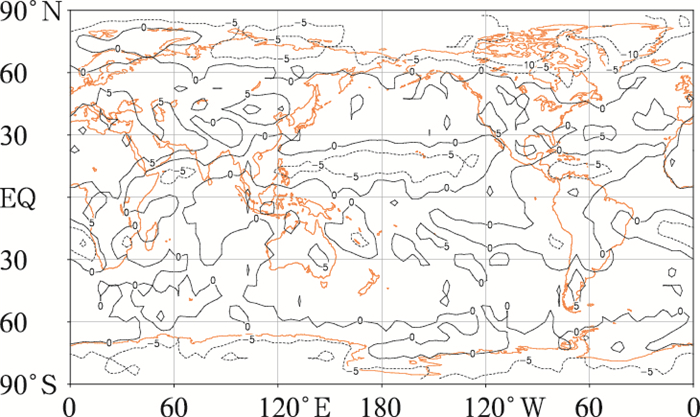
图 6a是新模式应用于FY-3B/VIRR L1数据资料处理得到的2016年7月平均OLR,图 6b是用于检验的CERES仪器多星融合OLR产品,图中两者相比:RMSE=5.69 W·m-2,Bias=0.8 W·m-2,表明新模式系数可反演出与CERES观测相比无系统偏差的OLR资料,尽管从理论上单通道反演整个长波段总辐射存在反演误差,但获得的精度还是可观的。图 7a是2016年7月10日FY-3B/VIRR日平均OLR,图 7b是与之对比的CERES日平均OLR,图中:RMSE=13.3 W·m-2,Bias=1.2 W·m-2,由于CERES日平均OLR产品是在24 h资料平均基础上得到的,而FY-3B为白天、夜间2次观测的平均,因此一天中的天气变化不可避免地增加了比较误差,我们对比了2016年1,3,7和10月的FY-3B与CERES OLR,得出:RMSE=9~15 W·m-2(日平均),RMSE=4~7 W·m-2(月平均),说明尽管单通道反演方法和OLR日变化带来误差,新模式系数估算的FY-3B/VIRR OLR资料与CERES产品是可以比拟的,图 8和图 9分别是2016年3和7月FY-3B/VIRR月平均OLR与CERES月平均OLR的差值图,图中偏差在-15~10 W·m-2,对比资料的观测频次固然是误差的原因之一,单通道反演模式的回归误差应是两种资料不同的另一主要原因。

|
图 6 2016年7月月平均OLR (a)FY-3B/VIRR, (b)AUQA-TERRA/CERES Fig. 6 Monthly average OLR in July 2016 (a)FY-3B/VIRR, (b)AUQA-TERRA/CERES |
|
图 8 2016的3月FY-3B/VIRR月平均OLR减去AQUA-TERRA/CERES月平均OLR Fig. 8 Monthly average OLR of FY-3B/VIRR minus that of AQUA-TERRA/CERES in March 2016 |
4 结论
由极轨气象卫星窗区通道亮温计算OLR的反演模式是一个经典的模型,应用于NOAA系列卫星AVHRR仪器的OLR产品处理已有40多年之久,产品广泛应用于气候分析、气候模式验证、ENSO监测和季风监测等方面,我国FY-3系列卫星的VIRR仪器因为有着与AVHRR相近的光谱特征,其OLR产品反演也采用了与AVHRR相类似的模型,但由于历史的原因,这两星的OLR业务产品与世界先进的CERES仪器观测OLR产品相比,都存在约为-10 W·m-2的偏差,NOAA是由于反演模式建立过程中匹配资料源的定标出现误差,FY-3是由于模式建立过程中辐射传输模拟的精度不够; 因此,在引进了国际最新逐线辐射传输模型计算软件LBLRTM后,利用该软件我们重新建立了FY-3系列VIRR仪器的OLR反演模式,应用模式处理得到了无系统偏差的、精度较为可观的FY-3卫星OLR资料,从新旧模式处理OLR资料的精度验证结果来看,新模式在精度上有了较大改进,尽管局限于观测通道,单通道OLR估算方法仍能得到较好精度的OLR产品。下一步我们将用新模式处理2008年以来的FY-3A,3B,3C历史OLR资料,以期该资料更好地应用于气候诊断和气候模式等方面的应用研究。
吴晓, 1998. 地球大气透过率及辐射率计算[J]. 应用气象学报, 9(1): 124-128. |
吴晓, 2011. 用卫星OLR资料估算中国大陆月降水量[J]. 气象, 37(1): 99-102. |
吴晓, 白文广, 2017. 基于FY-3/IRAS利用非线性模式反演OLR[J]. 应用气象学报, 28(2): 189-199. DOI:10.11898/1001-7313.20170206 |
吴晓, 鄢俊洁, 2011. 从FY-3B极轨气象卫星VIRR仪器通道5遥测数据计算射出长波辐射[J]. 科学通报, 56(31): 2604-2608. |
Clough S A, Shephard M W, Mlawer E J, et al, 2005. Atmospheric radiative transfer modeling:A summary of the AER codes[J]. J Quant Spectrosc Rad Transfer, 91(2): 233-244. DOI:10.1016/j.jqsrt.2004.05.058 |
Green R N, Wielicke B A, 1997. CERES inversion to instantaneous TOA flux[R]. CERES Algorithm Theoretical Basis Documents.
|
Gruber A, 1977. Determination of the Earth-atmosphere radiation budget from NOAA satellite data[R]. NOAA Technical Report NESS 76. Washington DC: US Department of Commerce.
|
Gube M, 1982. Radiation budget parameters at the top of the Earth's atmosphere derived from METEOSAT data[J]. J Appl Meteor, 21(12): 1907-1921. DOI:10.1175/1520-0450(1982)021<1907:RBPATT>2.0.CO;2 |
Jacobowitz H, Smith W L, Howell H B, et al, 1979. The first 18 months of planetary radiation budget measurements from the nimbus 6 ERB experiment[J]. J Atmos Sci, 36(3): 501-507. DOI:10.1175/1520-0469(1979)036<0501:TFMOPR>2.0.CO;2 |
Jacobowitz H, Tighe R J, 1984. The Earth radiation budget derived from the NIMBUS 7 ERB experiment[J]. J Geophys Res, 89(D4): 4997-5010. DOI:10.1029/JD089iD04p04997 |
Loeb N G, Priestley K J, Kratz D P, et al, 2001. Determination of unfiltered radiances from the clouds and the Earth's radiant energy system instrument[J]. J Appl Meteor, 40(4): 822-835. DOI:10.1175/1520-0450(2001)040<0822:DOURFT>2.0.CO;2 |
Ohring G, Gruber A, Ellingson R, 1984. Satellite determinations of the relationship between total longwave radiation flux and infrared window radiance[J]. J Climate Appl Meteor, 23(3): 416-425. DOI:10.1175/1520-0450(1984)023<0416:SDOTRB>2.0.CO;2 |
Wark D Q, Yamamoto G, Lienesch J H, 1962. Methods of estimating infrared flux and surface temperature from meteorological satellites[J]. J Atmos Sci, 19(5): 369-384. DOI:10.1175/1520-0469(1962)019<0369:MOEIFA>2.0.CO;2 |
 2018, Vol. 44
2018, Vol. 44