引言

脑卒中(俗称脑中风)是一种突然起病的脑血液循环障碍性疾病，也是脑血管疾病最严重的并发症。所以，脑卒中又被称为“人类沉默的杀手”。据统计，中国每年发生脑卒中的病人高达200万，每年脑卒中死亡120万。2012年，第三次全国死因调查显示(吕红霞和李志伟，2013)，脑卒中致死率排名第一，高达22.45%。

研究表明，脑卒中具有极高的致残率和较高的致死率，而这种疾病与诱发环境因素包括气温和湿度等之间存在密切的关系。国内外气象因素与心脑血管疾病的关系研究，我国最早可以追溯到20世纪80年代，王兴中和祝锦涛(1986)以合肥地区为例，研究了急性脑血管疾病的发病与异常气象的关系。许显福和裘建强(1990)、印佩芳等(1993)、杨贤为和邹旭恺(1998)分别探讨了气象因素和脑卒中发病之间的关系。初步证实了脑卒中发病与天气因素有关，但是具体什么天气因素与脑卒中发病相关，学者们仍然没有给出明确的结论。到了21世纪，梁丽英(2009)指出广州市脑卒中的日发病人数与当天的日平均气温、日最高气温、日最低气温、日平均水汽压、日平均露点温度呈显著负相关，与日平均气压呈显著正相关；凌佳(2013)利用半参数回归模型研究脑卒中的影响因素；方万里和马利娟(2014)利用2007—2010年宁波地区的脑卒中病例数据与气象资料，进行脑卒中的发病规律与气象因素的统计分析，发现脑卒中发病人数与前期的温差、高温和平均相对湿度情况呈负相关，与当期的气温和气压呈正相关。而在国外期刊上，Cowperthwaite and Burnett(2011)对2004—2008年155家美国医院的196439例脑卒中病人进行研究，并将脑卒中病人的发作类型分为缺血性、出血性、或短暂性脑缺血发作，研究结果表明天气和中风之间的季节性关联高度混淆。Wang et al(2017)对2004—2009年的中国济南地区1577例出血性脑卒中病人进行研究，发现出血性脑中风与环境温度近似呈线性关系，并给出了脑卒中的一个危险因素：低温。

当然，也有一些学者从医学机理的角度出发，分析气象因素对脑卒中发病的影响机制。张书余等(2013；2016)认为冷空气会影响血液的流动性，使得动脉粥样硬化以及血管收缩、心机细胞受损。同时，张书余等(2010)也指出高温、高湿天气将造成心脏排血量增加；强降温将导致肾上腺素水平上升，诱发冠状动脉痉挛甚至心肌梗死。阮烨等(2012；2013)、阮烨(2013)和赵娜娟等(2011)分别探讨了冷空气对人体血脂水平、血流变指标以及相关敏感指标的影响，证实了在冷空气活动影响心脑血管疾病的发病机制中，血管内皮素-1可能起到一定的作用；冷空气对HDL-C, ApoAL、TG及VLDL-C指标均有一定影响，这可能是造成心脑血管疾病的主要危险因素之一。

同时，对于脑卒中发病人数的预测以成为医学统计新的研究热点。董平和张敬华(2000)利用圆形统计探讨老年心血管病发病的季节规律，并说明发病的高峰时段大约在冬季12月至次年1月左右波动。随后，一些学者开始利用神经网络(谭英等，2013；闵晶晶等，2014)的方法来预测脑卒中的发病率，预测正确率分别为84.6%和60%。显然，传统的预测方法正确率还有待提升。而支持向量机具有一种自学习、自组织的非线性映射能力，高效地实现了从训练样本到预报样本的“转导推理”，大大简化了通常的分类和回归等问题。而且在医学数据中，存在大量的数据缺失、遗漏和误填，而支持向量机能够帮助我们抓住关键样本、“剔除”大量冗余样本，所以该算法具有较好的“鲁棒性”(即抗变换性，robustness)。因此，本文采用支持向量机来建立气象因素变化和脑卒中日就诊人数的预测模型，为提高医疗气象统计模型的预报准确率提供参考依据。

1 资料与方法 1.1 资料来源

本文选用2013年1月至2016年12月期间，某市四家医院脑卒中就诊人数与相应的逐日气象资料作为研究对象。时间跨度为4年(共1461 d)，四家医院共接诊脑卒中(包括脑出血、脑梗塞)病人61877例，病例信息包括发病时间、诊断报告时间、性别、职业和年龄。XX气象站逐日气象资料包括8个基本因素：日平均气压(单位：hPa)、日最高气压(单位：hPa)、日最低气压(单位：hPa)、日平均气温(单位：℃)、日最高气温(单位：℃)、日最低气温(单位：℃)、日平均湿度(单位：%)和日最低湿度(单位：%)。

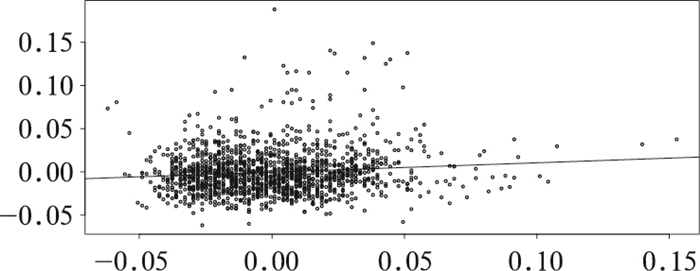
1.2 资料处理

从前人的研究成果看，天气因素能够从某种程度上诱发脑卒中发病。为了从统计学上分析天气因素与就诊人数之间的相关关系，本文选取日就诊人数与8个天气因素进行复相关分析，复相关系数R=0.107，说明天气因素和日就诊人数之间存在弱相关关系。其P值为0.033, 在0.05的显著水平下，可以说天气因素和日就诊人数之间的相关关系是显著的。具体的复相关系数如图 1所示。

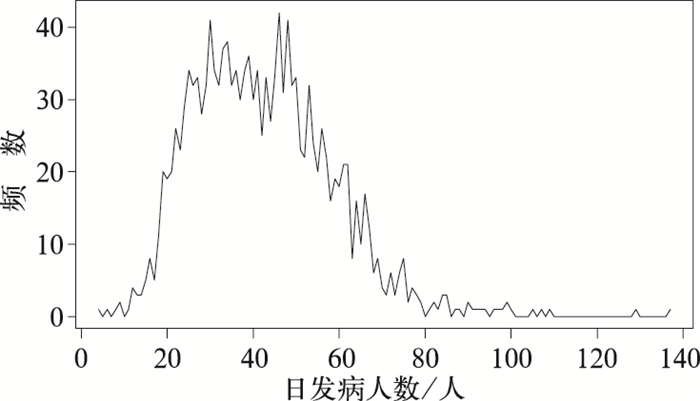
从图 1可以得出，虽然天气因素并不直接导致脑卒中的发病，但是之间的相关性还是存在的。为了进一步了解日就诊人数的分布特征，绘制频数分布折线如图 2所示。

研究发现，2013—2016年的1461天的脑卒中就诊人数不是简单的正态分布，而是呈现右偏分布，即日就诊人数处在[18，60]占据了总天数的84.74%。这种不平衡数据的存在，可能是导致传统的预测模型失效的因素之一。

1.3 支持向量机和随机森林方法 1.3.1 支持向量机方法

支持向量机(SVM)是一种基于VC维理论和结构风险最小原理的分类方法，根据有限样本在模型的复杂性和学习能力之间寻求最佳折中，以期获得最好的推广能力。而由SVM发展出来的回归方法称为支持向量回归(SVR)。

SVM最基础的原理就是将空间中的两类点(y=-1或y=1)用超平面w^Tx+b=0分开(在严格线性可分的情况下，存在这样的超平面)，而且希望这个超平面与两类的距离最大，也就是说，使得隔离带宽$ \mathit{\rho }\text{=}\frac{2}{\left\| \mathit{w} \right\|}$最大。这等价于用Lagrange乘子法求下式的极小值。

$ \mathit{L}\left(\mathit{w}{\rm, }\mathit{b}{\rm, }\mathit{\alpha } \right){\rm =}\frac{1}{2}\|\mathit{w}{{\|}^{{\rm 2}}}{\rm -}\sum\limits_{\mathit{i}{\rm =1}}^{\mathit{n}}{{{\mathit{\alpha }}_{\mathit{i}}}} [ {{\mathit{y}}_{\mathit{i}}}{\rm (}{{\mathit{w}}^{\mathit{T}}}{{\mathit{x}}_{\mathit{i}}}{\rm +}\mathit{b}{\rm)-1 } ] $

(1)

根据得到的解w^*, b^*, α^*得到最优分割超平面方程w^*Tx+b^*=0。任意点(x)的函数值w^*Tx+b^*的符号确定了该点的分类，或者说判别函数为sgn(w^*Tx+b^*)。

在实际的回归问题中，y的取值不仅仅是-1和1。令f(x)=w^Tx+b，希望y与f(x)的离差越小越好，SVR问题还是归结于求使得$ \frac{\left\| \mathit{w} \right\|}{2}=\frac{{{\mathit{w}}^{\text{T}}}\mathit{w}}{2}$最小的w，但约束条件是|y_i-f(x_i)|≤ε，这里ε为某目标值。类似于SVM，SVR允许一些误差，这样就可以把上面的约束放宽为(对于大于0的ξ_i, ξ_i^*)y_i-f(x_i)≤ε+ξ_i及f(x_i)-y_i≤ε+ξ_i^*，即得到Lagrange函数

$ \begin{align} &\mathit{L}\left(\mathit{w}{\rm, }\mathit{b}{\rm, }\mathit{\xi }{\rm, }\mathit{\alpha }{\rm, }\mathit{\eta } \right){\rm =}\frac{{\rm 1}}{2}\|\mathit{w}{{\|}^{{\rm 2}}}{\rm +}\mathit{C}\sum\limits_{\mathit{i}}{{\rm (}}{{\mathit{\xi }}_{\mathit{i}}}{\rm +}\mathit{\xi }_{\mathit{i}}^{*}{\rm)-} \\ &\ \ \ \ \ \ \ \sum\limits_{\mathit{i}}{{\rm (}}{{\mathit{\eta }}_{\mathit{i}}}{{\mathit{\xi }}_{\mathit{i}}}{\rm +}\mathit{\eta }_{\mathit{i}}^{*}\mathit{\xi }_{\mathit{i}}^{*}{\rm)-}\sum\limits_{\mathit{i}}{{{\mathit{\alpha }}_{\mathit{i}}}}{\rm (}\mathit{\varepsilon }{\rm +}{{\mathit{\xi }}_{\mathit{i}}}{\rm -}{{\mathit{y}}_{\mathit{i}}}{\rm +} \\ &\ \ \ {{\mathit{w}}^{\mathit{T}}}{{\mathit{x}}_{\mathit{i}}}{\rm +}\mathit{b}{\rm)-}\sum\limits_{\mathit{i}}{\mathit{\alpha }_{\mathit{i}}^{*}}{\rm (}\mathit{\varepsilon }{\rm +}\mathit{\xi }_{\mathit{i}}^{*}{\rm +}{{\mathit{y}}_{\mathit{i}}}{\rm -}{{\mathit{w}}^{{\rm T}}}{{\mathit{x}}_{\mathit{i}}}{\rm -}\mathit{b}{\rm)} \\ \end{align} $

(2)

需要在约束条件α＞0且η＞0下，解min_{w, b, ξ}{max_{α, η}L(w, b, ξ, α, η)}问题。对于非线性问题，可以基于对偶函数，猜测较为灵活的核函数K(x_i^T, x_j)=Φ(x_i)^TΦ(x_j)，其中Φ(x)为x的变换。

1.3.2 SVM针对不平衡数据的权重优化原理

非平衡数据是指数据集中某一类的样本数量明显少于其他类样本的数目。这类数据会带来一个问题，就是机器学习的泛化能力(generalization ability)的降低。针对不平衡数据的处理问题，2002年Chawla et al(2002)提出了SMOTE(synthetic minority over-sampling technique)算法，对向上抽样策略进行改进。而本文在交叉验证环节，从分类预测的结果出发，找出机器学习的泛化误差来源，从而人为地优化各个初始类别的比重，使得机器学习更加具有目的性和针对性。这样优化的方法，可以减少泛化误差，提高SVM算法的分类精度。

1.3.3 随机森林方法

随机森林(RF)是一种基于统计学的机器学习模型，它利用bootstrap重抽样方法从原始样本中抽取多个样本，然后对每个bootstrap样本进行决策树建模，然后组合多棵决策树的预测，平权投票出最终的预测结果。

随机森林中的每一棵决策树，使用相应的袋外(out of bag，OOB)数据计算它的袋外数据误差，记为errOOB₁。随机地对袋外数据所有样本的特征X加入噪声干扰(具体的操作方法就是随机地改变样本在特征X处的取值)，再次计算它的袋外数据误差，记为errOOB₂。假设随机森林中有N棵树，那么特征X的重要性为

$ \mathit{Importance}{\rm =}\sum{{\rm (}}\mathit{errOO}{{\mathit{B}}_{{\rm 2}}}{\rm -}\mathit{errOO}{{\mathit{B}}_{{\rm 1}}}{\rm)/}\mathit{N} $

(3)

用这个表达式来作为相应特征重要性的度量值是因为：若给某个特征随机加入噪声之后，袋外的准确率大幅度下降，则说明这个特征对于样本的分类结果影响很大，也就是说它的重要程度比较高。

2 优化建模与日就诊人数等级预测

经过数据统计发现，脑卒中日就诊人数最小值为4，最大值为134。基于此，本文将日就诊人数等分为六个等级(表 1)，方便接下来构建SVM模型对日就诊人数进行预测和检验。

根据表 1可知，脑卒中日就诊六类人数中，样本数量呈现巨大差异，为典型的非平衡数据。这种在原始数据集分布就不均衡的数据，又称为本质非平衡数据。研究发现，传统的分类算法如决策树、Bagging、Boosting对日就诊人数的预测正确率均为50%以下，随机森林回归的预测正确率为48%。在不平衡分类问题上，黄衍和查伟雄(2012)通过比较20个UCI数据集上随机森林和支持向量机的性能，证明了随机森林在不平衡数据上的表现显著逊色于支持向量机。因为SVM能够克服RF的等权投票机制，人为地优化各个类别的权重，从而达到更好的预测性能。

2.1 生成训练集和测试集

为了评价比较SVM算法，本文通过抽样将数据集分为训练集(train sample)和测试集(test sample)，两者之间的比例为3：1，即通过3/4的样本建立SVM模型，来预测另1/4样本的日就诊人数。为保持数据集分布，采用分层抽样，即在A1、A2、A3、B1、B2、B3各等级中分别抽取1/4作为测试集，剩下的1095个样本作为训练集。

2.2 建立SVM模型及预测判别

运用训练集建立SVM模型，所得结果如表 2所示。

表 2中SVM类型项目说明样本模型的类别为C分类器模型；SVM核函数项目说明本模型所使用的核函数为高斯内积函数且参数γ的取值为0.125；成本项目说明本模型确定的约束违反成本为1。模型找到了979个支持向量，六个等级各自对应的支持向量个数为7，461，186，290，34和1。根据以上建立的模型，对测试集进行预测，其预测的混淆矩阵如表 3所示。

从混淆矩阵可以发现，如果不对分类的权重进行优化的话(默认比重为1：1：1：1：1：1)，SVM针对不平衡数据的预测结果也比较差，预测正确率仅为52.46%，而且几乎把日就诊人数都预测为A2等级。

2.3 优化SVM模型及预测判别

从混淆矩阵和数据分析特征可知，每组的样本量不一样，如果采用等权赋值的话，预测结果就较差。所以下面将对六个类别进行不等权赋值优化，即提高前三类的权重，降低后三类的权重。具体优化的混淆矩阵如表 4所示，预测正确率即对应的初始分类权重如表 5所示。

结合表 4和表 5，可以得到：

(1) 由表 3的混淆矩阵可知，前三类的特征变量不明显。需要调高模型前三类的权重，于是将分类权重从1：1：1：1：1：1优化为100：100：100：10：2：1。正确率从52.46%上升到了59.56%，且由表 4混淆矩阵①可得，日就诊人数等级为A1的，有7个预测正确，终于实现了A1与A2的特征区分。A3被预测正确的个数已由原来的2个上升为20个；

(2) 由混淆矩阵①可知，适当升高前三类的比重是有效果的，但是A1与A3中的错误数依旧远高于正确数。于是将比重从100：100：100：10：2：1优化为1000：1000：1000：100：2：1，这时的错误个数减少了32，正确率上升了近10%。但是A1与A3的错误数还是很高，证明SVM模型还是不能够很好地区分前三类的具体特征；

(3) 明确了提高前三类的比重对正确率有正向影响，于是将比重从1000：1000：1000：100：2：1优化为100000：100000：100000：1000：2：1，这次权重优化的幅度更大一点，前三类都提高了两个数量级。错误数减少了72，比上次优化的效果还好一点，正确率从68.31%上升为87.98%。从混淆矩阵③可知，此时的A1，A2，A3基本能够正确区分，并且B1的预测正确率也已经达到了50%；

(4) 从混淆矩阵④可知，虽然前三类的正确率不错，但是B2和B3的错误率100%，而且错的比较离谱。于是在第四次优化的过程中，增大前三类权重的同时，适当增大第四类、第五类的比重，将优化权重调为1000000：2000000：2000000：10000：2000：1，错误个数为20个，说明一年366 d中，仅有20 d预测错误，正确率达到了94.56%。并且除了B3这一组的预测差距比较大之外，其他组的错误基本保持在上下等级浮动。这一预测结果对于医疗机构合理调配医务力量、床位和医疗药物，具有现实性的指导意义。

3 探索影响日就诊人数的天气因素-建立随机森林模型

虽然前一节给出的日就诊人数的预测，解决了医疗机构面临的问题。但是对于具体的病人来说，除了能够得到合理的救治之外，并没有给出具体的防范措施。于是，本节将建立随机森林模型，探索气象因素中的重要因素，帮助脑卒中高危人群及时采取干预措施。利用2013—2016年的脑卒中就诊人数与逐日气象数据，建立70棵树的随机森林模型，给出每个变量的重要性(表 6)。

表 6中的IM和INP指标都是重要性值的度量方式，数值越大，代表重要性越高。IM(increase in MSE)表示指标表示精度平均减少值，即表示误差的增加，准确性的降低；INP(increase in node purity)表示节点不纯度平均减少值，其实就是RSS(回归平方和)的减少；I是Importance，为相应特征重要性的度量值，对应变量的重要值越大，则说明变量对于模型进行分类越重要。本文的重要性排序主要以第二个指标为准，发现排名前三的分别是日最高气温、日最低气温和日平均气温。鉴于此，我们发现温度是诱发脑卒中就诊的最重要因素，气压次之，温度相关性较差。因此，脑卒中高危人群需要在温度变化异常的天气采取相应的预防措施，降低发病的风险。

4 结论

本文从机器学习算法的角度，对脑卒中的日就诊人数进行预测，并通过随机森林的方法找出影响脑卒中发病的重要气象因素。主要结论如下：

(1) 初期的数据挖掘发现，日就诊人数与8个气象因素呈现弱相关。但脑卒中的日就诊人数为不平衡数据，从折线图上反映出其为典型的右偏数据类型，这种数据特征是导致传统的预测模型预测脑卒中日就诊人数等级准确率较低的原因。

(2) 通过不断优化的SVM模型，使得日就诊人数等级的预测正确率达到94.56%，一年之中仅有20 d的日就诊人数等级预测错误。可以说，这种预测结果基本解决了医疗机构所面临的医务力量、床位和医疗药物的调配，具有一定的应用和推广价值。

(3) 最后，建立了日就诊人数关于气象变量的随机森林模型，探索出影响脑卒中发病率的三大重要气象因素：日最高气温、日最低气温、日平均气温。这将提醒脑卒中高危人群在温度变化异常的天气时，及时采取干预措施，降低发病风险。