引言

我国从20世纪90年代中期开始大规模建设具有定量测量降水和获得大气动力场结构能力的新一代多普勒天气雷达网。由于新一代天气雷达具有在线实时定标全自动体扫描工作模式较合理的地物杂波抑制以及科学的产品算法等特点，使得在定量测量降水以及对大尺度、中尺度天气系统的结构演变的监测能力方面得到很大的提高(李柏等，2013)。

天气雷达定量估测降水中最重要的环节之一是区分降水和非降水回波。非降水回波包括电磁干扰回波、地物杂波、超折射回波、生物回波(鸟、昆虫迁徙)和海浪回波等(马中元等，2010)。电磁波碰到近地面建筑物或高大山脉后反射而形成的回波称为地物杂波，而在逆温、高湿等特定大气条件下，电磁波发生弯曲碰到建筑物或山脉反射而形成的回波称为超折射回波(江源等，2009)。天气雷达数据质量控制目的是要最大程度地保留降水回波，剔除各种非降水回波对反射率因子数据带来的污染，在强天气分析、雷达定量估测降水以及资料同化应用中发挥着重要作用(张林等，2014)。

新一代天气雷达业务上通常采用模糊逻辑法对地物/超折射回波、海浪回波等进行质量控制，应用的变量包括反射率因子、速度和谱宽，效果较好，能过滤绝大多数的非降水回波带来的污染(刘黎平等，2007)。但对于晴空大气条件下的非降水回波而言效果不佳，特别是在春秋鸟、昆虫迁徙高峰季节下形成的生物回波，与层状云降水或降雪回波混杂在一起时更加难以区分(冷亮等，2012)，因此这类回波的质量控制仍然是一个困扰的难题。如何更好地实现非降水回波实时自动分类识别仍然是新一代天气雷达业务上面临的一大难题(李丰等，2012)。

双偏振雷达通过交替发射水平和垂直偏振波，并接收两个偏振方向回波信号的方法，可以探测到降水系统的水平偏振反射率因子(Z_H)、速度(V)、谱宽(σ_V)、差分反射率因子(Z_DR)、差分传播相位(ϕ_DP)、水平和垂直极化雷达返回之间的交叉相关系数(ρ_HV)。这些变量都是用来测量水平和垂直通道返回信号强度和相位之间的差异和相关性，而且能够提供散射粒子的形状、大小和状态等信息。美国已经实现了158部布网雷达(WSR-88D)偏振技术升级和业务化应用。

关于双偏振雷达数据质量控制，国内外相关专家和学者做过研究和分析。Hyangsuk et al(2009)发展了基于模糊逻辑法的WSR-88D回波分类算法(HCA)，将雷达回波分为10类，除了地物回波、生物回波这两种非气象回波之外，还有各种不同形态、不同尺度的降水粒子，HCA算法用到了所有的偏振雷达变量：Z_H，V，σ_V，ρ_HV，Z_DR，ϕ_DP。HCA算法区分降水和非降水回波的整体效果较好，但在模糊逻辑法处理过程中仍然存在一定的局限性，特别是距离较远处的生物回波和超折射回波的识别上并不理想。Lakshmanan et al(2007)发展了基于神经网络法的偏振雷达数据质量控制算法(dpQCNN)来区分降水和非降水回波，用到了6个变量信息(Z_H，V，σ_V，ρ_HV，Z_DR，ϕ_DP)，该方法对大量的降水和非降水回波样本进行计算和训练，得到降水回波发生的概率，再对未训练的样本进行分类识别。虽然神经网络法的HSS(Heidke skill score)评分达到0.8，但是神经网络模型过于依赖于训练的样本库，在识别降水或非降水回波的因果关系上存在局限。上述的模糊逻辑和神经网络方法在计算过程中都用到了6个变量信息，计算成本相对较高。Tang et al(2014)研究了基于相关系数法的WSR-88D偏振雷达回波分类算法，利用了相关系数、水平偏振反射率因子和大气环境温度场等变量(ρ_HV，Z_H，T)区分降水和非降水回波，在实时定量估测降水系统中(MRMS QPE)得到了应用，HSS评分高达0.83。

国内关于双偏振雷达数据质量控制的研究，Jiang et al(2013)基于模糊逻辑算法，对美国业务运行的KICT双偏振雷达的鸟类回波和昆虫回波分别进行了统计分析，发展了鸟类回波识别技术。杜牧云等(2012)通过大量ϕ_DP资料进行特征分析，根据实际情况将ϕ_DP资料分为非气象信号、较好、较差和差气象信号共4类，并根据不同需要，对较好气象信号不处理，对较差和差的气象信号分别进行订正和剔除，构建出一套系统的ϕ_DP资料分类处理方法。Liu et al(2010)分析了中国气象科学研究院研制的C波段双偏振雷达观测资料，认为信噪比(SNR)值对偏振变量测量值的影响至关重要，当SNR＜25 dB时，偏振变量的测量值就变得不可信了。

我国双偏振雷达处于试验和应用阶段，正在加快推进双偏振雷达业务化的发展进程，未来我国也要实现双偏振雷达业务化应用，以便于提高雷达探测和定量估测降水准确性。我国上海南汇雷达为WSR-88D双偏振业务雷达，观测模式为VCP21，其中有效数据的信噪比门限值为28 dB，因此可不考虑信噪比对偏振变量测量值的影响。本文以上海南汇WSR-88D双偏振雷达资料为例，利用相关系数、水平偏振反射率因子和差分反射率因子3个测量变量(ρ_HV，Z_H，Z_DR)着重研究S波段WSR-88D双偏振雷达非降水回波的识别方法。

1 识别方法

偏振变量中ρ_HV，Z_DR在降水和非降水回波特征上有明显的不同。对于降水回波而言，ρ_HV值接近于1，Z_DR也在一定范围内均匀变化，对于非降水回波如生物回波(鸟、昆虫)而言，ρ_HV较小(大多＜0.7)，Z_DR较大(大多>6)，且杂乱不均匀(Tang et al, 2014; Jiang et al，2013)。ρ_HV和Z_DR在区分降水和非降水回波特征上具有重要作用。

本文将ρ_HV，Z，Z_DR作为输入变量，先用简单的ρ_HV将多数非降水回波提取出来，但是冰雹、对流单体及非均一波束充塞的ρ_HV也较小，而且有些非降水回波(如生物回波)的ρ_HV较大，考虑到这些特殊情况对识别结果造成的影响，本文中算法采用回波顶高特征参数保留冰雹和对流单体，再采用ρ_HV和Z_DR去除非降水回波。

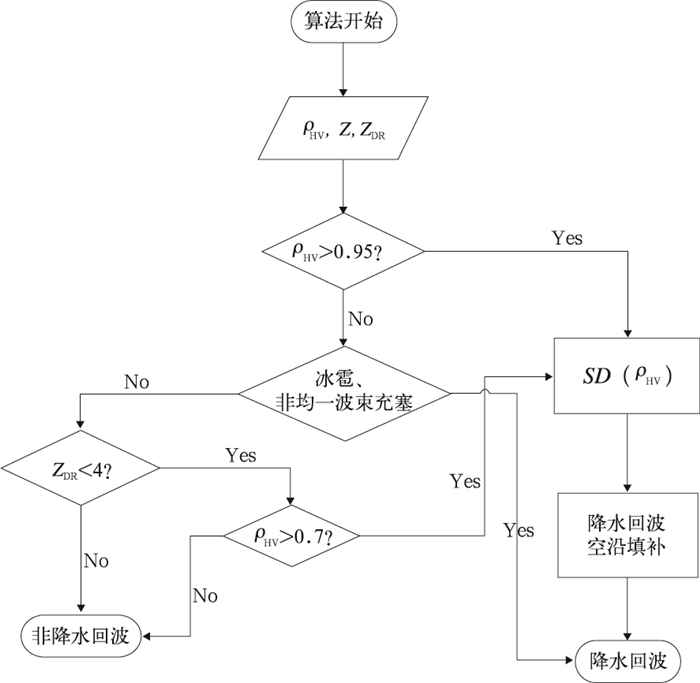
算法基于一般的气象原理，ρ_HV能够区分相当一部分降水和非降水回波，对于容易产生误判的冰雹及非均一波束充塞，则利用回波顶高特征参数进行保留，而对于一些ρ_HV较大的非降水回波可利用Z_DR和相关系数水平纹理等特征量进行识别。如图 1所示为算法执行步骤，共分为5步：(1)ρ_HV区分降水和非降水回波区域；(2)回波顶高特征参数保留冰雹和非均一波束充塞；(3)生物回波去除；(4)相关系数水平纹理(SD(ρ_HV))滤除非降水回波；(5)降水回波空洞填补。

1.1 基本相关系数法

图 2为上海南汇WSR-88D观测产品图像。由图可知，非降水回波(鸟、昆虫等生物回波)Z_H和V与层状云降水回波很相似，因此采用单偏振雷达不易完全区分两者，而偏振变量却比较容易区分两者的不同。

图 3为降水和非降水回波ρ_HV的统计直方图，统计了2016年上海南汇WSR-88D雷达两次观测过程共198个体扫数据，在统计之前首先根据雷达观测回波经验人工区分开降水和非降水回波，再利用上海14部自动气象站小时累积雨量值进行验证。根据统计结果不难发现，非降水回波的ρ_HV取值在0.2~1变化，而降水回波的相关系数ρ_HV在0.8~1取值，两者之间有一个重叠区域。

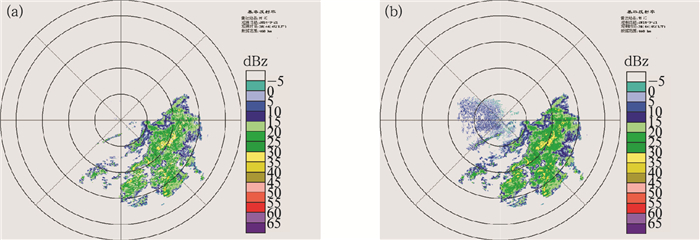
图 4为基本相关系数法识别图 2中的个例。由图 4可知，当ρ_HV=0.95时，多数非降水回波得到去除，但也会滤掉一些正常的降水回波，而当ρ_HV=0.7时，则会有一部分非降水回波保留下来。

1.2 冰雹及非均一波束充塞

当降水回波的ρ_HV＜0.95甚至更低时，考虑冰雹、对流单体及冰水混合物观测过程中发生非均一波束充塞的可能性较大。在一个脉冲周期内，当ρ_HV的减小伴随着较大的ϕ_DP梯度时，或者说是由于ϕ_DP的梯度变化而导致ρ_HV减小，这种现象称为非均一波束充塞。S波段WSR-88D双偏振雷达水平和垂直波束分辨率均为1°，在对流性降水观测过程中，当波束照射体内存在冰雹或对流单体时，若对流单体未被1°波束充满，则容易发生非均一波束充塞，且距离越远，随着雷达波束的展宽作用，非均一波束充塞现象越明显，ρ_HV越小。

那么如何在双偏振雷达数据质量控制中保留冰雹、对流单体和非均一波束充塞等正常降水回波呢？本文利用了回波顶高特征参数进行保留。由于冰雹、对流单体和非均一波束充塞通常发生在强对流降水过程中，伴随较高的回波强度和回波顶高。当一个距离库中的ρ_HV＜0.95时，检查该距离库对应的Z_H和回波顶高E_{TOP18 dBz}和E_{TOP0 dBz}值，式(1)和式(2)分别为冰雹和非均一波束充塞的识别标准。当距离库中ρ_HV＜0.95时，如式(1)，Z_H>45 dBz，且E_{TOP18 dBz}>8 km，则识别为冰雹；在低ρ_HV值和雷达站之间，算法搜索可能存在的风暴单体核，当径向上连续出现高的水平偏振反射率因子值(Z_H>45 dBz)，且长度超过1 km，则认为是风暴单体核，r_{storm_core}定义为风暴单体核到雷达站的距离。式(2)所示为识别非均一波束充塞的标准，在远于风暴单体核的位置，当E_{TOP0 dBz}>9 km时，则识别为非均一波束充塞。

Tang et al (2014)的研究表明，这两个识别标准不仅适用于冰雹和非均一波束充塞，在不同形状和大小的混合粒子或冰水混合物降水过程中，ρ_HV值较低，其识别标准也同样适用。

$ \begin{array}{l} {\rho _{{\rm{HV}}}}＜0.95 \cap ({E_{{\rm{TOP18}}\;\;{\rm{dBz}}}}＞8.0\;{\rm{km}}\; \cap \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{Z_{\rm{H}}}＞45\;\;{\rm{dBz}}) \end{array} $

(1)

$ \begin{array}{l} {\rho _{{\rm{HV}}}}＜0.95 \cap ({E_{{\rm{TOP0}}\;\;{\rm{dBz}}}}＞9.0\;{\rm{km}}\; \cap \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{r_{{\rm{ange}}}}＞{r_{{\rm{storm\_core}}}}) \end{array} $

(2)

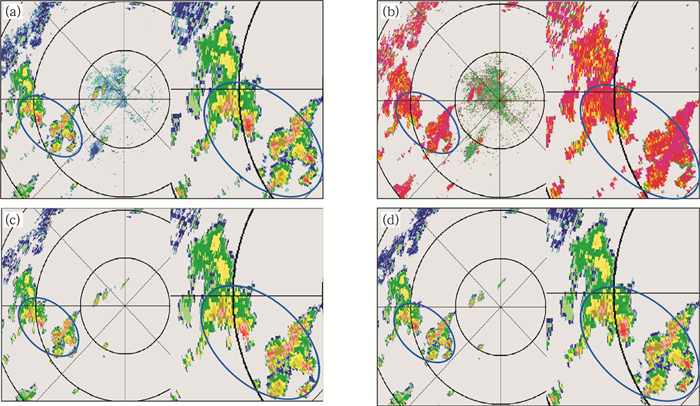
图 5为2016年7月5日上海南汇WSR-88D雷达一次冰雹观测过程，图 5a基本反射率中蓝圈标注处为冰雹影响区域，从图 5b中能直观看出在冰雹影响区域内的对流单体局部ρ_HV较小，低于0.95，当用ρ_HV=0.95阈值识别后，图 5c中部分对流单体被误判过滤了，图 5d为采用回波顶高特征参数式(1)保留冰雹和对流单体，同时雷达站周围的非降水回波也得到了识别。

图 6为2016年7月5日上海南汇WSR-88D雷达一次非均一波束充塞过程的观测个例，黑色圈标注为非均一波束充塞影响区域，如图 6b所示非均一波束充塞影响区域内ρ_HV较小，低于0.95。如图 6c所示，其ϕ_DP梯度变化明显。经过质量控制后，如图 6d所示，降水回波得到了保留，靠近雷达站的非降水回波也得到了识别。

1.3 生物回波识别

由昆虫后向散射导致的非降水回波中包含很多具有重要气象意义的信息，一般情况下是不宜被去除的，但在降水估测时是有必要将该类回波识别过滤的。

经过ρ_HV变量的初步筛选后，大致可区分为降水和非降水回波。非降水回波中包含生物回波、电磁干扰、超折射等各种类型的杂波。电磁干扰、超折射等杂波在新一代天气雷达业务中有较成熟的算法进行识别。而生物回波在新一代天气雷达业务上识别效果不理想，双偏振雷达中可利用偏振变量予以识别。

Jiang et al(2013)统计了大量WSR-88D偏振雷达的生物回波，认为Z_DR是识别生物回波的有效变量，其为水平和垂直返回信号强度之比，当降水回波较为均匀时，水平和垂直返回信号的相关性好，Z_DR在一定范围内均匀变化。生物回波Z_DR值很大，一般大于6以上。

本文利用2016年上海南汇雷达8—10月的晴朗天气资料，统计每天21:30左右时刻的数据，分析昆虫回波在100 km范围内Z_DR的平均值随时间的变化规律。横坐标为从8月1日起开始计数，直到10月31日截止，除去降雨天气的数据外，参与统计的昆虫数据有76个，如图 7所示。

由图 7b可知，昆虫回波ρ_HV随时间变化不明显，在0.7附近。而Z_DR随时间变化较为明显，存在降低趋势，总体在3~5之间变化(图 7a)，相比江源等(2009)对美国昆虫回波的统计结果值偏低。

图 1算法流程第三步为生物回波的识别，结合南汇雷达昆虫回波的统计规律，当Z_DR>4认为是生物回波给予滤出，若Z_DR＜4则对ρ_HV做进一步判定，若ρ_HV＜0.7则认为是非降水回波给予滤出。

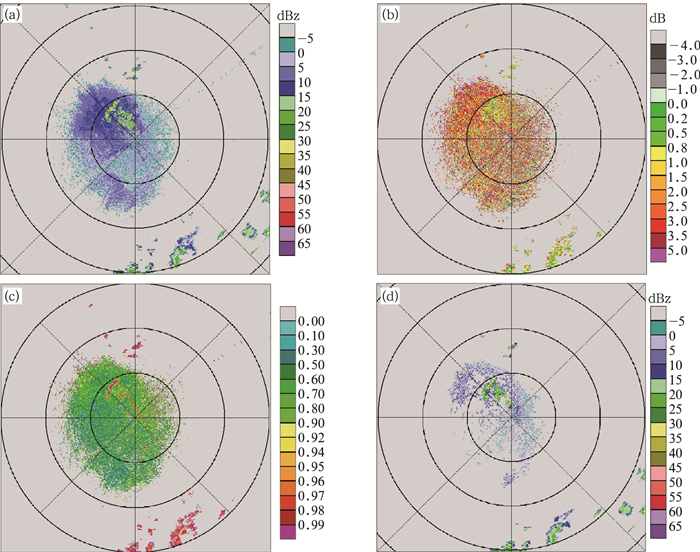
如图 8所示，为雷达站周围大面积生物回波，经过Z_DR和ρ_HV过滤后，多数生物回波得到识别，并且可以绝大程度上保留降水回波。

1.4 相关系数水平纹理SD(ρ_HV)

降水回波和非降水回波的区别不仅体现在ρ_HV上，两者相关系数水平纹理SD(ρ_HV)也表现出明显的不同特征，降水回波SD(ρ_HV)小，非降水回波SD(ρ_HV)大。图 1算法流程中，利用SD(ρ_HV)能有效识别ρ_HV>0.95的非降水回波，而且能过滤0.7＜ρ_HV＜0.95残留的非降水回波。

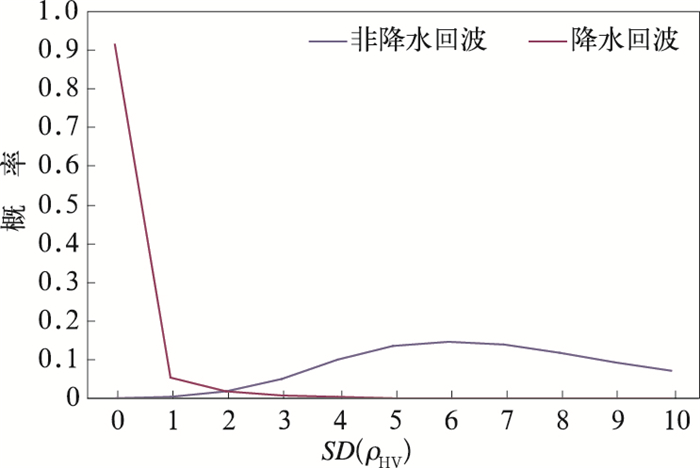
SD(ρ_HV)计算方法见式(3)所示，图 9为降水和非降水回波的SD(ρ_HV)特征统计概率分布图。统计前首先需要排除识别为冰雹、对流单体和非均一波束充塞等降水回波，采取先人工识别，再利用自动气象站雨量值进行验证的方法，分别统计了360620个降水回波样本点和865750个非降水回波样本点。由图可知，降水和非降水回波SD(ρ_HV)特征有非常明显的不同，SD(ρ_HV)一般在0~3，而非降水回波的SD(ρ_HV)一般都大于1。为了保证降水回波不会被误判，当SD(ρ_HV)>3时为识别非降水回波的最佳阈值。

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;SD\left({{\rho _{{\rm{HV}}}}} \right) = \\ \frac{{\sum\limits_{i = 1}^{{N_A}} {\sum\limits_{j = 1}^{{N_R}} {{{\left[ {10{\rho _{{\rm{HV}}}}\left({i, j} \right) - 10{\rho _{{\rm{HV}}}}\left({i, j + 1} \right)} \right]}^2}} } }}{{{N_A}{N_R}}} \end{array} $

(3)

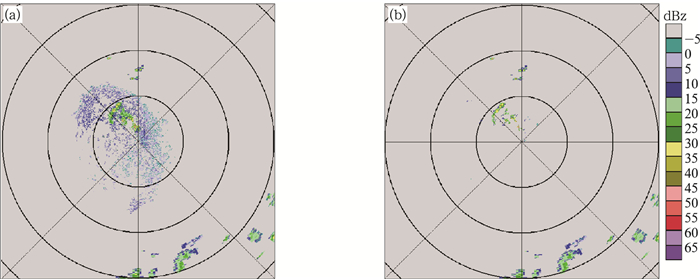
如图 10所示为处理图 8中生物回波识别后残留的非降水回波，经过相关系数水平纹理参数识别后，残留非降水回波得到了有效识别，降水回波基本上得到了保留。

1.5 降水回波空洞填补

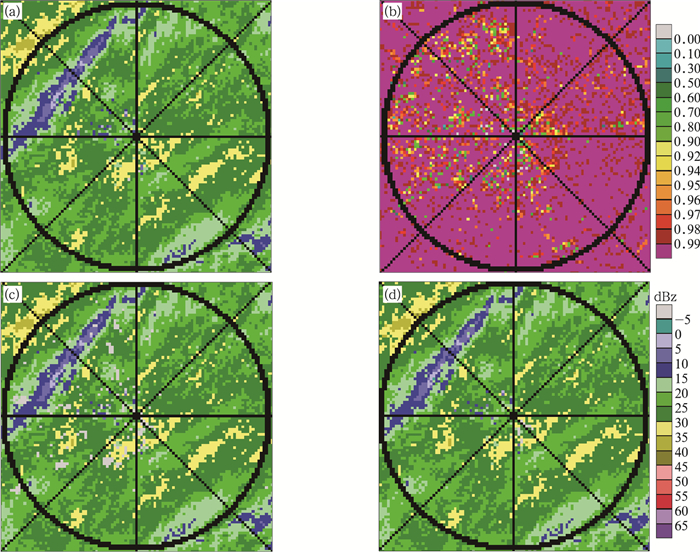
图 11为2015年7月11日08:12上海南汇雷达在灿鸿台风过程中的观测产品。由图 11b可知，大多数降水回波的ρ_HV>0.95，只有极少降水回波ρ_HV＜0.7。经过质量控制后，如图 11c所示，个别降水回波点会被误判为非降水回波而形成降水回波空洞。

算法的最后一步为降水回波空洞的填补。本文采用了中值法进行填补，以回波空洞点为中心9×9的窗口内，若有效回波的个数占窗口总数的70%以上，则采用9×9窗口内的有效回波的水平偏振反射率因子平均值代替回波空洞点的水平偏振反射率因子值，此时水平偏振反射率因子的单位为(mm⁶·m^-3)。具体过程为将9×9窗口内dBz值转换为(mm⁶·m^-3)后进行平均，最后再将平均后的(mm⁶·m^-3)值转换为dBz值。图 11d所示为降水回波空洞的填补效果，经过填补后，基本恢复到图 11a原来的降水回波形状。

2 效果评估

本文采用了算法测试个例之外的200个南汇体扫观测数据做效果评估分析，仍然采取先人工识别，再利用自动气象站雨量值进行验证的方法选取了6389760个非降水回波点和8356891个降水回波点样本数据。对文中算法的非降水回波识别准确率P_a、漏判率P_f以及降水回波误判率P_e进行评估。评估依据如下：

$ {P_a} = \sum {NP\_{\rm{Identify}}} /\sum {NP} $

(4)

$ {P_f} = \sum {NP\_{\rm{Unidentify}}} /\sum {NP} $

(5)

$ {P_e} = \sum {P\_{\rm{Identify}}} /\sum P $

(6)

式中∑NP和∑P分别为非降水回波和降水回波的样本总数，∑NP_Identify和∑NP_Unidentify分别为非降水回波识别和未识别的样本个数，∑P_Identify为降水回波识别样本个数。

经过评估后的效果如表 1所示。南汇S波段WSR-88D双偏振雷达非降水回波识别准确率为93.8%，漏判率为6.2%，降水回波的误判率为3.82%。

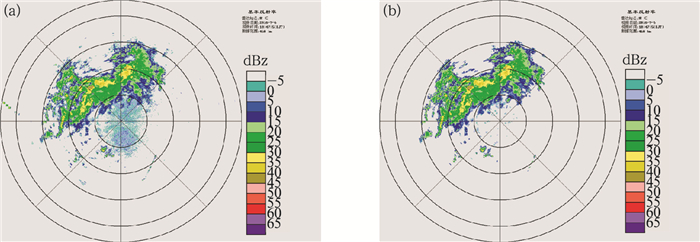
图 12a为上海南汇雷达2016年9月6日10:47观测数据，图 12b为经过质量控制后的效果。图 13a为南汇雷达2016年9月6日20:06观测数据，该观测个例中降水与非降水回波发生了混合，图 13d为经过质量控制后的效果，采用偏振变量能有效区分降水和非降水回波。

3 结论和讨论

本文分析S波段WSR-88D双偏振雷达非降水回波特征，利用偏振变量对降水和非降水回波特征进行了分类识别，并考虑了冰雹、非均一波束充塞等特殊情况下的处理，得到S波段WSR-88D双偏振雷达非降水回波识别算法流程，结论如下：

(1) ρ_HV，Z和SD(ρ_HV)为双偏振雷达识别非降水回波的有效特征量，能区分绝大多数降水和非降水回波。

(2) 当雷达回波中存在冰雹、对流单体和非均一波束充塞时，ρ_HV值小于0.95，算法利用了回波顶高特征参数对其进行保留。

(3) 极少的降水回波ρ_HV＜0.7，算法执行后形成了降水回波空洞，文中采用了中值法填补了降水回波空洞。

(4) 本文对算法进行了评估，结果表明，该算法对上海南汇S波段WSR-88D双偏振雷达非降水回波的识别准确率达到93%以上，降水回波误判率仅为3.82%。

我国双偏振雷达尚处于业务试验阶段，文中仅采用了一部上海南汇S波段WSR-88D偏振雷达数据做算法研究和测试。受到测试样本的局限，本文算法难免会有一些欠考虑的情况，未来需要在更多的偏振雷达中进行验证和完善。