2. 国家气象中心,北京 100081;
3. 中国气象局数值预报中心,北京 100081
2. National Meteorological Centre, Beijing 100081;
3. CMA Numerical Prediction Centre, Beijing 100081
暴雨灾害在我国频发,常带来巨大经济损失和人员伤亡,能否对其准确预报是社会关注的热点之一。暴雨是由不同尺度天气系统相互作用下产生的,大尺度系统为暴雨提供有利的环境条件,而中、小尺度系统是造成暴雨的直接系统(陆汉城和杨国祥, 2004)。目前,对暴雨的传统天气学人工预报存在很大的局限性,针对暴雨的研究和预报越来越多地采用数值模拟和预报技术(沈桐立等, 2010)。为保证数值模拟和预报中暴雨能及时触发和准确演变,数值模式的初值需要在不破坏大尺度环流形势场的同时,尽可能多地引入中小尺度信息。因此,模式初值场中是否包含多尺度信息具有重要意义。
在各主要业务数值预报中心,常使用变分资料同化(包括三维变分和四维变分)方法生成模式初值场(Lorenc, 2003; Bannister, 2008)。因此,在变分资料同化方案设计中包含多尺度信息对暴雨预报具有重要意义。在变分资料同化方法中,观测信息的传播方式主要由背景误差协方差矩阵B决定。其中,观测误差在水平方向主要通过B矩阵中的水平误差协方差传播。背景误差水平相关模型可以通过数学工具来近似描述,在全球模式中常采用谱滤波方法(庄世宇等, 2005),在区域模式中常采用递归滤波方法。递归滤波方法不需要显式地构造B矩阵,因此可以显著减小计算开销和内存(李冬等, 2011)。英国气象局(Purser and McQuigg, 1982)第一次将递归滤波的方法引入到区域预报模式中。目前,递归滤波被广泛应用于三维变分系统,如:SSI(spectral statistical interpolation)、GSI(gridpoint statistical interpolation)、MM5 3Dvar(the fifth-generation mesoscale model 3-dimensional variational data assimilation)和WRF 3Dvar(weather research forecast variational data assimilation system)等。我国自主研发的GRAPES中尺度三维变分同化系统中也采用了递归滤波方法(张华等, 2004)。
在GRAPES三维变分同化系统中,假定水平误差相关为高斯函数型,并利用递归滤波方法逼近。Skamarock(2004)研究表明,高斯型函数的功率谱比大气实际的谱衰减得快,但通过对多个递归滤波器进行线性拟合可得到衰减较慢的功率谱。何光鑫等(2011a;2011b)利用多元正态分布的可加性进行递归滤波的拟合(Wilks, 2005),将不同特征尺度的递归滤波进行拟合,使拟合后的滤波特征尺度接近一阶递归滤波器4倍网格距的特征尺度,拟合后的多尺度递归滤波在保持原有大尺度信息的基础上,更清晰地显示出了许多中小尺度的信息。
在研究与业务运行中发现,在递归滤波中特征尺度的选取对同化效果存在重要的影响。本文将基于何光鑫等(2011a;2011b)的研究,利用气候态的背景误差样本统计相关特征尺度,依据统计结果拟合新递归滤波器,并将新递归滤波器应用于江汉平原的一次暴雨预报。
1 多尺度资料同化方案设计 1.1 原滤波方案在GRAPES三维变分同化系统中假定水平误差相关为高斯型相关函数,为模拟高斯函数采用递归滤波方法进行逼近。一维情况下的递归滤波器为(朱宗申和胡铭, 2002):
| $ {B_i} = \alpha {B_{i - 1}} + \left( {1 - \alpha } \right){A_i}\;\;\;\;i = 1,2, \cdot \cdot \cdot ,n - 1,n $ | (1) |
| $ {C_i} = \alpha {C_{i - 1}} + \left( {1 - \alpha } \right){B_i}\;\;\;\;i = n,n - 1, \cdot \cdot \cdot ,2,1 $ | (2) |
式中,Ai为原始值,Bi为经过一次滤波后的值,Ci为经过两次滤波后的值,α是滤波系数。递归滤波的边界条件为:
一次滤波:
| $ {B_1} = \left( {1 - \alpha } \right){A_1} $ | (3) |
二次滤波:
| $ \left( {{C_n},{B_1}} \right) = \frac{{\left( {{B_n},{A_1}} \right)}}{{1 + \alpha }} $ | (4) |
二次以上滤波:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{C_n},{B_1}} \right) = \\ \frac{{1 - \alpha }}{{{{\left( {1 - {\alpha ^2}} \right)}^2}}}\left[ {\left( {{B_n},{A_1}} \right) - {\alpha ^3}\left( {{B_{n - 1}},{A_2}} \right)} \right] \end{array} $ | (5) |
滤波系数α:
| $ \alpha = 1 + E - \sqrt {E\left( {E + 2} \right)} $ | (6) |
其中
| $ E = {N_r}\delta {x^2}/{R^2} $ | (7) |
式中,Nr为滤波次数,R为特征尺度,δx为格距,i为格点。图 1中点线为利用递归滤波方法模拟出高斯型分布特征,图中横坐标为以格点为单位的距离,纵坐标为相关系数。为检验该方法与实际结果存在的差异,本文采用美国国家气象中心(National Meteorological Centre, NMC)方法计算背景误差样本,并利用该样本统计实际水平特征尺度。NMC方法(Parrish and Derber, 1992)是获取背景误差样本的一种常用方法,该方法利用预报到同一时刻的两个不同预报时效的预报场的差值作为背景误差近似样本。该方法首先在NMC同化系统中应用,因而简称NMC方法。在区域模式中,选用的两个预报时效一般为24和12 h(Derber and Bouttier, 1999)。本文研究中也采用了这样的方案。

|
图 1 不同变量的水平协相关结构 (a)流函数, (b)势函数, (c)非平衡质量场,(d)湿度场 (A为原方案,B为新方案,C为统计结果) Fig. 1 The horizontal co-correlation structure of different variables (a) stream function, (b) potential function, (c) unbalanced mass field, (d) humidity field (A original scheme, B new scheme, C statistical results) |
图 1中实线为实际统计结果,原方案(A)中高斯型函数的功率谱比估计的实际功率谱衰减得快,影响变分系统对中小尺度的分析同化能力。由于暴雨是由多尺度天气系统共同作用产生的,所以在暴雨数值预报中引入中小尺度信息是十分重要的。
1.2 新滤波方案为解决高斯型函数功率谱衰减较快这一问题,提高中小尺度的分析同化能力,将三种不同特征尺度的滤波器进行线性拟合(Wilks, 2005),即:
| $ {C'_i} = \frac{{C_i^1 + C_i^2 + C_i^3}}{3} $ | (8) |
式中,Ci1,Ci2和Ci3分别为三种不同特征尺度的递归滤波器,C′i为拟合后的递归滤波器。在原方案中,假定水平误差相关为高斯型函数,并利用递归滤波进行逼近。流函数、势函数和非平衡质量场在原方案递归滤波器中水平特征尺度为500 km,但是高斯型函数的功率谱比实际大气的功率谱衰减得快,对中小尺度信息的同化作用减弱。本文在保证新方案的水平特征尺度仍为500 km的基础上,根据样本估计结果选取三种特征尺度的递归滤波器进行拟合,减缓功率谱的衰减速度,与估计的实际情况更加接近。根据实际统计结果进行多次线性拟合得出经验性结果,流函数、势函数和非平衡质量场拟合的水平特征尺度分别为950、300和250 km;在原方案递归滤波中湿度场的水平特征尺度为200 km,新方案水平特征尺度选取方法与流函数、势函数和非平衡质量场水平特征尺度方法一致,湿度场拟合的水平特征尺度分别为350、150和100 km。本文利用多次线性拟合得出经验性的水平特征尺度并进行试验,在业务运用中对水平特征尺度的选取仍需细致调整。新方案的拟合结果如图 1中虚线B所示,新方案的功率谱衰减与实际统计结果更加接近,与原方案相比拓宽了水平相关矩阵的波谱空间。
1.3 单点试验单点同化试验可以清楚地表现出背景误差协方差矩阵对分析增量的影响,更好地看出新方案对中小尺度的同化能力。单点位置在30°N、113°E;湿度观测资料位于850 hPa,相对湿度为90%;u、v的观测资料位于500 hPa,其值均为10 m·s-1。
从比湿分析增量图(图 2a,2d)中可以看出新方案观测资料的影响范围较大,然后影响范围迅速减小,在观测点附近的影响强度明显小于原方案。从湿度场拟合方案(图 1d)中也可以看出,新方案对观测点附近的影响减弱;从u、v风场的分析增量图(图 2b,2c,2e,2f)中可以看出新方案对观测点附近的影响减弱。从流函数、势函数、非平衡质量场拟合方案(图 1a~1c)中也可以看出新方案在观测点附近的影响弱于原方案,与样本估计情况更加接近。

|
图 2 单点试验分析比湿(a, d;单位:g·kg-1)、纬向风(b,e;单位:m·s-1)和经向风(c,f;单位:m·s-1)增量的水平分布 (a, b, c)原方案,(d, e, f)新方案 Fig. 2 Increments of single test of specific humidity (a, d; unit: g·kg-1), u component of wind (b, e; unit: m·s-1), and v component of wind (c, f; unit: m·s-1) (a, b, c) original scheme, (d, e, f) new scheme |
为研究新方案在暴雨预报中对中小尺度信息的影响,本文将新方案应用于2015年6月1—2日江汉平原的一次暴雨预报。
2 个例分析 2.1 天气过程2015年6月1—2日一个中尺度对流系统在江汉平原地区造成一次强降水过程(王晓芳等, 2015;郑永光等, 2016),1日20时至2日08时在江汉平原、湖北中部、河南南部、湖南北部等地出现暴雨、局地特大暴雨(图 3)。研究表明(汪小康和廖移山, 2015),降水期间长江中下游地区受副热带高压外围西南暖湿气流的控制,在河套地区有短波槽东移的环流背景下,6月1日傍晚在江汉平原南部的暖切变线上新生成发展一个α中尺度低涡,在移动中不断加强发展,成为影响6月1日夜间江汉平原强降水的重要系统。

|
图 3 2015年6月1日20时至2日08时12 h累计降水(单位:mm) Fig. 3 Accumulated 12 h rainfall from 20:00 BT 1 to 08:00 BT 2 June 2015 (unit: mm) |
试验设计如表 1,起报时间为2015年6月1日08时(北京时,下同),模拟范围为(15°~45°N、100°~125°E),水平分辨率0.1°×0.1°,采用GRAPES-3Dvar同化系统,利用T639(T639L60全球中期数值预报系统)6 h预报场作为同化背景场,同化资料为常规探空资料。
|
|
表 1 试验设计 Table 1 Experimental design |
试验1为控制试验,湿度场、风场和质量场均采用原方案;试验2中湿度场为新方案,风场和质量场不变;试验3中湿度场不变,风场和质量场采用新方案;试验4中湿度场、风场和质量场均采用新方案;通过不同方案的对比,分别探究湿度场、风场与质量场利用新方案后对降水预报的影响。
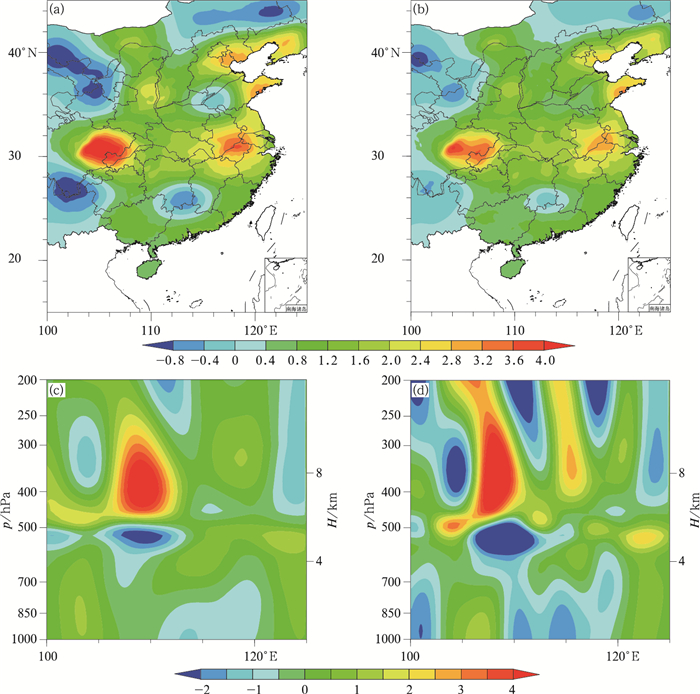
2.3 对同化分析的影响图 4a和4b分别为原方案与新方案850 hPa比湿分析增量场,新方案采用试验4预报结果进行分析(下文新方案均采用试验4预报结果进行分析)。如图所示,新方案的比湿分析增量中心强度较小,新方案对观测站点附近的影响减弱,与单点试验结果相同;图 4c和4d分别为原方案与新方案沿30°N散度场分析增量的垂直剖面图,如图所示新方案与原方案相比,除了大尺度信息外还反映出许多中尺度的散度场增量,与新方案的预期效果一致。
|
图 4 850 hPa比湿分析增量分布(a,b;单位:g·kg-1),沿30°N散度场分析增量的纬向垂直剖面(c,d;单位:10-5 s-1) (a,c)原方案,(b,d)新方案 Fig. 4 The 850 hPa increments of specific humidity (a, b, unit: g·kg-1), the vertical profiles of increments of divergence field along 30°N (c, d, unit: 10-5 s-1) (a, c) original scheme, (b, d) new scheme |
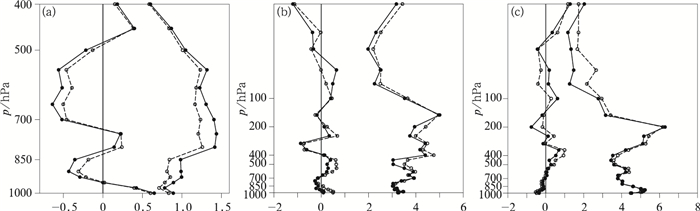
为检验新方案对分析场的影响,利用2015年6月1日08时0.1°×0.1°的欧洲中期数值天气预报中心再分析资料(EC数据)作为参考数据,计算各变量在新方案与原方案分析场的区域平均误差和绝对误差,区域范围为28°~33°N、109°~116°E。如图 5a所示,新方案与原方案相比,比湿在低层的误差减小;说明使用新方案后,比湿在低层对分析场有明显的改善,使低层湿度场更加接近实际情况。如图 5b和5c所示,新方案使散度场、涡度场在200 hPa也略向实况接近。
|
图 5 2015年6月1日08时分析场与EC数据差值的区域平均垂直廓线 (a)湿度场(单位:g·kg-1),(b)散度场(单位:10-5 s-1),(c)涡度场(单位:10-5 s-1) (左边线和右边线分别为区域平均的误差和绝对误差;实线为原方案,虚线为新方案) Fig. 5 Vertical profiles of regional means of difference values between analysis field and EC data at 08:00 BT 1 June 2015 (a) humidity field (unit: g·kg-1), (b) divergence field (unit: 10-5 s-1), (c) vorticity field (unit: 10-5 s-1) (Left line and right line represent the regional mean errors and absolute errors, respectively; solid line: original scheme; dotted line: new scheme) |
形势场的准确预报是降水预报提高的基础,因此本节对新方案与原方案在1日20时预报场中形势场的影响进行分析(图 6),探究新方案对形势场预报的影响,其检验方法与分析场的相同。
如图 6a所示,使用新方案后比湿在中低层更加接近实际情况,但弱于分析场。从图 6b和6c中可以看出,散度场、涡度场在中高层都有明显的改善,与实际情况更加接近。
通过预报场中形势场的偏差分析发现,新方案使湿度场、散度场和涡度场在预报场中均向实况接近,有利于降水预报的提高。
2.5 对降水预报的影响通过分析场和预报场分析可知,新方案使形势场更加接近实况,有利于降水预报的提高,但降水预报结果是否更加接近实况仍需进行检验。图 7中给出了2015年6月1日20时至2日08时降水量实况及4个试验预报的12 h累计降水分布。试验1(图 7a)预报的雨带呈东北—西南走向,降水范围偏小,强度明显偏弱,强降水中心向东北方偏移;试验2(图 7b)与试验1预报结果基本一致,但强降水中心在江汉平原地区变宽,与实况更加接近;试验3(图 7c)在湖北中部降水量达30 mm的预报范围明显大于试验1和试验2,强降水中心明显向西南地区移动,更加接近实况;试验4(图 7d)预报的强降水中心与实况基本一致,但降水范围偏小,强度偏弱,30 mm降水的预报范围明显大于试验3,与实际情况更加符合。从6月1日20时至2日08时12 h累积降水预报结果看,试验4的降水预报与实况更加接近。

|
图 7 2015年6月1日20时至2日08时累计降水量(单位:mm) (a)试验1,(b)试验2,(c)试验3,(d)试验4,(e)实况 Fig. 7 Accumulated 12 h rainfall (unit: mm) from 20:00 BT 1 to 08:00 BT 2 June 2015 (a) EXP1, (b) EXP2, (c) EXP3, (d) EXP4, (e) observed |
为检验模式对降水的预报能力和模拟效果,本文进行降水的客观检验。对6月1日20时至2日08时12 h内每组试验区域内的站点进行分级降水TS评分。降水量分为5个等级评估:0.1~5、5~15、15~30、30~50和50~70 mm。由于单独利用TS评分检验可能造成虚假预报导致预报技巧提高,因此配合预报偏差(Bias)检验降水预报(刘还珠和黄卓, 1998)。各组试验预报的格点降水量通过双线性插值方法插值到试验区域内的各个站点,实况降水量采用全国自动站降水资料。
从各组试验的TS评分(图 8a)中可以看出试验1在0.1~5和50~70 mm降水量的TS评分中较高,而在30~50 mm降水量的TS评分较低。试验2在15~30和30~50 mm降水量的TS评分较高,但在0.1~5 mm降水量中的TS评分较低。试验3在0.1~5和5~15 mm降水量的TS评分中最高,分别为0.74和0.61,说明试验3预报降水范围较大;试验4在15~30、30~50和50~70 mm降水量的TS评分均为最高,分别为0.48、0.31和0.1。试验4对这三个降水量级的偏差Bias(图 8b)也均小于1,说明不是由于强降水的虚假预报造成的TS评分较高,所以试验4在15 mm以上的降水预报技巧提高最为明显。通过客观检验发现,使用新方案后对降水范围和强度的预报都更加接近实况。
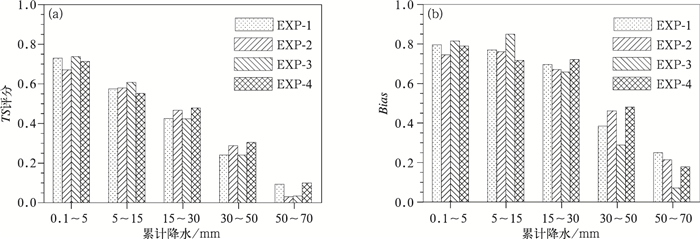
|
图 8 2015年6月1日20时至2日08时12 h累计降水TS评分(a)和偏差(b) Fig. 8 Accumulated 12 h simulated rainfall TS score (a) and Bias (b) from 20:00 BT 1 to 08:00 BT 2 June 2015 |
通过对形势场和降水的分析得知,新方案对这次强降水过程的形势场预报具有明显的调整,并提高模式对强降水的预报能力。为检验新方案与原方案差异在不同尺度内的表现,将新方案分析场、12 h预报场分别与原方案分析场、12 h预报场做差值,通过二维离散余弦变换(Denis et al, 2002)对该结果进行波谱能量分析(图 9),检验新方案在中小尺度的影响。
|
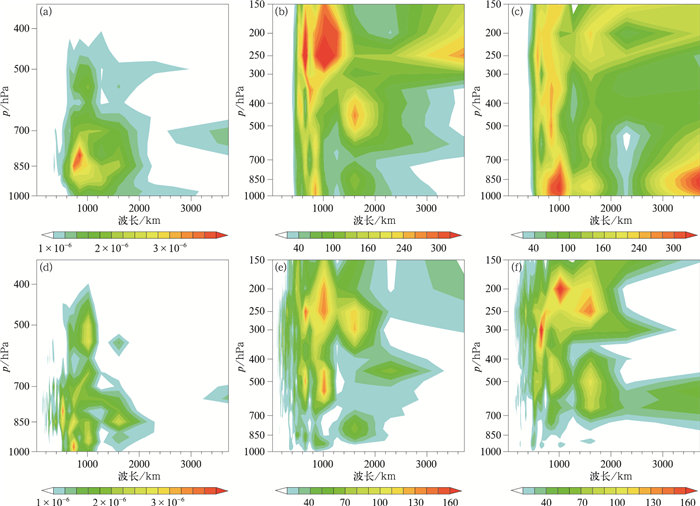
图 9 新方案与原方案差异在不同尺度湿度场(a,d)、经向风(b,e)和纬向风(c,f)的波谱能量(单位:K2)垂直分布 (a, b, c)分析场,(d, e, f)12 h预报场 Fig. 9 Distribution of the differences of spectrum energy (unit: K2) between new scheme and old scheme in different scales of (a, d) humidity field, (b, e) meridional wind, (c, f) zonal wind (a, b, c) analysis field, (d, e, f) 12 h forecast field |
通过分析场的比湿波谱能量(图 9a)发现,大值中心位于850~750 hPa、800 km波长处;经向风波谱能量(图 9b)在300~150 hPa、600~1200 km波长范围内具有最大波谱能量,550 hPa、1600 km波长处具有一个波谱能量大值中心;纬向风波谱能量(图 9c)大值中心出现在1000~850 hPa、800~1100 km波长和3400~3800 km波长范围内。
通过12 h预报场的比湿波谱能量(图 9d)发现,波谱能量明显减小,在1000~700 hPa、500~1000 km波长范围内存在4个大值中心,并在500 hPa、1000 km波长处也存在一大值中心。如图 9e所示,经向风波谱能量也明显减小,大值中心均出现在700、1000和1600 km波长处,分别位于500、250和300 hPa附近。纬向风波谱能量与湿度场波谱能量、经向风相同也明显较小,波谱能量大值中心明显向高层抬升,三个大值中心分别位于300 hPa、700 km波长处,200 hPa、1000 km波长处和250 hPa、1600 km波长处。通过12 h预报场的波谱能量图中还可以发现比湿、经向风和纬向风在200~400 km波长范围内波谱能量均略有增大。
通过上述分析可以看出,经向风、纬向风的新方案分析场与原方案分析场差值在α中尺度(200~2000 km)内从低层到高层都具有较大的波谱能量,大值中心则分别位于中高层和低层,比湿在中低层具有较大波谱能量。从12 h预报场中看出,经向风、纬向风和比湿的波谱能量均明显减小,大值中心出现在α中尺度内,风场波谱能量大值中心出现在中高层,比湿波谱能量大值中心出现在中低层。新方案在α中尺度内具有较大的波谱能量,但是新方案对江汉平原地区的暴雨预报是否具有正效果仍需进行验证,下一小节对新方案与原方案差值的α中尺度信息进行提取,并对江汉平原地区进行分析。
3.2 新方案反映的α中尺度信息对江汉平原暴雨的影响由图 10可以看出,在江汉平原、湖南东北部及湖北中部的850和500 hPa有辐合出现,而在200 hPa有辐散出现,但是强度较弱并且高低层配合较差,主要是由于在该时刻还未出现较强降水,但是从图 10中可以看出使用新方案后在江汉平原地区反映出许多中尺度信息。
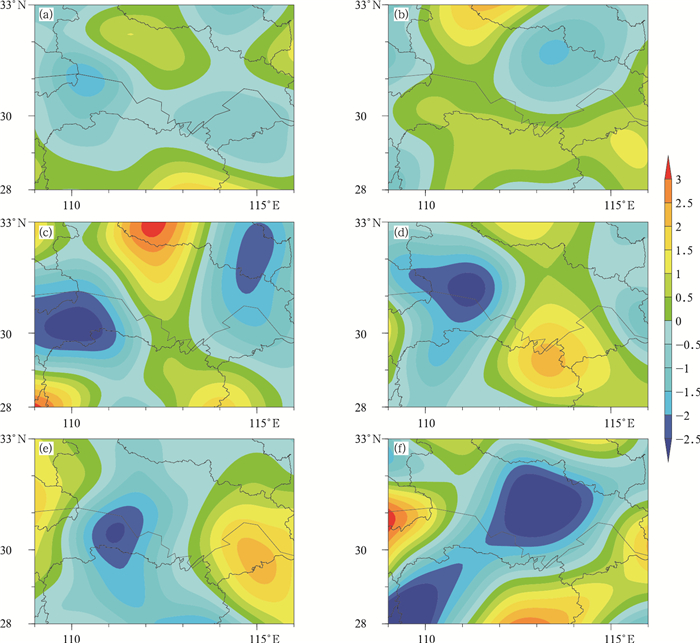
|
图 10 2015年6月1日08时新方案分析场与原方案分析场差异在α中尺度内散度场(a, c, e;单位:10-5 s-1)、涡度场(b, d, f;单位:10-5 s-1)的分布 (a, b)850 hPa, (c, d)500 hPa, (e, f)200 hPa Fig. 10 Divergence field (a, c, e; unit: 10-5 s-1) and vorticity field (b, d, f; unit: 10-5 s-1) of differences between the analysis fields of new scheme and original scheme in α mesoscale at 08:00 BT 1 June 2015 (a, b)850 hPa, (c, d)500 hPa, (e, f)200 hPa |
图 11为新方案12 h预报场与原方案12 h预报场差异在α中尺度内散度场和涡度场分布,从850 hPa散度场(图 11a)中可以看出,在江汉平原、湖南东北部以及湖北中部地区有明显的辐合,在江汉平原和湖北中部地区也出现较强的正涡度。江汉平原及湖南北部的散度场在500 hPa处辐散略有加强,涡度场依然维持为正涡度,说明强降水中心在中低层维持辐合状态。从200 hPa散度场中可以看出,在江汉平原和湖北北部出现较强的辐散,在江汉平原、湖北北部出现负涡度,说明在高层出现较强的辐散运动,与低层配合较好。通过分析发现,新方案在α中尺度内具有较大影响,在江汉平原等地出现低层辐合、高层辐散有利于产生降水的气象要素。通过对比08时与20时的散度场、涡度场发现,20时的尺度明显较小,这与图 9的分析结果一致,20时在200~400 km波长范围具有一定的影响。
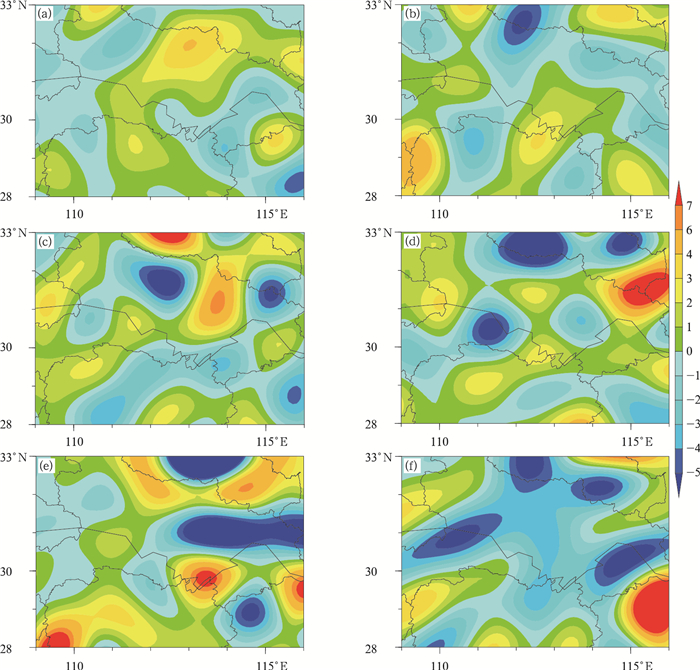
|
图 11 同图 10,但为2016年6月1日20时预报场 Fig. 11 Same as Fig. 10, but for the forecast field at 20:00 BT 1 June 2016 |
图 12为新方案12 h预报场与原方案12 h预报场差异在α中尺度内湿度场分布图。如图 12a所示,在113°~114.5°E、850~800 hPa存在比湿大值区,从比湿850 hPa水平分布也可以看出在江汉平原和湖北中部地区存在大值中心,比湿大值中心与散度场、涡度场配合较好。

|
图 12 新方案预报场与原方案预报场差异在α中尺度内比湿(单位:g·kg-1)分布 (a)沿30°N比湿经向垂直剖面,(b)比湿水平分布 Fig. 12 Specific humidity (unit: g·kg-1) of differences between the forecast field of new scheme and the forecast field of original scheme in α mesoscale (a) vertical profile of specific humidity along 30°N, (b) horizontal distribution of specific humidity |
本节采用连续试验检验新方案对降水预报的稳定性和普适性,连续试验采用业务化的GRAPES_Meso中尺度同化系统,水平分辨率为0.1°×0.1°,预报范围为15°~65°N、70°~145°E,试验采用T639 6 h预报场作为背景场,同化的观测资料包括:探空观测资料、飞机观测资料、云导风观测资料、船舶观测资料和地面观测资料。预报时间为:2015年6月15日08时至30日08时。在新方案中流函数、势函数、非平衡质量场和湿度场均采用三种水平特征尺度拟合方案。降水预报客观检验结果如图 13所示,新方案在小雨、中雨、大雨和暴雨四个量级的ETS评分均高于原方案,对降水预报有明显提高。图 13为新方案与原方案ETS平均评分、偏差平均评分差值,当折线落在黄色方框外表明通过了0.05显著性水平检验。如图所示,小雨、中雨和大雨量级的ETS平均评分通过了0.05显著性水平检验(图 13),说明新方案在这三个降水量级的改善更为明显。
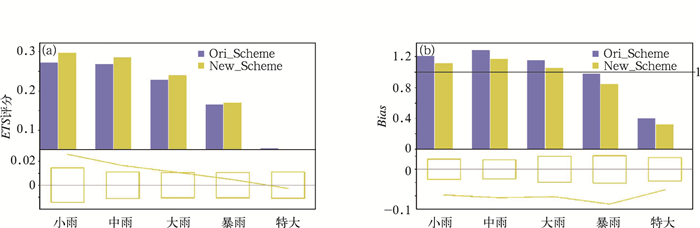
|
图 13 2015年6月15日08时至30日08时全国24 h降水预报累加检验 (a)ETS评分,(b)预报偏差 Fig. 13 Accumulated 24 h simulated rainfall verification over China during 08:00 BT 15-08:00 BT 30 June 2015 (a) ETS score, (b) forecast Bias |
本文根据统计的相关特征尺度设计新同化方案,将新方案应用于2015年6月1—2日江汉平原的暴雨预报中,研究结果表明:
(1) 新方案的功率谱与原方案的高斯型函数的功率谱相比衰减变慢,更加接近统计结果,拓宽水平相关矩阵的波谱空间。新方案对观测点附近的影响减弱,在散度场分析增量中除了反映出大尺度信息外还反映出许多中小尺度信息。
(2) 使用新同化方案后在分析场和预报场中湿度场、散度场和涡度场更加接近实际情况,使降水预报技巧明显提高。流函数、势函数、非平衡质量场和湿度场均使用三种特征水平特征尺度拟合的新方案对15 mm以上降水的预报技巧显著提高,流函数、势函数、非平衡质量场使用三种特征水平特征尺度拟合的新方案对15 mm以下降水的预报技巧提高明显。
(3) 新方案与原方案相比,湿度场、经向风和纬向风在α中尺度内具有较大的波谱能量。根据波谱能量与波长的关系,对江汉平原进行分析,结果表明:在江汉平原和湖北中部低层辐合、高层辐散和中低层湿度增加等有利于降水的要素,说明在这次暴雨预报中新方案引入了更多的中尺度信息。
(4) 本文进行了16 d的批量试验,通过24 h降水检验发现新方案在小雨、中雨、大雨和暴雨量级的ETS评分较高,验证了新方案对降水预报的稳定性。
新方案的降水预报技巧显著提高,试验结果表明新方案对α中尺度信息的引入效果较好,对小尺度信息的引入效果有待增加,下一步将对该方案进行优化,增加小尺度信息的引入;本文针对水平特征尺度进行了研究,未涉及垂直特征尺度的研究,今后将对垂直特征尺度以及垂直特征尺度与水平特征尺度的“匹配”问题进行探讨;本文研究的多尺度资料同化方案是在假定背景误差均匀和各向同性的基础上,而实际水平相关具有非均匀和各向异性(Derber and Bouttier, 1999),对于非均匀和各向异性的实际情况该如何进行模拟,将是下一步研究的重点。
何光鑫, 李刚, 张华, 2011a. GRAPES-3Dvar高阶递归滤波方案及其初步试验[J]. 气象学报, 69(6): 1001-1008. |
何光鑫, 李刚, 张华, 2011b. 高阶递归滤波在一次暴雨预报中的数值试验[J]. 大气科学学报, 34(4): 439-446. |
李冬, 王喜冬, 张学峰, 等, 2011. 基于扩散滤波的多尺度三维变分研究[J]. 海洋通报, 30(2): 164-171. |
刘还珠, 黄卓, 1998. NMC与HLAFS降水预报的比较[J]. 气象, 24(1): 47-52. DOI:10.7519/j.issn.1000-0526.1998.01.010 |
陆汉城, 杨国祥, 2004. 中尺度天气原理和预报:第2版[M]. 北京: 气象出版社, 278-284.
|
沈桐立, 曾瑾瑜, 朱伟军, 等, 2010. 2006年6月6—7日福建特大暴雨数值模拟和诊断分析[J]. 大气科学学报, 33(1): 14-24. |
王晓芳, 徐明, 王婧羽, 等, 2015. 2015年6月1—2日长江流域灾害性天气灾情、汛情和雨情特征[J]. 暴雨灾害, 34(2): 177-183. |
汪小康, 廖移山, 2015. 2015年6月1日江汉平原大暴雨过程诊断分析[J]. 暴雨灾害, 34(2): 184-190. |
张华, 薛纪善, 庄世宇, 等, 2004. GRAPES三维变分同化系统的理想试验[J]. 气象学报, 62(1): 31-41. DOI:10.11676/qxxb2004.004 |
郑永光, 田付友, 孟智勇, 等, 2016. "东方之星"客轮翻沉事件周边区域风灾现场调查与多尺度特征分析[J]. 气象, 42(1): 1-13. |
朱宗申, 胡铭, 2002. 一种区域格点三维变分分析方案——基本框架和初步试验[J]. 大气科学, 26(5): 684-694. |
庄世宇, 薛纪善, 朱国富, 等, 2005. GRAPES全球三维变分同化系统——基本设计方案与理想试验[J]. 大气科学, 29(6): 872-884. |
Bannister R N, 2008. A review of forecast error covariance statistics in atmospheric variational data assimilation.I:Characteristics and measurements of forecast error covariances[J]. Quart J Roy Meteor Soc, 134(637): 1951-1970. DOI:10.1002/qj.v134:637 |
Denis B, Cté J, Laprise R, 2002. Spectral decomposition of two-dimensional atmospheric fields on limited-area domains using the discrete cosine transform (DCT)[J]. Mon Wea Rev, 130(7): 1812-1829. DOI:10.1175/1520-0493(2002)130<1812:SDOTDA>2.0.CO;2 |
Derber J, Bouttier F, 1999. A reformulation of the background error covariance in the ECMWF global data assimilation system[J]. Tellus A-Dyn Meteor Oceanogr, 51(2): 195-221. DOI:10.3402/tellusa.v51i2.12316 |
Lorenc A C, 2003. Modelling of error covariances by 4D-Var data assimilation[J]. Quart J Roy Meteor Soc, 129(595): 3167-3182. DOI:10.1256/qj.02.131 |
Parrish D F, Derber J C, 1992. The national meteorological center's spectral statistical-interpolation analysis system[J]. Mon Wea Rev, 120(8): 1747-1763. DOI:10.1175/1520-0493(1992)120<1747:TNMCSS>2.0.CO;2 |
Purser R J, McQuigg R, 1982. A successive correction analysis scheme using recursive numerical filters[R]. Met Office Tech None, 154: 17.
|
Skamarock W C, 2004. Evaluating mesoscale NWP models using kinetic energy spectra[J]. Mon Wea Rev, 132(12): 3019-3032. DOI:10.1175/MWR2830.1 |
Wilks D S, 2005. Statistical Methods in the Atmospheric Sciences: 2nd ed[M].
San Diego: Academic Press, 449.
|
 2018, Vol. 44
2018, Vol. 44 

