引言

太行山区是海河众多支流的发源地，如大清河、子牙河、漳卫河等，其水资源量占海河流域水资源总量的40%(水利部海河水利委员会，2012)，山区径流又占地表水总径流量的75.9%(费宇红等，2004)。

太行山区径流量的变化会对海河的水资源量产生直接的影响，精确测算太行山区的径流量对于海河流域水资源的调控和京津冀协同发展具有十分重要的现实意义。太行山区径流的主要来源是夏季降水，其雨量占全年总降水量的65%～75%(闫冠华，2013)，精确估算太行山区夏季降水是准确测算山区径流的前提，但由于山区地形复杂，雨量观测站点有限，对山区降水的准确估算一直是个难题。

2000年以来，应用天气雷达反演降水成为气象和水文研究的重点(李柏等，2013；陈静等，2015；王红艳等，2015)，越来越完善的雷达观测系统和雷达观测技术使得多普勒雷达更广泛地应用到降水事件的分析中(张之贤等，2014)。1999年12月在合肥建立中国第一部新一代多普勒天气雷达，2004年石家庄多普勒雷达投入业务试运行，到目前华北地区共有20部多普勒雷达，已建成完善的雷达观测网。同时，多普勒天气雷达观测范围广、时空分辨率高、可及时准确地获取大范围降水空间分布数据，在山区雨量的估算方面有其独特优势，使山区降水精确反演成为可能(张亚萍等，2007；东高红和刘黎平，2012；潘旸等，2015)。

雷达估算降水普遍采用Z-I关系法，其中Z代表雷达反射率因子，I代表小时降水量，不同降水过程由于降水粒子的数密度、几何形状、相态及下落末速度不同，雷达反射率Z也不同，使得Z-I关系式也会随降水类型、降水强度、发生季节等产生变化(范江琳等，2014)。目前，我国广泛布局的S波段多普勒天气雷达是在美国WSR-88D雷达的基础上改进升级而来的，所以雷达反演降水算法也大多沿用美国Z=300I^1.4这一默认算法，相应的雷达降水产品，大多基于该算法得到(张培昌等，2001)。但研究表明，这一默认算法会造成对强降水的严重低估，并不完全适用于华北地区(王丽荣等，2008；袁晓清和倪广恒，2011)，因此，需要进行Z-I关系的本地化，提高反演精度。张家国等(1999)在三峡地区使用概率配对法，分别建立了不同降水类型随测距变化的Z-I关系，有效提升了反演精度。何宽科等(2007)发现：对于小雨量降水，应用美国默认的Z-I关系估测降水比较接近于实际，但应用默认Z-I关系估测台风降水，雨量会被严重低估，利用最小二乘法拟合出适合于舟山地区台风降水的Z-I关系：Z=70I^1.38，估测台风降水误差更小。

目前，雷达反演降水通常采用1小时尺度数据估算Z-I关系，其他尺度很少涉及。Legates(2000)在月尺度上建立雷达反射率和降水的对应关系，来减少不同降水类型和雷达观测带来的误差，进行Z-I关系的实时校准，而实际Z-I关系在更短的时间尺度上变化。Alfieri et al(2010)使用不同的时间窗，利用滑动平均法进行Z-I关系的统计计算，对于意大利西北部19次降水过程的反演验证表明：与传统算法相比，滑动时间窗Z-I算法反演精度提高了28%，尤其是当时间窗为2～5 h时，反演精度更高。国内采用多时间窗法进行降水反演的研究相对较少，有必要验证该方法在国内雷达降水反演的准确性，以及不同降水过程的最佳滑动时间窗。

本文应用太行山东部中低山区阜平、灵寿、平山3个县2013和2014年6—9月小时雷达反射率和对应雨量站降水数据，采用不同滑动时间窗拟合Z-I关系，并与其他研究建立的太行山Z-I关系、默认Z-I关系进行对比，验证不同反演方法的精度，旨在为太行山区雷达降水反演提供方法支撑。

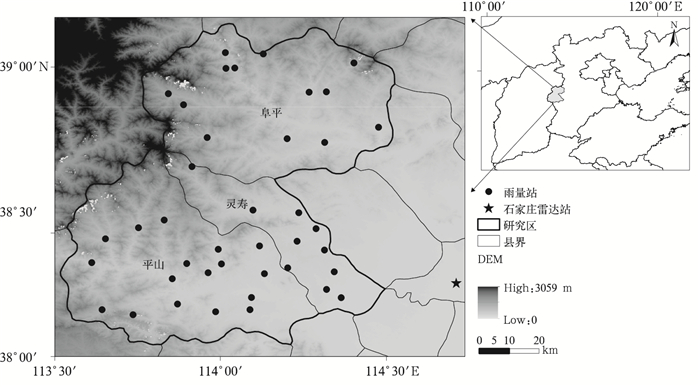
1 资料和方法 1.1 降水、雷达反射率数据及处理方法

选取太行山区东麓的平山县、灵寿县和阜平县(面积6213 km²)为研究区，该地区地形西北高东南低，最高海拔2263 m。选取3个县41个自动雨量站2013和2014年6—9月共45次降水过程的小时降水数据。雷达反射率数据使用石家庄多普勒天气雷达站2013和2014年6—9月6 min/次的基本反射率数据。研究区地形、石家庄雷达站、自动雨量站分布见图 1，雨量站属性见表 1。

多普勒雷达是锥型扫描，观测地物距离雷达站越远，所取的仰角越低。本研究区域内的雨量站与石家庄雷达站的直线距离大多超过50 km(表 1)，由表 2可知，本应选择0.5°仰角，但由于研究区地形复杂，使用0.5°仰角会产生一定遮挡，导致雷达反射率出现误差。而且，地面降雨强度、降水范围与1200 m高度层的雷达反射率关系较为密切(张培昌等，2001；白先达等，2011)，考虑到研究区海拔大多超过500 m，故将所探测的雷达回波高度范围设定为1500～2000 m，结合研究区域距离雷达站距离，使用三角函数公式tanα=H/L计算(α表示雷达仰角，H表示雷达观测到的气象目标高度，L表示观测目标对应地点到雷达的直线距离)，最终确定采用1.5°仰角的雷达反射率数据最为合适，可以比较理想地减少遮挡和地物杂波的干扰。

石家庄多普勒天气雷达每次体扫的时间间隔约是6 min，1 h之内有10次观测数据，参照邵月红等(2009)、白先达等(2011)的研究，将各点对应的10个雷达反射率值求算数平均，获取该小时的雷达反射率。

袁晓清和倪广恒(2011)、梁建茵和胡胜(2011)、陈静等(2015)的研究表明，以雨量站所在的格点为中心，周围9个格点雷达回波强度的平均值与地面观测降水的关系最为密切，以各雨量站为中心，选取周围9点的雷达反射率平均值，作为该点的雷达反射率值，与雨量站降水建立对应关系，来减小坐标转换产生的误差。

在使用雷达反射率-降水数据前，根据Fulton et al(1998)的研究方法对每个时次的雷达-雨量站数据进行质量控制。首先，去除雷达回波对应降水值小于0.1 mm·h^-1(可调参数)的数据对，保证数据对中对应的雨量站有降水，其次，去除雷达反演降水或者雨量站实测值高于150 mm·h^-1(可调参数，该值根据研究区多年最大小时降水统计得到)的数据对。最后，计算雷达-雨量站数据对的归一化绝对偏差，同时，计算数据对的标准偏差，若绝对偏差超过标准偏差的3倍(可调参数)，则删除该数据对，以减小0℃层亮带对雷达降水反演的影响(张亚萍等，2013)。

1.2 雷达反射率与降水关系反演算法 1.2.1 对比Z-I关系

概率配对法(probability-fitting technique, PFT)：王丽荣等(2008)在华北南部地区，利用概率配对法在不同月份、不同区域分别建立Z-I关系，来改善雷达降水反演的精度。尤其是建立了太行山区不同月份的Z-I关系：4—6月：Z=54.48I^2.43，7—8月：Z=23.11I^2.2，9—10月：Z=91.09I^1.82，由于该区域与本文研究区位置相近，将这3个Z-I关系作为概率配对法的计算公式，与本文中的其他Z-I关系算法进行对比，来验证不同方法的精度，为方便对比，下文统称概率配对法。

默认算法(default algorithm, DA)：根据美国夏半年大量对流云降水过程，统计得到的Z=300I^1.4，在美国东部大部分地区都得到了很好的验证(Battan，1973)，我国新一代多普勒天气雷达的降水算法也大多沿用了这一公式，因此将该默认算法也纳入对比，来验证其反演精度。

1.2.2 滑动时间窗Z-I关系法

由于不同时空雨滴谱分布不同，Z-I关系存在很强变异性，固定不变的Z-I关系很难同时兼顾到不同雨型、不同量级的降水过程(Richards and Crozier, 1983；Smith and Krajewski, 1993；Lee and Zawadzki, 2005；勾亚彬等，2014)。因此，理论上增加Z-I关系的数量，可以更为准确地反映Z和I之间的关系，反演效果会更好。本文由于是对过去发生降雨的反演，每次降水过程都可根据其反射率与降水强度，计算相应的Z-I关系，这样整体上可以增加Z-I关系的数量，减小反演误差。同时，雷达观测的降水目标与实际降雨之间受云团移动和风等复杂天气影响，可能存在一定的时间间隔，相同时刻雷达观测的反射率与雨量站降水可能并不完全相关，因此，参照Alfieri et al(2010)研究，采用不同时长时间窗滑动平均的方法来获取雷达反射率与降水数据对，分别反演不同时间窗数据对的Z-I关系，来给每次降水过程提供多个Z-I关系，从中选取最佳Z-I关系，来提高反演精度。

在每次降水过程中，空间上以每个站点为中心，选取周围9个格点雷达反射率的平均值，时间上取1 h内10个时次雷达反射率的算数平均数，作为该点对应的反射率，与雨量站小时降水组成雷达反射率和降水数据对，在此基础上分别采用1、2、3、4和5 h作为滑动时间窗进行滑动平均，取得相应的反射率和降水数据对，再利用最小二乘法拟合Z-I关系。

降水估测时，反射率的处理过程与反演时一致，取1 h 10个时次的反射率算术平均值，应用不同滑动时间窗反演得到的Z-I关系，得出小时尺度雷达估测降水。

反演时的滑动时间窗仅用于计算时间窗内反射率及降水的算术平均值，其意义在于解决同一时刻反射率和降水对应不准确的问题。降水估测时，直接将不同滑动时间窗Z-I关系应用于雷达小时反射率，得到小时尺度降水数据。如果个别站点降水时数小于滑动时间窗，则跳过该站点数据(在本文选取的降水事件中，绝大部分站点都有超过5 h的连续降水)。

本文针对不同等级降水过程分别进行验证，降水等级按24 h降水量的大小被划分为小雨(<10 mm·d^-1)、中雨(10～25 mm·d^-1)、大雨(25～50 mm·d^-1)、暴雨(>50 mm·d^-1)。

1.2.3 最小二乘法确定参数

最小二乘法的原理是通过最小化数据误差的平方和，来获得数据的最佳函数匹配，简单来说就是要使得观测点与估计点间距离的平方和达到最小，通过最小二乘法得到的函数可以准确反映数据变化的总体趋势(陈军红，2012)。

将Z=AI^b等式两边同时取对数变形后，得出lgZ=blgI+lgA，令y=lgZ，x=lgI，c=lgA，则y=bx+c，根据最小二乘法原理得到：

$ c = \overline y - b\overline x $

(1)

$ b = \frac{{n\sum\limits_{i = 1}^n {{x_i}{y_i} - \sum\limits_{i = 1}^n {{x_i}\sum\limits_{i = 1}^n {{y_i}} } } }}{{n\sum\limits_{i = 1}^n {x_i^2 - \sum\limits_{i = 1}^n {{x_i}} } }} $

(2)

式中，y 和x分别代表y与x的算数平均数，将已知的Z-I序列代入式(1)和式(2)，便可以推出A，b，求得相应的Z-I关系。

1.2.4 误差检验指标

为方便比较分析，引入平均误差(ME)、平均绝对误差(MAE)、均方根误差(RMSE)来反映雷达反演降水的准确性。

$ ME = \frac{1}{n}\left[ {\sum\limits_{i = 1}^n {\left({{R_i} - {G_i}} \right)} } \right] $

(3)

$ MAE = \frac{1}{n}\left[ {\sum\limits_{i = 1}^n {\left({\left| {{R_i} - {G_i}} \right|} \right)} } \right] $

(4)

$ RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{R_i} - {G_i}} \right)}^2}} } $

(5)

式中，R_i表示雷达估测降水量，G_i表示雨量站实测值，n表示样本容量。根据公式可知，ME，MAE，RMSE越小，反演精度越高，估测降水与实际降水越接近。

1.2.5 交叉验证

交叉验证法是目前最常见的误差检验法之一，参照Chen et al(2008)使用的交叉验证方法，将研究区41个雨量站点分成4组，每组10个(最后一组11个站点)，考虑到地形影响，尽量使每组站点均匀分布。每次选取3组站点作为反演站点用于反演Z-I关系，使用剩下一组站点进行验证，如此重复4次，保证所有站点都作为验证站点被选取一次。将验证站点对应的小时反射率代入反演出的Z-I关系计算小时降水，与雨量站实测小时降水、概率配对法和默认算法计算的小时降水进行对比，来验证不同算法的准确性。

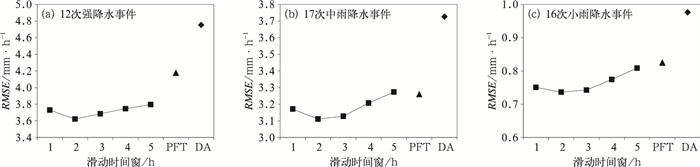
2 结果分析 2.1 不同雨量降水过程误差对比

选取2013和2014年6—9月的典型暴雨、中雨和小雨降水事件，使用默认算法、概率配对法、滑动时间窗Z-I算法反演降水，对降水误差进行交叉验证，得到不同反演算法的误差对比。图 2中可以看出，在三种不同雨量降水中，源于美国的默认算法误差最大，说明该算法基本不适用于太行山区的降水反演，有必要进行Z-I算法的本地化。

其次是概率配对法。滑动时间窗法的误差最小，无论滑动时间窗长短，误差基本都小于其他两种方法；不同的滑动时间窗对比，2 h时间窗取得的Z-I关系误差最小，反演效果最好。

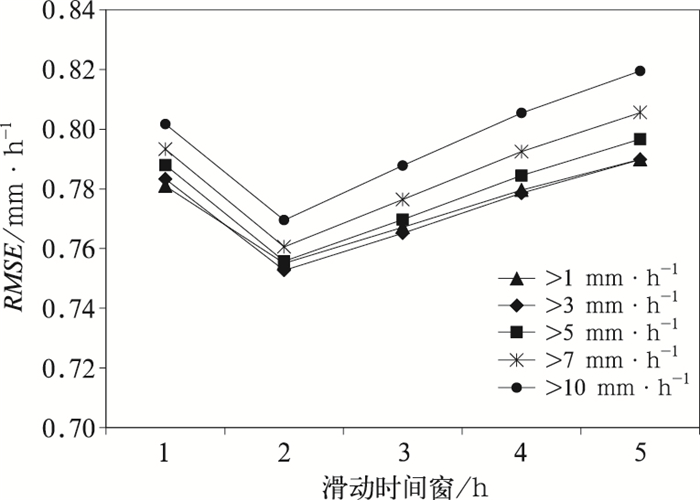
2.2 不同量级降水验证

为进一步分析不同量级降水的反演精度，研究将2013—2014年12次大到暴雨降水事件的小时降水，按>1 mm·h^-1、>3 mm·h^-1、>5 mm·h^-1、>7 mm·h^-1、>10 mm·h^-1进行分组，分别计算各组数据的RMSE。

图 3可以看出，在不同滑动时间窗RMSE对比中，2 h时间窗反演的Z-I关系计算的降水误差最小，说明2 h时间窗确实可有效提升降水反演精度。同时，不同雨量的对比表明：2 h时间窗对7 mm·h^-1以上降水的反演精度提升幅度最大。因此，接下来的验证将滑动时间窗设置为2 h。

选取2013—2014年暴雨(2013年7月9日)、中雨(2014年9月14日)和小雨(2013年9月19日)三次降水过程，分别利用默认算法、概率配对法和2 h滑动时间窗法进行降水反演，并与雨量站实测降水进行对比。

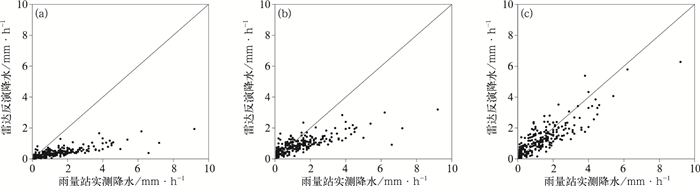
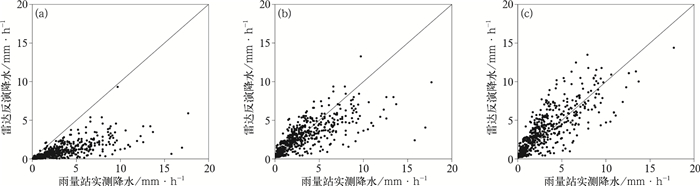
图 4和表 3是暴雨降水(2013年7月9日)条件下降雨反演的误差对比，可以看出：默认算法明显低估了实际降水，降水越大低估越明显，MAE和RMSE也都是最大的，反演精度最差。概率配对法反演的降雨精度提升明显，MAE为1.21 mm·h^-1，与2 h滑动时间窗法相当，但低估的散点仍然较多。2 h滑动时间窗法反演效果最好，散点基本都围绕在y=x函数附近，MAE和RMSE都较小，ME最小，仅为-0.06 mm·h^-1，与实际降水更为接近。

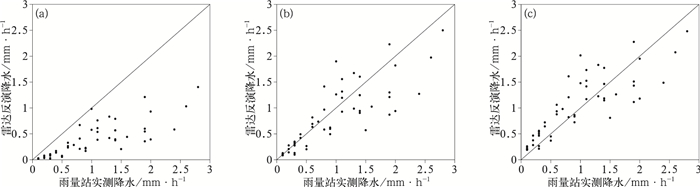
图 5和表 4是中雨降水(2014年9月14日)条件下不同方法的降雨反演对比，可以看出，默认算法明显低估了实际降雨，误差最大，ME，MAE和RMSE都表现最差。2 h滑动时间窗法反演的结果和概率配对法相比，提升明显，特别是改善了2 mm·h^-1以上降水的反演精度，降水散点主要收敛于在y=x函数附近。表 4的参数对比之中也可以看出，三者中默认算法精度最差，2 h滑动时间窗法反演误差最小，反演精度最高。

图 6和表 5是2013年9月19日小雨降水条件下的反演结果，可以看出，与暴雨和中雨条件相似，默认算法低估最明显；概率配对法和2 h滑动时间窗法估算结果相近，表 5的各参数对比也表明小雨降水过程中，后两种算法都能取得较好的反演效果。

综合三次降水的反演效果可以发现，默认算法低估显著，估算精度差，误差最大，基本不适用于研究区的降水反演。概率配对法对中雨和暴雨降水存在一定低估，但对小雨降水反演精度较高，说明概率配对法更适用于小雨降水反演。三种方法对比，2 h滑动时间窗法反演的降水散点分布最为收敛，无论暴雨、中雨、小雨，散点基本都能围绕y=x函数分布，表 3～表 5中各项误差指标基本保持最小，反演效果最好。

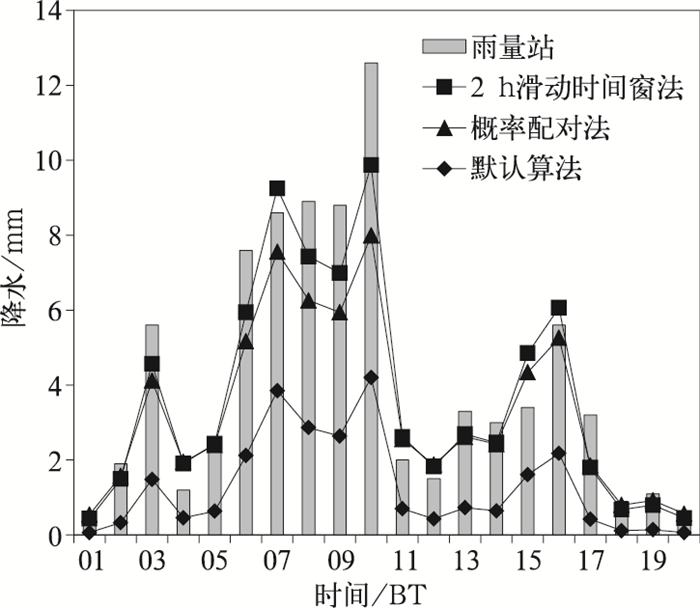
2.3 个例分析

为更直观地比较不同反演算法的误差大小，选取2013年7月9日下口站20 h连续降水事件，利用默认算法、概率配对法和2 h滑动时间窗法分别反演降雨，并与雨量站实测雨量进行对比。如图 7所示，除15:00时间段外，在其他降水时段2 h滑动时间窗法所估算的小时降水与雨量站实测降水都最为接近，其他算法均有一定程度的低估，默认算法低估最为严重。在降雨 < 2 mm的时段，概率配对法、2 h滑动时间窗法所计算的降水与实测降水都很接近，在>6 mm的时段，概率配对法估算的降水低估显著，2 h滑动时间窗法计算的降水与实测降水更为接近。

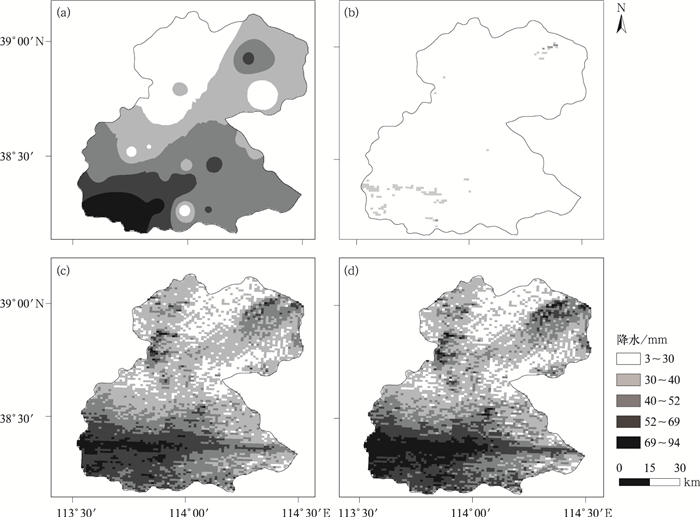
为检验不同反演方法的精度，进一步研究降水的空间分布，利用2013年7月9日41个雨量站日降水数据，采用反距离权重插值算法计算区域日降水量(图 8a)，默认算法、概率配对法和2 h滑动时间窗法计算的日降水分别见图 8b、8c和8d。可以看出：默认算法估算精度最差，整体都存在严重低估，已不能反映降水的空间分布特征；概率配对法和2 h滑动时间窗法计算的降水空间分布相似，都能比较准确地反映出研究区西南和东北的两个降水中心，尤其是2 h滑动时间窗法计算的降水中心附近降水量整体要高于概率配对法，与雨量站插值得到的降水空间分布更为接近。总体来看，2 h滑动时间窗法反演效果最好，概率配对法次之，默认算法反演效果最差。

3 讨论

滑动时间窗Z-I算法的主要优势在于：解决了同一时刻反射率和降水对应不准确的问题，通过灵活调整时间窗来获取最佳的Z-I关系，因此可以取得较好的降水反演效果。滑动时间窗的选择很关键，很多研究(邵月红等，2009；陈静等，2015)将1 h作为滑动时间窗，而Alfieri et al(2010)研究表明2～5 h的滑动时间窗取得的反演效果较好，本文在其基础上，进一步证明2 h是最佳的滑动时间窗，反演精度最高。使用2 h滑动时间窗计算可以进一步提升降水反演精度，获取高时空分辨率的雷达降水产品，提升雷达产品的业务应用价值，同时在当今全球气候异常的大背景下，区域降水的反演对于山区防灾减灾、水循环解析、变化预测及水资源管理具有重要现实意义。

本文使用的是1 h(10个时次)反射率的平均与小时降水对应的数据，相对6 min/次的雷达反射率与雨量对应的数据，物理意义较弱，但对于1 h以及更长时间尺度累计降水估测精度较高(白先达等，2011)。6 min尺度的短时降水估测可以详细地反映降水过程变化, 而1 h尺度的长时间降水估测可以较准确估测降水量的大小(伍静等，2010)，本文主要侧重降水量估测，因此选用1 h尺度的反射率与降水数据。同时，本文的目的主要是为山区水循环的估算提供更加可靠的数据支撑，更侧重于降水的反演，故与临近天气预报不同，可以选取小时尺度的时间窗，进行降水的估算。

对于时长较短的小雨降水过程，滑动时间窗Z-I算法相对概率配对法反演精度并没有明显提升，主要是因为小雨降水过程一般时长较短，不同时次间反射率和降水量差异较小，导致该算法对小雨降水过程的反演精度提升有限。

滑动时间窗Z-I算法在降水发生后，估算区域降雨量并分析降水的空间分布等场景，实用价值明显，本文并没有进行降水预估相关的应用研究，该方法对区域降水的预估能力有待进一步验证。滑动时间窗Z-I算法仍存在一定误差，这可能与山区的复杂地形、气候条件造成的雷达反射率和雨量站空间对应不一致(阮征等，2017)、雷达反射率降噪不彻底、雷达标定参数不恰当等因素有关(俞小鼎等，2006)，后续仍有优化提升的空间。本文应用2013—2014年夏季降水进行降水估算精度的分析，后续的研究中将利用更长时间序列的降水和雷达数据，同时扩大研究区，进行太行山复杂山地降水的空间反演，来获取更详细的山地降水空间变化规律信息，为山地水循环的估算提供更加可靠的数据支撑。

4 结论

本文利用雷达基本反射率因子数据和自动雨量站资料，按不同时长的滑动时间窗计算Z-I关系、反演降水，并与默认算法、概率配对法计算的雨量进行对比，在不同量级降水过程中进行验证，结果表明：

(1) 应用默认算法反演降水精度最差，低估严重，基本不能反映降水的实际情况；概率配对法，相比默认算法反演精度有了一定的提高，改善了小雨量降水的反演精度，但对强降水仍存在低估。

(2) 应用滑动时间窗Z-I关系法反演降水，不同时间窗反演精度不同，随时间窗的增大，误差呈现先下降后上升的趋势，其中2 h滑动时间窗拟合的Z-I关系反演精度最高，5 h滑动时间窗误差最大。

(3) 对于不同量级降水的反演对比，滑动时间窗Z-I关系法对中雨的改进最大，相比较默认算法，精度提高了50%左右。个例分析表明：滑动时间窗Z-I算法的主要优势在于改善早期算法对雨强较大降水的低估，2 h滑动时间窗反演降水的空间分布与实际更为接近。