引言

云是指停留在大气中的水滴或冰晶的集合体，是地球水分和能量循环的重要因子，是地球大气辐射收支平衡的主要调节者，也是影响地球大气热量平衡的重要因素，云的年、季节变化对于研究全球气候变化以及水汽收支平衡具有重要意义(徐兴奎，2012；马占山等，2008)。

随着科技发展，越来越多的新技术、新方法被应用于气象观测，国内外在云自动化观测方面已经做了大量研究工作，取得了卓有成效的进展。目前国内外对云高的观测主要采用主动设备如激光云高仪、毫米波测云仪等，而被动式云高观测主要基于红外波段大气传输方程反演云底高度；在云量自动化观测方面主要采用红外和可见光成像方式，利用图像处理技术实现云量探测(高太长等，2010；李肖霞等，2016；李思腾等，2015；赵静等2017；周毓荃和欧建军，2010)。由于激光云高仪等主动式云高观测设备采用单点测量方式，虽然能准确地获取云底高但是无法获取云量，红外和可见光成像仪能够得到全天空总云量，但是缺少云高信息，即使采用大气传输方程反演云底高，由于大气辐射传输的复杂性，使得云底高反演误差较大，很难实现云高、云量同时观测(陶法等，2013)。

双站可见光成像仪基于双站测距原理能够准确地获取云底高度，并进行全方位立体扫描得到全天空可见光云图，实现云高、云量同时观测，扫描式红外成像仪基于大气辐射传输方程获取云底高，利用全方位立体扫描获取全天空红外云图，实现云高、云量同时观测。由于双站可见光成像仪在可见光波段，受能见度影响较大，且在夜间无法观测，扫描式红外成像仪虽然能够昼夜实时观测，但是云高测量误差较大，且在云量观测上，受到大气气溶胶和大气传输路径的影响，使得低仰角获取云量误差较大；结合双站可见光成像仪和扫描式红外成像仪的优点，基于数据融合技术，构建地基双波段全天空成像仪，实现云高、云量同时观测。将双站可见光成像仪所测得的云底高，结合扫描式红外成像仪的红外辐射亮温，对云底到地面的温度递减梯度参数进行实时订正，反演云底高，提高红外云底高反演精度；充分利用可见光全天空云图分辨率高，而红外全天空云图受雾霾影响小, 能够全天候观测，将两者结合起来提高云量观测精度。

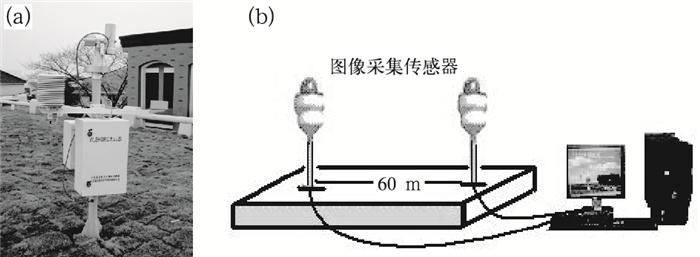
1 系统结构

地基双波段全天空成像仪，主要有两部分组成，一部分是扫描式红外成像仪(SIRIS-1)，其结构由热红外测温传感器、地面温湿度传感器、水平和俯仰旋转平台和控制箱等组成，红外测温传感器采用德国欧普士公司生产的CTlast，用于感应8~14 μm波段大气向下红外辐射，系统响应时间为120 ms，温度分辨率为0.1℃。距离比S=34：1，系统结构如图 1a所示(谭涌波等，2005；胡树贞等，2012)，另一部分为双站可见光成像仪，采用一对相机置于水平和俯仰可旋转的云台中，两个云台相距60 m，图像采集传感器采用Sony公司的FCB101P机芯，视场角为54°，图像分辨率为44万像素，最低照度为0.1 LX。旋转云台采用一体化高速球机，球机旋转角范围，水平角为0°~360°，俯仰角为0°~93°，球机预置位重复精度小于0.05°。系统结构如图 1b所示(胡树贞等，2013)。

2 云高数据融合技术 2.1 双站成像测量云高

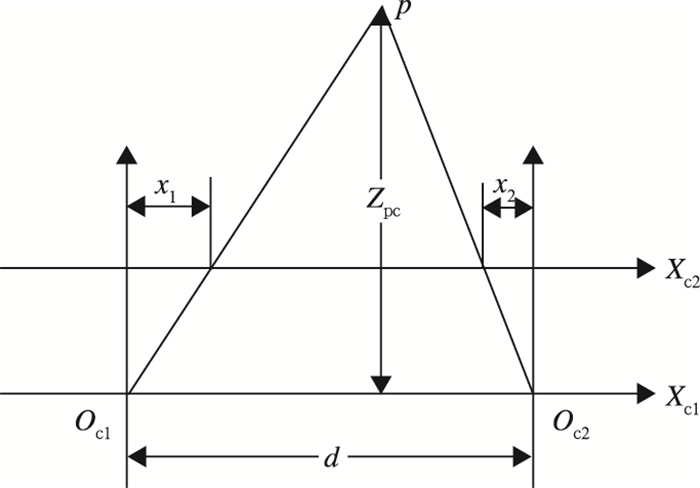
双站可见光成像仪利用一对相机同时拍摄一组图片，基于双站成像测距原理测得天顶方向的云底高度。基于双站成像测距原理示意图如图 2所示(陶法等，2013；谭涌波等，2005)。其中：d为两相机之间的距离(基线长)，p为目标物，Z_pc为目标物到相机的距离，x₁、x₂分别为目标物成像点到像主点(相片中心的)的距离。根据相似三角形原理可算得，目标物距离：

$ Z = f\frac{d}{{\left| {{x_1} - {x_2}} \right|}} $

(1)

式中f为相机焦距(单位:像素点)。

2.2 红外反演云高

红外测温传感器基于大气辐射传输方程反演云底高度(胡树贞等，2013；章文星等，2007)：

$ H = \frac{{{t_b} - {t_{{\rm{hum}}}} - {t_v} - t}}{\mathit{\Gamma }} $

(2)

式中，t_b为红外测温传感器采集一次天顶方向的辐射亮温温度，Γ=-6℃·km^-1，为大气温度垂直平均递减率，t_hum为湿度因子对辐射亮温的订正温度，t_v为能见度因子对辐射亮温的订正温度, t为地面温度。

2.3 云高数据融合

考虑温度垂直递减率随季节、时间、地理环境、地点以及大气气溶胶等影响，导致利用式(2)直接反演云底高度误差较大，结合双站可见光成像仪测得天顶云底高，对大气温度垂直递减率进行实时订正，提高红外反演云底高精度, 大气温度垂直递减率订正及云底高度反演公式为：

$ \left\{ \begin{array}{l} \mathit{\Gamma '} = \frac{{{{T'}_b} - t}}{h}\\ H = \frac{{{T_b} - t}}{{\mathit{\Gamma '}}} \end{array} \right. $

(3)

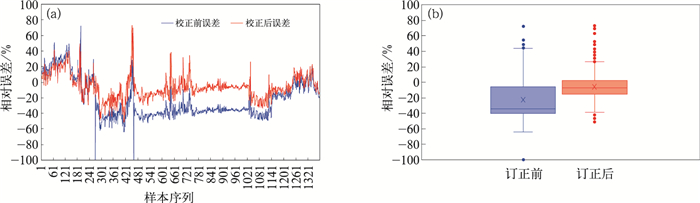
式中，Γ′为订正后的大气温度垂直递减率，T_b为红外测温传感器实时测得云体红外辐射亮温，t为地面环境温度，h为双站可见光成像仪所测天顶云高，T_b^′为双站可见光成像仪和红外测温传感器同时探测到云体的红外辐射亮温。由于天顶方向云底亮温与双站可见光成像仪所测云高在时间和空间对应上存在误差，造成Γ′值波动，需要对一段时间内计算得到的云底温度递减梯度参数进行统计平均，代替常规的大气温度垂直递减率，进行云高反演。利用2012年1—6月期间，激光云高仪测到天顶云高和扫描式红外全天空成像仪测得的云底高进行对比，订正前后散点分布图(图 3)中可以看出订正前相关系数为72%，订正后提高到94%，订正前后相对误差如图 4和表 1所示。

从图 4和表 1可以看出订正后相对误差平均值从订正前的-22.4%提高到-5.8%，标准偏差从订正前24.2%减小到15.6%，说明通过数据融合红外云高测量准确度得到有效提高。

3 云量数据融合技术 3.1 可见光全天空云图

通过对双站可见光成像仪云台控制实现全天空扫描，先水平方位扫描1圈得到9张照片，然后抬升30°后再水平扫描，依次往复扫描4圈共获得36个方位子图，先对子图进行预处理，消除畸变和光线不均匀，再进行球面投影，采用加权平均方法进行拼接，得到全天空可见光云图(陈青青等，2016)，球面投影示意图和全天空可见光云图(图 5)。

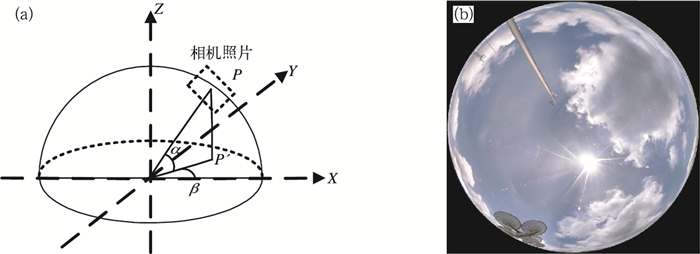
球体中心为坐标系原点, 球半径为相机焦距f, 相机仰角为α, 相机旋转角为β，图像中心是相机光轴与视平面的交点。设照片宽度为W, 高为H, 图像平面任意点P(x, y)在相机坐标系中的坐标为P(x, y, f), 世界坐标系中坐标为P(x_w, y_w, z_w)，相机坐标系转化成世界坐标系(曾文锋等，2001)为:

$ \begin{array}{l} \left({\begin{array}{*{20}{c}} {{x_w}}\\ {{y_w}}\\ {{z_w}} \end{array}} \right) = \\ \left({\begin{array}{*{20}{c}} {\cos \beta }&0&{\sin \beta }\\ 0&1&0\\ { - \sin \beta }&0&{\cos \beta } \end{array}} \right)\left({\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \alpha }&{ - \sin \alpha }\\ 0&{\sin \alpha }&{\cos \alpha } \end{array}} \right)\left(\begin{array}{l} x - W/2\\ y - H/2\\ f \end{array} \right) \end{array} $

(4)

过点P与球面交点P′的三维坐标为：

$ \left\{ \begin{array}{l} {{x'}_w} = \frac{f}{{\sqrt {x_w^2 + y_w^2 + z_w^2} }}{x_w}\\ {{y'}_w} = \frac{f}{{\sqrt {x_w^2 + y_w^2 + z_w^2} }}{y_w}\\ {{z'}_w} = \frac{f}{{\sqrt {x_w^2 + y_w^2 + z_w^2} }}{z_w} \end{array} \right. $

(5)

则点P′投影到水平面的二维坐标为P′(x_w^′, y_w^′)。根据投影变换式(4)和(5)，进行图像拼接，采用加权平均方法，实现图像间的平滑过度，消除拼接的痕迹，两幅图像加权平均融合公式(孙晓钢等，2008；杨燕等，2007；史金霞和王铮, 2005)为：

$ {I_{\left({i, j} \right)}} = \alpha \cdot {I_{1\left({i, j} \right)}} + \left({1 - \alpha } \right) \cdot {I_{2\left({i, j} \right)}} $

(6)

式中，α为加权系数，

$ \alpha = \frac{{{d_1}}}{{{d_1} + {d_2}}} $

式中，d₁, d₂分别为两幅图像重叠区域中的点到重叠区域边沿的距离。

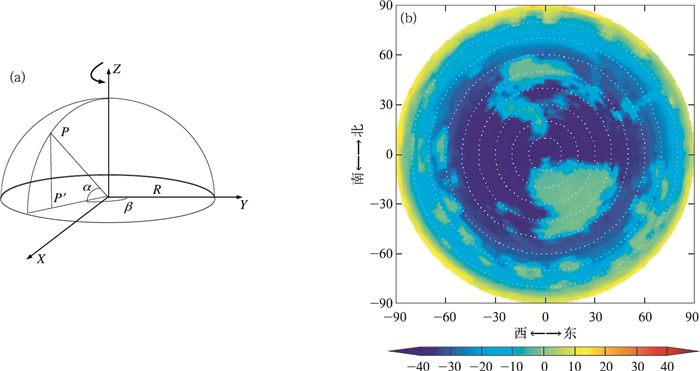
3.2 红外全天空云图

扫描式红外成像仪旋转平台带动红外测温传感器对全天空进行立体扫描，水平方位扫描1圈后抬升一定角度(2.25°)再水平扫描，依次往复扫描40圈共获得4023个方位点的辐射亮温信息，将不同方位和仰角观测的辐射亮温值拼接为半球全天空垂直向下辐射亮温分布图(章文星等，2010)。平面坐标中径向对应天顶角，原点对应天顶，径向与方位顺时针方向的夹角为方位角。球面投影示意图和全天空红外云图如图 6。

设天空任意一点P在球面坐标系中的坐标位置为

$ \left({\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right) = \left(\begin{array}{l} R \cdot \cos \alpha \cdot \cos \beta \\ R \cdot \cos \alpha \cdot \sin \beta \\ R \cdot \sin \alpha \end{array} \right) $

(7)

式中，α和β分别为该点所处位置的仰角和方位角。P点在平面坐标系中的投影点P′的坐标为：

$ \left(\begin{array}{l} {X'}\\ {Y'} \end{array} \right) = \left(\begin{array}{l} R \cdot \cos \alpha \cdot \cos \beta \\ R \cdot \cos \alpha \cdot \sin \beta \end{array} \right) $

(8)

根据式(8)可拼接出全天空红外云图。

3.3 图像配准

扫描式红外成像仪中红外温度测量单元的视场角为2.25°共扫描4023个点，拼接成一幅全天空红外云图，图像像素点为400×400，而双站可见光成像仪，相机视场角为56°共36张图片拼接成一幅全天空可见光云图，图像像素点为1338×1338。由于可见光和红外图像视场角、空间分辨率和传感器的空间位置等方面不一致，图像间不可避免地出现平移、旋转、比例缩放等差异，在图像融合之前需要对两幅图像进行配准(陶冰洁等，2004；王鲲鹏等，2009；苑津莎等，2009；闫钧华等，2013)。

在实际安装过程中很难保证两个扫描装置具有一致的姿态角[横滚(α)、俯仰(β)、旋转(γ)]，由于红外采用单点扫描所以不存在横滚，两个设备相距很近，约1 m左右，可以近似认为两云图之间没有平移，所以两幅全天空云图之间配准参数主要为：缩放(k)、俯仰(α)和旋转(γ)。

以焦点为中心建立坐标系，则两幅全天空云图中任意像点的三维坐标为(x₁, y₁, f₁)和(x₂, y₂, f₂)，根据放射变换模型：

$ \left(\begin{array}{l} {x_1}\\ {y_1}\\ {f_1} \end{array} \right) = k \cdot \mathit{\boldsymbol{R}}\left(\begin{array}{l} {x_2}\\ {y_2}\\ {f_2} \end{array} \right) $

(9)

其中旋转矩阵：

$ \begin{array}{l} \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \beta }&{ - \sin \beta }\\ 0&{\sin \beta }&{\cos \beta } \end{array}} \right] \cdot \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\cos \gamma }&{ - \sin \gamma }&0\\ {\sin \gamma }&{\cos \gamma }&0\\ 0&0&1 \end{array}} \right] \end{array} $

(10)

首先通过对可见光云图进行采样得到比例系数K，使两幅图像的投影半径相同f₁=f₂=f。再采用最小二乘方法求解旋转矩阵R，

令矩阵

$ \mathit{\boldsymbol{A = }}\left({\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1m}}}\\ {{y_{11}}}&{{y_{12}}}& \cdots &{{y_{1m}}}\\ f&f& \cdots &f \end{array}} \right) $

$ \mathit{\boldsymbol{B = }}\left({\begin{array}{*{20}{c}} {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2m}}}\\ {{y_{21}}}&{{y_{22}}}& \cdots &{{y_{2m}}}\\ f&f& \cdots &f \end{array}} \right) $

$ \mathit{\boldsymbol{R}} \cdot \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{A}} $

则

$ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\left({\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{T}}}} \right)^{ - 1}} $

(11)

选取能见度较好积云天气条件下的红外和可见光全天空云图，在两幅图像中选择3个以上的独立点，利用公式(11)可以求得旋转变换矩阵，达到图像配准目的。

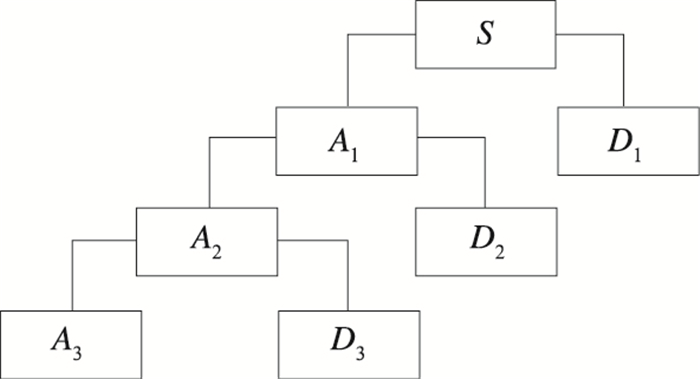
3.4 基于多分辨率分析的图像融合

在目前常用的图像融合技术中，基于多分辨率分析的图像融合方法应用非常广泛(刘贵喜等，2004；Zomet et al，2006；Lewis et al，2004；Buch and Sun, 1995；Su et al，2004)。由于其融合过程是在不同尺度、不同空间分辨率、不同分解层上分别进行，与其他融合方法相比，基于多分辨率分析的图像融合方法可以获得明显改善的融合效果。多分辨率图像融合的原理结构如图 7。

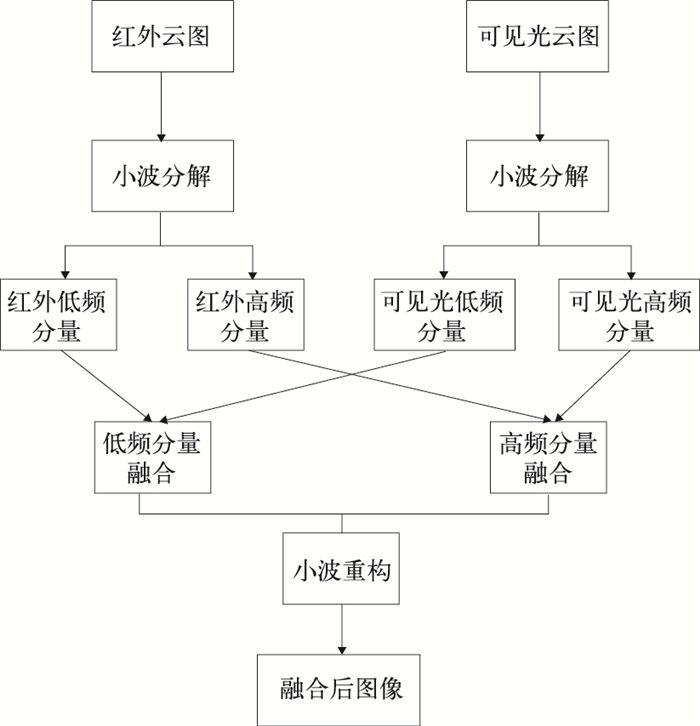
利用小波变换进行多分辨率图像融合，先对两幅图像进行小波分解，得到各自的低频近似分量和三个方向的高频细节分量，并分别对低频分量和高频分量采用不同的融合规则进行融合，得到融合后图像的低频分量和高频分量，最后对融合得到的低频分量和高频分量进行小波重构得到最后的融合图像。算法流程图如图 8。

图中图像低频分量反映图像的强度信息，采用均值法对图像进行融合，其融合系数计算公式为：

$ {F_l}\left({x, y} \right) = \left[ {{D_{lv}}\left({x, y} \right) + {D_{lr}}\left({x, y} \right)} \right]/2 $

(12)

式中，D_lv(x, y)表示可见光图像在点(x, y)处的低频分量上的分解系数，D_lr(x, y)表示红外图像在点(x, y)处的低频分量上的分解系数。

图像高频分量反映图像细节信息，如果采用均值法对图像进行融合会使图像更加平滑，图像细节信息损失较大，融合效果相对较差，为此采用最大值法对图像进行融合，其融合系数计算公式为：

$ {F_h}\left({x, y} \right) = \max \left\{ {{\rm{abs}}\left[ {{D_{hv}}\left({x, y} \right)} \right], {\rm{abs}}\left[ {{D_{hr}}\left({x, y} \right)} \right]} \right\} $

(13)

式中，D_hv(x, y)表示可见光图像在点(x, y)处的高频分量上的分解系数，D_hr(x, y)表示红外图像在点(x, y)处的高频分量上的分解系数。

3.5 融合后云量计算方法

采用最大类间方差法对图像进行分割一直被公认为是分割阈值选取的最佳方法(杨俊等，2009)。对一幅灰度图而言，假设其灰度级为M，灰度值为i的像素点数是n，总的像素点数是$N = \sum\limits_{i = 1}^M {ni} $，灰度值i出现的概率是P_i=n·i/N。然后用阈值T将其分成两组，背景类B={1, 2, …, T-1}和目标类O={T, T+1, …, M}，则：

背景类发生的概率：

$ {P_{\rm{B}}} = \sum\limits_{i = 1}^{T - 1} {{P_i}} $

(14)

灰度值均值：

$ {\mu _{\rm{B}}} = \frac{{\sum\limits_{i = 1}^{T - 1} {\left({{P_i} \cdot i} \right)} }}{{{P_{\rm{B}}}}} $

(15)

目标类发生的概率：

$ {P_{\rm{O}}} = \sum\limits_{i = T}^M {{P_i}} = 1 - {P_{\rm{B}}} $

(16)

灰度值均值：

$ {\mu _{\rm{O}}} = \frac{{\sum\limits_{i = T}^M {\left({{P_i} \cdot i} \right)} }}{{{P_{\rm{O}}}}} $

(17)

整幅图片灰度值均值

$ \mu = \sum\limits_{i = 1}^M {\left({{P_i} \cdot i} \right)} = {\mu _{\rm{B}}}{P_{\rm{B}}} + {\mu _{\rm{O}}}{P_{\rm{O}}} $

(18)

目标与背景的类间方差:

$ \begin{array}{l} \delta \left(T \right) = {\left({{\mu _{\rm{B}}} - \mu } \right)^2}{P_{\rm{B}}} + {\left({{\mu _{\rm{O}}} - \mu } \right)^2}{P_{\rm{O}}}\\ \;\;\;\;\;\;\;\; = {\left({{\mu _{\rm{B}}} - {\mu _{\rm{O}}}} \right)^2}{P_{\rm{B}}}\mu {P_{\rm{O}}} \end{array} $

(19)

让T依次在1~M取值，计算出每一个类间方差δ(T)，找出δ(T)的最大值，此时的T为该图片灰度值分割的最佳阈值。

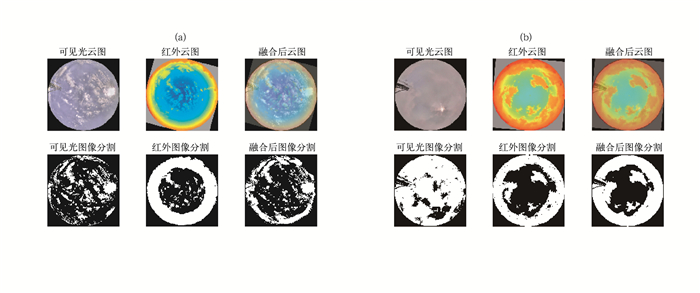
2012年7月7日(晴天)和8月23日(雾-霾天)图像融合前后分割图对比如图 9。

融合前后云量计算结果如表 2。

从图 9和表 2可以看出：(1)红外图像在低仰角受到大气气溶胶和传输路径影响比较突出，雾-霾对可见光云图影响比较大；(2)晴天条件下，融合后的云量更接近可见光云量，图像融合对红外全天空云量起到很好的修正作用；(3)雾-霾天气条件下，可见光云图很难区分云纹理结构，可见光云量偏高，雾-霾对红外云图的影响较小，融合后的云量更接近红外云量。

4 结论

(1) 在云高数据融合上，提出利用双站可见光成像仪测得天顶云底高，对大气温度垂直递减率进行订正，提高红外反演云底高精度。在能见度较高的天气条件下，利用双站可见光成像仪测得准确的天顶云底高，结合云底红外辐射亮温对大气温度垂直递减率进行订正，当夜间和雾-霾天气条件下，可见光云图纹理不清晰无法得到云底高时，利用云底红外辐射亮温结合订正后的大气温度垂直递减率实时反演云底高度。

(2) 在全天空云图拼接上，可见光全天空云图通过全方位立体扫描获得36个方位子图，对子图进行预处理消除畸变和光线不均匀，然后进行球面投影、加权平均方法进行拼接；红外全天空云图通过全方位立体扫描获得4023个方位点的辐射亮温信息，采用球面投影方式将不同方位和仰角观测的辐射亮温值拼接成全天空红外云图。

(3) 在图像配准上，建立放射变换模型，消除两幅全天空云图之间缩放、俯仰和旋转的影响，采用最小二乘方法求解旋转矩阵R，达到图像配准目的。

(4) 在云量数据融合上，采用小波变换进行多分辨率图像融合可以很好地消除红外低仰角大气气溶胶辐射的影响，并且保留可见光在高云、薄云时的观测能力，同时又能增强云纹理信息，提高云图识别率，改进云量观测。