引言

我国共规划建设216部新一代天气雷达，除西部地区一些山脉和沙漠以外，新一代天气雷达观测几乎覆盖了全国多数人口密集区。其中，东部地区年降水量多，多布设S波段新一代天气雷达，梅雨锋、台风及强对流等重大灾害性天气影响区域站点布设较为密集。而西部地区年降水量少，多布设C波段新一代天气雷达。S波段新一代天气雷达0.5°仰角有效观测范围在460 km，C波段新一代天气雷达有效观测范围在150 km(李柏等，2013；刘晓阳等，2010)。在站点布设密集的区域里，邻近雷达存在不同程度的重叠区，有些相邻的几部雷达中都存在重叠区，如青浦、南汇、杭州、宁波、舟山等。

经过长期的业务运行发现，相邻雷达在重叠区域中观测值并不完全相同。在相邻不同型号雷达的重叠区域，由于雷达参数及灵敏度不同而造成观测差异较大，对于相邻相同型号的两部雷达而言，当其中一部雷达存在遮挡、标定错误、发射机或接收机等故障问题时，重叠区域的回波观测值也存在较大的差异。

雷达回波强度不仅取决于雷达系统各参数的特性，而且和被观测的云、降水粒子的性质有关，还与雷达和被测目标之间的距离以及其间的大气状况有关。只有把这些要素都分析清楚，才能根据所测定的回波强度去推断云、降水的物理状况，雷达气象方程也是根据这个原理建立的(张培昌等，2000)。因此可以将造成相邻雷达重叠区回波差异的因素分为外界因素和内在因素。外界因素是由大气环境差异造成的，如遮挡，地物/超折射杂波，大气衰减等。内在因素是由雷达自身问题造成的，如标定错误、发射机、接收机等故障以及太阳法定位误差等。

万玉发等(2000)采用了极坐标与经纬度坐标的转换关系，利用雷达站周围的地形数据计算遮挡仰角。关于两部雷达观测值比较，国内一些学者也做过类似的研究和分析，吴翀等(2014)对新一代天气雷达与S-PAR相控阵天气雷达的观测值做了对比分析，也采用了经纬度匹配方法，在空间一致性上做了较好的匹配。但是多数学者在研究过程中仅用到了两部雷达相近时刻的观测资料，并没有在时间一致性上做严格匹配。而台风、强对流等快速移动的单体在很短的时间内能移动相当长的距离空间，在采样空间上容易造成较大的误差。文中首先对相邻两部雷达进行时间一致性匹配，再做空间一致性匹配，最终得到相邻两部雷达在重叠区域中相同时间、相同采样空间和相同海拔高度上的回波观测值。最后用实例验证该方法的检测效果，该方法在全国新一代天气雷达网实时运行监控业务中具有较高的应用价值。

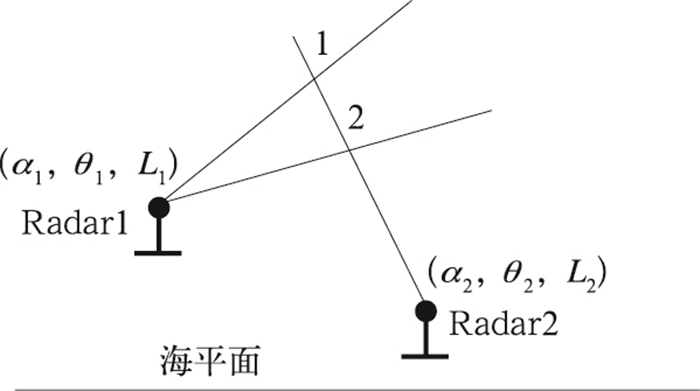
1 相邻雷达重叠区回波差异检测 1.1 相邻雷达观测示意图

图 1为相邻两部雷达立体观测示意图。由图可知，在两部雷达相距不远的情况下观测存在重叠区域，体扫数据在以每个雷达站为原点的极坐标下其仰角、方位角、斜距分别为(α₁, θ₁, L₁)和(α₂, θ₂, L₂)，两部雷达在重叠区存在相同的采样空间。

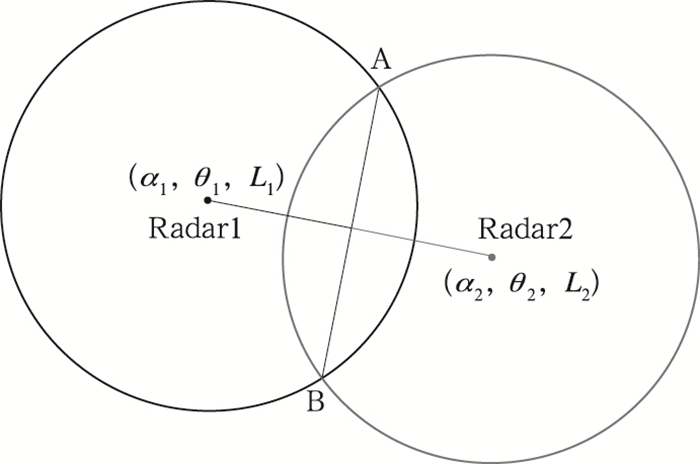
当两部雷达的扫描径向在平面位置显示器(PPI)投影上重合时，相同采样空间在两部雷达上的极坐标分别为(α₁, θ₁, L₁)，(α₂, θ₂, L₂)。当两部雷达最大探测距离和仰角都相同时，如图 2所示为PPI平面观测示意图。在重叠区中直线AB为两部雷达观测相同采样空间，重叠区其他区域观测海拔高度不同，不为同一采样空间。当两部雷达的仰角或最大探测距离不同时，则相同采样空间AB会向高仰角或最大探测距离较短的雷达靠近。

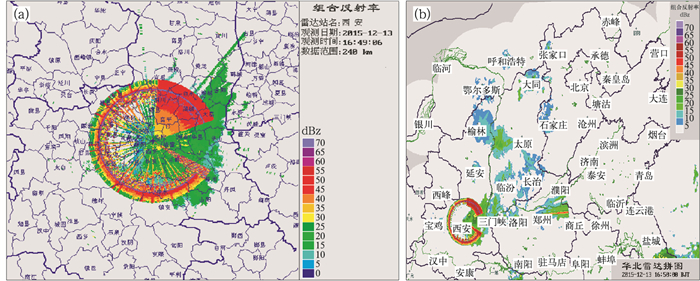
目前，天气雷达拼图系统为中国气象局气象探测中心实时业务系统之一。当几部雷达在重叠区观测值不同时，拼图系统采用最大值法取重叠区域的回波值。但如果其中一部雷达硬件系统故障造成回波值异常高时，则在拼图系统中显示为错误的回波值，如图 3所示。因此如何在业务上对邻近两部雷达回波观测值进行比较，及时检测差异和发现工作异常，引入本文的研究内容。

1.2 相邻雷达重叠区回波差异检测算法

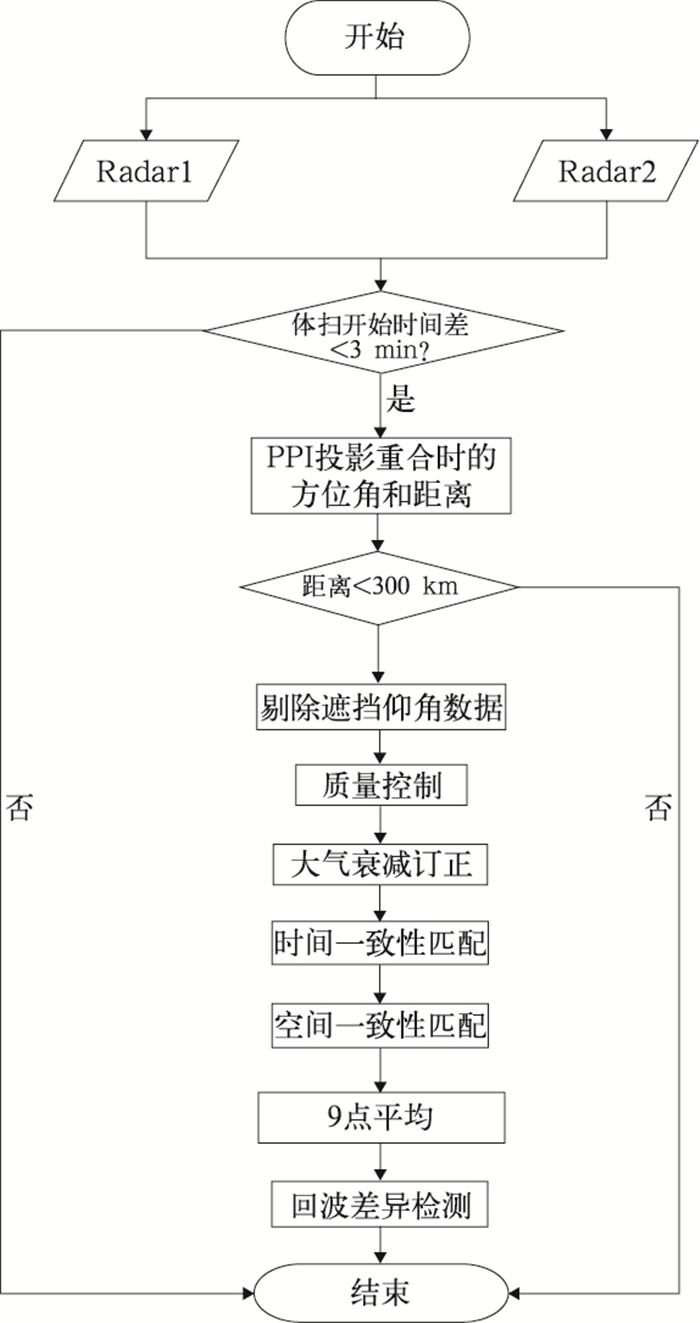
图 4为相邻两部雷达回波差异检测算法流程图，大概可以分为以下九步：

第一步：匹配体扫开始时间。若两部雷达基数据体扫开始时间差大于3 min，则匹配失败，重新匹配；

第二步：计算两部雷达在PPI投影上重合时的方位角和距离。根据空间一致性匹配算法，计算Radar2在Radar1上方位角、距离(θ₁, R₁)，和Radar1在Radar2上方位角、距离(θ₂, R₂)。R₁=R₂，为两部雷达的实际距离。当距离大于300 km时(可根据雷达最大探测距离调整阈值)，认为两部雷达相距较远，程序停止；

第三步：遮挡角计算。根据地形数据事先计算出两部雷达在重叠区域的遮挡角，剔除遮挡仰角以下的PPI观测数据；

第四步：数据质量控制。关于天气雷达的数据质量控制，目前业务上普遍采用模糊逻辑算法，目的都是滤除地物/超折射等杂波(江源等，2009；刘黎平等，2007；张林等，2014；肖艳姣和刘黎平，2006)；

第五步：大气衰减订正。本文采用逐库算法对雷达波在大气中的衰减进行订正(张培昌和王振会，2001；王振会和张培昌，2001)，见式(1)和式(2)。

$ {{\tau }_{i-1}}=\tau (i\Delta R)\left\{ \begin{align} &1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=0 \\ &{\rm{exp}}[-2\sum\limits_{j=1}^{i}{aZ_{r}^{b}\left(j \right)\Delta R}]\ \ \ \ i\ge 1 \\ \end{align} \right. $

(1)

$ \begin{matrix} {{Z}_{r}}\left(i \right)=[{{Z}_{M}}\left(i \right)/{{\tau }_{i-1}}]{\rm{exp}}\{a{{[{{Z}_{M}}\left(i \right)/{{\tau }_{i-1}}]}^{b}}\Delta R\} \\ i=1, 2, \cdots \\ \end{matrix} $

(2)

式中，Z_M为雷达测量值，Z_r为实际值，τ(R)为雷达与距离R之间雨区的双程透过率，a、b为球形粒子群降水正衰减系数。

第六步：时间一致性匹配。从基数据中计算得到两部雷达在重合方位上的观测时间，当时间接近时匹配成功，否则程序停止；

第七步：空间一致性匹配。将两部雷达极坐标数据进行经纬度匹配，根据测高公式分别计算两部雷达匹配后极坐标的海拔高度，当海拔高度接近时，则匹配成功；

第八步：9点平均。经过空间一致性匹配后，利用极坐标3×3空间上的反射率因子数据做9点平均，目的是排除匹配后某些观测奇异值对回波差异检测造成的影响；

第九步：回波差异检测。

2 时间一致性匹配

新一代天气雷达通常采用VCP21模式(0.5°、1.5°、2.4°、3.4°、4.3°、6°、10°、14°、19.5°)体扫。当邻近两部雷达扫描径向在PPI投影上重合时，仰角分别为α₁和α₂，方位角分别为θ₁和θ₂，对于敏视达(CINRAD/SA、SB和CB型号)雷达来讲，体扫基数据每根径向上都有记录的扫描时间，对于其他型号雷达来讲，可根据体扫观测开始时间和观测结束时间推算两部雷达在(α₁，θ₁), (α₂，θ₂)的扫描时间t₁和t₂。

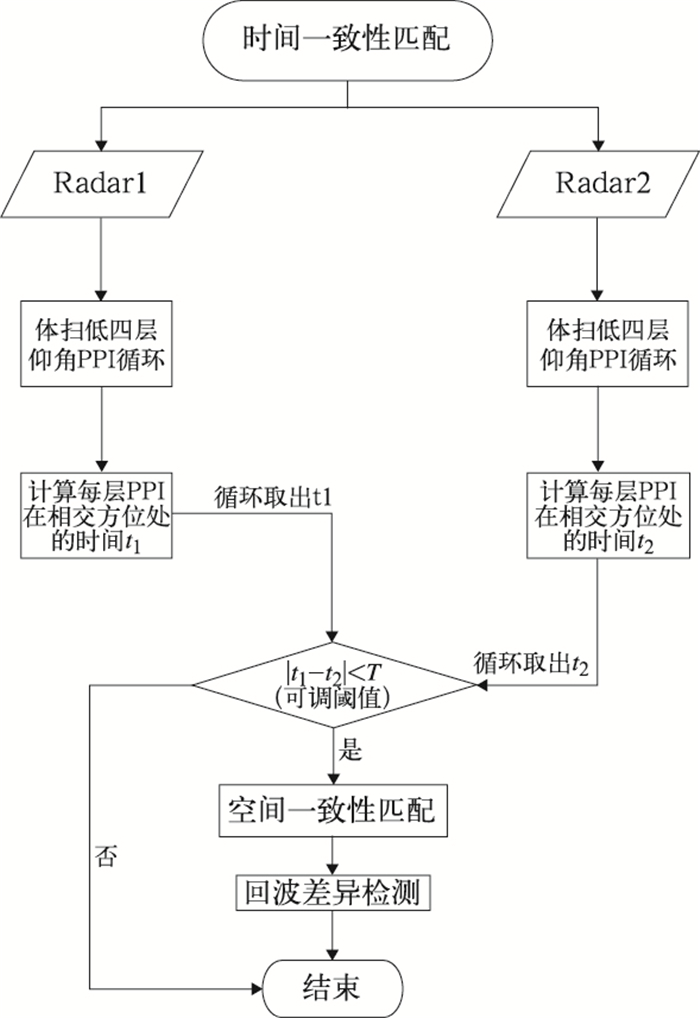
如图 5所示为时间一致性匹配算法流程，算法用到低四层仰角数据做循环，根据在每层PPI投影重合时的扫描时间，判断是否达到时间一致性匹配。例如，Radar1中0.5°仰角θ₁方位上扫描时间t₁与Radar2中1.5°仰角θ₂方位上扫描时间t₂满足和|t₁-t₂|＜T(T为可调阈值)，则Radar1的0.5°仰角层与Radar2的1.5°仰角层在重叠区时间一致性匹配成功(遮挡仰角层数据不进入计算过程)。

那么两部雷达每层PPI在投影重合时的扫描时间差取多少合适呢？本文研究过程中结合云雾降水形成的微物理过程，根据水滴下落末速度与水滴直径的关系确定其取值，表 1为1013 hPa、20℃条件下测定的静止空气中水滴的下落末速度(盛裴轩等，2003)。对于连续性降水而言，水滴直径在1 mm左右，水滴下落末速度在4 m·s^-1，当时，在同一采样空间垂直方向可造成20 m的误差，20 m的误差对连续性降水观测影响并不大。短时雷阵雨的水滴直径最大可达4 mm，水滴下落末速度为8.83 m·s^-1，当T=5 s时，在同一采样空间垂直方向造成45 m的误差，而45 m对短时雷阵雨的观测影响是不容忽视的。文中的个例为连续性降水过程，取T=5 s。

3 空间一致性匹配

吴翀等(2014)，张志强和刘黎平(2013)在定量分析S-PAR相控阵天气雷达与新一代天气雷达资料过程中，对两部雷达观测数据进行格点匹配，建立一一对应关系。在S-PAR相控阵天气雷达极坐标上每个格点(α₁, θ₁, L₁)数据都可以找到对应新一代天气雷达在该位置的极坐标(α₂, θ₂, L₂)数据。但在垂直方向上新一代天气雷达采用VCP21扫描模式，资料的俯仰分布不均匀，同时S-PAR相控阵天气雷达的垂直采样体积远超新一代天气雷达，因此使用了插值方法将仰角α₂与新一代天气雷达匹配，从而将新一代天气雷达的观测数据处理到S-PAR相控阵天气雷达格点上，达到格点一一匹配对应。

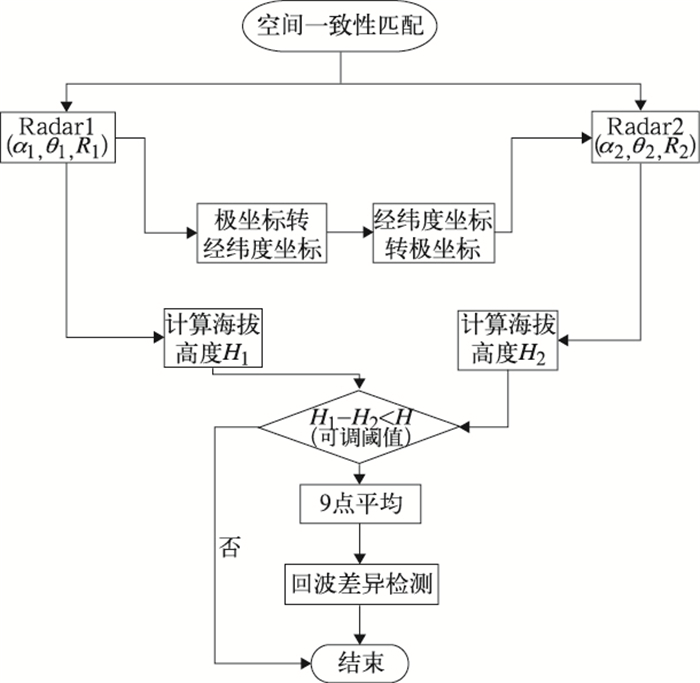
与吴翀等(2004)的处理方式不同，本文处理的是业务运行的新一代天气雷达基数据，两部雷达均采用VCP21模式体扫。时间一致性匹配后已经确定了两部雷达的仰角层α₁，α₂，如图 6为空间一致性匹配算法流程，将Radar1极坐标(α₁, θ₁, L₁)数据转换为经纬度坐标，再将经纬度坐标转换为Radar2极坐标(α₂, θ₂, L₂)数据，坐标转换公式见式(3)至式(9)，在坐标转换过程中两部雷达的仰角α₁，α₂是给定不变的，此时经过匹配后的两部雷达极坐标数据经纬度相同，但海拔高度可能不同。利用测高公式(10)计算两部雷达匹配后极坐标数据对应的海拔高度H₁和H₂，当海拔高度差|H₁-H₂|＜H(H为可调阈值)时，则匹配成功。

雷达资料是以极坐标形式分布于以天线为中心的圆锥面上，若将地球视为半径为R_e的圆球体(等效地球半径为R_m=K_mR_e，K_m=$\frac{4}{3}$)。设雷达站点的经度、纬度和海拔高度分别为(λ_r, φ_r, h_r)，体扫数据在以雷达站为原点的极坐标下的仰角、方位角和斜距分别为(α, θ, L)，该点在空间的经度、纬度及海拔高度记为(λ, φ, H)。使用球面三角公式进行坐标的转换。

(1) 雷达极坐标转经纬度坐标公式

$ \varphi ={\rm{si}}{{\rm{n}}^{-1}}\left({\rm{cos}}\beta {\rm{sin}}{{\varphi }_{r}}+{\rm{sin}}\beta {\rm{cos}}{{\varphi }_{r}}{\rm{cos}}\theta \right) $

(3)

$ \lambda ={\rm{si}}{{\rm{n}}^{-1}}\frac{{\rm{sin}}\theta {\rm{sin}}\beta }{~{\rm{cos}}\varphi }+{{\lambda }_{r}} $

(4)

β为该点与原点在地心处的夹角。

$\beta ={{K}_{m}}{\rm{ta}}{{{\rm{n}}}^{-1}}\left(\frac{L{\rm{cos}}\alpha }{{{R}_{m}}+{{h}_{r}}+L{\rm{sin}}\alpha } \right) $

(5)

通过式(5)计算得到β，再代入式(3)和式(4)即可得到该点的经纬度。

(2) 经纬度坐标转雷达极坐标

$ \rm{cos}\beta =\rm{sin}\varphi \rm{sin}{{\varphi }_{\mathit{r}}}+\rm{cos}\varphi \rm{cos}{{\varphi }_\mathit{r}}\rm{cos}\Delta \lambda $

(6)

$ \rm{cos}\varphi \rm{sin}\Delta \lambda =\rm{sin}\theta \rm{sin}\beta $

(7)

根据式(6)可计算出cosβ，从而推出sinβ(sinβ＞0)，然后代入式(7)中。

$ \rm{sin}\theta =\frac{\rm{cos}\varphi \rm{sin}\left(\lambda -{{\lambda }_\mathit{r}} \right)}{\rm{sin}\beta } $

若令|sin^-1θ=δ|，方位角θ确定如下：

$ \theta =\left\{ \begin{align} &\delta \ \ \ \ \ \ \ \ \ \ \ \ \ 当\varphi \ge {{\varphi }_{\bot }}, \lambda \ge {{\lambda }_{\bot }}时 \\ &\pi -\delta \ \ \ \ \ \ \ 当\varphi \ge {{\varphi }_{\bot }}, \lambda <{{\lambda }_{\bot }}时 \\ &\pi +\delta \ \ \ \ \ \ \ 当\varphi <{{\varphi }_{\bot }}, \lambda <{{\lambda }_{\bot }}时 \\ &2\pi -\delta \ \ \ \ \ 当\varphi <{{\varphi }_{\bot }}, \lambda \ge {{\lambda }_{\bot }}时 \\ \end{align} \right. $

(8)

$ L=\frac{{\rm{sin}}\left(\beta /{{K}_{m}} \right)}{{\rm{cos}}\left(\alpha +\beta /{{K}_{m}} \right)}\left({{R}_{m}}+{{h}_{r}} \right) $

(9)

(3) 雷达测高公式

将两部雷达经纬度匹配后的极坐标数据代入测高公式(10)，分别计算匹配后极坐标数据的海拔高度H₁，H₂。当|H₁-H₂|＜H (H可根据时间一致性算法中|t₁-t₂|＜T和雨滴下落末速度V_T确定，参数阈值可调，文中取20 m)，则认为达到了空间一致性匹配(张培昌等，2000)。

$ H={{h}_{r}}+L{\rm{sin}}\alpha +\frac{{{L}^{2}}{\rm{co}}{{{\rm{s}}}^{2}}\alpha }{2{{R}_{e}}} $

(10)

4 9点平均

根据云及降水粒子的雷达气象方程，见式(11)，N为波束有效照射体内所有产生的散射能量能同时返回天线处的云及降水粒子的总数，而不是单位体积内的粒子数。

$ {{P}_{r}}=\frac{{{P}_{t}}{{G}^{2}}{{\lambda }^{2}}}{~{{\left(4\pi \right)}^{3}}{{R}^{4}}}\sum\limits_{i=1}^{N}{{{\sigma }_{i}}} $

(11)

S波段新一代天气雷达的有效照射深度为250 m，反射率因子数据的最高分辨率是1 km，基本反射率因子数据最终是根据4个连续250 m距离库获取平均回波功率(P_r)后再进行计算，如式(12)所示。再根据雷达气象方程(13)求出反射率因子(单位：mm⁶·m^-3)，最后利用dBz=10lgZ将反射率因子值换算为dBz值(俞小鼎等，2006)。

$ P{{~}_{r}}=\frac{\overline{{{P}_{r1}}}+\overline{{{P}_{r2}}}+\overline{{{P}_{r3}}}+\overline{{{P}_{r4}}}}{4} $

(12)

$ Z={{P}_{r}}{{r}^{2}}/C $

(13)

S波段新一代天气雷达库长为1 km，经过空间一致性匹配后的两部雷达反射率因子数据是可以直接比较的，但是为了避免一些奇异值对回波观测差异的影响，本文采用3 km×3 km库上9点反射率因子平均值代替该点的反射率因子值，此时反射率因子的单位为mm⁶·m^-3，即将基本反射率因子dBz值转换为mm⁶·m^-3后进行9点平均，最后再将9点平均后的值转换为dBz值，方可进入回波差异检测分析。

5 个例分析 5.1 郑州一次频率源故障问题个例分析

2015年9月21—23日，郑州和商丘两部雷达在观测同一片降水回波过程中出现了明显的观测差异，两部雷达地面距离为179.1 km。9月25—26日，经过机外和机内仪表对两部雷达检测，结果表明郑州雷达发射机和接收机系统主要性能指标下降，超过了技术指标要求，包括发射机功率降低、相位噪声超标且不稳定、接收机动态下降。10月9—14日，通过对郑州雷达全面维修，检测到频率源输出定标功率偏低了5 dB，更换新频率源后，对雷达总体性能参数进行调整和标校，使其各项性能参数达到了技术指标要求。以这次频率源故障前后的数据为例，分析相邻雷达回波差异检测算法的准确性。

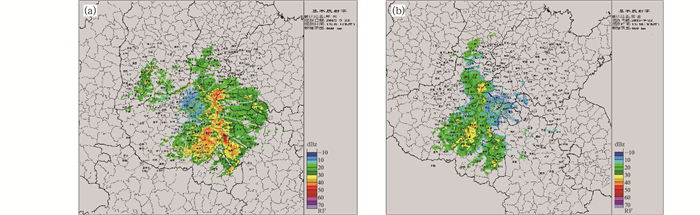
5.1.1 频率源故障数据分析

图 7为郑州和商丘两部雷达9月22日13:10的观测图像。从图中可以直观地看出两部雷达探测回波在重叠区存在一定的观测差异。

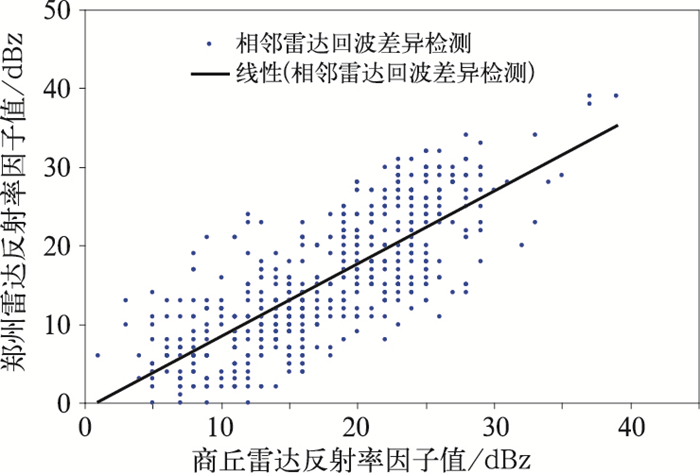
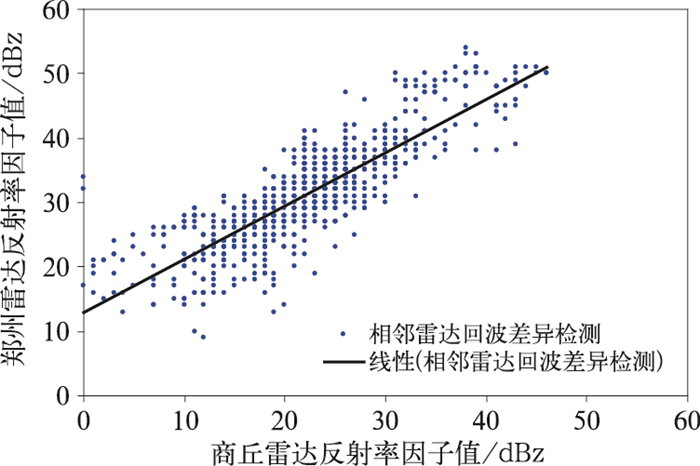
利用郑州和商丘两部雷达在9月22日12:00—14:00共20个体扫观测数据做相邻雷达重叠区回波差异检测个例分析。当T=5 s，V_T=4 m·s^-1，H=20 m时，经过回波差异算法检测后，符合时间一致性匹配的共有7对数据，经过空间一致性匹配算法后共生成739对反射率因子数据，散点图见图 8，两部雷达反射率因子测量值偏差较大。

将两部雷达回波差异进行定量分析，如表 2所示。在对同一采样空间观测过程中，两部雷达反射率因子相差10 dBz以上的占43.8%，相差5 dBz以上的回波高达87.7%。总体而言，回波差异平均值为9.1 dBz，即郑州雷达比商丘雷达回波值平均高9.1 dBz。

5.1.2 重新标校后数据分析

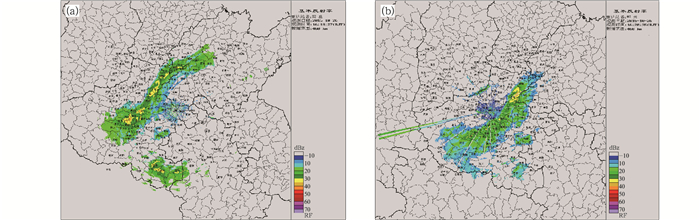
图 9为郑州和商丘雷达10月26日16:20的观测图像。由图可知，在故障维修及重新标校之后，两部雷达观测值比较接近。

利用郑州和商丘两部雷达在10月26日14:30—17:30共30个体扫观测资料，做相邻雷达重叠区回波差异检测个例分析。当T=5 s，V_T=4 m·s^-1，H=20 m时，经过回波差异算法检测后，符合时间一致性匹配的共有16对数据，经过空间一致性匹配算法后生成508对反射率因子数据，散点图见图 10。经过故障维修和重新标校后，两部雷达回波一致性变好。

表 3为两部雷达回波差异的定量分析数据，相比标校前的统计，标校后回波差异明显减小，在对同一采样空间观测过程中，两部雷达反射率因子相差10 dBz以上的缩小至9.6%。但由于两部雷达的型号略有不同，因此仍然存在一定的观测差异，定量统计结果表明，回波差异平均值为2.1 dBz。即郑州雷达经过故障维修后，比商丘雷达回波值平均低2.1 dBz。

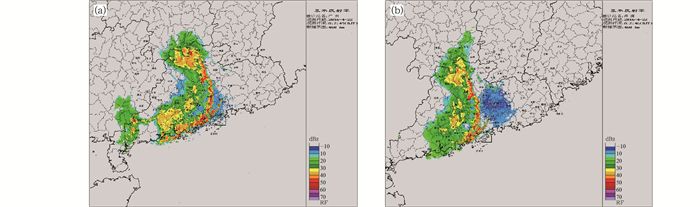
5.2 广东一次飑线过程个例分析

2016年4月22日07:00—11:00，一次强飑线过程扫过广东地区，造成大风和强降水，广州和河源两部雷达能同时观测到整个飑线过程资料，且最强时刻的飑线位置恰好在两部雷达的重叠观测区域，两部雷达地面距离为149.0 km。图 11为广州和河源两部雷达于4月22日08:00同时观测到的飑线过程资料。由图可知，两部雷达观测到飑线的形状、轮廓及反射率因子值非常接近。

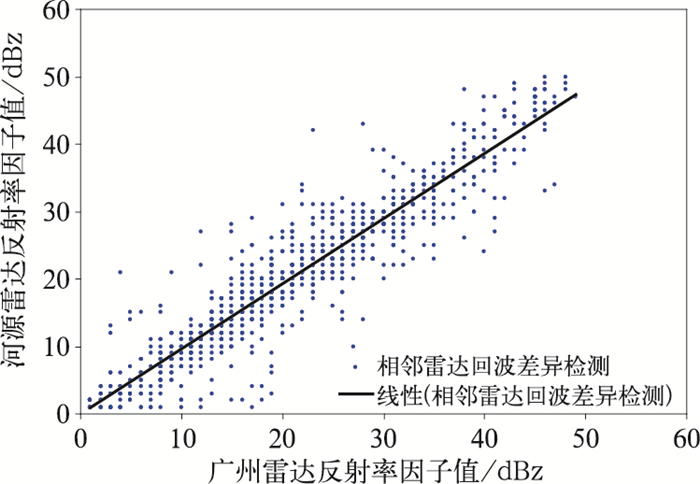
采用07:00—11:00广州和河源两部雷达40个体扫观测资料做相邻雷达重叠区回波差异检测个例分析。当T=5 s，V_T=4 m·s^-1，H=20 m时，经过回波差异算法检测后，符合时间一致性匹配的共有30对数据，经过空间一致性匹配算法后共生成872对反射率因子数据，散点图见图 12，由图可知，两部雷达在相同时间观测同一采样空间上的回波非常一致。

表 4为回波差异定量统计数据，广州和河源均为CINRAD/SA型号新一代天气雷达，在对同一采样空间观测过程中，两部雷达反射率因子相差10 dBz以上的仅为3.7%，相差3 dBz以上的也仅占到27.3%，回波差异平均值仅为0.79 dBz。

5.3 回波差异检测标准

当两部雷达存在重叠区，其中一部雷达发生故障时，利用本文介绍的方法能有效检测出两部雷达的观测差异，那么如何将该方法应用于实时业务中进行检测，即如何确定回波差异的检测标准，也是一个非常关键的问题。由以上个例可知，在正常情况下，相邻雷达在10 dBz以上观测差异非常少，且回波差异平均值小于3 dBz，若两部雷达反射率因子相差3 dBz，相当于两部雷达探测回波功率相差一倍。若观测差异持续很高，回波差异平均值大于3 dBz，则需要排查雷达故障等问题。

将该检测方法应用于新一代天气雷达实时运行业务中，对相邻每两部雷达经过时间一致性匹配后的每一对基数据进行一次检测分析，统计两部雷达在空间一致性匹配后的回波观测差异，大致确定如下标准：

(1) 10 dBz以上回波差异＞10%；

(2) 8 dBz以上回波差异＞20%；

(3) 5 dBz以上回波差异＞50%；

(4) 3 dBz以上回波差异＞70%；

(5) 回波差异平均值＞3 dBz。

以上5个条件判断中，若第5条件满足，且(1)~(4)中同时满足3个及以上的条件判断，则基本可以断定其中一部雷达存在异常，输出报警提示信息。在全国天气雷达网监控中，若发现一部雷达与邻近几部雷达都存在较大的观测差异，则确定是该部雷达存在故障，及时通知台站机务人员进行检修。该方法在全国新一代天气雷达网实时运行监控业务中具有较高的应用价值。

6 结论和讨论

我国东部地区新一代天气雷达站点布设较密，邻近几部新一代天气雷达存在重叠区，长期业务运行发现相邻雷达在重叠区观测值并不完全相同，当其中一部雷达存在硬件系统故障时，会存在较大的差异。文中重点介绍了相邻两部雷达回波差异的检测方法，并采用实际个例对该方法进行检验，结论如下：

(1) 影响两部雷达回波观测差异的因素包括外界因素和内在因素，文中排除了遮挡、杂波干扰和大气衰减等外界因素，只分析由雷达自身造成的回波差异。

(2) 新一代天气雷达采用VCP21模式扫描，对相邻两部雷达在低四层仰角在重叠区做时间一致性和空间一致性匹配，得到两部雷达在同一时间、同一采样空间上的回波观测值，从而进行分析比较。

(3) 文中采用郑州雷达在一次频率源故障前后的数据作为个例分析，比较郑州和商丘两部雷达在重叠区的观测值。频率源的故障造成两部雷达回波差异10 dBz以上的比例为43.8%，回波差异平均值为9.1 dBz，更换频率源重新标校之后，两部雷达回波差异在10 dBz以上的比例缩小至9.6%，回波差异平均值缩小为2.1 dBz。

(4) 文中采用2016年4月22日广东一次飑线过程中两部CINRAD/SA型号新一代天气雷达(广州和河源)的回波差异做了个例分析。结果表明，在这次飑线过程中，两部雷达回波一致性非常好，10 dBz以上的回波差异仅为3.7%，3 dBz以上的也仅占到27.3%，回波差异平均值为0.79 dBz。

(5) 在新一代天气雷达实时运行业务中，对相邻每两部雷达经过时间一致性匹配后的每一对基数据进行检测分析，统计两部雷达空间一致性匹配后的回波观测差异，文中给出了检测标准，若发现一部雷达与邻近几部雷达都存在较大的观测差异，则确定是该部雷达存在故障，及时通知台站机务人员进行检修。该方法在全国新一代天气雷达网实时运行监控业务中具有较高的应用价值。