2. 中国气象局数值预报中心,北京 100081;
3. 成都信息工程大学大气科学学院高原大气与环境四川省重点实验室,成都 610225;
4. 国家气象中心,北京 100081;
5. 中国核动力研究设计院,成都 610233
2. Numerical Weather Prediction Centre, CMA, Beijing 100081;
3. Key Laboratory of Plateau Atmospheric and Environment in Sichuan Province, College of Atmospheric Sciences, Chengdu University of Information Technology, Chengdu 610225;
4. National Meteorological Centre, Beijing 100081;
5. Nuclear Power Institute of China, CNNC, Chengdu 610005
在经典斜压不稳定理论中,对称不稳定(SI)是大气在垂直方向上对流稳定、水平方向上惯性稳定时,在重力和惯性力的共同作用下,空气作倾斜上升运动时的一种大气不稳定现象(Shou and Li, 1999; Hoskins, 1974; Bennetts and Hoskins, 1979;费建芳等,2009)。根据大气湿度把对称不稳定分为三类:饱和湿大气中的SI称为条件性对称不稳定(CSI),未饱和湿大气中的SI称为位势对称不稳定,这两者统称为湿对称不稳定;干大气中SI的则被称为干对称不稳定。由于在实际观测中,干大气中很少出现对称不稳定现象,Bennetts and Hoskins(1979)在研究中考虑了湿大气中的潜热释放,并把潜热释放产生的对称不稳定称为CSI。
自从CSI在带状云和降水形成过程中的重要作用被发现以后(Bennetts and Hoskins, 1979),学者们对CSI进行了深入研究,并将其作为冬季强降水的分析预报方法之一。这些研究结果揭示出CSI可能是暴雨、冬季暴雪、锋面带状降水等多种中尺度对流天气的形成机制(池再香等,2005;杜楠等,2008;王宗敏等,2014;张芳华等,2014;刘璐等,2015;周康辉等,2017)。在研究工作中,如何表征大气中的CSI是一个关键性的问题。目前,CSI的判定方法主要包括:湿位涡(MPV,moist potential vorticity)分析法、Mg-θ剖面图、倾斜对流有效位能(SCAPE)、Richarson数、增长率参数等(Hoskins, 1974; Emanuel, 1983; 费建芳等,2010)。其中,Moore and Lambert(1993)在研究中用相当位涡(EPV)方法诊断了CSI区域,并与Mg-θ剖面图(Mg面:等绝对地转角动量面;θ面:等位温面)方法比较发现,用EPV诊断CSI更有效。
近年来,随着数值模式的发展,模式输出的资料对CSI的诊断以及天气过程的机理分析提供了更有利的条件。目前,学者们已经利用MM5、WRF等数值模式模拟分析了不同个例中的不稳定现象。费建芳等(2009)以Kuo-Anthes方案的基础,在MM5模式中引入垂直-倾斜对流一体化方案以后模拟了2008年南方暴雪过程,模拟结果表明,CSI是造成暴雪加强的主要机制之一。王宗敏等(2014)利用WRF模式模拟了2009年一次副热带高压外围对流雨带的发生发展过程,发现雨带发展过程中,对流不稳定和对称不稳定同时存在。刘璐等(2015)用WRF模拟了2012年的“7·21”北京暴雨,并对该过程进行了条件不稳定性分析,结果表明,北京上空冷暖空气长期对峙触发对称不稳定,造成持续性降水。
综上,CSI作为锋面带状降水、暴雨、暴雪、热带气旋等多种中尺度对流天气的可能形成机制,在灾害天气的研究和预警预测方面得到广泛应用,用预报场资料、WRF等模式输出资料分析CSI的研究工作已经开展了不少。如果能采用高分辨率中尺度区域模式GRAPES-Meso模拟一次天气过程,并结合对流不稳定、惯性不稳定与对称不稳定判据诊断分析天气过程,将为对流性天气的预警预测提供一定的指示作用。
本文用GRAPES-Meso模拟了2015年8月2—4日的锋面带状降水过程,并利用模式输出的高分辨率资料,结合多种方法分析不稳定量,判定CSI的区域,并给出了CSI与锋面带状降水的关系、CSI与对流不稳定以及惯性不稳定的关系的初步结论。
1 资料与模式本文采用欧洲中期天气预报中心(ECMWF)的全球模式预报场资料作为初始场和侧边界条件。该资料截取的时段为2015年8月2日00时至4日00时,时间间隔为6 h,分辨率为0.125°×0.125°。实况资料为2015年8月2日00时至4日00时的国家级地面自动站降水观测资料与风云二号卫星的亮温资料。
该试验结合了中国气象局自主研究建立的新一代多尺度统一气象资料同化与数值预报系统GRAPES(Global and Regional Assimilation and PrEdiction System)中的中尺度区域模式GRAPES_Meso进行数值模拟。该模式采用半隐式-半拉格朗日差分方案和全可压/非静力平衡动力框架,包含可自由组合的、可优化的物理过程参数化方案与标准化、模块化、并行化的同化与模式程序,是全球、区域一体化的同化与预报系统。目前,GRAPES系统已在国家级、区域级气象业务中心运行, 在实际气象业务中发挥了重要应用(伍湘君等,2005;陈德辉等,2008;戴光丰和陈子通,2013;姜晓飞等,2015;万子为等,2015;陈炯等,2017)。
模式试验版本为GRAPES_Meso4.0.0.0。积分时间为2015年8月2日00时至4日00时(48 h),预报区域为15°~55°N、70°~145°E,模式分辨率为0.1°×0.1°(约10 km)。模式积分步长为60 s,模式的垂直层次为51层,模式输出时间间隔为3 h,模式输出垂直层次为26层。其他模式参数配置详见表 1。
|
|
表 1 模式参数配置 Table 1 Model parameter configuration |
参考了近年来GRAPES模式中各参数化方案的对比评估研究,因Kain-Fritsch Eta积云参数化方案(简称为KFeta方案,下同)在GRAPES模式中有较好的应用效果(王德立等,2013;郭云云等,2015),本文在本次试验中选择KFeta积云参数化方案。该方案以特征时间内消耗对流有效位能(ABE)作为闭合假设,以简单云模式判定积云对流和网格尺度的关系,云模式中考虑了上升、下沉气流的夹卷效率,并设定了夹卷率的最小阈值。
2 诊断分析方法 2.1 对流稳定度(1) 对流稳定度:大气的对流稳定性与气层的整层抬升有关,通过对流稳定度-∂θe/∂p来表征。-∂θe/∂p>0时,可以认为大气为对流稳定,-∂θe/∂p < 0时,大气为对流不稳定,-∂θe/∂p=0时,则为中性大气。其中,相当位温θe的公式为(盛裴轩等,2003),
| $ {\theta _{\rm{e}}} = \theta \exp (Lq/{c_p}T) $ | (1) |
式中,θ为位温,q为比湿,cp为定压比热容,cp=1.004 kJ·kg-1·K-1,L为凝结函数,单位:J·kg-1,公式(盛裴轩等,2003)如下:
| $ L = 2.5 \times {10^6} - 2323t $ | (2) |
式中,t为温度。
(2) 对流有效位能(CAPE):CAPE值对强对流天气具有较好的指示意义,是一个能定量反映大气环境中是否可能发生深厚对流的热力变量,是对流最终发展强弱的指标之一。CAPE值越大,对流发生的可能性越大(李万彪,2010;叶磊等,2015)。其表达式为:
| $ CAPE = g\int_{{z_{{\rm{LFC}}}}}^{{z_{{\rm{EL}}}}} {\left({\frac{{{T_{{\rm{vp}}}} - {T_{{\rm{ve}}}}}}{{{T_{{\rm{ve}}}}}}} \right)} {\rm{d}}z $ | (3) |
式中,Tvp与Tve分别为气块与环境的虚温,zLFC为自由对流高度,zEL为平衡高度(吴哲红,2007)。
2.2 惯性稳定度惯性不稳定是当水平面上原本处于地转平衡的基本气流受到横向扰动时,扰动被加速,气块具有远离原有平衡位置的趋势。惯性稳定度用绝对地转涡度(f+ζg)来表征,其中f为科氏参数,ζg是绝对地转涡度。(f+ζg)>0时,惯性稳定,反之为惯性不稳定(费建芳等,2009)。
2.3 对称不稳定(1) 天气学分析法:1) Vg随着高度增大,使得等Mg面的坡度更小,因此CSI容易在垂直风切大的区域产生;2)反气旋性风切越大的地方,绝对涡度将趋于零,从而产生弱的惯性稳定区域,因此CSI容易在反气旋风切大的地方产生;3)CSI容易在低静力稳定度的地方产生;4)CSI产生的天气现象多表现为一条或者多条带状云或者降水;与CSI有关的雨带与垂直风切变(等厚度线或者热成风)平行,含有向暖空气方向运动的分量,雨带宽度约为10~100 km;5)CSI引起的倾斜对流时间尺度约为3~4 h;6)与CSI相关的倾斜对流中最大垂直运动可达1~3 m·s-1(Moore and Lambert, 1993;费建芳等,2009)。
(2) M-θe剖面图:在湿大气中,当等Mg面的坡度小于等θe面时,空气倾斜上升而产生对称不稳定。考虑模拟资料中的Vg包含更多噪音(王宗敏等,2014),用沿锋区方向的风速V代替Vg,本文采用的绝对地转动量公式为:
| $ M = V + fx $ | (4) |
式中,f为地转参数,x为离开剖面左端的距离,向暖空气方向增大,单位:m。
(3) 湿位涡分析法(MPV):Hoskins(1974)提出用湿位涡来判定CSI的方法。在湿饱和大气中,可以认为θe=θse,用θe代替θse,展开湿位涡的公式:
| $ \begin{array}{l} MPV = g{\mathit{\boldsymbol{\xi }}_{\rm{a}}} \cdot \nabla {\theta _{\rm{e}}} = - g(\xi + f)\frac{{\partial {\theta _{\rm{e}}}}}{{\partial p}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;g\frac{{\partial v}}{{\partial p}}\frac{{\partial {\theta _{\rm{e}}}}}{{\partial x}} - g\frac{{\partial u}}{{\partial p}}\frac{{\partial {\theta _{\rm{e}}}}}{{\partial y}} \end{array} $ | (5) |
式中,θe为相当位温,ζ为相对涡度,
选取了2015年8月2—4日的一次华北锋面带状降水过程,此次天气过程的持续时间约为48 h。8月3日08时(UTC,下同)山东、河北、辽宁、吉林部分地区的24 h降水量达到大雨甚至暴雨级别,雨带稳定发展加强,8月4日08时的24 h降水量(图略)显示,大雨以及暴雨范围在上述区域继续扩大。发展旺盛阶段的雨带宽度约为250 km,长度约为2000 km。
利用EC高分辨率预报场资料对此次降水过程进行背景场分析。由500 hPa高空图(图 1a)可见,巴尔喀什湖附近的长波槽东移,槽线位于120°E附近,雨带正好位于槽前,长波槽下游的高压脊在135°E附近维持了约12 h,形成了下游阻挡形势,使低槽移动缓慢从而有利于降水的维持。588 dagpm线北抬至35°N附近,西太平洋副热带高压与贝加尔湖低槽下游的高压脊相叠加,进一步加强了下游高压的稳定性。此外,500 hPa温度槽落后于高度槽,在低槽东移的过程中,槽后的冷平流使槽加深,槽前正涡度平流又会促使低层的低值系统继续发展,有利于降水的形成以及维持。
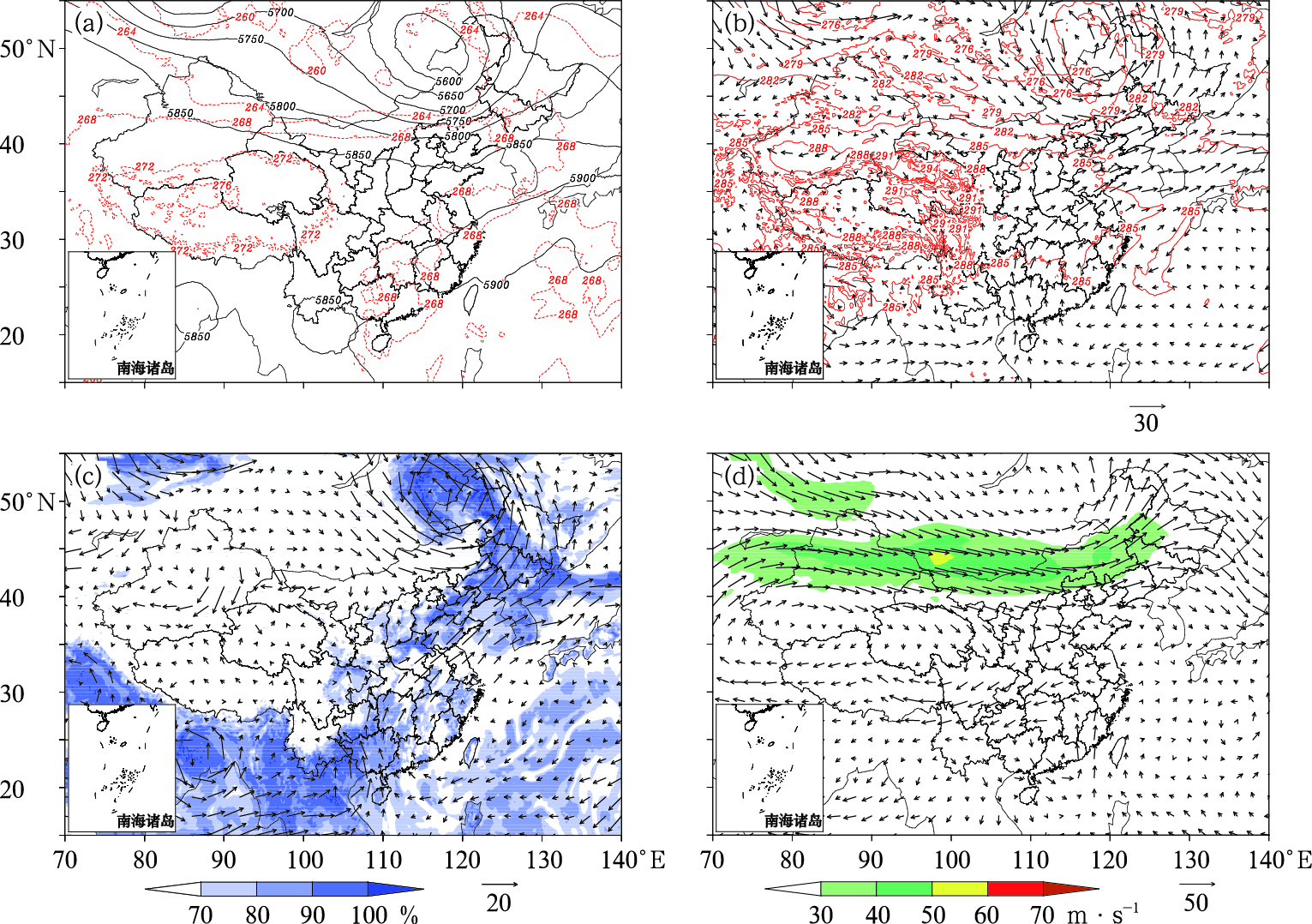
|
图 1 2015年8月2日06时(a)500 hPa高度场(黑实线,单位:gpm)与温度场(红虚线,单位:K),(b)700 hPa风场(风矢,单位:m·s-1)与温度场(红线,单位:K),(c)850 hPa风场与相对湿度(阴影),(d)200 hPa风场(阴影:高空急流) Fig. 1 (a) Geopotential height (black solid line, unit: gpm) and temperature (red dashed line, unit: K) at 500 hPa, (b) wind vector (unit: m·s-1) and temperature (red line, unit: K) at 700 hPa, (c) wind vector and relative humidity (shaded) at 850 hPa; (d) wind vector at 200 hPa (the shaded: high-level jet) at 0600 UTC 2 August 2015 |
由700 hPa(图 1b)风场可以看出,我国东北附近形成冷涡,西南气流把冷空气向雨区输送。华北至东北存在西南风向的低空急流,急流中心风速约为33 m·s-1,本次过程的雨区位于低空急流的左侧。再结合06时的红外云图与海平面气压场(图略)可知,地面有锋面气旋的存在。850 hPa上,西南风从孟加拉湾为此次降水输送来充分的水汽。此外,结合850 hPa水汽通量图(图略)可知,气流跨越渤海带来的水汽也为本次降水提供了有利条件。
200 hPa风场图(图 1d)上可见高空急流,急流随时间发展加强并逐渐东移,急流轴中心风速可达60 m·s-1。高低空急流耦合且华北地区刚好位于急流出口区右侧,具有反气旋切变,高空辐散进一步加强上升运动,有利于地面气旋发展。综上,高低空系统配置有利于此次华北锋面降水的形成和维持。
4 结果分析 4.1 模拟结果利用国家级自动站降水资料和GRAPES-Meso模式输出的资料分别绘制3日00时、4日00时的24 h降水量图(图 2),模拟雨带呈西南—东北走向,随着时间逐渐南移并加强。对比模拟与观测的雷达反射率因子拼图可知(图略),3日00时模拟雨带的位置较实况略偏北,模拟雨带中心偏西,整体强度偏大,但中心强度接近实况,约为50 dBz。
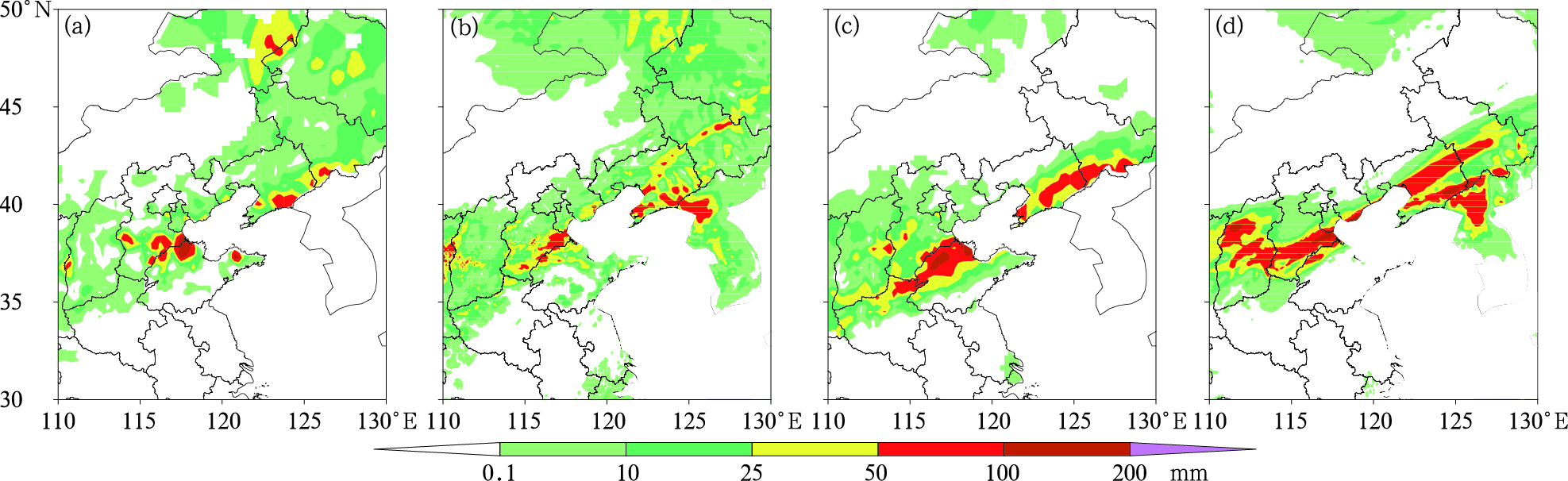
|
图 2 2015年8月3日00时(a, b)、4日00时(c, d)24 h累计降水量实况(a, c)和GRAPES-Meso模拟结果(b, d) Fig. 2 Observed (a, c) and simulated (b, d) 24 h rainfall at 0000 UTC 3 (a, b) and 0000 UTC 4 (c, d) August 2015 |
综上,模拟结果基本能够呈现此次降水过程的雨带走向、强度、落区等大致特征,模拟雨带的发展过程与实况接近。因此,可以利用模式输出的高分辨率资料来分析此次降水过程中的不稳定特征。
4.2 对流稳定度与垂直运动以横跨主雨区的A(50°N、110° E)、B(30°N、110°E)两点连线,作各时次对流稳定度与垂直运动的剖面图,剖线位置如图 3所示。
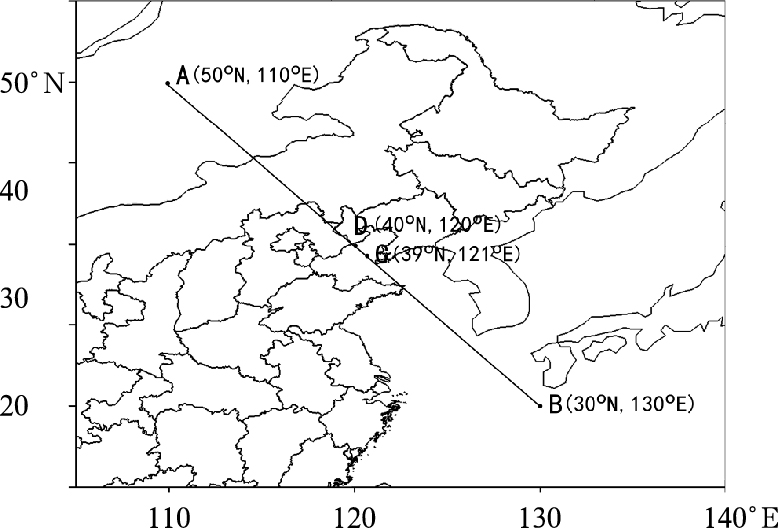
|
图 3 剖线AB以及C点(39°N、121°E)、D点(40°N、120°E)的位置 Fig. 3 Position of the line AB, Point C (39°N, 121°E), and Point D (40°N, 120°E) |
在模拟降水过程中,有两个时次的垂直运动强度最大(图 4)。垂直运动的第一次峰值出现在2日21时,锋前对流层高层有较强的垂直上升运动,强度可达0.35 m·s-1,上升运动的两侧有较弱的下沉运动,强度约为0.2 m·s-1。垂直运动在3日12时达到了第二次峰值,锋前对流层700 hPa以上为强烈的上升运动,强度可达0.75 m·s-1,700 hPa以下锋面附近为较弱的垂直下沉运动,强度约为0.3 m·s-1。对应两次垂直运动大值时刻,锋面附近的CAPE值也达到了峰值(图略)。

|
图 4 2015年8月2日21时(a),3日12时(b)θe(实线,单位:K)与垂直运动(阴影) (剖面位置如图 3) Fig. 4 Vertical cross-section of θe (solid line, unit: K) and vertical velocity (shaded area) at 2100 UTC 2 (a) and 1200 UTC 3 (b) August 2015 (Location of the cross-section is shown in Fig. 3) |
由图 4中的等θe线的分布可知,在118°~122°E上空存在一条由西向东移动的冷锋,随高度向西倾斜。锋前对流层600 hPa以下θe值随高度降低,这表明锋前对流层中低层有弱的对流不稳定。等θe线高值区呈现出由地面指向高空的舌状,θe的最大值可达350 K。而锋前600 hPa以上,θe的值随高度增加,锋前对流层中高层基本为对流稳定层结,等θe线呈现下凹状态或者自高空指向地面的舌状高值区,与垂直下沉运动对应较好。对流层中高层的等θe线呈现出的下凹状态,可能是由于水汽凝结释放潜热,使得相当位温陡然增大,在对流层中层形成大值区。
综上所述,锋前对流层低层存在弱的对流不稳定,当垂直运动增强时,会对不稳定能量区域造成一定的扰动,促使对流发展从而产生降水。选取8月2日21时垂直运动最大值对应到地面的C(39°N、121°E),与8月3日12时垂直运动最值对应的D点(40°N、120°E),分别分析C、D两点的降水量与各不稳定量之间的关系,C、D两点的地理位置如图 3所示。
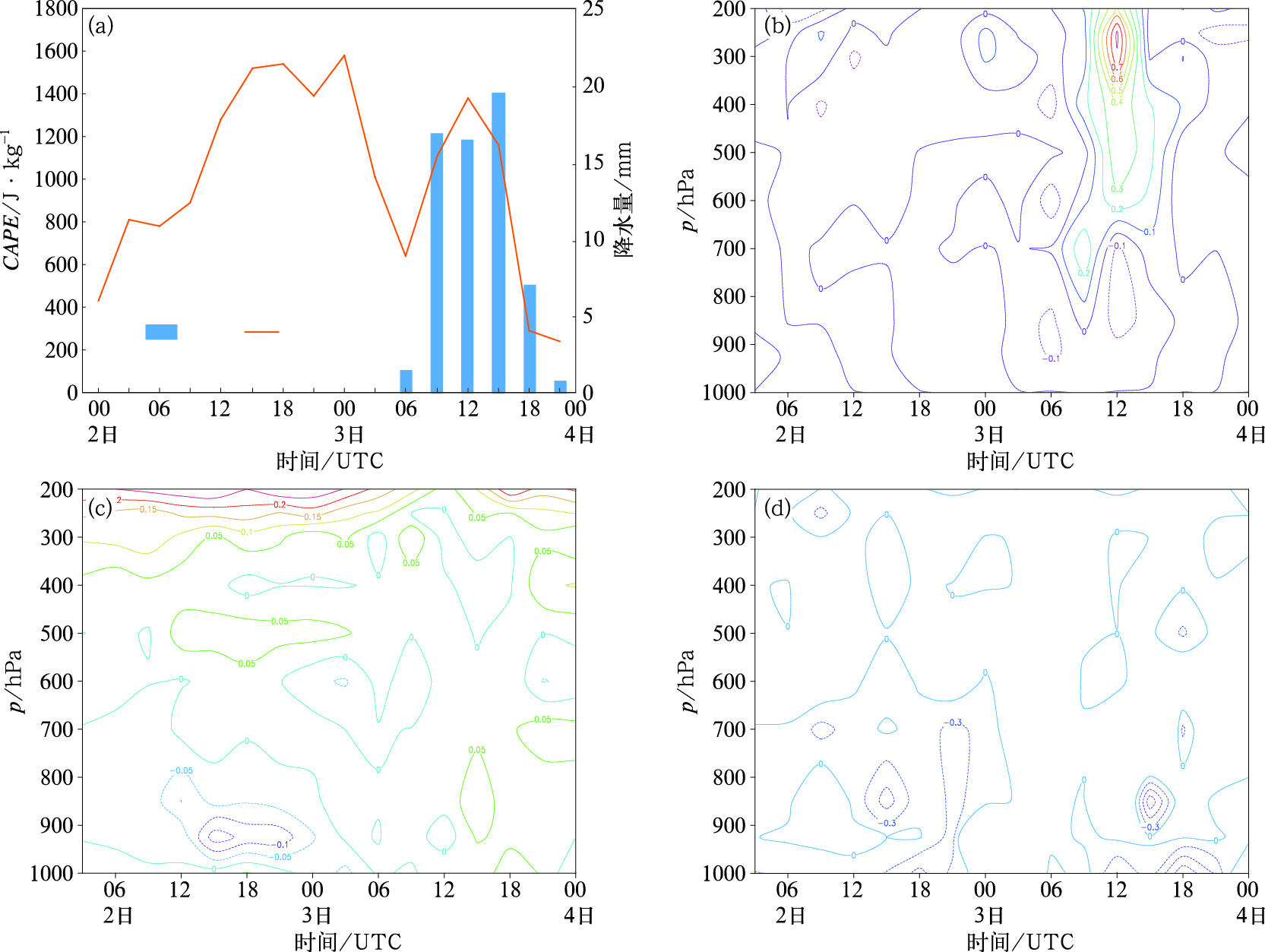
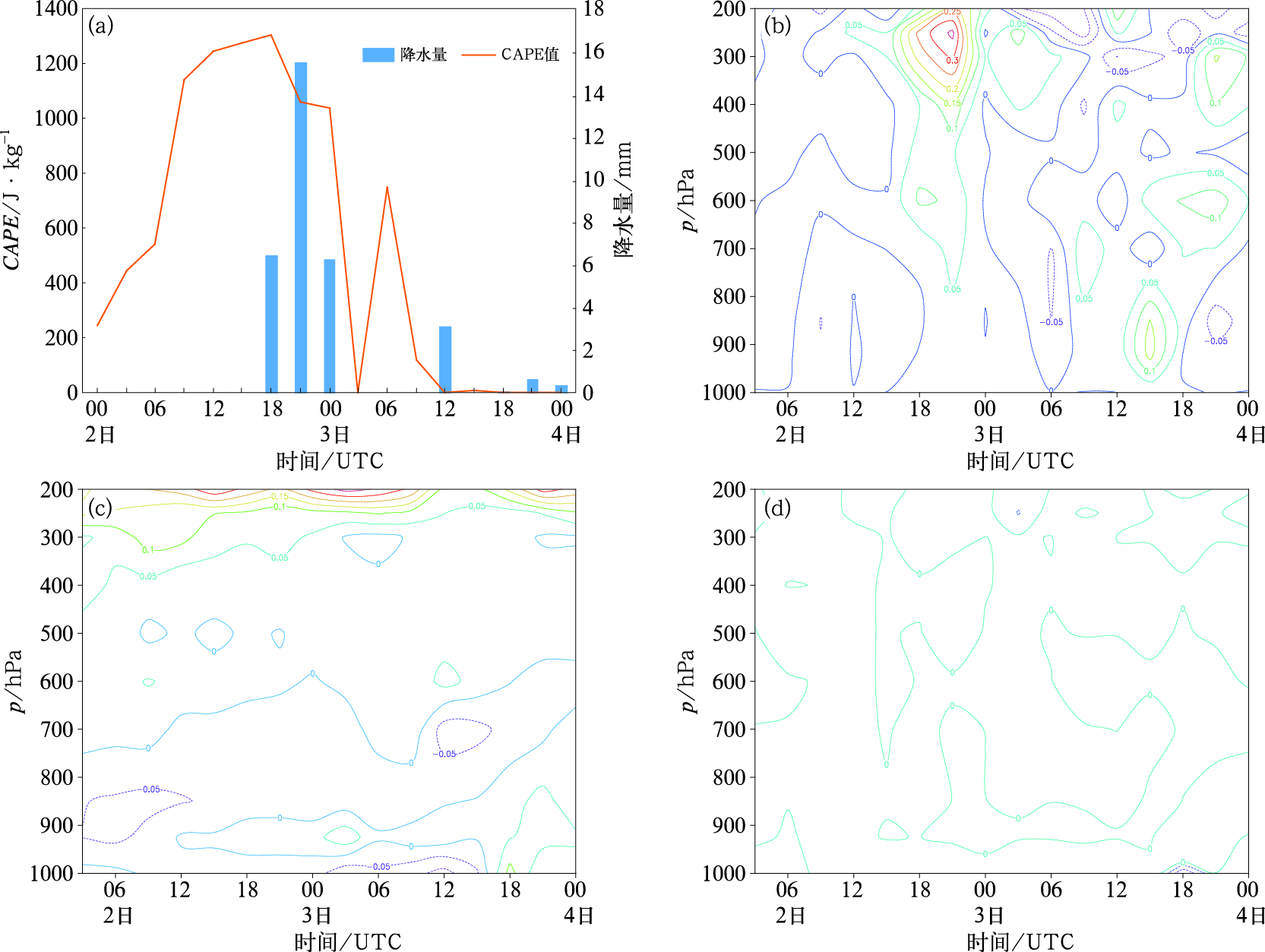
4.3 单站降水量与各不稳定量的关系如图 5所示,C点(39°N、121°E)的降水与垂直运动、对流不稳定、CAPE值均有较好的时间对应关系。8月2日18时至3日00时,垂直运动发展达到旺盛阶段,上升运动的强度可达0.35 m·s-1,CAPE也达到了峰值,约为1320 J·kg-1,降水在这个时段内产生;3日09时之后对流层低层有弱的垂直运动发展,伴随着弱的降水,CAPE值约为748 J·kg-1。降水的整个时段内,该点上空600 hPa以下基本为弱对流不稳定层结,而该点上空的湿位涡基本为正。综上,对流不稳定为C点降水过程的主要影响因子。
|
图 5 2015年8月2—4日C点(39°N、121°E)的(a)降水量与CAPE值的时间变化,(b)垂直运动(单位:m·s-1),(c)对流稳定度(单位:K·hPa-1),(d)湿位涡负值区(单位:PVU)的时间-高度变化剖面 Fig. 5 Temporal variation of simulated 3 h precipitation and CAPE (a), and time-height profiles of negative area of vertical velocity (b, unit: m·s-1), convective stability (c, unit: K·hPa-1), and moist negative potential vorticity (d, unit: PVU) at Point C (39°N, 121°E) during 2-4 August 2015 |
如图 6所示,D点的降水与垂直运动、湿位涡负值区都有良好的对应关系,而与对流不稳定没有明显的对应关系。8月3日06时之前,D点上空的CAPE值先逐渐增大再减小。在该时段,D点上空对流层中下层为对流不稳定层结。3日06时以后,垂直运动在900 hPa以上发展增强,在12时达到峰值0.75 m·s-1,而后逐渐减弱。随着垂直运动的发展,降水开始产生并于15时达到峰值。在这个阶段,D点上空的大气逐渐转为弱的对流不稳定或者中性层结;该点上空的MPV负值区在降水阶段发展旺盛,强度可以达到-0.5 PVU。
综上,CAPE值在降水前和降水过程中都有积累和释放的过程,降水产生阶段D点上空为弱的对流不稳定层结,湿位涡的负值区出现与降水有较好的时间对应关系,由此考虑发生在D点的降水可能受条件性对称不稳定(CSI)影响。为了深入探究CSI对此次降水的影响,进一步分析对流不稳定、对称不稳定、惯性不稳定的空间分布特征以及它们与降水的关系。
4.4 CSI的空间分布结合CSI的定义与第二章介绍的诊断分析方法,本文给出了CSI区域的判定方法:若一个区域同时满足-∂θe/∂p≥0(对流稳定或者中性层结),(f+ζg)≥0(惯性稳定),湿位涡MPV < 0(对称不稳定)这3个条件,则可以判定该区域存在CSI。
4.4.1 水平分布为了了解对流不稳定、对称不稳定、惯性不稳定在水平面上的分布以及变化情况。在850 hPa层面分别绘制8月3日03、12和21时的-∂θe/∂p负值区(图 7g~7i)、湿位涡负值区与绝对地转涡度负值区(图 7d~7f)的分布,以及滞后3 h的3 h累计降水量(图 7a~7c)。由850 hPa上3种不稳定量与降水量随时间的变化情况,把模拟降水过程分为3个阶段。

|
图 7 2015年8月3日06时(a),15时(b),4日00时(c)3 h累计降水量和8月3日850 hPa 03时(d),12时(e),21时(f)的湿位涡(蓝色阴影为MPV < 0的区域,单位:PVU)与绝对地转涡度负值区(红线,单位:10-3 s-1),8月3日03时(g),12时(h),21时(i)的-∂θe/∂p(单位:K·hPa-1) Fig. 7 The 3 h accumulated precipitation (unit: mm) at 0600 UTC 3 (a), 1500 UTC 3 (b), and 0000 UTC 4 (c) August, MPV (shaded area, unit: PVU) and absolute vorticity (red line, unit: 10-3 s-1) at 850 hPa at 0300 UTC (d), 1200 UTC (e) and 2100 UTC (f), and -∂θe/∂p (unit: K·hPa-1) at 850 hPa at 0300 UTC (g), 1200 UTC (h), 2100 UTC (i) 3 August 2015 |
在第一个阶段,降水开始产生并呈现出带状分布,3 h累计降水量可达25 mm。在这个阶段,华北上空有弱的对流不稳定,-∂θe/∂p的强度约为-0.1 K·hPa-1;该区域上空的湿位涡非常微弱,基本不存在CSI区域。可以认为对流不稳定为此阶段降水的主要原因(图 7a,7d,7g)。
在第二个阶段,雨带在华北上空发展增强,3 h累计降水量可达50 mm。在这个阶段,华北上空的对流不稳定逐渐增强,-∂θe/∂p < 0的区域基本与雨区平行,强度可达-0.2 K·hPa-1;CSI发展达到最旺盛的阶段,呈西南—东北向的一条窄带状区域,与雨带、对流不稳定区域平行,湿位涡的值可以达到-6 PVU。绝对地转涡度在雨带的后部发展增强,其值约为-3×10-3 s-1。此阶段的降水受对流不稳定、惯性不稳定、CSI的共同影响(图 7b,7e,7h)。
到了第三个阶段,华北雨带逐渐减弱东移。在这个阶段,华北上空的对流不稳定、CSI与惯性不稳定的强度均有所减弱,不稳定能量的强中心也随着雨带东移。此阶段的对流不稳定、惯性不稳定、CSI仍然维持着雨带的持续(图 7c, 7f, 7i)。
综上,对流不稳定、惯性不稳定、CSI在不同阶段对降水均有影响。对流不稳定在降水初期起主导作用;在随后的阶段,对流不稳定的减弱伴随着对称不稳定与惯性不稳定的增强,3种不稳定量共同影响降水;在降水后期,3种不稳定量影响着降水的持续。
4.4.2 垂直分布以横跨主雨区的AB线作3种不稳定量的垂直剖面图,剖线位置见图 3。
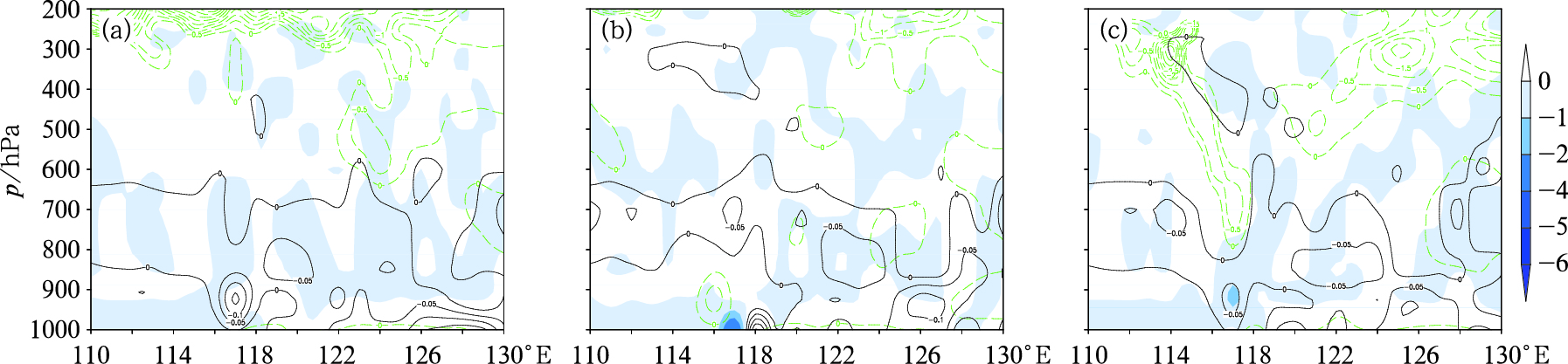
在第一阶段,对流层600 hPa以下基本为对流不稳定层结,越靠近近地面层,对流不稳定越强,117°E附近的-∂θe/∂p的强度可达-0.25 K·hPa-1;此时湿位涡强度很弱,可以认为不存在CSI区域(图 8a)。第二阶段,原本位于117°E附近的对流不稳定强中心东移,对应区域的CSI发展增强(图 8b),强度达到了-3 PVU。到了第三个阶段,对流层中下层的对流稳定与CSI均减弱(图 8c),-∂θe/∂p的强度为-0.05 K·hPa-1,湿位涡的强度约为-2 PVU。
|
图 8 2015年8月2日06时(a),21时(b),3日06时(c)不稳定量的垂直剖面(蓝色阴影:MPV < 0,单位:PVU;黑色实线:-∂θe/∂p < 0,单位:K·hPa-1,绿色虚线:惯性不稳定,单位:10-3 s-1,剖线位置见图 3) Fig. 8 Vertical cross-section of MPV (shaded area, unit: PVU), -∂θe/∂p (black line, K·hPa-1) and absolute vorticity (green line, 10-3 s-1) at 0600 UTC 2 (a), 2100 UTC 2 (b), 0600 UTC 3 (c) August 2015 (Location of the cross-section is shown in Fig. 3) |
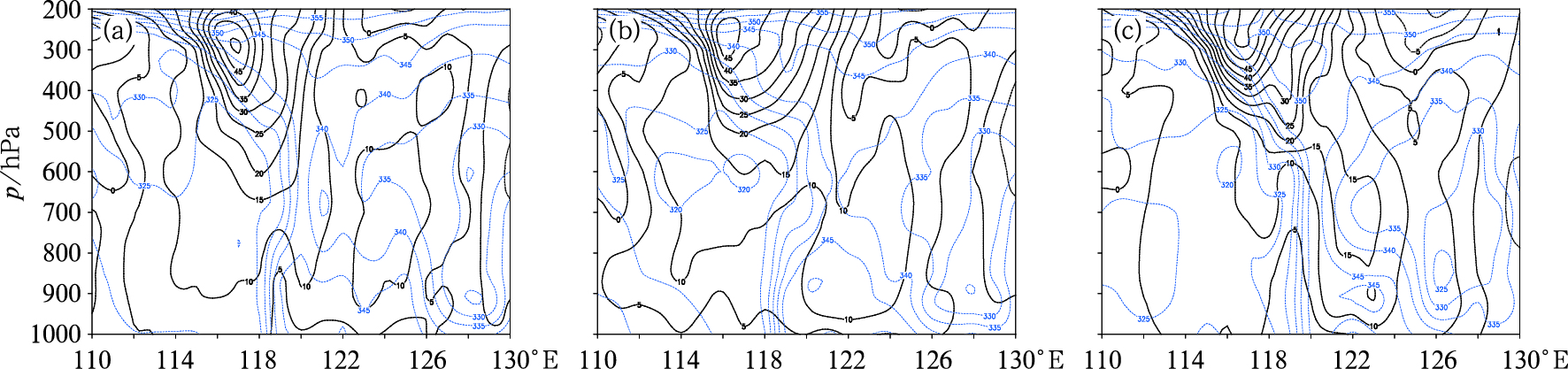
沿AB线作3个时刻的M-θe剖面(图 9),把等M面的坡度小于等θe面的区域判定为CSI。在3个时次的M-θe剖面图上,除了能诊断出与图 8基本对应的CSI区域,还能诊断出锋面(等θe线密集处)附近强度较弱的CSI区域。比较之后发现,对流稳定度、惯性稳定度、湿位涡结合诊断分析CSI区域的方法能比较各不稳定量的强弱,直观地反映出CSI的强度,排除与降水关系不大的弱CSI区域,因而比M-θe剖面图更准确有效。
|
图 9 2015年8月2日06时(a),21时(b),3日06时(c)M-θe剖面图(黑色实线:地转动量,单位:kg·m·s-1,蓝色虚线:相当位温,单位:K,剖线位置见图 3) Fig. 9 M-θe cross-section at 0600 UTC 2 (a), 2100 UTC 2 (b) and 0600 UTC 3 (c) August 2015 (Location of the cross-section is shown in Fig. 3; black solid line: M, unit: kg·m·s-1, blue dashed line: θe, unit: K) |
本文用EC高分辨率再分析资料在GRAPES_ Meso中模拟了2015年8月2—4日的一次华北锋面带状降水过程,模拟结果与实况接近,能呈现此次降水过程的雨带走向、强度、落区等大致特征。利用模式输出资料分析降水过程中的不稳定量,结果表明:
(1) 带状降水过程受对流不稳定、惯性不稳定以及CSI的影响。CSI的发展阶段伴随着对流不稳定的减弱和惯性不稳定的增强。
(2) 带状降水过程经历了3个阶段:在第一个阶段,降水区域上空基本为对流不稳定层结,降水主要受对流不稳定影响;第二个阶段,对流不稳定、对流层中层的CSI与惯性不稳定发展增强,降水受对流不稳定、CSI以及惯性不稳定的共同影响;第三个阶段,华北雨区上空的3种不稳定量均逐渐减弱,但仍然影响着降水的持续。
(3) 发展旺盛阶段的CSI在平面上呈带状分布,与雨区、对流不稳定区域平行,并随系统向东发展,随后减弱;CSI在剖面上主要活跃在对流层低层。
(4) 用湿位涡结合对流稳定度与惯性稳定度诊断CSI时,比M-θe剖面图诊断CSI区域更准确有效。
上述结论揭示了CSI的空间结构,对锋面雨带的形成机制研究有一定的参考意义,指出了CSI与锋面带状降水之间的联系,对暴雨的临近预报具有一定的指示作用。
陈德辉, 薛纪善, 杨学胜, 等, 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究[J]. 科学通报, 53(20): 2396-2407. DOI:10.3321/j.issn:0023-074X.2008.20.002 |
陈炯, 马占山, 苏勇, 2017. 适用于GRAPES模式C-P边界层方案的设计和实现[J]. 应用气象学报, 28(1): 52-61. |
池再香, 胡跃文, 白慧, 2005. "2003.1"黔东南暴雪天气过程的对称不稳定分析[J]. 高原气象, 24(5): 792-797. DOI:10.3321/j.issn:1000-0534.2005.05.020 |
戴光丰, 陈子通, 2013. GRAPES模式中地面通量在一次台风数值模拟中的敏感性试验研究[J]. 热带气象学报, 29(3): 403-410. DOI:10.3969/j.issn.1004-4965.2013.03.006 |
杜楠, 钟玮, 陆汉城, 等, 2008. 一次四川暴雨过程的非线性对流-对称不稳定分析[J]. 南京气象学院学报, 31(3): 308-316. DOI:10.3969/j.issn.1674-7097.2008.03.003 |
费建芳, 伍荣生, 宋金杰, 2009. 对称不稳定理论的天气分析与预报应用研究进展[J]. 南京大学学报(自然科学版), 45(3): 323-333. DOI:10.3321/j.issn:0469-5097.2009.03.001 |
费建芳, 伍荣生, 黄小刚, 等, 2010. 垂直-倾斜对流一体化参数化方案的实现及数值试验[J]. 气象学报, 68(2): 162-172. |
郭云云, 邓莲堂, 范广洲, 等, 2015. GRAPES中尺度模式中不同积云参数化方案预报性能对比研究[J]. 气象, 41(8): 932-941. |
姜晓飞, 刘奇俊, 马占山, 2015. GRAPES全球模式浅对流过程和边界层云对低云预报的影响研究[J]. 气象, 41(8): 921-931. |
李万彪, 2010. 大气物理:热力学与辐射基础[M]. 北京: 北京大学出版社.
|
刘璐, 冉令坤, 周玉淑, 等, 2015. 北京"7.21"暴雨的不稳定性及其触发机制分析[J]. 大气科学, 39(3): 583-595. |
盛裴轩, 毛节泰, 李建国, 等, 2003. 大气物理学[M]. 北京: 北京大学出版社.
|
万子为, 王建捷, 黄丽萍, 等, 2015. GRAPES-MESO模式浅对流参数化的改进与试验[J]. 气象学报, 73(6): 1066-1079. |
王德立, 徐国强, 贾丽红, 2013. GRAPES的积云对流参数化方案性能评估及其改进试验[J]. 气象, 39(2): 166-179. |
王宗敏, 丁一汇, 张迎新, 等, 2014. 副高外围对流雨带中的对流-对称不稳定及锋生的诊断分析[J]. 大气科学, 38(1): 133-145. |
伍湘君, 金之雁, 黄丽萍, 等, 2005. GRAPES模式软件框架与实现[J]. 应用气象学报, 16(4): 539-546. DOI:10.3969/j.issn.1001-7313.2005.04.015 |
吴哲红, 2007.一次西南地区暴雨的不稳定性诊断分析[D].南京: 南京信息工程大学. http://cdmd.cnki.com.cn/article/cdmd-10300-2007127771.htm
|
叶磊, 张梅, 赵定池, 等, 2015. 华东地区雷暴天气对流有效位能统计分析[J]. 安徽农业科学, 43(31): 160-162, 285. DOI:10.3969/j.issn.0517-6611.2015.31.062 |
张芳华, 陈涛, 杨舒楠, 等, 2014. 一次冬季暴雨过程中的锋生和条件对称不稳定分析[J]. 气象, 40(9): 1048-1057. |
周康辉, 郑永光, 王婷波, 等, 2017. 基于模糊逻辑的雷暴大风和非雷暴大风区分方法[J]. 气象, 43(7): 781-791. |
Bennetts D A, Hoskins B J, 1979. Conditional symmetric instability-a possible explanation for frontal rainbands[J]. Quart J Roy Meteor Soc, 105(446): 945-962. DOI:10.1002/(ISSN)1477-870X |
Emanuel K A, 1983. On assessing local conditional symmetric instability from atmospheric soundings[J]. Mon Wea Rev, 111(10): 2016-2033. DOI:10.1175/1520-0493(1983)111<2016:OALCSI>2.0.CO;2 |
Hoskins B J, 1974. The role of potential vorticity in symmetric stability and instability[J]. Quart J Roy Meteor Soc, 100(425): 480-482. DOI:10.1002/(ISSN)1477-870X |
Moore J T, Lambert T E, 1993. The use of equivalent potential vorticity to diagnose regions of conditional symmetric instability[J]. Wea Forecasting, 8(3): 301-308. DOI:10.1175/1520-0434(1993)008<0301:TUOEPV>2.0.CO;2 |
Shou Shaowen, Li Yaohui, 1999. Study on moist potential vorticity and symmetric instability during a heavy rain event occurred in the Jiang-Huai valleys[J]. Adv Atmos Sci, 16(2): 314-321. |
 2018, Vol. 44
2018, Vol. 44