引言

数值预报质量提高的关键因素之一就是初始场的改进。初始场的改进包含资料同化方法的发展和观测资料的增多。资料同化方法从最优插值方法(optimal interpolation, OI)、三维变分分析(three-dimensional variational analysis, 3Dvar)，四维变分分析(four-dimensional variational analysis, 4Dvar)发展到集合卡尔曼滤波(ensemble Kalman fitter, EnKF)和混合集合变分同化方法(hyborid variational analysis, Hybrid-Var)等，变分方法的应用使得大量非常规观测资料的同化成为可能；集合的引进使对背景误差协方差的描述从简单的模型化到随天气形势变化，从而观测资料的传播也更加合理，因此分析框架的改进对初始场质量的提高有很大的帮助。随着观测技术手段的提高，观测资料类型和数量也逐渐增多，从常规观测资料到卫星亮温、掩星反射率资料、雷达反射率和径向风、降水资料等，丰富的观测资料源为改善分析场质量提供更多可能，模式对天气系统发展的模拟也更准确和精细。

利用现有的全球和区域模式业务资源，结合全球和区域分析特点的混合分析方案是提高区域分析和预报质量的一种便捷可行的方法。高分辨率区域模式的分析更注重天气系统的中小尺度部分，天气系统大尺度特征的描述往往不如全球分析，一般也认为粗分辨率模式中的分析比嵌套模式能提供更好的大尺度特征；而且区域分析受区域范围的局限，模式区域边界以外特别是天气系统上游的有效观测信息难以影响分析，所以结合全球和区域分析特点的混合方案提了出来。混合技术的优点有以下几个方面：(1)结合全球分析，可以获得区域分析中所缺乏的观测资料信息，例如卫星亮温、掩星等资料；(2)减缓模式边界对分析的影响，利用区域边界外的观测信息；(3)全球分析能更好地描述大尺度信息；(4)可以获得区域分析更精细的中小尺度信息。混合分析可以通过在区域分析的目标函数中增加一项考虑全球分析信息的部分，从全球分析场中获得有益于区域分析的信息(Guidard and Fischer, 2008；Dahlgren and Gustafsson, 2012)。另外一种做法是对粗分辨率和高分辨率分析采用低通滤波，分别取两者的大(小)尺度波动部分。Yang(2005)以及Hsiao et al(2015)曾采用此方法，他们利用六阶隐式雷蒙德切线滤波器(6th order implicit Raymond tangent filter)来滤除小尺度部分。

国家气象中心业务运行的数值预报模式有GRAPES中尺度数值预报模式和T639全球中期数值预报模式。全球和区域同化预报系统(Global/Regional Assimilation and Prediction System，GRAPES)是我国自主研发的数值天气预报系统(薛纪善, 2006；Xue and Liu, 2007；薛纪善等，2008；陈德辉等, 2008；Zhang and Shen, 2008)，2006年GRAPES区域等压面三维变分分析系统和中尺度数值预报模式系统正式投入国家业务运行，2009年GRAPES区域等压面三维变分分析系统升级为模式面分析(马旭林等，2009)，并在2011年业务运行。目前GRAPES区域三维变分分析的分辨率为10 km，同化GTS传输的常规资料、雷达VAD风和GPS PW降水资料。全球T639中期数值预报模式从2008年在国家气象中心业务运行，该模式同化常规资料和美国极轨卫星系列NOAA 15/18全球的ATOVS资料。

考虑到全球分析系统采用了卫星等观测资料，由于和区域分析采用不同的框架结构，全球分析在大尺度部分的分析有一定优势；而且我国西部地区常规观测资料稀疏，中国区域以外西部地区属于天气系统的上游，其观测信息也影响着中国区域的预报，所以T639全球分析可以补偿区域分析在我国西部地区分析能力的不足和减缓区域分析边界的影响。为了提高区域模式的分析预报质量，同时更好地利用全球和区域模式的业务资源，文中采用离散余弦变换(discrete cosine transform，DCT)方法对全球和区域分析增量进行谱分解，从而混合全球分析的大尺度信息和区域分析的中小尺度信息。

1 模式系统及混合方案介绍 1.1 GRAPES区域模式系统

GRAPES区域中尺度数值预报模式系统(4.0版本)是采用地形追随坐标、半隐式半拉格朗日积分方案、全可压非静力平衡动力框架、可自由组合的物理过程参数化方案，模式变量分布在垂直方向采用Charney-Phillips跳层，水平方向采用Arakawa-C跳点，模式分层采用51层, 模式层顶达33 km。文中试验采用水平分辨率为10 km，格点数为751×501。GRAPES区域模式采用如下物理选项：辐射方案采用RRTM LW和Dudhia SW，积云对流方案采用Kain-Fritsch，微物理过程采用WSM6, 陆面过程采用NOAH，近地面层方案采用Monin-Obukhov方案，边界层方案采用MRF方案。

GRAPES区域分析采用模式面3Dvar系统(马旭林等，2009)，其采用非平衡的无量纲气压、流函数、非平衡的势函数和比湿作为控制变量。观测资料采用探空资料(TEMP)、地面报资料(SYNOP)、船舶资料(SHIPS)、飞机报资料(AIREP)、云导风资料(SATOB)、GPS降水资料(GPS PW)和雷达反演风场(RADAR VAD)。

1.2 T639全球模式

文中采用的全球分析来自国家气象中心业务运行的T639模式，其水平分辨率为30 km，垂直分辨率为60层，模式层顶达0.1 hPa。T639模式同化的观测资料主要为地面报、高空报、船舶报及美国极轨卫星系列NOAA-15/18的全球ATOVS资料(周慧等，2010；常飞，2015)。T639分析采用三维变分分析方法，针对不同观测采用多尺度同化方案。

1.3 混合方案

为了获得分析中大尺度和中小尺度信息，本文采用了DCT方法对有限区域二维气象场进行谱分解，这种方法可以不需要周期化气象场，也不需要去除倾向，能够比较真实地计算出气象场实际的谱结构(Denis et al, 2002；郑永骏等，2008)。本文将2D-DCT方法应用于有限区域二维气象场可以获得功能谱σ²(m, n)，其是随二维波数(m, n)变化的函数，公式如下：

$ {\sigma ^2}(m, n) = \frac{{{F^2}(m, n)}}{{M \circ N}}\;\;\;(m, n) \ne (0, 0) $

(1)

式中，M、N为X与Y方向的总波数，F(m, n)为二维谱系数。通过定义归一化波数获得只随一维波数变化的谱密度，

$ S(k) = S(\tilde k) \circ \Delta \circ \min (M - 1, N - 1) \circ {{\rm{ \mathsf{ π} }}^{ - 1}} $

(2)

式中，$S(\tilde k)$是当归一化波数$\alpha = \sqrt {\frac{{{m^2}}}{{{{(M - 1)}^2}}} + \frac{{{n^2}}}{{{{(N - 1)}^2}}}} $满足$\alpha \in \left[ {\frac{{\tilde k}}{{\min (M - 1, N - 1)}}, \frac{{\tilde k + 1}}{{\min (M - 1, N - 1)}}} \right]$区间的方差和，也是采用圆频率表示的波数$k \in \frac{{\rm{ \mathsf{ π} }}}{\Delta } \circ \left[ {\frac{{\tilde k}}{{\min (M - 1, N - 1)}}, \frac{{\tilde k + 1}}{{\min (M - 1, N - 1)}}} \right]$区间的方差和，其中$\tilde k = 1, 2, \cdots \min (M - 1, N - 1)-1$，因而$S(\tilde k)$由相应的方差σ²(m, n)组成。上式中Δ为格距，归一化波数α对应的波长为λ=2Δ/α，采用圆频率表示的波数为k=2π/λ=πα/Δ。

由于全球T639模式的分析和区域GRAPES分析都是在T639模式6 h预报场的基础上进行分析，因而文中分别针对全球T639模式和区域GRAPES模式的分析增量场进行尺度分离和混合。

具体步骤如下，首先获得全球T639模式和区域GRAPES模式的分析增量场。对T639模式的6 h预报场和分析场进行降尺度，获得与区域模式分辨率一致的气象场，从而获得T639模式的分析增量T_dxa：

$ {T_{dxa}} = {T_{xa}} - {T_{xb}} $

(3)

式中，T_xa为T639模式的分析场，T_xb为作为背景场的T639模式6 h预报场。同样，也可以得到区域GRAPES模式的分析增量G_dxa :

$ {G_{dxa}} = {G_{xa}} - {T_{xb}} $

(4)

式中G_xa为GRAPES模式的分析场。

然后，采用二维DCT方法对以上分析增量场进行谱分解，获得各自随波长变化的谱密度，针对不同变量和不同层次给定截断波长，保留大尺度部分的谱密度，再采用傅里叶逆变换获得格点空间的全球T639模式和区域GRAPES模式大尺度部分的分析增量T_dxa^L与G_dxa^L，公式如下：

$ T_{dxa}^L = {\rm{Filter}}({T_{dxa}}) $

(5)

$ G_{dxa}^L = {\rm{Filter}}({G_{dxa}}) $

(6)

式中Filter(T_dxa)与Filter(G_dxa)为获得大尺度部分分析增量的滤波过程。区域GRAPES模式的中小尺度分析增量G_dxa^S为：

$ G_{dxa}^S = {G_{dxa}} - G_{dxa}^L $

(7)

最后，在T639模式的背景场基础上，混合全球T639模式大尺度部分的分析增量T_dxa^L和区域GRAPES模式中小尺度部分的分析增量G_dxa^S，从而获得混合分析G_blnd，即：

$ {G_{\mathit{blnd}}} = {T_{xb}} + T_{dxa}^L + G_{dxa}^S $

(8)

文中根据T639模式和区域GRAPES模式各个变量的分析增量在每一层中谱密度随尺度变化情况确定截断波长，对无量纲气压(π)、U、V风场和位温(θ)按照不同层次用不同的截断波长进行了尺度分离，然后获得混合分析。其中对于湿度变量以区域分析为主。表 1为各个变量在不同层次采用的截断波长的情况。

1.4 试验设置

文中通过谱密度及动能谱的分析、批量试验的要素场和降水预报检验，分析了混合分析对预报的影响。文中进行以下批量试验：(1)GRAPES区域分析进行模式预报试验(以GRAPES表示)，其中同化的观测资料为探空资料(TEMP)、地面报资料(SYNOP)、船舶资料(SHIPS)、飞机报资料(AIREP)、云导风资料(SATOB)、GPS降水资料(GPS PW)和雷达反演风场(RADAR VAD)。(2)混合T639模式分析的大尺度部分与GRAPES区域分析的中小尺度部分，对混合分析进行GRAPES模式预报试验(以Blnd表示)。试验时间从2015年6月15日0000 UTC至7月15日0000 UTC(世界时，下同)，每日0000 UTC进行分析和48 h模式预报。

2 谱密度及动能谱分析

本文通过选取2015年7月2—4日的强降水个例，诊断全球T639分析和区域GRAPES分析的谱能量随不同尺度变化的情况。

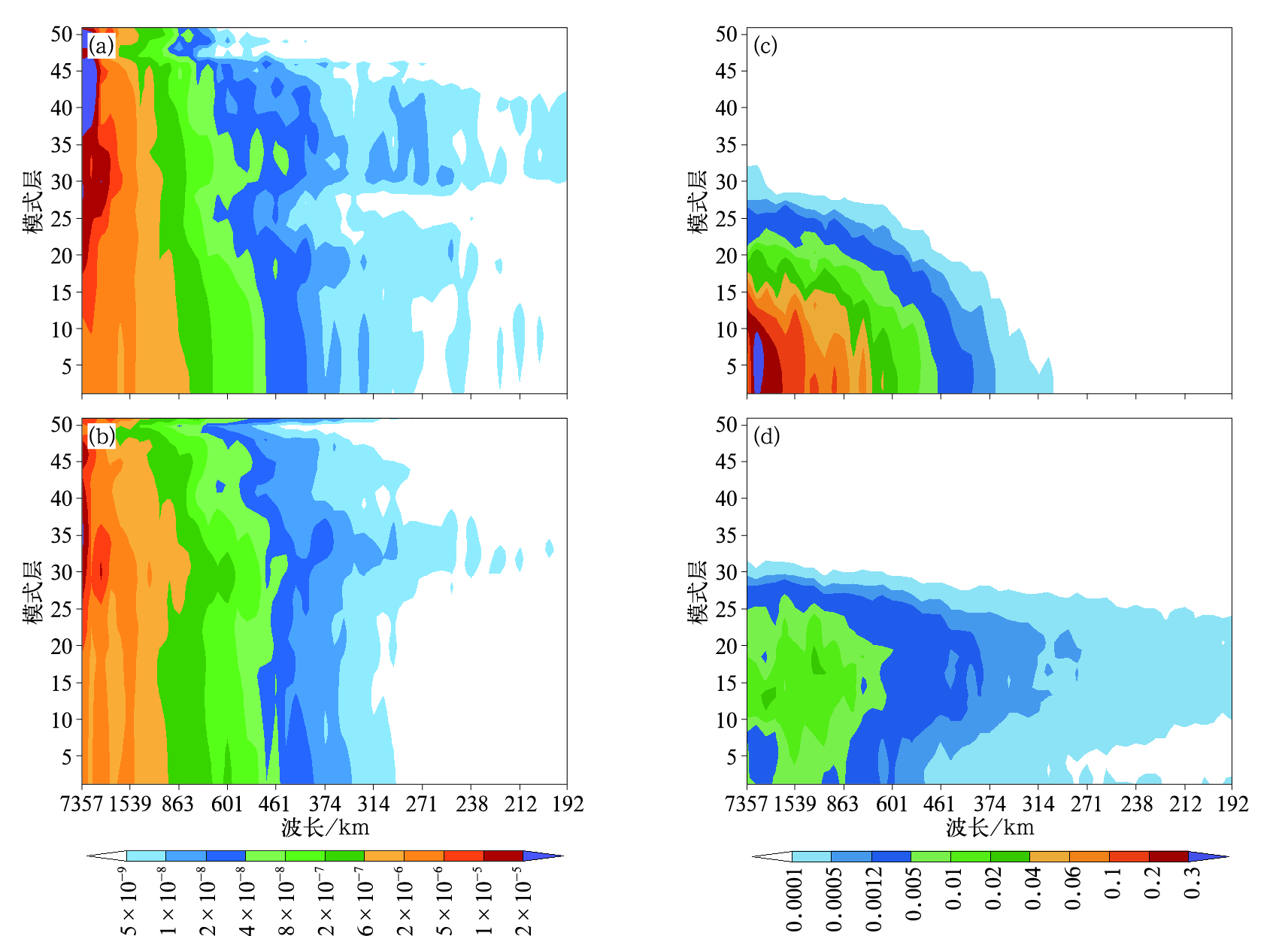
2.1 分析增量的谱密度

文中通过对分析增量进行谱分解，比较全球和区域分析增量场的谱密度随尺度变化的情况。图 1为GRAPES与T639试验分析增量经过谱分解后，无量纲气压的谱密度随不同尺度和不同层的变化情况。从图 1中可以看出，无量纲气压的谱密度都随着尺度的降低而减弱，区域GRAPES分析增量的谱密度在300 km以下的尺度部分略大于全球T639分析增量的谱密度，特别是中高层。

对于比湿变量，区域分析增量在大尺度部分的谱密度远远大于T639分析(图 1c，1d)，由于全球T639分析在中国区域使用的湿度观测资料较少，而GRAPES使用了加密地面站的湿度观测信息和GPS降水观测资料，区域GRAPES湿度分析在大尺度部分要优于全球T639分析，因此本文在混合分析中没有采用T639分析的大尺度信息。同时也可以看出，在中小尺度部分的中低层，T639分析增量的谱密度明显大于GRAPES分析，这可能是T639分析中背景误差结构把观测信息在中小尺度部分传播的更远造成的。

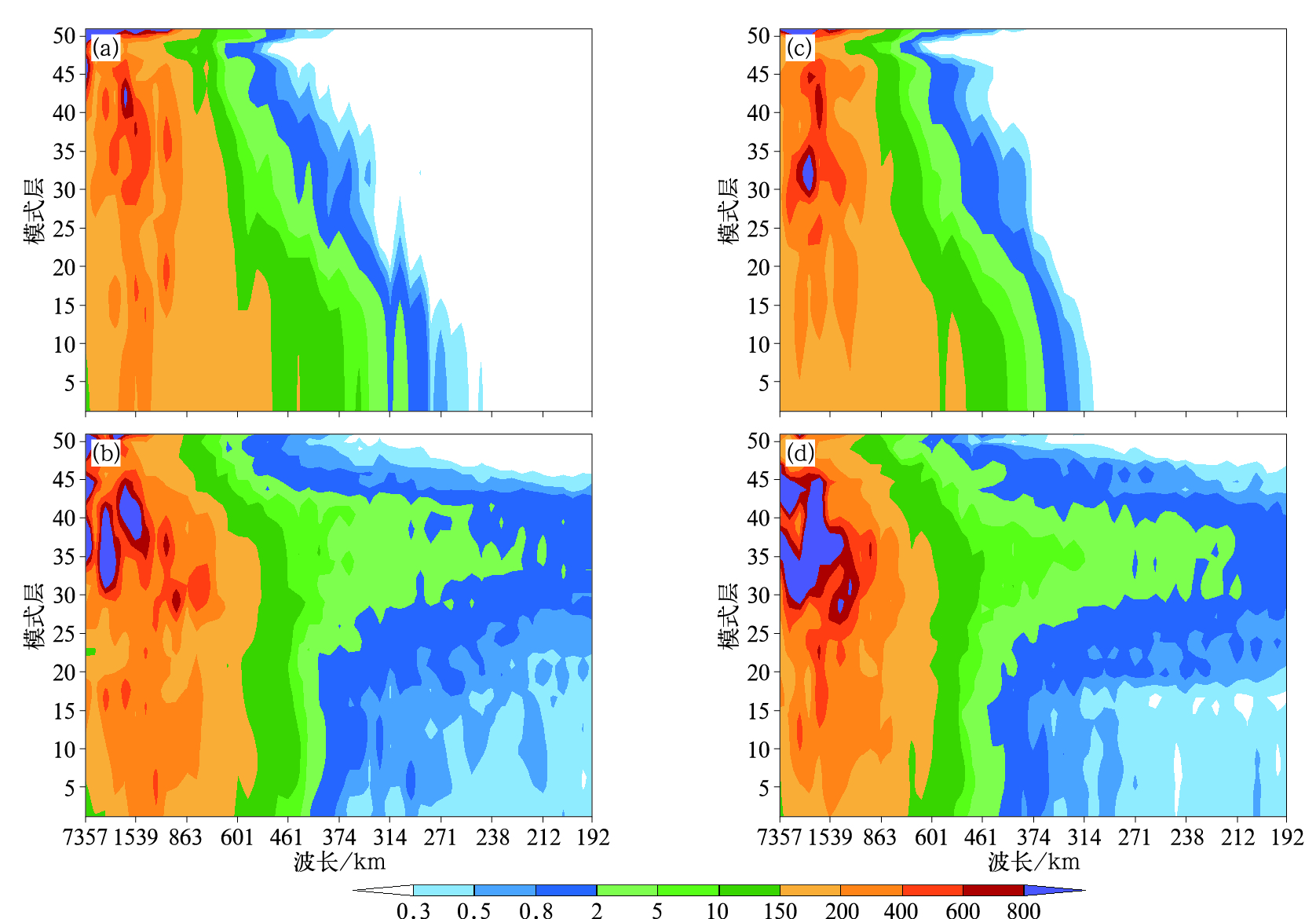
从分析增量U和V的谱密度随尺度的变化可以看出(图 2)，GRAPES(图 2a，2c)分析增量的谱密度随着尺度的降低在25层以上下降较快，T639分析增量在中高层的谱密度随尺度的降低下降较缓(图 2b，2d)；在25层以下GRAPES分析增量的谱密度在800~300 km略大于全球T639分析增量谱密度；T639分析增量和GRAPES区域分析增量谱密度的差别不仅和同化的不同观测信息有关，还和不同系统的背景误差协方差结构有关。

2.2 动能谱的比较

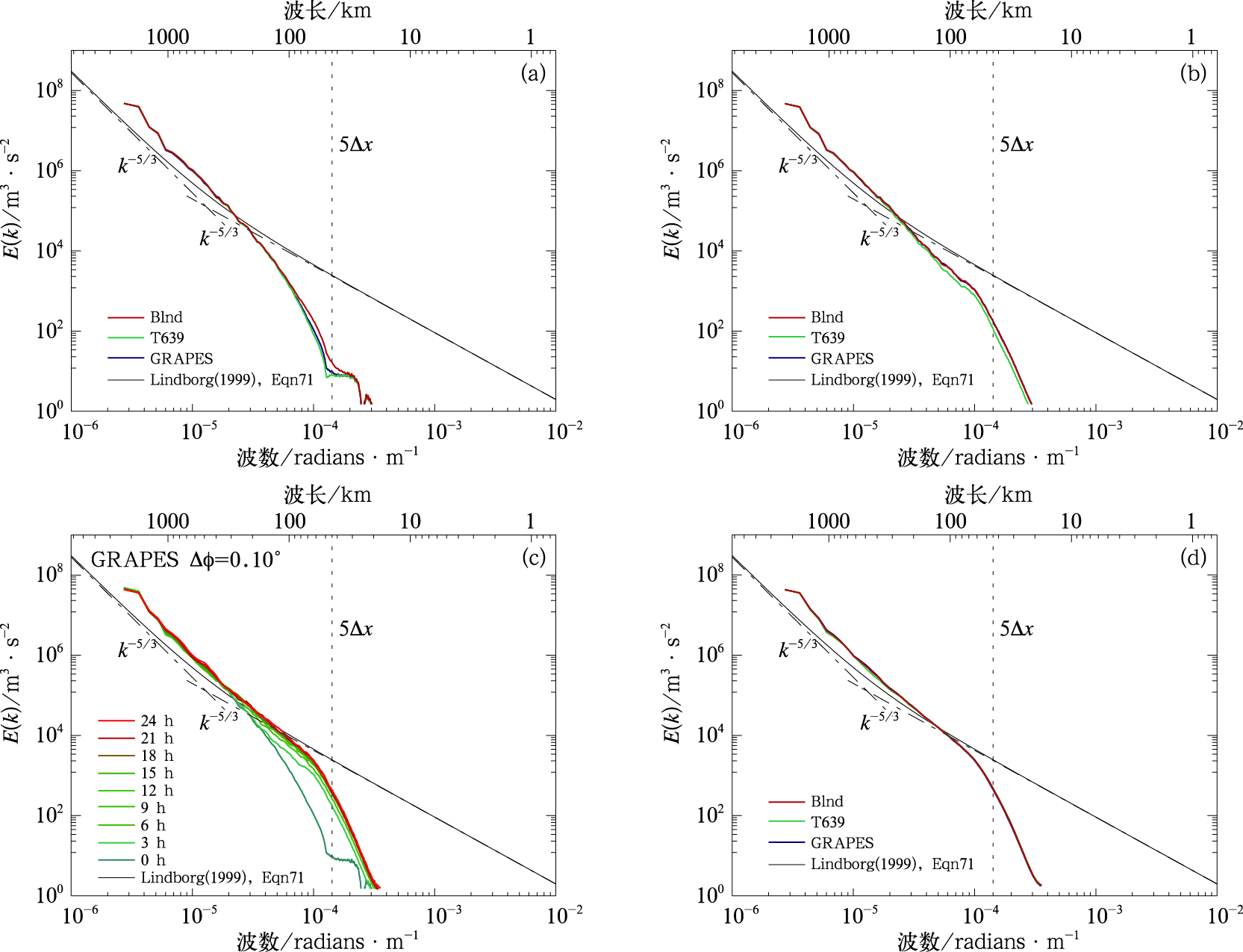
大量的观测事实表明大气动能谱具有如下分布特征：在大尺度区域动能(E)与波数(k)的关系满足E∝k^-3关系，过渡到中尺度区域表现为E∝k^-5/3关系。Lindborg(1999)使用MOZAIC资料主要集中在对流层顶部和平流层底部大约350~150 hPa的高度来统计动能谱，为了和Lindborg曲线比较，本文统计分析350~150 hPa高度，模式输出的U和V风场计算得到的平均动能谱分布。从分析的动能谱分布可以看出(图 3a)，在大尺度部分T639分析、GRAPES分析和Blnd分析试验的动能谱能量相当，而在中小尺度部分，由于在对流层高层以上，10 km分辨率模式统计的动能谱能量都低于Lindborg曲线，但可以看出T639分析的动能谱能量略微低于GRAPES分析的，经过大尺度和中小尺度信息混合后，Blnd分析的动能谱能量在中小尺度部分略微更接近观测。经过3 h预报后，在中小尺度部分，GRAPES分析和混合分析的预报平均动能谱能量相差不大，T639分析的预报平均动能谱能量略小(图 3b)。图 3c为spin up时间模式动能谱的演变特征，从图中可以看出，随着spin up时间发展模式动能谱逐渐在中尺度部分与Lindborg参考曲线靠近，6 h预报后的动能谱就变化不大，说明模式spin up过程基本完成，模式能够基本正确地生产和发展初始场中所不包含的中小尺度系统，模式的spin up时间约为6~9 h，比郑永骏等(2008)得到的结论略提前。考虑模式spin up时间，统计模式12~48 h预报平均的动能谱，从图 3d可以看出，几组试验的动能谱相当，说明12 h预报后初始场对模式动能谱的影响非常小。

从以上分析可以看出，GRAPES分析场的动能谱能量在中小尺度部分比T639全球分析略大，经过混合分析后，动能谱能量更接近理想曲线；而初始场对动能谱能量的影响可以到6 h左右。

3 分析预报试验结果 3.1 降水预报

从2015年6月15日0000 UTC至7月15日0000 UTC，在每日的0000 UTC进行分析预报试验，以下比较区域GRAPES分析(GRAPES)和混合尺度分析(Blnd)对降水和天气要素预报的影响。

从一个月批量试验平均的6 h累积降水ETS评分可以看出，经过大尺度分析和区域中小尺度分析混合后，预报降水ETS评分在不同降雨量级和不同预报时段上都有明显提高(图 4)。以上说明在区域中小尺度分析中加入协调的大尺度部分得到的初始场更容易被模式吸收，对区域模式的预报降水有明显正贡献。

3.2 要素场预报

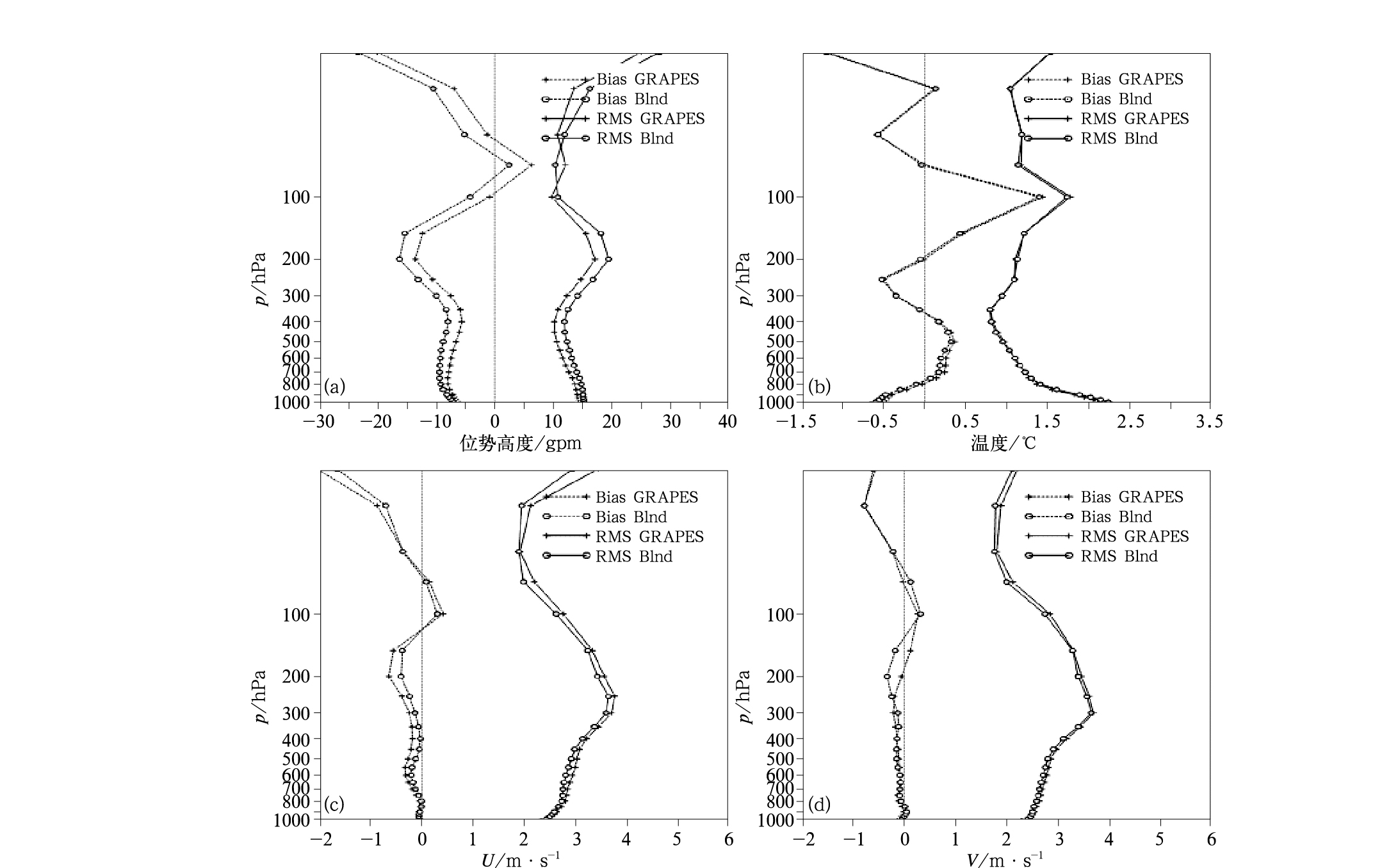
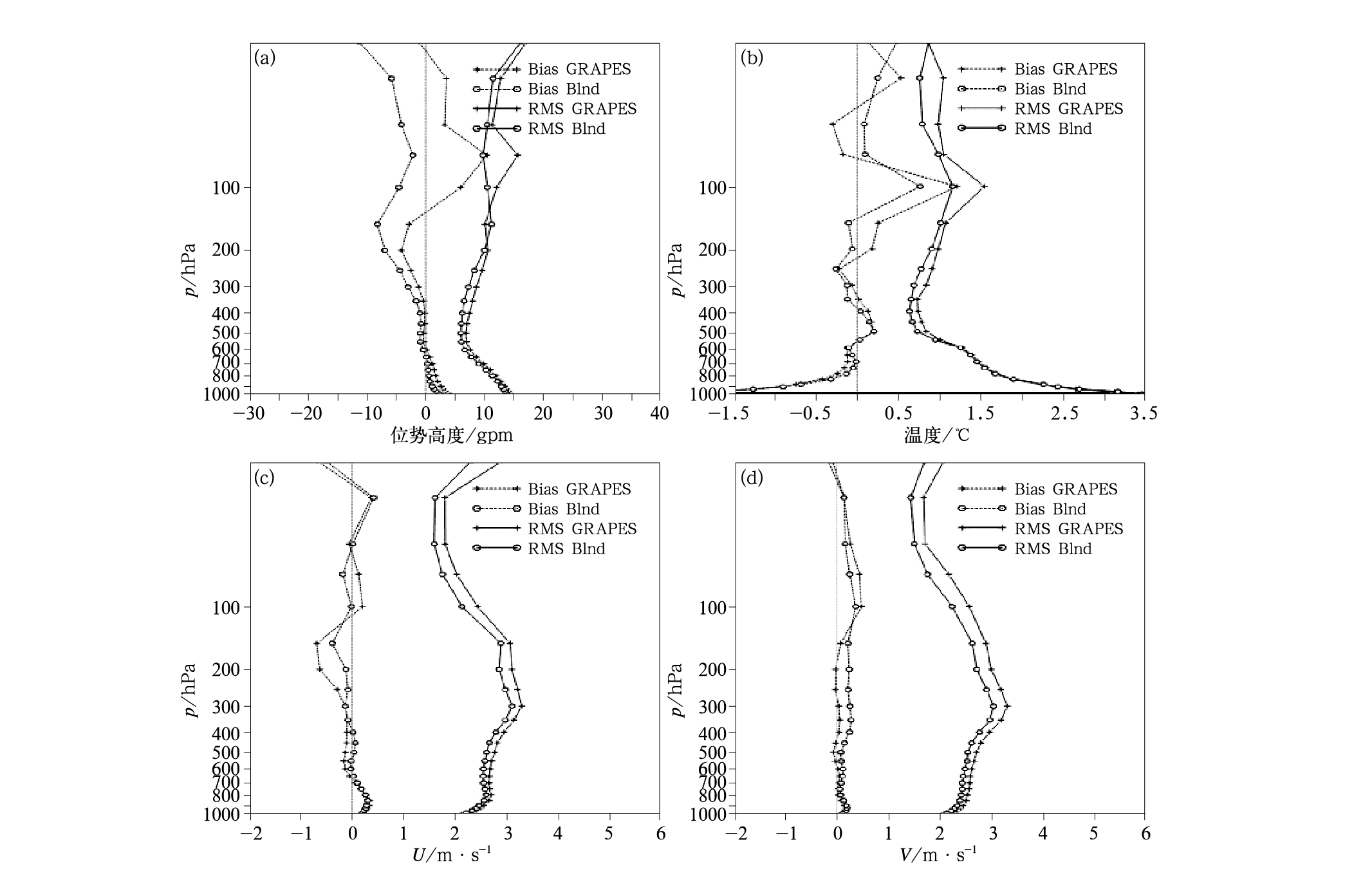
通过比较GRAPES和Blnd的位势高度、温度、U和V风场与FNL分析的均方根误差可以看出(图 5)，Blnd的风场、高度场和温度场的均方根误差从低层到高层都明显小于GRAPES的，而且温度和U风场的偏差整体也更小。以上说明Blnd的分析弥补了GRAPES的不足，分析质量有所提高。

图 6是GRAPES模式6 h预报的偏差与均方根误差，从图中可以看出，混合尺度方案的6 h预报位势高度均方根误差从低层到高层基本都大于区域分析的均方根误差；对于温度场，两组方案的均方根误差相差不大；对于风场，从低层到高层混合尺度分析后的预报更接近实况。预报12 h后，混合尺度方案的要素场预报质量和区域分析方案的相差不大，两组试验的均方根误差差别不大(图略)。

从以上分析可以看出，在区域分析中融合T639全球分析的大尺度部分可以明显提高风场、高度场和温度场的分析质量，而且前6 h的风场预报也有明显改进；同时也可以提高降水预报质量。

4 结论与讨论

本文为了提高区域GRAPES模式的预报能力，更有效地利用业务全球T639模式和区域GRAPES模式的资源，综合全球T639分析的大尺度部分和区域GRAPES分析的中小尺度部分获得混合分析。通过谱密度及动能谱分析，以及批量分析预报试验，初步得到如下结论：

(1) 由于同化不同的观测资料，以及在变分分析框架中采用不同的技术细节，区域GRAPES分析增量的谱密度与T639分析的有较大差别。GRAPES无量纲气压分析增量谱密度在300 km以下略大于T639分析的；对于湿度变量，T639分析增量大尺度部分的谱密度远远小于GRAPES；相对于U/V风场，GRAPES分析增量的谱密度在中小尺度部分下降较快，这说明区域GRAPES分析在动力场上中小尺度部分的分析还不够精细，还需要统计调节适合于区域模式的背景误差协方差的结构，例如采用更适合于中小尺度分析的二阶自回归水平相关模型替换区域分析中的高斯相关模型，考虑采用样本统计的垂直误差结构代替垂直相关模型，或者改进背景误差协方差中的平衡关系等(王瑞春和龚建东，2016)。同时GRAPES区域分析需要增加能改进中小尺度分析的高密度观测资料，例如采用雷达径向风观测资料(马昊等，2016)，也需要对同化的观测资料做更细致的应用分析，充分发挥观测资料对数据同化的价值(郝民等，2016)。

(2) 从动能谱上可以看出区域模式的分析和前6 h预报的动能谱比全球T639分析在中小尺度部分略微接近观测值，而经过大尺度和中小尺度部分分析的混合后，混合分析的动能谱在中小尺度部分明显最靠近观测动能谱。

(3) 分析预报试验表明，在区域分析中融合T639全球分析的大尺度部分可以明显提高风场、高度场和温度场的分析质量，以及6 h风场的预报质量；同时明显提高区域降水预报质量。

混合全球T639分析场的大尺度部分和区域GRAPES分析的中小尺度部分能有效改善区域模式初始场的质量，提高区域模式降水预报评分。但是目前GRAPES区域分析采用的观测资料类型和数量还较少，特别是西部地区的观测资料更少，今后将加强观测资料的使用，特别是时空高密度的雷达径向风和反射率资料的同化。同时区域三维变分分析中将进一步改进背景误差协方差，包括考虑随天气形势变化的背景误差结构来改进区域中小尺度分析。