强降雨是影响我国的主要重大灾害性天气之一,1998年长江流域的强降雨引发了历史罕见洪水,1991、2003和2007年淮河流域出现的强降雨也引发了流域性大洪水。强降雨及其引发的洪涝灾害不仅危及了人民的生命财产安全,同时还造成严重的国民经济损失,而减轻强降雨引发的洪涝灾害的关键则在于提高强降雨预报准确率。当今,数值预报已成为现代天气预报业务的基础,并在强降雨预报中发挥了非常重要的作用,但数值预报对于强降雨预报的精准度仍不够高,尤其是随着预报时效的延长,模式对强降雨预报的不确定性迅速增大,可靠性明显降低(陈静等,2006;赵琳娜等,2010;李勇,2016;沈学顺等,2017)。为此,加强对数值模式在中期预报时效的解释应用技术的研究就更为迫切(代刊等,2016;朱玉祥等,2016)。
已有研究表明,多模式集成预报技术能够充分利用不同模式的优点,并能有效减少不同模式的系统性误差(杜钧和陈静,2010),对强降雨预报技能提高有很好效果(Cartwright and Krishnamurti, 2007;Chakraborty and Krishnamurti, 2009;Krishnamurti et al,2009a;Sun and Chen, 2012;柯宗建等,2009;康红文等,2012;陈鹏翔等,2017)。许映龙等(2015)对1323号台风菲特的分析表明多模式集合预报订正技术能有效提高台风路径和风雨预报准确率。唐圣钧等(2015)利用高、低空间分辨率模式集成方法对2013年5月8日华南强降雨的分析表明,多模式集成相对单一模式有明显改善。Krishnamurti et al(2009b)利用多模式集成方法对中国季风区南海季风爆发时降雨、梅雨期降雨以及台风登陆强降雨进行研究,发现多模式集成方法的强降雨预报效果要优于任何一个单模式预报效果。王亚男和智协飞(2012)也指出多模式集成预报对降雨极大值的捕捉能力更高。
此外,已有数值模式释用应用技术研究表明,支持向量机(support vector machine, SVM)方法使用了统计学习理论中的结构风险最小化原则,在处理非线性特征的降雨预报时有明显优势(冯汉中和陈永义,2004;冯汉中等,2004;熊秋芬和曾晓青,2008)。韦惠红等(2009)也指出SVM方法在区域性暴雨预报中具有一定的预报能力和参考价值。陈超辉等(2010)采用相关加权、多元线性回归以及SVM回归方法,分别开展多模式集成预报研究,指出对于24 h时效降雨,基于SVM回归方法的多模式集成预报得到的均方根误差比多模式集合平均小,且同时也优于相关加权法和多元线性回归的多模式集成预报效果。
本文基于欧洲中期天气预报中心(ECMWF)和美国国家环境预报中心(NCEP)集合预报资料和SVM回归方法建立了多模式集成的动力-统计客观预报模型,考察了其在中期预报时效的预报效果,以期提高强降雨中期预报的准确率。
1 资料和方法 1.1 资料本文所用资料为TIGGE资料平台下的ECMWF和NCEP的全球集合预报资料及国家气象中心实时预报业务数据库逐日(24 h,下同)降雨量加密观测资料。
(1) ECMWF和NCEP集合预报资料
使用2011年3—10月和2012年3—9月ECMWF和NCEP每天12时(UTC)起报的108~180 h逐日累积降雨量集合预报资料。ECMWF和NCEP预报资料集合成员数分别为51和21个,资料格距均为1°×1°,空间范围为0°~60°N、70°~150°E。
(2) 实况降雨量加密观测资料
采用2011年4—10月和2012年4—9月全国2413个加密观测站点逐日累积降雨资料(时界:UTC 00时),并采用Barnes方法(Barnes, 1964)将站点资料插值为格点资料,格距为0.25°×0.25°,空间范围为0°~60°N、70°~150°E。
1.2 方法 1.2.1 SVM-多模式集成预报SVM-多模式集成预报(SVM multi-model ensemble forecasting, SVM-MEF)方法把时间轴分为两部分,即训练期和预报期。在训练期,利用ECMWF和NECP集合预报降雨量和实况降雨量(格点)资料,采用SVM回归方法构建回归预报模型;在预报期,将集合预报降雨量资料带入回归预报模型开展预报试验。
(1) SVM回归模型的构建
本文根据SVM回归理论,采用RBF核函数,针对某一预报时效的每一格点来构建非线性回归预报模型[式(1) 和式(2);冯汉中和陈永义,2004]:
| $ f({x}) = \sum\limits_{i = 1}^L {({{a}_i} - {a}_i^*)} K({x}, {{x}_i}) + {b} $ | (1) |
| $ K({x}, {{x}_i}) = \exp (- {\left\| {x - {{x}_i}} \right\|^2}/{\sigma ^2}) $ | (2) |
式中,f(x)为通过训练样本构造的预报函数,L为支持向量的个数,ai、ai*、b为通过训练样本确定的最优超平面参数,K(xi, x)是核函数,xi(xi∈RN)为M个预报因子。
(2) 预报因子的选取
对指定预报时效的任一格点,选取模式日降雨量预报≥指定量级的概率作为预报因子之一,对ECMWF和NCEP的日降雨量预报资料均同时指定5个量级,依次为小雨(≥0.1 mm)、中雨(≥10 mm)、大雨(≥25 mm)、暴雨(≥50 mm)、大暴雨(≥100 mm),也即每个样本共采用了10个因子。
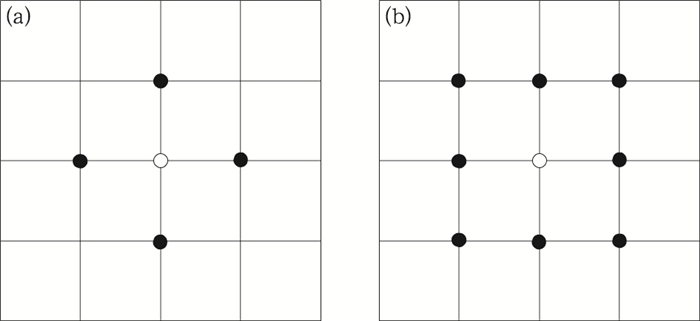
考虑到大雨及以上等级的强降雨实际发生次数相对较低,为此,在计算某格点大雨及以上等级的概率时,采取了升尺度方法,适度扩大了计算范围,即以某格点及与之格距(d)在指定范围内的格点中发生强降雨概率最大的值作为该降雨量级的预报因子。对于大雨和暴雨,采用d≤1.0°,参与计算的格点数为5(图 1a);对于大暴雨,采用d≤1.5°,参与计算的格点数为9(图 1b)。
|
图 1 升尺度方法示意图 (a)基于某格点(空心圆点)升尺度后大雨和暴雨的概率统计区间,(b)升尺度后大暴雨的概率统计区间 Fig. 1 Upscale method diagram (a) statistics area of heavy rain and rainstorm based on a grid point (hollow dot), (b) statistics area of heavy rainstorm based on a grid point |
(3) 训练样本的选取
研究采用了混合滑动训练期,即取预报日之前N d(30 d)和前一年预报日前后(2N+1) d(61 d)的样本混合,样本总量为(3N+1) d(91 d)。
1.2.2 集合平均预报集合平均预报(EC_M)采用等权重计算ECMWF集合预报所有成员(E)的数学平均值,能够反映出所有集合预报成员结果的总体趋势:
| $ EC\_M = \frac{{\sum\limits_{i = 1}^E {{E_i}} }}{E} $ | (3) |
式中Ei为集合预报各成员。
1.2.3 预报效果检验方法本文采用预报上常用的Threat Score(TS)评分作为衡量标准来检验某一量级降雨预报准确率,TS评分取值范围为0~1,对某一量级降雨的预报无预报技巧时值为0,对某一量级降雨预报准确率达100%时值为1,即无空报和漏报。
| $ TS = \frac{H}{{H + F + M}} $ | (4) |
式中,H为命中次数,F为空报次数,M为漏报次数。
2 SVM_MEF试验效果评估选用2012年5月1日至9月30日发生在淮河流域及其以南地区(18°~35°N、97°~123°E)的大雨和暴雨开展了SVM_MEF回报试验。鉴于前期已有预报业务实践和检验结果表明,在各业务模式中以ECMWF的总体预报效果最好(智协飞等,2016),为此在对SVM_MEF效果进行评估时选用了ECMWF的控制预报(EC_C)和集合平均预报(EC_M)作为参照对象进行了多角度比对评估。
2.1 总体预报效果对比表 1给出了2012年5—9月逐月的108 h预报SVM_MEF、EC_C、EC_M对大雨、暴雨和大暴雨的TS评分。由表 1清楚可见,SVM_MEF大雨预报的TS评分较EC_C提高了0.02~0.03,较EC_M提高了0.06~0.1,SVM_MEF暴雨预报的TS评分较EC_C提高了0.02~0.04,较EC_M提高了0.03~0.09。值得一提的是,SVM_MEF暴雨预报的TS评分较EC_C提高了5成至1倍及以上,较EC_M甚至提高了数倍。由上述可知,SVM_MEF对大雨和暴雨的总体预报效果最好,尤其对暴雨预报准确率的提高更为明显。
|
|
表 1 2012年5—9月SVM_MEF、EC_C、EC_M对大雨、暴雨和大暴雨108 h预报的TS评分 Table 1 Monthly TS score results of heavy rain forecasted by SVM_MEF, EC_C, EC_M from May to September 2012 (prediction time is 108 h) |
此外,表 1中,SVM_MEF大暴雨预报的TS评分与EC_C持平,预报效果并无明显提升,经分析认为原因主要在于大暴雨训练样本偏少。本文后续将重点针对SVM_MEF大雨和暴雨预报效果进行深入分析。
为深入了解SVM_MEF的预报效果,图 2和图 3还分别给出2012年5—9月逐日的108 h预报SVM_MEF、EC_C、EC_M对大雨和暴雨的TS评分,重点考察了该区域发生的20次暴雨过程(表 2)期间(共计75 d)SVM_MEF对大雨和暴雨的预报能力(表 3)。由表 3可知,SVM_MEF对大雨和暴雨预报明显具有优势,该方法大雨预报的TS评分高于TSEC_C和TSEC_M的日数分别为46 d和62 d,占总暴雨日数的61%和83%;对暴雨预报的TS评分高于TSEC_M的日数为41 d,占总暴雨日数的55%。
|
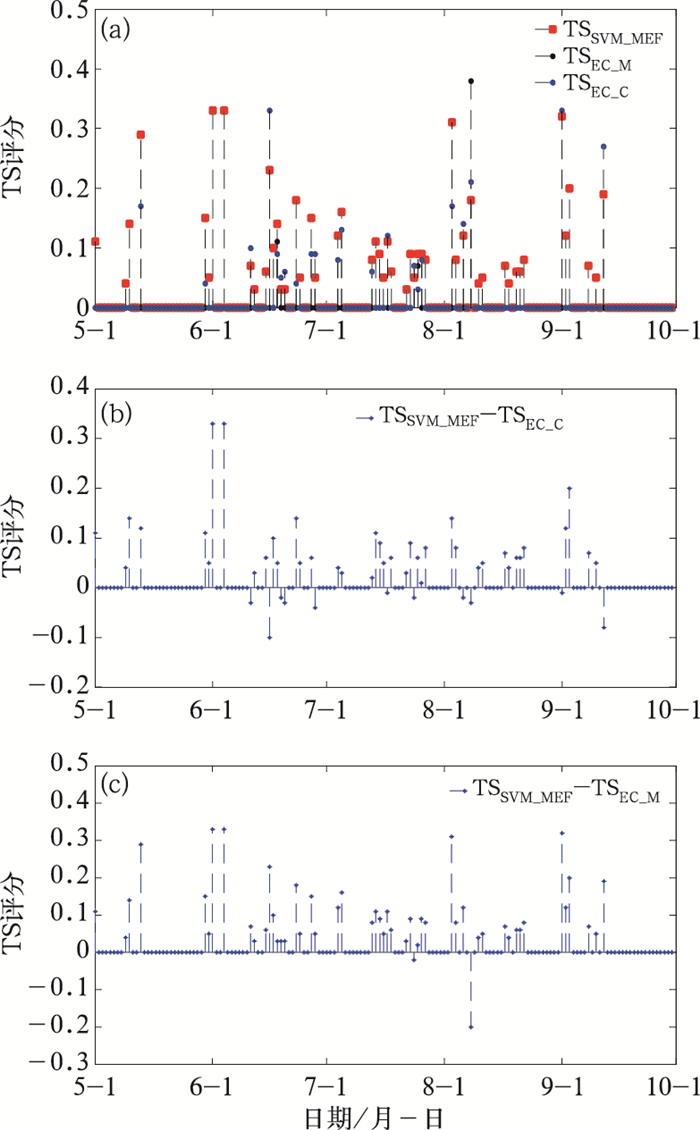
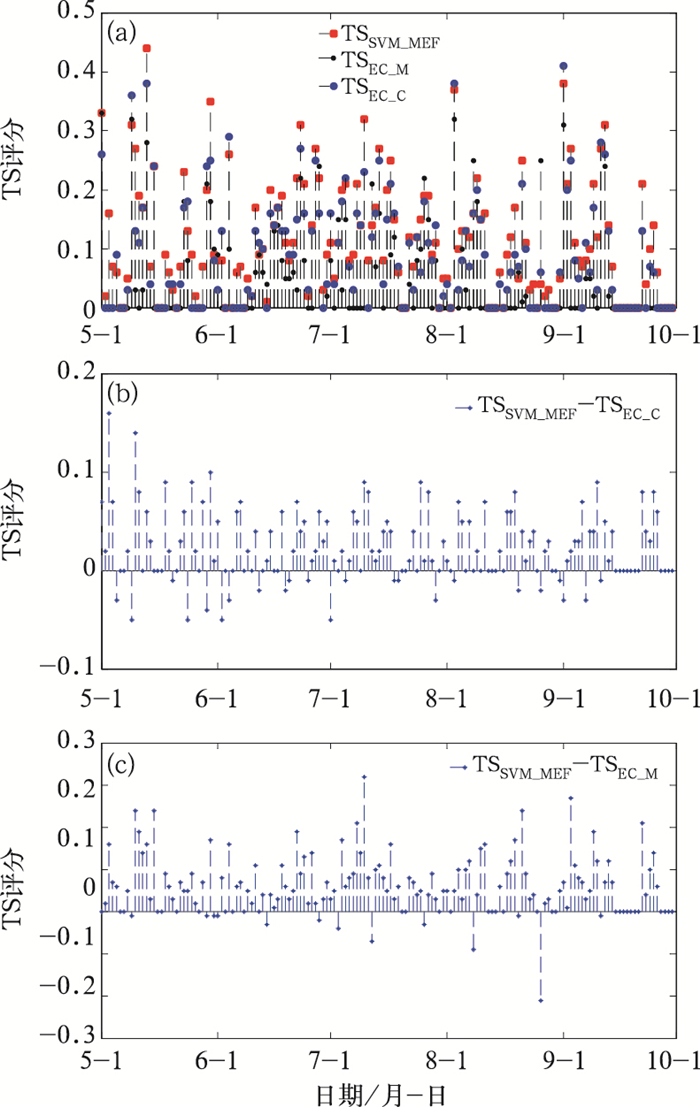
图 2 2012年5—9月SVM_MEF、EC_C、EC_M对大雨108 h预报逐日TS评分(a),以及SVM_MEF与EC_C、EC_M不同预报之间的TS评分差值: (b)TSSVM_MEF-TSEC_C,(c)TSSVM_MEF-TSEC_M Fig. 2 Daily TS score results of heavy rain forecasted by SVM_MEF, EC_C and EC_M from May to September 2012 (a), and the TS score difference between SVM_MEF and EC_C (b), and the TS score difference between SVM_MEF and EC_M (c) (Prediction time is 108 h) |
|
|
表 2 2012年5—9月20次暴雨过程(共计75 d) Table 2 20 heavy rain processes (75 d) from May to September 2012 |
|
|
表 3 2012年5—9月20次暴雨过程(共计75 d)SVM_MEF、EC_C、EC_M大雨和暴雨108 h预报的TS评分效果比较(单位:d) Table 3 Comparison of TS score results of 20 heavy rain processes (75 d) forecasted by SVM_MEF, EC_C and EC_M from May to September 2012 (prediction time is 108 h, unit: d) |
进一步分析表明(图 3),在SVM_MEF、EC_C、EC_M均预报出有暴雨发生的情况下,SVM_MEF预报评分最高;如对5月13日、5月30日、6月23日、8月3日的暴雨预报,SVM_MEF的TS评分较EC_C提高了0.1以上,其中6月23日和8月3日的TS评分提高达0.14;即使在EC_C和EC_M均没能报出暴雨情况下,SVM_MEF对暴雨具有较好的效果,如对5月1日、5月10日、6月17日、7月14日、9月1日、9月3日等的暴雨预报,SVM_MEF的TS评分均在0.1以上。
2.2 6月22—24日暴雨过程分析为更清楚地展示SVM_MEF的预报效果,本文选取了6月22—24日的暴雨过程对比分析了SVM_MEF、EC_C、EC_M预报结果(图 4)。此次过程期间,江南中东部和华南大部出现了大到暴雨,局部地区有大暴雨,过程日最大降雨量为230 mm。表 4给出了6月22—24日逐日的108 h预报TS评分。由表可见,SVM_MEF对大雨和暴雨的预报效果是最好的,SVM_MEF对大雨预报的TS评分较EC_C(EC_M)提高0.04~0.07(0.09~0.19),对暴雨预报的TS评分较EC_C(EC_M)提高0.05~0.14(0.05~0.18)。
|
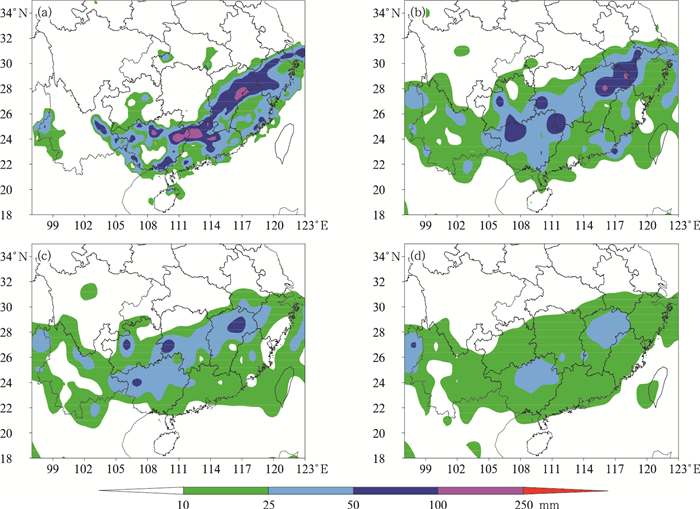
图 4 2012年6月23日降雨实况(a),以及SVM_MEF(b)、EC_C(c)和EC_M(d)的预报结果 Fig. 4 Observation (a) of the 23 June 2012 precipitation, and SVM_MEF forecast (b), EC_C forecast (c), EC_M forecast (d) (Prediction time is 108 h) |
|
|
表 4 2012年6月22—24日暴雨过程SVM_MEF、EC_C、EC_M对大雨和暴雨108 h预报的逐日TS评分结果 Table 4 Daily TS score results of the heavy rain process in 22-24 June 2012 forecasted by SVM_MEF, EC_C, EC_M (prediction time is 108 h) |
表 5还给出了过程期间雨势最强的6月23日的TS评分。由表可见,SVM-MEF预报性能仍具有明显优势。在108—180 h预报,SVM_MEF对大雨预报的TS评分较EC_C(EC_M)提高0.03~0.04(0.09~0.21);对暴雨预报的TS评分较EC_C(EC_M)提高0.02~0.14(0.05~0.18)。
|
|
表 5 2012年6月23日SVM_MEF、EC_C、EC_M对大雨和暴雨中期时效(108~180 h)预报的TS评分结果 Table 5 TS score results of the heavy rain on 23 June 2012 forecasted by SVM_MEF, EC_C, EC_M (prediction time is 108-180 h) |
图 4给出了6月23日降雨量实况及SVM_MEF、EC_C和EC_M 108 h的预报结果。图 4a显示,23日的强降雨中心主要分布在江南中北部、华南北部,同时在华南南部沿海等地也有分散的强降雨中心,与三种预报结果对比可见,SVM_MEF对上述强降雨中心分布范围和强度的预报均更接近实况,主要表现在:一是在江南中北部,50 mm以上降雨范围自江西中北部扩展延伸至赣浙皖三省交界,并有2个100 mm以上降雨点,较EC_C预报的强降雨中心范围更大,强度更强,EC_M则完全没有预报出暴雨;二是在华南北部,预报出自广西西北部及粤桂湘三省交界地区50 mm以上的强降雨中心,而EC_C仅在广西西北部局地预报有强降雨,EC_M同样没有预报出暴雨;三是在华南南部沿海,也预报出零星的暴雨点,而EC_C和EC_M均未体现。
3 结论与讨论本文采用ECMWF和NCEP集合预报资料和SVM回归方法建立了多模式集成的动力-统计客观预报模型,并选用2012年5—9月发生在淮河流域及其以南地区的大雨和暴雨开展了回报试验和效果评估,主要结论如下:
(1) 在中期预报时效,SVM_MEF对大雨和暴雨的总体预报效果最好,尤其对暴雨预报准确率明显提高。SVM_MEF逐月TS评分较EC_C提高了5成至1倍及以上,较EC_M甚至提高了数倍。对20次暴雨过程期间的检验结果,SVM_MEF大雨和暴雨预报的TS评分高于EC_C和EC_M TS评分的日数也明显占优。
(2) SVM_MEF优势在对强降雨中心分布范围和强度的把握上更为接近实况,其不仅在模式预报出有暴雨发生的情况下能够进一步提升预报效果,在模式没能报出暴雨情况下也仍具有较好的预报效果。
(3) 在中期预报时效中,数值模式对大气环流的预报效果较降雨量预报更为稳定,如何在本研究的基础上进一步结合环流场,提高强降雨的预报准确率,也是本工作下一步的研究方向。
陈超辉, 李崇银, 谭言科, 等, 2010. 基于交叉验证的多模式超级集合预报方法研究[J]. 气象学报, 68(4): 64-76. |
陈静, 矫梅燕, 龚建东, 等, 2006. 非绝热物理过程对北京暴雨数值预报不确定性影响[J]. 应用气象学报, 17(S1): 18-27. |
陈鹏翔, 江志红, 彭东梅, 2017. 基于BP-CCA统计降尺度的中亚春季降水的多模式集合模拟与预估[J]. 气象学报, 75(2): 236-247. DOI:10.11676/qxxb2017.017 |
代刊, 曹勇, 钱奇峰, 等, 2016. 中短期数字化天气预报技术现状及趋势[J]. 气象, 42(12): 1445-1455. DOI:10.7519/j.issn.1000-0526.2016.12.002 |
杜钧, 陈静, 2010. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 36(11): 1-11. DOI:10.7519/j.issn.1000-0526.2010.11.001 |
冯汉中, 陈永义, 2004. 处理非线性分类和回归问题的一种新方法(Ⅱ)——支持向量机方法在天气预报中的应用[J]. 应用气象学报, 15(3): 355-365. |
冯汉中, 徐会明, 徐琳娜, 2004. SVM方法与长江上游降水落区预报[J]. 高原气象, 23(S1): 63-68. |
康红文, 祝从文, 左志燕, 等, 2012. 多模式集合预报及其降尺度技术在东亚夏季降水预测中的应用[J]. 气象学报, 70(2): 192-201. DOI:10.11676/qxxb2012.019 |
柯宗建, 张培群, 董文杰, 等, 2009. 最优子集回归方法在季节气候预测中的应用[J]. 大气科学, 33(5): 994-1002. |
李勇, 2016. 2011年长江中下游梅雨期强降水延伸期集合预报性能初探[J]. 气象, 42(9): 1114-1123. DOI:10.7519/j.issn.1000-0526.2016.09.009 |
沈学顺, 苏勇, 胡江林, 等, 2017. GRAPES_GFS全球中期预报系统的研发和业务化[J]. 应用气象学报, 28(1): 1-10. DOI:10.11898/1001-7313.20170101 |
唐圣钧, 王东海, 杜钧, 等, 2015. 混合集合预报法在华南暴雨短期预报中的试验[J]. 应用气象学报, 26(6): 669-679. DOI:10.11898/1001-7313.20150603 |
王亚男, 智协飞, 2012. 多模式降水集合预报的统计降尺度研究[J]. 暴雨灾害, 31(1): 1-7. |
韦惠红, 李才媛, 邓红, 等, 2009. SVM方法在武汉区域夏季暴雨预报业务中的应用[J]. 气象科技, 37(2): 145-148. |
熊秋芬, 曾晓青, 2008. SVM方法在降雨预报中的应用及改进[J]. 气象, 34(12): 90-95. DOI:10.7519/j.issn.1000-0526.2008.12.012 |
许映龙, 吕心艳, 张玲, 等, 2015. 1323号强台风菲特特点及预报难点分析[J]. 气象, 41(10): 1222-1231. DOI:10.7519/j.issn.1000-0526.2015.10.005 |
赵琳娜, 吴昊, 田付友, 等, 2010. 基于TIGGE资料的流域概率性降水预报评估[J]. 气象, 36(7): 133-142. DOI:10.7519/j.issn.1000-0526.2010.07.020 |
智协飞, 王姝苏, 周红梅, 等, 2016. 我国地面降水的分级回归统计降尺度预报研究[J]. 大气科学学报, 39(3): 329-338. |
朱玉祥, 黄嘉佑, 丁一汇, 2016. 统计方法在数值模式中应用的若干新进展[J]. 气象, 42(4): 456-465. DOI:10.7519/j.issn.1000-0526.2016.04.009 |
Barnes S L, 1964. A technique for maximizing details in a numerical weather map analysis[J]. J Appl Meteor, 3(4): 396-409. DOI:10.1175/1520-0450(1964)003<0396:ATFMDI>2.0.CO;2 |
Cartwright T J, Krishnamurti T N, 2007. Warm season mesoscale superensemble precipitation forecasts in the southeastern United States[J]. Wea Forecasting, 22(4): 873-886. DOI:10.1175/WAF1023.1 |
Chakraborty A, Krishnamurti T N, 2009. Improving global model precipitation forecasts over India using downscaling and the FSU Superensemble Part Ⅱ: seasonal climate[J]. Mon Wea Rev, 137(9): 2736-2757. DOI:10.1175/2009MWR2736.1 |
Krishnamurti T N, Mishra A K, Chakraborty A, et al, 2009a. Improving global model precipitation forecasts over India using downscaling and the FSU Superensemble. Part Ⅰ: 1-5-day forecasts[J]. Mon Wea Rev, 137(9): 2713-2735. DOI:10.1175/2009MWR2568.1 |
Krishnamurti T N, Sagadevan A D, Chakraborty A, et al, 2009b. Improving multimodel weather forecast of monsoon rain over China using FSU superensemble[J]. Adv Atmos Sci, 26(5): 819-839. |
Sun Jianqi, Chen Huopo, 2012. A statistical downscaling scheme to improve global precipitation forecasting[J]. Meteorol Atmos Phys, 117(3/4): 87-102. |
 2017, Vol. 43
2017, Vol. 43