2. 上海市气象信息与技术支持中心,上海 200030
2. Shanghai Meteorological Information and Technological Support Centre, Shanghai 200030
随着全球经济的迅猛发展,城市化进程特别是在发展中国家进一步加速(谢志清等,2015;黄宏涛等,2016)。据联合国估计,在未来30年内,大多数城市人口的增长将主要集中在亚洲和非洲城市。快速城市化进程带来巨大经济效益的同时,也使得极端天气事件的增多,影响了人居生存环境和社会的可持续发展(白莹莹等,2015;李双双等,2015;刘伟东等,2016;尹志聪等,2015)。城市地区有着与乡村截然不同的下垫面覆盖,大量的建筑物、水泥道路等不透水下垫面取代了原有的耕地和森林,下垫面物理属性的巨大差异改变了原有地表与大气之间的能量、物质交换过程,这是产生城市气候效应的根本原因(王迎春等,2012;王晓峰等,2014;周莉等,2015)。由于城市下垫面的非均一性以及在城市地区建立地表能量通量观测塔的操作复杂性,目前城市地区的地表能量通量的直接观测还很欠缺。因此有必要设计参数化方案对城市地表能量平衡各项进行估算。目前在常见的中尺度模式中均包含有各类不同复杂程度的地表能量平衡陆面模式,对地表能量平衡的准确估算是改善中尺度预报模式模拟近地层热力、动力状态的关键因素(何晓凤等,2008;王咏薇等,2008;郑祚芳等,2013)。
城市地表能量平衡模式从形态学角度来说主要包括三类(Grimmond et al,2010;Chen et al,2011):第一类为平板(slab)模式,即通过外场观测试验获取如地表反照率、动力粗糙度、下垫面覆盖比率、建筑物高度等城市地表特征参数,并建立地表能量通量各项与短波辐射通量的经验关系来估算地表通量。这类模式的主要代表有地表城市能量(水分)平衡模式(Surface Urban Energy and Water Balance Scheme, SUEWS)(Grimmond and Oke, 2002;Offerle et al,2003;Järvi et al,2011)。这类模式的优点是需要的驱动量较少,均为常规气象观测资料,且计算简单,缺点是所需输入参数相对较多,且不同城市参数取值不同,需要观测试验确定。第二类为单层城市冠层模式(SL-UCM)(Kusaka et al,2001),SL-UCM区分了墙面、屋顶、地面的不同影响,城市街区为二维,但辐射处理过程为三维,考虑了不同街区走向和太阳方位角日变化的影响。第三类为多层城市冠层模式(ML-UCM)(Martilli et al,2002),多层模式不仅区分了建筑墙面、屋顶、路面的不同影响,而且城市冠层中划分了多层,考虑各层间相互作用,城市冠层建筑的几何形状为三维,模式也较为复杂。单层和多层城市冠层模式均忽略了城市植被以及水体对潜热通量的贡献,在耦合到中尺度模式中潜热通量由Noah陆面模式模拟(Chen and Dudhia, 2001)。Grimmond et al (2010)在首届国际城市地表能量平衡模式比较计划中表明并没有哪一单个模式对所有地表通量均有最佳模拟效果,而是使用多个模式进行集合模拟可以使模式误差最低化。
在将城市地表能量平衡(SEB)模式耦合到中尺度预报模式之前,必须首先对SEB模式进行不受中尺度模式影响的“离线”评估。前人对以上三类SEB模式在多个城市开展了评估和敏感性测试。如SUEWS (LUMPS)模式在墨西哥、波兰洛兹、美国巴尔的摩、洛杉矶、加拿大温哥华、芬兰赫尔辛基等城市进行了评估(Grimmond and Oke, 2002;Järvi et al, 2011;Loridan et al, 2011;Karsisto et al, 2016);SL-UCM模式利用美国温哥华、日本长滨、法国马赛、中国南京等地的观测资料进行了模拟评估(Masson, 2000;Kusaka et al, 2001;Lemonsu and Masson, 2002; Loridan et al, 2010;Zhao et al, 2014)。由于城市下垫面的非均一性和复杂多样性,城市下垫面与近地层大气间的相互作用每个城市均有其独特性。上海作为中国最大的城市,其城市化速率高于中国平均水平,人口极为密集。上海摩天大楼聚集,其城市下垫面相较于大多数欧美城市表现得更加复杂。因此有必要评估各类城市地表能量平衡模式在上海地区的适用性。本文将利用在上海徐家汇CBD区域观测的城市地表能量、辐射通量来驱动和验证简单而又考虑植被影响的SUEWS (LUMPS)模式在上海的模拟适用性并分析产生模式误差的可能原因。SUEWS模式整体结构较为简单,而又较为精细地考虑了城市下垫面非均一性,并可以模拟径流、灌溉等水文特征,这在各类城市陆面模式中具有较大的独特性。本文对SUEWS模式在上海中心城区的模拟评估一方面可以检验城市通量观测资料的合理性,另一方面也为SUEWS模式耦合到中尺度数值预报模式(例如WRF)以及应用于城市规划和气候减缓对策/灾害评估方面提供科学依据和前期准备。
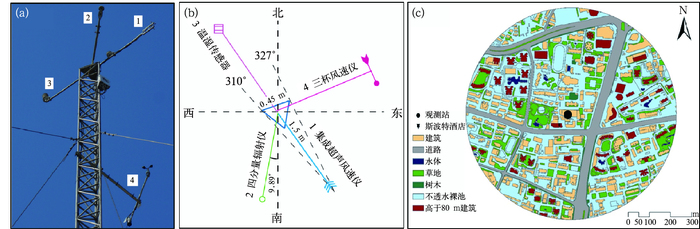
1 观测站点和资料介绍 1.1 仪器介绍本文用于检验模式的地表能量通量观测资料站点(图 1)位于上海市气象局(31.19°N、121.43°E)业务大楼楼顶的通量观测塔,楼高约55 m,铁塔高约25 m,因此观测仪器探测高度距地面约80 m。观测站点周边500 m范围内以混合商业区/居民区为主(徐家汇CBD区域),街道纵横、建筑物鳞次栉比,为典型的城市下垫面。结合上海测绘院的GIS数据和站点周边下垫面元数据调查,统计得到观测站点周边500 m范围内平均建筑物高度约为35.9 m,高大建筑物(图 1c红色标记建筑,高于80 m)主要集中在东面和西北方向,南北方向的建筑高度相对较低。三角铁塔(边长为0.45 m)上各观测仪器的安装位置如图 1a和1b所示,感热和潜热通量由集成开路红外气体分析仪和超声风速仪(infrared absorption gas analyzer integrated with a 3-D sonic anemometer, IRGASON)获取, 安装方位为东南向(145°),基本与盛行风向一致;向上、向下短波、长波辐射通量由荷兰Kipp & Zonen公司生产的四分量辐射通量观测仪(CNR4) 测量得到,安装方向在正南向偏西约10°;西北向温度/相对湿度传感器(HMP155A)小百叶箱用来测来塔层温、湿度;三杯风速仪(江苏省无线电研究所,ZQZ-A)架设方位为东北向,其分辨率为0.1 m·s-1, 最小启动风速为0.3 m·s-1。架设仪器的桅杆长度为1.5 m,除三杯风速仪架设在铁塔21 m处之外,其余仪器均架设在塔顶25 m处。数据采集器为CR3000,采样频率为10 Hz。本文选取的研究时段为2012年12月至2013年11月一年的观测资料,并按照季节常用划分方法分为冬(12—2月, DJF)、春(3—5月, MAM)、夏(6—8月,JJA)和秋季(9—11月,SON),以检验模式模拟能力的季节差异。
|
图 1 (a)上海徐家汇(XJH)通量观测塔仪器分布;(b)四组仪器的相对位置示意图;(c)观测站周边500 m范围内下垫面覆盖类型分布图 Fig. 1 (a) Instrumentation of the Shanghai Xujiahui flux tower; (b) schematic diagram of the instrument orientation; (c) land cover map within 500 m radius of the study site |
基于涡动相关仪对湍流通量的观测原理,为了合理准确运用观测数据,尤其是在城市复杂非均匀下垫面开展的涡动相关观测,需要对高频(10 Hz)原始数据进行严格的后处理和质量控制(徐自为等,2008;姜明等,2012)。国内外学者(Mauder et al, 2008;庄金鑫等,2013)对国际常用的几类涡动相关数据处理软件进行了评估比较,结果表明,相比之下,由爱丁堡大学开发的EdiRe软件(http://www.geos.ed.ac.uk/homes/rclement/micromet/EdiRe/)用户界面更为友好,具有模块功能较为完善且搭配灵活,运算速度快等优点。因此本文数据质量控制和后处理选用EdiRe软件,利用EdiRe软件编写了相关计算模块,使用方差检测法(徐自为等,2008)进行了野点剔除;对感热通量进行了超声虚温订正,主要是修正湿度对超声风速仪的影响,将直接观测的超声虚温转换为气温;对潜热通量WPL密度订正,消除因空气密度变化引起的误差;对原始数据进行2-D坐标旋转,主要消除非均匀地表对垂直风速的影响。Ao et al (2016a)计算了研究时段的垂直倾斜角度,表明95.7%的数据的旋转角度绝对值都在10°以内,可以得知本研究站点受垂直倾斜角度影响较小。最后统计得到30 min的通量时间序列。由于观测的风向为指南针所指方向(地磁北,Magnetic North),而航拍下垫面地图采用真北方向(True North),两者存在一个地磁偏角,本文将观测风向调整为真北方向,以使两者一致。地磁偏角在不同地理位置不同时间都会有所不同(https://www.ngdc.noaa.gov/geomag/geomag.shtml),在上海本文研究时段地磁偏角大约为5.5°,这对于非均匀下垫面也是容易造成影响的。
本文将摩擦速度(u*)小于0.1 m·s-1的数据视为湍流混合不够充分予以剔除(Grimmond et al, 2004),剔除数据占总数据的1%。对拖曳系数进行分析(Ao et al, 2016a),发现西南向(210°~247°)约60 m处距离观测站点最近的高大建筑(高于80 m)斯波特酒店(图 1c),以及观测塔身反面西北方位(图 1b,310°~327°)拖曳系数异常偏大,且数据相对较为稀少,考虑为高大建筑和塔身产生的小尺度湍流扰动,因此这两个方位的数据予以剔除。2012年12月11—17日和2013年3月8—16日为短期设备故障或维护期,这两个时段数据缺失。综合以上的数据质量控制,约有83%的30 min数据用于后续的模式评估分析。更加全面细致的观测站点仪器介绍和数据质量控制可参阅(Ao et al, 2016a;2016b)。
2 模式介绍 2.1 模式框架城市地表能量和水分平衡模式(Surface Urban Energy and Water Balance Scheme, SUEWS; Järvi et al, 2011)是在局地尺度城市气象模式(Local-Scale Urban Meteorological Parameterization Scheme, LUMPS; Grimmond and Oke, 2002)的基础上发展起来的。它是一个开源模式,可在英国雷丁大学网址下载(http://micromet.reading.ac.uk/software/)。SUEWS模式是建立在地表能量平衡框架之上的:
| ${Q^*} + {Q_{\rm{F}}} = {Q_{\rm{H}}} + {Q_{\rm{E}}} + \Delta {Q_{\rm{S}}}$ | (1) |
式中,Q*为净辐射通量,QF为人为热通量,QH, QE, ΔQS分别为感热、潜热和储热通量。SUEWS主要适用的空间尺度为局地尺度或小区尺度。
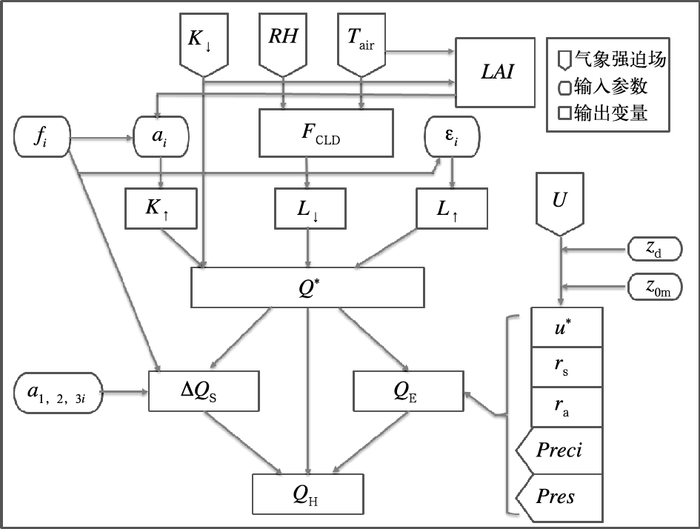
SUEWS模式计算各辐射、热通量的输入、输出以及主要的输入参数流程图如图 2所示。在SUEWS模式中,净辐射通量Q*是使用NARP (Net All-wave Radiation Parameterization scheme; Offerle et al, 2003)方案算得。NARP方案使用观测的入射短波辐射通量(K↓)、相对湿度(RH)和气温(Tair)来计算Q*:
|
图 2 SUEWS模式输入输出流程图 (图中变量含义均在文中有说明) Fig. 2 Flow chart of the processes of SUEWS (All the notations in the figure are defined in the text) |
| ${Q^*} = {K_ \downarrow } - {K_ \uparrow } + {L_ \downarrow } - {L_ \uparrow }$ | (2) |
其中向上短波辐射通量(K↑)计算公式如下:
| ${K_ \uparrow } = \sum ({f_i}{\alpha _i}){\rm{ }}{K_ \downarrow }$ | (3) |
式中,fi为各下垫面类型所占比率,αi为反照率,∑(fiαi)即为加权反照率。向下长波辐射通量(L↓)的计算采用公式如下:
| ${L_ \downarrow } = {\varepsilon _{{\rm{sky}}}}\sigma T_{{\rm{sky}}}^4$ | (4) |
式中,σ为斯蒂芬-玻尔兹曼常数,Tsky为整层气柱温度,在这里近似为观测的近地层气温(Tair),εsky为大气放射率,根据Prata (1996)计算晴天大气放射率εclear加入云的影响修正得到:
| ${\varepsilon _{{\rm{sky}}}} = {\varepsilon _{{\rm{clear}}}} + (1 - {\varepsilon _{{\rm{clear}}}}){\rm{ }}{F_{{\rm{CLD}}}}$ | (5) |
| $\begin{array}{l} {\varepsilon _{{\rm{clear}}}} = 1 - \left( {1 + w} \right)\exp [ - {\left( {1.2 + 3.0w} \right)^{0.5}}]\\ w{\rm{ }} = {\rm{ }}46.5{e_a}/{T_{{\rm{air}}}} \end{array}$ | (6) |
式中,w为大气可降水量,由水汽压(ea)和气温(Tair)决定,云量FCLD为相对湿度和气温的函数:
| ${F_{{\rm{CLD}}}}(RH,{T_{{\rm{air}}}}) = 0.185[{{\rm{e}}^{(0.015 + 1.9 \times {{10}^{ - 4}}{T_{{\rm{air}}}})}}^{ \times RH} - 1]$ | (7) |
最后得到向下长波辐射(L↓)的参数化方程为:
| $\begin{array}{l} {L_ \downarrow }({e_{\rm{a}}},{\rm{ }}{T_{{\rm{air}}}},{\rm{ }}RH) = \{ {\varepsilon _{{\rm{clear}}}}({e_{\rm{a}}},{\rm{ }}{T_{{\rm{air}}}}) + \\ \quad \quad \quad \quad \quad \quad \quad \quad [1 - {\varepsilon _{{\rm{clear}}}}({e_{\rm{a}}},{\rm{ }}{T_{{\rm{air}}}})] \times \\ \quad \quad \quad \quad \quad \quad \quad \quad {F_{{\rm{CLD}}}}(RH,{\rm{ }}{T_{{\rm{air}}}})\} \times \sigma T_{{\rm{air}}}^4 \end{array}$ | (8) |
向上长波辐射通量计算公式为:
| ${L_ \uparrow } = {\varepsilon _0}\sigma {T_0}^4 + (1 - {\varepsilon _0}){\rm{ }}{L_ \downarrow }$ | (9) |
式中T0为地表温度,式(9) 第二项为向下长波辐射的反射项;由于地表温度的观测是很难准确获取的,有必要使用气温来代替地表温度进行参数化,利用一阶泰勒公式对式(9) 第一项进行分解得到:
| ${\varepsilon _0}\sigma {T_0}^4 \approx {\varepsilon _0}\sigma T_{{\rm{air}}}^4 + 4{\varepsilon _0}\sigma T_{{\rm{air}}}^3({T_0} - {T_{\rm{a}}})$ | (10) |
以上式(10) 第二项可理解为气温与地表温度差的修正项,假设温差达到10 K, 气温为300 K, 该修正项可达到60 W·M-2。前人的研究表明(Offerle et al, 2003),该修正项与Q*或K↓具有很高的相关性,考虑到K↓为模式输入项,因此对其进行以下参数化:
| $4{\varepsilon _0}\sigma {T_{\rm{a}}}^3({T_0} - {T_{\rm{a}}}) = c{K_ \downarrow }[1 - (\sum {f_i}{\alpha _i})]$ | (11) |
式中, c=0.08,ε0=∑fiεi, εi为各下垫面类型的地表放射率,最终得到向上长波辐射通量的参数化方程为:
| $\begin{array}{l} {L_ \uparrow } = (\sum {f_i}{\varepsilon _i})\sigma {T_a}^4 + 0.08{K_ \downarrow }[1 - (\sum {f_i}{\alpha _i})] + \\ \quad \quad [1 - (\sum {f_i}{\varepsilon _i})]{L_ \downarrow } \end{array}$ | (12) |
储热通量(ΔQS)表征能量平衡系统中土壤、地表、城市冠层中的墙面等能量的吸收和释放。SUEWS模式中采用Grimmond et al (1991)提出的OHM (objective hysteresis model)模型将储热通量考虑为净辐射通量和地表属性的函数,其公式为:
| $\begin{array}{l} \Delta {Q_S} = \sum\limits_{i = 1}^n {} ({f_i}{a_{1i}}){\rm{ }}{Q^*} + \sum\limits_{i = 1}^n {} ({f_i}{a_{2i}})(\frac{{\partial {Q^*}}}{{\partial t}}) + \\ \quad \quad \quad \sum\limits_{i = 1}^n {} ({f_i}{a_{3i}}) \end{array}$ | (13) |
式中,n表示下垫面覆盖种类数,fi表示第i种下垫面类型所占比例,a1i, a2i, a3i为对应下垫面类型的经验参数,取值一般由文献给出,可在SUEWS模式中选取。早期的LUMPS中地表感热(QH)和潜热通量(QE)是根据简化的彭曼-蒙特斯公式来计算:
| ${Q_{\rm{H}}} = \frac{{\left( {1 - a} \right) + \left( {\gamma /s} \right)}}{{1 + \left( {\gamma /s} \right)}}({Q^*} - \Delta {Q_{\rm{S}}}) - b$ | (14) |
| ${Q_{\rm{E}}} = \frac{a}{{1 + \left( {\gamma /s} \right)}}({Q^*} - \Delta {Q_{\rm{S}}}) + b$ | (15) |
式中,s为饱和水汽压-温度曲线斜率,γ为湿度常数,a和b为经验参数,与植被覆盖、地表湿度相关。
SUEWS模式是在LUMPS模式的基础上加入水分平衡过程:
| $P + {I_{\rm{e}}} + F = E + R + \Delta S$ | (16) |
式中,P为降水(Preci),Ie为外部额外供水,F为人为水排放(如燃烧、空调、呼吸),E为蒸发,R为径流,ΔS为净水储量(如土壤湿度的改变),各水分平衡变量单位为mm·h-1。通过蒸发过程,水分平衡和地表能量平衡相联系(QE=LVE,LV为汽化潜热)。
SUEWS模式对Q*,ΔQS的计算与LUMPS相同,而对QH和QE的计算采用根据城市地区改进的彭曼-蒙特斯公式,重点考虑了表面阻抗、叶面积指数等的影响,QE的计算公式为:
| ${Q_{\rm{E}}} = \frac{{s{\rm{ }}({Q^*} + {Q_{\rm{F}}} - \Delta {Q_{\rm{S}}}) + {c_p}\rho VPD/{r_{\rm{a}}}}}{{s + \gamma (1 + {r_{\rm{s}}}/{r_{\rm{a}}})}}$ | (17) |
式中,cp为比热容,ρ为空气密度,VPD为水汽压差,为大气压(Pres)、相对湿度(RH)和气温(Tair)的函数。ra为空气动力阻抗,决定地表与大气之间湍流水汽传输速率;rs为表面阻抗,其参数化方法是从自然植被冠层阻抗类比而来的,表示整层城市表面对蒸发的影响。ra和rs的参数化方法对潜热通量的计算具有很大的影响(Järvi et al, 2011),ra的计算主要根据对数风廓线公式计算,为大气稳定度(ζ)、建筑物平均高度(zm)、动力学粗糙度(z0m)的函数;rs的倒数为表面传导率(gs),SUEWS中gs的模拟采用了Jarvis-Stewart公式(Jarvis,1976),为地表覆盖率,叶面积指数(LAI), 向下短波辐射通量(K↓),比湿亏缺(Δq)、气温(Tair)和土壤湿度亏缺(Δθ)的函数。
感热通量QH则基于地表能量平衡闭合的假设,由地表能量平衡剩余项得到:
| ${Q_{\rm{H}}} = {Q^*} + {Q_{\rm{F}}} - \Delta {Q_{\rm{S}}} - {Q_{\rm{E}}}$ | (18) |
由于缺乏建筑物、交通等能耗信息,本文未考虑人为热通量的排放;土壤湿度亏缺的计算采用默认参数模拟,土壤类型选取上海常见的黏土类型(史利江等,2010);模式积分步长为5 min。
2.2 模式输入参数本地化SUEWS模式输入参数主要包括常规气象观测资料(以及向下短波辐射通量)、下垫面参数两部分。风场、气温、相对湿度、向下短波辐射通量由徐家汇通量观测塔提供;降水资料来自徐家汇自动气象观测站(AWS) Vaisala MILOS500仪器(距离通量观测塔约60 m)。用于模式评估的辐射、能量通量观测资料也来自徐家汇通量观测塔。
下垫面共分为不透水路面、建筑物、常绿树、落叶树、草地、裸土和水体7种类型。并利用GIS技术统计了观测站点500 m范围内7种类型对应的覆盖比例,(表 1),可见不透水下垫面占主导地位,且裸土比例设为0暂未考虑该类型。此外,SUEWS模式还可以使用动态的下垫面覆盖信息,来更好地考虑复杂城市下垫面的空间不均匀性。模式所用7种下垫面反照率在Järvi et al (2011; 2014) 基础上基于观测值做了一定的调整,加权值为0.139,与观测得到的平均反照率0.14接近(Ao et al, 2016b)。下垫面动力粗糙度(z0)和零平面位移(zd)的计算使用Kanda et al (2013)的形态学方法。为了计算叶面积指数(LAI)的年变化,需要给出植物开始发芽(BaseT)和植物开始凋零(BaseTe)的日平均气温和日期,以及植物叶子完全长满和完全掉落的日期。本文通过对一年的观测时段站点周边植被物候变化的持续拍照以及上海天气软件城市街拍照片的收集,确定了观测时段植被大致开始发芽和凋零的日期分别为3月15日和9月15日,叶子完全长满和完全掉落的大致日期为5月20日和12月20日。因此得到BaseT和BaseTe分别为3月15日和9月15日的日平均温度:10和20℃。这与SUEWS模式根据北欧芬兰城市赫尔辛基给出的默认值5和10℃有很大差异。另外可以使用以下公式(Järvi et al, 2011)求得参数GDDFull (growing degree days needed for full capacity)和SDDFull (senescence degree days needed to initate leaf off), 求得GDDFULL≈400℃,SDDFULL≈-450℃,与模式默认值也有较大差别。
|
|
表 1 各下垫面类型对应的模式参数值 Table 1 Parameter values for each surface type |
GDDFULL=∑(DMTi-BaseT) 3月15日至5月20日, (DMTi-BaseT)>0
SDDFULL=∑(DMTi-BaseTe) 9月15日至12月20日, (DMTi-BaseT) < 0
通过实地考察观测站点附近的排水管道半径,取排水管道半径参数大约在100~750 mm,本文取500 mm作为尝试,但有必要进行更多的测试。
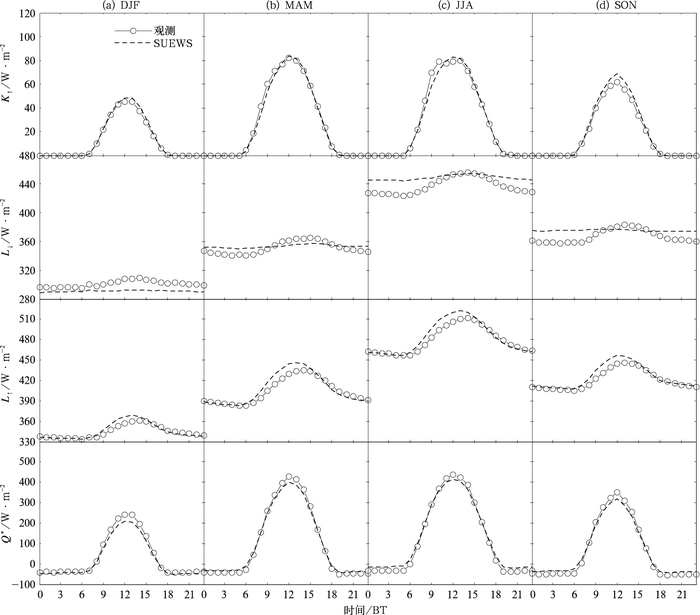
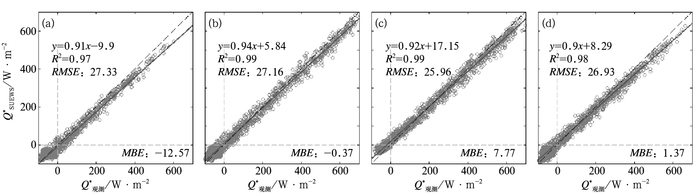
3 结果分析图 3给出各季节模拟和观测的平均辐射通量日变化曲线。由图可见,SUEWS模式成功地再现了各辐射通量的日变化形态,而系统地低估了四个季节的净辐射通量(Q*),特别是对中午日峰值处的低估约为25 W·M-2。SUEWS模式对夜间Q*亏损的模拟在春、夏、秋季都低估约15 W·M-2,而在冬季高估约5 W·M-2。各季节的均方根误差(RMSE)(图 4)为25.96~27.33 W·M-2,平均相对误差(MBE)为-12.57~7.77 W·M-2。
|
图 3 模拟和观测的徐家汇站点各个季节(a,DJF:冬季;b,MAM:春季;c,JJA:夏季;d,SON:冬季)辐射通量的平均日变化 (K↑:向上短波;L↓:向下长波;L↑:向上长波; Q*:净辐射通量) Fig. 3 Comparison of modeled and observed seasonal (a, DJF: winter; b, MAM: spring; c, JJA: summer; d, SON: autumn) mean diurnal variation of radiative fluxes (K↑, upward shortwave radiation flux; L↓, downward longwave radiation flux; L↑, upward longwave radiation flux; Q*, net all-wave radiation flux) |
|
图 4 模拟和观测的冬季(a),春季(b),夏季(c),秋季(d)小时净辐射通量(Q*)散点图 [实线为线性拟合曲线,虚线为1:1线,各季节的RMSE和MBE(单位:W·M-2)也有给出] Fig. 4 Scatter plots of the seasonal modelled versus observed hourly net all-wave radiation flux (Q*) [The RMSE and MBE (units: W·M-2), the linear regression (solid) and the 1:1 (dashed) lines are shown] |
SUEWS模式对向上短波辐射通量(K↑)除了在夏季为低估之外,其他三个季节均略为高估。线性拟合得到的决定系数R2为0.98~0.99,统计得到的RMSE为3.0(冬季)~5.7 W·M-2(夏季),MBE在秋季和冬季表现为正偏差(MBE:1.8/0.8 W·M-2),而在春季和夏季表现为负偏差(MBE:-0.6/-0.4 W·M-2)。SUEWS模式对K↑模拟的偏差来自模式对反照率参数的简化描述。
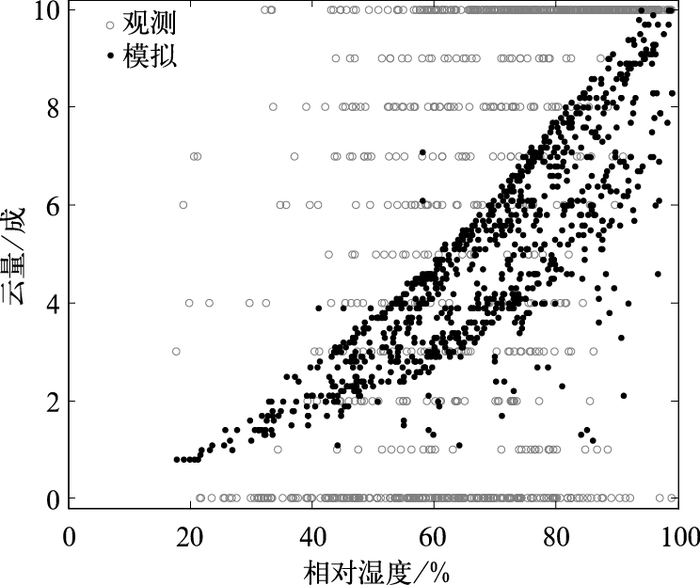
SUEWS模式较好地再现了春、夏季向下长波辐射通量(L↓)日变化形态,由图 3可见,模拟和观测的日极大值区均出现在午后。然而,SUEWS模式对秋、冬季的日变化形态没有较好的模拟。SUEWS模式对L↓四个季节的日变化幅度均被低估。SUEWS模式对冬季L↓量值全天时次均为低估,而对其他三个季节大致表现为夜间高估,白天低估,即SUEWS模式低估了L↓的日变化幅度。可见,对L↓的模拟表现为较大的不确定性和复杂性,从L↓的参数化方程(式8) 可以注意到云量的计算(式7) 是影响其模拟效果的关键因素。图 5给出了2012年12月至2013年9月(自2013年10月中国气象局取消了云量观测)一天三个时次(08、14、20时)模拟和观测的云量随相对湿度的变化情况,其中观测资料来自观测站点的月报表文件,可以看到,观测中出现晴天无云(云量为0) 和满云(云量为10成)的时次最多,分别占总时次的26%和37%;而模拟得到的云量几乎不会出现这两种情况。从式(7) 可以看到,只有当相对湿度(RH)等于0时,云量才为0,而现实中是无法满足RH=0的。此外,模拟的云量随RH分布在较狭长的范围,而观测则更加发散的分布。以上分析表明SUEWS模式无法模拟无云和满云的情况是导致对L↓日变化幅度低估的主要原因。线性统计得到L↓的决定系数R2为0.56(冬季)~0.82(秋季),RMSE为18.7(春季)~27.7 W·M-2(冬季),MBE为-9.7(冬季)~11.3 W·M-2(秋季),仅冬季为负值。SUEWS模式基本能模拟出L↑的日变化特征,但模拟的午后日峰值出现时次早于观测约1 h。四个季节的日峰值均有高估。线性统计得到L↑的决定系数R2为0.88(冬季)~0.97(秋季),RMSE为7.7(秋季)~9.6 W·M-2(春季),MBE为3.2(春季)~4.1 W·M-2(秋季)。
|
图 5 模拟和观测的云量随相对湿度的变化 Fig. 5 Scatter plot of the modeled and observed cloud cover amount as a function of relative humidity |
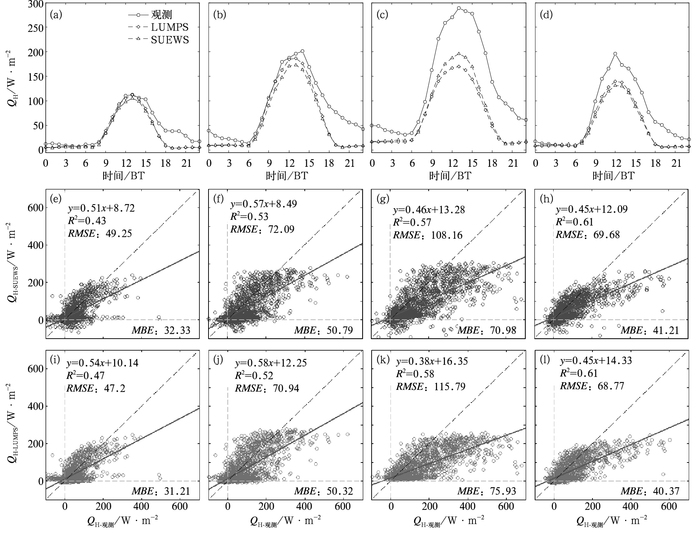
图 6同时给出各季节SUEWS和LUMPS模式对感热通量(QH)的模拟情况。由图可见,SUEWS和LUMPS模式对QH日变化形态均有较好模拟,除对春季日峰值出现时次偏早1 h外,对其他三个季节均有准确模拟。SUEWS和LUMPS模式对各个季节QH均为低估,尤其在下午到上半夜时段低估更为明显。两个模式对冬、春季节的模拟优于夏、秋季。SUEWS模式在冬、春、秋季对QH的模拟略逊于LUMPS模式,其均方根误差RMSE相差0.91~2.05 W·M-2,MBE相差0.47~1.12 W·M-2;而在夏季对QH的模拟优于LUMPS模式,其RMSE相差7.63 W·M-2,MBE相差4.95 W·M-2。线性统计得到SUEWS模式对QH的决定系数R2为0.43(冬季)~0.61(秋季)。
|
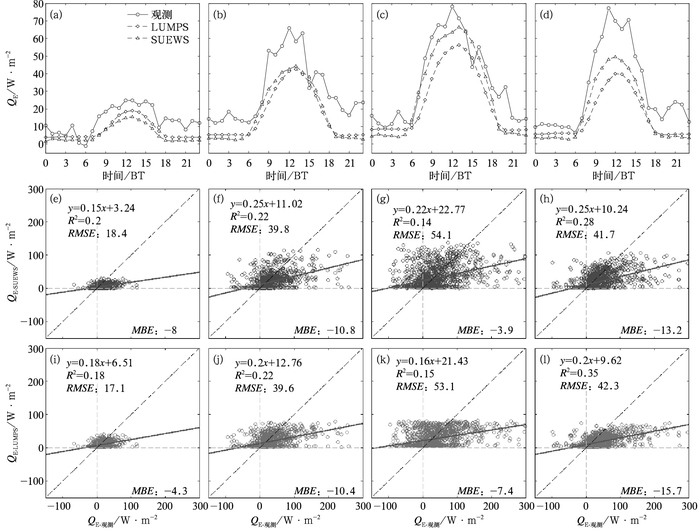
图 6 冬季(a,e,i),春季(b,f,j),夏季(c,g,k),秋季(d,h,l)模拟(SUEWS和LUMPS模式)和观测的感热通量(QH)平均日变化曲线(a~d)以及散点图(e~l) Fig. 6 Comparison of modeled and observed seasonal mean diurnal variations (a-d) of sensible heat flux (QH) in winter (a, e, i), spring (b, f, j), summer (c, g, k) and autumn (d, h, l); SUEWS/LUMPS versus observed hourly QH (e-l) |
图 7给出各季节模拟(SUEWS和LUMPS模式)和观测的潜热通量(QE)。可以看到,观测的冬季QE明显小于其他三个季节的QE。SUEWS和LUMPS模式较好地再现了各季QE的日变化趋势,但是四个季节均表现出对QE的低估(MBE < 0)。SUEWS模式在冬季和春季对QE的模拟与LUMPS模式非常接近,LUMPS模式在冬季的平均模拟效果略优于SUEWS模式; 而SUEWS模式在夏季和秋季对白天QE的模拟相比于LUMPS模式具有较明显改善,其MBE表现为负偏差,分别为-3.9、-13.2 W·M-2,LUMPS模式对应的MBE亦表现为负偏差,分别为-7.4、-15.7 W·M-2;两者的RMSE较为接近,SUEWS模式略大于LUMPS模式, 表现为SUEWS模式模拟结果更为发散。SUEWS模式对各季节QE的低估可能是由于研究区域存在一些灌溉活动,城市下垫面存在某些可透水的缝隙在模式中较难体现。
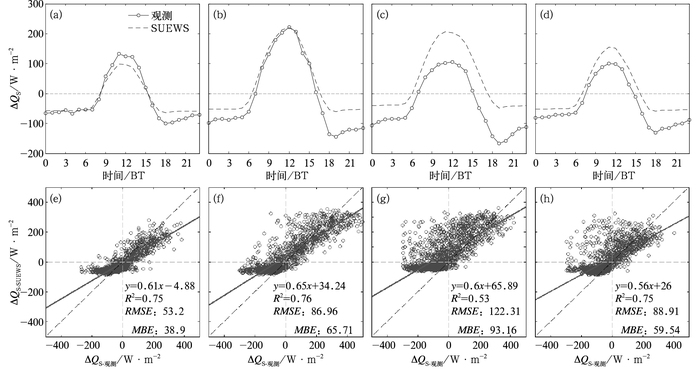
在城市地区对储热通量(ΔQS)的直接观测是极其困难的,因此本文用于模式评估的观测的ΔQS用残差项代替(ΔQS=Q*-QH-QE), 这种算法不可避免地将观测误差聚集于ΔQS,因此需要对其谨慎分析。图 8给出各个季节模拟和观测的ΔQS平均日变化曲线。由图可以看出,SUEWS模式对四个季节ΔQS日变化基本形态均有较好的模拟,对日最大值出现时次均有准确模拟;对冬、春、秋季早上(06—08时)和傍晚(15—17时)正负值(储热释放和存储)转换时间有很好的体现,而对夏季傍晚正负值转换时间滞后了2 h。SUEWS模式对冬季储热的存储(ΔQS>0) 为低估作用,平均日峰值低估约35 W·M-2,对上半夜(18—23时)的储热释放亦低估约30 W·M-2,而对后半夜(00—06时)储热释放量级具有很好地模拟,偏差在10 W·M-2以内。SUEWS模式很好地模拟了春季白天储热的存储,对夏季储热的模拟偏差最大,秋季次之,均表现为对储热存储的高估,而对储热释放为低估,且四个季节均对上半夜低估更明显。总的来说,冬、春、夏、秋季对应的RMSE分别为53.2、86.96、122.31、88.91 W·M-2,MBE分别为38.9、65.71、93.16、59.54 W·M-2。模拟和观测散点图线性拟合曲线与1:1线较为靠近,决定系数R2为0.53 (夏季)~0.76(春季)。
|
图 8 同图 6,但为SUEWS模拟和观测的储热通量(ΔQS) Fig. 8 Same as Fig. 6, but for SUZWS modeled and observed storage heat flux (ΔQS) |
模式误差的来源包括未考虑人为热释放、平流作用;使用不随方位变化的下垫面覆盖信息来表征非均匀复杂城市下垫面;未能获得详细的本地水文信息(如灌溉)等。而人为热释放、平流作用以及下垫面非均匀性主要是受气温、风速和风向的制约,本文将从分析以上气象因子和地表能量通量之间的关系来分析模式误差来源。
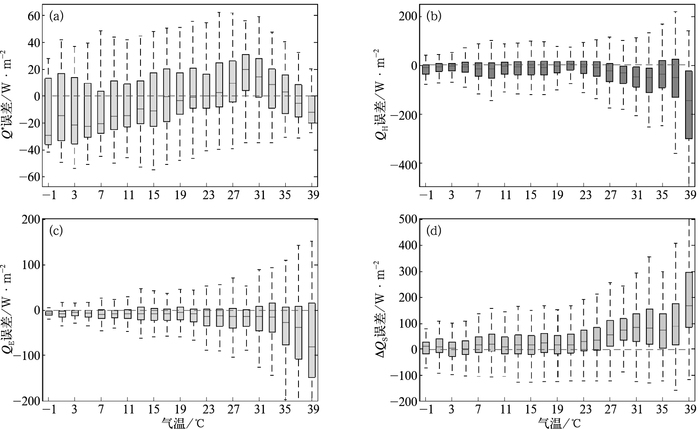
图 9~图 11给出Q*、QH、QE和ΔQS的模式误差(模拟值-观测值)随各气象因子(气温、风速、风向)变化的箱线图。由图 9可见,当气温>31℃时,SUEWS模式对QH和QE的模拟误差有较明显增大,而对于较低气温( < 5℃)模式误差无明显变化,这可能与上海夏季大量使用空调排放人为热有关,而本文SUEWS模式未考虑人为热通量造成模式对感热和潜热通量的低估。ΔQS模式误差则在气温>31℃左右表现出更加显著的高估,其误差中位值约为75 W·M-2。Q*误差与气温的关系更为复杂,在气温 < 23℃和>37℃模式为低估,最大误差达25 W·M-2左右,而在气温处于25~35℃时,模式为高估,误差约为10 W·M-2。
|
图 9 SUEWS模式误差(模拟-观测)随气温变化箱须图(a)净辐射通量, (b)感热通量, (c)潜热通量, (d)储热通量 [箱体上、下限和中位线分别表示上、下四分位和中位值,须线表示±1.5倍四分位距(IQR)] Fig. 9 Error between modeled (SUEWS) and observed values of (a) Q*, (b) QH, (c) QE and (d) ΔQS for the entire 1-yr period as a function of air temperature [Box plots show the median and inter-quartile range (IQR), whiskers indicate ±1.5 IQR] |
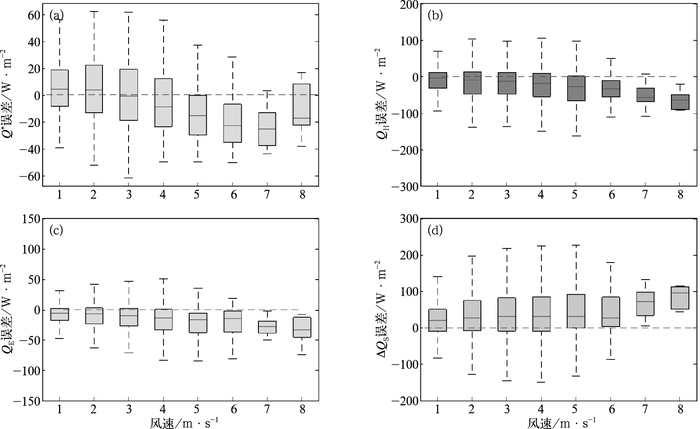
由图 10可见,当风速 < 6 m·s-1时,QH、QE和ΔQS模式误差变化不大,而当风速>6 m·s-1时,模式误差有明显增大,其中QH和QE为更加明显的低估,低估值分别约-60和-25 W·M-2,ΔQS与之相反,为更加明显的高估,高估值约80 W·M-2。这一结果与Loridan et al (2011)的结果一致。这主要由于较强风速条件下,城市储热效率将降低,而SUEWS模式未考虑这一平流作用。净辐射通量也是在强风下误差增大。
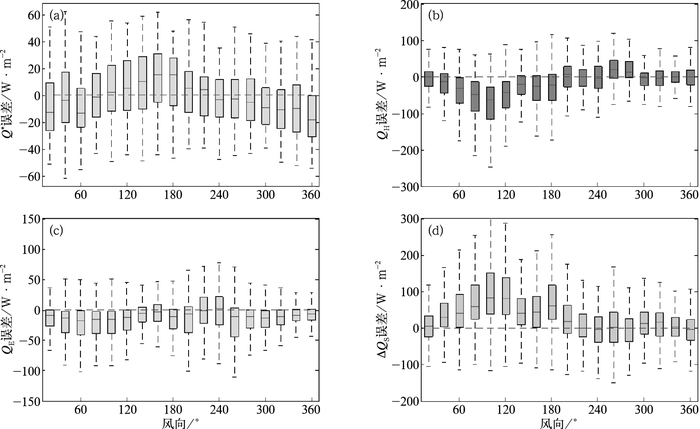
风向对模式误差的影响需结合观测站点周边环境来分析。周边环境主要特点(图 1c)是东面一条南北走向的主干道以及密集的商业建筑区,在西侧有一小型绿地公园(占地约8600 m2)。由图 11可见,Q*的模式误差随风向主要是100°~220°为正的误差,而其他方位则为负的误差,这可能主要是由于不同季节反照率等参数误差造成;QH的模式误差主要是在东面(80°~120°)有较明显的低估,误差约-50 W·M-2,而在西侧公园处(240°~280°)为高估,误差约15 W·M-2。这主要是由于本文SUEWS模式使用不随方位变化的陆地覆盖比例,东面密集建筑物对感热释放的贡献和西面公园对感热释放的削弱作用均被低估造成。ΔQS的模式误差走向与QH相反,QE的模式误差随风向变化不如QH明显。以上对SUEWS模式误差的分析表明风速的作用相对较小,只在较强风速误差明显增大,而考虑人为热通量以及随方位变化的动态下垫面信息非常重要。
为了更加客观地说明SUEWS模式在上海城区的模拟水平,将本文研究结果与世界其他城市的模拟结果进行比较,使用常用的RMSE为标准。美国巴尔的摩、波兰洛兹、加拿大温哥华和美国洛杉矶(Loridan et al, 2011;Järvi et al, 2011) Q*的RMSE大约为10~45 W·M-2, 本文徐家汇站大约为25 W·M-2, 可见SUEWS模式对上海净辐射通量(Q*)的模拟效果较好;温哥华和洛杉矶QH冬、春、夏、秋季RMSE分别为30~40, 40~45, 40~65, 40 W·M-2, 而本文徐家汇站分别约为45, 70, 100, 70 W·M-2,总体偏高,但需要注意的是,本文徐家汇站季节平均QH也是温哥华和洛杉矶站的两倍左右,因此也较合理;温哥华站和洛杉矶站QE冬、春、夏、秋季RMSE分别为18~25, 35, 30~55, 35 W·M-2, 而本文徐家汇站RMSE略高,分别约为18, 40, 50, 40 W·M-2,季节平均值较为接近,总体也较为合理;对于储热通量(ΔQS),波兰洛兹站各季节RMSE为30~40 W·M-2,季节平均日峰值为60~150 W·M-2;而本文徐家汇站各季节RMSE(图 8)为50~120 W·M-2,季节平均日峰值为100~220 W·M-2,可见SUEWS模式对ΔQS的模拟误差较为合理,但略逊于欧洲洛兹。
5 结论与讨论本文利用2012年12月至2013年11月一整年的上海徐家汇城市站点常规气象和地表能量平衡观测资料驱动和检验了局地城市地表能量(水分)平衡模式(SUEWS/LUMPS),对模式输入参数进行了部分本地化,并分析了模式误差随气象因子的变化关系,得到如下主要结论:
(1) SUEWS模式较好地再现了各辐射通量的日变化形态,对净辐射通量(Q*)中午日峰值低估约为25 W·M-2,各季节的RMSE为25.96~27.33 W·M-2,MBE为-12.57~7.77 W·M-2;模式对四个季节向下长波辐射通量(L↓)的日变化幅度均被低估,对向上长波辐射通量(L↑)的模拟明显优于L↓。
(2) SUEWS/LUMPS模式对感热通量(QH)各季节(春季除外)日峰值出现时次均有准确模拟,而对QH量值各季节均为低估,尤其在下午到上半夜时段低估更为明显,对应SUEWS模式四个季节RMSE分别为49.25、72.09、108.16和69.68 W·M-2。
(3) SUEWS模式对潜热通量(QE)的模拟在夏、秋季对白天QE的模拟相对于LUMPS模式有较大改善,而在冬季和春季两者模拟效果较为接近。
(4) SUEWS模式成功再现了储热通量(ΔQS)冬、春、秋季早、晚正负值转换(储热释放和存储)时间,而在夏季比观测滞后了2 h,对ΔQS量值的模拟季节差异性较大,冬季储热的存储(ΔQS>0) 为低估作用,平均日峰值低估约35 W·M-2,而对后半夜(0~6 h)储热释放量级具有很好地模拟,偏差在10 W·M-2以内。对夏季ΔQS的模拟偏差最大,秋季次之,均表现为对储热存储的高估,而对储热释放为低估。
(5) 当气温高于31℃和风速超过6 m·s-1时,QH、QE均表现为低估误差明显增大,而ΔQS则相反,表现为更显著的高估;风向的影响主要体现观测站点周边环境的非均一性,表现为模式使用不随风向变化的下垫面覆盖比率从而对东面密集建筑物对感热释放的贡献和西面公园对感热释放的削弱作用均被低估,误差分别约为-50和15 W·M-2。
以上模式评估结果表明局地尺度城市陆面模式SUEWS在上海具有较好的适用性,本文的研究为SUEWS模式耦合到中尺度数值预报模式(例如WRF)提供了科学依据和前期准备。SUEWS模式整体结构较为简单,在城市规划和气候减缓对策方面也有较好的应用前景。由于SUEWS模式的开发主要使用了欧美等城市观测资料,因此在上海的模拟效果较为必然的略逊于一些欧美城市。今后将继续根据上海的观测结果,收集较全面的人为热排放相关的人口、交通、建筑能耗信息,对模式参数化过程进行改进,提高其模拟能力。
致谢:感谢雷丁大学教授、上海市气象局特聘专家Sue Grimmond研究团队提供SUEWS模式源代码以及为本研究提供的科研指导。
白莹莹, 程炳岩, 王勇, 等, 2015. 城市化进程对重庆夏季高温炎热天气的影响[J]. 气象, 41(3): 319-327. DOI:10.7519/j.issn.1000-0526.2015.03.007 |
何晓凤, 蒋维楣, 刘红年, 等, 2008. 应用城市地表能量平衡方案研究城市冠层结构对城市热岛的热力影响[J]. 大气科学, 32(6): 1445-1457. |
黄宏涛, 吴荣军, 王晓云, 等, 2016. 城市化对珠三角地区气温及日较差的可能影响[J]. 气象, 42(7): 847-856. DOI:10.7519/j.issn.1000-0526.2016.07.008 |
姜明, 郭建侠, 景元书, 2012. 稳态与湍流特征测试对通量数据质量的评价[J]. 气象, 38(11): 1436-1442. |
李双双, 杨赛霓, 张东海, 等, 2015. 近54年京津冀地区热浪时空变化特征及影响因素[J]. 应用气象学报, 26(5): 545-554. DOI:10.11898/1001-7313.20150504 |
刘伟东, 尤焕苓, 孙丹, 2016. 1971—2010年京津冀大城市热岛效应多时间尺度分析[J]. 气象, 42(5): 598-606. DOI:10.7519/j.issn.1000-0526.2016.05.009 |
史利江, 郑丽波, 张卫国, 等, 2010. 上海土壤有机碳储量及其空间分布特征[J]. 长江流域资源与环境, 19(12): 1442-1447. |
王晓峰, 许晓林, 张蕾, 等, 2014. 上海"0731"局地强对流观测分析[J]. 高原气象, 33(6): 1627-1639. DOI:10.7522/j.issn.1000-0534.2013.00204 |
王迎春, 梁旭东, 苗世光, 等, 2012. 城市气象研究动向的思考[J]. 气象, 38(10): 1232-1237. DOI:10.7519/j.issn.1000-0526.2012.10.009 |
王咏薇, 蒋维楣, 刘红年, 2008. 大气数值模式中城市效应参数化方案研究进展[J]. 地球科学进展, 23(4): 371-381. |
谢志清, 杜银, 曾燕, 等, 2015. 上海城市集群化发展显著增强局地高温热浪事件[J]. 气象学报, 73(6): 1104-1113. DOI:10.11676/qxxb2015.075 |
徐自为, 刘绍民, 宫丽娟, 等, 2008. 涡动相关仪观测数据的处理与质量评价研究[J]. 地球科学进展, 23(4): 357-370. |
尹志聪, 郭文利, 李乃杰, 等, 2015. 北京城市内涝积水的数值模拟[J]. 气象, 41(9): 1111-1118. |
郑祚芳, 高华, 李青春, 2013. 城市化对北京一次极端降水过程影响的数值分析[J]. 气象, 39(3): 340-346. DOI:10.7519/j.issn.1000-0526.2013.03.008 |
周莉, 江志红, 李肇新, 等, 2015. 中国东部不同区域城市群下垫面变化气候效应的模拟研究[J]. 大气科学, 39(3): 596-610. DOI:10.3878/j.issn.1006-9895.1404.14157 |
庄金鑫, 王维真, 王介民, 2013. 涡动相关通量计算及三种主要软件的比较分析[J]. 高原气象, 32(1): 78-87. DOI:10.7522/j.issn.1000-0534.2012.00009 |
Ao X Y, Grimmond C S B, Chang Y Y, et al, 2016a. Heat, water and carbon exchanges in the tall megacity of Shanghai:challenges and results[J]. Int J Climatol, 36(14): 4608-4624. DOI:10.1002/joc.2016.36.issue-14 |
Ao X Y, Grimmond C S B, Liu D W, et al, 2016b. Radiation fluxes in a business district of Shanghai, China[J]. J Appl Meteor Climatol, 55(11): 2451-2468. DOI:10.1175/JAMC-D-16-0082.1 |
Chen F, Dudhia J, 2001. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modelling system.Part I:Model implementation and sensitivity[J]. Mon Wea Rev, 129: 569-585. DOI:10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2 |
Chen F, Kusaka H, Bornstein R, et al, 2011. The integrated WRF/urban modeling system:development, evaluation, and applications to urban environmental problems[J]. Int J Climatol, 31(2): 273-288. DOI:10.1002/joc.v31.2 |
Grimmond C S B, Blackett M, Best M J, et al, 2010. The international urban energy balance models comparison project:first results from phase 1[J]. J Appl Meteor Climatol, 49(6): 1268-1292. DOI:10.1175/2010JAMC2354.1 |
Grimmond C S B, Cleugh H A, Oke T R, 1991. An objective urban heat storage model and its comparison with other schemes[J]. Atmos Environ, 25B(3): 311-326. |
Grimmond C S B, Oke T R, 2002. Turbulent heat fluxes in urban areas:Observations and a Local-Scale Urban Meteorological Parameterization Scheme (LUMPS)[J]. J Appl Meteorol, 41(7): 792-810. DOI:10.1175/1520-0450(2002)041<0792:THFIUA>2.0.CO;2 |
Grimmond C S B, Salmond JA, Oke T R, et al, 2004. Flux and turbulence measurements at a densely built-up site in Marseille:heat, mass (water and carbon dioxide), and momentum[J]. J Geophys Res Atmos, 109: D24101. DOI:10.1029/2004JD004936 |
Järvi L, Grimmond C S B, Christen A, 2011. The surface urban energy and water balance scheme (SUEWS):evaluation in Los Angeles and Vancouver[J]. J Hydrol, 411(3-4): 219-237. DOI:10.1016/j.jhydrol.2011.10.001 |
Järvi L, Grimmond C S B, Taka M, et al, 2014. Development of the surface urban energy and water balance scheme (SUEWS) for cold climate cities[J]. Geosci Model Dev, 7(4): 1691-1711. DOI:10.5194/gmd-7-1691-2014 |
Jarvis P G, 1976. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field[J]. Phil Trans, Roy Soc London B, 273(927): 593-610. DOI:10.1098/rstb.1976.0035 |
Kanda M, Inagaki A, Miyamoto T, et al, 2013. A new aerodynamic parametrization for real urban surfaces[J]. Bound-Layer Meteor, 148(2): 357-377. DOI:10.1007/s10546-013-9818-x |
Karsisto P, Fortelius C, Demuzere M, et al, 2016. Seasonal surface urban energy balance and wintertime stability simulated using three land-surface models in the high-latitude city Helsinki[J]. Quart J Roy Meteor Soc, 142(694): 401-417. DOI:10.1002/qj.2016.142.issue-694 |
Kusaka H, Kondo H, Kikegawa Y, et al, 2001. A simple single-layer urban canopy model for atmospheric models:comparison with multi-layer and slab models[J]. Bound-Layer Meteor, 101(3): 329-358. DOI:10.1023/A:1019207923078 |
Lemonsu A, Masson V, 2002. Simulation of a summer urban breeze over Paris[J]. Bound-Layer Meteor, 104(3): 463-490. DOI:10.1023/A:1016509614936 |
Loridan T, Grimmond C S B, Grossman-Clarke S, et al, 2010. Trade-offs and responsiveness of the single-layer urban canopy parametrization in WRF:an offline evaluation using the MOSCEM optimization algorithm and field observations[J]. Quart J Roy Meteor Soc, 136(649): 997-1019. DOI:10.1002/qj.v136:649 |
Loridan T, Grimmond C S B, Offerle B D, et al, 2011. Local-scale Urban Meteorological Parameterization Scheme (LUMPS):longwave radiation parameterization and seasonality-related developments[J]. J Appl Meteor Climatol, 50(1): 185-202. DOI:10.1175/2010JAMC2474.1 |
Martilli A, Clappier A, Rotach M W, 2002. An urban surface exchange parameterisation for mesoscale models[J]. Bound-Layer Meteor, 104(2): 261-304. DOI:10.1023/A:1016099921195 |
Masson V, 2000. A physically-based scheme for the urban energy budget in atmospheric models[J]. Bound-Layer Meteor, 94(3): 357-397. DOI:10.1023/A:1002463829265 |
Mauder M, Foken T, Clement R, et al, 2008. Quality control of Carbo Europe flux data-Part 2:Inter-comparison of eddy-covariance software[J]. Biogeosciences, 5(2): 451-462. DOI:10.5194/bg-5-451-2008 |
Offerle B, Grimmond C S B, Oke T R, 2003. Parameterization of net all-wave radiation for urban areas[J]. J Appl Meteor, 42(8): 1157-1173. DOI:10.1175/1520-0450(2003)042<1157:PONARF>2.0.CO;2 |
Prata A J, 1996. A new long-wave formula for estimating downward clear-sky radiation at the surface[J]. Quart J Roy Meteor Soc, 122(533): 1127-1151. DOI:10.1002/(ISSN)1477-870X |
Zhao W J, Zhang N, Sun J N, et al, 2014. Evaluation and parameter-sensitivity study of a single-layer urban canopy model (SLUCM) with measurements in Nanjing, China[J]. J Hydrometeorol, 15(3): 1078-1090. DOI:10.1175/JHM-D-13-0129.1 |
 2017, Vol. 43
2017, Vol. 43